Introducing Exploratory Teaching in Preservice Teacher Education Through Lesson Study

Abstract

In exploratory teaching, the pupils learn from their work on tasks that aim to introduce new concepts, procedures, representations and mathematical ideas. Lesson study, with its focus on teachers’ collaborative and reflective work around issues of pupil learning, is a powerful formative process that may be used in preservice teacher education, sustaining an exploratory teaching approach. In this article, we present a lesson study experience in preservice teacher education, addressing the case of a preservice teacher who is preparing to teach in grades 1–6. Our aim is to identify what key aspects of knowledge of teaching practice does the preservice teacher use when preparing and leading an exploratory lesson during her participation in a lesson study. Our methodology is qualitative, with data collected from the lesson study sessions and the collection of documents produced during the lesson study work, and the data are analysed using a model that presents the key aspects of knowledge of teaching practice. The results show that the structure and the activities carried out in the lesson study, such as designing the lesson, selecting the task and anticipating questions to be posed to pupils, promoted the use of the preservice teacher’s didactic knowledge regarding the phases of an exploratory lesson.

1. Introduction

Initial teacher education is an important field of work within mathematics education. Great difficulties in this field have long been recognised (Lampert & Ball, 1998; Sims & Walsh, 2009). Its task is to prepare students in higher education for a demanding professional activity that, in the case of the early years, involves the teaching of various subject areas and transversal capacities. The work of the teacher has become increasingly difficult given the evolution of society that has provided a growing diversity in the pupil population, bringing out the importance of meeting the learning needs and learning styles of all pupils.

Research in mathematics education has shown that it is necessary to lead innovative and ambitious teaching that actively involves pupils in their learning process. For this, pupils need to have the opportunity to work on challenging tasks (Ponte, 2005) and to be able to experience productive struggle (NCTM, 2014). The curricula of many countries recommend this type of teaching that we may characterise as exploratory. However, preparing and leading an exploratory lesson is a challenge for many teachers and is even more challenging for preservice teachers, given their limited experience in teaching mathematics. They need to know how to select mathematical tasks, anticipate pupils’ work and prepare interventions and questions to ask in class (Burroughs & Luebeck, 2010; Martins et al., 2021). These are fundamental aspects of didactic knowledge that, to be learned effectively, require a close relationship between theory and practice. Therefore, it is essential that initial teacher education promotes opportunities for preservice teachers to become involved in preparing, leading and reflecting on lessons of this nature (Rodrigues & Cyrino, 2018).

This is possible through their participation in lesson study, a teacher education process that promotes the development of teachers’ knowledge, is focused on pupils’ learning, has a strong link to practice and has a collaborative and reflective nature. Lesson study is widely used with in-service teachers and also, increasingly, in initial teacher education (Tan et al., 2024). It allows participants to deepen the relationship between theory and practice, which is one of the major problems of initial teacher education, providing the experience of creating teaching situations aligned with curriculum guidelines and reflecting in a reasoned way on teaching practice (Burroughs & Luebeck, 2010; Ni Shuilleabhain & Bjuland, 2019).

There are studies, such as Martins et al. (2021), which show the use of knowledge in the preparation and leading of exploratory lessons by preservice secondary school mathematics teachers during their participation in lesson study. In this study, the preservice teachers were unfamiliar with the exploratory approach, and, at the first sessions of lesson planning, they focused on the role of the teacher, not putting the pupil at the centre of the learning process. However, the planning sessions for the research lesson of the lesson study enabled the preservice teachers to understand the structure of the exploratory lesson and to begin to consider aspects such as choosing challenging tasks and anticipating students’ responses and difficulties. They also began to consider moments in which students worked autonomously and discussed their ideas. In turn, leading the exploratory lesson was a great challenge for the preservice teachers, especially with regard to the management of the whole-class discussion, with its unforeseen events.

However, there is a lack of research on this topic concerning preservice teachers of the first years, and younger students also benefit greatly from exploratory lessons, as they have the opportunity to develop their learning in a meaningful way. Given the challenges of these lessons, it is important to understand what knowledge is mobilised by primary preservice teachers when they prepare and lead exploratory lessons. So, in this article we present a lesson study experience in preservice teacher education, addressing the case of a preservice teacher who is preparing to teach in grades 1–6, and we aim to answer the following research question: What key aspects of knowledge of teaching practice does the preservice teacher use when preparing and leading an exploratory lesson during her participation in a lesson study?

2. Exploratory Mathematics Teaching

In an exploratory lesson, the teacher challenges pupils to solve tasks using their previous knowledge and provides opportunities for them to take a central and active role in the learning process. This lesson, based on a strong teacher–pupil relationship, promotes the interaction between pupils, based on the mathematical content they are exploring. For an exploratory lesson to be productive and sustained by the work and interventions of the pupils, the teacher’s activity is essential (Ponte, 2005).

The exploratory approach is similar to the inquiry-based approach (Artigue & Blomhøj, 2013) and to structured problem-solving lessons (Stigler & Hiebert, 1999). In an exploratory lesson, it is intended that “an important part of the work of discovery and construction of knowledge [is] for pupils to carry out” (Ponte, 2005, p. 13). Therefore, in such lessons, the pupils are called upon to take an active role, making discoveries and building their knowledge. Exploratory lessons begin with the presentation of a task that is challenging for pupils, who interpret and solve it, engaging in exploration activity based on their previous knowledge. Subsequently, and under the guidance of the teacher, the pupils present the different strategies, concepts, representations and mathematical ideas they used to solve the task (Stein et al., 2008).

An exploratory lesson is usually organised in three phases: (i) introduction of the task; (ii) pupils’ autonomous work; and (iii) whole-class discussion and final synthesis (Canavarro, 2011). In the first phase, the teacher presents the task to the pupils, who are challenged to interpret and solve it. In the next phase, the pupils begin their autonomous work, while the teacher observes, supporting them without influencing or inducing them to respond, in order to avoid standardising solving strategies, procedures and mathematical representations. In this phase of the lesson, the teacher considers which strategies were used by the pupils, what mistakes they made and what difficulties they showed, in order to select and sequence the most pertinent solutions to consider in the whole-class discussion. Finally, the teacher leads the whole-class discussion, inviting pupils to explain and justify their solution strategies and manages these interventions in order to ensure the mathematical quality of their explanations. This moment promotes opportunities for pupils to relate their ideas and make mathematical connections. The exploratory lesson ends with a synthesis of the main mathematical ideas explored (Canavarro, 2011; Stein et al., 2008).

In the preparation of an exploratory lesson, there are several aspects to consider, namely the selection of the task, which should lead to “moments of reflection and discussion with the whole class” (Ponte, 2005, pp. 15–16). The teacher anticipates in detail possible solution strategies and difficulties that the pupils may present, foreseeing several possible ways to achieve the learning aim defined for the lesson and also considering the time established for each moment. After this careful planning of the lesson, the teacher teaches it, taking into account the degree of challenge of the task, as well as the diversity of the pupils’ productions, mathematical ideas and representations. During the lesson, the teacher also considers the management of time and the involvement and participation of pupils, not only during their autonomous work but also in the whole-class discussion, managing the various interventions and interactions, in order to create a challenging and stimulating learning environment that effectively contributes to pupils’ meaningful learning (Canavarro, 2011; Stein et al., 2008).

Given the demands and challenges associated with the exploratory approach, it is essential that preservice teachers have opportunities to get acquainted and reflect on lessons of this nature. Therefore, initial teacher education should enhance moments in which they can use and develop learning about this approach, namely how to organise and lead an exploratory lesson and understand its contribution to pupil learning (Rodrigues & Cyrino, 2018).

3. Development of Didactic Knowledge of Preservice Teachers Through Lesson Study

Didactic knowledge concerns, among other aspects, knowledge about teaching practices, which the teacher holds and develops through the observations made as a pupil and during initial teacher education, in professional development courses, through his/her own experience in the classroom and through many other informal contacts with colleagues and other educational agents (Ponte et al., 2024). This knowledge gained great prominence from the work of Shulman (1986), who coined the notion of pedagogical content knowledge, a concept that was deepened by authors such as Ball et al. (2008) and Carrillo-Yañez et al. (2018). In turn, for Ponte (2012), this knowledge has four main dimensions: (i) knowledge of school mathematics; (ii) knowledge of the curriculum; (iii) knowledge of pupils and their learning; and (iv) knowledge of teaching practice. In this model, the knowledge of teaching practice assumes a prominent role and includes aspects such as the planning of teaching, with the preparation of tasks, the planning of lessons and the organisation of pupils’ work during the lesson, as well as the creation of learning environments. Key aspects of this knowledge are (i) the design and enacting of the lesson, (ii) the tasks proposed to pupils and (iii) the communication established in the classroom (Ponte et al., 2024).

The design of an exploratory lesson involves two fundamental aspects: (i) lesson planning and (ii) the structuring of the lesson. Planning the lesson presupposes that the teacher considers the flow of the lesson, that is, the various moments of each phase and their connections, and also the anticipation of pupils’ strategies and difficulties, as well as the anticipation of interventions and questions to gather information about the pupils’ understanding and difficulties. Structuring the exploratory lesson implies considering each phase—the introduction of the task, pupils’ autonomous work, whole-class discussion and final synthesis (Canavarro, 2011; Stein et al., 2008).

The tasks that the teacher selects to propose to the pupils constitute the second key aspect of knowledge of teaching practice. Expository teaching privileges teachers’ explanations and exercises and tasks with solution strategies previously exemplified by the teacher. In turn, in exploratory teaching, the pupils are faced with tasks that present some degree of challenge, such as problems and explorations. These tasks are a starting point for new learning, an essential aspect in an exploratory lesson. According to Swan (2017), these new learnings include factual knowledge and procedural fluency, conceptual understanding, strategic competence for problem solving, and critical competence to analyse the solution strategies presented by others. In addition to the purpose of the tasks, the representations used, both in the statement and in the pupils’ solutions, are equally important. According to Bruner (1999), these representations can be enactive, when based on objects and movements; iconic, whether images or diagrams; and symbolic, verbal or algebraic. Ponte et al. (2024) highlight the fact that symbolic representations, although playing an important role in the teaching and learning of mathematics, only become meaningful for early-year pupils when other representations are also used and explored with meaning.

The last key aspect of didactic knowledge concerns communication (Brendefur & Frykholm, 2000). In expository teaching, communication is dominated by the teacher, who is the one who presents the ideas and just asks confirmation questions to the pupils in order to verify their knowledge (unidirectional communication). In exploratory teaching, the pupils assume a more relevant role, contributing to the communication that is established in the classroom, based on the teacher’s requests (contributive communication). Pupils are also invited to intervene in a reflective way, and their contributions are valued and may influence the course of the lesson (Ponte et al., 2024). Another important aspect of communication is the type of questions that the teacher asks the pupils. With confirmation questions, the teacher intends to understand if they understood the ideas presented. In this case, the teacher already knows the correct answer to the question and wants to know if the pupils are able to present it. Through focusing questions, “the teacher intends to draw the pupils’ attention to some aspect” (Ponte et al., 2024, p. 65). And, with inquiry questions, the teacher aims to challenge the pupils to think more deeply, which is why these are the most interesting questions.

The knowledge of teaching practice is developed “especially in initial teacher education and during professional practice, participating in projects and experiencing professional development opportunities, especially those that give a central role to classroom work, as is the case of lesson studies” (Ponte et al., 2024, p. 66). The lesson study is a teacher process of professional development in which a group of teachers address the improvement of pupils’ learning on a specific issue. This process consists of a “clear alternative to the traditional processes of reflection and improvement of educational practice and, as a consequence, we could say that they are a clear reconstruction of knowledge and teaching practices” (Gómez & Gómez, 2015, p. 16). It is based on moments of reflection and collaboration between the participants, who plan, lead and reflect on classroom situations, developing their knowledge in various domains (Fernández, 2010). Although initially designed for in-service teachers, lesson study has been adapted to initial teacher education (e.g., Clivaz & Miyakawa, 2020; Leavy & Hourigan, 2016). Lesson study can be organised in five stages: (i) goal setting, considering the mathematical topic to work on and the aims for the pupils’ learning; (ii) detailed lesson planning, based on the analysis of the curricular guidelines and teaching materials, selecting appropriate mathematical tasks, defining the teaching strategy, considering the possible solution strategies of the pupils and anticipating their possible difficulties and interventions necessary; (iii) a research lesson, as one of the teachers teaches the lesson, while the others observe the pupils’ work; (iv) post-lesson discussion, in which the participants share their observations; and, finally, (v) reflection, addressing all the work carried out with a focus on pupil learning, mathematical content and lesson design (Fujii, 2018).

In lesson study, the participants experience opportunities to develop their didactic knowledge, both in the preparation of the research lesson and in its observation and leading. In the post-lesson discussion and reflection sessions, they analyse the pupils’ learning, review their practice and think about how they can improve it. As Sims and Walsh (2009) state, through lesson study teachers can learn to think in more detail about long-term goals, improve lessons, learn valuable approaches and deepen their knowledge. As the authors indicate, they can learn to work collaboratively, learn to study pupils’ learning and behaviour and become more self-reflective.

Knowing how to prepare and lead exploratory lessons is a complex and challenging process for preservice teachers, and lesson study can play an important role in bringing together the theory that is taught during the initial teacher education courses and classroom practice (Burroughs & Luebeck, 2010; Leavy & Hourigan, 2016; Ni Shuilleabhain & Bjuland, 2019; Sims & Walsh, 2009).

4. Research Methodology

This research follows an interpretive and qualitative approach (Bogdan & Biklen, 2007) and considers as its data source the lesson planning and research lesson of a lesson study undertaken during the initial teacher education of primary teachers at a higher education institution in Portugal. The lesson study was carried out in the 2023/2024 academic year and involved two preservice teachers (Júlia and Alda, pseudonyms) who were attending the second semester of the first year of their master’s degree programme in teaching.

The preservice teachers had already completed a degree in general education, with a total of 180 ECTS credits, including 26 ECTSs in mathematics and 16 ECTSs in internships. During the master’s programme (120 ECTSs), the preservice teachers took several courses on mathematics (18 ECTSs) and had longer internships (50 ECTSs). Prior to the lesson study, they completed courses in subjects such as sociology and the psychology of education, the didactics of mathematics and school organisation. The preservice teachers observed several lessons taught by experienced teachers before the lesson study, so they were familiar with the students’ dynamics in the classroom. They had already participated in a lesson study carried out during the first semester of the same academic year, in which Júlia led the research lesson in a grade 2 class, following the exploratory approach.

The sessions of the second lesson study in which Júlia took part were organised as shown in

Table 1. Stages of the lesson study and the corresponding sessions.

Stages of the Lesson Study	Sessions (Sn)
Goal setting	S1, S2
Lesson planning	S3, S4, S5, S6
Research lesson	S7
Post-lesson discussion	S8
Reflection	S9

. They took place weekly and lasted approximately 90 min each.

The lesson study took place during the internship of the preservice teachers, which was being carried out in a grade 3 class with pupils that were between seven and eight years old. The preservice teachers were supervised by a teacher educator (the first author) from the higher education institution, who took on the role of facilitator, preparing and leading the lesson study sessions. These sessions always focused on the contributions of the preservice teachers, be it their interventions in the group discussions or the materials, resources, mathematical tasks and articles they selected and brought for discussion. The preservice teachers and the facilitator constituted the lesson study group.

After analysing the timetable and planning provided by the school where the preservice teachers were undertaking their internship, the group decided that the research lesson would focus on the theme of geometry and measurement and the introduction of the topic of area, with the learning aim of the lesson being to understand the concept of area and to recognise equivalent figures by solving an exploratory task with pentomino shapes. Then, the preservice teachers read and discussed articles, selected by the supervisor, on preparing and leading exploratory lessons and on teaching and learning about area in grade 3. All the work carried out for the research lesson was based on the exploratory approach. The preparation began with the selection of the task, chosen by Júlia, shown in Figure 1.

As suggested by Júlia, each group of pupils was given five equal squares so that they could manipulate them and build the various pentominoes, and a sheet to draw each construction they made. Larger squares were made available for the pupils to present their answers to their colleagues on the board during the whole-class discussion. To promote the final synthesis, the preservice teachers decided to explore with the pupils the conclusions summary sheet shown in Figure 2, which shows the twelve possible pentomino shapes and includes a space to fill in with suggestions from the pupils about the main mathematical ideas explored in the lesson, particularly relating the concepts of area and equivalent figures to pentomino shapes.

Júlia led and Alda observed the research lesson. We focus on the particular case of Júlia, since our goal is to identify what key aspects of knowledge of teaching practice she uses when preparing and leading an exploratory lesson during her participation in a lesson study.

The data were collected through observation of the goal-setting and lesson-planning sessions and of the research lesson and, also, through the collection of the documents produced: Júlia’s written report (written before the research lesson) that presents, based on the reading of articles and other documents, pupils’ usual difficulties in learning the topic of area; and the solutions of the task presented by Júlia. The lesson study sessions were recorded, and the relevant parts for this study were transcribed. The data were analysed deductively (Amado, 2013), considering

Table 2. Key aspects of knowledge teaching practice (adapted) (Ponte et al., 2024).

Design of the lesson	Planning the lesson	Flow of the lesson
		Anticipation of pupils’ strategies and difficulties
		Anticipation of teacher interventions and questioning
	Phases of an exploratory lesson	Introduction of tasks
		Pupils’ autonomous work
		Whole-class discussion and final synthesis
Tasks	Challenge and openness	Exercises
		Problems, explorations, investigations
	Purpose	To develop conceptual understanding
	Representations	Enactive (objects, movements)
		Iconic (images)
		Symbolic (verbal, algebraic)
		Mixed (tables, diagrams)
Communication	Basic forms	Unidirectional
		Contributive
		Reflexive
	Questioning	Confirmation questions
		Focusing questions
		Inquiry questions

, which presents the key aspects of knowledge of teaching practice from Ponte et al. (2024) that were of particular interest to this study.

Significant episodes from the lesson study sessions were identified, as well as extracts from Júlia’s written report, through which we sought to understand how she prepared and led the exploratory lesson.

5. Results

5.1. Lesson Planning

In the first session of the lesson study, the preservice teachers analysed the timetable and the annual plan provided by the school. They proposed that the research lesson should focus on introducing the topic of area, and, looking at the curriculum, they formulated the learning aim for this lesson. This analysis led the preservice teachers to think about the type of task that best suited the exploratory lesson they wanted to plan.

Júlia analysed documents on the usual difficulties pupils have in learning the concept of area and wrote “the difficulties pupils experience in learning area stem from the fact that they sometimes confuse the concepts of length and area, since both involve measuring length” and “[t]his type of confusion has consequences for the use of measurement units, i.e., selecting the most appropriate measurement unit” (Report). To help pupils overcome these difficulties, Júlia indicated that “the teacher should provide tasks that enable pupils to understand that the area of an object does not change by ‘displacement’ and that the measurement can be quantified by repeating a unit, with the resulting number depending on the size of the unit of measurement. The pupils develop this ability in contextualised situations, using materials and solving measurement problems” (Report). Analysing these documents also guided the two preservice teachers in clearly defining the learning aim, which in turn made them to reflect on the type of task to select. They opted for an exploratory task, since they were going to introduce the concept of area in this lesson. Writing this report led Júlia to analyse documents on the difficulties usually experienced by pupils in learning about the concept of area, which made anticipating the pupils’ answers more consistent. Júlia made a proposal based on a task that she had seen before in a piece of teaching material:

Alda:

We’re looking for a problem, right?

Júlia:

Instead of problems, we could use exploratory tasks…

Facilitator:

Why?

Júlia:

It depends on the task, I know. But I’ve seen some where they’re supposed to explore the pentomino squares and find out how many there are. And that seems to me to be more an exploration than a problem, because it seems more open, more challenging… with more possibilities for solution. (S2)

Júlia also suggested not “give them [pupils] a ‘normal’ statement. As it’s an exploratory task, we could use the message of the day” (S3). Based on her suggestions, the group created a task to present to the pupils in the research lesson, adapting the instructions that would be given to them through a statement shared orally by the preservice teacher (Figure 1). This task was challenging and required the pupils to work in a systematic way, and it was meant to provide a motivating context, suitable to introduce the concept of area, through the manipulation of squares.

After creating the task, the two preservice teachers anticipated the possible strategies that the pupils could use to solve it. As such, they solved the task by finding the different pentominoes, being attentive to the correctness of each possibility:

Júlia:

As for the correct answers, they can only be these [points to the 12 pentominoes]…

Facilitator:

What about the incorrect ones?

Alda:

Adding squares on top of the 5. Or using 4 or 3 squares instead of 5…

Júlia:

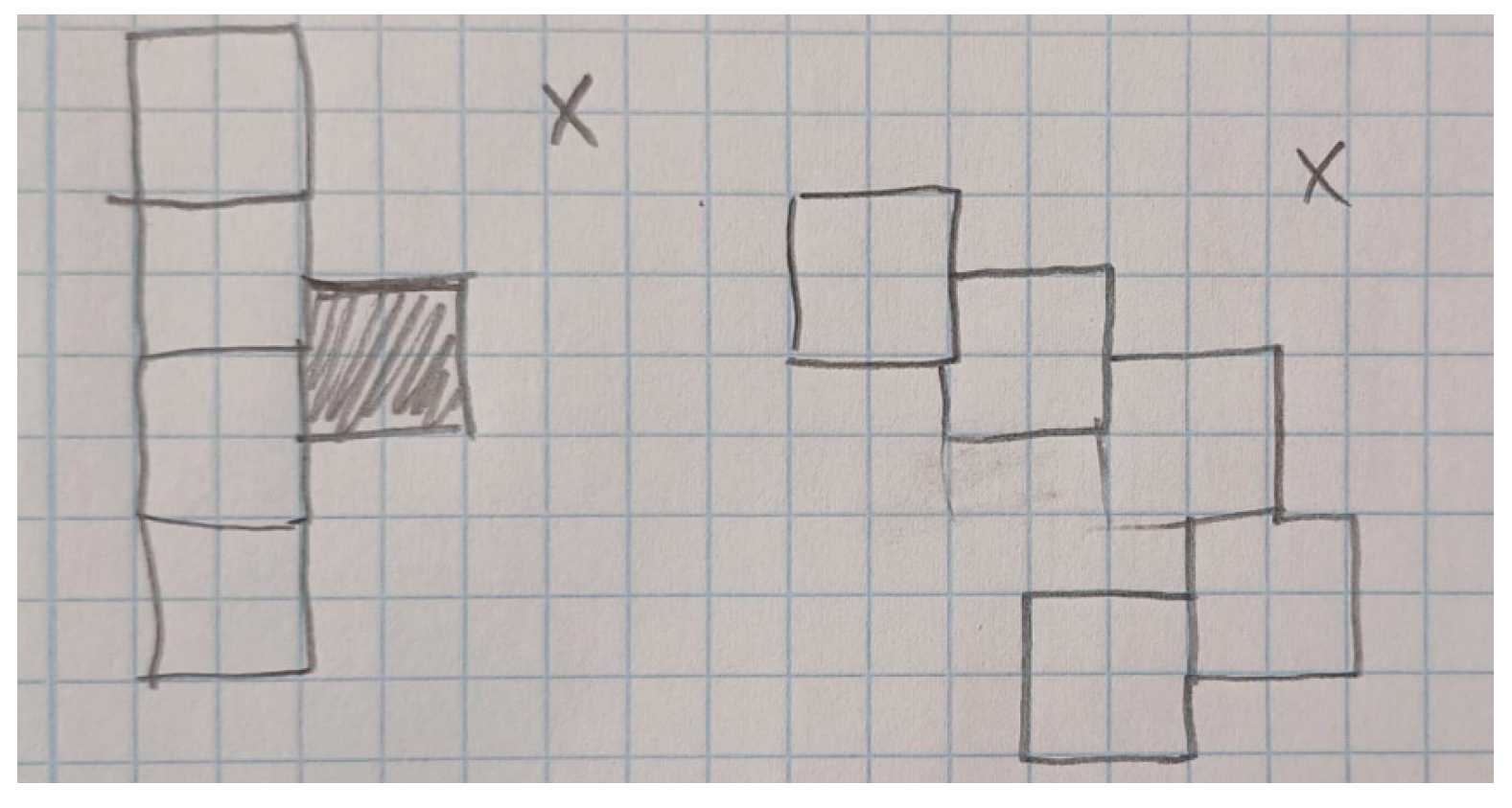
Putting a square in the middle, in other words, not joining sides and putting a square against two sides of other squares… Not putting side against side. Like this [draws Figure 3]. With regard to incomplete answers… We consider groups that reach less than 12 pentominoes, don’t we? (S4)

At the same time, the preservice teachers listed some difficulties that the pupils might have:

Alda:

I think they may have difficulties with the question of the directions of pentominoes. Realising that two pentomino shapes, even in different directions, are the same.

Facilitator:

And how are we going to help them overcome this difficulty?

Alda:

Take the pentomino and rotate it, so they realise that the shape doesn’t change, it’s the same.

Júlia:

They may even have difficulty in understanding what a pentomino is… The concept itself. But I’ll explain what it is in the introduction phase of the task and ask if there are any questions.

Alda:

But then they may also have difficulty in understanding the concepts of area and equivalent figures. They may have difficulty expressing themselves orally. (S4)

Júlia made a thorough effort in identifying possible difficulties, supported by analysing documents about pupils’ usual difficulties in learning the concept of area. In addition, this work also suggested strategies to overcome these difficulties, such as to use manipulative material, in this case pentominoes, and showing how they could be rotated so that the pupils could see for themselves that, although rotated in different directions, we may have the same pentomino. With regard to the possibility of pupils not understanding the concept of pentominoes, Júlia said that she would be attentive to their questions during the introduction of the task.

In the next planning session for the research lesson, the two preservice teachers prepared to carry out the task in class, considering how Júlia would select and sequence the pupils’ answers and establish connections between them and the aim of the lesson:

Júlia:

We have to select all the different pentominoes that appear in class. But also consider the wrong ones.

Facilitator:

So, which [pupils’ answers] are we going to begin with?

Júlia:

The correct ones are left for last.

Alda:

Yes, we’ll begin with the pupils who didn’t get all 12 pentominoes or who built them wrongly.

Júlia:

In other words, the wrong ones and the incomplete ones. And finish with the correct ones. The wrong ones are, for example, the “bad use” or incorrect fitting of the squares to create pentominoes, or even the use of less than 5 squares to create a pentomino; and the incomplete [answers] are all the ones that don’t include the 12 possible pentominoes, so 11, 10, 9…

Facilitator:

What about the sequencing of the correct answers?

Júlia:

So, I think it’s best to always begin with the group of pupils who have reached the fewest pentominoes. And also, from the simplest, most common [pentomino] and then on to the more complex ones.

Facilitator:

What if the class can’t find all 12 pentominoes?

Alda:

I think that as a class we have to try to find them all.

Júlia:

I could say “there are x more, find them”. And, as a last resort, I introduce the missing ones.

Facilitator:

Why?

Júlia:

I think it’s important to achieve the aim of the lesson. (S5)

In this way, the preservice teachers defined the overall strategy for selecting and sequencing the pupils’ responses. They decided to follow what is usually recommended in the exploratory approach, choosing to begin the whole-class discussion with the pupils’ wrong or incomplete answers and end with the correct ones. And in order to avoid repeating the pentominoes presented, Júlia suggested beginning with the group that had built the fewest pentominoes and then continue with the groups that had built the simplest ones. Since it was important to find all the pentominoes in order to achieve the aim of the lesson, the preservice teachers considered introducing those that the pupils had not presented.

In the sequence, the group prepared Júlia’s interventions, considering the degree of challenge of the questions she wanted to ask the pupils in order to promote their involvement in the discussion and to encourage them to explain their reasoning. In her former experience, Júlia recognised that she did not involve all pupils in the discussion:

Júlia:

I already know that I have to involve the class more. Not ask the whole-class so many open questions, but ask specific groups to participate while a pupil is presenting their answer. It’s important to ask a lot of challenging questions so that they can justify themselves.

Facilitator:

And what questions can we ask during the whole-class discussion?

Alda:

Imagine that one group came up with the T-shaped pentomino and another group came up with the upside-down T?

Júlia:

They both go to the board. And they have to conclude that it’s the same pentomino. But, questions to ask: the “why?” is obvious; “how did you think to create this pentomino?”; “group x, do you agree with your colleagues?”

Facilitator:

Knowing, based on monitoring the pupils’ autonomous work that you did before, that group x doesn’t agree, right?

Júlia:

Yes, yes, to create disagreement. “Pupil x, explain what your colleague said”, so that the same thing doesn’t happen [little pupils’ involvement]. Don’t ask the class closed questions [with yes or no answers]. Ask open questions to a particular pupil or group. (S5)

Therefore, the preparation of the lesson was based on the exploratory approach, addressing the selecting and sequencing of the presentation of pupils’ solutions and the questions to pose to them, considering what are equal and different pentominoes, aiming to figure out what is common about the 12 different shapes. In addition, the preservice teachers were careful in preparing questions in order to involve the pupils in the discussion, asking them to develop their answers, to explain and validate their colleagues’ interventions and to promote situations of disagreement.

5.2. Research Lesson

Júlia began the research lesson by presenting the task to the pupils. Given that they did not know the concept of a pentomino, as anticipated, she decided to clarify this aspect without giving them too much information or leading them to an answer to the task. She begun with three confirmation questions and then explained what a pentomino is and presented the task:

Júlia:

I was with a friend of mine this weekend and I was telling her that I knew five pentominoes. Do you know what pentominoes are?

Pupils:

No!

Júlia:

A pentomino is a polygon… Do you know what a polygon is?

Several pupils:

Yes!

Júlia:

Beatriz, what is a polygon?

Beatriz:

It’s a geometric figure…

Júlia:

…Bounded by line segments. What about a pentomino? It’s a polygon made up of five squares, and that’s the rule for pentominoes. After I told my friend that I found five pentominoes, she told me there were more. And I thought that a good challenge for my pupils would be to ask them to find out how many pentominoes there are in total. You already know that there are more than five. I want you to find out how many there are. I’m going to give each group five squares to create pentominoes and a sheet where you draw and colour each pentomino you discover. Any questions? Has anyone not understood?

Several pupils:

No! (S7)

The presentation of the task was in line with the planning, relating the new notion of the pentomino to the pupils’ known notion of polygons and providing the necessary information for the pupils to begin working.

During the phase of pupils’ autonomous work, Júlia circulated around the classroom, observing the work each group was doing and asking questions in order to understand the reasoning used to solve the task. At the same time, she selected and sequenced the pupils’ answers that she wanted them to share with their colleagues during the whole-class discussion. She observed the strategies used by the pupils and posed inquiry questions in order to understand the reasoning used by the pupils:

Júlia:

Have you discovered any pentominoes yet?

Group A:

Yes, this one! Is it right?

Júlia:

I don’t know. I’m not going to tell you if it’s right or not, you have to find out. What are you trying to do, Tomás?

Tomás:

Just moving a square.

Júlia:

Why?

Tomás:

It’s easier, so I don’t get mixed up.

After the pupils selected by the preservice teacher had built their pentominoes on the board (Figure 4), Júlia began the whole-class discussion with an invitation to the group that she chose as being the first to present their answer, making an inquiry question: “Dinis, how did your group come up with these pentominoes?” (S7)

These inviting actions led the pupils to share their answers and explain them to their colleagues, in the following way:

Dinis [group 1]:

We experimented.

Júlia:

Why these pentominoes and not others?

Dinis:

Because each one has five squares and no end is attached to another.

Júlia:

OK, what about Bianca?

Bianca [group 2]:

We always left four [fixed squares] and just moved one from side to side.

Júlia:

But which pentomino did you start with?

Bianca:

With this one. With all the squares next to each other.

Júlia:

In a line, yes.

Bianca:

And from this [pentomino], we took this [last] square over here and dragged it over here.

Júlia:

They kept moving this square. Good strategy!

Dinis:

They made a “T”.

Júlia:

Exactly. How did Tatiana’s group do it?

Tatiana [group 3]:

We just changed the squares and looked at which ones could be pentominoes. We tried a lot of them, but some turned out badly and we corrected them.

Júlia:

Why was it wrong? How did your group realise it was wrong?

Tatiana:

Because it was vertex to vertex.

Júlia:

What do you mean, Lourenço?

Lourenço:

We tried many, and the ones that were wrong were because we joined vertices. Then, we tried putting squares above and below them.

Júlia:

What about Simão’s group?

Simão [group 4]:

We tried several. We saw if they followed the rules, if they were glued to the sides, if they weren’t on top of each other, and if they were five. (S7)

At this point of the whole-class discussion, Júlia posed various inquiry questions to support the pupils in expressing their reasoning. Through her interventions, she also encouraged the pupils to take part in the discussion, and supported and guided them by rephrasing some of their interventions and encouraging them to continue their explanations, ensuring that the discussion stayed on track. And through those challenging questions, Júlia urged the pupils to clarify and justify their statements. Although none of the groups managed to find all twelve pentominoes, Júlia selected the incomplete answers of four groups who together came up with all the possibilities, and so she did not need to introduce missing pentominoes.

Júlia then continued the whole-class discussion aiming to establish connections among the various pentominoes and between them and the aim of the lesson. She used a variety of confirmation, focusing and inquiry questions:

Júlia:

OK, so how many pentominoes are there in total?

Several pupils:

Twelve!

Júlia:

We have 12 on the board. Are they all the same? Or are they all different?

Several pupils:

They’re all different!

Júlia:

But is there anything that’s always the same… Afonso?

Afonso:

They’re all five squares.

Júlia:

And what else?

Rita:

They all have the same corners.

Júlia:

We have 12 pentominoes here, and there are only 12. You’ve found them all. One of the characteristics of pentominoes is that they all have five squares. What other things can we say about these figures? Have you ever heard of equivalent figures?

Pupils:

Yes! No!

Dinis:

They’re the same as each other!

Júlia:

Tell me, Dinis? What are equivalent figures?

Dinis:

They’re equal figures.

Júlia:

So, are pentominoes equivalent figures?

Pupils:

Yes! No!

Olga:

Yes, because they always have five squares!

Júlia:

Very good. They may not be the same, but they always have five squares. So, all pentominoes are equivalent. There’s another very interesting thing about pentominoes, which has to do with the fact that they all have five squares… What could it be? I’ll give you a hint: they occupy the same space.

Olga:

Yes, they always occupy five squares.

Júlia:

And what does that mean, Inês?

Inês:

They use a measure of five squares.

Júlia:

What can I call this measure?

Pedro:

Square measure.

Carla:

Centimetre!

Júlia:

We once went outside to measure the perimeter of the part of the slide with our feet… Is this measurement called a perimeter?

Several pupils:

No…

Júlia:

What was the perimeter?

Several pupils:

It’s all round!

Júlia:

So, the five squares are just around?

Several pupils:

No, it’s inside!

Júlia:

What do we call this measurement? The space a figure occupies…

Ana:

Area!

Júlia:

Good, Ana! Area! (S7)

Based on the analysis of the pupils’ work, with a focus on their mathematical ideas, Júlia made connections between the answers presented on the board and those she had selected to be discussed in class. She did this through confirmation and focusing questions designed to encourage the pupils to list similarities and differences between the twelve pentominoes. The preservice teacher also emphasised important mathematical ideas, such as the concept of equivalent figures. Júlia managed to promote the pupils’ participation, much more than in her previous lesson study experience, encouraging them to listen, analyse and respond to their colleagues’ reasoning. At several times, she challenged the pupils through inquiry questions, insisting that they clarify and justify their statements, and informed or suggested with the intention of highlighting important mathematical ideas, such as the fact that all pentominoes are made up of the same number of squares, that they are equivalent figures and, therefore, have the same area.

The whole-class discussion ended with a final synthesis promoted through the use of the previously prepared conclusions summary sheet, which brought to the whole-class discussion the most important ideas:

Júlia:

Let’s recap. What are these figures called?

Rui:

Pentominoes.

Júlia:

And why are they pentominoes?

Ana:

Because they have five squares and occupy five squares.

Nádia:

They’re joined at the sides.

Bruna:

And they’re not on top of each other.

Tomás:

The vertices aren’t together.

Júlia:

What are these figures?

Several pupils:

Equivalent.

Júlia:

Very good, and why?

Several pupils:

Because they have the same area.

Júlia:

Which is…?

Several pupils:

Five squares.

Júlia:

On this sheet, we’re going to summarise what we’ve just been talking about. Let’s build our conclusions together. What do pentominoes have?

Bianca:

Always five squares.

Jorge:

And they have the area of five squares.

Júlia:

What else?

Susana:

They’re equivalent figures.

Júlia:

And?

Afonso:

They always have the same area.

Júlia:

Is there anything else missing? What is the unit of area of pentominoes?

Dinis:

The square.

Júlia:

All right. You can copy [Júlia’s written record on the board] onto your conclusion’s summary sheets. (S7)

In this segment of the final synthesis, Júlia encouraged the pupils to get involved, and they spoke up when she posed them mostly confirmation and focusing questions, reviewing the characteristics of the pentominoes, namely the fact that they all have the same area and are, therefore, equivalent figures. At the end of the final synthesis, Júlia made a record on the board (Figure 5) summarising the main ideas explored in the lesson and highlighting the relationship between pentominoes and the concepts of area and of equivalent figures.

6. Discussion

In the goal-setting and lesson-planning sessions, Júlia, given the aim set for the research lesson in the first session of the lesson study (as suggested by Fujii, 2018), said that the purpose of the task should be the development of a conceptual understanding, in this case, of the concept of area, since it was something that the pupils had not yet studied. Then, she reflected on the type of task she intended to propose to the pupils, taking into account the characteristics of an exploratory lesson, just as the preservice teachers who participated in Martins et al.’s (2021) study did. Thus, the preservice teacher considered selecting a problem or an exploratory task, given the degree of challenge and openness that they present, excluding closed tasks as exercises, given the nature of the lesson, as mentioned by Ponte (2005) and Ponte et al. (2024). Júlia opted for an exploratory task, which she found quite open and challenging, allowing a variety of solution strategies that pupils could use.

Júlia analysed documents about the difficulties that the pupils usually present in learning the concept of area and about the actions to be used by the teacher in order to support pupils in overcoming them, an activity characteristic of lesson study (Fujii, 2018). This study was very useful to the preservice teacher to anticipate in a consistent way the pupils’ strategies and difficulties in solving the task. It allowed her to relate important aspects of her knowledge about teaching practice, namely the challenge, openness and purpose of the exploratory task and the anticipation of pupils’ strategies and difficulties in learning the mathematical topic (Fujii, 2018; Ponte, 2005; Ponte et al., 2024). In other words, the preservice teacher understood that, in order to support pupils to overcome possible difficulties, such as confusing the concepts of length and area, she should select a task that promoted the understanding of the concept of area, presenting a contextualised situation using manipulative materials.

During the goal-setting and the lesson-planning sessions, Júlia constructed an exploratory task, taking into account the purpose (development of the concept of area), as mentioned by Swan (2017) and the characteristics of an exploratory task, such as challenge, openness and a motivating context for pupils, in line with Ponte (2005). She also defined that the task should allow the use of enactive representations (Bruner, 1999), in this case the manipulation of squares for the construction of pentominoes. Once the task was created, the preservice teacher solved it, anticipating the various strategies that the pupils could present in class, considering their degree of correctness, and reviewed possible difficulties that they could manifest. In parallel with this work and as suggested by Ponte et al. (2024), Júlia thought about the flow of the lesson when she suggested strategies to adopt to support pupils to overcome such difficulties, namely in the whole-class discussion, such as using manipulative material, and also when she planned each phase of the exploratory lesson and the interventions that she could make in the classroom. The preservice teacher planned to clarify possible questions from the pupils during the presentation of the task, ensuring that everyone could interpret it; she anticipated how to select and sequence pupils’ responses during autonomous work, thought about her interventions in the whole-class discussion and how to manage it to ensure that it remained on the desired to achieve the aim of the lesson, as indicated by Ponte (2005), Stein et al. (2008), Canavarro (2011) and Fujii (2018). The questions to ask the pupils were prepared in detail by the preservice teacher, considering that they should be challenging, to promote their involvement in the lesson and to encourage them to explain their reasoning, as indicated by Stein et al. (2008).

Thus, during the planning sessions of the research lesson, Júlia had the opportunity to use and deepen her knowledge of teaching practice about the following: (i) the tasks, with regard to the challenge and openness that they present, in this case the explorations, the purpose for which they are intended and the representations that can be used; and (ii) the design of the lesson, regarding its planning, in the frame of the three phases of the exploratory lesson, taking into account the flow and anticipation of pupils’ strategies and difficulties and the teacher’s interventions and questions.

The research lesson allowed Júlia to put into practice the detailed preparation she carried out in the previous lesson study sessions, namely her interventions and questioning, which were designed to promote contributive and reflexive communication, in which pupils assume a relevant role and their contributions are valued and used to further the development of the lesson (Brendefur & Frykholm, 2000). Fulfilling the three phases of the exploratory lesson, the preservice teacher began by introducing the task to the pupils, as suggested by Canavarro (2011), which she did according to what had been planned. During the pupils’ autonomous work, Júlia observed their productions and asked them inquiry questions in order to understand the reasoning involved in the solutions and to encourage them to explain their ideas, in line with the suggestions of Canavarro (2011) and Stein et al. (2008). At the whole-class discussion, the preservice teacher diversified the types of questions, meeting the aim that she had at each moment of the lesson. Júlia asked confirmation questions when, already knowing in advance the correct answer, she wanted to know if the pupils were able to give it; used focusing questions to draw pupils’ attention to some relevant aspect of the lesson; and posed inquiry questions to challenge pupils to think more deeply and to go further in their answers, as suggested by Stein et al. (2008) and Ponte et al. (2024). The lesson ended with the final synthesis (as suggested by Stein et al., 2008), which Júlia led using all the types of questions again, with emphasis on confirmation and focusing questions, since she intended, at this point in the lesson, to systematise the learning developed by the pupils in the previous moments, as indicated by Ponte (2005).

As Martins et al. (2021) suggest, the planning of this exploratory lesson, in the context of a lesson study, was carried out in detail, which may have contributed to the fact that Júlia did not encounter unexpected situations in the classroom, one of the main challenges that preservice teachers may face when leading exploratory lessons.

7. Conclusions

We present, in this article, a lesson study experience in preservice teacher education, addressing the case of a preservice teacher who is preparing to teach in grades 1–6, and we analyse the key aspects of the knowledge of teaching practice that she presented when preparing and leading an exploratory lesson during her participation in a lesson study.

In this study, we were able to verify that a preservice teacher used key aspects of their knowledge of teaching practice indicated by Ponte et al. (2024), and the work developed around the design of the lesson and the tasks in the planning phase of the exploratory lesson and communication were especially highlighted while leading the research lesson. Preparing and leading the research lesson allowed her to use and deepen her knowledge about teaching practice, carrying out all the phases of the exploratory lesson and overcoming the aspects in which she had more difficulty in her past teaching experience.

The structure of the lesson study, in particular the activities carried out during the preparation sessions for the research lesson, promoted the presentation of the preservice teacher’s didactic knowledge, in line with what Sims and Walsh (2009) say. Planning the research lesson in detail presupposes activities such as the analysis of mathematical tasks, the selection or construction and solving of the task to propose to the pupils, the anticipation of the strategies and difficulties that they may present, the preparation of interventions and questioning by the teacher and the different moments and flow of the lesson (Fujii, 2018). Leading the research lesson allows the teacher to put into practice the strategies previously defined and reflect on their results, as suggested by Fernández (2010) and by Rodrigues & Cyrino (2018). These are aspects that must be considered when it comes to preparing and leading exploratory lessons, namely because of the challenges it entails, especially for preservice teachers.