Mathematics Teachers’ Knowledge for Teaching with Digital Technologies: A Systematic Review of Studies from 2010 to 2025

Abstract

This systematic review examines mathematics teachers’ knowledge for teaching using digital technologies (DTs), understood as the intersection of disciplinary, pedagogical, and technological domains that teachers mobilize when designing, implementing, and assessing mathematics lessons. In this study, DTs refer to the digital hardware, software, and online environments used to represent, simulate, or analyze mathematical ideas (e.g., GeoGebra, Tinkerplots, spreadsheets, CAS tools, and learning management systems). We analyzed 50 peer-reviewed journal articles published between January 2010 and April 2025, retrieved from Web of Science, Scopus, ERIC, and Scielo. ResearchGate was consulted only as a supplementary repository to access the full texts already identified in the indexed databases. These articles were analyzed according to predefined analytical categories, including research themes, country of origin, and the digital technologies addressed in each study, allowing for cross-comparisons across theoretical frameworks and methodological approaches. The results reveal a strong interest in this topic in countries such as Turkey, the United States, Mexico, Indonesia, and Spain, with the participation of in-service mathematics teachers at the primary, secondary, and university levels, as well as preservice teachers. The most frequently studied themes in the past five years regarding teacher knowledge include teacher education through digital technologies, the analysis of lesson planning and tasks designed by teachers using DTs, and the assessment of their knowledge through self-perception questionnaires. The review concludes that only a few of the analyzed studies qualitatively examined teacher knowledge when using digital technologies, particularly those that employed non-participant observation, audio and/or video recordings, and semi-structured interviews.

1. Introduction

The study of mathematics teachers’ knowledge has its roots in the work of Shulman (1986), who introduced the concept of Pedagogical Content Knowledge (PCK) and emphasized the importance of integrating disciplinary knowledge with pedagogical expertise for effective teaching. Building on this foundational proposal, various models emerged that delved into the specificities of mathematics teachers’ knowledge (Fennema & Franke, 1992; Bromme, 1994; Ponte, 1999; Rowland et al., 2005; Ball et al., 2008). These models incorporated dimensions relevant to the study of mathematics teachers, such as content knowledge, pedagogical knowledge, student cognition, teachers’ beliefs, the philosophy of school mathematics, curriculum, instructional practice, and both common and specialized knowledge.

In parallel, the growing presence of digital technologies (DTs) in education has driven the development of models that integrate this component as part of teachers’ professional knowledge. In this review, digital technologies (DTs) are understood as digital hardware, software, and online environments that support the representation, simulation, and exploration of mathematical ideas (e.g., GeoGebra, TinkerPlots, spreadsheets, computer algebra systems, and learning management systems), with Mishra and Koehler’s (2006) Technological Pedagogical Content Knowledge (TPACK) framework being the most widely recognized. This model has had a significant influence on research concerning the use of digital technologies in teaching. However, it has faced criticism for the broadness of its definitions, which makes it challenging to clearly identify its components in actual teaching practice (Koehler et al., 2013).

More recently, the Mathematics Teacher’s Specialized Knowledge (MTSK) model, proposed by Carrillo et al. (2018), has represented a significant advancement by more precisely characterizing the specific knowledge a teacher requires to plan, teach, interact with colleagues, and reflect on their practice.

In this review, the term pedagogical practice refers to the instructional and decision-making processes through which mathematics teachers mobilize their professional knowledge disciplinary, pedagogical, and technological when designing, implementing, or reflecting on teaching with digital technologies.

Consistent with this view, the MTSK model integrates disciplinary knowledge, pedagogical-didactic knowledge, and teachers’ beliefs, recognizing that specialized knowledge encompasses the understanding of meanings, properties, and definitions of mathematical concepts, the connections among them, the strategies for teaching them, and the ways in which students learn them.

However, a limitation of the MTSK model lies in the fact that knowledge about digital technologies is mentioned only tangentially. While the use of digital resources is acknowledged within the MTSK subdomain “Knowledge of Mathematics Teaching” (KMT), it remains underdeveloped, in contrast with the profound impact digital technologies have had on education in recent years. In this regard, the OECD (2019) notes that DTs have transformed school dynamics and have become essential resources in pedagogical practice. This transformation became even more evident during the COVID-19 pandemic, when the need to enact technological–pedagogical competencies in real classrooms moved to the forefront of school systems worldwide, exposing gaps between self-reported knowledge and classroom practice.

In this review, classroom practice is understood broadly to encompass the pedagogical competencies and teaching actions through which mathematics teachers’ technological and pedagogical knowledge are enacted in real or simulated lessons, as described in the reviewed studies rather than directly observed by the authors.

In this context, it is pertinent to explore the intersection between TPACK and MTSK to analyze how mathematics teachers integrate DTs into the teaching of specific subject-area content. While previous reviews have addressed the integration of DTs in mathematics education (Willermark, 2018; Rivera-Robles et al., 2021; Noor-Kholid et al., 2023; Li et al., 2024; Kadluba et al., 2025), most focus on partial dimensions of teacher knowledge, with a predominance of self-perception studies and limited attention to the implementation of concrete DTs for teaching specific mathematical content.

Willermark (2018) conducted a systematic review of 107 articles (2011–2016) on the use of the TPACK model to identify teachers’ Technological Pedagogical Content Knowledge. The findings revealed a wide range of approaches and instruments, with self-report measures predominating over teacher performance assessments, the latter being scarce in the literature.

Rivera-Robles et al. (2021) reviewed 32 articles (2018–2020) retrieved from Web of Science, Scopus, and Scielo, focusing on empirical studies that examined mathematics teachers’ TPACK using quantitative, qualitative, or pedagogical approaches. Unlike Willermark, these authors found that research more frequently employed teacher performance assessments rather than self-reports, a difference attributable to their more specific inclusion criteria.

Noor-Kholid et al. (2023) analyzed 25 articles (2018–2020) in the Scopus and ERIC databases, aiming to explore the development of TPACK in mathematics teaching. Their results identified common barriers such as lack of confidence, resistance to change, and limited integration of DTs with pedagogical strategies. They also acknowledged methodological limitations, including the restricted use of databases and the exclusion of sources such as books, theses, or conference proceedings.

Li et al. (2024) conducted a review of 50 articles (2005–2022) on the TPACK of mathematics teachers in primary education, drawing on multiple databases (Scopus, Web of Science, ProQuest, PsycINFO, and ERIC). They identified a growing trend in research on the convergence of technology, pedagogy, and content, but also highlighted underexplored areas such as lesson design, teacher evaluation, and professional development.

Kadluba et al. (2025) focused their review on the assessment of TPACK in mathematics education, analyzing 123 articles (2005–2023). They examined the characteristics of the studies, the measurement instruments, and their operationalization, identifying a frequent use of self-report scales with less emphasis on knowledge tests, classroom observations, or analysis of instructional materials. They also noted that much of the assessment centers on general mathematical knowledge, without addressing specific subdomains, and that many instruments lacked statistical validation.

Taken together, previous reviews show a fragmented landscape. Most research has adopted the TPACK framework, often operationalized through self-report surveys, which captures general technological–pedagogical interactions, but overlooks disciplinary depth. In contrast, a smaller set of studies mobilized MTSK, offering sharper insights into mathematical specificity but without addressing digital integration. To date, no synthesis has systematically articulated both perspectives. This review addresses that gap by mapping how mathematics teachers’ knowledge with digital technologies has been studied through these frameworks, thus bridging generalist and specialized views of teacher knowledge.

Unlike previous reviews, the present study seeks to examine research that explores teachers’ knowledge when integrating digital technologies into teaching, regardless of the theoretical framework employed. It differs from prior reviews by integrating both generalist (TPACK) and mathematics-specific (MTSK) perspectives to provide a more comprehensive understanding of how teacher knowledge is conceptualized and enacted with digital technologies. This entails considering not only studies based on the TPACK model (Mishra & Koehler, 2006) but also those grounded in the Mathematics Teacher’s Specialized Knowledge (MTSK) model proposed by Carrillo et al. (2018).

These models were chosen because they represent two complementary perspectives on teachers’ professional knowledge: TPACK emphasizes the integration of technology, pedagogy, and content in teaching practice, while MTSK provides a domain-specific articulation of mathematical knowledge for teaching. Their joint consideration allows this review to bridge general technological–pedagogical frameworks with discipline-specific conceptualizations of mathematics teachers’ knowledge. For this reason, both models were included as keywords, reflecting their central role in the analytical framework of the study.

As well as research inspired by both perspectives, provided they offer relevant insights into how such knowledge influences the teaching of mathematics.

This study aimed to analyze research published between 2010 and 2025 related to mathematics teachers’ knowledge when integrating DTs into the teaching of specific subject-area content, identifying their characteristics, theoretical frameworks, methods, and evaluation instruments, as well as the patterns, categories, and connections that emerge across the reviewed studies. The choice of the 2010–2025 analysis period is justified for two reasons: (i) the publication of TPACK in 2006 spurred significant scholarly output during the following decade, and (ii) the period encompasses substantial changes in the educational use of DTs, particularly due to the COVID-19 pandemic.

Within this scope, particular attention was given to studies that explored teacher education through digital technologies and those analyzing lesson planning and task design involving DTs. Although these aspects were not treated as separate analytical categories, they emerged across several studies as key contexts in which mathematics teachers’ knowledge with digital technologies becomes visible in practice.

Analyzing the theoretical framework used in the studies makes it possible to identify how teachers’ knowledge, in relation to the use of technologies, has been conceptualized and examined from either a theoretical or empirical perspective. The countries of origin of the reviewed articles were examined because national contexts shape how digital technologies are adopted in mathematics education through variations in curriculum policies, teacher training systems, infrastructure, and research priorities. Identifying these contextual differences provides a comparative view of the maturity and equity of this research field across regions. Assessing teacher knowledge also allows for the identification of the characteristics of the instruments used and the dimensions they encompass. Based on these categories, the research questions that guide the analysis emerge.

In this review, the object of study is mathematics teachers’ knowledge when integrating digital technologies (DTs) to teach specific mathematical content. Building on PCK, we note how TPACK foregrounds the technological dimension while MTSK sharpens disciplinary and pedagogical specificity in mathematics. We operationalize this construct through (a) the theoretical frameworks used (e.g., TPACK, MTSK, and hybrid approaches) and (b) the assessment methods adopted (self-report instruments vs. competency-based, classroom observation tools). We focus on teachers’ knowledge because it is the enabler of classroom competence. Accordingly, we examine both declared knowledge (self-reports) and enacted competence (observation-based instruments) to understand how knowledge claims translate into practice.

This review contributes to the field by systematically mapping how mathematics teachers’ knowledge has been conceptualized and assessed in the integration of digital technologies. Its novelty lies in bridging two major frameworks—TPACK and MTSK—through a comparative analysis that highlights their convergences, limitations, and potential complementarities. By doing so, it offers a more comprehensive understanding of mathematics-specific technological knowledge and provides an analytical basis for the future design of hybrid models and instruments.

2. Research Questions Guiding the Review

RQ1. What are the characteristics (year, country/region, purpose) of articles (2010–April 2025) on mathematics teachers’ knowledge when integrating DTs to teach specific content?

RQ2. Which theoretical frameworks (TPACK, MTSK, hybrids approaches) are used and how is teachers’ knowledge operationalized within them?

RQ3. Which methods and instruments (self-report vs. observation/competency-based) are employed to assess teachers’ knowledge, and how robust are they?

RQ4. What patterns, categories, and connections emerge across the reviewed studies regarding the integration of digital technologies into the teaching of specific mathematical content?

3. Methods

3.1. Design and Reporting Standards

This study is a systematic literature review, grounded in the PRISMA 2020 guidelines (Page et al., 2021; Li et al., 2024) and the methodological approach proposed by Petticrew and Roberts (2008). This type of review was chosen because the aim of the study was to address previously defined research questions, thereby ensuring a reproducible and reliable synthesis of the existing literature. The review focused on identifying, evaluating, and analyzing empirical evidence on mathematics teachers’ knowledge when integrating digital technologies into the teaching of specific content.

Although The review protocol was not registered on platforms such as PROSPERO or OSF; however, all phases were carried out in accordance with the methodological steps established by PRISMA. The process included: (i) searches in indexed databases (WoS, Scopus, ERIC, Scielo); (ii) a reproducible query set; (iii) pre-defined inclusion/exclusion criteria; (iv) deduplication and multistage screening; (v) a PRISMA flow diagram; (vi) double coding of study characteristics and frameworks/instruments; and (vii) adjudication of discrepancies by the first and second authors.

The PRISMA process comprised the phases of identification, screening, eligibility, and inclusion (Figure 1), which helped confirm the validity of the findings and support evidence-based decision-making (Li et al., 2024). The search was conducted in the Web of Science (WOS), Scopus, Scielo and ERIC databases, selected for their broad coverage of scientific literature in mathematics education and technology. Additional sources such as ResearchGate were consulted informally to identify potentially relevant references, but no records from these sources were included in the systematic count. Filters and search strategies were applied based on study characteristics such as publication year (January 2010 to March 2025), country, theme, study purpose, and instruments used to assess mathematics teachers’ knowledge when integrating digital technologies into mathematics teaching. Only articles published in peer-reviewed academic journals were included.

3.2. Search Strategy

The search process was conducted between January 2010 and March 2025 across four databases Web of Science (WoS), Scopus, Scielo, and ERIC selected for their broad coverage of scientific literature in mathematics education and technology.

We set 2010–April 2025 to capture (i) the post-2006 diffusion of TPACK once indexing stabilized, (ii) pre-pandemic and pandemic/post-pandemic phases, and (iii) the emergence of MTSK (from 2018 onward) alongside DT integration in mathematics education.

Combinations of English and Spanish terms were used, carefully delimited to capture studies on mathematics teachers’ knowledge when integrating digital technologies. Core descriptors included mathematics teacher knowledge, TPACK, MTSK, digital technologies, and technology integration. These terms were combined with Boolean operators (AND, OR) and adapted to the syntax requirements of each database. To avoid over-expansion, the queries were restricted to titles, abstracts, and keywords, and were cross-checked against mathematics education subject categories. Synonyms and closely related terms were included only when they preserved relevance to the research questions.

3.3. Inclusion Criteria

Studies were included if they met the following conditions:

• Peer-reviewed publications (journal articles, book chapters from reputable academic publishers, and conference proceedings).
• Empirical or theoretical studies explicitly addressing mathematics teachers’ knowledge when integrating digital technologies into the teaching of specific content.
• Research conducted at any educational level.
• Publications written in English or Spanish.

Although research at any educational level (primary, secondary, and university) was accepted, the additional filters namely the focus on mathematics-specific content with digital technologies and the restriction to peer-reviewed journals produced a more focused corpus (n = 50). This explains the apparent contrast between the wide target population and the final number of studies retained for analysis.

3.4. Exclusion Criteria

The following were excluded:

• Non-scientific documents (unpublished theses, presentations, internal reports).
• Studies that did not directly address mathematics teaching or the professional knowledge of mathematics teachers in technology-mediated contexts.
• Duplicate publications found in more than one database.
• Works focused on disciplinary content other than mathematics, even if they included the use of digital technologies or pedagogical elements.
• Documents written in languages other than English or Spanish.

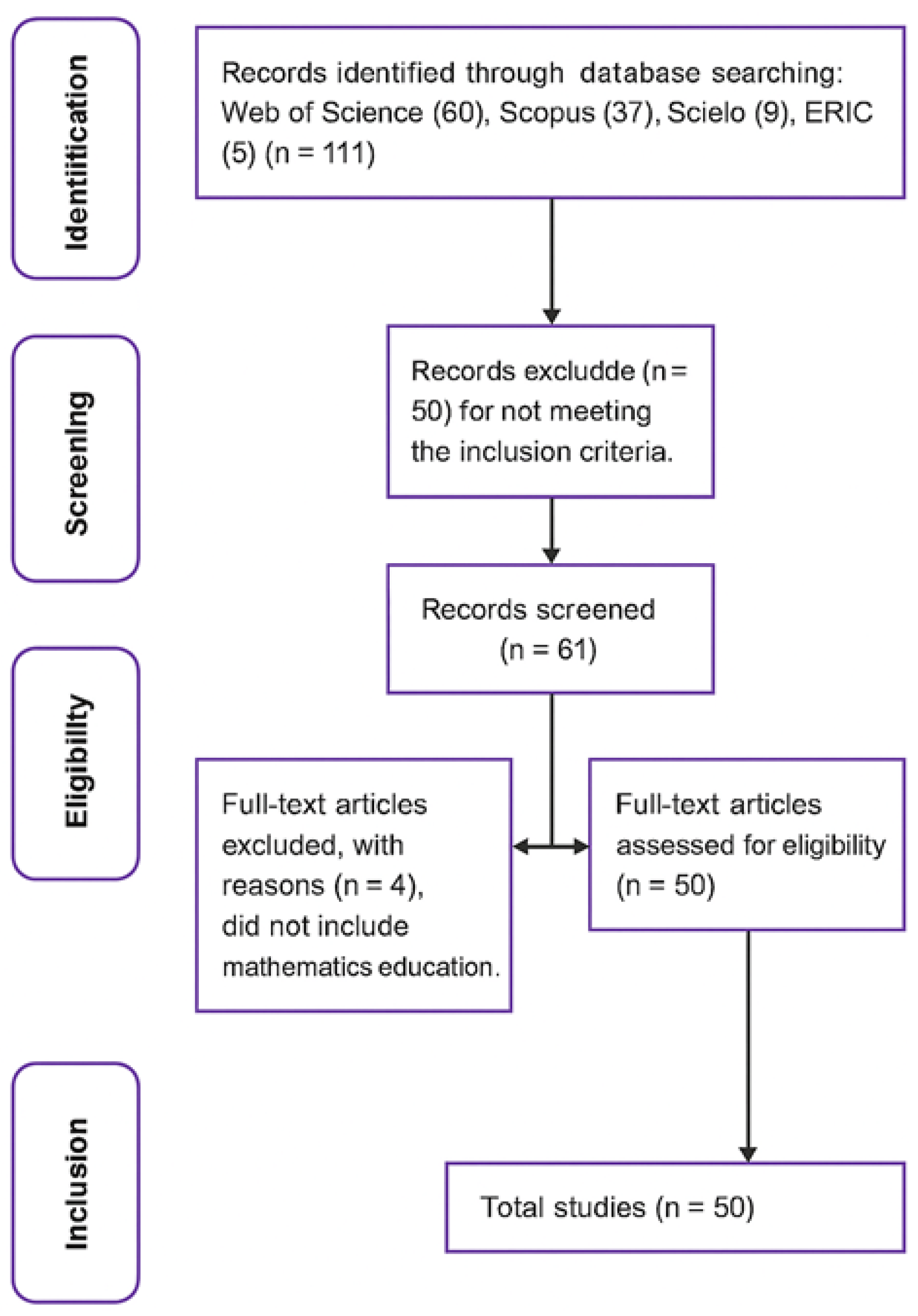
3.5. Screening Process

In the first stage, the combined keywords outlined in the search strategy were applied across the selected databases, resulting in the identification of a total of 111 records: Web of Science (53), Scopus (37), Scielo (8), ERIC (5), and ResearchGate (8).

In the second stage, the records were examined according to the established inclusion and exclusion criteria, leading to the elimination of 50 studies. This filtering was carried out because some were written in languages other than Spanish or English, were not peer-reviewed scientific publications, or did not directly address mathematics teachers’ knowledge when integrating digital technologies into teaching, focusing instead on other disciplinary areas.

In the third stage, the 61 articles that met the previous criteria were reviewed in detail, with 50 ultimately selected for analysis. In this process, four articles were excluded for not being related to mathematics education, and seven were identified as duplicates across different databases.

In the final stage, the 50 selected articles were analyzed to answer the research questions. For this purpose, an individual summary of each study was prepared based on a thorough and complete reading, identifying the most relevant themes and subthemes for the review. The final sample (n = 50) reflects stricter inclusion criteria than prior reviews, namely: (i) studies focusing specifically on mathematics teachers integrating digital technologies to teach content, (ii) peer-reviewed journal articles only, and (iii) a time window from 2010 to April 2025. This narrower scope enhanced comparability and yielded thematic saturation: after coding approximately 45 articles, no new categories emerged in the framework–instrument matrix.

3.6. Variables and Coding Scheme

To answer the research questions, each article was coded for the following variables:

• Year of publication, country/region, and research purpose—to characterize the sample and enable cross-comparisons. Country/region was coded because digital infrastructure, policy priorities, and teacher-education systems shape framework adoption, instrument availability, and DTs access, thus conditioning how knowledge with DTs is developed and assessed.
• Theoretical framework (TPACK, MTSK, or hybrid approaches) and operationalization of knowledge—to identify how mathematics teachers’ knowledge is conceptualized.
• Research methods and assessment instruments-distinguishing between self-report and observation/competency-based approaches.
• Mathematical content and contextual categories-to analyze patterns in how DTs are integrated with specific subject-area content across regions.

4. Results

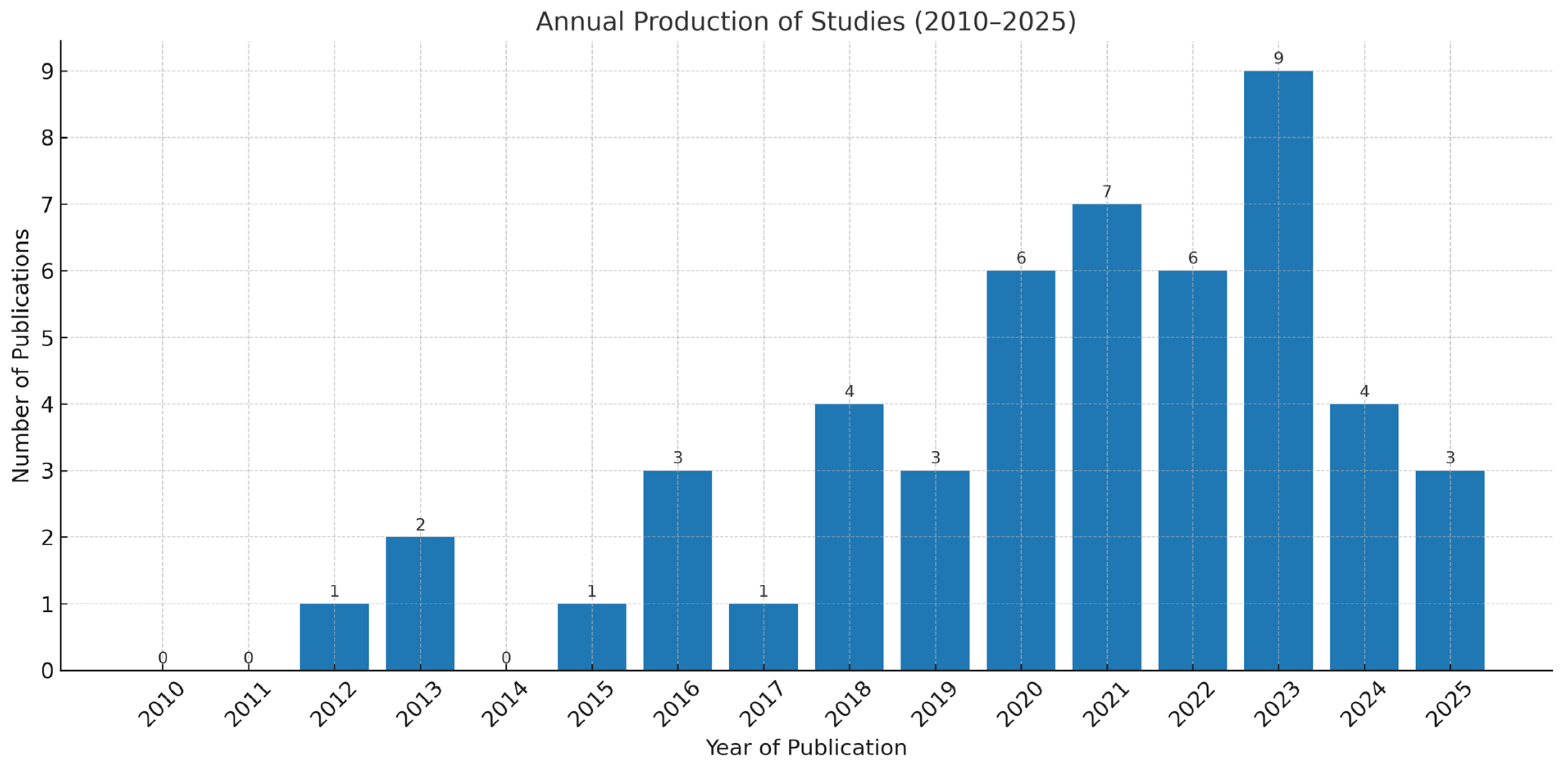
4.1. Characteristics of the Studies (Year, Country, and Purpose)

We first map the temporal and geographic distribution of the studies to contextualize the maturity and spread of the field, enabling comparison with prior reviews and highlighting where gaps persist. This descriptive layer also clarifies the purposes addressed in the selected studies, providing a baseline for the more detailed thematic analyses that follow.

A total of 50 research studies published between January 2010 and April 2025 were identified (Figure 2). The annual distribution reveals a steady growth in academic production in this field. In the early years of the period (2010, 2011, and 2014), no publications were recorded. In 2012, 2015, and 2017, one study was published per year (2.0% each), while in 2013, two studies were published (4.0%). Starting in 2016, there was an increase, with three articles (6.0%), a figure repeated in 2019 and 2025 (note: 2025 counts are partial, January–April). In 2018 and 2024, four publications were recorded each year (8.0% each), while in 2020, six studies were published (12.0%) and in 2021, seven (14.0%).

The most productive years were 2023, with nine articles (18.0%), and 2022, with six publications (12.0%), indicating a concentration of recent studies on mathematics teachers’ knowledge when integrating digital technologies into the teaching of specific content. The decline observed in 2024 and 2025 approximately 50% compared to the peak publication years may be explained by the fact that 2022 and 2023 saw an exceptionally high number of studies conducted during the COVID-19 pandemic. This period significantly accelerated the use of digital technologies in mathematics teaching, resulting in a temporary surge in academic output in this line of research.

Regarding the databases consulted, most studies originated from Web of Science (23 articles, 46.0%), followed by Scopus (18, 36.0%), Scielo (4, 8.0%), ResearchGate (3, 6.0%), and ERIC (2, 4.0%). It is worth noting that of the 18 articles identified in Scopus, eight were also indexed in Web of Science and were removed as duplicates, as shown in Figure 1. This finding underscores the pivotal role of Web of Science in identifying studies related to mathematics teachers’ knowledge when integrating digital technologies for teaching discipline-specific content.

The records retrieved in this review covered all five continents: America (44%), Asia (28%), Europe (14%), Africa (8%), and Oceania (6%), as illustrated in Figure 2. The countries with the highest number of publications were the United States, Mexico, and Turkey, with six studies each, followed by Spain (5) and Indonesia (4). Individual contributions were also identified from China, Israel, Peru, South Korea, Rwanda, the Netherlands, Portugal, among others. The Americas account for the largest number of studies included in this review, surpassing both Europe and Asia. This finding is noteworthy considering that, in the Americas, developing countries such as Colombia, Peru, and Costa Rica exhibit lower levels of digital technology implementation in educational institutions compared to European countries or global leaders such as South Korea and China. Nevertheless, most of the scholarly output from the Americas is concentrated in the United States and Mexico, whose investments in the use of digital technologies in the classroom far exceed those of the rest of the continent.

On the other hand,

Table 1. Classification of the articles included in the systematic review by analysis categories.

Author (year)	Country	Database
Li and Nugraha (2025)	China	WOS
Reyes-Yáñez et al. (2025)	Chile	Eric
Sánchez-Acevedo et al. (2025)	Chile	Eric
Saralar-Aras and Turker-Biber (2024)	United States	WOS
Kartal and Çınar (2022)	Turkey	WOS
Yildiz and Arpaci (2024)	Turkey	Scopus
Njiku (2024)	Tanzania	WOS
Sandoval et al. (2023)	Mexico	WOS
Seguí and Alsina (2023)	Spain	Scopus
Meléndez-Cruz et al. (2023)	Mexico	WOS
Padilla-Escorcia et al. (2023)	Colombia	Scopus
Aldemir-Engin et al. (2023)	Turkey	Scopus
Kohen et al. (2023)	Israel	WOS
Smith and Zelkowski (2023)	United States	WOS
Nzaramyimana and Umugiraneza (2023)	Rwanda	WOS
Cayo et al. (2023)	Spain	WOS
Muñoz-Catalán et al. (2022)	Spain	WOS
Advíncula et al. (2022)	Peru	WOS
Gamboa (2022)	Spain	Scielo
Morales-García et al. (2022)	Mexico	Scielo
Rizo-Cruz (2022)	Mexico	Scielo
Rakes et al. (2022)	United States	WOS
Almeida et al. (2021)	Brazil	WOS
Padilla-Escorcia and Acevedo-Rincón (2021)	Colombia	Scielo
Morales-López et al. (2021)	Costa Rica	Scopus
Van Leendert et al. (2021)	Netherlands	Scopus
Shin (2021)	South Korea	WOS
McLaughlin-Galanti et al. (2021)	United States	Scopus
Castro-Sierra and Gutierrez-Santiuste (2021)	Spain	WOS
León-Banguero et al.(2020)	Mexico	Scopus
Mailizar and Fan (2020)	Indonesia	WOS
Açıkgül and Aslaner (2020)	Turkey	Scopus
Zambak and Tyminski (2020)	United States	Scopus
Gutiérrez-Fallas and Henriques (2020)	Portugal	Scopus
Salas-Rueda (2020)	Mexico	WOS
Morales-López (2019)	Costa Rica	Scopus
Kafiyulio and Fisser (2019)	Tanzania	Scopus
Tabach and Trgalova (2019)	Canada	WOS
Fitriana and Mardiyana (2018)	Indonesia	Scopus
Saralar et al. (2018)	Turkey	Scopus
Ling Koh (2018)	New Zealand	WOS
Rohmitataati (2018)	Indonesia	WOS
Arevalo et al. (2017)	Colombia	Scielo
Muir et al. (2016)	Australia	WOS
Cangazoglu et al. (2016)	Turkey	WOS
Maesuri et al. (2016)	Indonesia	Scopus
Chizwina and Mhankure (2015)	South Africa	WOS
Handal et al. (2013)	Australia	WOS
Zelkowski et al. (2013)	United States	Scopus
Jang and Tsai (2012)	Taiwan	Scopus

presents the 50 articles included in this review, organized by author, year, country, and database. This classification allows for the observation of the geographical diversity of the studies, the temporal concentration of publications within the selected period (2010–2025), and the main indexing sources used, providing an overall view of the origin and dissemination of knowledge about mathematics teachers who use digital technologies in teaching.

Table 1 shows that, even in 2024, Web of Science (WOS) remained the database contributing the highest number of articles to the review, with a total of three records. Likewise, the United States stands out as the only one among the four countries with the highest output in this area whose articles were found in high-impact databases used in this review, such as Scopus and Web of Science. Furthermore, it was the only country in which publications related to teachers’ knowledge integrating digital technologies in mathematics teaching were identified continuously between 2020 and 2024. In contrast, in countries such as Mexico or Turkey, no publications were recorded in 2021. Although these countries had a total number of articles similar to that of the United States, their production was more evenly dispersed throughout the analyzed period, which shows less research continuity in this field of study.

4.2. Theoretical Approaches

In the 50 records included in this review, two main theoretical models were identified as the basis for studies related to teachers’ knowledge integrating digital technologies for teaching specific mathematics content. These are: Technological Pedagogical Content Knowledge (TPACK) and the Mathematics Teacher’s Specialized Knowledge (MTSK). The distribution of records was as follows: 35 studies (70%) grounded in TPACK, 12 (24%) in MTSK, and 3 (6%) that proposed combinations of both models or adaptations of TPACK to mathematics education.

4.3. TPACK

TPACK was the predominant theoretical model in the review, and its application focused on the following types of research:

• Teacher professional development: Açıkgül and Aslaner (2020) designed a microteaching experience with GeoGebra for 88 prospective teachers in the teaching of polygons, demonstrating more detailed planning and a more reflective integration of digital technologies (DTs).
• Technology-mediated lesson planning: Saralar-Aras and Turker-Biber (2024) worked with 44 pre-service teachers in the development of lesson plans following a training program with digital technologies (DTs), showing a strengthening of their TPACK.
• Inclusive course design: Van Leendert et al. (2021) adapted TPACK for teaching students with visual impairments, incorporating braille notation and resources for the tactile visualization of concepts.
• Design-based training: Gutiérrez-Fallas and Henriques (2020) integrated seven key tasks (such as the use of Tinkerplots and GeoGebra) to develop TPACK in prospective teachers, combining reflection, analysis, and technological application.
• Case studies on specific content: Morales-López et al. (2021) addressed quadratic functions and proposed categories for the seven TPACK components, although without specifying in detail the disciplinary knowledge involved.
• Conceptual adaptations: Zambak and Tyminski (2020) redefined the TCK component as Mathematical-Technological Knowledge (MKT) to better specify the technological competencies unique to mathematics teachers, classifying five proficiency levels: superficial, isolated, preserved, integrated, and expert.

Despite its widespread adoption, many TPACK studies do not specify precise criteria for evaluating the technological components of mathematics teachers and their integration into pedagogical practice, nor do they establish robust indicators to measure how technology transforms the teaching of specific content.

Beyond the general descriptions of TPACK provided in earlier reviews, this analysis contributes evidence of mathematics-specific adaptations (e.g., the incorporation of MKT) and training designs that explicitly connect technology with disciplinary content. This advances the construction of stronger indicators to evaluate teachers’ competence not only at the declarative level but also in enacted classroom practice with digital technologies.

4.4. MTSK

The studies that adopted the MTSK model (12 in total) focused primarily on disciplinary knowledge (MK) and pedagogical content knowledge (PCK), with less integration of the technological component, as outlined below:

• Targeted use of digital technologies (DTs): Sandoval et al. (2023) incorporated graphing calculators within the subdomain Knowledge of Mathematics Teaching (KMT) as a support resource, but without exploring them as a transformative element in task design.
• Analysis of GeoGebra in specific contexts: Padilla-Escorcia et al. (2023) and Padilla-Escorcia and Acevedo-Rincón (2021) examined its use in modeling trigonometric functions and conic sections, without establishing specialized technological indicators.
• Instruments to assess MTSK: Seguí and Alsina (2023) developed the MTSK-Stochastic questionnaire, including one item on technology use, although without delving into its pedagogical impact.
• Design of digital resources: Meléndez-Cruz et al. (2023) created a GeoGebra-based resource for teaching fractions with Cuisenaire rods, using MTSK to assess lesson plans and materials.
• Disciplinary studies without technological integration: Reyes-Yáñez et al. (2025), Sánchez-Acevedo et al. (2025), Cayo et al. (2023), and Advíncula et al. (2022) explored teachers’ knowledge of standard deviation, radicals, sequences, and polygons, respectively, from a disciplinary and pedagogical perspective, omitting the technological component.

Although MTSK-based studies are less frequent, their contribution is qualitatively significant: they provide disciplinary delimitation and precision in the description of mathematical tasks that are often absent in TPACK. These insights open the way for developing instruments that more rigorously capture teachers’ specialized knowledge in integrating digital technologies, with direct implications for professional preparation and evaluation.

4.5. Hybrid Proposals

In this review, hybrid approaches refer to proposals that integrate perspectives from models emphasizing digital technologies with those focused on mathematics-specific knowledge. These studies aim to connect technological, pedagogical, and mathematical dimensions more coherently within teaching and research on mathematics education.

Three studies proposed integrations between the TPACK and MTSK models or adaptations to the field of mathematics education:

• Replacement of Technological Content Knowledge (TCK) with Mathematical Technological Knowledge (MKT): Suggested for greater specificity in the knowledge of teachers who integrate technology into mathematics teaching, as a way to differentiate their TPACK from other professionals with disciplinary training in mathematics (Zambak & Tyminski, 2020).
• TPACK–MTSK combinations with adapted indicators: Applied to specific mathematical content (Gamboa, 2022; Rizo-Cruz, 2022).

The emergence of hybrid frameworks that articulate TPACK and MTSK stands out as one of the most promising contributions identified in this review. These integrated approaches not only enrich the understanding of teachers’ knowledge but also provide a viable path for designing indicators and instruments more consistent with the specificity of mathematics teaching mediated by digital technologies, fostering convergence between theory, assessment, and educational practice.

The inclusion of hybrid frameworks in this review responds to the growing effort within mathematics education research to overcome the limitations of analyzing teacher knowledge through a single model. Studies adopting these perspectives reveal that combining digital, pedagogical, and mathematical dimensions allows for a more precise characterization of teachers’ professional knowledge when technology is integrated into the teaching of mathematics. Therefore, the emergence of such frameworks represents a meaningful evolution toward models that better capture the complexity of teaching with digital technologies.

These tendencies are summarized in

Table 2. Summary of findings corresponding to the theoretical approaches of the records in the systematic review.

Summary of Findings
Model	Main Findings	Research Opportunities
TPACK (35 studies, 70%)	Broad applicability in teacher training programs and the design of technology-mediated instructional sequences. Examples of good practices include micro-teaching, inclusive courses, and lesson planning with resources such as GeoGebra, Tinkerplots, or simulators. Conceptual adaptations like MKT provide greater specificity in mathematics.	Need to establish more robust indicators to measure technological subdomains. Limited evidence on how the integration of digital technologies transforms the understanding of specific mathematical content. Low representation of Latin American contexts in empirical studies.
MTSK (12 studies, 24%)	Strong focus on disciplinary knowledge (MK) and pedagogical content knowledge (PCK) with specific applications of digital technologies (DTs). Use of specialized instruments (e.g., MTSK-stochastic) and experiences in designing digital resources in GeoGebra.	Systematically integrate the technological dimension into task analysis and the assessment of teacher knowledge. Develop measurement tools that include technological indicators adapted to MTSK. Explore applications in multicultural contexts or in settings with limited technological resources.
Hybrids/Adaptations (3 studies, 6%)	Proposals that combine TPACK and MTSK, or that replace TCK with MKT for greater specificity. These models are useful for situated analyses and for designing more integrated instruments.	Deepen the empirical validation of these hybrid models. Expand their application to different educational levels and diverse mathematical content. Systematize criteria for evaluating the effectiveness of integrating both frameworks.

, which highlights how the three main theoretical perspectives technology-oriented, mathematics-specific, and hybrid contribute differently to research on teacher knowledge with digital technologies. The findings show that while technology-oriented frameworks predominate in studies on training and lesson design, mathematics-specific models offer a stronger disciplinary foundation, and hybrid frameworks emerge as promising alternatives that combine both orientations to achieve greater conceptual precision and contextual relevance.

4.6. Instruments for Assessing Mathematics Teachers’ Knowledge in Using Digital Technologies (DTs) for Teaching

Across the corpus, most studies rely on self-report surveys, typically Likert scales grounded in TPACK, while validated observation rubrics that capture mathematics-specific technological indicators remain rare. This imbalance reveals the central gap: instruments often measure teachers’ perceived knowledge, but seldom their enacted competence in classrooms. Our review addresses this gap by mapping how theoretical frameworks (TPACK, MTSK, and hybrids) have been or not been translated into concrete instruments. In doing so, we identify design opportunities for competency-based assessment tools that integrate disciplinary precision from MTSK with the technological pedagogical emphasis of TPACK. Thus, the review not only synthesizes prior work but also delineates directions for building more rigorous and mathematics-specific instrumentation.

This review identified two main approaches for assessing teachers’ knowledge in integrating digital technologies into the teaching of specific mathematics content: self-reporting and competency-based assessment based on classroom observations.

4.7. Self-Report Approach

Across the corpus, self-report instruments emerged as the dominant approach to assessing mathematics teachers’ knowledge when integrating digital technologies. These tools, typically Likert-type questionnaires, capture teachers’ beliefs, levels of confidence, and perceived knowledge. While different authors contextualize their use in teacher education (Yildiz & Arpaci, 2024), professional development programs (Saralar-Aras & Turker-Biber, 2024), or classroom innovation (Açıkgül & Aslaner, 2020), what unites these instruments is their emphasis on self-perception rather than enacted practice. This reliance on subjective measures shapes the way knowledge is represented in the literature and highlights both their accessibility and their limitations. Representative examples include the works of Kohen et al. (2023), Castro-Sierra and Gutierrez-Santiuste (2021), Mailizar and Fan (2020), and Nzaramyimana and Umugiraneza (2023), among others, as described below:

• Mailizar and Fan (2020), with a sample of 355 Indonesian teachers, used the TPACK-M questionnaire adapted from Handal et al. (2013), distinguishing between knowledge of hardware, general software, mathematics-specific software, and online tools.
• Castro-Sierra and Gutierrez-Santiuste (2021) adapted the instrument developed by Schmidt et al. (2009), originally designed for early childhood or primary education teachers with generalist profiles, and implemented it with 183 university mathematics teachers. They evaluated seven components of TPACK using a four-point Likert scale, expanding the level of specificity regarding the skills teachers possess when integrating technology into their pedagogical practices.
• Kohen et al. (2023) combined pre- and post-intervention questionnaires with rubrics to assess TPACK in teaching tasks, showing significant improvements after training in dynamic geometry laboratories.
• Nzaramyimana and Umugiraneza (2023) analyzed the frequency and type of technology use among 118 teachers in Rwanda, finding a predominance of basic tools and low integration of advanced technologies.

Taken together, the evidence suggests that self-reports provide valuable insights into how teachers conceive of and value digital technologies, but they remain insufficient for assessing how such knowledge is mobilized in real classroom settings. Across the studies reviewed, improvements were mainly associated with increased confidence and awareness rather than observable changes in classroom practice. They rarely capture classroom orchestration, moment-to-moment decision-making, or the actual use of mathematics-specific digital tools. We therefore conclude that future research should move beyond isolated reliance on self-reports and systematically complement them with validated observation-based measures. Only through such triangulation can teachers’ knowledge claims be robustly linked to their professional practice.

4.8. Competency-Based Assessment Through Observation Units

Njiku (2024) proposed a qualitative method based on non-participant observation rubrics, applied to 30 mathematics teachers. This tool assessed conceptual understanding, use of prior knowledge, management of technological resources, and content representation, allowing for comparisons between what teachers reported and their actual classroom practice. It is the only instrument of this type identified in this systematic review (2010–2025). In fact, eight years earlier, Patahuddin et al. (2016) had used observation as a technique to assess the skills of a mathematics teacher (case study) who integrates DTs into mathematics teaching. However, they did not structure which specific aspects of the teacher should be observed, grounded in the TPACK components, so that the findings could be replicated in other studies of the same nature.

Table 3. Comparison of identified instruments.

Autor	Country	Educational Level	Type of Instrument	Model	Characteristics	Limitations
Jang and Tsai (2012)	Taiwan	Primary education	IBW-TPACK	TPACK	Evaluates knowledge of interactive whiteboards.	Not specific to mathematics education.
Handal et al. (2013)	Australia	Secondary education	TPACK-M	TPACK	Examines, through a mixed approach (self-reports and statements), teachers’ skills for teaching mathematics using digital technologies.	General nature of the items evaluated based on TPACK components.
Patahuddin et al. (2016)	Indonesia	Secondary education	Observation Log	TPACK	Studies the TPACK of a mathematics teacher who uses technology in teaching.	Difficulty in replicating the findings, as the instrument implemented is not structured according to TPACK components.
Mailizar and Fan (2020)	Indonesia	Secondary education	TPACK-M	TPACK	Establishes distinctions between hardware, general software, mathematical software, and online tools.	Self-report, perception bias.
Castro-Sierra and Gutierrez-Santiuste (2021)	Spain	Teacher Trainer	Adapted Questionnaire	TPACK	Evaluates the knowledge of university mathematics teachers who integrate technology into teaching using the TPACK model.	Adaptation without robust external validation of the Schmidt et al. (2009) model, from early childhood education to higher education.
Kohen et al. (2023)	Israel	Pre-service and in-service training	Questionnaire + Rubric	TPACK	Pre/post intervention, task evaluation.	Limited sample, specific context.
Nzaramyimana and Umugiraneza (2023)	Rwanda	Secundaria	Questionnaire	TPACK	Analysis of the use, frequency, and perception of ICT by a group of mathematics teachers.	Open-ended questionnaire, which makes it impossible to analyze specialized digital technologies specific to mathematics.
Smith and Zelkowski (2023)	United States	Secondary education	TPACK-US	TPACK	Evaluates the TPACK of secondary mathematics teachers who integrate technology into their pedagogical practices.	The items assessed focus on teachers’ technological skills, without addressing how these skills improve student learning.
Njiku (2024)	Tanzania	Secondary education	Observation Rubric	TPACK	Evaluates the actual practice of teachers integrating digital technologies into teaching, avoiding self-report bias.	Lower comparability with previous studies.
Li and Nugraha (2025)	China	Primary education	Questionnaire	TPACK	Evaluates teachers’ knowledge in integrating DTs for teaching, including items associated with the curriculum.	Self-reporting generates perception bias, with teachers overestimating their skills.

presents a comparison of some of the instruments identified in this review aimed at evaluating the knowledge of teachers who integrate DTs into the teaching of specific mathematics content.

5. Patterns, Categories, and Connections in Teachers’ Knowledge Integrating Digital Technologies (DTs) to Teach Specific Mathematics Content

5.1. Nature of DTs Integration

In most of the analyzed studies, technology was integrated to support the representation and exploration of mathematical concepts through dynamic constructions and visualization. Functions emerged as the mathematical object where teachers most frequently used DTs, such as GeoGebra, to facilitate instruction, as well as to design and plan mathematics tasks related to this topic using technology (Morales-López et al., 2021; Rizo-Cruz, 2022; Sandoval et al., 2023; Padilla-Escorcia et al., 2023; Wati et al., 2018). Other records focused on the construction and demonstration of properties in geometry concepts carried out by teachers through these specialized DTs for the subject area (Kartal & Çınar, 2022; Zambak & Tyminski, 2020).

In a smaller group of studies, the integration of DTs was aimed at transforming the pedagogical practice of both pre-service and in-service mathematics teachers through professional development activities designed to strengthen their technological knowledge. The ultimate goal was to integrate this knowledge pedagogically and didactically into the teaching of subject-specific content, supported by the implementation of instructional sequences grounded in DTs (Açıkgül & Aslaner, 2020; Yildiz & Arpaci, 2024; Saralar-Aras & Turker-Biber, 2024; Aldemir-Engin et al., 2023).

In summary, the use of dynamic visualization tools (GeoGebra/Sketchpad) and data analysis applications (TinkerPlots/spreadsheets) predominates in the teaching of mathematical objects. Planning with DTs is documented more frequently than sustained classroom implementation (with more lesson plans and micro-teaching experiences than follow-up studies), and the assessment of teacher knowledge remains largely based on self-report; rubric-based observation is minimal.

5.2. Educational Levels and Teacher Profiles

Regarding the educational level and profile of mathematics teachers in the studies included in this review, most of the research focused on pre-service and in-service mathematics teachers (Gutiérrez-Fallas & Henriques, 2020; Kartal & Çınar, 2022; Kohen et al., 2023; Morales-López, 2019), with a predominance in lower and upper secondary education. Studies were also found at the primary and university levels, though less frequently. In pre-service contexts, notable activities included task design courses/workshops and micro-teaching sessions; in in-service contexts, short- and medium-term professional development programs predominated. In addition, specific experiences in inclusive education were identified, involving tactile/Braille resources combined with dynamic mathematics software (Van Leendert et al., 2021).

5.3. Theorical Frameworks and Instruments

TPACK predominates as the theoretical foundation in studies related to teacher training, lesson planning, and the design of mathematics tasks integrating digital technologies (Yildiz & Arpaci, 2024; Saralar-Aras & Turker-Biber, 2024). In MTSK-based studies, the focus is mainly on disciplinary and pedagogical content knowledge, with less explicit attention to the technological component (Seguí & Alsina, 2023; Meléndez-Cruz et al., 2023). Hybrid proposals (e.g., replacing TCK with MKT) aim for greater mathematical specificity; however, these are scarce among the records gathered in this systematic literature review.

Regarding the instruments used to assess teachers’ knowledge in integrating digital technologies into the teaching of specific mathematical content, self-report tools (adapted TPACK questionnaires) are the most common (Mailizar & Fan, 2020; Smith & Zelkowski, 2023; Castro-Sierra & Gutierrez-Santiuste, 2021), while competency-based observation approaches (observation rubrics) are emerging as a means to contrast teachers’ self-reported knowledge with their actual classroom practices (Njiku, 2024; Patahuddin et al., 2016).

6. Discussion

This section discusses the main findings of the review in relation to previous studies and identifies conceptual and methodological gaps in the literature.

This systematic review broadened the perspective on mathematics teachers’ knowledge in the use of digital technologies (DTs) for teaching. Unlike previous studies, which relied almost exclusively on the TPACK framework, this work incorporated the Mathematics Teacher’s Specialized Knowledge (MTSK) model, enabling a more detailed analysis of the disciplinary and pedagogical dimensions of teacher knowledge required for teaching mathematics with digital tools. While TPACK (Mishra & Koehler, 2006) provides a broad description of the relationship between pedagogy, content, and technology, MTSK is specific to mathematics education and allows for a more precise characterization of knowledge in this domain.

Previous reviews, such as those by Rivera-Robles et al. (2021), Noor-Kholid et al. (2023), Li et al. (2024), and Kadluba et al. (2025), focused mainly on TPACK, emphasizing self-reports and general perspectives while placing less attention on mathematics-specific practices. However, their emphases varied: Rivera-Robles et al. (2021) addressed only TPACK-based studies, Noor-Kholid et al. (2023) explored its development in practice, and Li et al. (2024) and Kadluba et al. (2025) expanded the scope to methodological aspects and evaluation instruments.

Our analysis shows that, although MTSK has been applied less frequently, only 12 of the reviewed articles used it explicitly and just 5 examined the technological domain in depth its integration reveals an underexplored potential to connect disciplinary precision with the explicit use of digital technologies. At the same time, the predominance of TPACK, present in 35 studies, demonstrates its continued relevance, especially in teacher education programs, task design, and knowledge assessment. However, studies such as those by Zambak and Tyminski (2020) and Morales-García et al. (2022) show that TPACK alone is insufficient to capture the complexity of teachers’ knowledge when integrating technology for the teaching of specific mathematical content, reinforcing the need for hybrid approaches that combine the strengths of both frameworks. In this review, digital technologies are understood broadly, encompassing both mathematics-specific software (e.g., GeoGebra, Geometer’s Sketchpad) and general-purpose digital tools (e.g., spreadsheets, simulators). This inclusive focus allows capturing how teachers integrate digital resources to enhance mathematical reasoning, representation, and task design.

A central finding is the strong reliance on self-reports, which capture beliefs, confidence, or perceived knowledge, but rarely document classroom orchestration or real-time decision-making. With the exception of Njiku (2024), who proposed an observation rubric to assess TPACK in pedagogical practice, most studies fail to connect what teachers claim to know with what they actually implement in their classrooms. This gap underscores the urgency of developing validated, performance-based instruments that allow for the triangulation of knowledge claims with classroom evidence.

The geographical distribution of the corpus also shows important trends. Countries such as Turkey, the United States, Spain, and Mexico account for around 60% of the reviewed works, reflecting a concentration of research in certain contexts and leaving other regions underrepresented. This imbalance highlights the need to expand studies to emerging economies, where factors such as infrastructure, teacher education, and access to digital resources may shape the development of professional knowledge in different ways.

In summary, this review shows that, although TPACK dominates the literature, it lacks the disciplinary depth provided by MTSK. The combined analysis of both frameworks reveals that hybrid approaches offer a more robust and comprehensive understanding of mathematics teachers’ knowledge with DTs. Likewise, the scarcity of validated observation instruments constitutes a key gap in the literature, which this review makes explicit and identifies as a critical line for future research. The implications extend to teacher education—where micro-teaching, task design, and validated rubrics could help bridge the gap between what teachers declare and what they actually do to research, which should advance the validation of mathematics-specific technological indicators, and to educational policy, where prioritizing infrastructure and professional development in underrepresented regions is essential to ensure an equitable and effective integration of digital technologies in mathematics teaching.

Our contribution lies in specifying the areas where mathematics teachers’ knowledge in integrating digital technologies remains underdefined, showing how MTSK-informed descriptors can enrich TPACK-based measures, and proposing a hybrid instrumentation agenda for classroom assessment. Beyond synthesizing existing evidence, this review provides a conceptual and methodological foundation for future research seeking to operationalize mathematics-specific technological knowledge. It also offers practical guidance for teacher education programs aiming to bridge the gap between declared and enacted knowledge in technology-mediated mathematics instruction.

7. Conclusions

Over the past five years, research on mathematics teachers’ knowledge in using digital technologies (DTs) for teaching has remained concentrated in a small group of countries, while many others both developed and developing show little or no presence in this area. The absence of studies in contexts such as Peru or Rwanda, among others, may reflect differences in research priorities, visibility of local publications, or access to technological and academic resources rather than economic status alone. Nevertheless, regardless of context, there is a notable similarity in the topics addressed, which include: the formulation of indicators of teacher knowledge for integrating DTs into teaching, teacher training, the use of DTs in mathematics instruction, the design of tasks and learning units through DTs, and the assessment of teachers’ technological pedagogical content knowledge (TPACK).

In the review of the 50 records included, no significant differences were found regarding the study samples. The studies encompassed mathematics teachers across different educational levels: primary, secondary, higher education, and pre-service training. In particular, in the field of teacher education aimed at improving TPACK, Açıkgül and Aslaner (2020) focused on in-service teachers, whereas Saralar-Aras and Turker-Biber (2024) targeted pre-service teachers.

Another relevant finding was the limited number of studies employing a qualitative approach to analyze teachers’ knowledge regarding using DTs for teaching through non-participant observation units or audio and video recordings. Most studies relied on self-reports as a strategy to categorize what teachers claim to know about teaching mathematics. However, this methodology has been questioned in the literature due to the potential overestimation of self-reported knowledge.

Mathematics teachers’ knowledge with DTs is framed by TPACK (technology–pedagogy–content) and sharpened by MTSK (disciplinary and pedagogical subdomains). The DTs considered (e.g., GeoGebra, Tinkerplots, Sketchpad) afford dynamic representation, simulation, modeling, and data analysis. Accordingly, key teacher skills include linking mathematical objects to technological representations, orchestrating tools to meet content goals, designing investigable tasks, and interpreting evidence generated through DT interactions. Most studies rely on self-reports; validated classroom rubrics for mathematics-specific indicators remain limited an actionable avenue for future work.

In conclusion, this review reveals that mathematics teachers’ knowledge with digital technologies emerges through complementary lenses. TPACK illuminates how technological, pedagogical, and content domains interact in practice, while MTSK brings disciplinary precision to the foreground. Our synthesis shows that combining both perspectives is necessary to capture how teachers actually mobilize knowledge when integrating digital technologies. By articulating these frameworks, this review not only consolidates what is known but also points to a conceptual pathway for future studies.

8. Limitations and Future Directions

One of the limitations of this review lies in the search strategy employed, as it was restricted to the databases Scopus, WOS, ERIC, and Scielo. Future research could expand the scope to include other databases such as ScienceDirect, SAGE, ProQuest, Springer, and Taylor & Francis, as well as regional repositories like Latindex, Redalyc, and Dialnet.

Moreover, this review focused exclusively on studies published as scientific journal articles. For future reviews, it would be beneficial to include a broader range of sources in other languages, such as Portuguese, and to give greater consideration to short conference papers, books, book chapters, editorials, theses, and dissertations, given that a high percentage of the records analyzed corresponded to research articles. Such inclusion would allow for a more comprehensive exploration of mathematics teachers’ technological pedagogical content knowledge (TPACK) when integrating digital technologies into mathematics teaching.