Theoretical Foundation and Validation of the Record of Decision-Making (RODM)
Abstract
1. Introduction
1.1. Theoretical Frame
1.1.1. Overlapping Wave Theory
1.1.2. Visual Perceptual Demands of Beginning Reading
1.1.3. Observed Strategies in Use
The prolegomenous study of pancreatic enzymes revealed that trypsinogen plays a key role in digestion, its activation sparking a cascade of chemical reactions. Yet, the path to understanding its behavior was anything but straightforward, marked by the anfractuosity of cellular structures and the intricacies of interfascicular signaling within tissues.
1.2. Administering and Interpreting the RODM
1.2.1. RODM Backup Strategies
Using Phonic Elements (Sub-Word Parts) as a Backup Strategy
Using Rereading as a Backup Strategy
Text: Jack and Jill went up the hillExample 1 (rereading a line): “Jack and Jill went up the hill, Jack and Jill went up the hill.”Example 2 (rereading multiple words): “Jack and Jill, Jack and Jill”Example 3 (rereading a single word): “Jack, Jack,”Example 4 (rereading a subword part): “ Ja- Ja-,
1.2.2. Other Oral Reading Behaviors Included
Outcomes of Applying Backup Strategies: Unsuccessful or Successful Outcomes
Text: Jerry was the fastest runner in the whole school.Student: “Jerry was the fastest runner in the /wuh/, /wuh/. Jerry was the fastest runner in the, in the wole school.”
Correcting an Error: Successful Use of Backup Strategies
Text: Jerry was the fastest runner in the whole school.Student: “Jerry was the fastest runner in the /wuh/, /wuh/. Jerry was the fastest runner in the, in the wole school. In the whole school.”
1.2.3. Observed Reading Behaviors Excluded from Analysis
1.3. Theory-Driven Validation Analysis
2. Materials and Methods
2.1. Data Sources
2.2. Scoring the Oral Reading Records
2.3. Data Analysis
3. Results
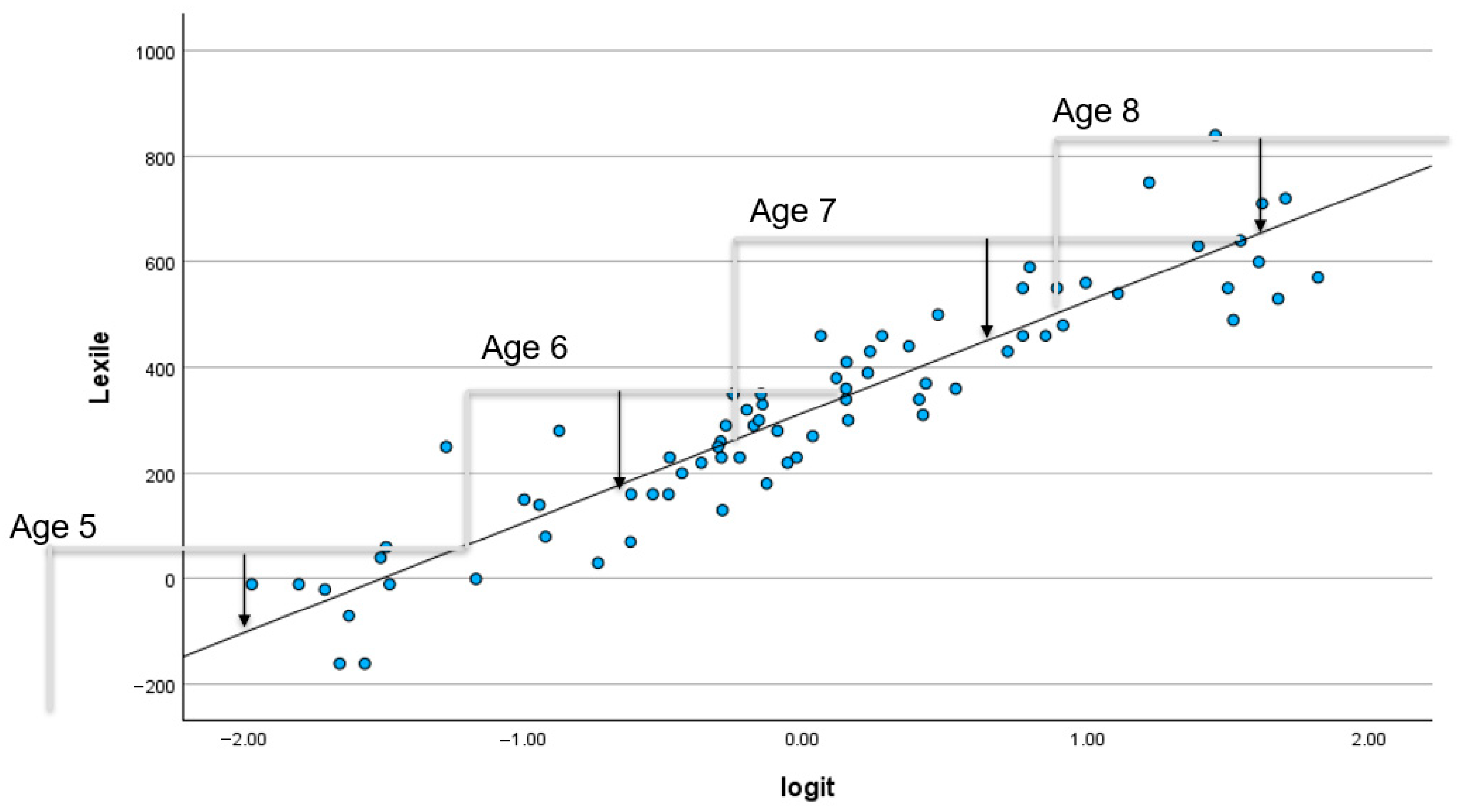
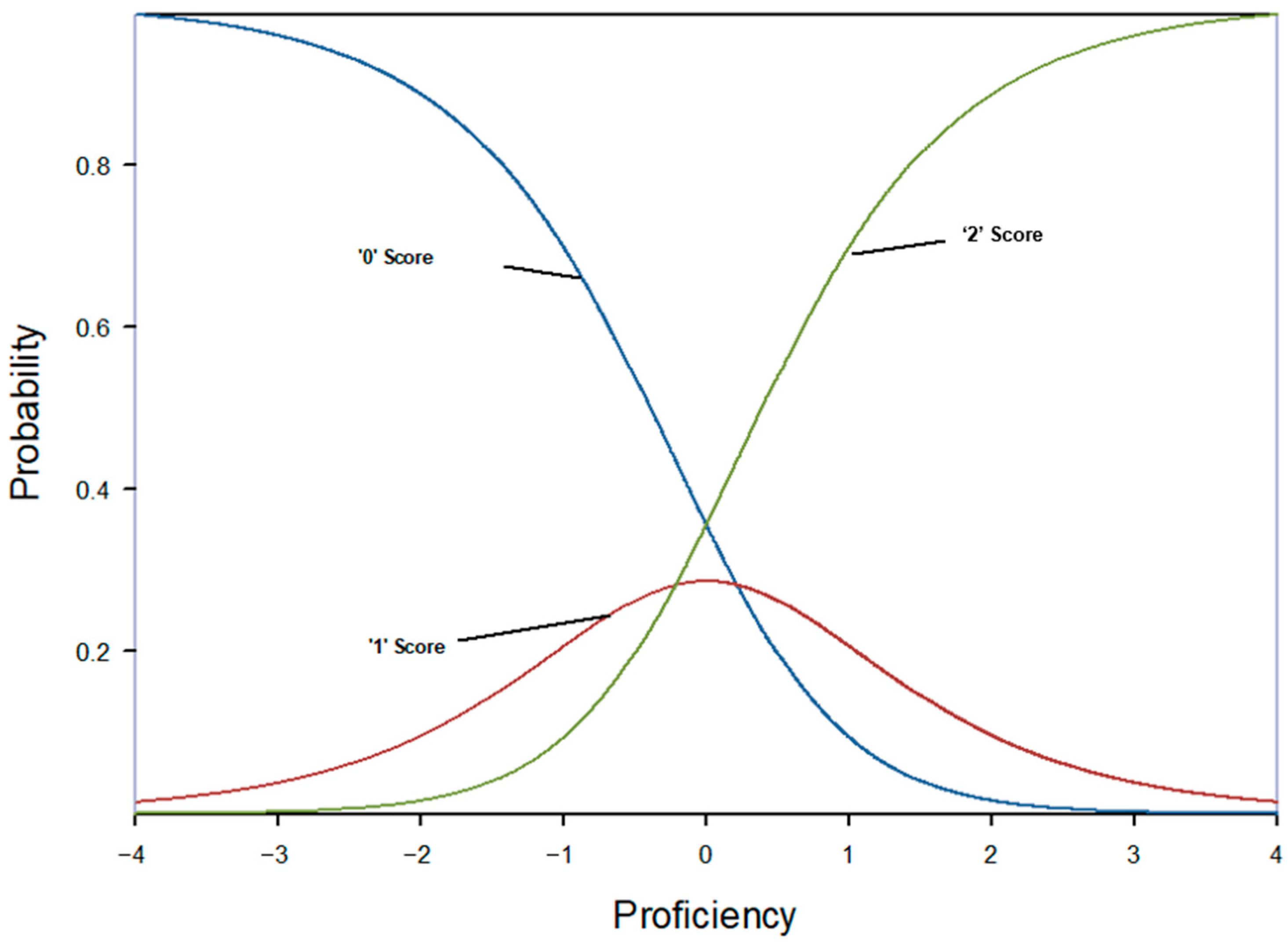
3.1. Identifying the Optimal Response Scale
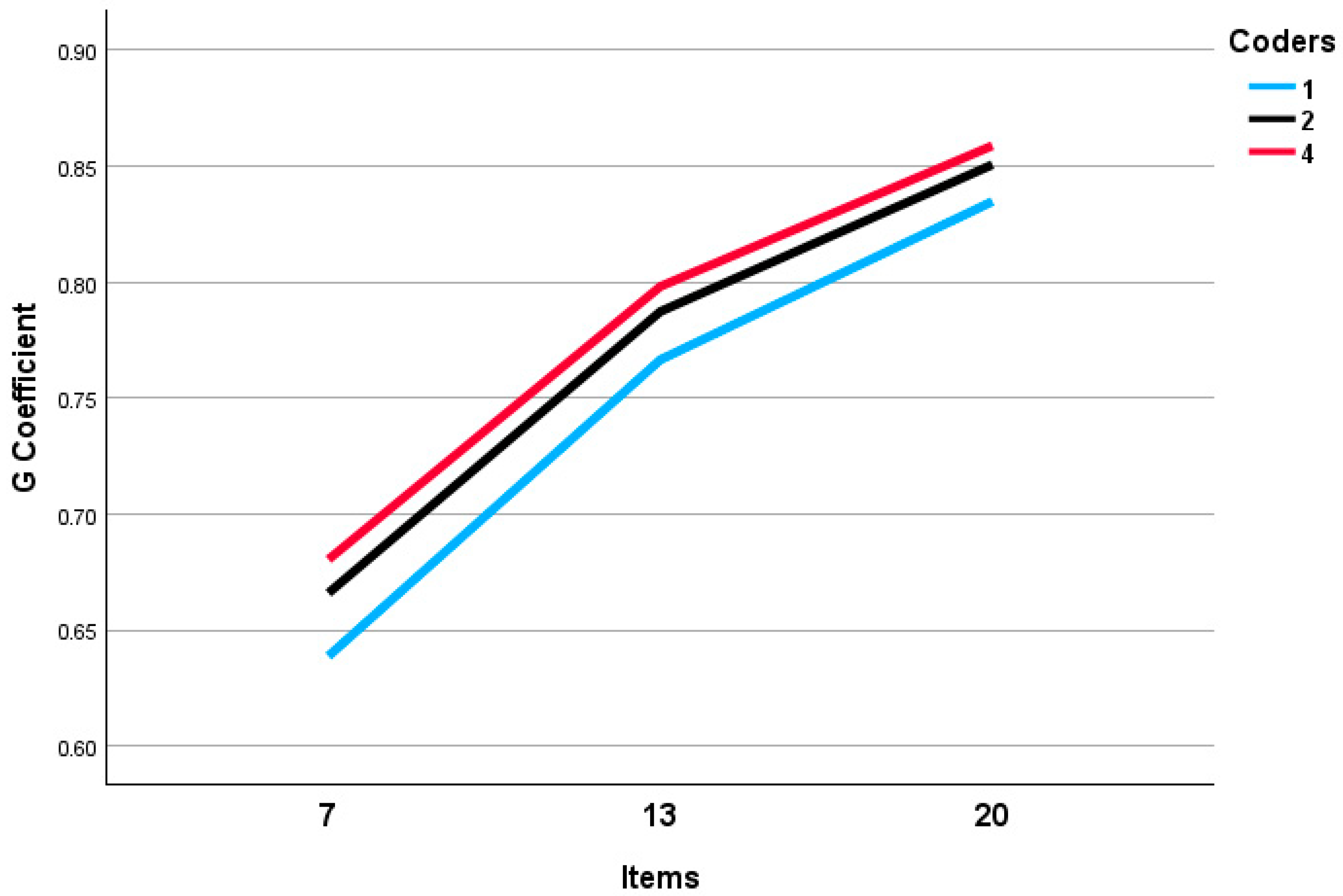
3.2. Interrater Reliability and Accuracy
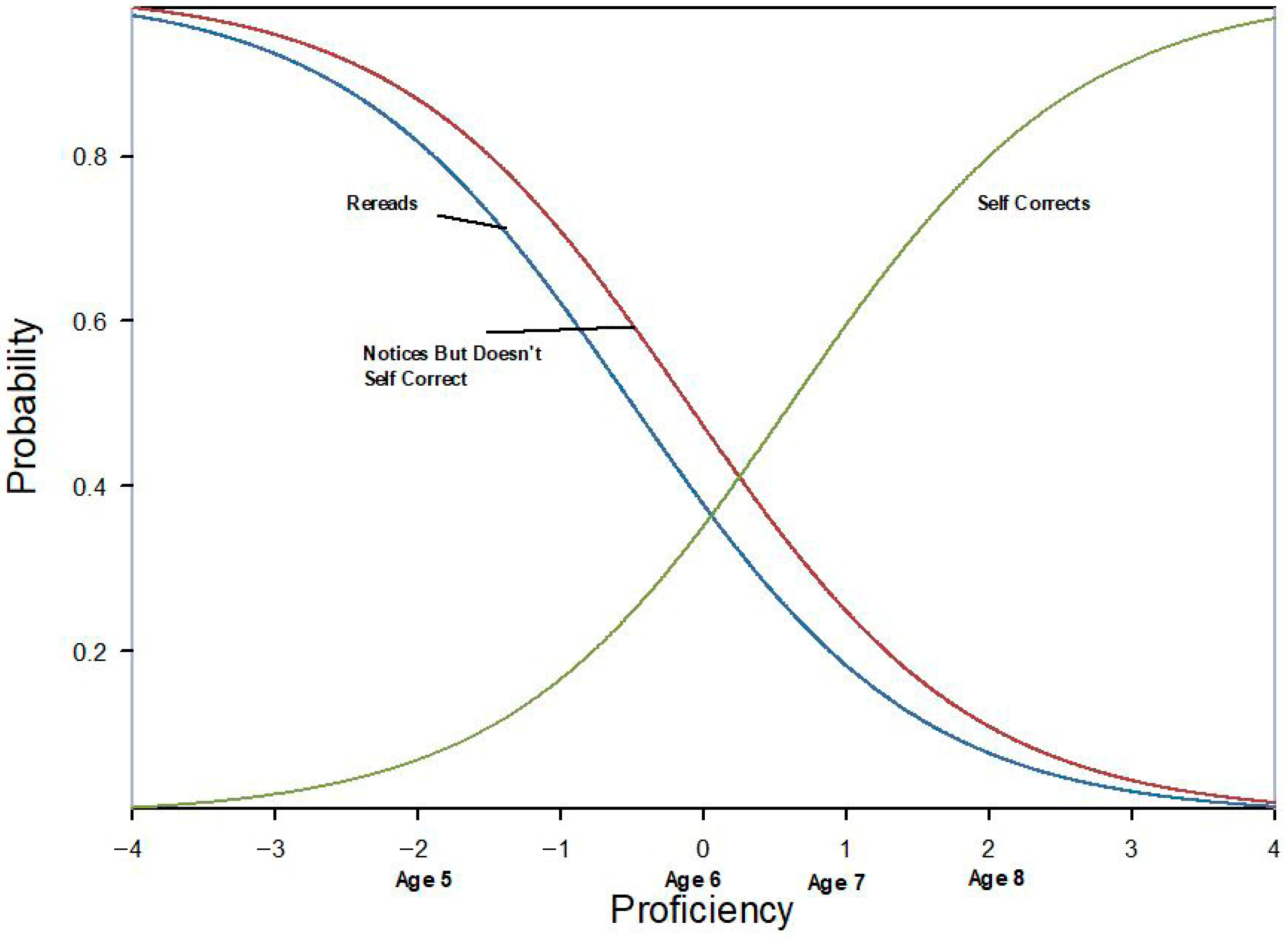
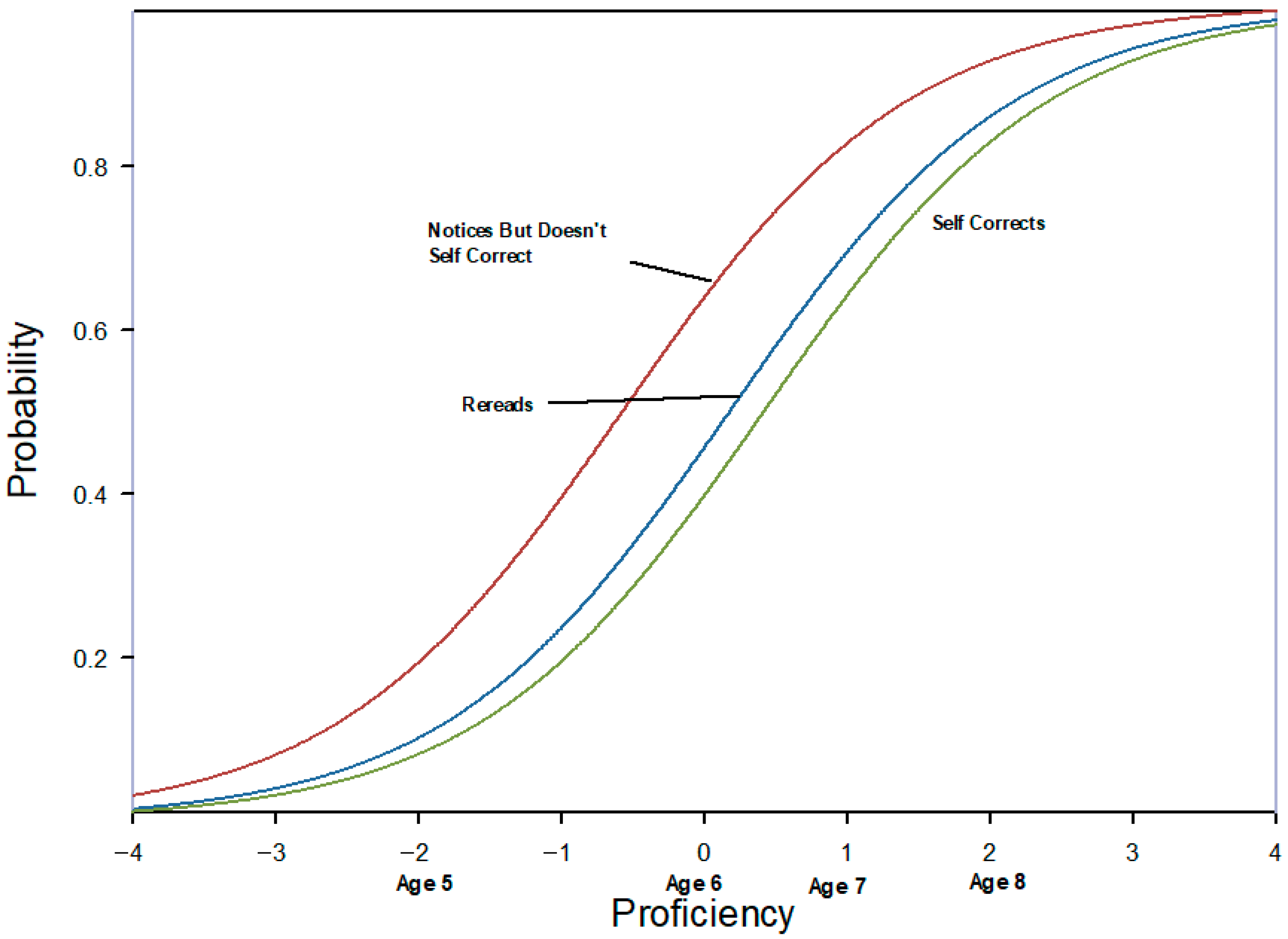
3.3. Testing Assumptions 1 and 2
3.4. Testing Assumption 3
3.5. Testing Assumptions 4 and 5
4. Discussion
4.1. Summary of Findings
4.2. Practical Implications
4.3. Future Considerations Based on the Findings
4.3.1. Response Scale Findings
4.3.2. Including Medial-Final and Medial Items
4.3.3. Adding More Items to Increase Reliability
Coding Multiple Attempts
Analogies
Appealing for Help
Meaning and Structure Cues
4.4. Next Steps
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Adams, M. A. (1990). Beginning to read: Thinking and learning about print. MIT Press. [Google Scholar]
- Adams, M. A. (2004). Modeling the connections between word recognition and reading. In R. B. Ruddell, & N. Unrau (Eds.), Theoretical models of reading (pp. 1219–1243). International Reading Association. [Google Scholar]
- Coombs, C. H. (1964). A theory of data. Wiley. [Google Scholar]
- Cunningham, A. E., Perry, K. E., & Stanovich, K. E. (2001). Converging evidence for the concept of orthographic processing. Reading and Writing, 14(5), 549–568. [Google Scholar] [CrossRef]
- D’Agostino, J. V., & Briggs, C. (2025). Validation analysis during the design stage of text leveling. Education Sciences, 15(5), 607. [Google Scholar] [CrossRef]
- D’Agostino, J. V., Kelly, R. H., & Rodgers, E. (2019). Self-corrections and the reading progress of strugglingbeginning readers. Reading Psychology, 40(6), 525–550. [Google Scholar] [CrossRef]
- Davis, B. J., & Evans, M. A. (2021). Children’s self-reported strategies in emergent reading of an alphabet book. Scientific Studies of Reading, 25(1), 31–46. [Google Scholar] [CrossRef]
- Ehri, L. C. (1975). Word consciousness in readers and prereaders. Journal of Educational Psychology, 67(2), 204–212. [Google Scholar] [CrossRef]
- Ehri, L. C. (1998). Grapheme-phoneme knowledge is essential for learning to read words in English. In J. L. Metsala, & L. Ehri (Eds.), Word recognition in beginning literacy (pp. 41–63). Routledge. [Google Scholar]
- Ehri, L. C. (2005). Learning to read words: Theory, findings, and issues. Scientific Studies of Reading, 9(2), 167–188. [Google Scholar] [CrossRef]
- Ehri, L. C. (2022). What teachers need to know and do to teach letter–sounds, phonemic awareness, word reading, and phonics. The Reading Teacher, 76(1), 53–61. [Google Scholar] [CrossRef]
- Fagan, W. T., & Eagan, R. L. (1986). Cues used by two groups of remedial readers in identifying words in isolation. Journal of Research in Reading, 9(1), 56–68. [Google Scholar] [CrossRef]
- Farrington-Flint, L., & Wood, C. (2007). The role of lexical analogies in beginning reading: Insights from children’s self-reports. Journal of Educational Psychology, 99(2), 326–338. [Google Scholar] [CrossRef]
- Gaskins, I. W. (2010). Interventions to develop decoding proficiencies. In A. McGill-Franzen, & R. Allington (Eds.), Handbook of reading disability research (pp. 289–306). Routledge. [Google Scholar]
- Gibson, E. J., & Levin, H. (1975). The psychology of reading. MIT Press. [Google Scholar]
- Goswami, U. (1988). Orthographic analogies and reading development. The Quarterly Journal of Experimental Psychology, 40(2), 239–268. [Google Scholar] [CrossRef]
- Goswami, U. (2013). The role of analogies in the development of word recognition. In J. L. Metsala, & L. Ehri (Eds.), Word recognition in beginning literacy (pp. 41–63). Routledge. [Google Scholar]
- Harmey, S., D’Agostino, J., & Rodgers, E. (2019). Developing an observational rubric of writing: Preliminary reliability and validity evidence. Journal of Early Childhood Literacy, 19(3), 316–348. [Google Scholar] [CrossRef]
- Johnson, T., Rodgers, E., & D’Agostino, J. V. (2024). Learning to read: Variability, continuous change and adaptability in children’s use of word solving strategies. Reading Psychology, 45(2), 105–142. [Google Scholar] [CrossRef]
- Kaye, E. L. (2006). Second graders’ reading behaviors: A study of variety, complexity, and change. Literacy Teaching and Learning, 10(2), 51–75. [Google Scholar]
- Kuhfeld, M., Lewis, K., & Peltier, T. (2023). Reading achievement declines during the COVID19 pandemic: Evidence from 5 million US students in grades 3–8. Reading and Writing, 36(2), 245–261. [Google Scholar] [CrossRef]
- Linacre, J. M. (2021). FACETS (Many-Facet Rasch measurement) software (Version 3.83.6). [Computer software]. FACETS.
- Lindberg, S., Lonnemann, J., Linkersdörfer, J., Biermeyer, E., Mähler, C., Hasselhorn, M., & Lehmann, M. (2011). Early strategies of elementary school children’s single word reading. Journal of Neurolinguistics, 24(5), 556–570. [Google Scholar] [CrossRef]
- Lupker, S. J., Acha, J., Davis, C. J., & Perea, M. (2012). An investigation of the role of grapheme units in word recognition. Journal of Experimental Psychology: Human Perception and Performance, 38(6), 1491. [Google Scholar] [CrossRef]
- Marchbanks, G., & Levin, H. (1965). Cues by which children recognize words. Journal of Educational Psychology, 56(2), 57. [Google Scholar] [CrossRef]
- Messick, S. (1995). Validity of psychological assessment: Validation of inferences from persons’ responses and performances as scientific inquiry into score meaning. American psychologist, 50(9), 741. [Google Scholar] [CrossRef]
- MetaMetrics. (2024). Lexile grade level charts. Available online: https://hub.lexile.com/account-membership/ (accessed on 22 July 2025).
- Microsoft CoPilot. (2025). Prompt: “Use these words in a passage: Trypsinogen, anfractuosity, prolegomenous, and interfascicular”. Available online: https://copilot.microsoft.com/ (accessed on 25 June 2025).
- Miles, K. P., & Ehri, L. C. (2019). Orthographic mapping facilitates sight word memory and vocabulary learning. In D. Kilpatrick, R. Joshi, & R. Wagner (Eds.), Reading development and difficulties. Springer. [Google Scholar] [CrossRef]
- Mushquash, C., & O’Connor, B. P. (2006). SPSS and SAS programs for generalizability theory analyses. Behavior Research Methods, 38(3), 542–547. [Google Scholar] [CrossRef]
- National Assessment of Educational Progress. (2024). 2024 NAEP reading assessment. Available online: https://www.nationsreportcard.gov/reports/reading/2024/g4_8/?grade=4 (accessed on 22 July 2025).
- Roberts, J. S., Laughlin, J. E., & Wedell, D. H. (1999). Validity issues in the Likert and Thurstone approaches to attitude measurement. Educational and Psychological Measurement, 59(2), 211–233. [Google Scholar] [CrossRef]
- Rodgers, E., D’Agostino, J. V., Berenbon, R., Johnson, T., & Winkler, C. (2023). Scoring Running Records: Complexities and affordances. Journal of Early Childhood Literacy, 23(4), 665–694. [Google Scholar] [CrossRef]
- Rodgers, E., D’Agostino, J. V., Kelly, R. H., & Mikita, C. (2018). Oral reading accuracy: Findings and implications from recent research. The Reading Teacher, 72(2), 149–157. [Google Scholar] [CrossRef]
- Rumelhart, D. E. (2004). Toward an interactive model of reading. In R. B. Ruddell, & N. Unrau (Eds.), Theoretical models of reading (pp. 1149–1179). International Reading Association. [Google Scholar]
- Savage, R., & Stuart, M. (2006). A developmental model of reading acquisition based upon early scaffolding errors and subsequent vowel inferences. Educational Psychology, 26(1), 33–53. [Google Scholar] [CrossRef]
- Savage, R., Stuart, M., & Hill, V. (2001). The role of scaffolding errors in reading development: Evidence from a longitudinal and a correlational study. British Journal of Educational Psychology, 71(1), 1–13. [Google Scholar] [CrossRef]
- Seidenberg, M. S., Cooper Borkenhagen, M., & Kearns, D. M. (2020). Lost in translation? Challenges in connecting reading science and educational practice. Reading Research Quarterly, 55, S119–S130. [Google Scholar] [CrossRef]
- Seidenberg, M. S., & McClelland, J. L. (1989). A distributed, developmental model of word recognition and naming. Psychological Review, 96(4), 523. [Google Scholar] [CrossRef]
- Shanahan, T. (2019). Why children should be taught to read with more challenging texts. Perspectives on Language and Literacy, 45(4), 17–19. [Google Scholar]
- Sharp, A. C., Sinatra, G. M., & Reynolds, R. E. (2008). The development of children’s orthographic knowledge: A microgenetic perspective. Reading Research Quarterly, 43, 206–226. [Google Scholar] [CrossRef]
- Siegler, R. S. (1984). Strategy choice in addition and subtraction: How do children know what to do. Origins of Cognitive Skills, 229–294. [Google Scholar]
- Siegler, R. S. (1995). How does change occur: A microgenetic study of number conservation. Cognitive Psychology, 28(3), 225–273. [Google Scholar] [CrossRef] [PubMed]
- Siegler, R. S. (1996). Emerging minds: The process of change in children’s thinking. Oxford University Press. [Google Scholar]
- Siegler, R. S. (2005). Children’s learning. American Psychologist, 60(8), 769. [Google Scholar] [CrossRef]
- Siegler, R. S. (2016). Continuity and change in the field of cognitive development and in the perspectives of one cognitive developmentalist. Child Development Perspectives, 10(2), 128–133. [Google Scholar] [CrossRef]
- Siegler, R. S., & Robinson, M. (1982). The development of numerical understandings. In H. W. Reese, & L. P. Lipsitt (Eds.), Advances in child development and behavior (Vol. 16, pp. 242–312). Academic Press. [Google Scholar]
- Stanovich, K. E. (1980). Toward an interactive-compensatory model of individual differences in the development of reading fluency. Reading Research Quarterly, 16, 32–71. [Google Scholar] [CrossRef]
- Stanovich, K. E. (2004). Mattew effects in reading: Some consequences of individual differences in the acquisition of literacy. In R. B. Ruddell, & N. Unrau (Eds.), Theoretical models of reading (pp. 454–516). International Reading Association. [Google Scholar]
- Stanovich, K. E., & West, R. F. (1989). Exposure to print and orthographic processing. Reading Research Quarterly, 24, 402–433. [Google Scholar] [CrossRef]
- Stanovich, K. E., West, R. F., & Cunningham, A. E. (2013). Beyond phonological processes: Print exposure and orthographic processing. In S. A. Brade, & D. P. Shankweiler (Eds.), Phonological processes in literacy (pp. 219–236). Routledge. [Google Scholar]
- Steffler, D. J., Varnhagen, C. K., Friesen, C. K., & Treiman, R. (1998). There’s more to children’s spelling than the errors they make: Strategic and automatic processes for one-syllable words. Journal of educational psychology, 90(3), 492. [Google Scholar] [CrossRef]
- Thurstone, L. L. (1927). A law of comparative judgment. Psychological Review, 34, 273–286. [Google Scholar] [CrossRef]
- United States Department of Education. (1995). Listening to children read aloud (Vol. 22). National Center for Education Statistics. [Google Scholar]
- Vellutino, F. R., & Scanlon, D. M. (2002). The interactive strategies approach to reading intervention. Contemporary Educational Psychology, 27(4), 573–635. [Google Scholar] [CrossRef]
- Wood, H., & Wood, D. (1999). Help seeking, learning and contingent tutoring. Computers & Education, 33(2–3), 153–169. [Google Scholar] [CrossRef]
- Yan, Z., & Chiu, M. M. (2023). The relationship between formative assessment and reading achievement: A multilevel analysis of students in 19 countries/regions. British Educational Research Journal, 49(1), 186–208. [Google Scholar] [CrossRef]
- Yao, Y., Amos, M., Snider, K., & Brown, T. (2024). The impact of formative assessment on K-12 learning: A meta-analysis. Educational Research and Evaluation, 29(7–8), 452–475. [Google Scholar] [CrossRef]




| Element | Average Agreement |
|---|---|
| Reread | 100% |
| Notices But Does Not SC | 92% |
| No IMF | 98% |
| Initial | 94% |
| Initial Medial | 94% |
| Initial Final | 75% |
| IMF | 86% |
| Final | 77% |
| Blends Digraphs | 90% |
| Rimes | 65% |
| SC Ratio | 96% |
| Total | 88% |
| Element | Measure | SE | Infit MNSQ | Outfit MNSQ |
|---|---|---|---|---|
| Medial | 2.56 | 0.13 | 0.85 | 1.12 |
| Final | 1.08 | 0.08 | 1.04 | 1.13 |
| Medial Final | 0.96 | 0.08 | 1.01 | 1.04 |
| Initial Final | −0.09 | 0.07 | 1.24 | 1.32 |
| IMF | −0.40 | 0.07 | 1.23 | 1.35 |
| Initial | −0.60 | 0.07 | 1.34 | 1.56 |
| Rimes | −0.71 | 0.08 | 1.22 | 1.32 |
| Initial Medial | −0.89 | 0.08 | 1.29 | 1.51 |
| No IMF | −0.89 | 0.08 | 1.32 | 1.54 |
| Blends Digraphs | −1.01 | 0.09 | 1.25 | 1.44 |
| Element | Measure | SE | Infit MNSQ | Outfit MNSQ | Infit MNSQ Reversed | Outfit MNSQ Reversed |
|---|---|---|---|---|---|---|
| Medial | 2.67 | 0.17 | 0.53 | 0.54 | ||
| Final | 1.26 | 0.11 | 0.78 | 0.78 | ||
| Medial Final | 0.86 | 0.11 | 0.92 | 0.93 | ||
| Initial Final | −0.06 | 0.11 | 1.40 | 1.55 | ||
| Initial | −0.39 | 0.11 | 1.60 | 1.86 | 1.25 | 1.26 |
| IMF | −0.47 | 0.12 | 1.59 | 1.83 | 1.43 | 1.50 |
| No IMF | −0.87 | 0.13 | 1.78 | 2.11 | 1.19 | 1.22 |
| Rimes | −0.87 | 0.13 | 1.74 | 1.90 | 1.34 | 1.45 |
| Initial Medial | −0.89 | 0.13 | 1.82 | 2.12 | 1.21 | 1.26 |
| Blends Digraphs | −1.24 | 0.18 | 1.98 | 2.42 | 1.21 | 1.24 |
| Element | Measure | SE | Infit MNSQ | Outfit MNSQ |
|---|---|---|---|---|
| SC Ratio | 0.61 | 0.05 | 1.27 | 1.33 |
| Notices But Does Not SC (reversed) | −0.11 | 0.05 | 0.87 | 0.85 |
| Reread (reversed) | −0.50 | 0.05 | 1.21 | 1.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodgers, E.M.; D’Agostino, J.V. Theoretical Foundation and Validation of the Record of Decision-Making (RODM). Educ. Sci. 2025, 15, 1483. https://doi.org/10.3390/educsci15111483
Rodgers EM, D’Agostino JV. Theoretical Foundation and Validation of the Record of Decision-Making (RODM). Education Sciences. 2025; 15(11):1483. https://doi.org/10.3390/educsci15111483
Chicago/Turabian StyleRodgers, Emily M., and Jerome V. D’Agostino. 2025. "Theoretical Foundation and Validation of the Record of Decision-Making (RODM)" Education Sciences 15, no. 11: 1483. https://doi.org/10.3390/educsci15111483
APA StyleRodgers, E. M., & D’Agostino, J. V. (2025). Theoretical Foundation and Validation of the Record of Decision-Making (RODM). Education Sciences, 15(11), 1483. https://doi.org/10.3390/educsci15111483






