Teaching and Learning Trochoid Curves: The Importance of LEGO^® Drawing Robots and Educational Robotics in Tertiary Mathematics Education

Abstract

An innovative, STEAM-based educational approach uses LEGO^® robots to improve the visualisation and understanding of trochoid curves in tertiary mathematics education. The method involves a two-step process: first, the curves are drawn based on the classical definition of trochoids using a custom-designed LEGO^® robot that employs LED light to trace the shapes. Then, the same process is replicated with a marker, with the robot controlling the movement of the drawing head to reproduce the curves accurately. To deepen students’ comprehension and visualisation, Desmos dynamic geometry software was used in parallel to draw all three types of trochoids (prolate, curtate, and cusped). This hands-on technique aims to make these motion curves more tangible and engaging within a classroom setting. A quantitative experiment involving 94 first-year IT BSc students was conducted during the spring semester of the 2024/2025 academic year using a quasi-experimental design. We had one control group and two experimental groups. One of the experimental groups did not use educational robotics; participants could only see how the robots worked via video. The other experimental group gained first-hand experience by building and testing LEGO^® drawing robots. The aim was to evaluate the effectiveness of an innovative teaching method that used educational robotics to improve understanding of the mathematical properties of trochoids, compared to traditional teaching methods and presentations containing short videos. The Mann–Whitney U test was used in all cases during hypothesis testing. Only watching videos of drawing robots does not have a statistically significant effect on learning outcomes. In this case, the effect size was only 0.12. However, the results of the group performing educational robotics activities showed a statistically significant difference compared to the other two groups, with large effect sizes (0.68 and 0.7). Our results suggest that visualisation using LEGO^® robots significantly improves students’ knowledge of parametric curves. Educational robotics offers promising opportunities because it is an attractive and interactive teaching tool. Its great advantage is that it combines abstract mathematical concepts with modern technology, thus creating an effective learning environment.

1. Introduction

Trochoid curves are generated by rolling a circle along a straight line (Morley, 1894). Trochoids are a group of curves including three primary types: the cycloid, which is created by a point on a circle as the circle rolls; the curtate cycloid, which occurs when the point is inside the circle; and the prolate cycloid, which is created by a point outside the circle. All these curves are formed due to the same basic process: a circle rolls along a line without slipping. However, their specific shape varies depending on the position of the tracking point relative to the centre of the circle (Johnston, 2019).

By the late 17th century, mathematicians had thoroughly explored and documented all the fundamental properties, geometrical characteristics, and mathematical complexities of trochoid curves (Yates, 1974). These investigations included understanding the unique properties of the cycloid, such as its tautochrone and brachistochrone characteristics, which demonstrated the importance of the curve in problems related to the fastest descent and the timing of pendulums (Kimball, 1955). Pioneers like Christiaan Huygens and Jacob Bernoulli made groundbreaking contributions by analysing the nature of the cycloid as the solution to classical problems in calculus and physics (Blåsjö, 2023). Their work laid the foundation for further developments in differential geometry and the calculus of variations, making the cycloid one of the most studied and celebrated curves in the history of mathematics. Although their basic properties have already been mapped out, cycloids continue to excite the imagination of mathematicians and educators, and serve as a rich example for teaching fundamental concepts in mathematics and physics (Dhombres, 2024; Johnston, 2019).

For more than two centuries, these fascinating curves have been a vital component of higher education curricula in geometry and mathematical analysis, particularly in the study of plane curves. Although they have rich historical roots, cycloids remain a relevant and engaging topic for modern teaching approaches, which can benefit significantly from innovative pedagogical methods (Kabaca, 2013; Körei & Szilágyi, 2024b). In the slow but steady development of higher education, new teaching techniques must be introduced alongside traditional lectures (Alenezi et al., 2023). From a pedagogical point of view, it is important to use various teaching methods, which is also emphasised by constructivist learning theories (Zajda, 2021). Therefore, teachers should use modern and innovative teaching strategies that are tailored to the individual needs of students.

A well-structured STEAM framework that integrates mathematics, engineering, arts, and technology into the teaching and learning process can significantly promote the development of interdisciplinary connections and provide a solid foundation for effective knowledge transfer (Belbase et al., 2022; Leavy et al., 2023). Hands-on approaches capture students’ attention and stimulate interest, making abstract mathematical concepts more tangible (Gnawali, 2025; Lee et al., 2024). Rapid advances in educational robotics in recent years have expanded the possibilities of interactive and hands-on learning experiences (Ryalat et al., 2025). Many universities now have access to various robotic kits that can serve as powerful didactic tools. Integrating robotics into mathematics education has numerous benefits (Torres & Inga, 2025). for example, it enables creative, student-centred teaching approaches that resonate with contemporary learning preferences. It encourages active participation and experimentation, which are important for developing a comprehensive understanding of complex mathematical phenomena.

The systematic review of Samuel et al. (2025) revealed that the United States led in integrating educational robotics into mathematics education. LEGO^® robots were the most frequently used type of robot, with programming, building, and coding as the primary methods of integration. Most of the studies focused on applied mathematics topics. Constructivist learning theory was the most prevalent framework, and a qualitative methodology was commonly employed. The participants mainly consisted of primary and early secondary school students. Regarding research focus, emotional or affective factors were the most frequently examined, often yielding positive outcomes. The research of Szilágyi et al. (2024) explored a novel four-stage STEAM-based methodology using educational robotics and dynamic geometry software to teach two families of cycloidal curves (epi- and hypotrochoids) to engineering students. A control group study with 98 students revealed that the experimental group, taught with the new methodology, significantly outperformed the control group in understanding epi- and hypotrochoids, regardless of prior calculus knowledge. The findings support the effectiveness of combining frontal teaching with motivating activities and technological integration, such as educational robotics and dynamic geometry software, aligning with recent advances in educational practices that emphasise active learning and hands-on experiences in STEM education. This study proves that if mathematics is supported with hands-on exercises, students are more engaged and learning outcomes are significantly better.

In this research, we tested and evaluated an alternative, new STEAM-based teaching strategy in a classroom environment that employs LEGO^® robotic kits (The LEGO Group, Billund, Denmark) and the Desmos Graphing Calculator as practical tools for demonstrating the construction and properties of trochoids. This approach emphasises visualisation to foster a deeper understanding of the curves. One of the most important elements of valuable STEAM projects is selecting or constructing the right educational robot. In this experiment, we used our own LEGO^® robot designs developed two years ago (Körei & Szilágyi, 2024b). The aim of this study is to determine the added value of video-based and/or first-hand experiential learning compared to the traditional method when teaching trochoids. The research seeks to answer two key questions: First, does video-based experience alone sufficiently improve students’ understanding of trochoids compared to traditional teaching methods? Second, is there a significant difference in learning outcomes between students who engage in hands-on robotic activities and those who only observe demonstrations through videos?

Our paper is structured as follows. After the introduction, we describe the current state of LEGO^® robots in tertiary education, followed by an overview of the historical and theoretical background of trochoids. We deal in detail with the representation opportunities and present the possibilities of using educational robotics. The Methodology section describes the experimental setup, research questions, and the sample. The Data Analysis and Results section presents data, hypothesis testing, and summary tables. Next, in the Discussion session, we answer the research questions. Then, the Conclusions and Recommendations section can be read. The study ends with the Limitation section.

2. Current Trends of Using LEGO^® Robots in Tertiary Education

Educational robotics (ER) is a field of robotics and a growing trend in STEAM education that deals with robots and robotic devices used in education to enrich the learning experience and facilitate a more effective acquisition of subject knowledge. ER includes the design, development, and application of robots used for learning purposes, such as mathematics, physics, programming, and other subjects. The goal is to encourage students to learn more actively and develop their problem-solving skills, creativity, and technical and engineering skills through robotics (Atman Uslu et al., 2023; Bano et al., 2024).

2.1. Robotic Platforms

Programmable robot platforms are one of the most essential tools in educational robotics, enabling students to explore the fundamentals of robotics construction and programming. These devices serve as versatile systems that can be customised, controlled, and programmed according to specific learning objectives. Programmable robot platforms provide practical experience, all while engaging learners through hands-on, interactive activities (Kyprianou et al., 2023). As innovative teaching methods become increasingly important, these tools stand at the forefront of educational robotics (Rayner et al., 2022). Krause et al. (2024) presented comprehensive guidelines for the selection of programmable robot platforms, which addresses the growing need for careful consideration in the face of market diversity. It outlines a seven-step process and details 15 criteria, ranging from price and purpose to software development and expandability. The paper provides a structured framework to help educators choose the best robot to align with their specific educational settings and goals.

Educational robotics platforms range from beginner-friendly systems like LEGO^® Education SPIKE Prime and micro:bit, which foster basic programming and problem-solving skills, to more advanced options like VEX Robotics, Arduino, Fischertechnik sets and iRobot^®Create^®3, enabling the implementation of complex algorithms and real-world applications. LEGO^® robotics kits are often used because they are affordable and easily accessible. Commercial robotics platforms can be expensive, limiting access for institutions with fewer resources.

LEGO^® robotics kits, especially LEGO^® Education SPIKE Prime (Figure 1), are renowned for their intuitive, hands-on learning approach, which makes them accessible to students of all ages. The modular design of LEGO^® bricks and the combination of versatile sensors allow for easy construction and experimentation, promoting creativity and problem-solving skills. Block-based programming environments such as Scratch further simplify the coding process, allowing students to focus on logical thinking and algorithm development without being distracted by complex syntax. LEGO^® kits are excellent for teaching basic robotics concepts and fundamental programming; they can also be used in mathematics education at all levels. The LEGO^® Education SPIKE Prime hub can also be programmed in Python 3.11, providing a playful way to learn the basics of object-oriented programming even in tertiary education (Körei & Szilágyi, 2022b).

For first-year university students, integrating LEGO^® robots into mathematics education is a good choice because the knowledge level of those entering tertiary education is generally not uniform. Therefore, it is worth using a platform that caters to students with different levels of knowledge. Other advantages and disadvantages of using LEGO^® robots in education were collected in (Körei & Szilágyi, 2024a).

2.2. LEGO^® Robots in Tertiary STEAM Education

There are numerous examples of LEGO^® robots being used for educational purposes in tertiary education. The LEGO^® Education SPIKE Prime robotics kit was launched in 2020. This kit played a significant role in many areas of education in the last five years. Good practices can be found in all STEAM areas. For example, in science education (Petrovič, 2021), in engineering and technology education (Assante et al., 2024), in nanoscience education (Nguyen et al., 2023), in robotics education (Brown & Tsugawa, 2024; Petrovič et al., 2024), and in mathematics education (Petrovič, 2022; Szilágyi et al., 2024).

One of the stereotypes about LEGO^® robots is that they are not necessarily suitable for high-precision mathematical measurements and experiments. We demonstrated that by combining theoretical analysis with rigorous experimentation and data processing techniques, LEGO^® Education SPIKE Prime robots can indeed be used for precise tasks (Körei et al., 2025). Our previous study focused on understanding and improving the turning accuracy of LEGO^® SPIKE Prime robots, using mathematical derivations and refining these models through regression analysis. We developed a method where the robot itself collects performance data, enabling autonomous regression modelling and reducing human error. Statistical validation further strengthened the findings, confirming that, with careful consideration and advanced techniques, LEGO^® robots can overcome inherent limitations and be effectively used in applications requiring precision, such as educational robotics and robot competitions (Körei et al., 2025).

Both Gervais and Patrosio (2022) and Buchsteiner et al. (2025) demonstrated the benefits of integrating LEGO^® Education SPIKE Prime robot kits with the Robot Operating System (ROS) in education, but with different approaches. The primary benefit lies in affordability. Petrovič et al. (2024) showed that the capabilities of the LEGO^® Education SPIKE Prime system can be significantly extended towards advanced projects by using the Raspberry Pi Build Hat as an alternative to the SPIKE Prime Hub. This opens up opportunities to incorporate internet connectivity, a camera, powerful computational resources, and the ability to connect Arduino and hundreds of low-cost sensors and actuators, thus broadening the educational potential of the system.

3. Historical and Theoretical Background of Trochoids

During the first third of the seventeenth century, the number of known curves was slightly greater than two thousand years ago. However, the situation changed entirely between 1634 and 1644 (Boyer, 1945). The cycloid curve had been noted several times before, but when Marin Mersenne in 1634 and Galileo Galilei in 1639 again suggested it as a curve worthy of study, its shape, parametric equation and properties were promptly determined through the composition of motions.

3.1. Importance and Uniqueness of Cycloid in Calculus

The cusped cycloid, or cycloid, is the simplest member of roulettes. The original discoverer of the cycloid is unknown (Whitman, 1943). No mention of the cycloid has been found in writings before the 15th century. Historians of mathematics have identified several individuals who are considered potential discoverers of the cycloid (Al-ossmi, 2024). As a curve generated by a moving circle, the cycloid was first noted by Cardinal Cusanus (Nicolaus de Cusa) as early as 1451 (Bartolini Bussi et al., 2010), and later by Charles de Bouvelles in 1501. The name “cycloid” was given by Galileo Galilei in 1599 (Henry & Wanner, 2017; Raicu & Rugescu, 2015).

Although Galilei tried to find a mathematical way to determine the area under the cycloid arch, he was unsuccessful, but observed the area to be three times the area of the generating circle using a physical comparison of metallic shapes (Whitman, 1943). Marin Mersenne probably heard about the curve from Galilei, introduced it to Gilles Persone de Roberval, and urged him to determine its area (Shirali, 2013). Roberval confirmed Galilei’s observation that the area under the arch is three times that of the generating circle. Roberval later found the area under the cycloid arch in 1634 using Cavalieri’s method. Roberval, Fermat, and Descartes found different ways to determine the tangent lines to the cycloid (Shim, 2015). English mathematician John Wallis significantly contributed to studying cycloids in the mid-17th century. In 1658, he addressed Pascal’s challenge concerning the curve, building on prior work by Roberval and others. His treatise, dating back to 1659, showcased his solutions to cycloid-related problems and disseminated Christopher Wren’s elaborations on cycloid rectification (Florio, 2022). In 1658, Christopher Wren found that the length of one arch of the cycloid is four times the diameter of the generating circle. Although Wren’s mathematical results were not directly published, John Wallis provides a valuable record of his work in a tract titled De Cycloide (Dhombres, 2024). Figure 2 shows a cycloid illustration from 1659. Further discoveries about the cycloid continued, including Christian Huygens’ work in 1673, where he demonstrated that a pendulum swinging along a cycloid path would have a constant period and created a clock based on this property (Ben-Abu et al., 2018; Shim, 2015).

The cycloid continued to be a topic of front-line investigation well beyond this period. Notably, the solution to the brachistochrone problem (finding the curve of steepest descent), posed by Johann Bernoulli in 1696 and solved independently by himself, Jacob Bernoulli, Newton, Leibniz, and L’Hôpital, turned out to be the cycloid. Johan Bernoulli used the optical Fermat concept to solve the problem. Using the calculus of variations, Euler addressed the method that gave a rigorous proof of the brachistochrone problem (Abdul-Hafidh, 2022). From a mathematical history perspective, it is significant that the title page of Johann Bernoulli’s Opera Omnia features an unexpected vignette (Figure 3), which illustrates Johann’s competitors as a dog barking at a mathematical illustration nailed to a tree. This illustration shows a cycloid accompanied by the phrase “Supra invidiam”, which can be interpreted as “beyond envy”. Additionally, in the engraved portrait on the left page, we observe him holding a piece of paper displaying a drawing of a cycloid (Henry & Wanner, 2017).

Likewise, the solution to the tautochrone problem (finding the curve for which the time taken by a particle sliding down the curve to its lowest point is independent of its starting point) also proved to be the cycloid (Shirali, 2013). Pascal calculated its centre of gravity and area, Huygens calculated the movement of a material point along a cycloid (Matsuura et al., 2013). The cycloid is not an algebraic curve, meaning that it cannot be expressed by a polynomial equation. This fact challenged early mathematicians, leading to the development of new techniques (Gindikin, 2007). Cycloid studies were important in the birth and development of analytical geometry and calculus, particularly in integral and variational calculus (Shim, 2015). Mathematicians frequently used the cycloid as an example when they presented their new mathematical methods and ideas. The cycloid was not just an interesting curve, but a powerful tool for mathematicians to explore, test, and refine their mathematical ideas and methods (Gindikin, 2007). The cycloid has been referred to as Helen of Geometry or Apple of Discord, both for its remarkable characteristics and for the disputes it sparked among renowned mathematicians of the 17th century (Martin, 2010; Phillips, 1967).

Today, engineers and designers often use cycloids to design roller coasters (Figure 4). Being a brahistochronous curve, a cycloid allows one to obtain the highest speeds between the two different heights of the circuit (Raicu & Rugescu, 2015). The roof structure of the Kimbell Art Museum is widely recognised and well-documented for its use of cycloid curves. This architectural solution allows for the creation of a lightweight, strong, and aesthetically pleasing roof. By utilising the unique properties of cyloid arches, the design provides optimal shading and natural lighting within the building. The cycloid shapes of the Kimbell Art Museum in Texas are perhaps the most singular example ever applied in building design (Park et al., 2007). The most distinctive design element of the museum is the series of sixteen parallel cycloid vaults (see Figure 4).

Cycloidal patterns are widely distributed on the surface of Jupiter’s moon Europa (Groenleer & Kattenhorn, 2008; Hoppa et al., 1999). Violin makers use curtate cycloids to design the arching of the top and bottom plates, as these curves closely match the profiles of historic Cremonese instruments and provide ideal acoustic properties (Playfair, 2003). Cycloid-like mirrors are important in advanced optical systems (Lemaitre et al., 2022).

3.2. Classification of Cycloidal Curves

A cycloid is a specific form of trochoid and is an example of a roulette (Al-ossmi, 2024). Roulette is a path traced by the point fixed on a curve that is rolling on another fixed curve (Lockwood, 1967). Cycloidal curves are a family of roulettes generated by the motion of a point attached to a circle as the circle rolls along a fixed straight line or another circle (Yates, 1974). This family includes trochoids, epitrochoids and hypotrochoids, as shown in

Table 1. Classification of cycloidal curves. Source: Szilágyi et al. (2024).

	Cycloidal curves
	(a circle rolling on another circle or a line)
	Epitrochoids	Trochoids	Hypotrochoids
	(a circle rolling outside another circle)	(a circle rolling on a line)	(a circle rolling inside another circle)
The tracing point is on the circumference of the moving circle.	Epicycloid	Cusped cycloid	Hypocycloid
The tracing point is inside the moving circle.	Curtate epitrochoid	Curtate cycloid	Curtate hypotrochoid
The tracing point is outside the moving circle.	Prolate epitrochoid	Prolate cycloid	Prolate hypotrochoid

.

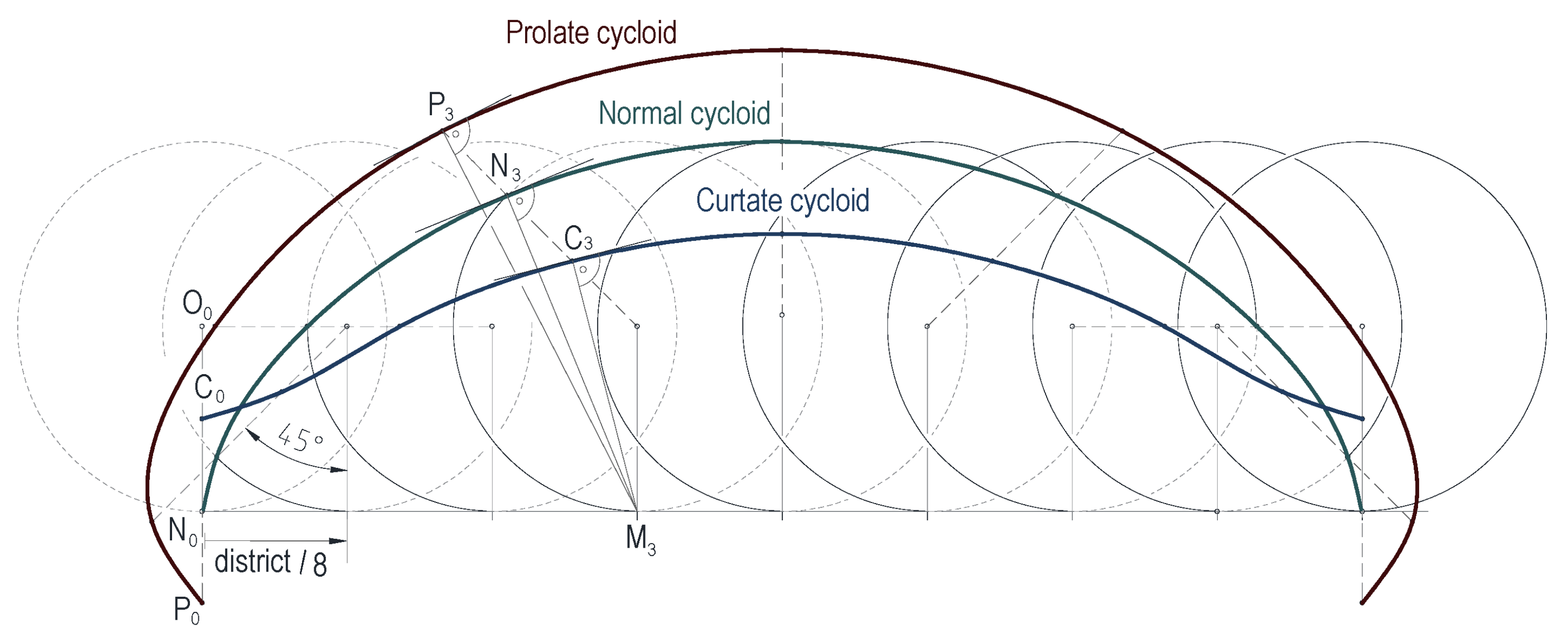
3.3. Parametric Equations of Trochoids

The parametric equations of trochoids are

$$\left(x\right(t),y(t\left)\right)=(rt-dsint,r-dcost),t\in \mathbb{R},$$

(1)

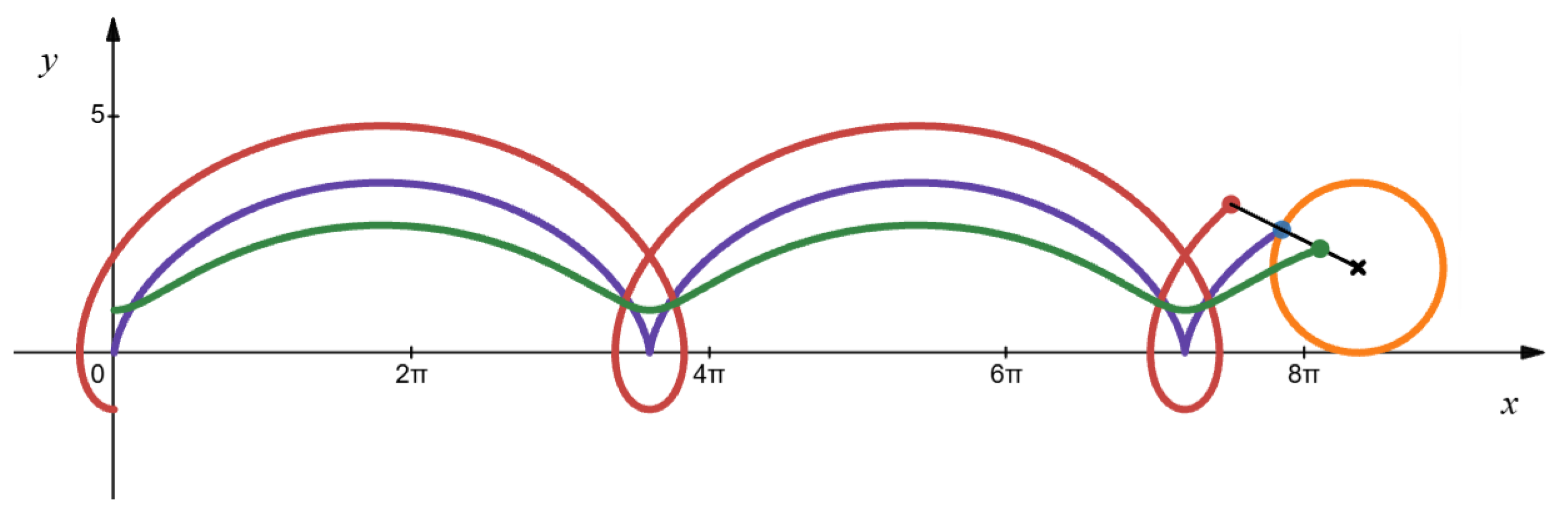
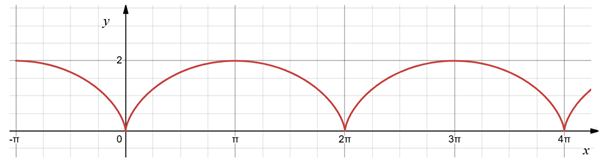
where $r,d\in {\mathbb{R}}^{+}.$ In Equation (1), r denotes the radius of the moving circle and d denotes the distance of the examined point from the centre of the circle. If $d<r$, then we obtain a prolate cycloid, for $d=r$ we obtain a cusped cycloid, and for $d>r$ we have a curtate cycloid from Equation (1). A detailed derivation of Equation (1) can be found in (Körei & Szilágyi, 2024b). Figure 5 shows the three types of trochoids. The caption of Figure 5 contains a link that can be used to generate various trochoids using Desmos.

3.4. Manual Drawing of Cycloids

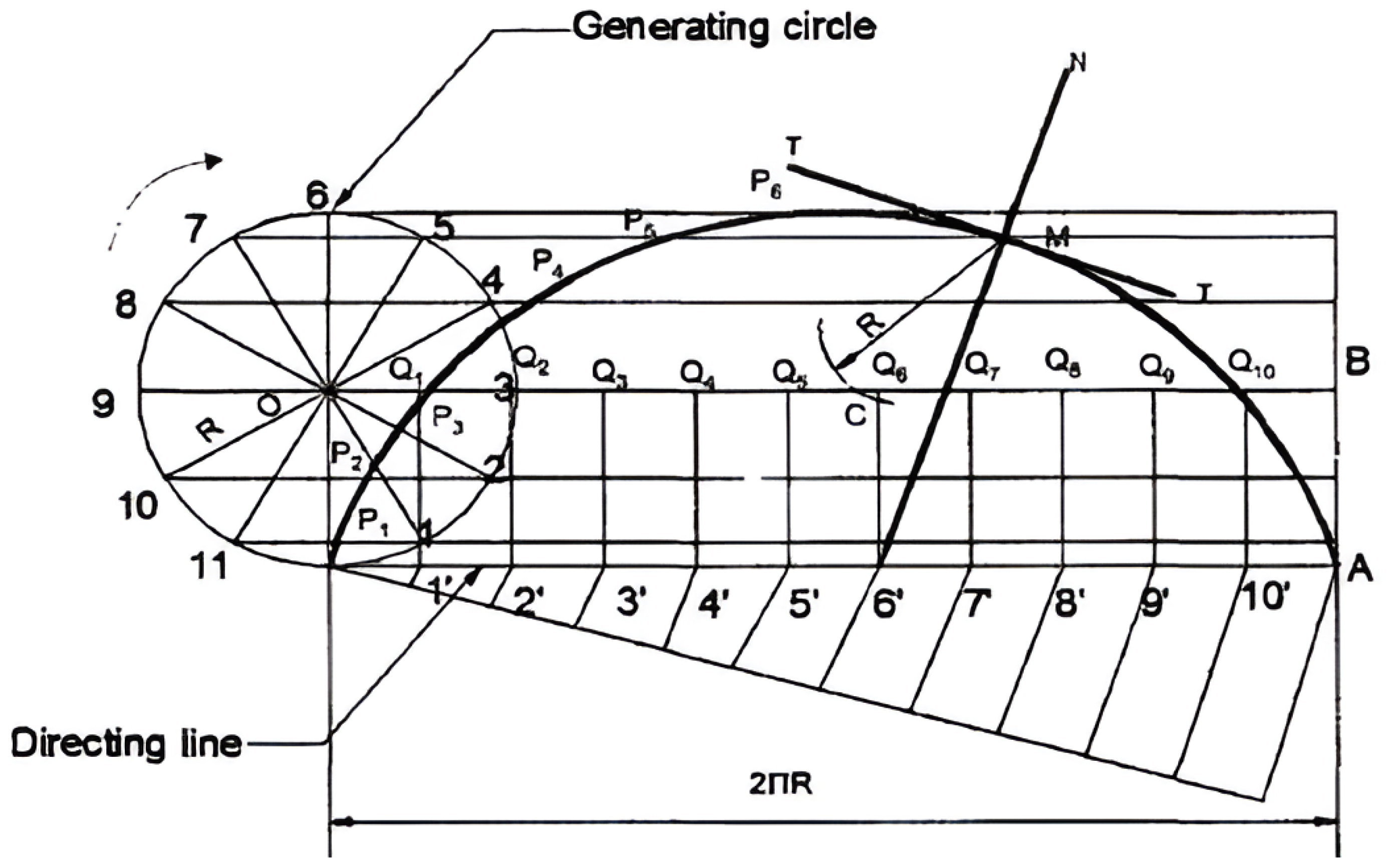
Lockwood (1967) presents two different methods for manually drawing a cycloid. The first method involves drawing a series of rolling circles and their radii, marking the cycloid’s path point-by-point. The second method uses a semicircle and a series of horizontal lines and cutting points to define the curve, offering a quicker manual construction alternative. At present, engineering drawing uses a third method for constructing a cycloid. It combines geometric construction with principles of the rolling circle to define points along the curve (Reddy, 2008). This method is designed to create an accurate representation of the cycloid using basic drafting tools (see Figure 6).

However, in descriptive geometry, the core is not the manual nature of the drawings, but rather the principles and methods it employs to represent three-dimensional objects through two-dimensional drawings. As highlighted in Stachel (2007), the essence lies in conceptual and geometrical techniques, not in whether the drawings are made by hand. Even Gaspar Monge, the founder of descriptive geometry, did not consider hand-drawing an essential feature, underscoring that the discipline is fundamentally about the mathematical and geometrical ideation behind the drawings rather than the manual process itself (Balajti, 2024). Today, CAD (Computer-Aided Design) tools are used in almost all technical, engineering, and architectural design instead of manual drawing (Fakhry et al., 2021). Computer-aided design offers numerous advantages, such as greater accuracy, easier modification, faster editing, and simpler sharing and storage thanks to digital file formats (Nyemba, 2022). CAD software, such as AutoCAD 2024, allows for the precise creation of complex drawings and models that would be much more time-consuming and less accurate if done by hand (Liu, 2021). AutoCAD’s precision tools provide a far more accurate and efficient method for generating cycloids than manual drafting techniques. Although the manual methods described earlier help to understand the geometric principles of a cycloid, engineers primarily rely on AutoCAD to create them in practical applications. AutoCAD, using parametric equations, can precisely define and draw cycloids, which are essential for complex engineering designs that incorporate these curves. Figure 7 shows all three types of trochoids created using AutoCAD.

At the same time, Fakhry et al. (2021) found in a student experiment that hand-drawing remains relevant and beneficial when combined with CAD in architectural drafting courses. The article emphasises that hand-drawing remains valuable for specific tasks, such as taking notes during site visits, and is potentially better at promoting creativity in the details of working drawings than the exclusive use of CAD. Therefore, the recommendation is to integrate both methods, starting with manual drawing for larger tasks and then moving on to CAD to take advantage of the strengths of both approaches.

4. Displaying Trochoids

The connection between geometry and kinematics has deep historical roots (Farouki, 2000). Mathematical models have been used for centuries to study curves from motion, enabling a precise analysis of the geometric properties of these interesting curves (Gray et al., 2016).

4.1. Schilling’s Kinematic Model

The Chicago World’s Columbian Exposition of 1893, held to mark the 400th anniversary of Columbus’s discovery of America, remains one of the largest international exhibitions ever organised. This event was a notable milestone in the history of mathematics, as it featured geometric models displayed by German mathematicians. These models were designed by mathematics educators and researchers to aid in teaching, illustrate geometric concepts, and enhance student understanding. Felix Klein highlighted the importance of constructing such models during his lectures at the exhibition, emphasising their role in fostering intuition and addressing the abstract nature of mathematics. The success of the German exhibit sparked the development of similar mathematical model collections across various higher education institutions in Europe, America, and Russia (Kuteeva et al., 2017). In addition to Felix Klein, the primary influences on the visual depiction of geometric objects were the renowned German mathematicians Eduard Kummer and Alexander von Brill. Their students created the initial plaster models, which generated considerable interest among mathematicians and subsequently led to their commercial production and distribution. One of the first companies to enter this market was a factory established in Darmstadt in 1880 by Ludoville von Brill, Alexander von Brill’s brother. In 1899, Martin Schilling acquired the factory, relocating it first to Halle and later to Leipzig after 1903 (Shell-Gellasch, 2015). The company’s first catalogue was issued in 1903, with a subsequent edition published in 1911. The 1903 Schilling catalogue is considered a culturally valuable publication, which prompted a reprint in 2010 in a modern edition that remained faithful to the original (Schilling, 2010).

At the beginning of the 20th century, most mathematical models were static, non-interactive, and typically constructed from wood, paper, or plaster. Kinematic models, which are capable of demonstrating motion, were subsequently developed. These devices incorporated moving parts such as cranks and hinges to illustrate mathematical concepts. The primary components of these kinematic models were usually made of metal, predominantly brass. The kinematic models featured in the Schilling catalogue were designed by Frederick Schilling, a mathematics professor at Göttingen who also served as the scientific director of the Schilling company (Snyder, 1904). These models are listed in the 1903 and 1911 editions of the Schilling Catalogue of Mathematical Models. The 1911 catalogue details 377 items organised into forty series, with Series XXIV dedicated to kinematic models demonstrating movement (Shell-Gellasch, 2015). Among these, Frederick Schilling’s twelve kinematic models are included (Snyder, 1904). Made of brass and celluloid and mounted on wood, Model 7 features three trochoids drawn directly on the glass plate, as shown in Figure 8.

Schilling’s 1911 catalogue includes the names of the models, brief mathematical descriptions, and, in certain instances, illustrations of the models (Gray et al., 2016). Model 7 features a toothed metal disc connected to a similarly toothed bar on one side. A radius extending from the circle includes designated positions for pins: one inside the circumference, one on the circumference, and one outside the circle. Turning a crank located beneath the baseplate causes the circle to move along the edge of the bar, producing a curve above each pin position. These generated curves are displayed on a glass overlay situated above the mechanism. The point in the circumference of the circle traces a cycloid, shown in blue; the point outside the circle produces a prolate cycloid, indicated in orange; and the point inside the circle creates a curtate cycloid, represented in green (Schilling, 1911).

4.2. Using Dynamic Geometry Software

GeoGebra is one of the best-known dynamic geometry software programs (Carneiro et al., 2021). GeoGebra empowers learners to explore and construct mathematical concepts dynamically, bridging the gap between abstract theory and concrete visualisation with free accessibility. Kabaca (2013) explored the use of dynamic software, specifically GeoGebra, as a tool for teaching cycloid curves at the tertiary level. His study aims to visualise the cycloid curve, understand the underlying mathematical principles, and abstract more complex cycloidal curves, such as epicycloids and hypocycloids. Key aspects of the paper include a focus on dynamic mathematics software, mathematical modelling, and the use of multiple representations. The research defined the whole process as a cyclical interaction between mathematics and the real world by constructing visual models using GeoGebra and relating them to corresponding mathematical equations. The paper provided step-by-step instructions and equations for using GeoGebra to create a cycloid and demonstrate that dynamic software and multiple representations can enhance students’ understanding of advanced mathematical concepts. Gunčaga et al. (2019) focused on visualising mathematical concepts with computers, using the cycloid curve as a prime example. It highlights how computer-based visualisation tools, especially GeoGebra, can enhance understanding of complex mathematical ideas, drawing on historical approaches such as Torricelli’s method for determining the area under a cycloid. The paper explains how GeoGebra provides a dynamic and accessible way to illustrate Torricelli’s geometrical method, making it suitable for secondary school students and pre-service teachers. By connecting historical approaches with modern technology, the study demonstrates that students can gain deeper insights into the properties of the cycloid curve and the logic behind its area calculation. GeoGebra enables students to explore, construct, and experiment with mathematical models, improving engagement in and understanding of mathematical concepts, especially the cycloid.

Desmos is primarily an online graphing calculator, but in many ways it is similar to dynamic geometry software, as it offers live, real-time drawings and visualisations that can be easily modified. Its primary focus is on providing user-friendly and straightforward representations of functions and graphs. The research paper of Chechan et al. (2023) examines the effect of using the Desmos Graphing Calculator on Swedish high school students’ understanding of functions. Using a mixed-methods approach, it combines pre- and post-tests with student opinion surveys. The study finds that students using Desmos show a greater improvement in understanding functions than those using traditional methods. Qualitative feedback indicates that students perceive Desmos positively, especially for visualisation and analysis. The paper highlights that, while Desmos enhances conceptual grasp, effective implementation and time for exploration are crucial. Desmos is a valuable educational tool that improves students’ mathematical understanding, creativity, and visualisation when properly integrated.

Körei and Szilágyi (2022a) highlighted Desmos as a valuable free tool for visualising and exploring parametric curves, especially hypotrochoids, in a classroom setting. With Desmos, users can easily input curve equations in various forms, including parametric equations, and then interactively manipulate variables using sliders to observe the impact on the resulting curve. The paper explicitly mentions the Hypotrochoid Equation Tracer application made with Desmos, which animates the formation of hypotrochoids, displaying the trajectory of a fixed point and the moving and fixed circles, enhancing the learning experience. The paper of Körei and Szilágyi (2024a) focused on epitrochoid curves, and Desmos was used as an integral component of the presented STEAM-based learning method. The paper introduces an improved virtual Epitrochoid Tracker built with the Desmos Graphing Calculator, designed to check the parametric equations for curves drawn by a physical LEGO^® robot. Desmos is selected due to its accessibility as an easy-to-use online application compatible with various devices, allowing students to use their personal devices for assignments. It supports the teaching of parametric curves through dynamic animations, and the Epitrochoid Tracker specifically animates the curve formation process, displaying the position of the moving circle and the connection between its centre and the pole. In the classroom, Desmos is used in two ways: first, as a post-check function where the dimensions of the robot are entered to plot the resulting curve, and second, as a pre-planning tool, where the Epitrochoid Tracker visualises the curves that the robot can draw, allowing for simulations and exploration of parametric constants and spectacular epitrochoids.

4.3. Drawing Robots

Two years ago, we designed and built two distinct LEGO^® robots to draw trochoid curves (see Figure 9). The first, the “hanging rail” model, follows the traditional method of drawing trochoids: a gear rolls along a long rack, with a pen attached to the moving gear to draw the curve. This robot includes a programmable hub, a motor, and a drawing head that can be fixed at different distances from the gear’s centre, allowing it to draw three types of trochoids (prolate, cusped, and curtate cycloids). The second, the “moving tray” model, moves the paper in a straight line under the drawing head. The drawing head moves in a circular motion around a given centre, and horizontal motion is achieved by moving the paper. This robot uses two separate motors to achieve these two types of motion. The challenge lies in synchronising the two movements to ensure the curve is accurate (Körei & Szilágyi, 2024b). The building guide of the “hanging rail” model can be found in the Supplementary Materials.

We displayed two different methods for visualising cycloid curves with the “hanging rail” model in Körei and Szilágyi (2024b), focusing on the tools used to create the visual representation. The first approach involved using an LED light source attached to a LEGO^® robot. By capturing the robot’s movement in a darkened room with long exposure photography, the path of the LED light visualises the cycloid curve (see Figure 10).

This method allows for visualising the curve without physically drawing it. The second approach involved physical drawing, where the LEGO^® robot is equipped with a felt-tip pen (or similar drawing instrument). As the robot moves according to the principles of cycloid generation, the pen leaves a visible trace of the curve on paper (see Figure 9, right).

After creating the drawing robots, this year we tested them in a classroom environment to determine the significance of first-hand experiences in facilitating the learning process when teaching parametric curves.

5. Methodology

The experiment was conducted at a Hungarian university during the spring semester of the academic year 2024/2025. The 94 students participating in the study attended lectures by the same teacher at the University of Miskolc. We established a control group experiment using a quasi-experimental design.

Students from the Faculty of Mechanical Engineering and Informatics of the University of Miskolc participated in the experiment. In the spring semester of the academic year 2024/2025, 101 students studied the Calculus II course. The course material covers curve theory, integral calculus, and its applications, among other topics. A total of 94 students participated in the study. In this experiment, we worked with two different experimental groups. There were 61 participants in the two experimental groups and 33 in the control group. The experimental and control groups attended the same lecture. Throughout the semester, they were exposed to the same concepts, theorems, and problems.

5.1. Experimental Setup

We worked with two experimental groups and one control group. The groups were approximately equal in size, with around 30 participants each. The control group studied in the usual way, attending compulsory on-site lectures and practical classes at the university. To ensure the integrity and clarity of the research results, the control group did not receive any specific treatment or intervention. This decision was made because it was not possible to require university students to participate in additional activities outside of the regular coursework if they did not want to. By keeping the control group unchanged, we aimed to obtain a pure comparison between the groups, allowing us to accurately attribute any observed differences or effects to the experimental interventions.

In addition to the lectures and practical classes required by the curriculum, both experimental groups participated in a 120 min on-site seminar on trochoids. Both types of drawing robots were showcased during the seminars, and their operating principles were thoroughly explained in a detailed PowerPoint presentation. The participants studied the functioning robots through short videos. The videos are short, lasting around 3 to 4 min, and focus on trochoid drawing. They are silent videos, so students rely on visual cues and the teacher’s explanation. The students watched these videos at least twice to understand the topic. The teacher provided additional narration and context to complement the videos. We brought pre-built robot models to the seminars and used them as teaching aids. No building took place during these seminars.

Only half of the experimental group received further treatment. Thirty participants, members of the EG (ER) group, participated in two 90 min practical sessions, where they had the opportunity to build the hanging rail model (see Figure 9, right) to draw trochoids in small groups. The three types (cusped, prolate, and curtate cycloids) were drawn using felt-tip pens and LED lights. The participants used Desmos dynamic geometry software to check the parametric equations corresponding to the drawn curves. The steps of the student projects can be found in the Appendix A. To ensure equal treatment time, members of EG(V) worked on two complex homework tasks related to trochoids, for which they created animations using dynamic geometry software and solved problems involving area and arc length calculations. The recommended homework tasks can be found in the Appendix B.

The effectiveness of the intervention was measured based on the scores obtained in the midterm exam tasks related to trochoids. The tasks can be found in the Appendix C.

5.2. Research Questions

The purpose of having two separate experimental groups is to evaluate the effectiveness and importance of different teaching methods. This design allows us to determine whether video-based demonstrations alone are sufficient for achieving the desired learning outcomes, or if direct, hands-on experience is essential for a deeper understanding and mastery of the subject matter. Our comparison aims to clarify the added value of video-based and/or first-hand experiential learning over purely traditional instruction within the context of the study. We searched for answers to the following two research questions:

RQ1 

Does video-based experience alone sufficiently improve students’ understanding of trochoids compared to traditional teaching methods?

RQ2 

Is there a significant difference in learning outcomes between students who receive hands-on building activities and those who only observe demonstrations via videos?

5.3. Sample

The experiment involved 94 full-time, mostly first-year IT students from the Faculty of Mechanical Engineering and Informatics of the University of Miskolc. The control group (CG) consisted of 33 students. The average age was 21.30 years. Of the two experimental groups, the one that received treatment only through videos consisted of 31 students. This will be referred to as EG(V) in the following. In EG(V), the average age was 21.39 years. The other experimental group, which received educational robotics treatment, consisted of 30 participants. The average age was 20.8 years. We use the abbreviation EG(ER) for this group.

Table 2. Gender distribution in the total sample and in the groups.

	Participants
	CG		EG(V)		EG(ER)		Total
Gender	N	%	N	%	N	%	N	%
Female	4	12.12	2	6.45	5	16.67	11	11.70
Male	29	87.88	29	93.55	25	83.33	83	88.30
Total	33	100.00	31	100.00	30	100.00	94	100.00

shows the breakdown of participants by gender for the total sample and also for three groups. The low number of female participants reflects the global trend in IT higher education, where women are often underrepresented. This does not necessarily cause bias or distortion in our results, as the study focuses on overall group comparisons. The primary goal is to analyse the data within the existing sample.

The distribution of participants by their field of study in the full sample reveals that 45.74% were pursuing a Bachelor’s degree in Computer Science (CS), 40.43% were studying Computer Science Engineering (CSE), and 13.83% were in Business Informatics (BI).

Table 3. Number of participants per group and BA program.

	Participants
	CG		EG(V)		EG(ER)		Total
BA Program	N	%	N	%	N	%	N	%
CS	19	57.58	12	38.71	12	40.00	43	45.74
CSE	12	36.36	13	41.94	13	43.33	38	40.43
BI	2	6.06	6	19.35	5	16.67	13	13.83
Total	33	100.00	31	100.00	30	100.00	94	100.00

shows the distribution of the total sample across various BA programs.

5.4. Ethics

At the start of the experiment, students were briefed on the research goals and provided their informed consent to participate. The researchers explained the entire procedure in detail to ensure transparency. Participation in extracurricular activities was voluntary. To maintain confidentiality, each participant was assigned pseudonymous codes for data recording and analysis. Throughout the study, participants engaged in all scheduled activities. The entire research process adhered to the ethical guidelines outlined in the University of Miskolc’s Code of Ethics, ensuring responsible conduct of the study.

6. Data Analysis and Results

The midterm exam scores were manually recorded in a Microsoft Excel spreadsheet, then imported into the DATAtab application for further data analysis. Scores related to trochoid curve tasks in the midterm exam were collected and analysed for the 94 participants.

6.1. Descriptive Statistics

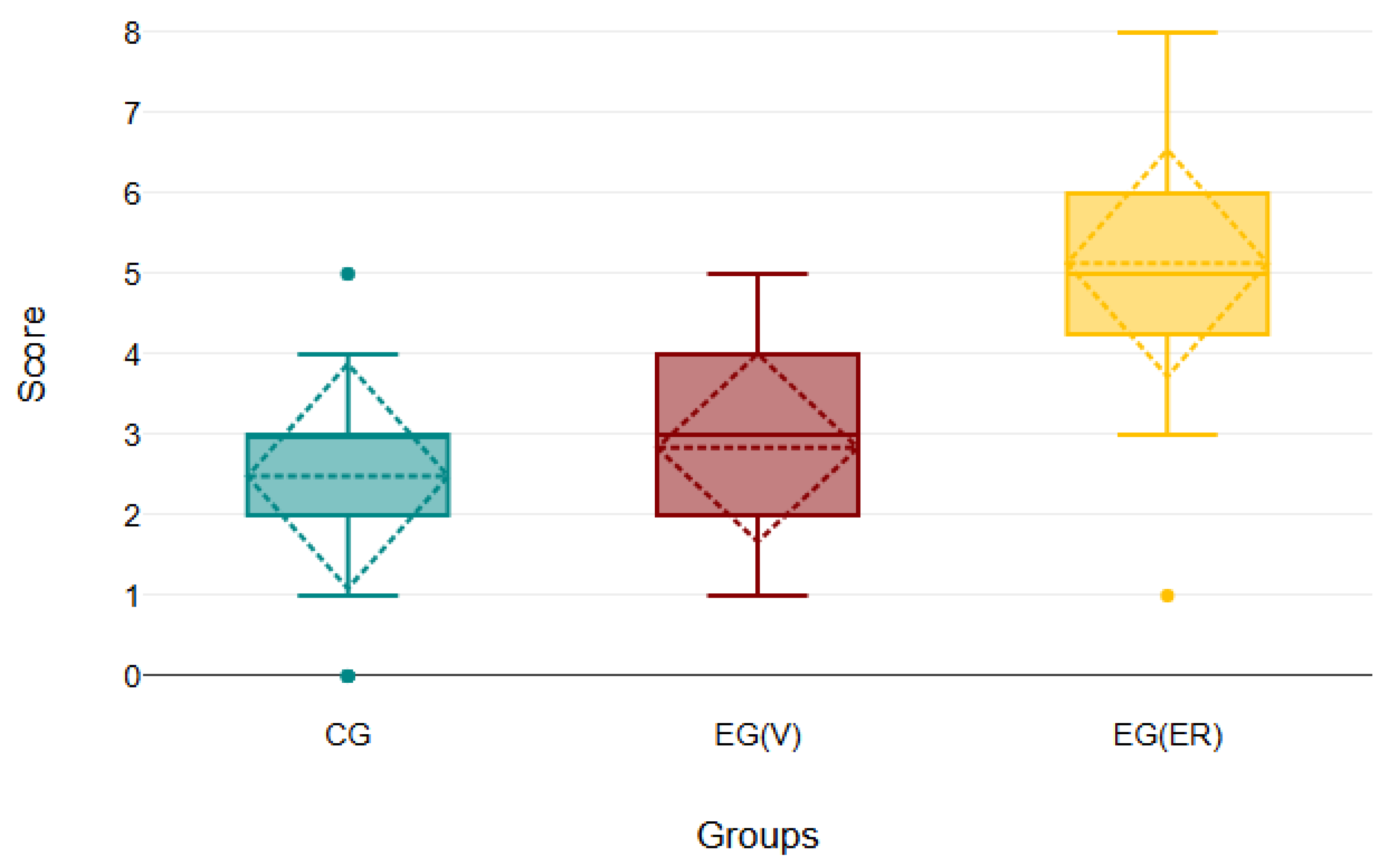
The descriptive statistics are summarised in

Table 4. Descriptive statistics for midterm exam scores.

	Groups
	CG	EG(V)	EG(ER)
N	33	31	30
Mean (M)	2.48	2.84	5.13
Median	3	3	5
Mode	3	3	6
Standard Deviation (SD)	1.42	1.19	1.43
Minimum	0	1	1
Maximum	5	5	8
Median Absolute Deviation (MAD)	1	1	1

, while Figure 11 provides a visual representation of the key characteristics of the scores of the relevant mid-term exam tasks for three groups, highlighting the data distribution and outliers.

The descriptive statistics for the midterm exam scores in the three groups reveal notable differences in performance. CG had an average score of 2.48, with a median of 3 and a mode of 3. The scores in this group ranged from 0 to 5, with a standard deviation of 1.42. In contrast, EG(V) showed a slight improvement, with a mean score of 2.84. At the same time, this group maintained a median of 3 and a mode of 3, similar to the control group, but demonstrated a lower standard deviation of 1.19. The scores ranged from 1 to 5, with no participants scoring zero, which shows a somewhat more consistent performance among group members. Most notably, EG(ER) achieved a much higher average score of 5.13, with a median of 5 and a mode of 6. The score range extends from 1 to 8, because some participants reached significantly higher scores. The value of the standard deviation is 1.43, suggesting improved performance and that the scores were more concentrated at the higher end of the scale.

Similar standard deviations suggest that, although the groups differ in average scores, each group’s degree of performance variability remains relatively consistent. This indicates that interventions or conditions did not significantly affect the spread of individual scores within the groups. So, the interventions primarily influence mean performance levels rather than reducing or increasing score dispersion.

6.2. Normality Testing

Examining normality is an important step in selecting the appropriate statistical method.

Table 5. Different statistical tests to check the normality.

	CG		EG(V)		EG(ER)
	Stat.	p	Stat.	p	Stat.	p
Kolmogorov–Smirnov	0.19	0.173	0.17	0.317	0.2	0.173
Kolmogorov–Smirnov (Lilliefors)	0.19	0.050	0.17	0.028	0.20	0.005
Shapiro–Wilk	0.93	0.039	0.91	0.017	0.92	0.23
Anderson–Darling	0.88	0.022	1.04	0.008	1.14	0.005

shows the statistics and p values of four different statistical tests. A high p-value, greater than 0.05, shows that the data does not significantly deviate from normality (Khatun, 2021).

Since some of these tests have p-values below the usual significance level of 0.05, this suggests that the data do not follow a normal distribution in either case of groups, especially according to the Shapiro–Wilk and Anderson–Darling tests. Therefore, non-parametric statistical methods are required for hypothesis testing.

6.3. Hypothesis Testing

The groups are independent of each other and have different sample sizes, so we employed the Mann–Whitney U test, a nonparametric method, for hypothesis testing. This test is appropriate because it does not assume a normal distribution and can effectively compare two independent groups with unequal sizes (Steyn, 2020).

The descriptive statistics in Table 4 show that EG(V) performed slightly better than CG. Statistical testing must be performed to validate this conclusion. The following hypotheses were formulated to answer research question RQ1:

• Null hypothesis: There is no difference between the CG and EG(V) groups with respect to the dependent variable.
• Alternative hypothesis: There is a difference between the CG and EG(V) groups with respect to the dependent variable.

Table 6. Mann–Whitney U-test results CG versus EG(V).

CG vs. EG(V)	U	z	Asymptotic p	Exact p	r
Mann–Whitney U-test	444.5	−0.92	0.356	0.373	0.12

shows the results of the Mann–Whitney U-test CG versus EG(V). In this case, whether there is a significant difference between the CG and EG(V) groups was tested.

The Mann–Whitney U statistic obtained is 444.5. This value represents the sum of ranks for one of the groups in the comparison, reflecting how the data points in the two samples are ordered relative to each other. A smaller U value indicates greater differences between the groups, while a larger U value suggests that the groups are more similar. In this case, the U value of 444.5 suggests no significant difference between the two groups regarding their ranks, which is supported by the high p-values (0.356 and 0.373). The asymptotic p-value is 0.356. This value represents the probability of observing a test statistic as extreme as, or more extreme than, the observed value under the null hypothesis (which posits no difference between the groups). A p-value of 0.356 is above the common significance threshold of 0.05, suggesting that the result is not significant at the 5% level. The exact p-value is 0.373. This is an alternative method for calculating the p-value, which is often used when sample sizes are small. It is slightly higher than the asymptotic p-value (0.356), reinforcing the conclusion that the result is not statistically significant at the 5% level. Both p-values suggest that there is no significant difference between the groups. This indicates that the two groups’ results are statistically similar. The z-value is −0.92. This standardised score represents the deviation of the observed U-statistic from the expected mean under the null hypothesis, expressed in units of standard deviation. It is used to assess the significance of the U-statistic by comparing it to a standard normal distribution. In this case, a z-value of −0.92 indicates that the observed difference is close to what would be expected by chance, and combined with the p-values, further supports the conclusion that the difference between the groups is not statistically significant. The effect size (r) is calculated to be 0.12, which is a small effect size according to Cohen (2013). Since both p-values are above the common significance threshold of 0.05, we fail to reject the null hypothesis. This indicates that there is no statistically significant difference between the two groups in this comparison. The effect size of 0.12 suggests a small or negligible practical difference.

We performed a similar statistical analysis for CG and EG(ER). We created the following hypotheses to answer the research question RQ2:

• Null hypothesis: There is no difference between the CG and EG(ER) groups with respect to the dependent variable.
• Alternative hypothesis: There is a difference between the CG and EG(ER) groups with respect to the dependent variable.

Table 7. Mann–Whitney U-test results CG versus EG(ER).

CG vs. EG(ER)	U	z	Asymptotic p	Exact p	r
Mann–Whitney U-test	94	−5.59	<0.001	<0.001	0.7

shows the results of the Mann–Whitney U-test CG versus EG(ER). The Mann–Whitney U-test produced a U value of 94. The z-score of −5.59 shows how many standard deviations the observed U is from the expected mean under the null hypothesis of no difference. Such an extreme z-value indicates that the likelihood of obtaining these results by chance is very low. The asymptotic and exact p-values are less than 0.001, confirming that the difference between groups is statistically significant. With an effect size (r) of 0.7, which is considered large according to Cohen (2013), this suggests a strong and meaningful difference. The results provide robust evidence that the intervention has a substantial effect, leading us to reject the null hypothesis.

We obtained similar results when comparing EG(V) and EG(ER).

Table 8. Mann–Whitney U-test results EG(V) versus EG(ER).

EG(V) vs. EG(ER)	U	z	Asymptotic p	Exact p	r
Mann–Whitney U-test	104	−5.28	<0.001	<0.001	0.68

shows the results of the Mann–Whitney U-test EG(V) versus EG(ER).

• Null hypothesis: There is no difference between the EG(V) and EG(ER) groups with respect to the dependent variable.
• Alternative hypothesis: There is a difference between the EG(V) and EG(ER) groups with respect to the dependent variable.

Both p values are below 0.001, i.e., the test indicates a highly significant difference between the groups. The large effect size of 0.68 shows that this difference is statistically significant. The z-value confirms that the observed difference is very unlikely to have occurred by chance under the null hypothesis.

7. Discussion and Answer to Research Questions

In this study, we tested the effectiveness of different teaching methods for the topic of trochoid curves. While adding video demonstrations to traditional instruction showed a slight increase in test scores, it was not statistically significant. So, simply providing visual aids, even in a dynamic format, may not be enough to fundamentally alter student understanding. Students in group EG(V) still learned more than those in the control group, but the difference was not statistically significant in the learning results. This could be due to the passive nature of videos; students may not have been actively engaged in constructing their own knowledge or applying the concepts in a meaningful way.

In contrast, the group that participated in hands-on building activities with LEGO^® robots (EG(ER)) exhibited a significantly higher level of understanding. This highlights the power of active learning and the importance of directly engaging with the material. Building the drawing robots, programming their movements, and observing the curves being traced firsthand led to a deeper and more intuitive grasp of the mathematical principles involved. This is likely due to the multi-sensory and problem-solving nature of these activities, which require students to actively think and apply their knowledge in the midterm exam tasks.

The violin plots in Figure 12 display the distribution of the data set for each group, visualising the shape, spread, and central tendency. They combine a box plot with a density plot, allowing us to see where the data is concentrated and how it varies across different values.

7.1. Answer to Research Question RQ1

We investigated whether video-based visualisation alone was enough to significantly improve student understanding of trochoids, compared to traditional lecture-based teaching. To answer this, a control group (CG) received traditional instruction, while an experimental group (EG(V)) received the same traditional instruction and video demonstrations of the robots drawing the curves. The descriptive statistics (Table 4) and the shape of the violin plots (Figure 12) also suggest that there is no statistically significant difference between the CG and EG(V) groups. The overlapping distributions and similar medians indicate comparable central tendencies and variances. A Mann–Whitney U test was then conducted to compare the performance of the CG and EG(V) groups on midterm exam questions related to trochoids. The results showed a U statistic of 444.5 with an asymptotic p-value of 0.356 and an exact p-value of 0.373, as shown in Table 6. Since both p-values are greater than 0.05 (the standard significance level), we failed to reject the null hypothesis. This means that there was no statistically significant difference in the midterm exam scores between the CG and EG(V).

Furthermore, the effect size (r = 0.12) was small, suggesting any observed difference was negligible in practical terms. Although EG(V) had slightly higher average scores (2.84 vs. 2.48), these improvements were not statistically significant. Based on these findings, our answer to research question RQ1 is that simply adding video demonstrations to traditional teaching methods did not result in a measurable improvement in student understanding of trochoids compared to the students who only received traditional instruction.

7.2. Answer to Research Question RQ2

We aimed to examine whether hands-on building activities with educational robotics provided a significant advantage in learning outcomes compared to observing video-based visualisation. To investigate this, we compared two groups: an experimental group that received only video-based instruction (EG(V)) and another experimental group that participated in hands-on building activities using LEGO^® robots (EG(ER)). Both groups received the same traditional instruction in addition to their respective treatments. The violin plot in Figure 12 shows that the scores in the EG(ER) group are higher and more widely distributed than those in the EG(V) group. The descriptive statistics (Table 4) and the shape of the violin plots also suggest that there is a statistically significant difference between the EG(V) and EG(ER) groups.

A Mann–Whitney U test was used to compare the performance of these two groups on midterm exam questions related to trochoids. The results are shown in Table 7. The results of the Mann–Whitney U test revealed a statistically significant difference between EG(V) and EG(ER). The U statistic was 104, with asymptotic and exact p-values less than 0.001. Based on the data, the probability of observing such a large difference between the groups by chance is very low. With such small p-values that are less than 0.05 (the standard significance level), we rejected the null hypothesis, meaning there was a real difference between the learning outcomes of the two groups. Furthermore, the effect size (r = 0.68) was large, showing a strong difference between the groups. The answer to the research question RQ2 is that hands-on building activities had a substantial positive impact on learning outcomes compared to simply watching the videos. The EG(ER) group performed significantly better than the EG(V) group. Our findings indicate that hands-on building activities with educational robotics resulted in significantly improved learning outcomes regarding trochoids compared to learning based solely on video demonstrations. The hands-on approach provided a deeper level of understanding and knowledge retention.

When performing statistical calculations, we also aimed to compare the results of the CG group with those of the EG(ER) group. The results of the Mann–Whitney test indicate that the EG(ER) group statistically significantly outperformed the CG group in terms of points scored, as shown in Table 8.

7.3. Connection to Previous Results

Our findings align with constructivist learning theories, emphasising the importance of actively constructing knowledge through experience and environmental interaction. The core principle of constructivism is that meaningful knowledge and critical thinking are actively built through cognitive, cultural, emotional, and social processes. It emphasises that individual learning is an active process, involving engagement and participation within the learning environment (Zajda, 2021). The results contribute positively to the growing body of research highlighting the benefits of integrating educational robotics and STEAM-based approaches into mathematics education (Lopez-Caudana et al., 2020; López-Belmonte et al., 2021; Ouyang & Xu, 2024; Suarez et al., 2023; Zhong & Xia, 2020). The experience showed that if mathematics is supported with hands-on exercises, students are more engaged and learning outcomes are significantly better.

The findings of this study complement previous research in mathematics education and the integration of technology (Cirneanu & Moldoveanu, 2024; Szilágyi et al., 2024). The fact that video demonstrations alone were insufficient for a significant improvement aligns with studies questioning the effectiveness of passive learning methods and the need for active engagement. The study of Shao et al. (2024) examines whether science education videos can replace practical experiments. The results show that science education videos should only provide an alternative to practical experiments if the appropriate equipment is not available. The significant improvement observed in the hands-on robotics group (EG(ER)) supports the growing body of literature highlighting the benefits of constructivist approaches in learning. Specifically, the research by Samuel et al. (2025), which indicated that LEGO^® robots were the most frequently used robot type in mathematics education and that most studies focused on applied mathematics topics, has some relation. While previous studies have been conducted, they focused primarily on secondary school children; in our research, we focus on university students.

This study also reinforces the findings of Szilágyi et al. (2024), which found that a four-stage STEAM-based methodology using educational robotics and dynamic geometry software significantly improved engineering students’ understanding of cycloidal curves (specifically epi- and hypotrochoids). However, the current study focuses on trochoids. The previous studies explored Desmos as an aid, and our current research uses it to plot results and check equations. The current study offers evidence that the advantages of adding technology to education are worth it. As seen through the research, adding robots creates a space to test mathematical equations in a physical sense. In conclusion, the results of this study are consistent with and build upon the findings of prior research, solidifying the idea that active, hands-on learning experiences, particularly those facilitated by educational robotics, are powerful tools for enhancing mathematical understanding and fostering deeper engagement in STEM/STEAM disciplines.

The use of LEGO^® SPIKE Prime kits in tertiary engineering education is growing. For example, Nguyen et al. (2023) presented a novel approach to science education by constructing an atomic force microscope (AFM) using the LEGO^® Education SPIKE Prime kit. This innovative method provides a cost-effective and accessible alternative to traditional, expensive AFMs, making it easier to teach nanoscale science principles. Assante et al. (2024) introduced a LEGO-based online laboratory for remote industrial robotics education. It leverages pre-assembled LEGO^® SPIKE robots that are accessible and controllable remotely, overcoming the need for physical interaction. The authors detail the remote laboratory architecture and hardware and present a practical implementation of industrial robots.

Trochoids play an important role in the design of effective gear systems. A related concept is the epitrochoid, which describes the path traced by a point on a circle that rolls around the outside of a fixed circle. Epitrochoid curves offer benefits in gear design by enabling greater rolling contact, which helps minimise friction on tooth surfaces and improves the overall durability of the gears (Jeong et al., 2025). Understanding trochoids and other cycloidal curves is crucial in engineering and IT education because these curves remain fundamental in a wide range of active research fields nowadays, as demonstrated in the works of Gao et al. (2025); González-Durán et al. (2024); Jeong et al. (2025); Lemaitre et al. (2022); Song et al. (2023); Vasić et al. (2025), among others. Cycloidal curves have been used in optics, mechanics, biomechanics and advanced machine design, becoming essential to modern engineering knowledge and innovation.

8. Conclusions and Recommendations

Traditional visual representation methods, such as kinematic models used to illustrate motion-related curves, gradually disappeared from university mathematics education in the second half of the 20th century. This trend can be explained primarily by changes in learning methods, the development of computer technology, and the spread of interactive teaching tools. Modern digital tools have partially replaced the old illustrative tools. The importance of traditional, hand-drawn illustrations and physical models has decreased, and the emphasis has shifted towards information and communication visualisation techniques, such as computer graphics, simulations, and dynamic models. This process accelerated in the 1980s, when computers became more widely available in education. Rapid technological advances of the last century have made it possible to create more interactive, dynamic, and personalised visualisation methods that are also effective for modern learners. However, this does not necessarily mean the old methods have lost value. The educational toolkit constantly expands and is worth using to achieve the best results. Traditional kinematic models and demonstration tools were very valuable because they helped students understand the basic concepts of motion more easily by visually perceiving the changes. They provided first-hand experience.

Personal experience and practical activities are very valuable in education, especially in mathematics and physics. With models built from LEGO^® robot kits, students can create kinematic models and see how they work first-hand. They can study the movements. They can easily modify the models they have built, making it easy to study the changes. This method not only deepens theoretical knowledge but also develops problem-solving skills, creativity, and collaboration. At the same time, modern visualisation tools allow for simulations and the study of more complex movements and dynamics, resulting in a richer, more comprehensive learning experience. This pedagogical approach allows students to actively participate in the learning process and understand the theoretical background through their own experience.

Using Desmos Graphing Calculator or other interactive visualisation tools can be an optimal complement to practical activities. By creating animations, students can dynamically see and interpret motion processes, changes, and relationships, resulting in a deeper understanding. These tools allow students to create, modify, and analyse models themselves, making them active participants in the learning process. In addition, they develop their graphical, analytical and applied skills and help to connect complex concepts in an easily understandable visual form. This combination of gaining experience with LEGO^® robots and then visualising and animating theoretical models using Desmos is an effective, modern, and enjoyable way to teach mathematics and physics.

In the future, educators should consider incorporating hands-on activities and active learning strategies into their mathematics courses to promote deeper understanding and greater student engagement. Educational robotics provides a powerful tool for achieving these goals, and further research is needed to explore the optimal ways to integrate such technologies into the curriculum and assess their long-term impact on student learning and motivation. While video demonstrations can be valuable as supplementary resources, the findings suggest that they are not a sufficient replacement for direct, hands-on engagement with the material. The integration of practical, hands-on activities is essential to acquire deeper, more active, and more applicable knowledge. For this reason, we recommend that instructors prefer practical activities over video instruction whenever possible.

9. Limitations

The findings of this study should be interpreted considering several limitations. The study was conducted with a specific group of students (first-year IT BSc students at a Hungarian university). The results may not be generalisable to other populations, such as students in different fields of study, at different types of institutions, or in different cultural contexts. Moreover, the sample had a low number of female participants, reflecting the global trend of underrepresentation of women in IT. Replicating the study with a more gender-balanced sample could provide additional information on the effectiveness of the intervention in different demographic groups and address potential gender-specific learning patterns.

In this study, we only relied on midterm exam scores. However, the sole measure of learning outcomes may not capture the full extent of student understanding and retention, potentially overlooking the development of deeper conceptual knowledge or problem-solving skills. Longitudinal studies are needed to assess the long-term impact of the intervention on students’ mathematical proficiency and attitudes toward STEM fields.

LEGO^® robot-based activities require a significant number of building elements, limiting the number of students who can participate effectively in a single session, potentially making them challenging to implement with large classes. Alternative hands-on activities or technologies could be explored to achieve similar learning outcomes in different contexts. Furthermore, the construction and experimentation phases with the LEGO^® robots require a suitable space to accommodate building and drawing, which could pose logistical constraints for certain institutions or classrooms. The LEGO^® robot activities also necessitate attention to practical matters such as ensuring that the robot hubs are adequately charged before and during sessions, and providing technical support to troubleshoot any mechanical or programming issues that may arise. These demands could create additional burdens for instructors and potentially disrupt the learning flow.

Furthermore, the study may be subject to self-selection bias, as students who chose to participate in the experimental groups (particularly the EG(ER) group involving hands-on LEGO^® activities) might already have had a pre-existing interest in or aptitude for robotics, mathematics, or hands-on learning, which could have influenced their performance. This self-selection effect could lead to an overestimation of the impact of the intervention. Future research could consider strategies to mitigate self-selection bias, such as the random assignment of students to treatment groups or collecting data on students’ pre-existing interests and skills to control for these factors in the analysis. At the same time, in educational experiments in tertiary education, it is often challenging to mitigate self-selection bias, as students cannot be required to participate in activities outside the regular curriculum.