Preservice Mathematics Teachers’ Mathematical Modeling Competencies: Mathematical Beliefs Perspective

Abstract

This study investigated the relationship between preservice elementary mathematics teachers’ beliefs about mathematics and their mathematical modeling competencies. In the study, the belief categories of the preservice teachers were first determined using Q methodology and then classified into traditional and non-traditional belief. A Mathematical Modeling Competencies Rubric was developed in line with the literature and expert opinions. Three independent experts used this rubric to evaluate holistic modeling tasks that the participants completed. The resulting scores were analyzed using the Many-Facet Rasch Model to test for differences in modeling competencies among the belief groups. The findings revealed that preservice mathematics teachers with non-traditional beliefs demonstrated higher modeling competencies than those with traditional beliefs (χ² = 84.7, df = 3, p < 0.001). In conclusion, the study highlights that preservice mathematics teachers’ beliefs about mathematics play a crucial role in developing modeling competencies and suggests that belief structures should be considered in teacher education programs.

1. Introduction

In recent years, rapid technological advancement has accelerated societal change and reshaped the knowledge and skills required of individuals. Especially in the face of complex real-world problems—such as pandemics—that may affect future living conditions, enabling individuals to make informed, evidence-based decisions highlights the importance of mathematics, and particularly mathematical modeling (Siller et al., 2024). Similarly, OECD (2024) emphasizes that mathematics education should not only foster conceptual understanding but also develop problem-solving and modeling skills, support the effective use of technology, and encourage collaboration in addressing real-world problems. In this context, it has been highlighted that students should be introduced to modeling activities that provide opportunities to analyze real-life situations and to engage with a variety of mathematical concepts and tools (Niss et al., 2007; R. A. Lesh & Doerr, 2003). Therefore, implementing mathematical modeling activities is important in enabling students to apply their mathematical knowledge, formulate problems, and interpret their solutions. Moreover, beliefs about mathematics play a significant role in students’ mathematics learning and problem-solving (Op’t Eynde et al., 2002). Additionally, the literature suggests that students’ beliefs about mathematics have a significant impact on their mathematical modeling competencies (Ärlebäck, 2009; Ferri, 2011; Kaiser & Maaß, 2007). However, empirical research directly examining how preservice teachers’ mathematical modeling competencies differ across distinct belief profiles is lacking, leaving a gap in understanding the relationship between beliefs and modeling skills in teacher education. In this context, the present study examines the mathematical modeling competencies of preservice teachers across different belief profiles.

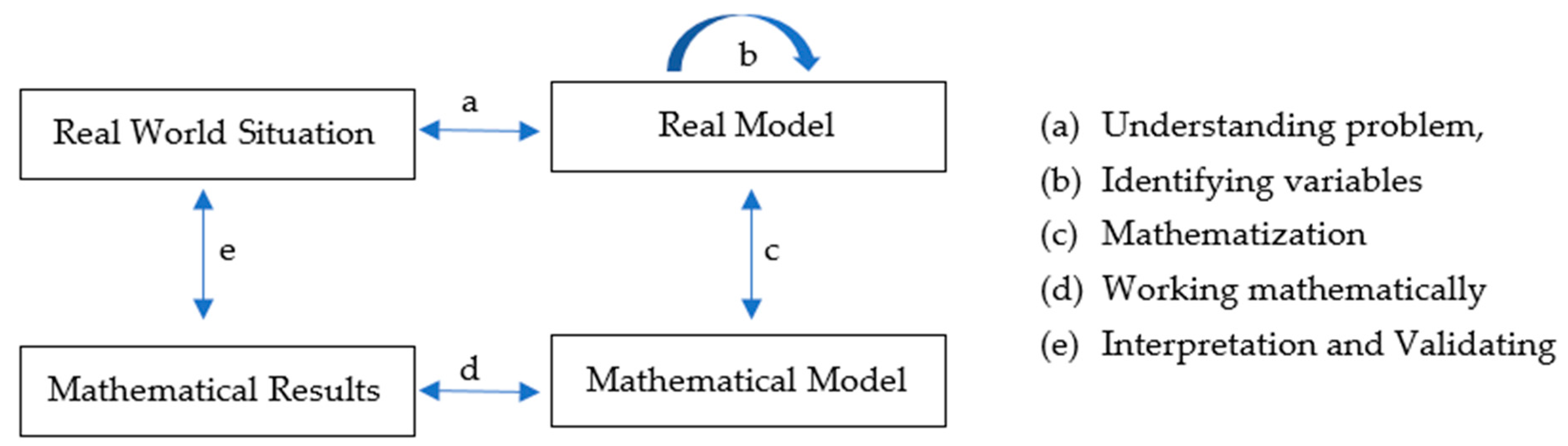
1.1. Mathematical Modeling and Mathematical Modeling Competencies

Mathematical modeling is an iterative, cyclical process used in numerous fields, ranging from the natural to the social sciences (Czocher et al., 2020). It encompasses selection, assumption, and decision-making processes, with the objective of elucidating real-world phenomena or forecasting the future behavior of systems (Cirillo et al., 2016). In other words, mathematical modeling is a process that enables problem-solving, making predictions, and examining observable phenomena arising in real life or other disciplines (English, 2006; Neunzert, 2015; Taite & DiNapoli, 2025). As different researchers have approached mathematical modeling through various perspectives in the literature, this process has been explained by different modeling cycles (Blum & Leiß, 2007; R. A. Lesh & Doerr, 2003; Stillman et al., 2007; Kaiser & Stender, 2013; Ferri, 2018). Nevertheless, examining these cycles reveals that mathematical modeling is essentially a cyclical process comprising four essential stages: first, understanding of the problem; then, its mathematization; next, the production of mathematical results; and finally, their interpretation and validation. Mathematical modeling competencies, on the other hand, are defined as the processes involved in the modeling cycle (Niss et al., 2007; Kaiser, 2007; Maaß, 2006; Zöttl et al., 2010; Mischo & Maaß, 2012). Similarly, mathematical modeling competencies are described as the ability to possess the necessary skills, capabilities, and attitudes to effectively carry out the modeling process (Maaß, 2006; Zöttl et al., 2010). As a result, mathematical modeling competencies are often defined in the literature as a set of cognitive and motivational skills necessary to complete the modeling cycle successfully. In this study, based on the definitions outlined in the literature, mathematical modeling competencies (selected from Blum & Leiß, 2007) are addressed in Figure 1.

1.2. Mathematical Beliefs

Beliefs are defined as emotions, understandings, and thoughts that can be conscious or unconscious and are shaped by an individual’s experiences (Furinghetti & Pehkonen, 2002; Pehkonen & Pietilä, 2003), guiding their behaviors (Pajares, 1992; Philipp, 2007), attributed to truth (Goldin, 2002), and influencing their cognitive and affective characteristics (Cross, 2009; Philipp, 2007). Mathematical beliefs, on the other hand, are defined as personal perspectives and worldviews that shape an individual’s approach to mathematical engagement and understanding, stemming from their past mathematical experiences (Cross, 2009; Raymond, 1997), and include cognitive and affective features (Schoenfeld, 1992; Ernest, 1989; Grigutsch & Törner, 1998). In this regard, researchers have examined mathematical beliefs from various perspectives (see Ernest, 1989; Törner & Pehkonen, 1999; Dede & Karakuş, 2014). For example, Ernest (1989) addresses mathematical beliefs as operational, platonist, and problem-solving, while Törner and Pehkonen (1999) examine them as toolbox, system, and process. A thorough examination of these definitions reveals aspects that are conceptually similar between them. Indeed, Ernest’s (1989) operational view aligns with Törner and Pehkonen’s (1999) toolbox perspective, both emphasizing the rule, operation, and definition dimensions of mathematics. In this study, the categories of traditional belief, transitional belief, and non-traditional belief, proposed by Dede and Karakuş (2014) based on different perspectives of mathematical beliefs, are utilized. This classification is found to align with the definitions of Ernest (1989) and Törner & Pehkonen (1999). The characteristics of the mathematical belief categories are as follows: Traditional belief views mathematics as a set of rules and operations, associating mathematics with using formulas and methods. This view is often reflected in statements by preservice teachers such as “Only talented people can learn mathematics,” “Mathematics is best learned by memorization,” or “Mathematics consists of unrelated rules.” Transitional belief views mathematics as static and dynamic, absolute and relative, incorporating characteristics of both traditional and non-traditional belief categories. Typical expressions of this view, as stated by preservice teachers, include “Mathematics is both dynamic and static,” “Mathematics learning should be both student-centered and teacher-centered,” and “Mathematics is abstract but also concrete.” Non-traditional belief, on the other hand, views mathematics as dynamic, continuously evolving, discovered, related to real life, and interconnected. Preservice teachers expressing this view often state that “Mathematics is an integral part of our lives,” “Mathematics is learned by doing and experiencing,” and “Mathematics provides a foundation for other disciplines.”

1.3. Mathematical Modeling and Mathematical Beliefs

The mathematical modeling process begins with the understanding of a real-life problem. Ferri (2006) states that after understanding the real situation, the next phase involves the mental representation of the real model, while Blum and Leiß (2007) suggest that a “situational model” is created during this phase. As the mental representation of the real model is developed, individuals simplify the model into a more manageable form through their cognitive processes. Lawson and Marion (2008/2023) argue that the model developed in this process also reflects individuals’ beliefs about the model. Similarly, Blum and Leiß (2007) emphasize that the situational model, which emerges during the problem understanding phase, is unique to the individual and shaped according to personal differences. Therefore, it can be said that individuals’ personal views and perceptions of the given situation are incorporated into the modeling process when creating the situational model. Ferri and Lesh (2013) have stated that in problem-solving, mathematical modeling, interpretation, and decision-making processes, individuals utilize not only their cognitive characteristics but also their affective traits, beliefs, and tendencies. Similarly, De Corte et al. (2000) also point out that students’ problem-solving behaviors are related to their knowledge and beliefs. Schoenfeld (1992) highlights that beliefs about mathematics influence how individuals engage in mathematical actions and, therefore, may be related to their problem-solving competency. In this context, it can be said that mathematical modeling competencies can also be influenced by individuals’ affective characteristics, beliefs, and tendencies. Neunzert (2015) states that models reflect our beliefs about how the external world operates, and mathematical modeling can be viewed as a transformation of our thoughts into mathematical language. Similarly, R. A. Lesh and Doerr (2003) indicate that models are created for specific situations and purposes; therefore, they reflect individuals’ personal views and beliefs. Furthermore, Ferri and Lesh (2013) emphasize that beliefs have a significant effect on modeling processes, which can be considered part of mathematical modeling competencies. Mischo and Maaß (2012) also suggest that beliefs about mathematics affect all stages of mathematical modeling, including mathematical modeling competencies. Ärlebäck (2009) specifically points out the importance of beliefs for mathematizing and interpreting competencies. Consequently, it can be said that the role of beliefs and affective traits in mathematical modeling is frequently noted in the literature (see Ferri, 2011; Kaiser & Maaß, 2007).

1.4. Aim and Rationale of the Study

A growing body of literature is exploring the development of mathematical modeling competencies. Prior research has examined these competencies at various educational levels, including middle school (Biccard & Wessels, 2017), high school (Kaiser & Brand, 2015; Beckschulte, 2020), and university (de Villiers & Wessels, 2020; Durandt & Lautenbach, 2020). In addition, topic-focused studies (Engel & Kuntze, 2011; Fakhrunisa & Hasanah, 2020) and research employing various methodological approaches (e.g., Durandt & Lautenbach, 2020; Kaiser & Brand, 2015) have investigated different dimensions of mathematical modeling competencies. However, most of these studies have focused on the development of students’ modeling competencies and have not addressed participants’ mathematical beliefs in relation to these competencies. Although some studies have examined both mathematical modeling competencies and beliefs about mathematics (Wess et al., 2021; Mischo & Maaß, 2012, 2013), they typically treated beliefs as a single variable rather than categorizing individuals according to belief profiles to explore differences in modeling competencies. Moreover, while previous research has highlighted the importance of beliefs in problem-solving (Schoenfeld, 2015) and in mathematical modeling processes (Mischo & Maaß, 2012; Ferri & Lesh, 2013), no empirical study has investigated the modeling competencies of preservice teachers across different mathematical belief profiles. In this context, to address this gap, it is crucial to identify students’ beliefs about mathematics, explore the relationship between these beliefs and mathematical modeling competencies, and examine the modeling competencies of students in different belief categories. Thus, this study examines the mathematical modeling competencies of preservice elementary mathematics teachers in relation to their beliefs about mathematics. The research question is as follows:

Do preservice mathematics teachers in different mathematical belief categories exhibit statistically significant differences in their mathematical modeling competencies?

2. Materials and Methods

In this study, the modeling competencies of preservice teachers were examined according to their beliefs about mathematics. The type of mathematical belief held by the preservice teachers was determined statistically using Q methodology. Random assignment reduces bias by ensuring that participants are assigned to groups in a statistically grounded, chance-based manner (Duchateau et al., 2024); therefore, similarly, determining the belief categories of preservice teachers in a statistically grounded manner may support the validity of the obtained results. The study was conducted at the university level in Türkiye. The study group consists of 12 preservice teachers. The preservice teachers involved in the study have taken courses such as General Mathematics, Abstract Mathematics, Geometry, Analysis, and Linear Algebra. Given that they have taken these courses, it is expected that they will be able to provide adequate responses and offer interpretations for the mathematical modeling activities during the research process. Therefore, these preservice teachers were considered an appropriate study group for determining their mathematical modeling competencies. Prior to data collection, all participants were fully informed about the study’s objectives and procedures. They were assured of confidentiality and anonymity, informed that participation was voluntary, and that they could withdraw at any time without consequences. Written informed consent was obtained from all adult participants, and parental consent was obtained for student participants. While forming these groups, attention was paid to ensuring that there was no statistically significant difference in the preservice teachers’ academic achievements, as well as their beliefs about mathematics. According to the analysis conducted using Q methodology, the preservice teachers fell into two categories: traditional and non-traditional beliefs. Accordingly, the groups listed in

Table 1. Groups According to Belief Categories Related to Mathematics.

	Groups According to Belief Categories
	NTB	MB1	MB2	TB
Individuals According to Belief Categories	NTB	NTB	NTB	TB
	NTB	TB	NTB	TB
	NTB	TB	TB	TB

have been formed: Non-Traditional Belief [NTB], Traditional Belief [TB], Mixed Belief 1 Group [MB1], Mixed Belief 2 Group [MB2]. Four groups have been formed based on these criteria to examine their modeling competencies. The details of these groups are provided in Table 1.

In the NTB group, all individuals hold non-traditional beliefs about mathematics, whereas in the TB group, all individuals hold traditional beliefs. The MB1 group consists of one individual with a non-traditional belief and two individuals with traditional beliefs, while the MB2 group consists of two individuals with non-traditional beliefs and one individual with a traditional belief. It has also been determined that there is no statistically significant difference in the general academic achievement scores of the preservice teachers in the NTB, TB, MB1, and MB2 groups [H(3) = 1.66, p > 0.05]. The mean general academic achievement scores of the preservice teachers’ belief groups are presented in

Table 2. Number of Participants in Each Group Based on Their Belief Categories Related to Mathematics.

Groups According to Belief Categories	n	Mean
NTB	3	3.26
TB	3	3.1
MB1	3	3.04
MB2	3	3.29

.

Two approaches to developing students’ mathematical modeling competencies stand out in the literature: holistic and atomistic (Blomhøj, 2007; Blomhøj & Jensen, 2003; Haines et al., 2003; Kaiser & Brand, 2015). The holistic approach aims for students to experience the entire process and develop all modeling competencies, while the atomistic approach focuses on specific modeling competencies such as mathematical analysis, mathematization, and mathematical work (Blomhøj & Jensen, 2003). However, it is emphasized that both approaches should be used together, as purely holistic practices may overlook some competencies (Blomhøj & Kjeldsen, 2006; Zöttl et al., 2010). In line with this, the present study designs an instructional environment that integrates holistic and atomistic modeling competencies based on Swanson and Law’s (1993) whole-part-whole teaching model. Thus, by combining the holistic and atomistic approaches, the aim is to create a more effective learning environment that leverages the strengths of both methods. To this end, the learning plan was structured into three sections in accordance with the whole-part-whole learning model. In the first section, basic information on mathematical modeling was provided to the preservice teachers, and two activities aligned with the holistic approach, involving real-life situations, were introduced. In the second section, atomistic activities focusing on each modeling competency were applied in accordance with the whole-part-whole model. The preservice teachers first solved the activities individually and then had the opportunity to discuss them in class, allowing them to identify errors and improve their solutions. In the third section, preservice teachers were encouraged to reassemble the knowledge and experiences gained in the previous stages, establish connections between modeling competencies, and make these competencies more meaningful and relevant. As a result, the preservice teachers had the opportunity to approach and restructure their modeling competencies holistically through modeling activities. The activities conducted through group work enabled participants to engage more deeply in modeling competencies by enhancing their participation, communication, and collaboration skills throughout the process. The holistic activities used in the study were adapted from well-established and widely documented tasks in the literature that include all stages of the modeling cycle to ensure the validity of the results (see Blum & Ferri, 2009; Ferri, 2006; R. Lesh et al., 1997; R. A. Lesh & Doerr, 2003; Maaß & Gurlitt, 2009). The atomistic activities, on the other hand, were developed by drawing on studies from the literature on mathematical modeling (see Berry & Houston, 1995; Edwards & Hamson, 1996; Giordano et al., 2014; Kaur & Dindyal, 2010; Masterton-Gibbons, 2007). For example, in the Lighthouse Modelling Task adapted to local context from the study by Blum and Ferri (2009), participants are asked to determine how far from the shore a ship is when its crew first sees the light of the lighthouse. This activity requires students to interpret a real-world context, identify relevant variables (such as the height of the lighthouse and the curvature of the Earth), formulate mathematical relationships to represent the situation, carry out the necessary calculations, and finally interpret and validate their results.

A Mathematical Modeling Competency Rubric was developed to thoroughly examine the mathematical modeling competencies of the preservice teachers in groups formed according to their belief categories. The analytical rubric method was chosen to evaluate each competency separately, and a general rubric type was used to evaluate solutions for all modeling activities, not just a single activity. When developing the rubric categories, modeling cycles in the literature were reviewed (see Kaiser & Stender, 2013; Ferri, 2006; Blum & Leiß, 2007; Houston, 2007; Lingefjärd, 2004), and the opinions of two mathematics educators with experience in modeling were utilized. As a result of this process, consensus was reached that modeling competencies consist of five main components, and the rubric was structured accordingly. These components are (a) understanding the problem, (b) identifying variables, (c) mathematization, (d) working mathematically, and (e) interpretation and validation (see Figure 1). When determining the performance levels for each modeling competency, the highest performance level was defined first, and other levels were created in reference to this benchmark. In this context, it was decided that each competency would consist of four performance levels. As emphasized by Brookhart (2013), the defined levels were ensured to be clear, understandable, observable, distinct, and free from relative expressions. The solutions to the five holistic modeling activities were evaluated by three independent raters experienced in mathematical modeling, using the developed rubric. The resulting scores were analyzed quantitatively through the Many-Facet Rasch Model (MFRM). The rubric is presented in Appendix A.

3. Results

Unlike classical test theory, the Many-Facet Rasch Analysis can predict facet parameters independently of item, rater, test, and group characteristics (Toffoli et al., 2016). Furthermore, it calibrates each facet independently of the others and standardizes them on a common logit scale, thus providing the ability to not only predict individuals’ abilities in assessments using rubrics with multiple and ordinal categories but also to compare the strictness of raters and the difficulty of items (Prieto & Nieto, 2014). In this context, the potential significant differences in the modeling competencies of groups formed according to belief types were examined using the Many-Facet Rasch Analysis. The data were obtained by evaluating the solutions of five holistic modeling activities by preservice teachers, which were assessed by three experts using the rubric. The general equation of the Many-Facet Rasch Analysis is as follows (Eckes, 2015):

$$\log \left[{\displaystyle \frac{P_{nljk}}{P_{nljk-1}}}\right]={\theta }_n-{\delta }_l-{\alpha }_j-{\tau }_k$$

$P_{nljk}$: The probability of individual n obtaining score k from rater j on item l;

$P_{nljk-1}$: The probability of individual n obtaining score k − 1 from rater j on item l;

${\theta }_n$: The ability of individual n;

${\delta }_l$: The difficulty of item l;

${\alpha }_j$: The strictness level of rater j;

${\tau }_k$: The difficulty level of category k related to category k – 1.

Table 3. Modeling Competency Performance Based on Mathematical Belief Types with Many-Facet Rasch Analysis.

Group	Logit	Standard Error	Infit	Outfit
NTB	2.33	0.25	1.23	1.22
TB	−0.60	0.23	0.88	0.86
MB1	0.76	0.25	0.72	0.64
MB2	1.76	0.25	1.15	1.07
Mean	1.06	0.25	0.99	0.95
Standard Deviation (Population)	1.11	0.01	0.20	0.22
Standard Deviation (Sample)	1.29	0.01	0.24	0.25
Model, Population:	RMSE: 0.25 Standard Deviation: 1.09 Separation: 4.41 Reliability: 0.95
Model, Sample:	RMSE: 0.21 Standard Deviation: 1.68 Separation: 5.12 Reliability: 0.96
Model, Fixed (All Same) Chi-Square: 84.7 sd: 3 p = 0.000
Model, Random (Normal) Chi-Square: 2.9 sd: 2 p = 0.23

presents the Many-Facet Rasch analysis measurements for the modeling competency performances of the groups formed according to belief types. The highest logit measurement is 2.33, while the lowest logit measurement is −0.60 (higher logit values indicate stronger modeling competency performance). The logit measurement range for the groups’ modeling competency performances is 2.93. The NTB group showed the highest performance, while the TB group demonstrated the lowest performance. As seen in Table 3, the fit statistics for both in-fit and out-fit fall between the accepted values of 0.5 and 1.5. This finding indicates that the model and data fit well (Wright & Linacre, 1994). Additionally, the reliability statistic, which shows the repeatability of the same results (Linacre, 2012), was found to be 0.96. This value demonstrates that the groups formed according to belief types can be reliably differentiated based on their modeling competency performances. The separation index is 5.12, and the reliability statistic is 0.96. The hypothesis “Groups constructed according to belief types show a significant difference in mathematical modeling competencies” was tested using the Chi-Square test, and the results revealed that the null hypothesis was rejected (χ² = 84.7, sd = 3, p = 0.00). In other words, at least two of the groups formed according to belief types show a significant difference in modeling competency performance. To identify which groups show significant differences from each other, it is necessary to calculate the t-value for each group’s measurements (Eckes, 2015; Myford & Wolfe, 2004; Vianello & Robusto, 2010). To test this, the Wald statistic, originally proposed by Fischer and Scheiblechner (1970) and described in detail by Eckes (2015), can be used to examine model–data fit:

$$t_{n,m}={\displaystyle \frac{{\widehat{\theta }}_n-{\widehat{\theta }}_m}{{\left({SE}_n^2+{SE}_m^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}}.$$

Here, n and m represent the individuals whose ability levels are being compared. ${\widehat{\theta }}_n$ and ${\widehat{\theta }}_m$ represent the logit measurements of the relevant individuals, and ${SE}_n$ and ${SE}_m$ represent the standard errors of the measurements for these individuals.

The logit measurements and scoring of the groups’ modeling competencies are presented in

Table 4. Logit Measurements and Scoring of the Groups’ Modeling Competencies.

Groups	Logit	Standard Error	Scorings
NTB	2.33	0.25	15
TB	−0.60	0.23	15
MB1	0.76	0.25	15
MB2	1.76	0.25	15

.

There is a difference of 0.57 logit between the NTB and the MB2, as can be seen in Table 4. This difference is not statistically significant $t_{NTB,MB2}\left(28\right)=$ 1.6, p > 0.05. No significant difference was found in modeling competency performance between the group consisting of preservice teachers in the non-traditional belief category (NTB) and those in other belief categories (MB2). There is a 1.57 logit difference between the NTB and the MB1. This difference is statistically significant $t_{NTB,MB1}\left(28\right)=$ 4.4, p < 0.01. It can be stated that there is a significant difference in modeling competency performance between the group consisting of preservice teachers in the non-traditional belief category (NTB) and the group consisting of teachers with different belief types (MB1). There is a 2.93 logit difference between the NTB and the TB. This difference is statistically significant $t_{NTB,TB}\left(28\right)=$ 8.9, p < 0.01. It can be said that there is a significant difference in modeling competency performance between the group consisting of preservice teachers in the non-traditional belief category (NTB) and the group consisting of preservice teachers in the traditional belief category (TB). There is a 1 logit difference between the MB1 and the MB2 groups. This difference is statistically significant $t_{MB2,MB1}\left(28\right)=$ 2.8, p < 0.01. It can be stated that there is a significant difference in modeling competency performance between the groups formed by preservice teachers in different belief types (MB2 and MB1), and this difference is in favor of the group with a higher number of preservice teachers in the non-traditional belief category (MB2). There is a 2.36 logit difference between the MB2 and TB groups. This difference is statistically significant $t_{MB2,TB}\left(28\right)=$ 7.1, p < 0.01. It can be stated that there is a significant difference in modeling competency performance between the group consisting of preservice teachers in different belief types (MB2) and the group consisting of teachers in the traditional belief category (TB). There is a 1.36 logit difference between the MB1 and TB groups. This difference is statistically significant $t_{MB1,TB}\left(28\right)=$ 4.1, p < 0.01. It can be stated that there is a significant difference in modeling competency performance between the group consisting of preservice teachers in different belief types (MB1) and the group consisting of teachers in the traditional belief category (TB). The Wald test results summarizing these group differences in modeling competencies are presented in

Table 5. Groups’ Modeling Competencies Logit Measurement Difference Wald Test Results.

Groups	sd	t	p
NTB-MB2	28	1.6	p > 0.05
NTB-MB1	28	4.4	p < 0.05
NTB-TB	28	8.9	p < 0.05
MB2-MB1	28	2.8	p < 0.05
MB2-TB	28	7.1	p < 0.05
MB1-TB	28	4.1	p < 0.05

.

4. Discussion

According to the Many-Facet Rasch Analysis results, the difference between the NTB group and the MB2 group was not statistically significant. However, the differences between the NTB group and the MB1 group, the NTB group and the TB group, the MB1 group and the MB2 group, the MB2 group and the TB group, and the MB1 group and the TB group were statistically significant. When the MFRA findings are evaluated overall, it can be said that the groups of preservice teachers in the non-traditional belief category performed better in modeling competencies than the other groups. These results are consistent with the findings of Mischo and Maaß (2012), who stated that viewing mathematics as unchanging, which can be considered a traditional belief, has a negative impact on modeling competencies, whereas viewing mathematics as a useful tool (non-traditional belief) has a positive impact on modeling competencies. Similarly, Kaiser and Maaß (2007) stated that preservice teachers in the non-traditional belief category exhibit a positive attitude towards mathematical modeling. In contrast, those in the traditional belief category exhibit a negative attitude towards mathematical modeling. The difference in the logit scores of the mathematical modeling competencies of preservice teachers in different belief categories, in favor of the non-traditional belief category, may be due to the positive impact of preservice teachers’ perspectives and affective traits related to mathematical modeling, as noted by Mischo and Maaß (2012) and Kaiser and Maaß (2007). Additionally, this result may be related to the characteristics of the belief types about mathematics. This is because preservice teachers in the non-traditional belief category tend to believe that mathematics is intertwined with everyday life and forms the foundation of other scientific disciplines, whereas those in the traditional belief category regard mathematics as consisting of immutable, isolated rules with only one correct solution path (Ernest, 1989; Grigutsch & Törner, 1998). In this context, the mathematical modeling process—which requires expressing real-world problems in mathematical terms and thus aligns more closely with the non-traditional perspective—may have been associated with increased engagement among preservice teachers in the non-traditional belief category. Consistent with this interpretation, Mischo and Maaß (2012) found that students holding traditional and rigid beliefs about mathematics were less motivated to solve modeling tasks compared to those who regarded mathematics as a useful tool for addressing real-world problems. This factor may therefore help explain the differences in modeling competencies observed between preservice teachers in the non-traditional and traditional belief categories.

5. Conclusions

In conclusion, it can be stated that the types of beliefs held by preservice teachers about mathematics play a significant role in their mathematical modeling competencies in this study. Preservice teachers with non-traditional beliefs, whose perspectives on mathematics are grounded in life experiences and exploration (see Ernest, 1989; Grigutsch & Törner, 1998), demonstrated higher performance in modeling activities. In contrast, it can be said that preservice teachers with traditional beliefs, who view mathematics as a set of unchanging rules, were more limited in their modeling processes. This finding suggests that beliefs about mathematics are an important factor that should be considered in developing preservice teachers’ modeling competencies. Therefore, it may be argued that fostering changes in preservice teachers’ beliefs about mathematics throughout their educational life has the potential to contribute to the development of their mathematical modeling competencies. In this context, considering that students’ beliefs about mathematics stem from their past mathematical experiences (Cross, 2009; Raymond, 1997) and that teachers play a significant role in shaping these experiences, as highlighted by Mischo and Maaß (2012), the adoption of teaching approaches grounded in non-traditional beliefs about mathematics may encourage students to develop such beliefs; consequently, this may help them to engage more effectively with mathematical modeling processes and to achieve greater success in this area. Additionally, the Q methodology used in this study, which effectively classifies pre-service teachers according to their belief profiles and enables the examination of individuals’ subjective perspectives by grouping them according to their personal viewpoints, can also be applied to investigate other perceptual characteristics, such as attitudes, values, and perceptions related to mathematics education. Furthermore, in future research, the use of the Many-Facet Rasch Model (MFRM) can account for and separate the effects of item, rater, test, and group characteristics, allowing measurements to be estimated more independently and impartially, thereby helping to reduce potential statistical biases.