Number Line Strategies of Students with Mathematical Learning Difficulties and Students with General Learning Difficulties: Findings Through Eye Tracking
Abstract
1. Introduction
1.1. Number Line
1.2. Students with Mathematical Learning Difficulties
1.3. Students with General Learning Difficulties
1.4. Eye Tracking and Conceptual Framework
1.5. Aim and Research Question
2. Materials and Methods
2.1. Participants
2.2. Eye Tracking Device
2.3. Tasks
2.4. Procedure
2.5. Qualitative Data Analysis
2.6. Statistical Analysis
3. Results
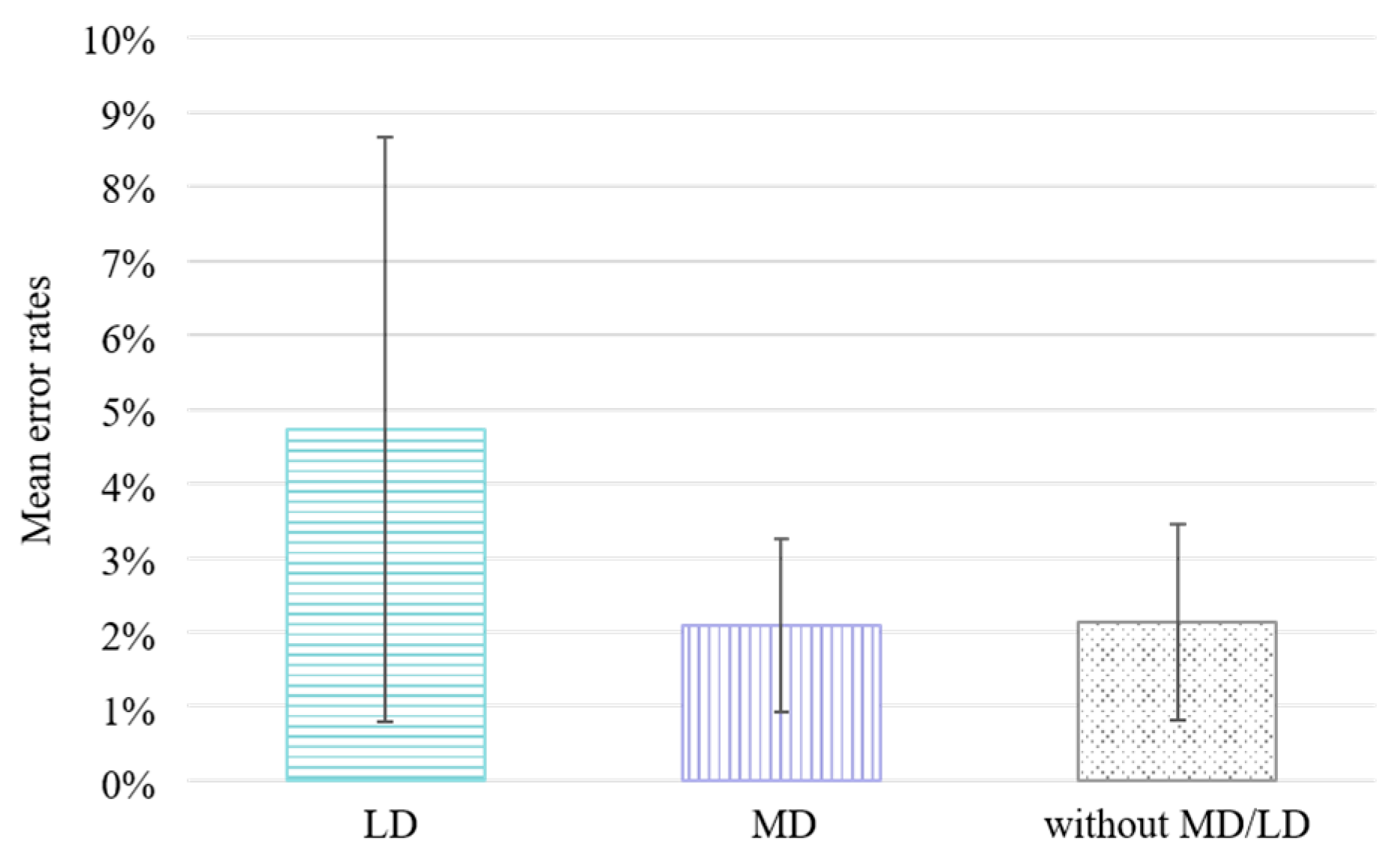
3.1. Error Rates
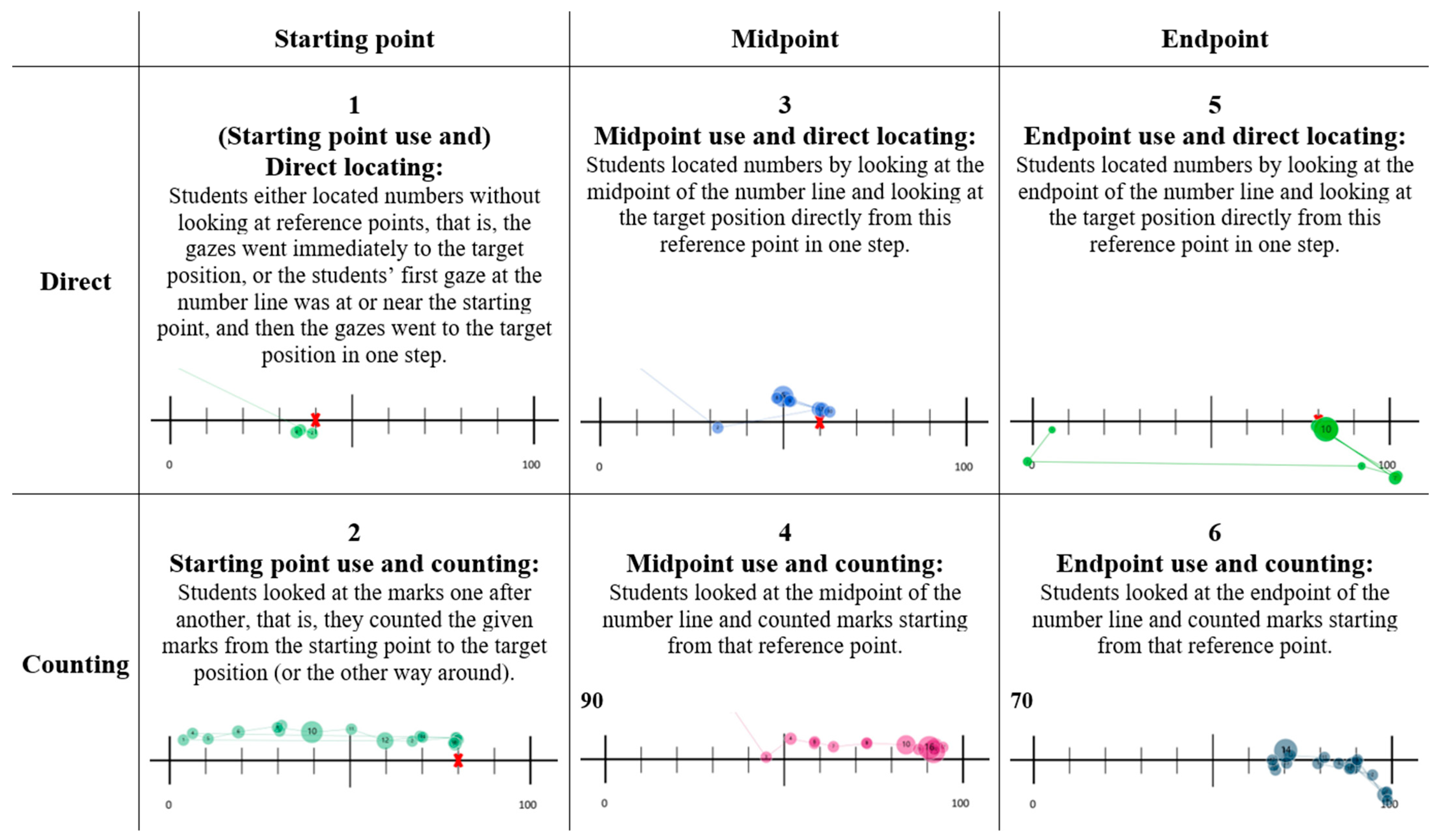
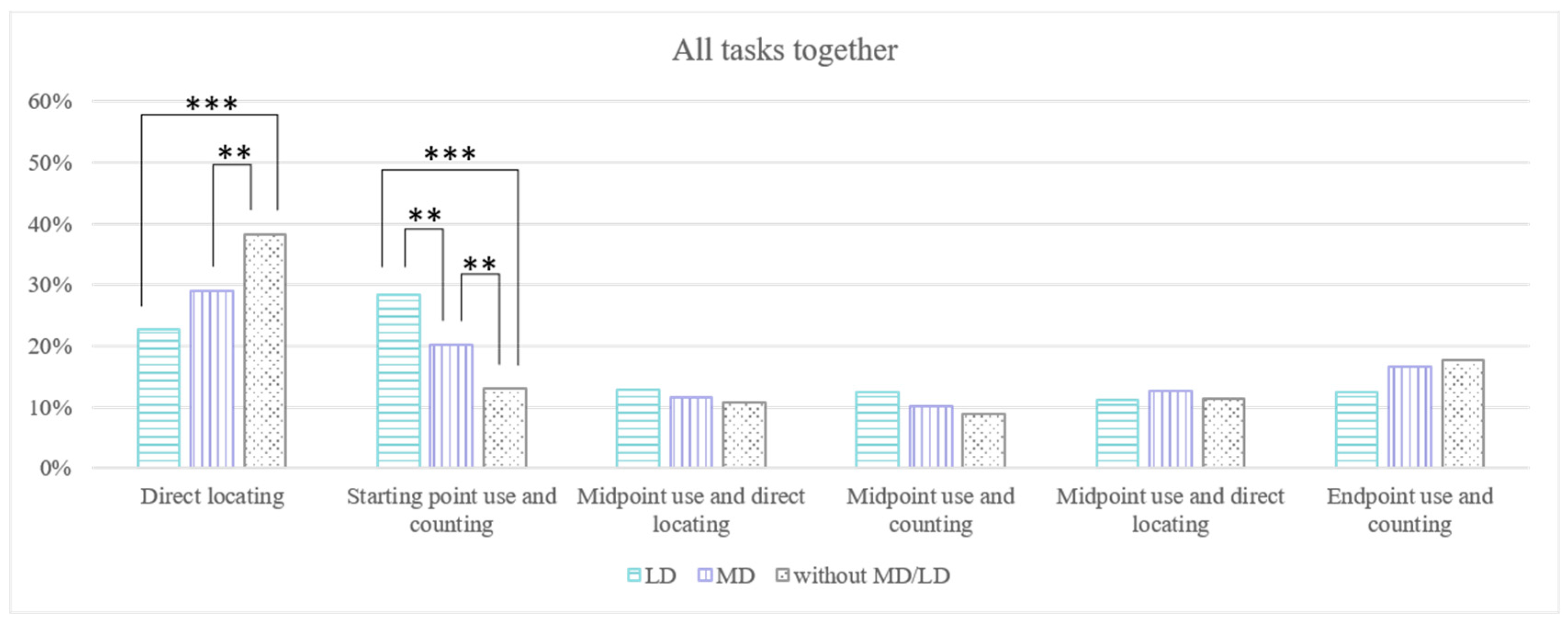
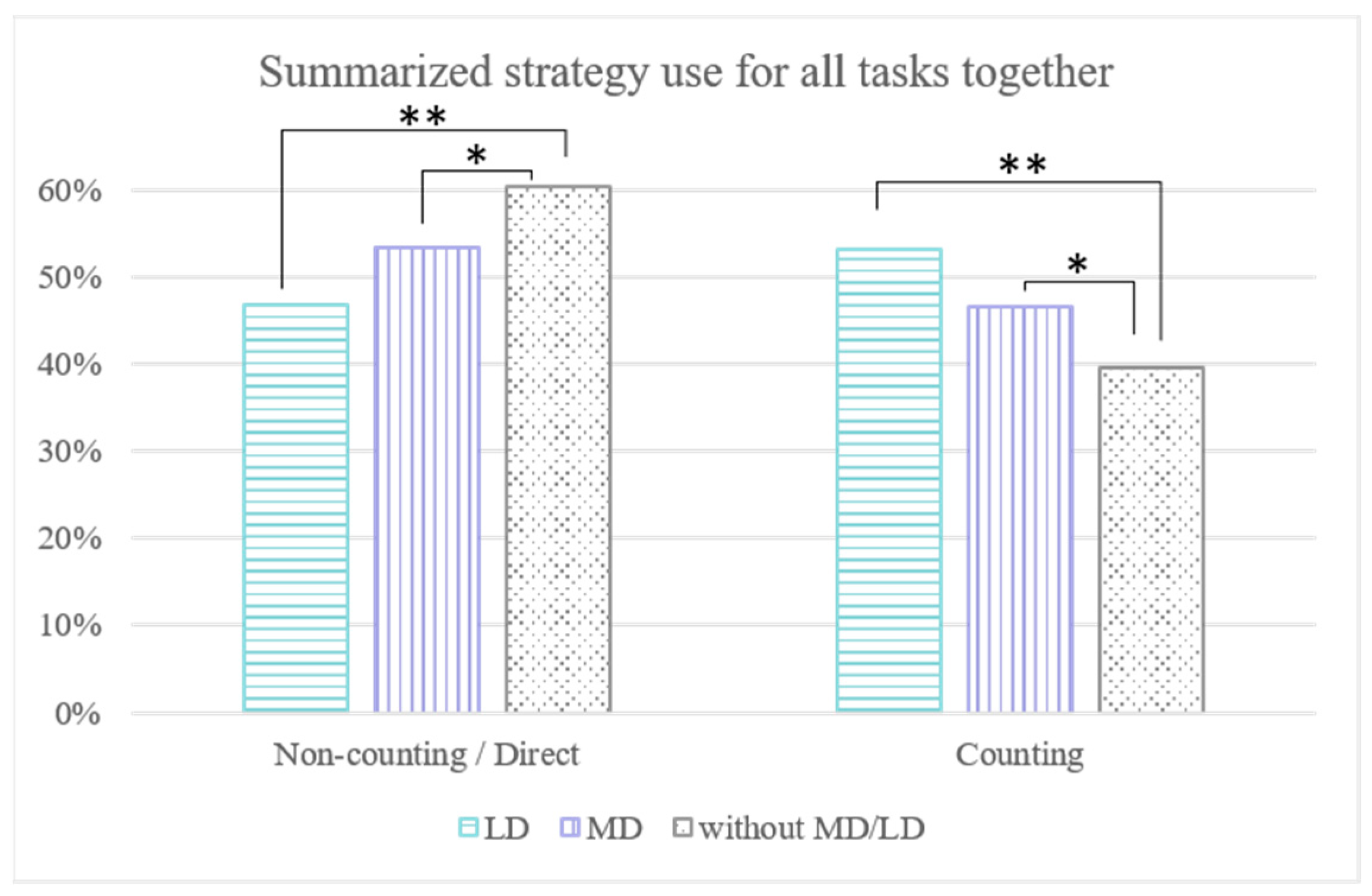
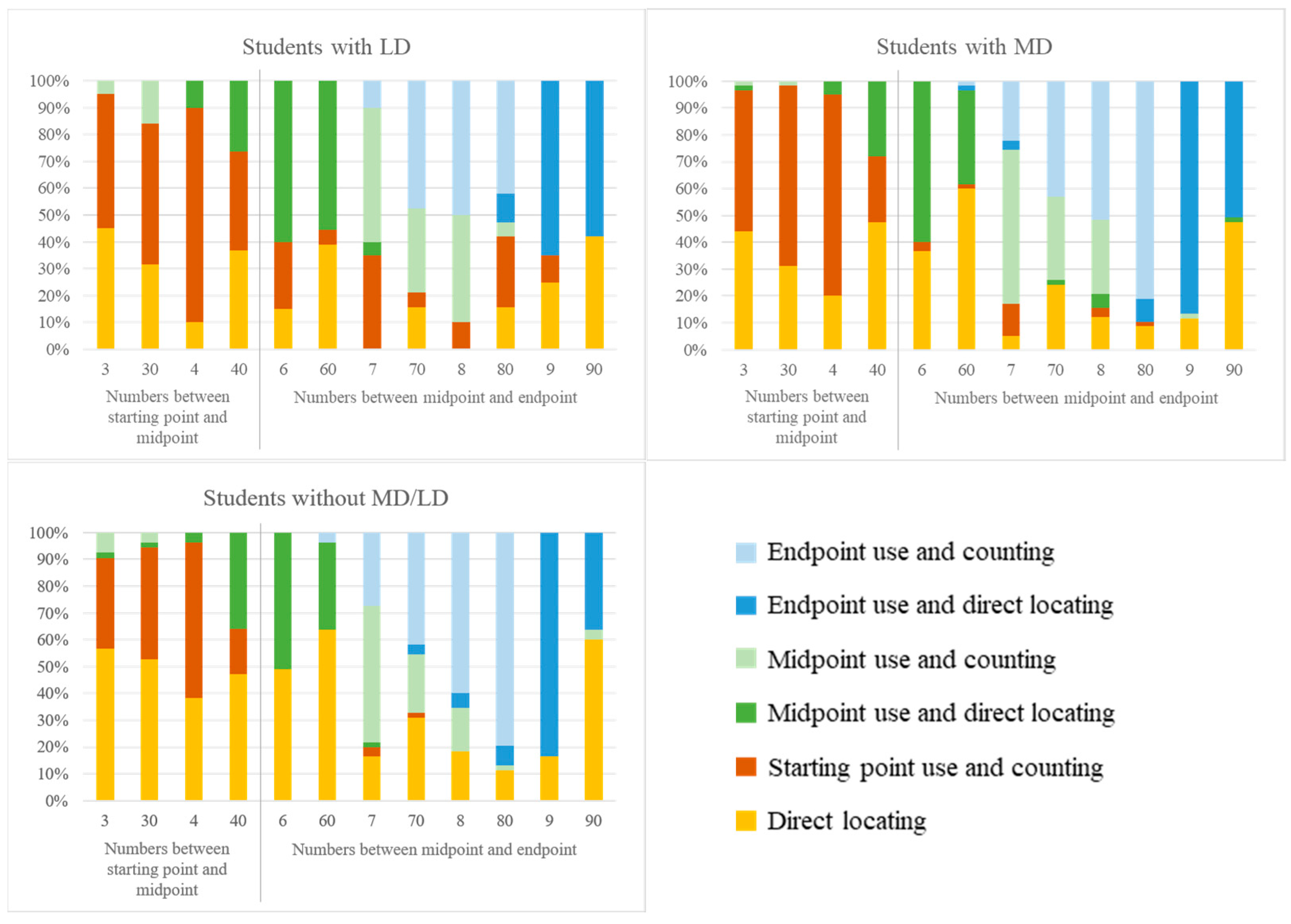
3.2. Students’ Strategy Use
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | For better comparability of the error rates, we visualize the mean error rates, even though the Kruskal–Wallis test is a non-parametric test and is based on rank-sums. |
| 2 | Due to the relatively small sample size of students with LD, we refrained from further statistical analyses at the task level. |
References
- Andrá, C., Lindström, P., Arzarello, F., Holmqvist, K., Robutti, O., & Sabena, C. (2015). Reading mathematics representations: An eye tracking study. International Journal of Science and Mathematics Education, 13, 237–259. [Google Scholar] [CrossRef]
- AO-SF NRW (Ausbildungsordnung sonderpädagogische Förderung). (2022). Verordnung über die sonderpädagogische Förderung, den Hausunterricht und die Schule für Kranke. Bereinigte amtliche Sammlung der Schulvorschriften NRW. Available online: https://bass.schule.nrw/6225.htm (accessed on 7 July 2025).
- APA (American Psychiatric Association). (2013). Diagnostic and statistical manual of mental disorders (5th ed.). American Psychiatric Publishing, Inc. [Google Scholar] [CrossRef]
- Ashcraft, M. H., & Moore, A. M. (2012). Cognitive processes of numerical estimation in children. Journal of Experimental Child Psychology, 111, 246–267. [Google Scholar] [CrossRef] [PubMed]
- Baddeley, A. (2012). Working memory: Theories, models, and controversies. Annual Review of Psychology, 63, 1–29. [Google Scholar] [CrossRef] [PubMed]
- Baroody, A. J. (1984). Children’s difficulties in subtraction: Some causes and questions. Journal for Research in Mathematics Education, 15(3), 203–213. [Google Scholar] [CrossRef]
- Bartolini Bussi, M. G. (2015). The number line: A “western” teaching aid. In X. Sun, B. Kaur, & J. Novotna (Eds.), Conference proceedings of the ICMI study 23: Primary mathematics study on whole numbers (pp. 298–306). University of Macau. [Google Scholar]
- Bikner-Ahsbahs, A. (2025). How eye tracking may advance the field of mathematics education: A commentary on the ESM Special Issue on eye-tracking research in mathematics education. Educational Studies in Mathematics, 118, 555–574. [Google Scholar] [CrossRef]
- Büttner, G., & Hasselhorn, M. (2011). Learning disabilities: Debates on definitions, causes, subtypes, and responses. International Journal of Disability, Development and Education, 58(1), 75–87. [Google Scholar] [CrossRef]
- Carrasco, M. (2011). Visual attention: The past 25 years. Vision Research, 51, 1484–1525. [Google Scholar] [CrossRef]
- Chumachenko, D., Shvarts, A., Dreneva, A., & Krichevets, A. (2024). Eye movements in the development of geometric shape recognition: From sensory-motor processes to theoretical perception. Educational Studies in Mathematics, 118, 529–554. [Google Scholar] [CrossRef]
- Cohen, J. (1988). Statistical power analysis for the behavioral sciences. L. Erlbaum Associates. [Google Scholar]
- Diezmann, C., & Lowrie, T. (2007). The development of primary students’ knowledge of the structured number line. In J. H. Woo, H. C. Lew, K. S. Park, & D. Y. Seo (Eds.), Proceedings of the 31st conference of the international group for the psychology of mathematics education, Seoul, Republic of Korea, 8–13 July 2007 (Vol. 2, pp. 201–208). PME. [Google Scholar]
- Dröse, J., Prediger, S., Neugebauer, P., Delucchi Danhier, R., & Mertins, B. (2021). Investigating students’ processes of noticing and interpreting syntactic language features in word problem solving through eye-tracking. International Electronic Journal of Mathematics Education, 16(1), em0625. [Google Scholar] [CrossRef]
- Duchowski, A. (2017). Eye tracking methodology: Theory and practice. Springer. [Google Scholar] [CrossRef]
- Dudley-Marling, C. (2004). The social construction of learning disabilities. Journal of Learning Disabilities, 37(6), 482–489. [Google Scholar] [CrossRef]
- Ebersbach, M., Luwel, K., & Verschaffel, L. (2015). The relationship between children’s familiarity with numbers and their performance in bounded and unbounded number line estimations. Mathematical Thinking and Learning, 17, 136–154. [Google Scholar] [CrossRef]
- Freudenthal, H. (1973). Mathematics as an educational task. Kluwer. [Google Scholar]
- Freudenthal, H. (1999). Didactical phenomenology of mathematical structures. Kluwer. [Google Scholar]
- Friso-van den Bos, I., Kroesbergen, E. H., Van Luit, J. E. H., Xenidou-Dervou, I., Jonkman, L. M., Van der Schoot, M., & Van Lieshout, E. C. D. M. (2015). Longitudinal development of number line estimation and mathematics performance in primary school children. Journal of Experimental Child Psychology, 134, 12–29. [Google Scholar] [CrossRef] [PubMed]
- Frykholm, J. (2010). Learning to think mathematically with the number line: A resource for teachers, a tool for young children. Math Learning Center. [Google Scholar]
- Fuson, K. (1984). More complexities in subtraction. Journal for Research in Mathematics Education, 15(3), 214–225. [Google Scholar] [CrossRef]
- Gabriel, T., & Börnert-Ringleb, M. (2023). The intersection of learning difficulties and behavior problems–a scoping review of intervention research. Frontiers in Education, 8, 1268904. [Google Scholar] [CrossRef]
- Gaidoschik, M. (2024). Number line estimation tasks: Ein fachdidaktischer Blick auf einen in den kognitiven Neurowissenschaften prominenten Aufgabentyp. Journal für Mathematik-Didaktik, 45, 1. [Google Scholar] [CrossRef]
- Gaidoschik, M., Moser Opitz, E., Nührenbörger, M., & Rathgeb-Schnierer, E. (2021). Besondere Schwierigkeiten beim Mathematiklernen. Special Issue der Mitteilungen der Gesellschaft für Didaktik der Mathematik, 111S, 3–19. [Google Scholar]
- Geary, D. C., Hoard, M. K., Nugent, L., & Byrd-Craven, J. (2008). Development of number line representations in children with mathematical learning disability. Developmental Neuropsychology, 33, 277–299. [Google Scholar] [CrossRef]
- Gebhardt, M., Oelkrug, K., & Tretter, T. (2013). Das mathematische Leistungsspektrum bei Schülerinnen und Schülern mit sonderpädagogischem Förderbedarf in der Sekundarstufe. Ein explorativer Querschnitt der fünften bis neunten Klassenstufe in Münchner Förderschulen. Empirische Sonderpädagogik, 2, 130–143. [Google Scholar]
- Gebhardt, M., Sälzer, C., Mang, J., Müller, K., & Prenzel, M. (2015). Performance of students with special educational needs in Germany: Findings from programme for international student assessment 2012. Journal of Cognitive Education and Psychology, 14(3), 343–356. [Google Scholar] [CrossRef]
- Gebhardt, M., Zehner, F., & Hessels, M. (2014). Basic arithmetical skills of students with learning disabilities in the secondary special schools: An exploratory study covering fifth to ninth grade. Frontline Learning Research, 2(1), 50–63. [Google Scholar] [CrossRef]
- Gomez, A., Piazza, M., Jobert, A., Dehaene-Lambertz, G., & Huron, C. (2017). Numerical abilities of school-age children with developmental coordination disorder (DCD): A behavioral and eye-tracking study. Human Movement Science, 55, 315–326. [Google Scholar] [CrossRef] [PubMed]
- Grünke, M., & Cavendish, W. (2016). Learning disabilities around the globe: Making sense of the heterogeneity of the different viewpoints. Learning Disabilities: A Contemporary Journal, 14, 1–8. [Google Scholar]
- Haffner, J., Baro, K., Parzer, P., & Resch, F. (2005). Heidelberger Rechentest (HRT 1-4). Hogrefe. [Google Scholar]
- Hanich, L. B., Jordan, N. C., Kaplan, D., & Dick, J. (2001). Performance across different areas of mathematical cognition in children with learning difficulties. Journal of Educational Psychology, 93, 615–626. [Google Scholar] [CrossRef]
- Hecht, T., Sinner, D., Kuhl, J., & Ennemoser, M. (2011). Differenzielle Effekte eines Trainings der mathematischen Basiskompetenzen bei kognitiv schwachen Grundschülern und Schülern der Förderschule mit dem Schwerpunkt Lernen—Reanalyse zweier Studien. Empirische Sonderpädagogik, 3, 308–323. [Google Scholar] [CrossRef]
- Heeffer, A. (2011). Historical objections against the number line. Science & Education, 20, 863–880. [Google Scholar] [CrossRef]
- Heimlich, U. (2016). Pädagogik bei Lernschwierigkeiten [Pedagogy for learning difficulties]. UTB. [Google Scholar] [CrossRef]
- Heimlich, U., Hillenbrand, C., & Wember, F. B. (2016). Lernen. In Ministerium für Schule und Weiterbildung des Landes Nordrhein-Westfalen (Ed.), Sonderpädagogische Förderschwerpunkte in NRW: Ein Blick aus der Wissenschaft in die Praxis. Available online: https://www.staedteregion-aachen.de/fileadmin/user_upload/A_40/Dateien/Foerderschulen/Broschuere_Sonderpaed_Foerderschwerpunkte.pdf (accessed on 8 July 2025).
- Heyd-Metzuyanim, E. (2013). The co-construction of learning difficulties in mathematics—Teacher–student interactions and their role in the development of a disabled mathematical identity. Educational Studies in Mathematics, 83, 341–368. [Google Scholar] [CrossRef]
- Holmqvist, K., Nyström, M., Andersson, R., Dewhurst, R., Jarodzka, H., & Van de Weijer, J. (2011). Eye tracking: A comprehensive guide to methods and measures. Oxford University. [Google Scholar]
- Jansen, B. R. J., Schmitz, E. A., & van der Maas, H. L. J. (2016). Affective and motivational factors mediate the relation between math skills and use of math in everyday life. Frontiers in Psychology, 7, 513. [Google Scholar] [CrossRef]
- Jordan, N. C., Kaplan, D., & Hanich, L. B. (2002). Achievement growth in children with learning difficulties in mathematics: Findings of a two-year longitudinal study. Journal of Educational Psychology, 94, 586–597. [Google Scholar] [CrossRef]
- Klein, C., & Ettinger, U. (2019). Eye movement research: An introduction to its scientific foundations and applications. Springer. [Google Scholar]
- KMK (Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland). (2022). Sonderpädagogische Förderung in Förderschulen 2021/2022 [Special educational support in special schools 2021/2022]. Available online: https://www.kmk.org/fileadmin/Dateien/pdf/Statistik/Dokumentationen/Aus_Sopae_2021.pdf (accessed on 10 July 2025).
- Landerl, K., Vogel, S., & Kaufmann, L. (2017). Dyskalkulie: Modelle, Diagnostik, Intervention [Dyscalculia: Models, diagnostics, intervention]. Ernst Reinhardt. [Google Scholar] [CrossRef]
- Landis, J. R., & Koch, G. G. (1977). The measurement of observer agreement for categorical data. Biometrics, 33, 159–174. [Google Scholar] [CrossRef]
- Lehmann, R. H., & Hoffmann, E. (2009). BELLA. Berliner Erhebung arbeitsrelevanter Basiskompetenzen von Schülerinnen und Schülern mit Förderbedarf “Lernen”. Waxmann. [Google Scholar]
- Lloyd, J. W., Keller, C., & Hung, L. (2007). International understanding of learning disabilities. Learning Disabilities Research & Practice, 22(3), 159–160. [Google Scholar] [CrossRef]
- Lutz, S., Ebenbeck, N., & Gebhardt, M. (2023). Mathematical skills of students with special educational needs in the area of learning (SEN-L) in pre-vocational programs in Germany. International Journal for Research in Vocational Education and Training, 10(1), 1–23. [Google Scholar] [CrossRef]
- Moser Opitz, E. (2008). Zählen, Zahlbegriff, Rechnen. Theoretische Grundlagen und eine empirische Untersuchung zum mathematischen Erstunterricht in Sonderklassen. Haupt. [Google Scholar]
- Moser Opitz, E. (2013). Rechenschwäche/dyskalkulie. Theoretische Klärungen und empirische Studien an betroffenen Schülerinnen und Schülern. Haupt. [Google Scholar]
- Moser Opitz, E., Freesemann, O., Prediger, S., Grob, U., Matull, I., & Hußmann, S. (2017). Remediation for students with mathematics difficulties: An intervention study in middle schools. Journal of Learning Disabilities, 50, 724–736. [Google Scholar] [CrossRef]
- Moser Opitz, E., Grob, U., Wittich, C., Häsel-Weide, U., & Nührenbörger, M. (2018). Fostering the computation competence of low achievers through cooperative learning in inclusive classrooms: A longitudinal study. Learning Disabilities: A Contemporary Journal, 16, 19–35. [Google Scholar]
- Müller, K., Prenzel, M., Sälzer, C., Mang, J., Heine, J.-H., & Gebhardt, M. (2017). Wie schneiden Schülerinnen und Schüler an Förderschulen bei PISA ab? Analysen aus der PISA 2012-Zusatzerhebung zu Jugendlichen mit sonderpädagogischem Förderbedarf. Unterrichtswissenschaft, 45, 175–192. [Google Scholar]
- Namkung, J. M., & Fuchs, L. S. (2016). Cognitive predictors of calculations and number line estimation with whole numbers and fractions among at-risk students. Journal of Educational Psychology, 108(2), 214–228. [Google Scholar] [CrossRef] [PubMed]
- NCTM (National Council of Teachers of Mathematics). (2000). Principles and standards for school mathematics. NCTM. [Google Scholar]
- Newman, R. S., & Berger, C. F. (1984). Children’s numerical estimation: Flexibility in the use of counting. Journal of Educational Psychology, 76, 55–64. [Google Scholar] [CrossRef]
- Nicchiotti, B., & Spagnolo, C. (2024). Gender differences in relation to perceived difficulty of a mathematical task. In T. Evans, O. Marmur, J. Hunter, G. Leach, & J. Jhagroo (Eds.), Proceedings of the 47th conference of the international group for the psychology of mathematics education, Auckland, New Zealand, 17–21 July 2024 (Vol. 3, pp. 257–264). PME. [Google Scholar]
- Nuraydin, S., Stricker, J., Ugen, S., Martin, R., & Schneider, M. (2023). The number line estimation task is a valid tool for assessing mathematical achievement: A population-level study with 6484 Luxembourgish ninth-graders. Journal of Experimental Child Psychology, 225, 105521. [Google Scholar] [CrossRef]
- OECD. (2007). Students with disabilities, learning difficulties and disadvantages. policies, statistics and indicators. Available online: https://www.oecd-ilibrary.org/education/students-with-disabilities-learning-difficulties-and-disadvantages_9789264027619-en (accessed on 7 July 2025).
- Okoli, M. L., Ogbu, C. E., Enyi, C. O., Okoli, I. C., Wilson, R. E., & Kirby, R. S. (2022). Sociodemographic and socioeconomic correlates of learning disability in preterm children in the United States. BMC Public Health, 22, 212. [Google Scholar] [CrossRef]
- Peeters, D., Degrande, T., Ebersbach, M., Verschaffel, L., & Luwel, K. (2016). Children’s use of number line estimation strategies. European Journal of Psychology of Education, 31, 117–134. [Google Scholar] [CrossRef]
- Peeters, D., Verschaffel, L., & Luwel, K. (2017). Benchmark-based strategies in whole number line estimation. British Journal of Psychology, 108, 668–686. [Google Scholar] [CrossRef]
- Peng, P., & Fuchs, D. (2016). A meta-analysis of working memory deficits in children with learning difficulties: Is there a difference between verbal domain and numerical domain? Journal of Learning Disabilities, 49(1), 3–20. [Google Scholar] [CrossRef]
- Petitto, A. L. (1990). Development of number line and measurement concepts. Cognition and Instruction, 7(1), 55–78. [Google Scholar] [CrossRef]
- Pitta-Pantazi, D., Demosthenous, E., Schindler, M., Lilienthal, A. J., & Christou, C. (2024). Structure sense in students’ quantity comparison and repeating pattern extension tasks: An eye-tracking study with first graders. Educational Studies in Mathematics, 118, 339–357. [Google Scholar] [CrossRef]
- Posner, M. I. (1980). Orienting of attention. Quarterly Journal of Experimental Psychology, 32, 3–25. [Google Scholar] [CrossRef]
- Pullen, P. C. (2016). Historical and current perspectives on learning disabilities in the United States. Learning Disabilities: A Contemporary Journal, 14, 25–37. [Google Scholar]
- Reinert, R. M., Huber, S., Nuerk, H.-C., & Moeller, K. (2015). Strategies in unbounded number line estimation? Evidence from eye-tracking. Cognitive Processing, 16, 359–363. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, D., Parmer, R. S., & Signer, B. R. (2001). Fourth-grade culturally and linguistically diverse exceptional students’ concepts of number line. Exceptional Children, 67, 199–210. [Google Scholar] [CrossRef]
- Scherer, P., & Moser Opitz, E. (2010). Fördern im Mathematikunterricht der Primarstufe [Fostering in mathematics education at the primary level]. Spektrum. [Google Scholar]
- Schindler, M., & Lilienthal, A. J. (2018). Eye-tracking for studying mathematical difficulties—Also in inclusive settings. In E. Bergqvist, M. Österholm, C. Granberg, & L. Sumpter (Eds.), Proceedings of the 42nd conference of the international group for the psychology of mathematics education, Umeå, Sweden, 3–8 July 2018 (Vol. 4, pp. 115–122). PME. [Google Scholar]
- Schindler, M., & Schindler, F. (2022). Förderung der strukturierten Anzahlerfassung bei Kindern mit Schwierigkeiten im Rechnenlernen: Eine explorative Eye-Tracking Studie zur Evaluation schulischer Förderung in Klasse 5. In P. Klein, N. Graulich, J. Kuhn, & M. Schindler (Eds.), Eye-tracking in der Mathematik- und Naturwissenschaftsdidaktik (pp. 75–90). Springer. [Google Scholar] [CrossRef]
- Schindler, M., Schovenberg, V., & Schabmann, A. (2020). Enumeration processes of children with mathematical difficulties: An explorative eye-tracking study on subitizing, groupitizing, counting, and pattern recognition. Learning Disabilities: A Contemporary Journal, 18, 193–211. [Google Scholar]
- Schindler, M., Shvarts, A., & Lilienthal, A. J. (2025a). Introduction to eye tracking in mathematics education: Interpretation, potential, and challenges. Educational Studies in Mathematics, 118, 309–321. [Google Scholar] [CrossRef]
- Schindler, M., Simon, A. L., Baumanns, L., & Lilienthal, A. J. (2025b). Eye-tracking research in mathematics and statistics education: Recent developments and future trends. A systematic literature review. ZDM Mathematics Education, 57, 727–743. [Google Scholar] [CrossRef]
- Schmidt, M. C. S. (2016). Dyscalculia ≠ maths difficulties. An analysis of conflicting positions at a time that calls for inclusive practices. European Journal of Special Needs Education, 31(3), 407–421. [Google Scholar] [CrossRef]
- Schneider, M., Heine, A., Thaler, V., Torbeyns, J., De Smedt, B., Verschaffel, L., Jacobs, A. M., & Stern, E. (2008). A validation of eye movements as a measure of elementary school children’s developing number sense. Cognitive Development, 233, 409–422. [Google Scholar] [CrossRef]
- Schneider, M., Merz, S., Stricker, J., De Smedt, B., Torbeyns, J., Verschaffel, L., & Luwel, K. (2018). Associations of number line estimation with mathematical competence: A meta-analysis. Child Development, 89, 1467–1484. [Google Scholar] [CrossRef]
- Schulz, A., & Wartha, S. (2021). Zahlen und Operationen am Übergang Primar-/ Sekundarstufe. Grundvorstellungen aufbauen, festigen, vernetzen. Springer. [Google Scholar]
- Simon, A. L., Asghari, P., Lilienthal, A. J., & Schindler, M. (2023). Strategy use in number line tasks of students with and without mathematical difficulties: A study using eye tracking and AI. In M. Ayalon, B. Koichu, R. Leikin, L. Rubel, & M. Tabach (Eds.), Proceedings of the 46th conference of the international group for the psychology of mathematics education, Haifa, Israel, 16–21 July 2023 (Vol. 4, pp. 211–218). PME. [Google Scholar]
- Simon, A. L., Rott, B., & Schindler, M. (2025). Exploring strategies for the identification of triangles by students with learning difficulties: An eye-tracking study. Mathematics Education Research Journal, 1–27. [Google Scholar] [CrossRef]
- Simon, A. L., & Schindler, M. (2021). A comparative analysis of eye tracking and thinking aloud in number line estimation tasks: A study on students with and without mathematical difficulties. In M. Inprasitha, N. Changsri, & N. Boonsena (Eds.), Proceedings of the 44th conference of the international group for the psychology of mathematics education, Khon Kaen, Thailand, 19–22 July 2021 (Vol. 4, pp. 65–72). PME. [Google Scholar]
- Simon, A. L., & Schindler, M. (2022). Strategy use in number line tasks of students with mathematical difficulties: An eye-tracking study. In C. Fernández, S. Llinares, A. Gutiérrez, & N. Planas (Eds.), Proceedings of the 45th conference of the international group for the psychology of mathematics education, Alicante, Spain, 18–23 July 2022 (Vol. 4, pp. 3–10). PME. [Google Scholar]
- Spagnolo, C., Capone, R., & Gambini, A. (2021). Where do students focus their attention on solving mathematical tasks? An eye tracker explorative study. In M. Inprasitha, N. Changsri, & N. Boonsena (Eds.), Proceedings of the 44th conference of the international group for the psychology of mathematics education, Khon Kaen, Thailand, 19–22 July 2021 (Vol. 4, pp. 89–96). PME. [Google Scholar]
- Strohmaier, A. R., MacKay, K. J., Obersteiner, A., & Reiss, K. M. (2020). Eye-tracking methodology in mathematics education research: A systematic literature review. Educational Studies in Mathematics, 104, 147–200. [Google Scholar] [CrossRef]
- Sullivan, J. L., Juhasz, B. J., Slattery, T. J., & Barth, H. C. (2011). Adults’ number-line estimation strategies: Evidence from eye movements. Psychonomic Bulletin & Review, 18, 557–563. [Google Scholar] [CrossRef] [PubMed]
- Teppo, A., & van den Heuvel-Panhuizen, M. (2014). Visual representations as objects of analysis: The number line as an example. ZDM Mathematics Education, 46, 45–58. [Google Scholar] [CrossRef]
- Tikhomirova, T., Malykh, A., Lysenkova, I., Kuzmina, Y., & Malykh, S. (2022). The development of number line accuracy in elementary school children: A cross-country longitudinal study. British Journal of Educational Psychology, 93(2), 423–436. [Google Scholar] [CrossRef]
- Tzouriadou, M. (2020). Concepts and ambiguities in the field of learning disabilities. In S. Misciagna (Ed.), Learning disabilities-neurological bases, clinical features and strategies of intervention. IntechOpen. [Google Scholar] [CrossRef]
- van der Sluis, S., de Jong, P. F., & van der Leij, A. (2004). Inhibition and shifting in children with learning deficits in arithmetic and reading. Journal of Experimental Child Psychology, 87, 239–266. [Google Scholar] [CrossRef]
- van der Weijden, F., Kamphorst, E., Willemsen, R., Kroesbergen, E., & van Hoogmoed, A. (2018). Strategy use on bounded and unbounded number lines in typically developing adults and adults with dyscalculia: An eye-tracking study. Journal of Numerical Cognition, 4, 337–359. [Google Scholar] [CrossRef][Green Version]
- van’t Noordende, J. E., van Hoogmoed, A. H., Schot, W. D., & Kroesbergen, E. H. (2016). Number line estimation strategies in children with mathematical learning difficulties measured by eye tracking. Psychological Research, 80, 368–378. [Google Scholar] [CrossRef]
- van Viersen, S., Slot, E. M., Kroesbergen, E., van’t Noordende, J., & Leseman, P. (2013). The added value of eye-tracking in diagnosing dyscalculia: A case study. Frontiers in Psychology, 4, 679. [Google Scholar] [CrossRef]
- Verschaffel, L., Greer, B., & De Corte, E. (2007). Whole number concepts and operations. In F. K. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 557–628). Information Age Publishing. [Google Scholar]
- Werner, B., Berg, M., & Höhr, R. (2019). “Math, I Don’t Get It”: An exploratory study on verbalizing mathematical content by students with speech and language impairment, students with learning disability, and students without special educational needs. In D. Kollosche, R. Marcone, M. Knigge, M. G. Penteado, & O. Skovsmose (Eds.), Inclusive mathematics education (pp. 377–399). Springer. [Google Scholar] [CrossRef]
- WHO (World Health Organization). (2019). ICD-11: International classification of diseases (11th revision). Available online: https://icd.who.int/en (accessed on 7 July 2025).
- Winkel, K., & Zipperle, I. (2023). Children with mathematical learning difficulties—How do their working memory skills differ from typically developing first graders? Journal für Mathematik-Didaktik, 44, 417–440. [Google Scholar] [CrossRef]
- Woods, D. M., Ketterlin Geller, L., & Basaraba, D. (2018). Number sense on the number line. Intervention in School and Clinic, 53(4), 229–236. [Google Scholar] [CrossRef]
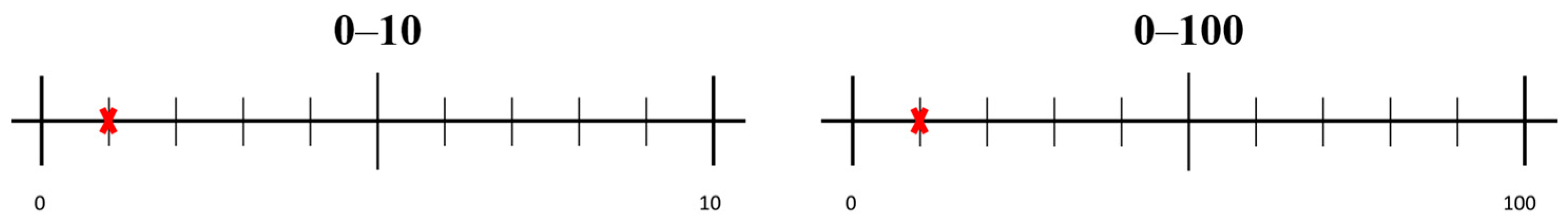
| LD (n = 20) | MD (n = 60) | Without MD/LD (n = 55) | |
|---|---|---|---|
| Participant information | |||
| Age: mean (SD) | 11.7 (0.7) | 10.8 (0.6) | 10.6 (0.6) |
| Mathematical abilities | |||
| HRT: mean t-value (SD) | 24.95 (5.91) | 33.68 (2.77) | 48.84 (4.98) |
| Mathematical learning difficulties: n (%) | 20 (100.00) | 60 (100.00) | 0 (0.00) |
| Position-to-Number-Task | Number-to-Position-Task | |||
|---|---|---|---|---|
| Number range | 0–10 | 0–100 | 0–10 | 0–100 |
| Numbers | 9, 3, 6 | 80, 40, 60 | 7, 4, 8 | 70, 30, 90 |
| Numbers | |||||||
|---|---|---|---|---|---|---|---|
| 3 30 | 4 40 | 6 60 | 7 70 | 8 80 | 9 90 | ||
| Direct | x | x | x | x | x | x | |
| Starting point | Counting | x | x | x | x | x | x |
| Midpoint | Direct | x | x | x | x | x | x |
| Counting | x | x | x | x | |||
| Endpoint | Direct | x | x | x | x | ||
| Counting | x | x | x | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simon, A.L.; Rott, B.; Schindler, M. Number Line Strategies of Students with Mathematical Learning Difficulties and Students with General Learning Difficulties: Findings Through Eye Tracking. Educ. Sci. 2025, 15, 1461. https://doi.org/10.3390/educsci15111461
Simon AL, Rott B, Schindler M. Number Line Strategies of Students with Mathematical Learning Difficulties and Students with General Learning Difficulties: Findings Through Eye Tracking. Education Sciences. 2025; 15(11):1461. https://doi.org/10.3390/educsci15111461
Chicago/Turabian StyleSimon, Anna Lisa, Benjamin Rott, and Maike Schindler. 2025. "Number Line Strategies of Students with Mathematical Learning Difficulties and Students with General Learning Difficulties: Findings Through Eye Tracking" Education Sciences 15, no. 11: 1461. https://doi.org/10.3390/educsci15111461
APA StyleSimon, A. L., Rott, B., & Schindler, M. (2025). Number Line Strategies of Students with Mathematical Learning Difficulties and Students with General Learning Difficulties: Findings Through Eye Tracking. Education Sciences, 15(11), 1461. https://doi.org/10.3390/educsci15111461






