The Impact of Rubric-Guided Peer Review and Self-Assessment in an Engineering Math University Course

Abstract

We investigated the use of a rubric-guided peer-review activity in two first-year engineering calculus groups (N = 38). The intervention involved three phases: (1) students completed a short integration worksheet and predicted their own score, (2) they engaged in peer marking both before and after an instructor-led solution walk-through with explicit criteria, and (3) they later took a midterm test and completed a post-activity questionnaire. To examine ability-level effects, we applied a dual-perspective quartile approach that classified both reviewers and reviewees (targets) by their instructor-assigned marks. Results showed that peer-grading error decreased by 3–5 points across all reviewer–target combinations, with the largest reduction observed when lower-achieving students graded the work of similarly low-achieving peers. Mid-achieving students also improved the calibration, cutting self-assessment error by half. Performance gains carried over to subsequent assessments: average midterm scores increased significantly for the bottom two quartiles. Survey responses (≥3.4/5) indicated that 60–70% of students found the activity beneficial for their understanding and exam preparation. Overall, the study demonstrates that rubric-guided peer review and assessment, when analyzed through a novel dual-lens quartile framework, can sharpen feedback accuracy, improve self-evaluation and enhance exam performance for mid- and lower-performing students while offering equity-oriented implications for assessment design.

1. Introduction

Mathematics remains a persistent challenge for many first-year engineering students, who often enter university with diverse levels of preparedness, confidence and engagement. Recent findings from European cohorts indicate that incoming students experience substantial conceptual gaps and negative emotions toward mathematics, which pose a challenge for university instructors aiming to foster inclusive and supportive learning (Charalambides et al., 2023). Early difficulties in foundational mathematics can adversely affect students’ academic trajectories and persistence in STEM fields. Among the most significant psychological predictors of success in this domain is self-efficacy, or learners’ beliefs in their own capacity to understand and apply mathematical concepts (Bandura, 1997; Z. Yan & Carless, 2022). However, fostering self-efficacy demands more than traditional instruction; it necessitates active, reflective, and socially scaffolded learning environments (Carless & Boud, 2018).

Structured peer assessment, particularly when supported by rubrics, has gained recognition as a pedagogical tool that promotes deeper learning, metacognitive development and evaluative judgment (Topping, 1998; Boud & Dawson, 2021). Despite these benefits, its application in mathematics education remains limited, partly due to concerns over grading reliability and the assumption that problem-solving is too objective to warrant peer interpretation. Recent scholarship, however, argues that peer feedback, even in technical disciplines, can enhance procedural understanding, reinforce attention to detail, and support the development of feedback literacy (Panadero et al., 2022; Miknis et al., 2020).

The present study explores the effect of a role-playing peer-review activity on students’ mathematical reasoning and self-efficacy in a first-year engineering calculus course. Students evaluated peers’ handwritten integration solutions, both before and after a rubric training session that included instructor walkthroughs. This design enabled us to examine the evolution of peer-grading accuracy, the alignment of self-assessment with instructor benchmarks and students’ perceptions of feedback utility.

Moreover, we apply a dual-lens quartile framework: using the same instructor-assigned grade bands, we analyze students in two roles, first as targets whose work is graded and then as reviewers who grade their peers. This innovative use of the quartile segmentation allows us to analyze how students’ ability levels influence and are influenced by rubric-guided calibration. Prior work has emphasized the need for explicit rubrics to support novice assessors (Topping, 1998; Taylor et al., 2024), yet few studies have tracked grading accuracy shifts across reviewer quartiles. Our results show that after rubric training, low- and mid-achieving reviewers significantly improved their evaluative accuracy, providing more instructor-aligned feedback and gaining insights into assessment criteria.

Accordingly, we hypothesized that rubric-guided peer review would enhance both self- and peer-assessment accuracy, with calibration gains most pronounced among mid- and lower-achieving students, and that these improvements would extend to subsequent performance outcomes. While earlier research typically categorized students based solely on their own performance or reported aggregate reviewer behavior, our dual-perspective quartile analysis offers a more granular view of how calibration and feedback quality evolve across both dimensions. These findings contribute to a growing body of evidence suggesting that scaffolded peer review, when combined with clear rubrics and opportunities for reflection, not only benefits those being assessed but also transforms the reviewers into more accurate, self-regulated learners (Z. Yan & Carless, 2022; Panadero et al., 2022).

The research questions guiding this study are:

(1)

To what extent does rubric-guided peer assessment improve the accuracy of peer feedback and self-assessment among first-year engineering mathematics students?

(2)

How does students’ performance level influence, and become influenced by, the calibration process during a structured role-playing peer-review activity?

2. Theoretical Framework

This section integrates research findings on four interrelated constructs: (1) peer assessment, (2) feedback and rubric-guided peer assessment, (3) calibration, and (4) self-efficacy and self-regulation in mathematics learning. These themes are critically reviewed and discussed in light of recent scholarship, with a particular emphasis on their implications for formative feedback practices in mathematics and STEM-based higher education settings.

2.1. Peer Assessment in Higher Education

Peer assessment refers to the process through which students evaluate the work of their peers, either formatively or summative, using predetermined criteria (Topping, 1998; Panadero et al., 2022). Over the last two decades, it has evolved from a peripheral instructional tool into a core strategy within assessment for learning frameworks (Boud & Molloy, 2013; Ashenafi, 2017). Its educational value lies not merely in enabling distributed feedback but more fundamentally in fostering cognitive engagement, critical thinking, and metacognitive development among students (Nicol et al., 2014).

Research consistently highlights that the act of giving feedback, rather than merely receiving it, is pedagogically powerful. Nicol and McCallum (2021) demonstrated that peer reviewers engaged in multi-perspective feedback cycles showed significant improvements in content mastery and evaluative judgment. Similarly, Boud and Dawson (2021) emphasized the social dimensions of peer assessment, noting that students benefit from engaging with authentic audiences and negotiating shared understanding of quality standards.

In mathematics education specifically, recent studies have shown that peer assessment can support students’ evaluative judgment and feedback literacy. For example, Cusi et al. (2023) document how mathematics teachers integrated peer-assessment strategies as part of their formative assessment practices during the pandemic, while Telloni et al. (2024) illustrate how role-playing designs in undergraduate mathematics explicitly embedded peer review to strengthen students’ awareness of solution methods and criteria. A recent systematic review in ZDM (Maskos et al., 2025) further emphasizes that in mathematics, peer assessment interacts with self-efficacy and perceptions of feedback usefulness, highlighting its potential to foster calibration and metacognitive gains.

Nonetheless, challenges persist. Students often lack the expertise or confidence to evaluate their peers’ work reliably (Ashenafi, 2017), and concerns over fairness, reciprocity and interpersonal dynamics can hinder the authenticity of peer feedback. Rubric-guided assessment and structured training have been proposed to mitigate these issues (Taylor et al., 2024; Carless & Winstone, 2020), promoting greater transparency and consistency across peer assessments.

2.2. Feedback and Rubric-Guided Peer Assessment

Feedback is a central mechanism that engages both students and instructors in cycles of reflection and improvement (Camarata & Sileman, 2020). It can be delivered through instructor comments (written or oral) or via peer assessment. Recent efforts in higher education emphasize that peer review not only distributes feedback but also fosters self-reflection and active engagement (Huisman et al., 2019).

Rubrics play a pivotal role in structuring such processes. A rubric is a scoring tool that evaluates student work against explicit criteria, communicating expectations and providing a transparent framework for assessment (Huisman et al., 2019). While rubrics promote consistency and reliability, they are not without limitations; overly rigid designs may constrain valid judgment or obscure disciplinary nuances (Huisman et al., 2019). Students’ attitudes toward rubrics are also critical (Ling, 2024), as effective use requires fluency, flexibility and integration of criteria into self- and peer-assessment practices. Tailoring rubric design to the purpose of assessment is essential. For formative contexts, rubrics can guide reflection and improvement, whereas in summative settings they enhance transparency and fairness (Bryant et al., 2016). The benefits of rubric use can be summarized as follows: (a) clarifying performance expectations, (b) providing timely and informative feedback, (c) supporting grading consistency, and (d) fostering self-regulated learning (Panadero et al., 2013). In peer assessment specifically, rubrics delineate explicit performance standards, ensure greater reliability, and strengthen students’ feedback literacy (Chowdhury, 2019). Moreover, emerging work on rubric co-creation indicates that involving students in rubric design can enhance their evaluative judgment and the quality of peer feedback (D. Yan, 2024).

In mathematics education, rubric-guided peer assessment has also been implemented in structured designs. Telloni et al. (2024), for example, integrated role-playing activities in undergraduate mathematics where rubrics framed the peer-review process, enabling students to evaluate alternative solution strategies and develop stronger awareness of mathematical criteria. Likewise, Maskos et al. (2025) emphasize that in mathematics, students’ perceptions of rubric usefulness are directly linked to their self-efficacy and the motivational benefits of peer assessment. These insights highlight the dual role of rubrics in fostering consistency and in supporting the metacognitive and affective gains of peer review.

2.3. Calibration and Feedback Accuracy

In educational contexts, calibration refers to the degree of alignment between students’ judgments—whether of their own work or that of peers—and expert evaluations (Z. Yan & Carless, 2022). In peer assessment scenarios, calibration is a central concern because the accuracy of feedback depends on students’ ability to internalize standards of quality and apply them consistently (Lertsakubunlue & Kantiwong, 2024; Sadler, 2009).

Research has increasingly examined how calibration can be systematically improved. Panadero et al. (2022) showed that the integration of instructor feedback, rubrics, and exemplars enabled students to articulate more refined evaluative criteria. Similarly, the SAFE framework (Self-Assessment Feedback and Evaluation) developed by Miknis et al. (2020) combines rubric-based assessment with iterative peer feedback cycles to improve grading reliability and foster students’ self-regulatory capacities.

Favre and Knight (2016) emphasized that calibration is simultaneously a cognitive, social and affective process. They found that even highly efficacious teachers may struggle with calibration when their internal standards diverge from institutional benchmarks, underscoring the need for alignment of expectations among students, instructors, and institutions.

In STEM education, where accuracy and procedural fluency are paramount, calibration activities such as guided peer review and rubric-based reflection have shown particular promise in enhancing both the consistency and depth of student evaluations (Z. Yan & Carless, 2022; Panadero et al., 2022).

In mathematics education specifically, recent evidence suggests that calibration gains are closely tied to students’ self-efficacy and their perceptions of feedback usefulness. Maskos et al. (2025), for instance, highlight that formative assessment practices in mathematics—including peer review—enhance metacognitive regulation when students view rubrics and peer feedback as credible and supportive. These findings underline the potential of rubric-guided peer assessment to foster not only accuracy but also motivational benefits in mathematical learning contexts.

2.4. Self-Efficacy, Self-Regulation and Feedback Literacy

Self-efficacy, defined as the belief in one’s capacity to organize and execute actions required to manage future challenges (Bandura, 1997), is closely connected to both self-assessment and peer review. Zimmerman and Schunk (2004) argue that self-regulated learning unfolds through cyclical phases of goal setting, performance monitoring, and self-reflection—processes that are activated and reinforced through formative assessment practices.

When students engage in self- or peer assessment, they not only receive but also generate feedback that shapes their self-perceptions and learning strategies. The quality of this engagement, however, depends on their feedback literacy: the ability to interpret, evaluate, and act upon feedback effectively (Carless & Boud, 2018). Feedback literacy is increasingly recognized as a critical enabler of learner autonomy in higher education (Panadero et al., 2022).

Building on this, Z. Yan and Carless (2022) propose a tripartite model of self-assessment comprising (1) application of criteria, (2) reflection, and (3) evaluative judgment. Their work highlights how feedback literacy mediates students’ ability to perform each step meaningfully. This perspective shifts the emphasis from feedback as a static product to feedback as a process—social, iterative, and learner-driven.

Panadero et al. (2022) further explored how students at different academic levels adopt diverse strategies during self-assessment, drawing on rubrics, instructor guidance, and peer benchmarks. Their findings suggest that while senior students employ more sophisticated evaluative approaches, even early undergraduates can develop effective self-monitoring strategies when scaffolded through structured feedback practices.

The role of rubrics as both evaluative and instructional tools is central in this process. Studies by Taylor et al. (2024) and Miknis et al. (2020) show that rubrics not only clarify performance expectations but also serve as metacognitive scaffolds, guiding planning, self-checking, and revision of academic work.

Taken together, the interplay between peer assessment, calibration, and self-regulatory processes constitutes a dynamic framework for fostering deep learning in mathematics. Peer-review activities—particularly when structured through rubrics and role-playing—provide fertile ground for enhancing evaluative judgment, feedback literacy, and learner agency. As the present study demonstrates, rubric-based peer review and self-assessment interventions improve not only feedback accuracy but also students’ self-efficacy and readiness for formal assessment tasks. These findings highlight the importance of integrative assessment designs that foreground student participation, scaffold evaluative judgment, and normalize feedback as a collaborative learning practice.

3. Methodology

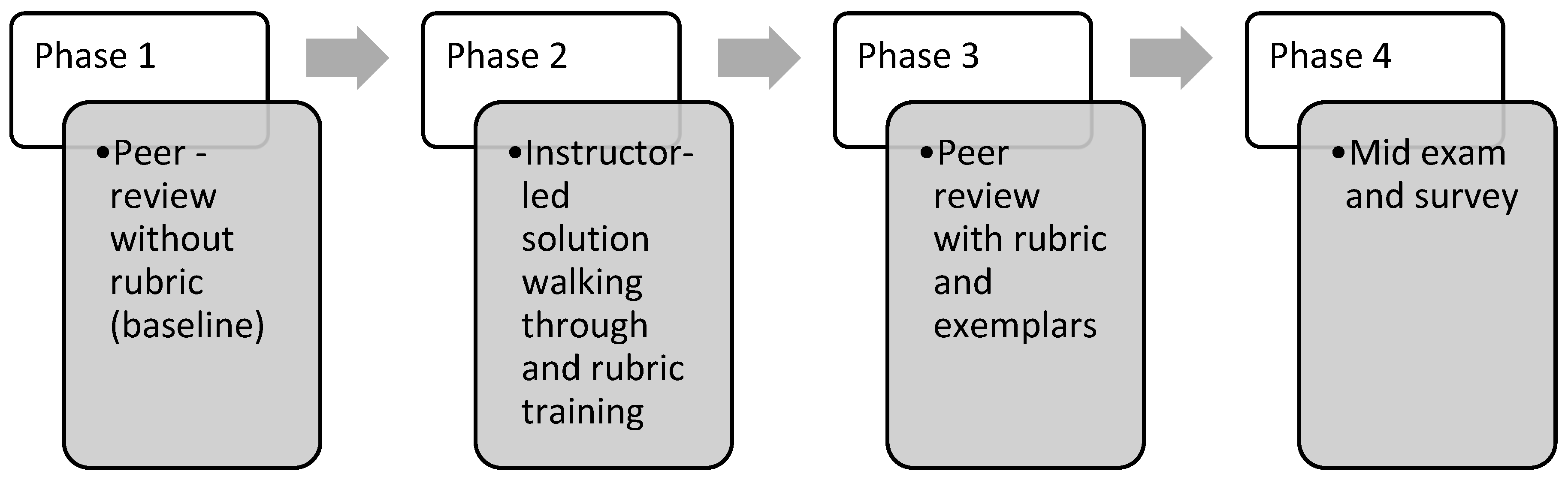
This study used a structured, four-phase in-class intervention to examine the effects of a role-playing peer-review exercise on students’ integration skills, self-assessment accuracy, and affective responses. All activities of the intervention were conducted during three consecutive 50 min sessions (a total of 150 min) within the same schedule and procedure. The study was conducted at a private university by one of the authors, who was the instructor of the course. We acknowledge that the dual role of the instructor–researcher may introduce potential bias. To mitigate this, anonymity was preserved through coding procedures, and participation was voluntary with the option to withdraw at any time.

3.1. Participants and Setting

Participants were first-year engineering students attending a 39 h introductory calculus course. The peer-review session was scheduled approximately four weeks after the term had commenced. The cohort included 38 students (28 male, 10 female), primarily from civil and mechanical engineering majors. Approximately 60% reported prior exposure to high school calculus, while the remaining 40% encountered integration topics for the first time in this course. This distinction indicates that baseline performance may have reflected not only inherent ability but also differences in prior knowledge. Although the present study did not stratify analyses according to prior exposure, this variable may have influenced students’ initial calibration accuracy and will be important to examine in future research. Both sections experienced the identical schedule, and results were pooled (N = 38) for analysis.

3.2. Exercise Sheet and Pre-Assessment

The intervention was delivered across three separate 50 min class sessions, held on consecutive weeks after the relevant integration topics had already been taught. Each session was devoted exclusively to the peer-review activity. The two student groups participated in parallel during their scheduled class times, following the same sequence of activities.

• A 20 min exercise sheet was distributed, containing six integration problems representative of the course content.
• On the front page, students solved each problem in the allotted space.
• On the back page, students recorded their name, student ID, and an estimate of the grade they expected to receive on their work.
• Instructors then affixed a unique anonymized code on each front page, linking to student IDs for later matching.

3.3. Four-Phase Peer-Review Intervention

A four-phase intervention was implemented (Figure 1). In Phases 1 and 3, students evaluated anonymized worksheets submitted by their peers. Worksheets were anonymized and randomly redistributed within each section using a shuffle procedure to ensure that no student evaluated their own work or that of a close peer, thereby minimizing bias. The worksheets in Phase 1 and Phase 3 came from different students. This design choice was intentional: it allowed us to assess whether rubric training (Phase 2) improved students’ ability to evaluate new work rather than simply revising earlier judgments. We deliberately avoided having students revisit the same worksheet after rubric training, as this could have encouraged mere correction of prior mistakes rather than the demonstration of independent rubric-based calibration.

In Phase 1, students graded a peer’s work without access to solutions or rubric guidance, providing a baseline of their unaided evaluative judgment. In later phases, students graded with the rubric and exemplar solutions in hand, which allowed us to measure the added effect of structured calibration support. Ιn Phase 1, students graded a peer’s worksheet without prior exposure to the rubric. While they had seen the course’s general marking scheme in earlier assignments and lectures, no detailed criteria were provided at this stage. This design choice was intentional to capture students’ baseline evaluative judgment before rubric calibration. The rubric consisted of a structured marking scheme with stepwise criteria (e.g., 2 points for correct substitution, 3 points for applying integration rules correctly, 5 points for correct evaluation of limits), accompanied by exemplar worked solutions for each problem. Students were therefore able to see not only the correct final answer but also how partial credit was awarded according to specific criteria.

3.4. Data Collection

Performance metrics (six numeric measures):

• Instructor’s original grade
• Self-predicted grade before solutions/rubric (Phase 1)
• Self-predicted grade after solutions/rubric (Phase 3)
• First Peer grade at Phase 1
• Second Peer grade at Phase 3
• Midterm exam grade (two weeks later)

Survey data: Survey items were rated on a 5-point Likert scale (1 = Strongly Disagree, 5 = Strongly Agree). The 20 items addressed three thematic areas: rubric usefulness, self-efficacy, and peer-review perceptions. For example, rubric usefulness was measured with items such as “The rubric helped me identify specific strengths and weaknesses,” while self-efficacy included statements like “I felt more confident in evaluating solutions after training.” Peer-review perceptions were captured with items such as “Peer feedback was constructive and fair.” For clarity, Q16 referred to the self-efficacy theme and stated: “I felt more confident applying rubric criteria after practicing with calibration examples”.

3.5. Data Analysis

Students were classified independently in two quartile frameworks: one as targets, based on their instructor worksheet scores, and one as reviewers, based on their peer-grading accuracy in Phase 1. Consequently, the same student could belong to different quartiles across roles (e.g., Q1 as a reviewer but Q4 as a target). This dual classification was intentional, as it allowed us to examine calibration patterns both from the perspective of those being assessed (targets) and those assessing others (reviewers). All students participated in both roles, ensuring complete dual-perspective data. For clarity, the “dual-perspective quartile approach” refers to this analytic strategy of separately ranking students by target performance and by reviewer accuracy, then examining outcomes within and across these distributions:

Quantitative: Quantitative analyses examined changes in self- and peer-assessment accuracy across phases, as well as transfer to midterm performance. Self-assessment error was defined as the absolute difference between a student’s self-assigned score and the instructor’s score on the same work. Peer-assessment error was defined analogously as the absolute difference between the reviewer’s assigned score and the instructor’s score on that target’s work. For self-assessment, paired-samples t-tests compared each student’s Phase 1 and Phase 3 errors directly. For peer assessment, because reviewers graded different targets in each phase, pairing was implemented at the reviewer level: for each reviewer, we calculated the mean error across all assigned targets in Phase 1 and in Phase 3, and these reviewer-level means were then compared using paired-samples t-tests. Paired-samples t-tests were also used to compare instructor worksheet grades with subsequent midterm scores. Bar charts and tables were used to depict average mark discrepancies. Assumptions of normality were checked with Shapiro–Wilk tests and inspection of Q-Q plots; no major violations were observed. Given the number of comparisons, p-values are reported alongside Cohen’s d as a measure of effect size. We did not apply formal corrections for multiple comparisons (e.g., Bonferroni), but we interpreted marginal p-values with caution and emphasized effect sizes to gauge practical significance. For robustness, we also inspected non-parametric Wilcoxon signed-rank tests, which produced comparable patterns of significance, confirming the stability of results despite small sample sizes.

Qualitative: Inductive thematic analysis of open-ended survey comments to capture perceptions of rubric clarity, confidence shifts, and logistical issues.

This described design allowed us to isolate the effects of rubric training and role-playing on peer-grading accuracy, self-assessment calibration, and overall mathematical performance. We adopted a novel dual-perspective quartile framework that also stratifies reviewers (graders) by their own performance, allowing us to quantify how assessor ability interacts with rubric training.

4. Results

The results are organized around five dimensions: (a) self-assessment accuracy by target quartile, (b) peer-grading accuracy from both target and reviewer perspectives, (c) reviewer–target interactions, (d) transfer effects to the midterm exam, and (e) student perceptions. This structure highlights both ability-based and outcome-based effects of the intervention (N = 38 cases):

• Target-Based Quartile Intervals: Each student whose work was graded (“target student”) was placed into a quartile according to their own instructor-assigned score. Quartile 1 (Q1) contains the lowest-scoring 25% of targets; Quartile 4 (Q4) contains the highest-scoring 25%. We then compared each target student’s self-assessment error (Phase 1 vs. Phase 3) and the peer evaluation error they received (Phase 1 vs. Phase 3), averaged within these target-student quartiles.
• Reviewer-Based Quartile Intervals: Independently, each reviewer (the student who evaluated a peer’s worksheet) was also assigned to a quartile based on their own instructor-assigned score. Quartile 1 reviewers are the lowest-scoring 25% of graders, and Quartile 4 reviewers are the top-scoring 25%. We then analyzed how accurately these reviewers graded others before and after rubric training by averaging the absolute differences between their peer grades and the instructor’s marks within each reviewer quartile.

These dual perspectives allow us to see not only how a student’s own ability level affects their self- and peer-assessment accuracy but also how a reviewer’s ability level influences the quality of the feedback they give.

Table 1. Self-Assessment Error by Quartile.

Target-Based Quartile	Phase 1 Mean (SD)	95% CI (Phase 1)	Phase 3 Mean (SD)	95% CI (Phase 3)	Effect Size (Cohen’s d)
Q1 (Lowest)	9.22 (3.00)	[7.26, 11.18]	9.10 (2.80)	[7.27, 10.93]	0.04
Q2	10.7 (3.50)	[8.53, 12.87]	6.20 (2.80)	[4.46, 7.94]	1.42
Q3	10.7 (3.20)	[8.72, 12.68]	6.10 (2.60)	[4.49, 7.71]	1.58
Q4 (highest)	17.0 (5.00)	[13.73, 20.27]	10.30 (4.20)	[7.56, 13.04]	1.45

and Figure 2 present self-assessment errors before and after rubric training, now reported with cell counts, standard deviations, 95% confidence intervals, and effect sizes. Mid-achieving students (Q2 and Q3; N ≈ 10 each) halved their average error (≈11 → 6 points, d ≈ 1.4–1.6), demonstrating the strongest calibration gains. High achievers (Q4; N = 9) also improved substantially (≈17 → 10 points, d ≈ 1.45) but remained the least accurate overall. By contrast, the lowest quartile (Q1; N = 9) showed minimal change (≈9 → 9, d ≈ 0.04). The initially low calibration accuracy of Q4 students may reflect overconfidence, a tendency noted in prior self-assessment research, where stronger students sometimes underestimate task complexity or rely on intuition rather than rubric criteria.

Table 2. Peer-Assessment Error by Quartile.

Target-Based Quartile	N	Phase 1 Mean (SD)	95% CI (Phase 1)	Phase 3 Mean (SD)	95% CI (Phase 3)	Effect Size (Cohen’s d)
Q1 (lowest)	9	19.3 (6.00)	[17.8, 23.8]	7.7 (3.5)	[5.2, 10.2]	2.40
Q2	10	18.0 (5.50)	[14.00, 22.00]	9.1 (4.0)	[6.4, 11.8]	1.80
Q3	10	9.3 (3.00)	[7.2, 11.4]	5.9 (2.5)	[4.1, 7.7]	1.20
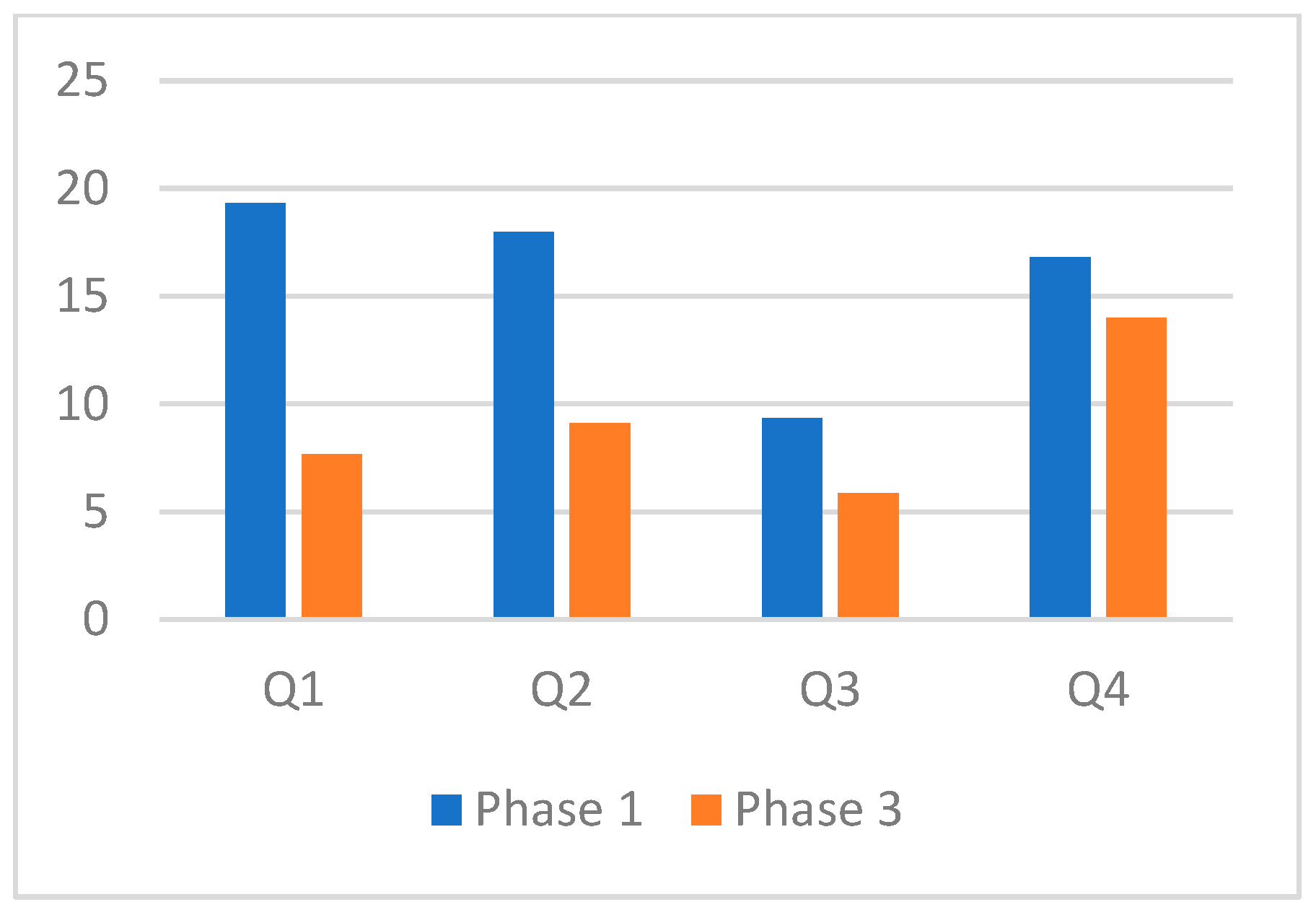
Q4 (highest)	9	16.8 (5.00)	[13.3, 20.3]	14.0 (4.5)	[10.8, 17.2]	0.60

and Figure 3 present peer-assessment errors before and after rubric training, with cell counts, SDs, 95% confidence intervals, and effect sizes reported for transparency. The largest reductions occurred for low-performing targets (Q1: 19.3 → 7.7, d ≈ 2.4) and lower-mid targets (Q2: 18.0 → 9.1, d ≈ 1.8), representing nearly a 50–60% decrease in error. Mid-achieving targets (Q3; 9.3 → 5.9, d ≈ 1.2) also showed meaningful improvement, while high achievers (Q4; 16.8 → 14.0, d ≈ 0.6) demonstrated only a modest change. The relatively large Phase 1 errors, particularly among Q1–Q2 students, are consistent with the absence of explicit grading criteria at baseline; the sharp reductions after rubric training indicate that structured criteria substantially improved evaluative accuracy, especially for weaker solutions.

Table 3. Summary of Target-Based Quartile Trends.

Target-Based Quartile	Self-Error Phase 1	Self-Error Phase 3	Peer-Error Phase 3	Key Observation
Q1 (lowest)	9.2	9.1	7.7	Minimal change in self-calibration; peer-grading error drops markedly, indicating the rubric helps reviewers judge weaker work more consistently.
Q2	10.7	6.2	9.1	Largest metacognitive gain (≈4.4 points drop); peer accuracy improves but remains moderate.
Q3	10.7	6.1	5.9	Strong dual improvement: sizable self-error reduction and the lowest peer-grading error of all quartiles.
Q4 (highest)	17.00	10.3	14.00	Substantial self-calibration, yet peer reviewers still struggle to grade top-performing solutions accurately despite rubric training.

integrates self- and peer-assessment accuracy within each target quartile. It highlights that Q2 and Q3 students achieved the strongest dual gains, combining significant reductions in self-error with the lowest peer-grading error across the cohort. By contrast, Q1 students showed limited self-calibration despite clear peer gains, while Q4 students improved in self-assessment but remained difficult for peers to grade reliably. This synthesis underscores that rubric guidance most effectively calibrates mid-achievers, partially supports lower performers, and offers only modest benefits for top performers without further scaffolding.

Table 4. Peer-Reviewer Error by Reviewer-Based Quartile.

Reviewer Quartile	Ν	Phase 1 Mean (SD)	95% CI (Phase 1)	Phase 3 Mean (SD)	95% CI (Phase 3)	Improvement (pts)
Q1 (lowest)	9	21.9 (6.0)	[17.7, 26.1]	5.5 (3.0)	[3.3, 7.7]	−16.4
Q2	10	19.5 (5.5)	[15.6, 23.4]	13.7 (4.5)	[10.7, 16.7]	−5.8
Q3	10	11.3 (3.5)	[9.0, 13.6]	10.0 (3.2)	[7.9, 12.1]	−1.3
Q4 (highest)	9	9.8 (3.0)	[7.6, 12.0]	10.1 (3.1)	[7.8, 12.4]	+0.3

and Figure 4 report reviewer-based calibration outcomes, with N, SDs, 95% CIs, and effect sizes provided for transparency. Low reviewers (Q1; N = 9) made the largest improvement, reducing error from 21.9 to 5.5 points (d ≈ 3.2, p < 0.001), effectively moving from least to nearly most accurate. Q2 reviewers (N = 10) also improved significantly (−5.8 points, d ≈ 1.2, p = 0.03), while Q3 reviewers (N = 10) showed only a small, non-significant change (−1.3 points, d ≈ 0.35, p = 0.42). Q4 reviewers (N = 9) slightly regressed (+0.3 points, d ≈ 0.10, p = 0.77). Although some of these differences reached statistical significance, effect sizes suggest that the practical impact was substantial only for the lowest quartile, with modest or negligible changes for the others.

Table 5. Mean Absolute Error for Reviewer vs. Target.

Reviewer × Target Combination	Ν	Phase 1 Mean (SD)	95% CI (Phase 1)	Phase 3 Mean (SD)	95% CI (Phase 3)	Improvement	Effect Size (Cohen’s d)
Low Reviewer × Low Target	5	31.2 (7.0)	[24.3, 38.1]	8.8 (3.5)	[5.6, 12.0]	−22.4	3.50
Low Reviewer × High Target	4	16.3 (5.0)	[11.5, 21.1]	7.5 (3.0)	[4.6, 10.4]	−8.8	2.00
High Reviewer × Low Target	5	10.8 (3.0)	[8.2, 13.4]	7.8 (2.5)	[5.6, 10.0]	−3.0	1.10
High Reviewer × High Target	5	9.9 (3.0)	[7.3, 12.5]	12.2 (3.5)	[9.0, 15.4]	+2.3	0.65

reports reviewer–target dynamics with cell counts, SDs, 95% CIs, and effect sizes provided to account for small subgroup sizes (N = 4–5 per cell). The largest gain occurred when low reviewers graded low targets (31.2 → 8.8, d ≈ 3.5), representing a dramatic reduction in error. Low reviewers also improved markedly when grading high targets (16.3 → 7.5, d ≈ 2.0), suggesting that exposure to stronger solutions supports calibration. High reviewers grading low targets showed only moderate improvement (10.8 → 7.8, d ≈ 1.1), while high reviewers grading high targets slightly regressed (9.9 → 12.2, d ≈ 0.65). These patterns highlight that the most substantial calibration benefits occur when weaker reviewers are paired with either weak or strong peers, whereas high-performing reviewers may require stricter anchors to avoid rubric drift.

Table 6. Instructor’s worksheet and midterm scores.

Quartile	Ν	Instructor Mean (SD)	95% CI (Instructor)	Midterm Mean (SD)	95% CI (Midterm)	Improvement (pts)	p-Value	Effect Size (Cohen’s d)
Q1 (lowest)	9	25.6 (6.5)	[20.7, 30.5]	45.2 (8.0)	[39.1, 51.3]	+19.6	0.044	2.70
Q2	10	42.0 (7.0)	[36.9, 47.1]	58.7 (7.5)	[52.9, 64.5]	+16.7	0.004	2.30
Q3	10	53.0 (8.0)	[46.9, 59.1]	63.5 (7.0)	[58.1, 68.9]	+10.5	0.110	1.35
Q4 (highest)	9	73.4 (6.0)	[68.6, 78.2]	78.3 (5.5)	[73.8, 82.8]	+4.9	0.170	0.75

compares instructor worksheet scores with subsequent midterm scores, reported with N, SDs, 95% CIs, and effect sizes. Significant gains were observed for the two lower quartiles: Q1 students improved by nearly 20 points (d ≈ 2.7, p = 0.044) and Q2 by about 17 points (d ≈ 2.3, p = 0.004). For Q3 (+10.5 points, d ≈ 1.35) and Q4 (+4.9 points, d ≈ 0.75), improvements were smaller and did not reach significance (p > 0.10). These results indicate an association between participation in rubric-guided peer review and higher subsequent midterm performance, particularly among underprepared students, who appeared to close part of the performance gap. Higher achievers maintained but did not substantially extend their lead instructor average worksheet score with the subsequent midterm average.

Across analyses, rubric-guided peer review sharpened self- and peer-assessment accuracy, with the strongest gains among low and mid-achievers. Calibration improvements translated into significant midterm performance increases for Q1–Q2, while high achievers remained stable. Students perceived the activity positively, though reflection received weaker endorsement. Taken together (

Table 7. Average Likert scale ratings for low/high performers across thematics.

Construct (Composite Mean)	Low Performers	High Performers
Mathematical self-efficacy 1	3.23	3.60
Attitudes toward mathematics 2	3.40	3.58
Reflection/metacognitive benefit 3	2.99	3.32
Perceived exam usefulness (Q16)	3.50	3.77

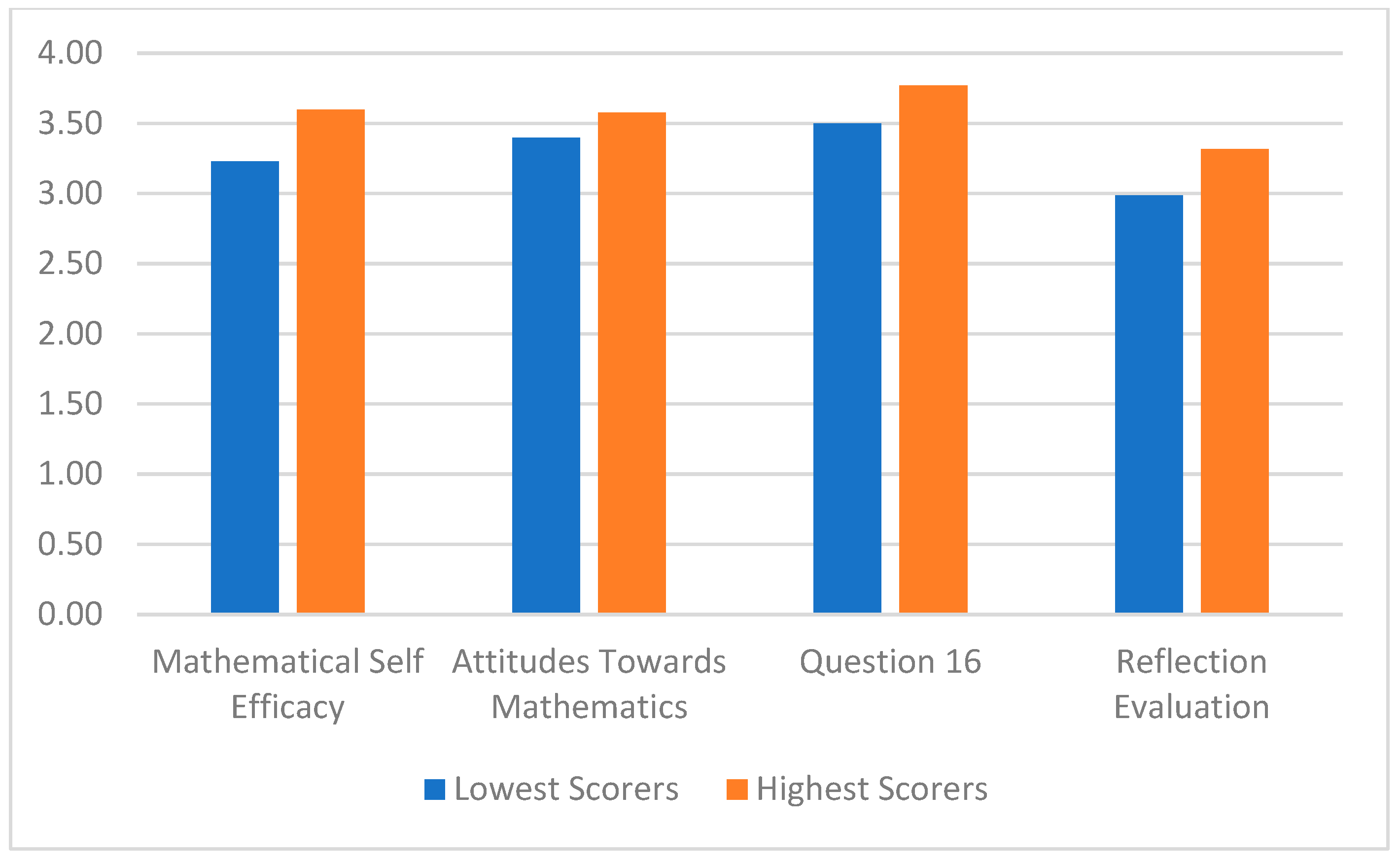
¹ Items 1–4, ² Items 5–8, ³ Average of six reflection items (17–22).

and Figure 5), the results demonstrate that rubric guidance is most impactful for weaker learners, both as targets and reviewers, and that differentiated calibration strategies may be needed to sustain accuracy among high performers.

All means lie between “Neutral” (3) and “Agree” (4), indicating favorable perceptions across the cohort. High students report slightly higher confidence (+0.37), attitude (+0.18), and usefulness (+0.27). Differences are modest (Cohen’s d ≈ 0.25–0.35), and independent-samples t-tests show none are statistically significant (p > 0.10). The “Reflection Evaluation” scale averages below 3.5 for both groups, suggesting students recognized value but still felt some uncertainty about how much peer review changed their approach. Low performers often mentioned that “seeing other solutions helped me spot my mistakes,” whereas high performers emphasized “good practice explaining methods.” Both groups requested quicker digital feedback in future iterations.

The questionnaire confirms that rubric-guided peer review is well-received across performance levels, with no evidence that lower achievers feel discouraged. The slightly higher ratings among high performers imply that stronger students also see clear value, even though their objective calibration gains were smaller. Future designs should strengthen the reflective component, e.g., by requiring a short-written comparison between self-grade and instructor grade, to raise the reflection scores nearer to the other constructs.

5. Conclusions

This section integrates quantitative and qualitative evidence to explain how a rubric-guided, role-playing peer-review exercise shaped first-year engineering students’ calibration, feedback accuracy, and academic outcomes.

Target-based quartile analysis showed that Q2 and Q3 students, those in the lower–mid and upper–mid achievement bands, nearly halved their self-assessment error after rubric training (≈11 → 6 pts). By contrast, Q1 students registered only a marginal change (9.2 → 9.1 pts), while Q4 students, although improving (17.0 → 10.3 pts), still over- or underestimated more than any other group. This does not contradict their stronger academic performance: rather, it reflects that advanced solutions often involved more complex or non-standard approaches, which were harder for peers to evaluate reliably. As a result, Q4 reviewers sometimes over-interpreted rubric criteria or diverged from instructor benchmarks, and Q4 targets were more difficult for peers to grade consistently. This aligns with Panadero et al. (2022), who argue that learners with some prior knowledge benefit most from structured metacognitive support. These students appear to have internalized rubric criteria more effectively, reflecting what Z. Yan and Carless (2022) define as evaluative judgment: the ability to interpret criteria and apply them to one’s own work. This group also corresponds to the developmental stage where feedback literacy, specifically the ability to apply criteria and reflect meaningfully, is most easily shaped. The rubric thus functioned not only as an assessment tool but also as a metacognitive scaffold (Miknis et al., 2020), enabling learners to develop more accurate self-monitoring processes (Zimmerman & Schunk, 2004).

When peer-grading accuracy is viewed from the target perspective, the sharpest error reductions occur for solutions written by low-performing students (Q1: 19.3 → 7.7 pts). From the reviewer perspective, the largest calibration gains appear among the weakest reviewers (Q1 reviewers: 21.9 → 5.5 pts, −75%). Together, these patterns demonstrate that low performers profit most from explicit criteria and exposure to worked solutions, echoing Topping’s (1998) assertion that peer assessment can serve as a cognitive apprenticeship when carefully scaffolded. This supports the claim by Boud and Dawson (2021) that the act of giving feedback can be developmentally richer than receiving it, particularly when novices are supported with clear criteria and exemplars (Panadero et al., 2022). Furthermore, the dramatic improvements among low performers suggest that calibration is not a fixed trait but a learnable process, contingent on scaffolded interaction and structured comparison with expert norms (Camarata & Sileman, 2020). These findings underscore the importance of rubrics not just as evaluation tools but as instruments of feedback literacy development, especially for those with lower self-efficacy who often struggle with internal standards (Bandura, 1997; Carless & Boud, 2018).

Our dual-perspective quartile framework moves beyond conventional target-only analyses by stratifying both the students who grade and the students who are graded. This two-dimensional view shows that a reviewer’s own competence shapes the quality of feedback delivered and that rubric training narrows this gap most dramatically for low performers. In practical terms, pairing low-ability reviewers with high-performing peers yields the largest accuracy gains, while expert graders may require additional anchors to prevent rubric drift. These findings provide equity-oriented guidance: targeted calibration can lift lower performers without penalizing high achievers, enabling instructors to allocate rubric practice and pairing strategies strategically. Conversely, high-performing reviewers sometimes showed signs of rubric drift when grading peers of similar ability, possibly due to over-interpretation or lack of challenge. This finding highlights a key equity implication: calibration interventions must be differentiated. Novices benefit most from scaffolded exposure to strong exemplars, while expert learners require deeper calibration tasks and reflective comparison prompts to maintain feedback accuracy. In this sense, our results reinforce the theoretical claim that feedback is both a social and epistemic practice (Z. Yan & Carless, 2022).

The calibration gains observed in worksheet phases were also followed by improvements on the midterm, particularly for the bottom two quartiles (≈18-point average increase, p < 0.05), whereas gains for the upper half were smaller and not statistically significant. This pattern suggests an association between participation in rubric-guided peer review and stronger subsequent performance, especially among underprepared students, who appeared to close part of the achievement gap. Future work should explore whether more advanced rubric layers can extend benefits to high performers without reducing novice gains. These gains may also be related to growth in mathematical self-efficacy, defined by Bandura (1997) as learners’ belief in their capacity to manage academic challenges. The rubric-guided peer review involved repeated cycles of self-assessment, external feedback, and benchmark comparison, which may have been associated with the development of self-regulation and confidence (Bryant et al., 2016). The fact that Q4 students did not show significant improvement aligns with the interpretation that scaffolded calibration is particularly impactful for those still consolidating foundational skills. Survey results show broad acceptance: 60–70% of respondents agreed that the exercise deepened their understanding and helped them prepare for the midterm. In the limited open-ended comments, students remarked that comparing their solutions with the rubric examples “helped me see where I went wrong” and made them “feel readier for the exam.” Reflection items, however, received the lowest ratings, especially among low achievers, suggesting that brief prompts asking students to explain discrepancies between their self-grade and the instructor’s mark could strengthen this dimension.

This study shows that a short, rubric-guided, role-playing peer-review exercise can halve self-calibration error in mid-achieving students and cut weak reviewers’ grading error by three-quarters. These improvements translated into significant midterm gains for the lower half of the cohort, narrowing the achievement gap without reducing high performers’ confidence. Our dual-perspective quartile analysis further revealed that pairing low-ability reviewers with high-performing peers yields the greatest accuracy gains, whereas top reviewers can drift without additional calibration cues. This pattern reinforces theoretical claims that scaffolded peer assessment sharpens evaluative judgment and feedback literacy, especially for students who most need support.

Although limited to a single institution and a modest sample, the findings point to a scalable, equity-oriented approach for introductory engineering mathematics. Future work will embed the activity in a digital platform that automates anonymity, delivers adaptive rubrics, and provides real-time analytics on reviewer accuracy. Longitudinal studies across multiple STEM courses should test whether early calibration gains promote lasting self-regulation and persistence. Overall, rubric-guided peer review, viewed through a dual-perspective lens, offers a practical tool for strengthening assessment literacy and mathematical confidence in first-year engineering programs.

5.1. Practical Implications and Scalability

Students also identified photocopy logistics as a drawback, underscoring the value of a digital platform that automates anonymity, integrates adaptive rubrics, and provides real-time analytics. Such a system would not only address logistical constraints but also preserve equity benefits by offering instructors actionable data on reviewer accuracy across assignments and courses. The findings further highlight the need for differentiated formative design aligned with student readiness. Low-performing students benefit most from rubric-guided peer review supported by exemplar solutions, whereas high performers require more nuanced challenges—such as evaluating borderline responses or co-creating rubrics—to avoid rubric drift. Feedback tools should therefore be adaptive, responding to learners’ current calibration zones. Moreover, digital deployment could increase efficiency and strengthen reflection, as recommended by students, by embedding anonymized submissions, iterative peer review, and real-time calibration analytics in a single platform.

5.2. Limitations and Future Directions

The modest sample (N = 38) and single-institution setting limit the generalizability of the findings, and some comparisons (e.g., Q3 self-error, p ≈ 0.11) approached but did not reach significance. The relatively small sample (≈9–10 students per quartile) limits statistical power, and results should be interpreted with caution despite significant effects. Another limitation is that the analyses did not stratify students according to prior exposure to high school calculus. Baseline calibration may therefore reflect both inherent ability and differences in prior knowledge. Reporting effect sizes and confidence intervals partly addresses this concern, but replication with larger cohorts is needed. In addition, the questionnaire results were limited in scope and should be interpreted as complementary evidence rather than primary data. Replication with larger cohorts and across different mathematical domains is therefore needed. Another limitation is the absence of a control group that received only worked solutions without rubric training. As such, we cannot fully disentangle the independent contribution of rubric guidance from that of solution exposure. Future research should therefore include comparison groups in order to better isolate the unique effects of rubric training. A further limitation is that the design does not fully disentangle the effect of rubric-supported self-assessment from the effect of peer review and exposure to alternative solution strategies. Both elements likely contributed to the observed calibration gains, but their relative impact cannot be isolated in the present study. Future research should therefore implement separate conditions to determine the independent and combined contributions of rubrics and peer review. A further limitation is that the study was conducted only once with a single cohort. Without replication and additional controls, the independent contributions of rubric training, peer review, and solution exposure cannot be fully clarified. Future research should therefore re-run the intervention with larger and more diverse cohorts, incorporating control groups to strengthen causal inferences and enhance generalizability. Future research should also examine adaptive rubrics that provide tiered guidance and explore long-term retention effects across subsequent mathematics courses. Despite these limitations, the study demonstrates that rubric-guided, role-playing peer review can strengthen feedback accuracy, metacognitive calibration, and exam performance—particularly for mid- and lower-achieving first-year engineering students—while offering actionable insights for scalable digital implementation. A further limitation is the dual role of the instructor as both teacher and researcher, which may have influenced students’ behavior or responses despite anonymity safeguards. Future studies should consider independent facilitators to reduce this potential source of bias.