Playing Gebeta in Preschool: Informal Pathways to Early Numeracy Through Directionality and Bundling
Abstract
1. Introduction
- How do preschool children unfamiliar with Gebeta learn and play the game? What do they master, and where are they challenged?
- Which mathematical skills do the children learn by playing Gebeta?
1.1. Play in Early Mathematics Education
1.2. The Gebeta Game and Mathematics
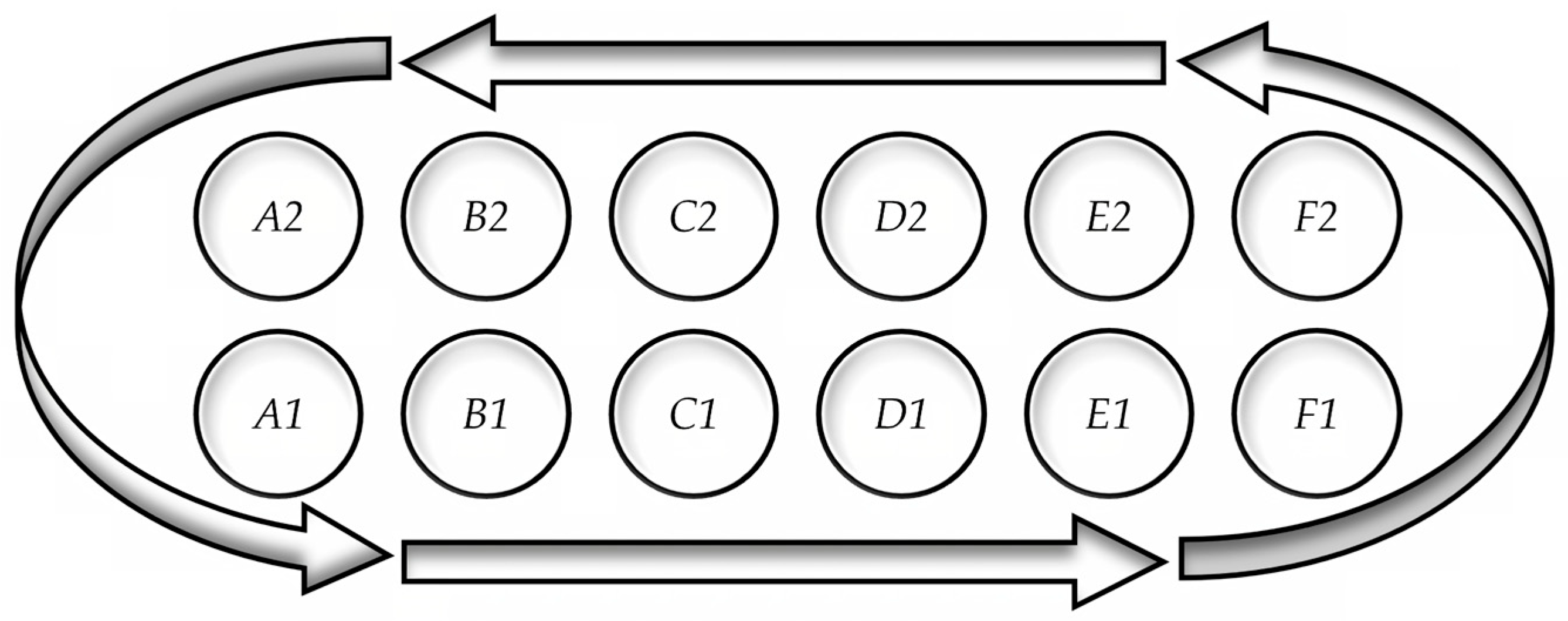
1.2.1. The Gebeta Game Rules
1.2.2. Mathematical Concepts Embedded in the Gebeta Game
2. Theoretical Framework
2.1. Counting
- One-to-one correspondence is needed to compare the cardinality of two sets. Two sets have the same cardinality, i.e., the same number of elements, if you can allocate each element of one set to one and only one element of the other set and vice versa (Piaget & Szeminska, 1941). When playing Gebeta, the players sow counters by placing one counter in each of the homes. Thus, there is a one-to-one correspondence between the sown counters and the homes that received a counter.
- Subitising is the ability to “see” how many items a set contains. This is easy for up to three elements. For larger sets, we subitise by structuring the set. For example, we can see that a set contains five elements when we subitise a group of two and a group of three. This skill is called conceptual subitising (Clements, 1999). When playing Gebeta, the players must identify “families” of four counters.
- Systematic counting is the ability to determine the cardinality of a set by enumerating. It requires an understanding of the five counting principles (Gelman & Gallistel, 1978):
- The one-to-one principle demands that children maintain one-to-one correspondence between objects and number words when counting.
- The stable-order principle demands that children can recite the number words in the correct order “one, two, three, four, five, …”
- The cardinal principle says that the final number word used in the counting process is the total number of counted objects.
- The abstraction principle is about what can be counted, i.e., both tangible and abstract objects. In the context of Gebeta, these can include counters, homes, steps, families, players, matches, and wins.
- The order-irrelevance principle highlights that the same cardinal number results regardless of the enumeration order.
When playing Gebeta, players count, for example, how many counters or families they have captured. - Basic arithmetic is the ability to add or subtract small numbers, eventually by using tangible objects (Barth et al., 2005). Gebeta players must understand that a set of three counters will become a family of four if one is added.
- Bundling is the ability to understand sets of objects as units (Wege et al., 2023). In the Gebeta game, sets of four counters are treated as units, known as families. Before the game starts, the families are distributed into the homes. During the game, the players capture families. At the end of the game, players count the number of families they have captured. Bundling plays a crucial role in the number system. We bundle ten ones into a group of ten, ten groups of ten into a group of one hundred and so on.
- Children’s concept of zero develops over time. Nieder (2016) distinguishes four stages of zero-like concepts: (1) the sensory representation of zero as the absence of stimulation; (2) the categorial representation of zero as “nothing” in contrast to “something”; (3) the quantitative representation of zero as the cardinality of the empty set; and (4) the mathematical representation of zero as an abstract number. In the game Gebeta, empty homes have a special meaning. This can be used to introduce zero as the cardinality of the empty set, i.e., the number of counters that remain in a pit after all counters have been removed.
2.2. Measuring
2.3. Locating
2.4. Designing
2.5. Playing
2.6. Explaining
3. Materials and Methods
3.1. Study Design
- The focus is on individuals observed throughout a period of developmental change, making the child the primary unit of analysis. In this study, the focus was placed on five children in a Norwegian kindergarten (see Section 3.2).
- Observations occur before, during, and after a phase of change within a specific domain, not just before and after. Thus, I observed the children during four play sessions over a one-month period. This is a realistic timeframe to become familiar with a new game.
- There is a high frequency of observations during the transition period, with intervals considerably shorter than the time needed for the developmental change. Here, the transition is from not knowing the game to playing the game without help. Thus, in the first session, I introduced the game and helped the children learn the rules. In the following sessions, support was gradually reduced, allowing the children to play more independently.
- Behaviours are analysed in depth. Microgenetic studies usually combine qualitative and quantitative methods (Siegler & Crowley, 1991). However, due to the small sample size, only a qualitative method was employed: Interaction Analysis (see Section 3.3).
3.2. Data Collection

3.3. Interaction Analysis
- The first step is a content log. The log entries are indexed by videotape number and timestamp and contain summary listings of events as they occur on the tape (Jordan & Henderson, 1995, p. 43). The log entries are broad descriptions of what is happening, not detailed transcripts.
- Instead of Group Work, I coded the data alone. First, a deductive classification was conducted using the predefined coding scheme, i.e., Bishop’s fundamental mathematical activities as presented in Section 2. Afterwards, the data was coded inductively by identifying patterns of repeated actions in the children’s interactions with the material and each other. Through repeated replays, increasingly detailed aspects of the participants’ social skills and their abilities to collaboratively construct meaning became clearer (Jordan & Henderson, 1995, p. 43).
- As specific tape segments became significant, content logs were expanded into transcriptions (Jordan & Henderson, 1995, p. 47). Focusing solely on relevant segments enables me to transcribe those parts more thoroughly.
4. Results
4.1. Bishop’s Fundamental Mathematical Activities
4.1.1. Counting
4.1.2. Measuring
4.1.3. Locating
4.1.4. Designing
4.1.5. Playing
- On day 2 (timestamp 44:23), during Emil’s match against me, Emil had one counter in C1 and D1, three in E1 and two in F1. Instead of choosing the home with the most counters, he moved the counter from D1 to E1 and captured a family (cf., Table A2, line 1267).
- In his next move (timestamp 44:43), he avoided moving the counters from F1 to my side. He instead moved the counter from C1 to D1 (cf., Table A2, line 1277).
- On day 3 (timestamp 07:22), during Emil’s match against Dan, Dan had one counter in E2 and C2, and three in B2. He took three counters from B2 and started to sow them. Then, he realised that there was only one counter in C2. Thus, he put the three counters back into B2, took the counter from C2, and moved it to B2. And captured the family in B2.
- On day 4 (timestamp 12:02), during Emil’s match against Britt, Britt had one counter in B2 and D2, and three in E2. Emil showed Britt how she could capture a family by moving the counter from D2 to E2 (cf., Table A3, line 395).
4.1.6. Explaining
4.2. Patterns of Repeated Actions
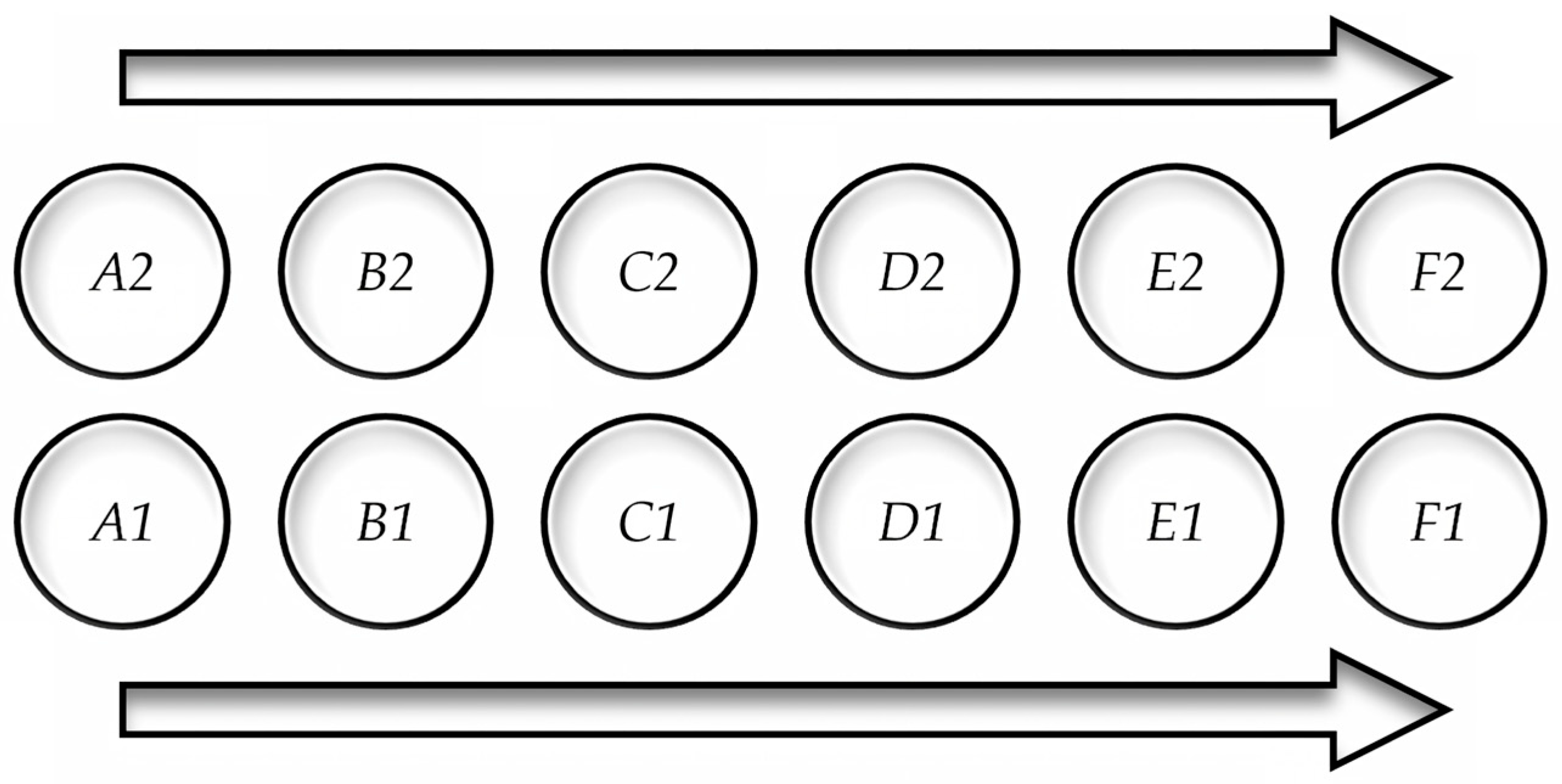
4.2.1. Directionality
4.2.2. Bundling
- Ada: On day 1 (timestamp 17:30), after their first match, I showed Ada and Britt how to bundle the counters, and they did it. Then (timestamp 18:38), I asked them to count the families, but they counted the counters separately. However, after I had shown them how to count the families (timestamp 19:57), both girls were able to do it. Already after the second match on day 1 (timestamp 32:54), Ada grouped her counters on her own initiative, but she counted the individual counters instead of the families as units. This remained unchanged during all four days. On day 4 (see Table 2), Ada grouped, but preferred to count the counters: “I do it just as I want to” (line 314), even though Dan insisted that she must count the groups (line 315):
| Line | Timestamp | Activity * | Comments |
|---|---|---|---|
| 296 | 08:49 | Ada (starts to group her counters): Here are just four. | |
| 299 | 08:55 | Ada: I believe I have six. | Britt still wants to sow left-to-right in her row. |
| 300 | 08:57 | Dan: Six? That are more. | Dan estimates the amount. |
| 301 | 08:59 | Dan: I think so. | |
| 302 | 09:01 | Ada makes a group of five counters. | |
| 304 | 09:07 | Ada (removes the fifth counter from her group of five and starts a new group): I do it just as I want to. | |
| 307 | 09:15 | Ada makes a new group of four. | Ada groups correctly. |
| 308 | 09:17 | Dan: No, you must do it right. | |
| 310 | 09:21 | Dan: That’s not good. Ada: Let me think. | |
| 311 | 09:23 | Ada (has four groups of four): Just here. | |
| 313 | 09:27 | Ada (counts the counters in the first group): 1, 2, 3, 4. | Ada does not count the groups. |
| 314 | 09:29 | Ada: I do it just as I want to. | |
| 315 | 09:31 | Dan: But you must only count the four counters. |
- Britt: On day 4 (see Table 3), she bundled the counters on demand. She even insisted on doing it by herself without help (line 425).
| Line | Timestamp | Activity * | Comments |
|---|---|---|---|
| 421 | 13:06 | Britt starts grouping her counters. | Britt can group. |
| 423 | 13:08 | R: Since you capture groups of four, you can just count how many groups of four you have. | |
| 424 | 13:12 | The practitioner helps Britt group her counters. | |
| 425 | 13:14 | Britt pushes together the groups that the practitioner had created. Practitioner: I have just made groups of four. | Britt wants to group on her own. |
| 426 | 13:17 | Practitioner: What do you do now? | |
| 427 | 13:19 | R: But Britt can do it on her own. | |
| 429 | 13:22 | Britt continues grouping her counters. |
| Line | Timestamp | Activity * | Comments |
|---|---|---|---|
| 468 | 14:33 | Britt finished her grouping. | |
| 469 | 14:34 | R: Now, you can count how many groups of four you have. | |
| 470 | 14:37 | Britt (counts the counters in one group): 1, 2, 3, 4. | |
| 471 | 14:39 | R: How many groups? | |
| 472 | 14:41 | Britt (starts counting the counters in the next group): 1, 2. Emil (shows Britt how to count groups): No, like this 1, 2, 3, 4. | Britt does not count how many counters she has nor how many groups. She checks if there are four counters in each group. |
| 473 | 14:45 | Britt: No. I don’t do it like this. Emil (continues counting Britt’s groups): 5, 6. | |
| 474 | 14:47 | Britt counts the counters in the first group again. | |
| 475 | 14:49 | Britt: 1, 2. | |
| 476 | 14:51 | Emil: It is not like this. | |
| 477 | 14:53 | Britt: 3, 4. | |
| 478 | 14:55 | Britt (counts the counters in the second group): 1. | |
| 479 | 14:57 | Britt: 2. | |
| 480 | 14:58 | Britt (starts over again in the second group): 1. | |
| 481 | 14:59 | Britt: 2 | |
| 482 | 15:00 | Britt: 3. | |
| 483 | 15:01 | Britt: 4. | |
| 484 | 15:02 | Practitioner: Let her count. | |
| 485 | 15:03 | Britt (counts the counters in the third group): 1. | |
| 486 | 15:04 | Britt: 2, 3, 4. | |
| 487 | 15:06 | Britt (counts the counters in the fourth group): 1, 2, 3, 4. | |
| 488 | 15:12 | Britt (counts the counters in the fifth group): 1, 2, 3, 4. | |
| 489 | 15:13 | Britt (counts the counters in the sixth group): 1, 2, 3, 4. | |
| 490 | 15:15 | Britt (counts the counters in the seventh group): 1, 2, 3, 4. | |
| 491 | 15:18 | Britt (counts the counters in the third group again): 1, 2, 3, 4. | |
| 493 | 15:21 | Britt: Four. | |
| 494 | 15:22 | Britt: I have four. | Does she mean ‘groups of four’? |
| 495 | 15:24 | R (points at Britt’s families): Britt, can you count how many groups of four you have? | |
| 497 | 15:29 | R (points at Britt’s families): 1, 2, 3, 4, … | |
| 498 | 15:31 | Britt (counts the families): 1, 2, 3, 4. | |
| 499 | 15:33 | Britt (continues counting the families correctly): 5, 6, 7. | Britt can count the groups. |
| 500 | 15:38 | Emil distributes his counters into the homes on the board. | |
| 501 | 15:40 | Practitioner: So, Britt, how many groups do you have? | |
| 502 | 15:44 | Britt: 7. Emil starts picking up Britt’s counters. | Britt is a CP-knower. |
- Carl: In all his matches, Carl bundled the counters and counted the families on his own initiative. He must have learnt this skill before the project.
- Dan: On day 1 (timestamp 19:26), he bundled his counters but counted them individually. On subsequent days, he bundled them himself and insisted that the other children count the bundles as well (e.g., Table 2, line 315). Only when Ada refused to count the families did Dan do the same (timestamp 09:37). At the end of day 4 (timestamps 12:59–13:22), he even tried to count the bundles without grouping the counters, but this was too difficult.
- Emil was familiar with the game already before the project started. He bundled and counted families all by himself (e.g., day 2, timestamp 45:11). On several occasions, he showed the other children how to do it. You can find examples in Appendix A (Table A3, lines 326, 329, 331, and 419). Nevertheless, he sometimes preferred to count the individual counters. On day 2 (timestamp 44:07), after he had counted his 16 counters, I stated that I had 16, too. Emil acknowledged. How did he know? Most likely, he subitised that my four groups of four contain the same amount as his four groups. However, when he later compared his five families to my six families, he counted the groups (see Figure 6).
4.2.3. Algorithmic Thinking
5. Discussion
5.1. Directionality
5.2. Bundling
5.3. The Adults’ Role
5.4. Summary
5.5. Limitations
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| IPA | International Phonetic Alphabet |
| Sikt | Norwegian Agency for Shared Services in Education and Research |
| GDPR | General Data Protection Regulation |
Appendix A
Appendix A.1. Britt’s First Turn on Day 2
| Line | Timestamp | Activity * | Comments |
|---|---|---|---|
| 314 | 10:34 | Britt takes all the counters from A1. | |
| 315 | 10:38 | Britt puts the first counter back to A1. R: Here is the first one. (points to B1) | She starts at the same place where the counters came from. |
| 316 | 10:40 | R: That was well the one you had taken. R takes the counter from A1. | |
| 317 | 10:42 | R: This is the first one. I put the counter in B1. | |
| 318 | 10:44 | R: The second. Britt puts a counter in C1. | |
| 319 | 10:46 | R: The third. Britt puts a counter in D1 and E1. R: And the fourth. | |
| 320 | 10:48 | R (points to E1): And now you take all here. | |
| 321 | 10:50 | Britt takes the counters from E1. | |
| … | |||
| 325 | 10:58 | R (is focused on the other match): Yes. Britt starts sowing at E1. | She starts at the same place where the counters came from. |
| 327 | 11:02 | Britts puts a counter in F1. | |
| 328 | 11:04 | Britt (looks at the three counters in her hand): There are only these left here. | |
| 329 | 11:06 | R (points at the homes in the second row): Yes, you must continue. | |
| 330 | 11:08 | Britt puts a counter in A1. R (points at F2): Here, you must continue here. | She attempts to continue in the same row, not the other one. |
| 331 | 11:10 | Britt moves the counter from A1 to A2. R (points again at F2): Here! | She attempts to sow clockwise. |
| 332 | 11:12 | R (points at A2 and moves finger to F2): Here, here, here. Britt takes the counter from A2. | |
| 333 | 11:14 | R (points at F2): Here. Britt puts the counter in F2. | |
| 334 | 11:16 | R (points at E2): And there. Britt puts a counter in E2 and D2. | |
| 335 | 11:18 | R (points at D2): And now, you must take all these. | |
| 336 | 11:20 | Britt takes all counters from D2. R (points at C2): And continue. | |
| 337 | 11:22 | Britt puts the counters on the table. | She thinks she has won the counters. |
| 338 | 11:24 | Britt picks the counters up. R (points at C2): You must continue from here. | |
| … | |||
| 341 | 11:30 | Britt sows the counters to C2, B2, and A2. | She sows correctly. |
| … | |||
| 344 | 11:38 | R (points at A1): Here. Britt puts a counter in A1. | She needs help at the transition from one row to the other. |
| 345 | 11:40 | R (points at B1): And here. Britt puts a counter in B1. | |
| 346 | 11:42 | R (points at B1): And now, you take all these. Britt takes all the counters from B1. | |
| 347 | 11:44 | R (points at C1): And distribute. | |
| 348 | 11:46 | Britt looks at the counters and asks something unintelligible. | |
| 349 | 11:48 | Britt puts the counters on the table. R: You must distribute them. | She thinks she has won the counters. |
| … | |||
| 353 | 11:56 | Britt starts sowing at B1. R (points at C1): Here. It starts here. | She starts at the same place where the counters came from. |
| 354 | 11:58 | R (takes the counter from B1): Not here. | |
| 355 | 12:00 | R (puts the counter in C1): It starts here. | |
| 356 | 12:02 | R (points at D1): And then here. Britt puts counters in D1, E1, and F1. | |
| … | |||
| 362 | 12:14 | Britt (looks at the two remaining counters in her hands): I have only two. | |
| 363 | 12:16 | R (points at C2): Yes. | Because I thought the two counters came from the empty home D2. |
| 364 | 12:18 | R (points at C2): Here. Britt hesitates. R: Where do they come from? | |
| 365 | 12:20 | R (points at D2): They have been here? | |
| 366 | 12:22 | Britt puts a counter in D2. R (takes the counter from D2): But you must distribute... | She starts at the same place where the counters supposedly came from. |
| 367 | 12:24 | R (puts the counter in C2): ...here and here. (points at B2) | |
| 368 | 12:26 | Britt puts the counter in B2 and waits. | She does not know how to continue. |
| 373 | 12:36 | Britt still waits. R (points at B2): Was the last one here, now? | |
| 374 | 12:38 | Britt: Yes. R: Then you must take all these here. | |
| … | |||
| 382 | 12:54 | R (points at A2): Then, you continue here. | |
| 383 | 12:56 | Britt puts a counter in A2 and the next one in B2. | She sows in a clockwise direction. |
| 384 | 12:58 | R (moves the counter from B2 to A1): No. | |
| Britt’s first turn continues for a while in the same manner. | |||
| 498 | 17:12 | Britt distributes counters from A2... | She sows in a clockwise direction. |
| … | |||
| 505 | 17:25 | ... to F2. | |
| 507 | 17:31 | Britt continues distributing from A1… | In her row, she sows in an anticlockwise direction. |
| 508 | 17:36 | ... to E1. | |
| 510 | 17:40 | Britt (attempts to take the counters from C1): Can I take these because there are so many? | She does not remember that she must continue from E1. |
| 511 | 17:42 | R: Hm? Britt: Can I take these because there are so many? | |
| 513 | 17:46 | R: Was the last one there? | |
| 514 | 17:48 | Britt: Yes. | |
| 515 | 17:49 | R: Really? | |
| 516 | 17:50 | R: Yes, then you can take these. | |
| … | |||
| 522 | 18:03 | Britt (looks at the counters in her hand): There are so many. | |
| 523 | 18:05 | Britt starts sowing at C1 and continues to D1 and E1. | She starts at the same place where the counters came from. |
| 525 | 18:09 | R points at F1. Britt puts a counter in F1. | |
| 527 | 18:11 | R points at F2. Britt puts a counter in F2. | |
| 529 | 18:15 | Britt sows counters in D2, E2, and F2. | She sows in a clockwise direction. |
| … | |||
| 532 | 18:20 | R (moves the counter from F2 to C2): The last one is here. | |
| 533 | 18:23 | R takes the counters from C2 and distributes them to B2 and A2. | R finishes Britt’s turn. |
| 534 | 18:26 | R takes the counters from A2 and distributes them to A1, B1, and C1. | |
| 535 | 18:27 | R (takes the counters from C1 and distributes them to D1 and E1): Yes. Now, here are four and here are four. | |
| 536 | 18:30 | R (takes the four counters from B1 and E1 and moves them to Britt’s site): And now, you win these. | |
Appendix A.2. Emil’s Match Against Me on Day 2
| Line | Timestamp | Activity * | Comments |
|---|---|---|---|
| Emil and I have each captured 16 counters. There are still 16 counters remaining on the board. One counter is in C1, D1, and C2; two in F1 and F2; and three in E1, E2, and D2. | |||
| 1261 | 44:05 | R: I have four groups of four. | I have grouped my counters. |
| 1262 | 44:07 | Emil (groups his counters): It is easier to count like this. | |
| 1263 | 44:09 | Emil (counts the counters): 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16. | He counts the individual counters even though they are grouped. |
| 1264 | 44:17 | R (looks at his 4 groups of 4): I have 16, too. | |
| 1265 | 44:19 | Emil: Yes. | He seems to know that 4 times 4 is 16. |
| 1266 | 44:21 | R: So, we have the same amount. It is your turn. | |
| 1267 | 44:23 | Emil moves a counter from D1 to E1 and creates a family. | This is a strategic move. |
| 1268 | 44:25 | R: Yes, you win this one. | |
| 1269 | 44:27 | Emil (moves the family from E1 to his side): Do you want to continue? | |
| 1270 | 44:29 | R: Yes, it is my turn. | |
| 1271 | 44:31 | R (picks up the counters from F2): I take these. | |
| 1272 | 44:33 | R (sows into E2 and D2): Then, I win those. | |
| 1273 | 44:35 | R moves the two captured families to my side. | |
| 1274 | 44:37 | Emil: Do you have more than I now? | This is a reasonable conclusion. |
| 1275 | 44:39 | R: Yes, I believe I have a little more. | |
| 1276 | 44:41 | R: But if you win all remaining ones… | |
| 1277 | 44:43 | Emil moves a counter from C1 to D1. | This is a strategic move. He avoids moving the counters from F1 to my side. |
| 1278 | 44:45 | R (moves the last counter in my row from C2 to B2): I must take this one. | This is a move without agency. |
| 1279 | 44:47 | Emil moves the counter from D1 to E1. | Emil proceeds with his strategy. |
| 1280 | 44:49 | R moves the counter from B2 to A2. | The last phase is like a race. Unfortunately, Emil lost this time. We would have succeeded if his single counter had started at B1 instead of C1 or if my last counter had started at B2 instead of C2. |
| 1281 | 44:51 | Emil moves the counter from E1 to F1. | |
| 1282 | 44:53 | R: Unfortunately, you must continue with this one. | |
| 1283 | 44:55 | Emil picks up the counters from F1. | |
| 1284 | 44:57 | Emil sows the counters into F2, E2, and D2. | |
| 1285 | 44:59 | R: Now, it is finished. | |
| 1286 | 45:01 | Emil: It is your turn. | |
| 1287 | 45:03 | R: Yes, but you have nothing in your row. | |
| 1288 | 45:05 | Emil: So what? | |
| 1289 | 45:07 | R: The game is finished. | |
| 1290 | 45:09 | R: I believe I have a little more. | |
| 1291 | 45:11 | Emil silently counts both his and my families by pointing at each bundle from a distance. | Emil counts the bundles. |
| 1292 | 45:13 | Emil (pushes his counters together): Yes, you win! | Emil mentally compares the numbers. |
Appendix A.3. Day 4
| Line | Timestamp | Game: Emil vs. Britt * | Game: Dan vs. Ada * | Comments |
|---|---|---|---|---|
| 166 | 05:33 | Emil and Britt restart their game. | Dan and Ada have already played some turns. Dan has captured three families, and Ada has one. It is Dan’s move. | |
| 167 | 05:34 | Emil (takes the counters from F1): Well! I play. | R (points at D2 and talk to Ada): Those are yours. | |
| 168 | 05:35 | Ada collects the family from D2. | ||
| 169 | 05:36 | R (points at B2 and talk to Dan): You must continue here. | ||
| 170 | 05:37 | Emil sows into E1, D1, C1, and B1. | Emil sows clockwise. | |
| 171 | 05:38 | Ada attempts to take the counters from B2. | ||
| 172 | 05:40 | R (points at Dan): No, he shall do it. | ||
| 173 | 05:41 | Ada shrugs her shoulders. | ||
| 174 | 05:42 | Dan: But that is on Ada’s side. | ||
| 175 | 05:43 | Emil (takes the counters from B1): Right? | ||
| 176 | 05:44 | Practitioner: Yes. | ||
| 177 | 05:45 | Dan attempts to take counters from B1. R (points at B2): Here. | ||
| 178 | 05:47 | Emil (sows into A1): One. | Emil counts while he sows. | |
| 179 | 05:48 | Emil (sows into A2): Two. | Dan takes all counters from B2. | |
| 180 | 05:49 | Emil (sows into B2): Three. | ||
| 181 | 05:50 | Emil (sows into C2): Four. | ||
| 182 | 05:51 | Emil (sows into D2): Five. | ||
| 183 | 05:53 | Emil (takes all counters from D2): Well. | ||
| 184 | 05:54 | One of Dan’s counters falls into A2. R (points at A2): You can start with this one. | ||
| 185 | 05:56 | Emil continues sowing into E2 and F2. | Dan sows into A1. | |
| 186 | 05:57 | Emil sows into F1. | Dan sows into B1. Ada: This one is full. | |
| 187 | 05:59 | Emil sows into E1. | Carl: Yes. | |
| 188 | 06:00 | Emil (sows into D1): Five. | Emil has counted silently. | |
| 189 | 06:01 | Britt: Yes. | Dan sows into C1. | |
| 190 | 06:02 | Emil takes all counters from D1. | ||
| 191 | 06:03 | Dan sows into D1. | ||
| 192 | 06:04 | Ada (reaches to Dan’s side): Oh, you have forgotten this one. | ||
| 193 | 06:05 | Emil sows into C1, B1, and A1. | Ada takes a counter from Dan’s side and sows it into E1. | |
| 194 | 06:07 | Dan sows into F1. | ||
| 195 | 06:08 | Emil sows into A2, B2, and C2. | Dan sows into F2. | |
| 196 | 06:09 | Dan sows into E2 and picks up the four counters from E2. | ||
| 197 | 06:10 | Dan moves the counters to his side. R: But–yes, now it is your turn (points at Ada). | ||
| 198 | 06:12 | Emil takes all counters from C2. | R (points at D1): Then you can take out these, too. | |
| 199 | 06:14 | Dan: These? | ||
| 200 | 06:15 | One of Emil’s counters falls into B2. | R: Yes. | |
| 201 | 06:16 | Practitioner: Oh. Emil tries to pick up the extra counter from B2. | Dan takes the counters from D1 and moves them to his side. R (to Ada): And now, it is your turn. | |
| 202 | 06:17 | The practitioner picks up the counter and moves it to D2. | Ada (attempts to take counters from B1): Okay, I take this one. | |
| 203 | 06:19 | R: No, you must take from your side. | ||
| 204 | 06:20 | Practitioner (points at E2): Now, you must continue here. | Ada picks up the counters from C2. | |
| 205 | 06:21 | Ada sows into A2. | ||
| 206 | 06:22 | Emil sows in E2 and F2. | Ada sows into A1. | |
| 207 | 06:24 | Ada sows the last counter into B1. | ||
| 208 | 06:25 | Emil continues sowing in F1 and E1 | R: Now, you can take these. | |
| 209 | 06:26 | Emil (puts the last counter in the empty home D1): Britt, it is your turn now. | Ada picks up all the counters from B1. | |
| 210 | 06:28 | Practitioner (points at D2): Yes, then you take this one. | ||
| 211 | 06:29 | Practitioner moves the counter from D2 to Emil’s side. | Ada sows into B1. | Ada starts at the same place where the counters came from. |
| 212 | 06:30 | Practitioner (points at D1): Because the last one was here, you win this one. | The practitioner knows the Kalaha rules and believes that we are playing this version. | |
| 213 | 06:33 | Ada sows into C1. | ||
| 214 | 06:34 | Practitioner (looks at me): Is it like this? Britt takes all counters from F2. | ||
| 215 | 06:35 | R: No. | Ada sows into D1. | |
| 216 | 06:36 | Emil shakes his head and moves the counter back to D2. R comes over to look at the game. Britt starts sowing at F2. | Ada sows into E1. | |
| 217 | 06:38 | Britt sows into E2 and D2. Practitioner: Don’t you do it like this? | Ada sows into F1. | Britt starts at the same place where the counters came from, and sows left to right, anticlockwise. |
| 218 | 06:40 | Britt sows into C2. Emil: No, wait! That’s the wrong way, wrong way, wrong way. | Ada sows into F2. | Emil started the game clockwise. Therefore, anticlockwise is the wrong direction. |
| 219 | 06:43 | Britt sows into B2. Emil: Wrong way. | Ada sows into E2. | |
| 220 | 06:44 | Emil (picks up a counter from C2): That’s the wrong way! | Ada sows into D2. | |
| 221 | 06:45 | Emil (picks up the counter from B2): That’s the wrong way! | Ada sows into C2. | |
| 222 | 06:47 | Emil: No, not this way! You do it the wrong way! | ||
| 223 | 06:49 | Ada sows the last counter into B2. | ||
| 224 | 06:50 | Emil: That’s the wrong way! | ||
| 225 | 06:52 | Ada (points at B2): I did this one at the end. | ||
| 226 | 06:54 | Ada: I have finished it. | ||
| 227 | 06:57 | Emil picks up the extra counter from B2. | ||
| 228 | 06:58 | Practitioner: I think I see how you do it. | Dan groups his families. | Dan groups on his own. |
| 229 | 07:00 | R: He has started the other way. | ||
| 230 | 07:02 | R: Therefore, you must continue playing the other way. | ||
| 231 | 07:04 | Britt points at E2. | Dan looks at Britt’s game. | |
| 232 | 07:06 | Britt (points at Emil’s row and moves her finger from F1 to A1): I must distribute here? Emil sows Britt’s counters into F1 and E1. | Dan and Ada watch what Emil is doing. | Britt is confused but starts to understand. |
| 233 | 07:08 | Dan: It is not like this. | Does he mean the direction? | |
| 234 | 07:09 | Emil continues sowing into D1 and C1. | ||
| 235 | 07:10 | Carl attempts to take the counters that Ada has captured. | ||
| 236 | 07:11 | Emil puts the last counter into B1 and picks up the two counters from B1. | Ada pushes Carl’s hand away. | |
| 237 | 07:13 | Emil sows the counters into A1 and A2. | Dan (to Ada): Are you ready? | |
| 238 | 07:14 | Ada: Yes! | ||
| 239 | 07:15 | Emil hesitates. | ||
| 240 | 07:17 | R (points at A2): Just take these here. | Ada (points at B2): This was the last one. Carl takes a counter from B1 and pretends to eat it. | |
| 241 | 07:19 | Britt picks up all counters from A2. Emil (points at B2): And then you give this one, (at C2) this one, (at D2) this one, (at E2) this one. | Dan points at B1, and Carl puts the counter back. | |
| 242 | 07:23 | Britt sows the counters into B2, C2, and D2. | Dan takes all counters from B1. | Britt sows correctly. |
| 243 | 07:25 | Emil: Right. | Dan sows into C1. | Dan sows correctly. |
| 244 | 07:27 | Britt attempts to put the next counter into A2. | Dan sows into D1. | Britt loses track when she gets disturbed. |
| 245 | 07:29 | Practitioner (stops her): No, we continue here, Britt (points at E2). | Dan sows into E1. | |
| 246 | 07:31 | Dan picks up all counters from E1. | ||
| 247 | 07:33 | Britt puts a counter in D2 and E2. | Dan sows into F1. | |
| 248 | 07:35 | Emil moves a counter from D2 to F2. | Dan sows into F2. | |
| 249 | 07:37 | R (points at E2): You must take these and continue. | Dan sows into E2. | |
| 250 | 07:39 | Dan: This one. | ||
| 251 | 07:41 | Emil puts a counter in F1. | Dan: It is yours. | The children help each other. |
| 252 | 07:43 | R (points at F1): Then you win those here now. | Ada: What? (takes the four counters from F2.) | |
| 253 | 07:45 | Emil takes all counters from F1. | ||
| 254 | 07:46 | Emil moves the counters to Britt’s side. | Ada (looks at the counters in her hand): Okay. | |
| 255 | 07:47 | Carl (points at A2): Whose are those? | ||
| 256 | 07:48 | Ada: Do I get four? | ||
| 257 | 07:49 | Carl: Whose are those? | ||
| 258 | 07:50 | Ada: I get four. | ||
| 259 | 07:51 | R: Yes. | ||
| 260 | 07:52 | Practitioner: If she finishes on your side. | ||
| 261 | 07:57 | Emil: If I finish with four, they belong to me. | Ada: I have got four, and you have one more. | Ada now has three families, and Dan has four. |
| 262 | 08:03 | Dan puts his hand into C1. R (points at C1): Then you win these. | ||
| 263 | 08:05 | Emil takes all counters from E1. | Dan picks up the four counters from C1 and moves them to his side. | Dan now has five families. |
| 264 | 08:06 | R: Now, it is Ada’s turn. | ||
| 265 | 08:07 | Emil sows counters into D1. | R points at Ada’s row, which starts with A2. | |
| 266 | 08:09 | Emil sows counter into C1. | Ada takes all counters from E2. | |
| 267 | 08:10 | Dan groups his counters. | ||
| 268 | 08:11 | Emil sows counter into B1. | Dan: I will group them. | |
| 269 | 08:12 | Ada attempts to sow from A2. R (points at D2): No. | ||
| 270 | 08:13 | Ada sows into D2. | ||
| 271 | 08:14 | Ada sows into C2 and picks up all counters from C2. | ||
| 272 | 08:17 | Emil sows into A1. Britt (shows me the counters in her hands): Four. | Ada sows into B2. | |
| 273 | 08:18 | Ada sows into A2. R: And now, you get these. | ||
| 274 | 08:19 | Emil sows a counter into A2. | Ada: Yes! (picks up the four counters from A2.) | |
| 275 | 08:20 | Emil sows counters into B2 and C2. | Ada: I have got four. | |
| 276 | 08:21 | Emil takes all counters from C2. | Ada shows Dan the four counters in her hand. | |
| 277 | 08:22 | Ada: I have got four. | ||
| 278 | 08:23 | Emil sows into D2. | Ada (shows Britt the counters): I have got four, Britt. | |
| 279 | 08:24 | Emil sows into E2. Britt raises her hand, holding the four counters. | Ada: I have got more than you. Dan picks up counters from F1. | Ada has four families, and Britt has one. |
| 280 | 08:25 | Emil sows into F2. | Ada: But that’s fine, because you can get more later. | |
| 281 | 08:28 | Emil picks up the four counters from F2. | Dan sows into E1 and D1. | Dan sows clockwise (the wrong direction). |
| 282 | 08:29 | Emil moves the counters to his side. | Dan sows into C1. | |
| 283 | 08:31 | Dan: I have the most of all. | ||
| 284 | 08:32 | Ada (points at her counters): Look at me! | ||
| 285 | 08:33 | Emil looks at Ada’s counters. | ||
| 286 | 08:34 | Emil (points at Britt): Okay! | ||
| 287 | 08:35 | Ada (points at A1): I have started from there. | ||
| 288 | 08:36 | Ada (points at A2): Not here. Dan (counts his families): I have one, two. | ||
| 289 | 08:38 | Emil (points at the homes on his side): You cannot take from this, this, and this one. | ||
| 290 | 08:39 | R (points at Britt’s homes): You must well take from your side. | ||
| 291 | 08:40 | Dan (still counts his families): Three, four. | ||
| 292 | 08:41 | Britt moves her hand to E2. | ||
| 293 | 08:42 | Britt: Can I take these? | ||
| 294 | 08:43 | R: Yes. | ||
| 295 | 08:45 | Britt picks up all counters from E2. | ||
| 296 | 08:49 | Ada (starts to group her counters): Here are just four. | ||
| 297 | 08:51 | R (moves his finger over F2, F1, and E1): And then it goes this way. | ||
| 298 | 08:53 | Britt sows into F2. | ||
| 299 | 08:55 | Britt attempts to sow into E2. R (points at F1): Here. | Ada: I believe I have six. | Britt still wants to sow left-to-right in her row. |
| 300 | 08:57 | Britt sows into F1. | Dan: Six? That are more. | Dan estimates the amount. |
| 301 | 08:59 | Britt sows into E1. | Dan: I think so. | |
| 302 | 09:01 | Britt sows into D1. | Ada makes a group of five counters. | |
| 303 | 09:03 | Emil picks up the four counters in D1 and moves them to his side. Britt sows into C1. | ||
| 304 | 09:07 | Britt sows into B1. | Ada (removes the fifth counter from her group of five and starts a new group): I do it just as I want to. | |
| 305 | 09:11 | Emil moves a counter from C1 to A1. R (asks him): What do you do? | ||
| 306 | 09:13 | Emil: She had two here (points at C1). | ||
| 307 | 09:15 | R: Ah, yes. | Ada makes a new group of four. | Ada groups correctly. |
| 308 | 09:17 | R (asks Britt): Do you still have one? | Dan: No, you must do it right. | |
| 309 | 09:19 | Emil points at B2. | ||
| 310 | 09:21 | Britt sows into B2. | Dan: That’s not good. Ada: Let me think. | |
| 311 | 09:23 | Ada (has four groups of four): Just here. | ||
| 312 | 09:25 | Britt sows into C2. | ||
| 313 | 09:27 | Emil picks up all counters from C1. | Ada (counts the counters in the first group): 1, 2, 3, 4. | Ada does not count the groups. |
| 314 | 09:29 | Ada: I do it just as I want to. | ||
| 315 | 09:31 | Emil sows into B1 and A1. | Dan: But you must only count the four counters. | |
| 316 | 09:33 | Emil sows into A2. | ||
| 317 | 09:35 | Ada: No, I just count like this. | ||
| 318 | 09:37 | Emil sows into B2. | Dan: Okay, I do the same as you. | |
| 319 | 09:39 | Emil sows into C2. | Dan starts counting the counters in each group. | |
| 320 | 09:41 | Emil sows into D2. | Dan: 1, 2, 3, 4. | |
| 321 | 09:43 | Emil sows into E2 and F2. | Dan: 5, 6, 7, 8. | |
| 322 | 09:45 | Emil sows into F1. | Dan: 9, 10, 11, 12. | |
| 323 | 09:47 | Emil takes the counters from F1 and sows them to E1 and D1. | ||
| 324 | 09:49 | Emil (to Britt): It is your turn. | Dan and Ada continue counting silently. | |
| 325 | 09:51 | Ada (to Emil): I have 14. | Ada has 16 counters (4 times 4). | |
| 326 | 09:53 | Emil (counts Ada’s families): 1, 2, 3, 4. | ||
| 327 | 09:55 | Ada: No, I have 14. Dan: I have 15. | Dan has 20 (5 times 4). Errors of perseveration (Radatz, 1979)? | |
| 328 | 09:57 | Dan: I have ... (starts counting again) 1, 2, 3, 4,... | He is unsure if 15 was correct. | |
| 329 | 09:59 | Emil (counts Ada’s families again): 1, 2, 3, 4. | ||
| 330 | 10:01 | Ada: No, I have 14. | ||
| 331 | 10:03 | Emil (counts Dan’s families): 1, 2, 3, 4, 5. | ||
| 332 | 10:05 | Emil: It is like this. | ||
| 333 | 10:07 | Ada: No, I have 14. | ||
| 334 | 10:09 | Dan (starts counting once again): 1, 2, 3, 4,... | ||
| 335 | 10:11 | Emil (points at one of Dan’s families): No, but you see, this one is here like this. | Dan (continues counting with the next group): 5, 6, 7, 8,... | |
| 336 | 10:14 | Emil: Look here. This is a group of four. Practitioner (to Britt): It is your turn. | Dan (continues counting with the next group): 9, 10, 11, 12,... | |
| 337 | 10:16 | Ada rearranges her counters in a row. | ||
| 338 | 10:18 | Practitioner (asks me): Is it she who shall start? | ||
| 339 | 10:19 | Dan (continues counting with the next group): 13, 14, 15, 16,... Ada: We can do it as we want to. | ||
| 340 | 10:21 | Britt looks at Ada. | Dan counts the last group silently. | |
| 341 | 10:22 | Practitioner: Britt? | Dan: I have 20. | He is correct now. |
| The children continue playing. | ||||
| 394 | 11:59 | Britt has one counter in B2, one in D2, and three in E2. | Dan has one counter each in A1, B1, C1, and E1, and three in D1. | |
| 395 | 12:02 | Emil shows Britt how she can capture a family by moving the counter from D2 to E2. | Dan moves the counter from C1 to D1 and captures the family. | The children make strategic moves. |
| 396 | 12:05 | Britt moves the counter from D2 to E2. | Ada: Don’t take from me! | |
| 397 | 12:06 | Emil picks up the family from E2 and moves it to Britt’s side. | R: Now, he is finished. It was his turn. Now it is your turn. | |
| 398 | 12:09 | Emil picks up the counters from F1. | Ada moves a counter from B2 to A2. | |
| 399 | 12:11 | Emil sows into E1 and D1. | R: Your turn is finished. | |
| 400 | 12:14 | Emil captures the family from D1. | ||
| 401 | 12:18 | Britt (looks at her counters): Look here, look how many I have. | ||
| 402 | 12:21 | Emil: Britt, it is your turn. | ||
| 403 | 12:25 | Emil (to me): Can you look at us? | R moves to Emil’s side. | |
| 404 | 12:27 | Emil (points at the board): There are only four left. | ||
| 405 | 12:29 | Ada (talks to Britt): I have done it very well. Dan looks at Britt’s counters. | ||
| 406 | 12:32 | Ada pushes her counters together. Dan: Britt has very much. | ||
| 407 | 12:34 | Ada: Britt and I did a lot yesterday. | ||
| 408 | 12:37 | Ada: It is summer. | ||
| 409 | 12:39 | Dan (counts the counters on the board): 1, 2, 3, 4. | ||
| 410 | 12:43 | Carl (points at E1): And this one. | ||
| 411 | 12:45 | R: Now, at the end, we can say that it is finished. Emil groups his counters. | Ada and Dan point at E1. | The number of counters on the board must always be a multiple of four. |
| 412 | 12:50 | R: Then you can count how many you have. | ||
| 413 | 12:52 | Emil (points at Britt’s counters): You must count these here. | ||
| 414 | 12:54 | Britt: I can count. | ||
| 415 | 12:55 | Ada: I have 17. I have 17. | ||
| 416 | 12:59 | Dan (counts groups of four even though his counters are arranged in a row): One. | ||
| 417 | 13:02 | Dan: Two. | ||
| 418 | 13:03 | Emil: You must just count like this. | ||
| 419 | 13:04 | Emil (shows Britt how he counts his families): 1, 2, 3, 4. | ||
| 420 | 13:05 | Dan: Three. | ||
| 421 | 13:06 | Britt starts grouping her counters. | Britt can group. | |
| 422 | 13:07 | Dan: Four. | ||
| 423 | 13:08 | R: Since you capture groups of four, you can just count how many groups of four you have. | ||
| 424 | 13:12 | The practitioner helps Britt group her counters. | Dan (repeats his count of the fourth group): Four. | |
| 425 | 13:14 | Britt pushes together the groups that the practitioner had created. Practitioner: I have just made groups of four. | Britt wants to group on her own. | |
| 426 | 13:17 | Practitioner: What do you do now? | ||
| 427 | 13:19 | R: But Britt can do it on her own. | ||
| 428 | 13:21 | Dan (repeats his count of the fourth group): Four. | ||
| 429 | 13:22 | Britt continues grouping her counters. | Dan stops his attempt to count groups of counters that are not grouped. | |
| 468 | 14:33 | Britt finished her grouping. | Dan and Ada distribute the counters back on the board into the starting arrangement. | |
| 469 | 14:34 | R: Now, you can count how many groups of four you have. | ||
| 470 | 14:37 | Britt (counts the counters in one group): 1, 2, 3, 4. | ||
| 471 | 14:39 | R: How many groups? | ||
| 472 | 14:41 | Britt (starts counting the counters in the next group): 1, 2. Emil (shows Britt how to count groups): No, like this 1, 2, 3, 4. | Britt does not count how many counters she has nor how many groups. She checks if there are four counters in each group. | |
| 473 | 14:45 | Britt: No. I don’t do it like this. Emil (continues counting Britt’s groups): 5, 6. | ||
| 474 | 14:47 | Britt counts the counters in the first group again. | ||
| 475 | 14:49 | Britt: 1, 2. | ||
| 476 | 14:51 | Emil: It is not like this. | ||
| 477 | 14:53 | Britt: 3, 4. | ||
| 478 | 14:55 | Britt (counts the counters in the second group): 1. | ||
| 479 | 14:57 | Britt: 2. | ||
| 480 | 14:58 | Britt (starts over again in the second group): 1. | ||
| 481 | 14:59 | Britt: 2 | ||
| 482 | 15:00 | Britt: 3. | ||
| 483 | 15:01 | Britt: 4. | ||
| 484 | 15:02 | Practitioner: Let her count. | ||
| 485 | 15:03 | Britt (counts the counters in the third group): 1. | ||
| 486 | 15:04 | Britt: 2, 3, 4. | Ada: Can we change, Britt? | Ada wants to start a new match with Britt. |
| 487 | 15:06 | Britt (counts the counters in the fourth group): 1, 2, 3, 4. | Ada: Britt, you and I can play against each other. | |
| 488 | 15:12 | Britt (counts the counters in the fifth group): 1, 2, 3, 4. | ||
| 489 | 15:13 | Britt (counts the counters in the sixth group): 1, 2, 3, 4. | ||
| 490 | 15:15 | Britt (counts the counters in the seventh group): 1, 2, 3, 4. | ||
| 491 | 15:18 | Britt (counts the counters in the third group again): 1, 2, 3, 4. | ||
| 492 | 15:20 | Dan leaves the table. Ada (collects Dan’s counters): I can take yours. | ||
| 493 | 15:21 | Britt: Four. | ||
| 494 | 15:22 | Britt: I have four. | Does she mean ‘groups of four’? | |
| 495 | 15:24 | R (points at Britt’s families): Britt, can you count how many groups of four you have? | ||
| 496 | 15:27 | Ada distributes Dan’s counters into the homes on the board. | ||
| 497 | 15:29 | R (points at Britt’s families): 1, 2, 3, 4,... | ||
| 498 | 15:31 | Britt (counts the families): 1, 2, 3, 4. | ||
| 499 | 15:33 | Britt (continues counting the families correctly): 5, 6, 7. | Britt can count the groups. | |
| 500 | 15:38 | Emil distributes his counters into the homes on the board. | ||
| 501 | 15:40 | Practitioner: So, Britt, how many groups do you have? | ||
| 502 | 15:44 | Britt: 7. Emil starts picking up Britt’s counters. | Britt is a CP-knower. | |
References
- Alehegn, D. (2022). Want to teach early learners math in Ethiopia? Early Childhood Education Ethiopia. Available online: https://www.earlyeducationethiopia.org/play-gebeta (accessed on 31 August 2025).
- Barth, H., La Mont, K., Lipton, J., & Spelke, E. S. (2005). Abstract number and arithmetic in preschool children. Proceedings of the National Academy of Sciences of the United States of America, 102(39), 14116–14121. [Google Scholar] [CrossRef]
- Bishop, A. J. (1988). Mathematics education in its cultural context. Educational Studies in Mathematics, 19(2), 179–191. [Google Scholar] [CrossRef]
- Bishop, A. J. (1991). Mathematical enculturation. A cultural perspective on mathematics education. Kluwer. [Google Scholar]
- Brock, R., & Taber, K. S. (2017). The application of the microgenetic method to studies of learning in science education: Characteristics of published studies, methodological issues and recommendations for future research. Studies in Science Education, 53(1), 45–73. [Google Scholar] [CrossRef]
- Clements, D. H. (1999). Subitizing: What is it? Why teach it? Teaching Children Mathematics, 5(7), 400–405. [Google Scholar] [CrossRef]
- Clements, D. H., & Sarama, J. A. (2021). Learning and teaching early math: The learning trajectories approach (3rd ed.). Routledge. [Google Scholar]
- Dehaene, S., Bossini, S., & Giraux, P. (1993). The mental representation of parity and number magnitude. Journal of Experimental Psychology: General, 122(3), 371–396. [Google Scholar] [CrossRef]
- European Parliament. (2016). Regulation (EU) 2016/679 of the European Parliament and of the Council of 27 April 2016 on the protection of natural persons with regard to the processing of personal data and on the free movement of such data, and repealing Directive 95/46/EC (General Data Protection Regulation). Official Journal of the European Union, L 119, 1–88. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32016R0679 (accessed on 31 August 2025).
- Gasteiger, H., & Moeller, K. (2021). Fostering early numerical competencies by playing conventional board games. Journal of Experimental Child Psychology, 204, 105060. [Google Scholar] [CrossRef]
- Gelman, R., & Gallistel, C. R. (1978). The child’s understanding of number. Harvard University Press. [Google Scholar]
- Gifford, S. (2005). Teaching mathematics 3–5: Developing learning in the foundation stage: Developing learning in the foundation stage. McGraw-Hill Education. [Google Scholar]
- Ginsburg, H. P. (2006). Mathematical play and playful mathematics: A guide for early education. In D. G. Singer, R. M. Golinkoff, & K. Hirsh-Pasek (Eds.), Play = Learning: How play motivates and enhances children’s cognitive and social-emotional growth (pp. 145–166). Oxford University Press. [Google Scholar] [CrossRef]
- Ginsburg, H. P., Lee, J. S., & Boyd, J. S. (2008). Mathematics education for young children: What it is and how to promote it. Social Policy Report, 22(1), 1–24. [Google Scholar] [CrossRef]
- Ginsburg, K. R. (2007). The importance of play in promoting healthy child development and maintaining strong parent-child bonds. Pediatrics, 119(1), 182–191. [Google Scholar] [CrossRef]
- Göbel, S. M., McCrink, K., Fischer, M. H., & Shaki, S. (2018). Observation of directional storybook reading influences young children’s counting direction. Journal of Experimental Child Psychology, 166, 49–66. [Google Scholar] [CrossRef]
- Hartmann, J., Herzog, M., & Fritz, A. (2022). Zero—An uncommon number: Preschoolers‘ conceptual understanding of zero. International Electronic Journal of Elementary Education, 14(3), 353–361. [Google Scholar] [CrossRef]
- Huizinga, J. (1949). Homo Ludens: A study of the play-element in culture. Routledge & Kegan Paul. [Google Scholar]
- Jordan, B., & Henderson, A. (1995). Interaction analysis: Foundations and practice. The Journal of the Learning Sciences, 4(1), 39–103. [Google Scholar] [CrossRef]
- Kieran, C. (2013). The False dichotomy in mathematics education between conceptual understanding and procedural skills: An example from Algebra. In K. R. Leatham (Ed.), Vital directions for mathematics education research (pp. 153–171). Springer. [Google Scholar] [CrossRef]
- Krajcsi, A., Kojouharova, P., & Lengyel, G. (2021). Development of preschoolers’ understanding of zero. Frontiers in Psychology, 12, 583734. [Google Scholar] [CrossRef] [PubMed]
- Lavelli, M., Pantoja, A., Hsu, H., Messinger, D., & Fogel, A. (2005). Using microgenetic designs to study developmental change processes. In D. M. Teti (Ed.), Handbook of research methods in developmental science (pp. 40–65). Blackwell Publishing Ltd. [Google Scholar] [CrossRef]
- Lundvin, M., & Palmér, H. (2025). A play-responsive approach to teaching mathematics in preschool, with a focus on representations. Education Sciences, 15(8), 999. [Google Scholar] [CrossRef]
- MacDonald, A. (2025). Everyday mathematical activities of babies and toddlers in early childhood education settings. Early Childhood Education Journal. [Google Scholar] [CrossRef]
- Maffia, A., Morais, A., & Silva, L. (2025). Using boardgames to develop mathematical competence: A systematic review. In A. Cusi, A. Maffia, S. Palha, & A. M. Vogler (Eds.), Proceedings of the GAME conference (pp. 61–64). ERME. [Google Scholar]
- Maffia, A., & Silva, L. (2025). Adapting boardgames for the primary mathematics classroom: The Italian project “Numeri & Pedine”. In A. Cusi, A. Maffia, S. Palha, & A. M. Vogler (Eds.), Proceedings of the GAME conference (pp. 139–140). ERME. [Google Scholar]
- Martinez, K., Menéndez-Menéndez, M. I., & Bustillo, A. (2022). A new measure for serious games evaluation: Gaming Educational Balanced (GEB) model. Applied Sciences, 12(22), 11757. [Google Scholar] [CrossRef]
- Moll, L. C., Amanti, C., Neff, D., & Gonzalez, N. (1992). Funds of knowledge for teaching: Using a qualitative approach to connect homes and classrooms. Theory into Practice, 31(2), 132–141. [Google Scholar] [CrossRef]
- Nelson, G., & Powell, S. R. (2018). Computation error analysis: Students with mathematics difficulty compared to typically achieving students. Assessment for Effective Intervention, 43(3), 144–156. [Google Scholar] [CrossRef]
- Nieder, A. (2016). Representing something out of nothing: The dawning of zero. Trends in Cognitive Sciences, 20(11), 830–842. [Google Scholar] [CrossRef]
- Norwegian Directorate for Education and Training. (2017). Framework plan for the kindergartens content and tasks. Ministry of Education and Research. Available online: https://www.udir.no/contentassets/5d0f4d947b244cfe90be8e6d475ba1b4/framework-plan-for-kindergartens--rammeplan-engelsk-pdf.pdf (accessed on 31 August 2025).
- Öngören, S., & Gündoğdu, S. (2021). Mathematical skills in traditional children’s games in early childhood. Kastamonu Education Journal, 29(5), 1052–1064. [Google Scholar] [CrossRef]
- Pankhurst, R. (1971). Gabata and related board games of Ethiopia and the horn of Africa. Ethiopia Observer, 14(3), 154–206. [Google Scholar]
- Papandreou, M., & Tsiouli, M. (2022). Noticing and understanding children’s everyday mathematics during play in early childhood classrooms. International Journal of Early Years Education, 30(4), 730–747. [Google Scholar] [CrossRef]
- Perry, B., Thiel, O., & Severina, E. (2020). Reflexivity and early childhood mathematics education—Applying Bishop’s universality to vignettes of young children’s learning. In O. Thiel, E. Severina, & B. Perry (Eds.), Mathematics in early childhood-research, reflexive practice and innovative pedagogy (pp. 1–10). Routledge. [Google Scholar] [CrossRef]
- Piaget, J., & Inhelder, B. (1991). La génèse des structures logiques élémentaires—Classification et sériations [The genesis of elementary logical structures—Classification and seriations]. Delachaux et Niestlé. [Google Scholar]
- Piaget, J., & Szeminska, A. (1941). La genèse du nombre chez l’enfant [The development of the number concept in the child]. Delachaux et Niestlé. [Google Scholar]
- Piette, É., & Stephenson, M. (2022). Gabata (Ghinda). In Github (Version 1.3.4) [Ludeme program]. Digital Ludeme Project. Available online: https://github.com/Ludeme/GameDatabase/blob/master/games/lud/Gabata%20(Ghinda).lud (accessed on 31 August 2025).
- Pyle, A., & Danniels, E. (2017). A continuum of play-based learning: The role of the teacher in play-based pedagogy and the fear of hijacking play. Early Education and Development, 28(3), 274–289. [Google Scholar] [CrossRef]
- Radatz, H. (1979). Error analysis in mathematics education. Journal for Research in Mathematics Education, 10(3), 163–172. [Google Scholar] [CrossRef]
- Ramani, G. B., & Siegler, R. S. (2008). Promoting broad and stable improvements in low-income children’s numerical knowledge through playing number board games. Child Development, 79(2), 375–394. [Google Scholar] [CrossRef] [PubMed]
- Rengifo-Herrera, F. J. (2025). When using objects is not enough: Microgenetic analysis of an educational situation in early childhood education. Estudos de Psicologia, 42, e230120. [Google Scholar] [CrossRef]
- Rohrbough, L. (1955). Count and capture: The world’s oldest game. Cooperative Receation Service. [Google Scholar]
- Sfard, A. (2015). Learning, commognition and mathematics. In D. Scott, & E. Hargreaves (Eds.), The SAGE handbook of learning (pp. 129–138). SAGE. [Google Scholar] [CrossRef]
- Shaki, S., & Fischer, M. H. (2008). Reading space into numbers—A cross-linguistic comparison of the SNARC effect. Cognition, 108(2), 590–599. [Google Scholar] [CrossRef]
- Siegler, R. S., & Crowley, K. (1991). The microgenetic method. A direct means for studying cognitive development. The American Psychologist, 46(6), 606–620. [Google Scholar] [CrossRef]
- Siegler, R. S., & Ramani, G. B. (2009). Playing linear number board games—But not circular ones—Improves low-income preschoolers’ numerical understanding. Journal of Educational Psychology, 101(3), 545–560. [Google Scholar] [CrossRef]
- Skemp, R. R. (1976). Relational understanding and instrumental understanding. Mathematics Teaching, 77, 20–26. [Google Scholar]
- Sousa, C., Rye, S., Sousa, M., Torres, P. J., Perim, C., Mansuklal, S. A., & Ennami, F. (2023). Playing at the school table: Systematic literature review of board, tabletop, and other analog game-based learning approaches. Frontiers in Psychology, 14, 1160591. [Google Scholar] [CrossRef]
- Stelzer, J. (2023). The seriousness of play: Johan Huizinga’s Homo Ludens and the demise of the play-element. International Journal of Play, 12(3), 337–348. [Google Scholar] [CrossRef]
- Stohlmann, M. (2022). Two Modes of game-based learning for middle school mathematics. Journal of Mathematics Education at Teachers College, 12(2), 9–20. [Google Scholar] [CrossRef]
- Tesfamicael, S. A., & Farsani, D. (2024). Creating a culturally responsive mathematics education: The case of Gebeta game in Ethiopia. In M. A. Ashraf, & S. M. Tsegay (Eds.), STEM education—Recent trends and new advances. IntechOpen. [Google Scholar] [CrossRef]
- Thiel, O. (2025). Rechnen mit Gebeta: Ein äthiopisches Spiel für den Unterricht [Calculating with Gebeta: An Ethiopian game for the classroom]. Grundschule, 57(4), 28–33. [Google Scholar]
- Thiel, O., Nakken, A. H., & Tesfamicael, S. A. (2024, July 7–14). Affordances of Gebeta game in early childhood mathematics education [Paper presentation]. 15th International Congress on Mathematics Education (ICME-15), Sydney, Australia. Available online: https://www.researchgate.net/publication/384597488_Affordances_of_Gebeta_Game_in_Early_Childhood_Mathematics_Education (accessed on 31 August 2025).
- Usta, N., & Cagan, B. (2022). The effect of mangala, the intelligence game taught by distance education, on the mathematical motivations and problem-solving skill levels of 6th-grade students. Higher Education Studies, 12(1), 9–25. [Google Scholar] [CrossRef]
- Vlassis, J., Ariane, B., Amélie, A., Anne-Françoise, d. C., Christophe, D., Nadine, G., Sylvie, K., Christophe, L., Débora, P., Mélanie, T.-V., Youssef, T., & Fagnant, A. (2023). Developing arithmetic skills in kindergarten through a game-based approach: A major issue for learners and a challenge for teachers. International Journal of Early Years Education, 31(2), 419–434. [Google Scholar] [CrossRef]
- Vogt, F., Hauser, B., Stebler, R., Rechsteiner, K., & Urech, C. (2018). Learning through play—Pedagogy and learning outcomes in early childhood mathematics. European Early Childhood Education Research Journal, 26(4), 589–603. [Google Scholar] [CrossRef]
- Vogt, F., & Rechsteiner, K. (2016). Regelspiele entwickeln [Developing rule games]. In B. Hauser, E. Rathgeb-Schnierer, R. Stebler, & F. Vogt (Eds.), Mehr ist mehr: Mathematische Frühförderung mit Regelspielen [More is more: Early mathematical education with rule games] (pp. 46–55). Kallmeyer. [Google Scholar] [CrossRef]
- Vygotsky, L. S. (1967). Play and its role in the mental development of the child. Soviet Psychology, 5(3), 6–18. [Google Scholar] [CrossRef]
- Vygotsky, L. S. (1978). Mind in society. The development of higher psychological processes. Harvard University Press. [Google Scholar]
- Walsh, G., McMillan, D., & McGuinness, C. (2017). Playful teaching and learning. Sage. [Google Scholar] [CrossRef]
- Wege, T. E., De Smedt, B., Gilmore, C., & Inglis, M. (2023). Counting many as one: Young children can understand sets as units except when counting. Journal of Experimental Child Psychology, 225, 105533. [Google Scholar] [CrossRef]
- Whitacre, I., Henning, B., & Atabaș, Ș. (2020). Disentangling the research literature on number sense: Three constructs, one name. Review of Educational Research, 90(1), 95–134. [Google Scholar] [CrossRef]
- Wood, D. J., Bruner, J. S., & Ross, G. (1976). The role of tutoring in problem solving. Journal of Child Psychiatry and Psychology, 17(2), 89–100. [Google Scholar] [CrossRef]
- Wood, E. A. (2022). Play and learning in early childhood education: Tensions and challenges. Child Studies, (1), 15–26. [Google Scholar] [CrossRef]
- Yusuf, A., & Noor, N. M. (2024). Modeling students’ algorithmic thinking growth trajectories in different programming environments: An experimental test of the Matthew and compensatory hypothesis. Smart Learning Environments, 11(1), 38. [Google Scholar] [CrossRef]
- Zaslavsky, C. (1994). “Africa counts” and ethnomathematics. For the Learning of Mathematics, 14(2), 3–8. Available online: http://www.jstor.org/stable/40248107 (accessed on 31 August 2025).



| Activity | Percentage |
|---|---|
| counting | 69% |
| measuring | 0% |
| locating | 11% |
| designing | 6% |
| playing | 13% |
| explaining | 1% |
| Line | Timestamp | Activity * |
|---|---|---|
| 16 | 00:30 | R: Do you remember how to start? |
| 17 | 00:32 | Ada (moves her hand to Britt’s A1): Well, first you must do it … |
| 18 | 00:34 | Ada (picks up the counters): …like… |
| 19 | 00:36 | Ada (shows the counters in her hand): …this. |
| 20 | 00:38 | Ada (closes her hand and moves it to Bitt’s A2): Then, we take one… |
| 21 | 00:40 | Ada (points with her thumb down at Britt’s A2): …here. |
| 22 | 00:42 | Ada (points with her thumb down at Britt’s A3): And here. |
| 23 | 00:44 | Ada (points with her thumb down at Britt’s A4): Here. |
| 24 | 00:46 | Ada (points with her thumb at Britt’s A5): And there. |
| 25 | 00:48 | Ada: And so on and on and on. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thiel, O. Playing Gebeta in Preschool: Informal Pathways to Early Numeracy Through Directionality and Bundling. Educ. Sci. 2025, 15, 1365. https://doi.org/10.3390/educsci15101365
Thiel O. Playing Gebeta in Preschool: Informal Pathways to Early Numeracy Through Directionality and Bundling. Education Sciences. 2025; 15(10):1365. https://doi.org/10.3390/educsci15101365
Chicago/Turabian StyleThiel, Oliver. 2025. "Playing Gebeta in Preschool: Informal Pathways to Early Numeracy Through Directionality and Bundling" Education Sciences 15, no. 10: 1365. https://doi.org/10.3390/educsci15101365
APA StyleThiel, O. (2025). Playing Gebeta in Preschool: Informal Pathways to Early Numeracy Through Directionality and Bundling. Education Sciences, 15(10), 1365. https://doi.org/10.3390/educsci15101365






