Mathematical Creativity: A Systematic Review of Definitions, Frameworks, and Assessment Practices
Abstract
1. Introduction
1.1. Defining Mathematical Creativity
1.2. Theoretical Perspectives on Mathematical Creativity
1.3. Linking Definitions and Frameworks
1.4. Significance of Study
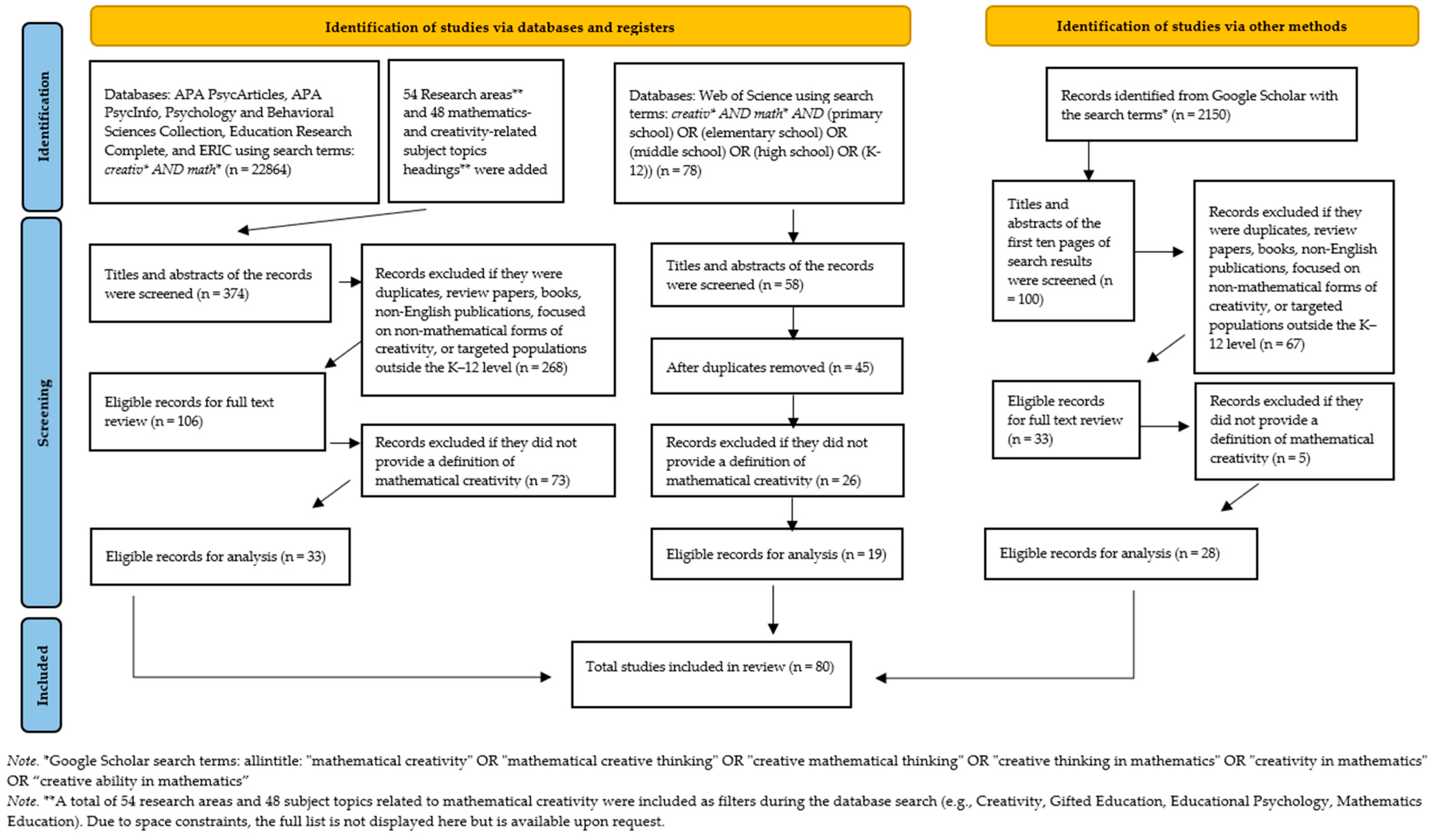
2. Methodology
2.1. Literature Selection
2.1.1. Major Databases
2.1.2. Google Scholar
2.1.3. Web of Science (WoS)
2.2. Coding and Analysis
3. Findings
3.1. Definition of Mathematical Creativity
3.1.1. Divergent Thinking-Oriented Definitions (n = 61)
3.1.2. Problem-Solving and Problem-Posing-Oriented Definitions (n = 37)
3.1.3. Affective–Motivational Emphasis (n = 6)
3.2. Theoretical Frameworks in the Reviewed Studies
3.2.1. Domain-Specific Frameworks (n = 34)
3.2.2. Multidimensional Frameworks (n = 27)
3.2.3. Domain-General Frameworks (n = 25)
3.3. Assessment of Mathematical Creativity
3.3.1. Scoring Approaches in Mathematical Creativity Assessments
3.3.2. Format of Assessments
3.3.3. Components Scored in Assessments
3.3.4. Types of Tasks Used in Assessments
3.3.5. Target Groups of Studies
4. Discussion
4.1. Implications for Research
4.2. Implications for Practitioners
4.3. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Akgul, S., & Kahveci, N. G. (2016). A study on the development of a mathematics creativity scale. Eurasian Journal of Educational Research, 62, 57–76. [Google Scholar] [CrossRef]
- Aljarrah, A. (2020). Describing collective creative acts in a mathematical problem-solving environment. The Journal of Mathematical Behavior, 60, 100819. [Google Scholar] [CrossRef]
- Al-Mayahi, A., & Hassan, A. K. (2022). Creative problem-solving (cps) skills in mathematics and their correlation to the perceptual speed among the fourth-class high school students. International Journal of Early Childhood Special Education, 14(2), 3958–3966. [Google Scholar]
- Amabile, T. M. (1982). Social psychology of creativity: A consensual assessment technique. Journal of Personality and Social Psychology, 43(5), 997–1013. [Google Scholar] [CrossRef]
- Amabile, T. M. (1983). The social psychology of creativity: A componential conceptualization. Journal of Personality and Social Psychology, 45, 357–376. [Google Scholar] [CrossRef]
- Ariba, O. T. (2019). Enhancing children’s early years mathematical creativity through the visual arts [Doctoral dissertation, University of Johannesburg]. [Google Scholar]
- Assmus, D., & Fritzlar, T. (2022). Mathematical creativity and mathematical giftedness in the primary school age range: An interview study on creating figural patterns. ZDM–Mathematics Education, 54(1), 113–131. [Google Scholar] [CrossRef]
- Ayvaz, Ü., & Durmuş, S. (2021). Fostering mathematical creativity with problem posing activities: An action research with gifted students. Thinking Skills and Creativity, 40, 100846. [Google Scholar] [CrossRef]
- Azaryahu, L., Broza, O., Sasson, O., Hershkovitz, S., & Adi-Japha, E. (2025). Can creative musical and mathematical thinking be developed among first and second graders? Thinking Skills and Creativity, 58, 101916. [Google Scholar] [CrossRef]
- Bahar, A. K., & Maker, C. J. (2011). Exploring the relationship between mathematical creativity and mathematical achievement. Asia-Pacific Journal of Gifted and Talented Education, 3(1), 33–48. [Google Scholar]
- Bahar, A. K., & Maker, C. J. (2020). Culturally responsive assessments of mathematical skills and abilities: Development, field testing, and implementation. Journal of Advanced Academics, 31(3), 211–233. [Google Scholar] [CrossRef]
- Balka, D. S. (1974). The development of an instrument to measure creative ability in mathematics (Publication No.7515965) [Doctoral dissertation, University of Missouri-Columbia]. [Google Scholar]
- Bal-Sezerel, B., & Sak, U. (2022). Mathematical Creativity Test (MCT) development for middle school students. Turkish Journal of Education, 11(4), 242–268. [Google Scholar] [CrossRef]
- Barraza-García, Z. M., Romo-Vázquez, A., & Roa-Fuentes, S. (2020). A theoretical model for the development of mathematical talent through mathematical creativity. Education Sciences, 10(4), 118. [Google Scholar] [CrossRef]
- Bicer, A. (2021). A systematic literature review: Discipline-specific and general instructional practices fostering the mathematical creativity of students. International Journal of Education in Mathematics, Science and Technology, 9(2), 252–281. [Google Scholar] [CrossRef]
- Bicer, A., & Bicer, A. (2023). Understanding young students’ mathematical creative thinking processes through eye-tracking-stimulated recall interview. Mathematics Education Research Journal, 35(2), 361–399. [Google Scholar] [CrossRef]
- Bicer, A., Lee, Y., Perihan, C., Capraro, M. M., & Capraro, R. M. (2020). Considering mathematical creative self-efficacy with problem posing as a measure of mathematical creativity. Educational Studies in Mathematics, 105(3), 457–485. [Google Scholar] [CrossRef]
- Bishara, S. (2016). Creativity in unique problem-solving in mathematics and its influence on motivation for learning. Cogent Education, 3(1), 1202604. [Google Scholar] [CrossRef]
- Chamberlin, S. A., & Moon, S. M. (2005). Model-eliciting activities as a tool to develop and identify creatively gifted mathematicians. Journal of Secondary Gifted Education, 17(1), 37–47. [Google Scholar] [CrossRef]
- Chart, H. E., Grigorenko, E. L., & Sternberg, R. J. (2008). Identification: The aurora battery. In J. A. Plucker, & C. M. Callahan (Eds.), Critical issues and practices in gifted education (pp. 345–365). Prufrock Press. [Google Scholar]
- Coxbill, E., Chamberlin, S. A., & Weatherford, J. (2013). Using model-eliciting activities as a tool to identify and develop mathematically creative students. Journal for the Education of the Gifted, 36(2), 176–197. [Google Scholar] [CrossRef]
- El-Sahili, A., Al-Sharif, N., & Khanafer, S. (2015). Mathematical creativity: The unexpected links. The Mathematics Enthusiast, 12(1), 417–464. [Google Scholar] [CrossRef]
- Fatah, A., Suryadi, D., Sabandar, J., & Turmudi, T. (2016). Open-ended approach: An effort in cultivating students’ mathematical creative thinking ability and self-esteem in mathematics. Journal on Mathematics Education, 7, 11–20. [Google Scholar] [CrossRef]
- Fortes, E. C., & Andrade, R. R. (2019). Mathematical creativity in solving non-routine problems. The Normal Lights, 13(1), 108–135. [Google Scholar] [CrossRef]
- García-García, J., Martinez-Artero, M. R. N., & Olivares-Carrillo, P. (2024). Exploring the influence of musical training on mathematical creativity. Thinking Skills and Creativity, 52, 101498. [Google Scholar] [CrossRef]
- Guilford, J. P. (1956). The structure of intellect. Psychological Bulletin, 53(4), 267–293. [Google Scholar] [CrossRef] [PubMed]
- Guilford, J. P. (1965). Intelligence: 1965 model. American Psychologist, 21(1), 20–26. [Google Scholar] [CrossRef]
- Guilford, J. P. (1968). Intelligence has three facets: There are numerous intellectual abilities, but they fall neatly into a rational system. Science, 160(3828), 615–620. [Google Scholar] [CrossRef]
- Haavold, P. Ø. (2013). What are the characteristics of mathematical creativity? An empirical and theoretical investigation of mathematical creativity [Unpublished doctoral dissertation, University of Tromsø]. [Google Scholar]
- Haavold, P. Ø. (2016). An empirical investigation of a theoretical model for mathematical creativity. The Journal of Creative Behavior, 52(3), 226–239. [Google Scholar] [CrossRef]
- Haavold, P. Ø. (2018). An investigation of the relationship between age, achievement, and creativity in mathematics. The Journal of Creative Behavior, 54(3), 555–566. [Google Scholar] [CrossRef]
- Hall, J. A. (2009). Problem solving and creativity: A gender and grade level comparison (Publication No. 3356163) [Doctoral dissertation, Tennessee State University]. [Google Scholar]
- Haylock, D. W. (1987). A framework for assessing mathematical creativity in school chilren. Educational Studies in Mathematics, 18(1), 59–74. [Google Scholar] [CrossRef]
- Haylock, D. W. (1997). Recognising mathematical creativity in schoolchildren. ZDM, 29(3), 68–74. [Google Scholar] [CrossRef]
- Hu, L., & Wang, H. (2024). Unplugged activities in the elementary school mathematics classroom: The effects on students’ computational thinking and mathematical creativity. Thinking Skills and Creativity, 54, 101653. [Google Scholar] [CrossRef]
- Huang, P. S., Peng, S. L., Chen, H. C., Tseng, L. C., & Hsu, L. C. (2017). The relative influences of domain knowledge and domain-general divergent thinking on scientific creativity and mathematical creativity. Thinking Skills and Creativity, 25, 1–9. [Google Scholar] [CrossRef]
- Hwang, W. Y., Chen, N. S., Dung, J. J., & Yang, Y. L. (2007). Multiple representation skills and creativity effects on mathematical problem solving using a multimedia whiteboard system. Educational Technology & Society, 10(2), 191–212. [Google Scholar]
- Jensen, L. R. (1973). The relationships among mathematical creativity, numerical aptitude, and mathematical achievement [Doctoral dissertation, The University of Texas]. [Google Scholar]
- Joklitschke, J., Rott, B., & Schindler, M. (2022). Notions of creativity in mathematics education research: A systematic literature review. International Journal of Science and Mathematics Education, 20(6), 1161–1181. [Google Scholar] [CrossRef]
- Junaedi, Y., Wahyudin, W., & Juandi, D. (2021). Mathematical creative thinking ability of junior high school students’ on polyhedron. Journal of Physics: Conference Series, 1806(1), 012069. [Google Scholar] [CrossRef]
- Kattou, M., Kontoyianni, K., Pitta-Pantazi, D., & Christou, C. (2013). Connecting mathematical creativity to mathematical ability. ZDM, 45(2), 167–181. [Google Scholar] [CrossRef]
- Kaufman, J. C., & Baer, J. (Eds.). (2005). Creativity across domains: Faces of the muse. Psychology Press. [Google Scholar]
- Kaufman, J. C., & Sternberg, R. J. (Eds.). (2010). The Cambridge handbook of creativity. Cambridge University Press. [Google Scholar]
- Kim, H., Cho, S., & Ahn, D. (2003). Development of mathematical creative problem-solving ability test for identification of the gifted in math. Gifted Education International, 18(2), 164–174. [Google Scholar] [CrossRef]
- Kirisci, N., Sak, U., & Karabacak, F. (2020). The effectiveness of the selective problem solving model on students’ mathematical creativity: A Solomon four-group research. Thinking Skills and Creativity, 38, 100719. [Google Scholar] [CrossRef]
- Kontoyianni, K., Kattou, M., Pitta-Pantazi, D., & Christou, C. (2013). Integrating mathematical abilities and creativity in the assessment of mathematical giftedness. Psychological Test and Assessment Modeling, 55(3), 289. [Google Scholar]
- Krutetskii, V. A. (1976). The psychology of mathematical abilities in schoolchildren. University of Chicago Press. [Google Scholar]
- Kulsum, S. I., Wijaya, T. T., Hidayat, W., & Kumala, J. (2019). Analysis on high school students’ mathematical creative thinking skills on the topic of sets. Jurnal Cendekia, 3(2), 431–436. [Google Scholar] [CrossRef]
- Lee, K. S., Hwang, D., & Seo, J. J. (2003). A development of the test for mathematical creative problem-solving ability. Journal of the Korea Society of Mathematical Education Series D: Research in Mathematical Education, 7(3), 163–189. [Google Scholar]
- Leikin, M., & Tovli, E. (2019). Examination of creative abilities of preschool children with and without specific language impairment (SLI). Communication Disorders Quarterly, 41(1), 22–33. [Google Scholar] [CrossRef]
- Leikin, R. (2009). Exploring mathematical creativity using multiple solution tasks. In Creativity in mathematics and the education of gifted students (vol. 9, pp. 129–145). Sense Publishers. [Google Scholar] [CrossRef]
- Leikin, R. (2013). Evaluating mathematical creativity: The interplay between multiplicity and insight. Psychological Test and Assessment Modeling, 55(4), 385–400. [Google Scholar]
- Leikin, R., & Kloss, Y. (2011, February 9–13). Mathematical creativity of 8th and 10th grade students. Seventh Conference of the European Society for Research in Mathematics Education—CERME7 (pp. 1084–1093), Rzeszów, Poland. [Google Scholar]
- Leikin, R., & Lev, M. (2013). Mathematical creativity in generally gifted and mathematically excelling adolescents: What makes the difference? ZDM, 45(2), 183–197. [Google Scholar] [CrossRef]
- Leikin, R., & Pitta-Pantazi, D. (2013). Creativity and mathematics education: The state of the art. ZDM, 45(2), 159–166. [Google Scholar] [CrossRef]
- Leikin, R., & Sriraman, B. (2022). Empirical research on creativity in mathematics (education): From the wastelands of psychology to the current state of the art. ZDM–Mathematics Education, 54(1), 1–17. [Google Scholar] [CrossRef]
- Leu, Y. C., & Chiu, M. S. (2015). Creative behaviours in mathematics: Relationships with abilities, demographics, affects and gifted behaviours. Thinking Skills and Creativity, 16, 40–50. [Google Scholar] [CrossRef]
- Lev, M. (2013). Relationship between high mathematical ability and mathematical creativity in secondary school students [Doctoral dissertation, University of Haifa]. [Google Scholar]
- Levav-Waynberg, A., & Leikin, R. (2012). The role of multiple solution tasks in developing knowledge and creativity in geometry. The Journal of Mathematical Behavior, 31(1), 73–90. [Google Scholar] [CrossRef]
- Levenson, E. (2011). Exploring collective mathematical creativity in elementary school. The Journal of Creative Behavior, 45(3), 215–234. [Google Scholar] [CrossRef]
- Lin, C. Y., & Cho, S. (2011). Predicting creative problem-solving in math from a dynamic system model of creative problem solving ability. Creativity Research Journal, 23(3), 255–261. [Google Scholar] [CrossRef]
- Lithner, J. (2008). A research framework for creative and imitative reasoning. Educational Studies in Mathematics, 67(3), 255–276. [Google Scholar] [CrossRef]
- Livne, N. L., & Milgram, R. M. (2000). Assessing four levels of creative mathematical ability in Israeli adolescents utilizing out-of-school activities: A circular three-stage technique. Roeper Review, 22(2), 111–116. [Google Scholar] [CrossRef]
- Livne, N. L., & Milgram, R. M. (2006). Academic versus creative abilities in mathematics: Two components of the same construct? Creativity Research Journal, 18(2), 199–212. [Google Scholar] [CrossRef]
- Lucas, B., Claxton, G., & Spencer, E. (2012). Progression in creativity: Developing new forms of assessment (pp. 1–27). Background paper for OECD conference “Educating for Innovative Societies”. Centre for Real-World Learning, University of Winchester. [Google Scholar]
- Mann, E. L. (2005). Mathematical creativity and school mathematics: Indicators of mathematical creativity in middle school students [Doctoral dissertation, University of Connecticut]. [Google Scholar]
- Mann, E. L. (2009). The search for mathematical creativity: Identifying creative potential in middle school students. Creativity Research Journal, 21(4), 338–348. [Google Scholar] [CrossRef]
- Marrone, R., Cropley, D. H., & Wang, Z. (2022). Automatic assessment of mathematical creativity using natural language processing. Creativity Research Journal, 35(4), 661–676. [Google Scholar] [CrossRef]
- Martin, L., Towers, J., & Pirie, S. (2006). Collective mathematical understanding as improvisation. Mathematical Thinking and Learning, 8(2), 149–183. [Google Scholar] [CrossRef]
- Meyer, M. S., Shen, Y., & Plucker, J. A. (2024). Reducing excellence gaps: A systematic review of research on equity in advanced education. Review of Educational Research, 94(1), 33–72. [Google Scholar] [CrossRef]
- Moher, D., Liberati, A., Tetzlaff, J., & Altman, D. G. (2009). Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. PLoS Medicine, 6(7), e1000097. [Google Scholar] [CrossRef]
- Munahefi, D. N., Kartono, Waluya, B., & Dwijanto. (2022). Analysis of self-regulated learning at each level of mathematical creative thinking skill. Bolema: Boletim de Educação Matemática, 36(72), 580–601. [Google Scholar] [CrossRef]
- Muzaini, M., Rahayuningsih, S., Ikram, M., & Nasiruddin, F. A.-Z. (2023). Mathematical creativity: Student geometrical figure apprehension in geometry problem-solving using new auxiliary elements. International Journal of Educational Methodology, 9(1), 139–150. [Google Scholar] [CrossRef]
- National Council of Teachers of Mathematics (NCTM). (2000). Principles and standards for school mathematics. NCTM. [Google Scholar]
- Page, M. J., McKenzie, J. E., Bossuyt, P. M., Boutron, I., Hoffmann, T. C., Mulrow, C. D., Shamseer, L., Tetzlaff, J. M., Akl, E. A., Brennan, S. E., Chou, R., Glanville, J., Grimshaw, J. M., Hróbjartsson, A., Lalu, M. M., Li, T., Loder, E. W., Mayo-Wilson, E., McDonald, S., … Moher, D. (2021). The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ, 372(71), n71. [Google Scholar] [CrossRef]
- Pelczer, I., & Rodríguez, F. G. (2011). Creativity assessment in school settings through problem-posing tasks. The Mathematics Enthusiast, 8(1), 383–398. [Google Scholar] [CrossRef]
- Pellegrino, J. W., & Hilton, M. L. (2012). Educating for life and work: Developing transferable knowledge and skills in the 21st century. NRC, the National Academies Press. [Google Scholar]
- Petticrew, M., & Roberts, H. (2006). Systematic reviews in the social sciences: A practical guide. Blackwell Publishing. [Google Scholar]
- Pham, L. H. (2014). Validation of predictive relationship of creative problem-solving attributes with math creativity (Publication No. 3579944) [Doctoral dissertation, St. John’s University]. [Google Scholar]
- Pitta-Pantazi, D., Christou, C., Kontoyianni, K., & Kattou, M. (2011). A model of mathematical giftedness: Integrating natural, creative, and mathematical abilities. Canadian Journal of Science, Mathematics and Technology Education, 11(1), 39–54. [Google Scholar] [CrossRef]
- Polya, G. (1945). How to solve it: A new aspect of mathematical method. Princeton University Press. [Google Scholar]
- Potters, O. T., van Schijndel, T. J., Jak, S., & Voogt, J. (2023). Two decades of research on children’s creativity development during primary education in relation to task characteristics. Educational Research Review, 39, 100532. [Google Scholar] [CrossRef]
- Rahyuningsih, S., Nurhusain, M., & Indrawati, N. (2022). Mathematical creative thinking ability and self-efficacy: A mixed-methods study involving Indonesian students. Uniciencia, 36(1), 318–331. [Google Scholar] [CrossRef]
- Riling. (2021). Expanding mathematical creativity by understanding student actions [Doctoral dissertation, Boston University]. [Google Scholar]
- Sadak, M., Incikabi, L., Ulusoy, F., & Pektas, M. (2022). Investigating mathematical creativity through the connection between creative abilities in problem posing and problem solving. Thinking Skills and Creativity, 45, 101108. [Google Scholar] [CrossRef]
- Sahliawati, M., & Nurlaelah, E. (2020). Mathematical creative thinking ability in middle school students. Journal of Physics: Conference Series, 1469(1), 012145. [Google Scholar] [CrossRef]
- Sawyer, R. K. (2004). Creative teaching: Collaborative discussion as disciplined improvisation. Educational Researcher, 33(2), 12–20. [Google Scholar] [CrossRef]
- Schoevers, E. M., Kroesbergen, E. H., & Kattou, M. (2018). Mathematical creativity: A combination of domain-general creative and domain-specific mathematical skills. The Journal of Creative Behavior, 54(2), 242–252. [Google Scholar] [CrossRef]
- Schoevers, E. M., Leseman, P. P., Slot, E. M., Bakker, A., Keijzer, R., & Kroesbergen, E. H. (2019). Promoting pupils’ creative thinking in primary school mathematics: A case study. Thinking Skills and Creativity, 31, 323–334. [Google Scholar] [CrossRef]
- Schrauth, M. A. (2014). Fostering mathematical creativity in the middle grades: Pedagogical and mathematical practices (Publication No. 3665425) [Doctoral dissertation, Texas State University]. [Google Scholar]
- Sengil-Akar, S., & Yetkin-Ozdemir, I. E. (2022). Investigation of mathematical collective creativity of gifted middle school students during model-eliciting activities: The case of the quilt problem. International Journal of Mathematical Education in Science and Technology, 53(2), 337–363. [Google Scholar] [CrossRef]
- Shaw, S. T., Luna, M. L., Rodriguez, B., Yeh, J., Villalta, N., & Ramirez, G. (2022). Mathematical creativity in elementary school children: General patterns and effects of an incubation break. Frontiers in Education, 7, 835911. [Google Scholar] [CrossRef]
- Sholihah, F., Suyitno, H., & Dwijanto, D. (2020). Creative mathematical thinking ability in creative problem solving model viewed from gender. Journal of Primary Education, 9(1), 58–65. [Google Scholar]
- Silver, E. A. (1997). Fostering creativity through instruction rich in mathematical problem solving and problem posing. ZDM, 29(3), 75–80. [Google Scholar] [CrossRef]
- Singer, F. M. (2012). Exploring mathematical thinking and mathematical creativity through problem posing. In R. Leikin, B. Koichu, & A. Berman (Eds.), Proceedings of the international workshop of the israeli science foundation on exploring and advancing mathematical abilities in high achievers (pp. 119–124). Simon Fraser University. [Google Scholar]
- Singer, F. M., & Voica, C. (2013). A problem-solving conceptual framework and its implications in designing problem-posing tasks. Educational Studies in Mathematics, 83(1), 9–26. [Google Scholar] [CrossRef]
- Sriraman, B. (2005). Are giftedness and creativity synonyms in mathematics? Journal of Secondary Gifted Education, 17(1), 20–36. [Google Scholar] [CrossRef]
- Sriraman, B. (2009). The characteristics of mathematical creativity. ZDM: The International Journal on Mathematics Education, 41, 13–27. [Google Scholar] [CrossRef]
- Stolte, M., García, T., Van Luit, J. E., Oranje, B., & Kroesbergen, E. H. (2020). The contribution of executive functions in predicting mathematical creativity in typical elementary school classes: A twofold role for updating. Journal of Intelligence, 8(2), 26. [Google Scholar] [CrossRef]
- Stolte, M., Kroesbergen, E. H., & Van Luit, J. E. (2019). Inhibition, friend or foe? Cognitive inhibition as a moderator between mathematical ability and mathematical creativity in primary school students. Personality and Individual Differences, 142, 196–201. [Google Scholar] [CrossRef]
- Suherman, S., & Vidákovich, T. (2022). Assessment of mathematical creative thinking: A systematic review. Thinking Skills and Creativity, 44, 101019. [Google Scholar] [CrossRef]
- Suherman, S., & Vidákovich, T. (2024a). Relationship between ethnic identity, attitude, and mathematical creative thinking among secondary school students. Thinking Skills and Creativity, 51, 101448. [Google Scholar] [CrossRef]
- Suherman, S., & Vidákovich, T. (2024b). Role of creative self-efficacy and perceived creativity as predictors of mathematical creative thinking: Mediating role of computational thinking. Thinking Skills and Creativity, 53, 101591. [Google Scholar] [CrossRef]
- Suherman, S., & Vidákovich, T. (2025). Creative self-efficacy, attitudes, creative style, and environmental literacy: Promoting mathematical creative thinking. The Journal of Educational Research, 118, 475–485. [Google Scholar] [CrossRef]
- Tabach, M., & Friedlander, A. (2013). School mathematics and creativity at the elementary and middle-grade levels: How are they related? ZDM Mathematics Education, 45, 227–238. [Google Scholar] [CrossRef]
- Tan, M., Mourgues, C., Bolden, D. S., & Grigorenko, E. L. (2013). Making numbers come to life: Two scoring methods for creativity in Aurora’s Cartoon Numbers. The Journal of Creative Behavior, 48(1), 25–43. [Google Scholar] [CrossRef]
- Tan, S. (2015). Assessing creative problem solving ability in mathematics: Revising the scoring system of the DISCOVER mathematics assessment (Publication No. 3740385) [Doctoral dissertation, The University of Arizona]. [Google Scholar]
- Teseo, R. F. (2019). The development of an instrument to measure creative ability in mathematics (Publication No. 13834341) [Doctoral dissertation, University of Missouri-Columbia]. [Google Scholar]
- The Organization for Economic Co-operation and Development (OECD). (2021). PISA 2021 creative thinking framework (third draft). PISA 2022. Available online: https://www.oecd.org/en/about/programmes/pisa/pisa-publications.html (accessed on 10 July 2025).
- Torrance, E. P. (1974). Torrance tests of creative thinking. Scholastic Testing Service. [Google Scholar]
- Tubb, A. L., Cropley, D. H., Marrone, R. L., Patston, T., & Kaufman, J. C. (2020). The development of mathematical creativity across high school: Increasing, decreasing, or both? Thinking Skills and Creativity, 35, 100634. [Google Scholar] [CrossRef]
- Tyagi, T. K. (2016). Mathematical creativity and mathematical aptitude: A cross-lagged Panel analysis. Creativity Research Journal, 28(3), 328–333. [Google Scholar] [CrossRef]
- Van Harpen, X. Y., & Sriraman, B. (2013). Creativity and mathematical problem posing: An analysis of high school students’ mathematical problem posing in China and the USA. Educational Studies in Mathematics, 82, 201–221. [Google Scholar] [CrossRef]
- Wang, X., Somasundram, P., & Zhang, J. (2025). The influence of flow experience on mathematical creativity among primary school students in China. Frontiers of Education, 10, 1580126. [Google Scholar] [CrossRef]
- Wardani, S., Sumarmo, U., & Nishitani, I. (2011). Mathematical creativity and disposition: Experiment with grade-10 students using Silver inquiry approach. Journal of the Faculty of Education, Gunma University. Natural Science Series, 59, 1–16. [Google Scholar]
- Wei, S. N. (2023). The relationship among mathematics anxiety, mathematics self-efficacy and mathematics creativity in junior high school students [Master’s thesis, Hubei University]. CNKI. Available online: https://link.cnki.net/doi/10.27130/d.cnki.ghubu.2023.000709 (accessed on 7 October 2025).
- Yackel, E., & Cobb, P. (1996). Sociomathematical norms, argumentation, and autonomy in mathematics. Journal for Research in Mathematics Education, 27(4), 458–477. [Google Scholar] [CrossRef]
- Yang, S., Zhu, S., Qin, W., Mai, Y., Guo, Q., & Li, H. (2025). Assessing the impact of problem-based digital learning on mathematics proficiency and creative problem solving for vocational high students. Education and Information Technologies. [Google Scholar] [CrossRef]
- Yaniawati, P., Kariadinata, R., Sari, N. M., Pramiarsih, E. E., & Mariani, M. (2020). Integration of e-learning for mathematics on resource-based learning: Increasing mathematical creative thinking and self-confidence. International Journal of Emerging Technologies in Learning (iJET), 15(06), 60–78. [Google Scholar] [CrossRef]
- Yuan, X. (2009). An exploratory study of high school students’ creativity and mathematical problem posing in China and the United States (Publication No. 3528254) [Doctoral dissertation, Illinois State University]. [Google Scholar]
- Yuliardi, R., Kusumah, Y. S., & Juandi, D. (2024). Development of a STEM-based digital learning space platform to enhance students’ mathematical creativity in future learning classrooms. Eurasia Journal of Mathematics, Science and Technology Education, 20(12), 1–17. [Google Scholar] [CrossRef]
- Zainudin, M., Subali, B., & Jailani. (2019). Construct validity of mathematical creativity instrument: First-order and second-order confirmatory factor analysis. International Journal of Instruction, 12(3), 595–614. [Google Scholar] [CrossRef]
| Study | Study Goal | Sample | Country | Type of Assessment Tasks |
|---|---|---|---|---|
| Akgul and Kahveci (2016) | To develop a valid and reliable scale of math creativity for use with middle school students | Fifth to Eighth Graders (10- to 15-year-old) (N = 297) | Türkiye | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Aljarrah (2020) | To explore and refine an emergent definition of collective creativity in elementary mathematics classrooms by analyzing students’ collaborative problem-solving processes | Sixth Graders (N = 25) | Canada | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Al-Mayahi and Hassan (2022) | To examine the correlation between creative problem-solving skills in mathematics and the perceptual speed | Fourth grade High Schoolers (N = 209) | Iraq | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Ariba (2019) | To explore the use of the skills and contents of the visual arts to enhance children’s mathematical creativity in the early years, using a specially designed intervention | First Graders (N = 15) | Nigeria | Self-Report or Questionnaire/Inventory, Observational and Interview-Based Task |
| Assmus and Fritzlar (2022) | To investigate whether mathematically gifted primary school students differ from non-gifted ones in high creativity in dealing with mathematical patterns and structures | Third Graders (N = 24) | Germany | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Ayvaz and Durmuş (2021) | To foster the problem-posing and mathematical creativity skills of gifted students who struggle with problem-posing | Seventh Graders (N = 6) | Türkiye | Problem-Posing Tasks or Situations |
| Azaryahu et al. (2025) | To investigate the development of creative thinking in math and music among first-and second-grade students through an integrated study program | First and second-graders N = 206) | Israel | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Bahar and Maker (2011) | To investigate the relationship between students’ creative performance and achievement in the mathematical domain across grade levels | First to Fourth Graders (N = 78) | US | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Bahar and Maker (2020) | To develop, field test, and implement a culturally responsive mathematics assessment to identify mathematically talented high school students from underrepresented and low-income backgrounds for participation in a special STEM internship program | High Schoolers (N = 57) | US | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Balka (1974) | To explore the nature of creative ability in mathematics | Sixth to Eighth Graders (N = 500) | US | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Bal-Sezerel and Sak (2022) | To present the development of a mathematical creativity test and exploration of its psychometric properties | Fifth to Eighth Graders (N = 1129) | Türkiye | Open-Ended Problem-Solving Tasks with Multiple Solutions, Problem-Posing Tasks or Situations |
| Barraza-García et al. (2020) | To propose and apply a theoretical model, called the Praxeological Model of Mathematical Talent (PMMT), to analyze and promote the development of mathematical talent through mathematical creativity in school-aged students | Fifth and Sixth Graders (10- to 12-year-old) (N = 26) | México | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Bicer et al. (2020) | To reveal both the effects of problem-posing interventions on the mathematical creative ability of students and how students’ creative self-efficacy in mathematics was related to their mathematical creative ability | Third to Fifth Graders (N = 205): 89 third graders, 62 fourth graders, and 54 fifth graders | US | Problem-Posing Tasks or Situations |
| Bicer and Bicer (2023) | To investigate four young elementary school students’ creative processes through eye-tracking (ET) and stimulated recall interview (SRI) techniques while they engaged in multiple representations (MRs) of mathematical problems | First to fifth grader (N = 4) | US | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Bishara (2016) | To investigate the ability of students to tackle the solving of unique mathematical problems in the domain of numerical series, verbal and formal, and its influence on the motivation of junior high students with learning dis- abilities in the Arab sector | Seventh grade junior high schoolers (N = 50) | Israel | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Coxbill et al. (2013) | To examine student groups’ written mathematical models to open-ended problems presented during three MEAs in alternating weeks | Third and Sixth Graders (N = 39): 24 third graders and 15 sixth graders | US | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| El-Sahili et al. (2015) | To design problems that express unexpected links in mathematics and suit students of intermediate and secondary levels | Seventh graders (N = 16) | Lebanon | Open-Ended Problem-Solving Tasks with Multiple Solutions, Observational and Interview-Based Task |
| Fatah et al. (2016) | To examine the use of open-ended approach in cultivating students’ mathematical creativity and self-esteem in mathematics of senior high school students | Eleventh Graders (N = Not specified) | Indonesia | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Fortes and Andrade (2019) | To explore the students’ mathematical creativity in terms of fluency, flexibility, and originality in solving six non-routine problems | Tenth Graders (N = 30) | Philippines | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| García-García et al. (2024) | To validate the positive effects of musical training on mathematical performance and explore the role of mathematical creativity in this relationship, addressing a research gap | Third Graders (14-to 15-year-old) (N = 220) | Canada | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Haavold (2013) | To examine the mathematical reasoning of high-achieving students when faced with an unfamiliar trigonometric equation | Eighth and Eleventh Graders (N = 308). | Norway | Open-Ended Problem-Solving Tasks with Multiple Solutions, Problem-Posing Tasks or Situations |
| Haavold (2016) | To empirically investigate the characteristics of mathematical creativity | 13- and 14-year-old (N = 184) | Norway | Open-Ended Problem-Solving Tasks with Multiple Solutions, Problem-Posing Tasks or Situations, Self-Report or Questionnaire/Inventory |
| Haavold (2018) | To investigate the relationship between age, knowledge, and creativity in mathematics, specifically examining which grade level, when controlled for mathematical achievement, influences mathematical creativity, and what characterizes the relationship between grade level, mathematical achievement, and mathematical creativity | Eighth and Eleventh Graders (13- and 14-year-old) (N = 301): 184 eighth graders and 117 eleventh graders | Norway | Open-Ended Problem-Solving Tasks with Multiple Solutions, Problem-Posing Tasks or Situations |
| Hall (2009) | To determine if there are creative differences by gender and grade level in the solving of non-routine mathematical problems and to investigate the relationship between students’ level of creativity and the various solution methods utilized when solving non-routine math problems | Sixth and Seventh Graders (N = 170). | US | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Haylock (1997) | To identify the kinds of responses in school mathematics that might justifiably be identified as “creative” | 11- and 12-year-old (N = Not specified). | England | Open-Ended Problem-Solving Tasks with Multiple Solutions, Problem-Posing Tasks or Situations |
| Hu and Wang (2024) | To investigate the impact of unplugged activities on students’ mathematical creativity and computational thinking | Third-grader (8-and 9-year-old) (N = 97) | China | Open-Ended Problem-Solving Tasks with Multiple Solutions and Problem-Posing Tasks or Situation |
| Huang et al. (2017) | To explore the relationship among domain-general divergent thinking ability, domain-specific scientific creativity, and mathematical creativity | Sixth Graders (11- to 14-year-old) (N = 187) | Taiwan | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Jensen (1973) | To investigate the relationships among creativity in mathematics, numerical aptitude, and mathematical achievement | Sixth Graders (N = 232) | US | Problem-Posing Tasks or Situations |
| Junaedi et al. (2021) | To describe the mathematical creative thinking level on polyhedron problems | Eighth Graders (N = 35) | Indonesia | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Kattou et al. (2013) | To investigate whether there is a relationship between mathematical ability and mathematical creativity, and to examine the structure of this relationship | Fourth to Sixth Graders (9- to 12-year-old) (N = 359): 143 fourth graders, 118 fifth graders, and 98 sixth graders | Cyprus | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Kirisci et al. (2020) | To explore, in a Solomon Four-Group research design, the effectiveness of the Selective Problem-Solving Model (SPS) on students’ analogical problem construction and selective thinking as major components of creative thinking in mathematics | Seventh Graders (N = 201) | Türkiye | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Kontoyianni et al. (2013) | To propose an equitable identification process accompanied by a new identification instrument aiming to recognize mathematical giftedness in students | Fourth to Sixth Graders (10- to 12-year-old) (N = 359): 143 fourth graders, 118 fifth graders, and 98 sixth graders | Cyprus | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Kulsum et al. (2019) | To find students’ mathematical creative thinking skills in solving mathematical problems by using several indicators | Tenth Graders (N = 22) | Indonesia | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| R. Leikin (2013) | To develop and refine a multidimensional model for assessing mathematical creativity using Multiple Solution Tasks (MSTs) | Tenth and Eleventh Graders (N = 191): 4 groups: Gifted (G), Non-Gifted (NG), Excelling in Math (EM), and Not Excelling in Math (NEM) students | Israel | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| R. Leikin and Kloss (2011) | To investigate and compare the mathematical creativity of students by evaluating their performance on Multiple Solution Tasks (MSTs), focusing on three creativity components: fluency, flexibility, and originality | Eighth and Tenth Graders (N = 258): 108 tenth graders and 158 eighth graders | Israel | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| R. Leikin and Lev (2013) | To examine relationships between mathematical creativity, general giftedness, and mathematical excellence, and to explore the power of different types of mathematical tasks for the identification of between-group differences related to mathematical creativity as reflected in multiple solutions produced by the students | Eleventh and Twelfth Graders (N = 51): Students a) gifted students (G) who excel in mathematics. (b) The HL group consists of students who learn math at a high level of mathematical instruction. (c) The RL group consists of students who learn math at an RL of mathematical instruction | Israel | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| M. Leikin and Tovli (2019) | To examine the relationship between developmental language deficit and children’s creative ability | Monolingual Preschoolers (3- to 5-year-old) (N = 45): 16 with formally diagnosed SLI and with developmental language disorders (5.98-year-old), 15 (5.73-year-old), and 14 from a younger kindergarten group (3.78-year-old) of children | Israel | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Leu and Chiu (2015) | To identify key creative behaviors in mathematics learning based on the perspective of multiplicity in creativity and drawing on the characteristics of creative mathematicians | Fourth Graders (N = 372) | Taiwan | Open-Ended Problem-Solving Tasks with Multiple Solutions, Problem-Posing Tasks or Situations, Self-Report or Questionnaire/Inventory |
| Lev (2013) | To examine relationships between mathematical creativity, general giftedness (G factor), and excellence in school mathematics (EM factor) | Tenth and Eleventh Graders (16- to 18-year-old) (N = 184): 38 students identified as being generally gifted and excelling in mathematics, 38 students identified as being generally gifted but not excelling in mathematics, 51 students excelling in mathematics who are not identified as being generally gifted, 57 students who are neither identified as being generally gifted nor excelling in mathematics, Super Mathematically Gifted) group: Additionally, 7 students who satisfied all criteria for the G-EM group and were characterized by mathematics professors as being students with extraordinary mathematical abilities | Israel | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Levav-Waynberg and Leikin (2012) | To explore the effectiveness of MSTs as a tool for the development of students’ mathematical knowledge and creativity associated with attending MSTs in geometry | Tenth Graders (N = 303): 209 students studied mathematics at a high level (HL), and 94 students at the regular level (RL) | Israel | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Levenson (2011) | To explore both the process involved in collective mathematical creativity as well as the product of collective mathematical creativity | Fifth and Sixth Graders (N = 88) | Israel | Open-Ended Problem-Solving Tasks with Multiple Solutions, Observational and Interview-Based Task |
| Livne and Milgram (2000) | To describe a three-stage technique for assessing creative ability in mathematics utilizing out-of-school activities | Eleventh and Twelfth Graders (N = 139) | Israel | Self-Report or Questionnaire/Inventory |
| Livne and Milgram (2006) | To examine the research question of whether the 4 by 4 model is the best model to support the postulation of general and domain-specific abilities in mathematics, each at four levels in mathematics | Tenth and Eleventh Graders (Average: 16-year-old) (N = 1090) | Israel | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Mann (2005) | To explore the relationship between mathematical creativity and mathematical achievement, attitude towards mathematics, self-perception of creative ability, gender and teacher perception of mathematical talent and creative ability. | Seventh Graders (N = 89) | US | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Mann (2009) | To explore simpler methods for identifying creative potential in middle school students and examine the relationship between creativity and variables like achievement, attitude, and self-perception | Seventh Graders (N = 89) | US | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Munahefi et al. (2022) | To determine the effect of SRL on mathematical creative thinking skill and analyze in detail the components of SRL at each level of creative mathematical thinking | Eleventh Graders (N = 36) | Indonesia | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Muzaini et al. (2023) | To explore the relationship between students’ mathematical creativity and figure apprehension when solving geometric problems with additional auxiliary elements, such as straight and curved lines | Twelfth Graders (14- and 15-year-old) (N = 38) | Indonesia | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Pelczer and Rodríguez (2011) | To focus on the relation between problem posing and mathematical creativity; in particular, on the issue of defining criteria for creativity assessment through problem posing tasks in classroom settings | High Schoolers (16-and 17-year-old) (N = 44) | México | Problem-Posing Tasks or Situations, Self-Report or Questionnaire/Inventory |
| Pham (2014) | To investigate the predictive relationship of the creative problem-solving attributes and math creativity of students | Sixth Graders (12-and 13-year-old) N = 560) | Vietnam | Open-Ended Problem-Solving Tasks with Multiple Solutions, Problem-Posing Tasks or Situations, Self-Report or Questionnaire/Inventory |
| Pitta-Pantazi et al. (2011) | To examine the structure and relationships among the components of mathematical giftedness and to identify groups of students that differ across these components | Fourth to Sixth Graders (N = 239): 108 fourth graders, 64 fifth graders, and 67 sixth graders | Cyprus | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Rahyuningsih et al. (2022) | To investigate the extent to which self-efficacy affects students’ mathematical creative thinking ability and to determine the characteristics of students with high mathematical creative thinking ability and high self-efficacy | 14-year-old (N = 96) | Indonesia | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Riling (2021) | To examine the nature of student mathematical creativity and identify how it can be influenced by social and aesthetic factors | High Schoolers (N = 211) | US | Observational and Interview-Based Task |
| Sadak et al. (2022) | To examine constructs of creative ability in mathematical problem posing (CAMPP) and creative ability in mathematical problem solving (CAMPS) | Sixth Graders (12-and 13-year-old) (N = 187) | Türkiye | Open-Ended Problem-Solving Tasks with Multiple Solutions, Problem-Posing Tasks or Situations |
| Sahliawati and Nurlaelah (2020) | To determine the mathematical creative thinking ability of junior high school students in solving the problem of the plane figure | Seventh Graders (12-and 13-year-old) (N = 28) | Indonesia | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Schoevers et al. (2018) | To investigate the relations between domain-general creativity (GC), domain-specific mathematical creativity (MC), and mathematical ability (MA) in a new and integrated way | Fourth Graders (Average: 9-year-old) (N = 342) | Netherlands | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Schoevers et al. (2019) | To gain an in-depth understanding of promoting mathematical creativity in educational practice | Fourth Graders (9-and 10-year-old) (N = 22) | Netherlands | Observational and Interview-Based Task |
| Schrauth (2014) | To help fill gaps in the research on mathematical creativity in the classroom and to provide insightful descriptions of how teachers foster mathematical creativity that teachers and administrators find relatable and useful | Seventh Graders (N = 5) | US | Observational and Interview-Based Task |
| Sengil-Akar and Yetkin-Ozdemir (2022) | To examine the collective mathematical creativity of gifted middle school students within a group through model- eliciting activities | Seventh and Eighth graders (N = 4) | Türkiye | Open-Ended Problem-Solving Tasks with Multiple Solutions, Observational and Interview-Based Task |
| Shaw et al. (2022) | To investigate whether a brief incubation break during a mathematical strategy generation task could improve elementary students’ ability to generate strategies and think more creatively | First to fifth graders (N = 211): including 53 first graders, 55 s graders, 25 third graders, 37 fourth graders, and 41 fifth graders | US | Problem-Posing Tasks or Situations |
| Sholihah et al. (2020) | To test the effectiveness of Creative Problem Solving (CPS) research and to analyze mathematical creative thinking skills based on gender | Seventh Graders (N = 6) | Indonesia | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Singer (2012) | This essay draws on the conclusions obtained by a few studies that dealt with students of various ages who won mathematical contests | Fourth to Sixth Graders (11- and 13-year-old) (N = 17) | Romania | Problem-Posing Tasks or Situations |
| Stolte et al. (2019) | To test the hypothesis that inhibition moderates the relationship between mathematical ability and mathematical creativity in primary school children | Third to fifth Graders (N = 80 to 82): 80 for fluency, 82 for flexibility, and 81 for originality | Netherlands | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Stolte et al. (2020) | To investigate the role of executive functions in mathematical creativity | 8- to 13-year-old (N = 278) | Netherlands | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Suherman and Vidákovich (2024a) | To investigate the relationship between attitude, ethnicity, and mathematical creative thinking among secondary school students | Seventh to Ninth graders (Average: 13-year-old) (N = 896) | Indonesia | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Suherman and Vidákovich (2024b) | To examine the predictors of MCT by specifically focusing on the roles of perceived creativity (PC), creative self-efficacy (CS), and computational thinking (CT) | Secondary School (Average: 13-year-old) (N = 896) | Indonesia | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Suherman and Vidákovich (2025) | To explore the indirect effect of creative self-efficacy and attitude toward mathematics in the promotion of creative mathematical thinking and as a mediator of creative style and environmental literacy | 11- to 15-year-old (N = 896) | Indonesia | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Tabach and Friedlander (2013) | To evaluate students’ creativity, as expressed in the solution methods of three problems for groups of students in different grades | Fourth to ninth graders (N = 76) | Israel | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| S. Tan (2015) | To revise and revalidate the scoring procedure of the DISCOVER Mathematics Assessment | First to Fifth Graders (N = 233): 57 first graders, 48 s graders, 37 third graders, 49 fourth graders, and 42 fifth graders | Australia | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| M. Tan et al. (2013) | To present an assessment developed for creativity that provides a score for mathematical creativity (MaC) in addition to a score for general creativity in the numeric domain, or what we might call numerical creativity (NuC) | Fourth to Sixth Graders (Average: 10-year-old) (N = 205): 22.3% fourth graders, 43.2% fifth graders, and 34.5% sixth graders | England | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Teseo (2019) | To investigate the relationships among attributes of creative problem-solving ability to find out the contribution patterns of these attributes to mathematics creative problem-solving of 6th-grade students on Long Island, New York | Sixth Graders (N = 632) | US | Open-Ended Problem-Solving Tasks with Multiple Solutions, Self-Report or Questionnaire/Inventory |
| Tubb et al. (2020) | To focus on mathematical creativity in children across grades six-12 at a large Australian school | Eighth to Twelfth Graders (13- to 17-year-old) (N = 896): 82 eighth graders, 235 ninth graders, 191 tenth graders, 189 eleventh graders, and 199 twelfth graders | Australia | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Tyagi (2016) | To explore if mathematical creativity and mathematical aptitude are causally related, and if so, what the direction of causation is | 13-year-old (N = 480) | India | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Van Harpen and Sriraman (2013) | To investigate mathematically advanced high school students’ abilities in posing mathematical problems | Eleventh and Twelfth Graders (16- and 19-year-old) (N = 123): 55 Jiaozhou, 44 Shanghai, and 30 U.S. students | Jiaozhou, Shanghai, and US | Problem-Posing Tasks or Situations |
| Wang et al. (2025) | To explore the influence of Chinese primary school students’ flow experience in mathematics class on their mathematical creativity | Sixth Graders (N = 273) | China | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Wardani et al. (2011) | To analyze in depth the roles of inquiry approach, school level, and students’ previous mathematics ability on the quality of students’ mathematical creative and disposition, and to analyze teachers’ opinions on the inquiry approach | Tenth Graders (N = 240) | Indonesia | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Yang et al. (2025) | To focus on the dynamic nature of students’ ability development and employed a longitudinal effectiveness diagnostic research approach to measure the impact of PBDL on vocational high school students’ mathematics proficiency and creative problem-solving using time-series data | 16- to 18-year-old (N = 37) | China | Self-Report or Questionnaire/Inventory |
| Yaniawati et al. (2020) | To introduce the utilization of e-learning for mathematics on Resource-Based Learning (RBL) with a scientific approach to increase mathematical creative thinking ability and to develop students’ self-confidence | Seventh graders N = 40) | Indonesia | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Yuan (2009) | To compare students’ creativity and mathematical problem-posing abilities in China and the United States | Eleventh and Twelfth Graders (16- and 19-year-old) (N = 123): 55 Jiaozhou, 44 Shanghai, and 30 U.S. students | Jiaozhou, Shanghai, and US | Problem-Posing Tasks or Situations |
| Yuliardi et al. (2024) | To develop a STEM-based DLS platform that is valid, practical, and effective in enhancing students’ mathematical creativity | Junior High Schoolers (N = 190) | Indonesia | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Zainudin et al. (2019) | To prove empirically whether or not all items in each dimension measure constructs, where all items in each dimension match one-factor model, and whether all items in each dimension have a significant effect. | Junior high schoolers (12- to 15-year-old) (N = 313) | Indonesia | Open-Ended Problem-Solving Tasks with Multiple Solutions |
| Assessments | Studies Using the Assessment | Target Group | Scoring Types | Components Scored in Assessments | Format |
|---|---|---|---|---|---|
| A Creativity Assessment Tool (CAT) (was adapted from the assessment tool for creativity developed by Lucas et al. (2012)) | Ariba (2019) | First Grade | No formal scoring | Socio-Emotional and Attitudinal Components | Paper-based |
| A Mathematical Creativity Scale (MCS) (developed by Akgul and Kahveci (2016)) | Akgul and Kahveci (2016) | Fifth to Eighth Graders (10- to 15-year-old) (N = 297) | Criterion & Norm-referenced | Divergent thinking Components | Paper-based |
| A Mathematical Creativity Instrument (developed by Zainudin et al. (2019)) | Zainudin et al. (2019) | (12- to 15-year-old) | Criterion & Norm-referenced | Divergent thinking Components | Paper-based |
| Analogical Problem Construction Test (APCT) (developed by Kirisci et al. (2020)) | Kirisci et al. (2020) | Seventh Grade | Criterion-referenced | Problem-Solving and Thinking Processes Components | Paper-based |
| A test of Mathematical Creativity (developed by Tubb et al. (2020)) | Tubb et al. (2020) | 13- to 17-year-old | No formal scoring | Divergent thinking Components | Paper-based |
| Cartoon Numbers (CN), one of the subtests of the Aurora Battery (developed by Chart et al. (2008)) | M. Tan et al. (2013) | 10-year-old | Criterion & Norm-referenced | Divergent thinking Components | Paper-based |
| Creative Ability in the Mathematical Problem-Posing (CAMPP) Test (developed by Sadak et al. (2022) and translated into Turkish) | Sadak et al. (2022) | 12- and 13-year-old | Criterion & Norm-referenced | Divergent thinking Components | Paper-based |
| Creative Ability in the Mathematical Problem-Solving (CAMPS) Test (developed by Sadak et al. (2022) and translated into Turkish) | Sadak et al. (2022) | 12- and 13-year-old | Criterion & Norm-referenced | Divergent thinking Components | Paper-based |
| Discovering Intellectual Strengths and Capabilities while Observing Varied Ethnic Responses (DISCOVER) (developed by Bahar and Maker (2011)) | Bahar and Maker (2011, 2020), S. Tan (2015) | First to Fifth Grade, and high school senior | Criterion & Norm-referenced | Divergent thinking Components | Paper-based |
| Geometrical Figure Apprehension Creative Test (GFACT) (developed by Muzaini et al. (2023)) | Muzaini et al. (2023) | 14- and 15-year-old | Criterion-referenced | Divergent thinking Components | Paper-based |
| Mathematics Creative Thinking Ability Scale (developed by Rahyuningsih et al. (2022)) | Rahyuningsih et al. (2022) | 14-year-old | Criterion-referenced | Divergent thinking Components | Paper-based? |
| Mathematics Creative Problem-Solving Ability Test (MCPSAT) (developed by Kim et al. (2003) and translated into English and Vietnamese) | Pham (2014) and Teseo (2019) | 12- and 13-year-old and Sixth Grade | Criterion & Norm-referenced | Divergent thinking Components | Paper-based |
| Mathematical Creativity Test (MCT) (developed by Bal-Sezerel and Sak (2022)) | Bal-Sezerel and Sak (2022) | Fifth to Eighth Grade | Criterion & Norm-referenced | Divergent thinking Components | Paper-based |
| Multiple-Solution Task (MST) (developed by R. Leikin (2009)) | R. Leikin (2013), R. Leikin and Kloss (2011), R. Leikin and Lev (2013), Lev (2013), and Levav-Waynberg and Leikin (2012), Tabach and Friedlander (2013) | Fourth to ninth, Tenth to Twelfth Grade, and 16- to 18-year-old | Criterion & Norm-referenced | Divergent thinking Components | Paper-based |
| Observational and Interview-Based tasks developed by the researchers | El-Sahili et al. (2015), Levenson (2011), Riling (2021), Schoevers et al. (2019), Schrauth (2014), and Sengil-Akar and Yetkin-Ozdemir (2022) | Fifth to Eighth Grade and High School, and 9- and 10-year-old | Criterion-referenced & Norm-referenced and No Formal Scoring | Divergent thinking Components, Problem-Solving and Thinking Processes Components, Socio-Emotional and Attitudinal Components | Paper-based |
| Open-ended Multiple-solution tasks developed by the researchers | Aljarrah (2020), Assmus and Fritzlar (2022), Azaryahu et al. (2025), Barraza-García et al. (2020), Bicer and Bicer (2023), Bishara (2016), Coxbill et al. (2013), El-Sahili et al. (2015), Fatah et al. (2016), Fortes and Andrade (2019), Hall (2009), Haylock (1997), Hu and Wang (2024), Junaedi et al. (2021), Kattou et al. (2013), Kulsum et al. (2019), Kontoyianni et al. (2013), M. Leikin and Tovli (2019), Levenson (2011), Leu and Chiu (2015), Livne and Milgram (2006), Munahefi et al. (2022), Pitta-Pantazi et al. (2011), Sahliawati and Nurlaelah (2020), Sengil-Akar and Yetkin-Ozdemir (2022), Sholihah et al. (2020), Tyagi (2016), Wardani et al. (2011), Yaniawati et al. (2020), and Yuliardi et al. (2024) | 1- to 5-year-old, fourth to eighth grade, tenth, eleventh grade, 8- to 16-year-old, and Junior High School | Criterion & Norm-referenced, No formal scoring, and Unclassified Approach | Divergent thinking Components, Problem-Solving and Thinking Processes Components, Socio-Emotional and Attitudinal Components | Paper-based and online |
| Problem-Posing Tasks/Activities developed by the researchers | Ayvaz and Durmuş (2021), Bicer et al. (2020), Hu and Wang (2024), Jensen (1973), Leu and Chiu (2015), Pelczer and Rodríguez (2011), Shaw et al. (2022), Singer (2012), and Yuan (2009) | First to seventh grade, 11- to 13-year-old, and 16- to 19-year-old | Criterion- & Norm-referenced and No formal scoring | Divergent thinking Components | Paper-based |
| Self-report or Questionnaire/Inventory generated by researchers | Haavold (2016), Leu and Chiu (2015), Livne and Milgram (2000), and Pelczer and Rodríguez (2011), and Yang et al. (2025) | 13- and 14-year-old, fourth grade, eleventh and twelfth grade and 16- and 17-year-old | Criterion & Norm-referenced and No formal scoring | Divergent thinking Components, Problem-Solving and Thinking Processes Components, Socio-Emotional and Attitudinal Components | Paper-based |
| Test of Creative Problem-Solving Skills in Math (developed by Al-Mayahi and Hassan (2022)) | Al-Mayahi and Hassan (2022) | Fourth grade high schoolers | Criterion-referenced | Problem-Solving and Thinking Processes Components | Paper-based |
| The Creative Ability in Mathematics Test (CAMT) (developed by Balka (1974)) | Balka (1974), Haavold (2013, 2016, 2018), and Mann (2005, 2009) | Sixth to Eighth Grade, Eleventh Grade, and 13- and 14-year-old | Criterion & Norm-referenced | Divergent thinking Components | Paper-based |
| The Creative Problem-Solving Attributes Inventory (CPSAI) (developed by Lin and Cho (2011) and translated into English and Vietnamese) | Pham (2014), and Teseo (2019) | Sixth grade and 12- and 13-year-old | Criterion & Norm-referenced | Divergent thinking Components | Paper-based |
| The Divergent Production (DP) subtest (developed by Haylock (1987, 1997) and translated into Taiwanese) | Huang et al. (2017) | 11- to 14-year-old | Criterion & Norm-referenced | Divergent thinking Components | Paper-based |
| The Mathematical Creative Thinking based Ethnomathematics Test (MCTTBE) (developed by Suherman and Vidákovich (2022)) | Suherman and Vidákovich (2024a) | Average 13-year-old | Criterion & Norm-referenced | Divergent thinking Components | Online |
| The Mathematical Creative Thinking based Ethnomathematics Test (MCTTBE) (developed by Suherman and Vidákovich (2024a)) | Suherman and Vidákovich (2024b, 2025) | 11- to 15-year-old | Criterion & Norm-referenced | Divergent thinking Components | Online |
| The Mathematical Creative Scale (developed by Wei (2023) for Chinese students) | Wang et al. (2025) | Sixth Graders | Criterion & Norm-referenced | Divergent thinking Components | Paper-based |
| The Mathematical Creativity Test (MCT) (developed by Kattou et al. (2013) and translated into Dutch) | Schoevers et al. (2018) | 9-year-old | No formal scoring | Divergent thinking Components | Paper-based |
| The Mathematical Creativity Test (MCT) (developed by Kattou et al. (2013) and translated by Schoevers et al. (2018) into Dutch) | Stolte et al. (2019) | Third to Fifth Grade | Criterion & Norm-referenced | Divergent thinking Components | Paper-based |
| The Mathematical Creativity Test (MCT) (developed by Kattou et al. (2013) and translated by Stolte et al. (2020) into Dutch) | Stolte et al. (2020) | 8- to 13-year-old | Criterion & Norm-referenced | Divergent thinking Components | Paper-based |
| The Test for Mathematical Creative Problem-Solving Ability (created by Lee et al. (2003) and adapted by García-García et al. (2024) into Spanish) | García-García et al. (2024) | 14- to 15-year-old | Criterion & Norm-referenced | Divergent thinking Components | Paper-based |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sipahi, Y.; Bahar, A.K. Mathematical Creativity: A Systematic Review of Definitions, Frameworks, and Assessment Practices. Educ. Sci. 2025, 15, 1348. https://doi.org/10.3390/educsci15101348
Sipahi Y, Bahar AK. Mathematical Creativity: A Systematic Review of Definitions, Frameworks, and Assessment Practices. Education Sciences. 2025; 15(10):1348. https://doi.org/10.3390/educsci15101348
Chicago/Turabian StyleSipahi, Yasemin, and A. Kadir Bahar. 2025. "Mathematical Creativity: A Systematic Review of Definitions, Frameworks, and Assessment Practices" Education Sciences 15, no. 10: 1348. https://doi.org/10.3390/educsci15101348
APA StyleSipahi, Y., & Bahar, A. K. (2025). Mathematical Creativity: A Systematic Review of Definitions, Frameworks, and Assessment Practices. Education Sciences, 15(10), 1348. https://doi.org/10.3390/educsci15101348






