Mathematical Creativity: A Systematic Review of Definitions, Frameworks, and Assessment Practices

Abstract

Mathematical creativity (MC) plays an important role in mathematics and education; however, its conceptualization and assessment remain inconsistent across empirical studies. This systematic review examined how MC has been defined, conceptualized, and assessed across 80 empirical studies involving K-12 populations. Through thematic analysis, the study identified three definition types: divergent thinking, problem-solving, and problem-posing, as well as affective–motivational emphasis. We organized theoretical frameworks into three categories: domain-general, domain-specific, and multidimensional frameworks. Results showed that the most common definitions emphasized divergent thinking components while fewer studies highlighted affective and dispositional factors. Domain-specific frameworks were the most frequently used, followed by multidimensional frameworks. Regarding assessment, studies predominantly relied on divergent-thinking scoring. Most assessments used criterion-referenced rubrics with norm-based comparisons. They were delivered mainly in paper-pencil format. Tasks were typically open-ended multiple-solution problems with fewer studies using self-reports or observational methods. Overall, the field prioritizes product-based scoring (e.g., fluency, flexibility, originality) over evidence about students’ solution processes (e.g., reasoning, metacognitive monitoring). To improve cross-context comparability, future work should standardize and transparently report age, grade, and country coding and scoring practices.

1. Introduction

Creativity has been seen as an important skill for the 21st century because it helps drive innovation, problem-solving, and intellectual growth in societies (Meyer et al., 2024; OECD, 2021). In this manner, mathematical creativity (MC) has become an important topic in mathematics education, as it can support deeper understanding and problem-solving (R. Leikin & Sriraman, 2022). However, research on MC is still limited and often takes a backseat to studies on procedural skills and test performance (Joklitschke et al., 2022).

The importance of nurturing mathematical creativity is underscored by international organizations such as the National Council of Teachers of Mathematics (NCTM, 2000), the National Academy of Sciences (NAS) (Pellegrino & Hilton, 2012), and the OECD (2021). All of them emphasize the value of creativity across many mathematical abilities and grade levels (R. Leikin & Sriraman, 2022). Mathematical creativity is also relevant to gifted education since many gifted students demonstrate the capacity for original and flexible thinking in mathematics (Bal-Sezerel & Sak, 2022; Bicer, 2021; Chamberlin & Moon, 2005). Yet, the field still lacks conceptual clarity and consistency in defining and assessing mathematical creativity, especially in the context of identifying and supporting gifted learners.

In particular, the lack of consistent and reliable assessment practices gives a significant problem for both researchers and educators. It is difficult to understand how mathematical creativity develops or how instructional strategies can foster or hinder it without valid tools to define and measure it. Assessment is not completely a technical topic. It is central to the conceptualization of creativity, as definitions often shape what is measured. Any effort to define and model mathematical creativity must also critically examine how it is operationalized and assessed in empirical studies. Therefore, a systematic review is needed to synthesize the various approaches to assessment, identify gaps in current practices, and provide directions for future research.

Despite theoretical contributions, the empirical literature on mathematical creativity remains fragmented. There is no universally accepted definition or framework. Measurement practices vary across studies (R. Leikin & Pitta-Pantazi, 2013). Some researchers focus on domain-general characteristics such as divergent thinking (Guilford, 1968; Torrance, 1974), while others emphasize domain-specific abilities (Bicer, 2021; Silver, 1997). This heterogeneity makes it difficult to draw coherent conclusions, which limits the effectiveness of educational interventions.

The present study addresses this gap by conducting a systematic review of empirical research on mathematical creativity. The review synthesizes how MC has been defined, conceptualized, and framed across the literature rather than endorsing a single definition or framework. Specifically, it focuses on three guiding questions: (1) how is mathematical creativity defined? (2) Which theoretical frameworks are adhered to conceptualize MC? (3) How is mathematical creativity operationalized and assessed?

1.1. Defining Mathematical Creativity

Defining mathematical creativity (MC) has challenges for both researchers and mathematics educators. While early research on creativity focused on domain-general definitions (e.g., Guilford, 1968; Torrance, 1974), more recent researchers have focused on contextualizing creativity within specific domains such as mathematics. Guilford conceptualized creativity as divergent thinking. Building upon this framework, Torrance developed the Torrance Tests of Creative Thinking (TTCT). It became a widely adopted tool in creativity research. These general models have mainly influenced how creativity is defined and assessed in mathematics education (R. Leikin, 2009; Silver, 1997).

Haylock (1987) suggested that mathematical creativity has two parts: overcoming fixation and divergent production. This model shows that being creative in mathematics requires both flexible thinking and the ability to generate ideas.

Building on these earlier perspectives, Silver (1997) defined mathematical creativity as the generation of multiple solution strategies to solve problems. That is, MC integrates divergent thinking into mathematical activity. In the context of gifted education, Sriraman (2005) defined mathematically creative students as those who can engage in problem-solving, pose original problems, and construct multiple solution strategies. From a more classroom-centered perspective, Bicer (2021) defined MC as “an ability to generate new mathematical ideas, processes, or products that are new to the students but may not necessarily new to the rest of the world” (p. 253).

Despite the fact that there have been many variations, most definitions agree that mathematical creativity is the ability to produce solutions that are both novel and appropriate within a mathematical context (Kaufman & Sternberg, 2010). However, some researchers warn us against misinterpretations. For example, Amabile (1982) argued that focusing only on creative products without considering the process and context may lead to misunderstandings in measuring creativity. Similarly, Joklitschke et al. (2022) emphasized the importance of transparency and strong theory when inferring mathematical creativity.

In summary, while early conceptualizations emphasized general cognitive processes, contemporary definitions of mathematical creativity increasingly reflect a domain-specific, multidimensional, and context-dependent view. These definitions form the conceptual basis upon which measurement tools, frameworks, and pedagogical models have been developed.

1.2. Theoretical Perspectives on Mathematical Creativity

Theoretical perspectives on mathematical creativity have long been built upon foundational models of general creativity, such as those of Guilford (1968) and Torrance (1974). Guilford’s Structure-of-Intellect (SOI) model conceptualizes creativity across three dimensions: operations (e.g., cognition, memory, divergent production, convergent production, evaluation), contents (e.g., figural, symbolic, semantic; later also behavioral), and products (e.g., units, classes, relations, systems, transformations, implications). This approach shaped the idea that creativity is something that can be measured in different ways. Torrance continued this work by outlining four main components of creativity: fluency, flexibility, originality, and elaboration. These four components are important in tests measuring divergent thinking.

Amabile’s (1983) Component Model of Creativity introduced a sociopsychological perspective by emphasizing the interaction of domain-relevant skills, creativity-related processes, and intrinsic task motivation. In mathematics education, R. Leikin (2009) and Silver (1997) have been influential in transferring general theories of creativity to the field of mathematics. Drawing on the work of Torrance (1974), Silver proposed a framework emphasizing differential production in mathematical tasks, particularly multiple solution tasks (MSTs). Leikin expanded on this approach by creating a model of mathematical creativity that includes fluency, flexibility, originality, and elaboration. Sriraman (2005) proposed a theoretical model that frames mathematical creativity around five guiding principles: motivation, uncertainty, risk, effort, and aesthetics. Their work emphasized the role of open-ended, ill-structured problem solving in the development and determination of creativity among mathematically gifted students.

Another influential contribution came from Krutetskii (1976) and Polya (1945), who underscored the importance of heuristic thinking, pattern recognition, and flexible strategy use in mathematical problem-solving. Building on these cognitive views, Haylock (1987) proposed that MC involves (1) overcoming fixation, which means moving beyond routine methods, and (2) divergent production, which is about coming up with many different solutions to a problem

Balka (1974) presented a set of specific cognitive abilities that characterize mathematical creativity: (1) formulating mathematical hypotheses, (2) determining patterns, (3) breaking mental set, (4) evaluating unusual ideas, (5) identifying missing information and posing relevant questions, and (6) decomposing problems into sub-problems. Their task-specific model remains relevant for classroom-based assessments and curriculum design. In more recent work, Kattou et al. (2013) emphasized that mathematical creativity is a domain-specific subcomponent of mathematical ability, best investigated through problem-solving and problem-posing tasks. Similarly, the work of R. Leikin and Pitta-Pantazi (2013) and Sriraman (2009) highlighted the contribution of creative thinking to students’ conceptual understanding, reinforcing creativity.

Some frameworks have integrated sociocultural perspectives to explore how creative thinking develops within classroom interactions. For instance, frameworks combining Silver’s (1997) components with socio-mathematical norms (Yackel & Cobb, 1996) and collective creativity theories (Martin et al., 2006; Sawyer, 2004) provide insight into the collaborative and contextual nature of MC in real learning environments.

In summary, the theoretical frameworks that inform mathematical creativity have a rich spectrum, from cognitive-divergent production models to sociocultural classroom-based perspectives, and from individual problem-solving heuristics to collaborative meaning-making processes. This diversity reflects the multifaceted nature of creativity and underscores the need for strong tools to study and foster MC in educational settings.

1.3. Linking Definitions and Frameworks

We present definitions and conceptualisations separately to keep the narrative clear and the evidence comparable. We used definition to refer to a concise statement of what mathematical creativity (MC) is, its semantic core (for example, emphasis on originality and appropriateness). In contrast, we used conceptualisation to refer to the theoretical lens that explain how MC is organized into components and how it becomes measurable in tasks and scoring. These two layers are naturally connected; definitions enable particular lenses, and lenses make definitions observable, but combining them in the same analytic stream easily blurs claims and reduces the interpretability of later assessment results. Accordingly, in our coding, we tagged explicit “what is MC” statements as definitions, while we classified the models, components, and operational choices as conceptualisations. When the same source contributed to both layers, we explained it once in detail under the conceptual lens and used cross-references from the definition side to avoid redundancy. This analytic boundary improves reliability (coders can agree more consistently on definitions than on full frameworks), reduces repetition (key historical sources appear in one place rather than two), and builds a clean bridge to the assessment synthesis that follows. By doing so, definitions tell the meaning; conceptualisations provide the structure; assessment shows the evidence. Treating them as distinct but tightly linked allows us to answer the guiding questions separately while still showing how meaning, structure, and measurement work together across the literature.

1.4. Significance of Study

Despite the increasing attention to the field, empirical studies related to mathematical creativity have continued to yield inconsistent results, especially regarding the definition, conceptualization, and assessment of the construct (R. Leikin & Sriraman, 2022). This study addresses a critical gap by systematically synthesizing existing research to clarify what is meant by “mathematical creativity,” what theoretical frameworks support it, and how it has been operationalized and measured in educational settings. Importantly, the findings of this review are not only relevant to researchers and curriculum developers but are also crucial for practitioners in education. In this sense, our K-12 review complements earlier syntheses of assessment in mathematical creative thinking (e.g., Suherman & Vidákovich, 2022) by connecting what MC is and how it is structured to what is actually scored and how it is delivered in schools.

Furthermore, this study contributes to ongoing discussions about the need for domain-specific creativity research, as general creativity assessments may fail to capture the unique cognitive processes (Bal-Sezerel & Sak, 2022; Kaufman & Baer, 2005). By focusing specifically on K-12 student populations, this review informs both research and practice aimed at nurturing mathematical creativity from an early age, particularly among students who might otherwise be overlooked by traditional measures of creativity.

Assessment practices may vary by age/grade and by task design. Evidence suggests that creativity generally rises across the primary years but shows dips around grades 3–4 and 5–6. In this sense, task form also matters, with age-related gains in fluency and flexibility less pronounced on tasks that require both figural and verbal responses (Potters et al., 2023). In mathematics, originality tends to lag behind fluency and flexibility. Although the number of strategies increases from grades 1–5, creativity scores can decline from grade 4 to 5 (Shaw et al., 2022; Tubb et al., 2020). Accordingly, in our findings (RQ3), we interpreted operationalizations and scoring alongside age/grade bands and task characteristics. Given the predominance of cross-sectional designs and limited longitudinal evidence, we treated these patterns as descriptive rather than causal (Tubb et al., 2020).

2. Methodology

This study used a systematic review to provide a transparent and reproducible synthesis of research on mathematical creativity. In line with the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) 2020 (Page et al., 2021), we specified eligibility criteria and a coding scheme in advance and reported the full search and selection process. These procedures minimize selection bias and make the evidence base comparable across studies (Moher et al., 2009; Petticrew & Roberts, 2006). The approach is particularly useful in fragmented literature, where single studies can mislead. A structured synthesis yields a more reliable view of what is known and where better evidence is needed. Details of databases, screening, and coding were explained below.

2.1. Literature Selection

To explore how mathematical creativity is defined, conceptualized, and assessed, a comprehensive literature search was conducted using three sources: scholarly databases, Google Scholar, and Web of Science. The search aimed to identify both peer-reviewed articles and dissertations/theses relevant to K-12 creativity and mathematics education.

2.1.1. Major Databases

We searched APA PsycArticles, APA PsycInfo, Education Research Complete, ERIC, and Psychology & Behavioral Sciences Collection. Our search strategy integrated systematically selected keywords with Boolean operators to maximize the retrieval of relevant literature: creativ* (terms beginning with creativ, e.g., creativity) AND math* (terms beginning with math, e.g., mathematics). This approach limited the results to studies explicitly categorized under both creativity and mathematics to increase the precision of the search. Our search was conducted across abstracts, keywords, and titles using these terms. English-language records and relevant publication types were retained. All inclusion/exclusion criteria matched those shown in Figure 1 (PRISMA). Initial hits, filters, and de-duplication counts are reported in Figure 1.

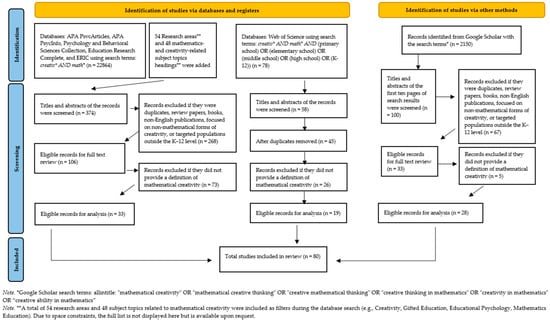
Figure 1. PRISMA Flowchart of Literature Search and Selection.

2.1.2. Google Scholar

In parallel, we ran an allintitle search: “mathematical creativity” OR “mathematical creative thinking” OR “creative mathematical thinking” OR “creative thinking in mathematics” OR “creativity in mathematics” OR “creative ability in mathematics.” We screened the first 10 pages (100 records) by relevance and applied the same inclusion/exclusion criteria. Then we de-duplicated against the five databases. Counts for screening and retention are summarized in Figure 1.

2.1.3. Web of Science (WoS)

To enhance coverage and reduce cross-index selection bias, a third source, the Web of Science (WoS), was searched. The search was conducted using the following query in the title, abstract, and keyword fields: creativ* AND math* AND (primary school OR elementary school OR middle school OR high school OR K-12). English-language records and document types appropriate to our study scope were retained. The previously defined inclusion/exclusion criteria were applied directly. Duplicates were removed from the results of five databases and Google Scholar. Records lacking a clear definition of mathematical creativity were eliminated. Finally, 19 studies were eligible for review. With this addition, total number of studies were 80 (13 doctoral dissertations and 67 journal articles) were retained for analysis. The complete selection process is illustrated in a PRISMA diagram (Figure 1).

2.2. Coding and Analysis

Thematic analysis was conducted by the research team on the 80 empirical studies to examine how mathematical creativity was defined, framed, and assessed. The research team included two researchers: a doctoral student and a mid-career researcher. Table 1 provides a summary of the studies, including their aims, samples, countries, and type of assessment tasks. Table 2 provides an overview of the assessments used across the studies, including their associated studies, grade levels, scoring types, components scored, and formats. For both RQ1 (definitions) and RQ2 (frameworks), we followed the same steps. We read each study in full, pulled key phrases and keywords, and grouped recurring patterns. For RQ1, an author-by-author scheme was first considered but proved too granular. Our recluster yielded three definition themes: divergent-thinking, problem-solving/problem-posing, and affective/motivational. For RQ2, we likewise began inductively. The first pass mirrored two of the definition themes and a third “multidimensional” cluster. Because definitions and frameworks address different questions, we re-grouped frameworks across all studies and adopted domain-general, domain-specific, and multidimensional as the final categories (multiple codes allowed). Definitions and frameworks were analyzed on separate axes to avoid forcing one-to-one matches. Coding was led by the doctoral student. After that the mid-career researcher reviewed category boundaries and provided feedback. Disagreements were resolved in meetings.

Table 1. Overview of Studies Included in the Systematic Review.

Study	Study Goal	Sample	Country	Type of Assessment Tasks
Akgul and Kahveci (2016)	To develop a valid and reliable scale of math creativity for use with middle school students	Fifth to Eighth Graders (10- to 15-year-old) (N = 297)	Türkiye	Open-Ended Problem-Solving Tasks with Multiple Solutions
Aljarrah (2020)	To explore and refine an emergent definition of collective creativity in elementary mathematics classrooms by analyzing students’ collaborative problem-solving processes	Sixth Graders (N = 25)	Canada	Open-Ended Problem-Solving Tasks with Multiple Solutions
Al-Mayahi and Hassan (2022)	To examine the correlation between creative problem-solving skills in mathematics and the perceptual speed	Fourth grade High Schoolers (N = 209)	Iraq	Open-Ended Problem-Solving Tasks with Multiple Solutions
Ariba (2019)	To explore the use of the skills and contents of the visual arts to enhance children’s mathematical creativity in the early years, using a specially designed intervention	First Graders (N = 15)	Nigeria	Self-Report or Questionnaire/Inventory, Observational and Interview-Based Task
Assmus and Fritzlar (2022)	To investigate whether mathematically gifted primary school students differ from non-gifted ones in high creativity in dealing with mathematical patterns and structures	Third Graders (N = 24)	Germany	Open-Ended Problem-Solving Tasks with Multiple Solutions
Ayvaz and Durmuş (2021)	To foster the problem-posing and mathematical creativity skills of gifted students who struggle with problem-posing	Seventh Graders (N = 6)	Türkiye	Problem-Posing Tasks or Situations
Azaryahu et al. (2025)	To investigate the development of creative thinking in math and music among first-and second-grade students through an integrated study program	First and second-graders N = 206)	Israel	Open-Ended Problem-Solving Tasks with Multiple Solutions
Bahar and Maker (2011)	To investigate the relationship between students’ creative performance and achievement in the mathematical domain across grade levels	First to Fourth Graders (N = 78)	US	Open-Ended Problem-Solving Tasks with Multiple Solutions
Bahar and Maker (2020)	To develop, field test, and implement a culturally responsive mathematics assessment to identify mathematically talented high school students from underrepresented and low-income backgrounds for participation in a special STEM internship program	High Schoolers (N = 57)	US	Open-Ended Problem-Solving Tasks with Multiple Solutions
Balka (1974)	To explore the nature of creative ability in mathematics	Sixth to Eighth Graders (N = 500)	US	Open-Ended Problem-Solving Tasks with Multiple Solutions
Bal-Sezerel and Sak (2022)	To present the development of a mathematical creativity test and exploration of its psychometric properties	Fifth to Eighth Graders (N = 1129)	Türkiye	Open-Ended Problem-Solving Tasks with Multiple Solutions, Problem-Posing Tasks or Situations
Barraza-García et al. (2020)	To propose and apply a theoretical model, called the Praxeological Model of Mathematical Talent (PMMT), to analyze and promote the development of mathematical talent through mathematical creativity in school-aged students	Fifth and Sixth Graders (10- to 12-year-old) (N = 26)	México	Open-Ended Problem-Solving Tasks with Multiple Solutions
Bicer et al. (2020)	To reveal both the effects of problem-posing interventions on the mathematical creative ability of students and how students’ creative self-efficacy in mathematics was related to their mathematical creative ability	Third to Fifth Graders (N = 205): 89 third graders, 62 fourth graders, and 54 fifth graders	US	Problem-Posing Tasks or Situations
Bicer and Bicer (2023)	To investigate four young elementary school students’ creative processes through eye-tracking (ET) and stimulated recall interview (SRI) techniques while they engaged in multiple representations (MRs) of mathematical problems	First to fifth grader (N = 4)	US	Open-Ended Problem-Solving Tasks with Multiple Solutions
Bishara (2016)	To investigate the ability of students to tackle the solving of unique mathematical problems in the domain of numerical series, verbal and formal, and its influence on the motivation of junior high students with learning dis- abilities in the Arab sector	Seventh grade junior high schoolers (N = 50)	Israel	Open-Ended Problem-Solving Tasks with Multiple Solutions
Coxbill et al. (2013)	To examine student groups’ written mathematical models to open-ended problems presented during three MEAs in alternating weeks	Third and Sixth Graders (N = 39): 24 third graders and 15 sixth graders	US	Open-Ended Problem-Solving Tasks with Multiple Solutions
El-Sahili et al. (2015)	To design problems that express unexpected links in mathematics and suit students of intermediate and secondary levels	Seventh graders (N = 16)	Lebanon	Open-Ended Problem-Solving Tasks with Multiple Solutions, Observational and Interview-Based Task
Fatah et al. (2016)	To examine the use of open-ended approach in cultivating students’ mathematical creativity and self-esteem in mathematics of senior high school students	Eleventh Graders (N = Not specified)	Indonesia	Open-Ended Problem-Solving Tasks with Multiple Solutions
Fortes and Andrade (2019)	To explore the students’ mathematical creativity in terms of fluency, flexibility, and originality in solving six non-routine problems	Tenth Graders (N = 30)	Philippines	Open-Ended Problem-Solving Tasks with Multiple Solutions
García-García et al. (2024)	To validate the positive effects of musical training on mathematical performance and explore the role of mathematical creativity in this relationship, addressing a research gap	Third Graders (14-to 15-year-old) (N = 220)	Canada	Open-Ended Problem-Solving Tasks with Multiple Solutions
Haavold (2013)	To examine the mathematical reasoning of high-achieving students when faced with an unfamiliar trigonometric equation	Eighth and Eleventh Graders (N = 308).	Norway	Open-Ended Problem-Solving Tasks with Multiple Solutions, Problem-Posing Tasks or Situations
Haavold (2016)	To empirically investigate the characteristics of mathematical creativity	13- and 14-year-old (N = 184)	Norway	Open-Ended Problem-Solving Tasks with Multiple Solutions, Problem-Posing Tasks or Situations, Self-Report or Questionnaire/Inventory
Haavold (2018)	To investigate the relationship between age, knowledge, and creativity in mathematics, specifically examining which grade level, when controlled for mathematical achievement, influences mathematical creativity, and what characterizes the relationship between grade level, mathematical achievement, and mathematical creativity	Eighth and Eleventh Graders (13- and 14-year-old) (N = 301): 184 eighth graders and 117 eleventh graders	Norway	Open-Ended Problem-Solving Tasks with Multiple Solutions, Problem-Posing Tasks or Situations
Hall (2009)	To determine if there are creative differences by gender and grade level in the solving of non-routine mathematical problems and to investigate the relationship between students’ level of creativity and the various solution methods utilized when solving non-routine math problems	Sixth and Seventh Graders (N = 170).	US	Open-Ended Problem-Solving Tasks with Multiple Solutions
Haylock (1997)	To identify the kinds of responses in school mathematics that might justifiably be identified as “creative”	11- and 12-year-old (N = Not specified).	England	Open-Ended Problem-Solving Tasks with Multiple Solutions, Problem-Posing Tasks or Situations
Hu and Wang (2024)	To investigate the impact of unplugged activities on students’ mathematical creativity and computational thinking	Third-grader (8-and 9-year-old) (N = 97)	China	Open-Ended Problem-Solving Tasks with Multiple Solutions and Problem-Posing Tasks or Situation
Huang et al. (2017)	To explore the relationship among domain-general divergent thinking ability, domain-specific scientific creativity, and mathematical creativity	Sixth Graders (11- to 14-year-old) (N = 187)	Taiwan	Open-Ended Problem-Solving Tasks with Multiple Solutions
Jensen (1973)	To investigate the relationships among creativity in mathematics, numerical aptitude, and mathematical achievement	Sixth Graders (N = 232)	US	Problem-Posing Tasks or Situations
Junaedi et al. (2021)	To describe the mathematical creative thinking level on polyhedron problems	Eighth Graders (N = 35)	Indonesia	Open-Ended Problem-Solving Tasks with Multiple Solutions
Kattou et al. (2013)	To investigate whether there is a relationship between mathematical ability and mathematical creativity, and to examine the structure of this relationship	Fourth to Sixth Graders (9- to 12-year-old) (N = 359): 143 fourth graders, 118 fifth graders, and 98 sixth graders	Cyprus	Open-Ended Problem-Solving Tasks with Multiple Solutions
Kirisci et al. (2020)	To explore, in a Solomon Four-Group research design, the effectiveness of the Selective Problem-Solving Model (SPS) on students’ analogical problem construction and selective thinking as major components of creative thinking in mathematics	Seventh Graders (N = 201)	Türkiye	Open-Ended Problem-Solving Tasks with Multiple Solutions
Kontoyianni et al. (2013)	To propose an equitable identification process accompanied by a new identification instrument aiming to recognize mathematical giftedness in students	Fourth to Sixth Graders (10- to 12-year-old) (N = 359): 143 fourth graders, 118 fifth graders, and 98 sixth graders	Cyprus	Open-Ended Problem-Solving Tasks with Multiple Solutions
Kulsum et al. (2019)	To find students’ mathematical creative thinking skills in solving mathematical problems by using several indicators	Tenth Graders (N = 22)	Indonesia	Open-Ended Problem-Solving Tasks with Multiple Solutions
R. Leikin (2013)	To develop and refine a multidimensional model for assessing mathematical creativity using Multiple Solution Tasks (MSTs)	Tenth and Eleventh Graders (N = 191): 4 groups: Gifted (G), Non-Gifted (NG), Excelling in Math (EM), and Not Excelling in Math (NEM) students	Israel	Open-Ended Problem-Solving Tasks with Multiple Solutions
R. Leikin and Kloss (2011)	To investigate and compare the mathematical creativity of students by evaluating their performance on Multiple Solution Tasks (MSTs), focusing on three creativity components: fluency, flexibility, and originality	Eighth and Tenth Graders (N = 258): 108 tenth graders and 158 eighth graders	Israel	Open-Ended Problem-Solving Tasks with Multiple Solutions
R. Leikin and Lev (2013)	To examine relationships between mathematical creativity, general giftedness, and mathematical excellence, and to explore the power of different types of mathematical tasks for the identification of between-group differences related to mathematical creativity as reflected in multiple solutions produced by the students	Eleventh and Twelfth Graders (N = 51): Students a) gifted students (G) who excel in mathematics. (b) The HL group consists of students who learn math at a high level of mathematical instruction. (c) The RL group consists of students who learn math at an RL of mathematical instruction	Israel	Open-Ended Problem-Solving Tasks with Multiple Solutions
M. Leikin and Tovli (2019)	To examine the relationship between developmental language deficit and children’s creative ability	Monolingual Preschoolers (3- to 5-year-old) (N = 45): 16 with formally diagnosed SLI and with developmental language disorders (5.98-year-old), 15 (5.73-year-old), and 14 from a younger kindergarten group (3.78-year-old) of children	Israel	Open-Ended Problem-Solving Tasks with Multiple Solutions
Leu and Chiu (2015)	To identify key creative behaviors in mathematics learning based on the perspective of multiplicity in creativity and drawing on the characteristics of creative mathematicians	Fourth Graders (N = 372)	Taiwan	Open-Ended Problem-Solving Tasks with Multiple Solutions, Problem-Posing Tasks or Situations, Self-Report or Questionnaire/Inventory
Lev (2013)	To examine relationships between mathematical creativity, general giftedness (G factor), and excellence in school mathematics (EM factor)	Tenth and Eleventh Graders (16- to 18-year-old) (N = 184): 38 students identified as being generally gifted and excelling in mathematics, 38 students identified as being generally gifted but not excelling in mathematics, 51 students excelling in mathematics who are not identified as being generally gifted, 57 students who are neither identified as being generally gifted nor excelling in mathematics, Super Mathematically Gifted) group: Additionally, 7 students who satisfied all criteria for the G-EM group and were characterized by mathematics professors as being students with extraordinary mathematical abilities	Israel	Open-Ended Problem-Solving Tasks with Multiple Solutions
Levav-Waynberg and Leikin (2012)	To explore the effectiveness of MSTs as a tool for the development of students’ mathematical knowledge and creativity associated with attending MSTs in geometry	Tenth Graders (N = 303): 209 students studied mathematics at a high level (HL), and 94 students at the regular level (RL)	Israel	Open-Ended Problem-Solving Tasks with Multiple Solutions
Levenson (2011)	To explore both the process involved in collective mathematical creativity as well as the product of collective mathematical creativity	Fifth and Sixth Graders (N = 88)	Israel	Open-Ended Problem-Solving Tasks with Multiple Solutions, Observational and Interview-Based Task
Livne and Milgram (2000)	To describe a three-stage technique for assessing creative ability in mathematics utilizing out-of-school activities	Eleventh and Twelfth Graders (N = 139)	Israel	Self-Report or Questionnaire/Inventory
Livne and Milgram (2006)	To examine the research question of whether the 4 by 4 model is the best model to support the postulation of general and domain-specific abilities in mathematics, each at four levels in mathematics	Tenth and Eleventh Graders (Average: 16-year-old) (N = 1090)	Israel	Open-Ended Problem-Solving Tasks with Multiple Solutions
Mann (2005)	To explore the relationship between mathematical creativity and mathematical achievement, attitude towards mathematics, self-perception of creative ability, gender and teacher perception of mathematical talent and creative ability.	Seventh Graders (N = 89)	US	Open-Ended Problem-Solving Tasks with Multiple Solutions
Mann (2009)	To explore simpler methods for identifying creative potential in middle school students and examine the relationship between creativity and variables like achievement, attitude, and self-perception	Seventh Graders (N = 89)	US	Open-Ended Problem-Solving Tasks with Multiple Solutions
Munahefi et al. (2022)	To determine the effect of SRL on mathematical creative thinking skill and analyze in detail the components of SRL at each level of creative mathematical thinking	Eleventh Graders (N = 36)	Indonesia	Open-Ended Problem-Solving Tasks with Multiple Solutions
Muzaini et al. (2023)	To explore the relationship between students’ mathematical creativity and figure apprehension when solving geometric problems with additional auxiliary elements, such as straight and curved lines	Twelfth Graders (14- and 15-year-old) (N = 38)	Indonesia	Open-Ended Problem-Solving Tasks with Multiple Solutions
Pelczer and Rodríguez (2011)	To focus on the relation between problem posing and mathematical creativity; in particular, on the issue of defining criteria for creativity assessment through problem posing tasks in classroom settings	High Schoolers (16-and 17-year-old) (N = 44)	México	Problem-Posing Tasks or Situations, Self-Report or Questionnaire/Inventory
Pham (2014)	To investigate the predictive relationship of the creative problem-solving attributes and math creativity of students	Sixth Graders (12-and 13-year-old) N = 560)	Vietnam	Open-Ended Problem-Solving Tasks with Multiple Solutions, Problem-Posing Tasks or Situations, Self-Report or Questionnaire/Inventory
Pitta-Pantazi et al. (2011)	To examine the structure and relationships among the components of mathematical giftedness and to identify groups of students that differ across these components	Fourth to Sixth Graders (N = 239): 108 fourth graders, 64 fifth graders, and 67 sixth graders	Cyprus	Open-Ended Problem-Solving Tasks with Multiple Solutions
Rahyuningsih et al. (2022)	To investigate the extent to which self-efficacy affects students’ mathematical creative thinking ability and to determine the characteristics of students with high mathematical creative thinking ability and high self-efficacy	14-year-old (N = 96)	Indonesia	Open-Ended Problem-Solving Tasks with Multiple Solutions
Riling (2021)	To examine the nature of student mathematical creativity and identify how it can be influenced by social and aesthetic factors	High Schoolers (N = 211)	US	Observational and Interview-Based Task
Sadak et al. (2022)	To examine constructs of creative ability in mathematical problem posing (CAMPP) and creative ability in mathematical problem solving (CAMPS)	Sixth Graders (12-and 13-year-old) (N = 187)	Türkiye	Open-Ended Problem-Solving Tasks with Multiple Solutions, Problem-Posing Tasks or Situations
Sahliawati and Nurlaelah (2020)	To determine the mathematical creative thinking ability of junior high school students in solving the problem of the plane figure	Seventh Graders (12-and 13-year-old) (N = 28)	Indonesia	Open-Ended Problem-Solving Tasks with Multiple Solutions
Schoevers et al. (2018)	To investigate the relations between domain-general creativity (GC), domain-specific mathematical creativity (MC), and mathematical ability (MA) in a new and integrated way	Fourth Graders (Average: 9-year-old) (N = 342)	Netherlands	Open-Ended Problem-Solving Tasks with Multiple Solutions
Schoevers et al. (2019)	To gain an in-depth understanding of promoting mathematical creativity in educational practice	Fourth Graders (9-and 10-year-old) (N = 22)	Netherlands	Observational and Interview-Based Task
Schrauth (2014)	To help fill gaps in the research on mathematical creativity in the classroom and to provide insightful descriptions of how teachers foster mathematical creativity that teachers and administrators find relatable and useful	Seventh Graders (N = 5)	US	Observational and Interview-Based Task
Sengil-Akar and Yetkin-Ozdemir (2022)	To examine the collective mathematical creativity of gifted middle school students within a group through model- eliciting activities	Seventh and Eighth graders (N = 4)	Türkiye	Open-Ended Problem-Solving Tasks with Multiple Solutions, Observational and Interview-Based Task
Shaw et al. (2022)	To investigate whether a brief incubation break during a mathematical strategy generation task could improve elementary students’ ability to generate strategies and think more creatively	First to fifth graders (N = 211): including 53 first graders, 55 s graders, 25 third graders, 37 fourth graders, and 41 fifth graders	US	Problem-Posing Tasks or Situations
Sholihah et al. (2020)	To test the effectiveness of Creative Problem Solving (CPS) research and to analyze mathematical creative thinking skills based on gender	Seventh Graders (N = 6)	Indonesia	Open-Ended Problem-Solving Tasks with Multiple Solutions
Singer (2012)	This essay draws on the conclusions obtained by a few studies that dealt with students of various ages who won mathematical contests	Fourth to Sixth Graders (11- and 13-year-old) (N = 17)	Romania	Problem-Posing Tasks or Situations
Stolte et al. (2019)	To test the hypothesis that inhibition moderates the relationship between mathematical ability and mathematical creativity in primary school children	Third to fifth Graders (N = 80 to 82): 80 for fluency, 82 for flexibility, and 81 for originality	Netherlands	Open-Ended Problem-Solving Tasks with Multiple Solutions
Stolte et al. (2020)	To investigate the role of executive functions in mathematical creativity	8- to 13-year-old (N = 278)	Netherlands	Open-Ended Problem-Solving Tasks with Multiple Solutions
Suherman and Vidákovich (2024a)	To investigate the relationship between attitude, ethnicity, and mathematical creative thinking among secondary school students	Seventh to Ninth graders (Average: 13-year-old) (N = 896)	Indonesia	Open-Ended Problem-Solving Tasks with Multiple Solutions
Suherman and Vidákovich (2024b)	To examine the predictors of MCT by specifically focusing on the roles of perceived creativity (PC), creative self-efficacy (CS), and computational thinking (CT)	Secondary School (Average: 13-year-old) (N = 896)	Indonesia	Open-Ended Problem-Solving Tasks with Multiple Solutions
Suherman and Vidákovich (2025)	To explore the indirect effect of creative self-efficacy and attitude toward mathematics in the promotion of creative mathematical thinking and as a mediator of creative style and environmental literacy	11- to 15-year-old (N = 896)	Indonesia	Open-Ended Problem-Solving Tasks with Multiple Solutions
Tabach and Friedlander (2013)	To evaluate students’ creativity, as expressed in the solution methods of three problems for groups of students in different grades	Fourth to ninth graders (N = 76)	Israel	Open-Ended Problem-Solving Tasks with Multiple Solutions
S. Tan (2015)	To revise and revalidate the scoring procedure of the DISCOVER Mathematics Assessment	First to Fifth Graders (N = 233): 57 first graders, 48 s graders, 37 third graders, 49 fourth graders, and 42 fifth graders	Australia	Open-Ended Problem-Solving Tasks with Multiple Solutions
M. Tan et al. (2013)	To present an assessment developed for creativity that provides a score for mathematical creativity (MaC) in addition to a score for general creativity in the numeric domain, or what we might call numerical creativity (NuC)	Fourth to Sixth Graders (Average: 10-year-old) (N = 205): 22.3% fourth graders, 43.2% fifth graders, and 34.5% sixth graders	England	Open-Ended Problem-Solving Tasks with Multiple Solutions
Teseo (2019)	To investigate the relationships among attributes of creative problem-solving ability to find out the contribution patterns of these attributes to mathematics creative problem-solving of 6th-grade students on Long Island, New York	Sixth Graders (N = 632)	US	Open-Ended Problem-Solving Tasks with Multiple Solutions, Self-Report or Questionnaire/Inventory
Tubb et al. (2020)	To focus on mathematical creativity in children across grades six-12 at a large Australian school	Eighth to Twelfth Graders (13- to 17-year-old) (N = 896): 82 eighth graders, 235 ninth graders, 191 tenth graders, 189 eleventh graders, and 199 twelfth graders	Australia	Open-Ended Problem-Solving Tasks with Multiple Solutions
Tyagi (2016)	To explore if mathematical creativity and mathematical aptitude are causally related, and if so, what the direction of causation is	13-year-old (N = 480)	India	Open-Ended Problem-Solving Tasks with Multiple Solutions
Van Harpen and Sriraman (2013)	To investigate mathematically advanced high school students’ abilities in posing mathematical problems	Eleventh and Twelfth Graders (16- and 19-year-old) (N = 123): 55 Jiaozhou, 44 Shanghai, and 30 U.S. students	Jiaozhou, Shanghai, and US	Problem-Posing Tasks or Situations
Wang et al. (2025)	To explore the influence of Chinese primary school students’ flow experience in mathematics class on their mathematical creativity	Sixth Graders (N = 273)	China	Open-Ended Problem-Solving Tasks with Multiple Solutions
Wardani et al. (2011)	To analyze in depth the roles of inquiry approach, school level, and students’ previous mathematics ability on the quality of students’ mathematical creative and disposition, and to analyze teachers’ opinions on the inquiry approach	Tenth Graders (N = 240)	Indonesia	Open-Ended Problem-Solving Tasks with Multiple Solutions
Yang et al. (2025)	To focus on the dynamic nature of students’ ability development and employed a longitudinal effectiveness diagnostic research approach to measure the impact of PBDL on vocational high school students’ mathematics proficiency and creative problem-solving using time-series data	16- to 18-year-old (N = 37)	China	Self-Report or Questionnaire/Inventory
Yaniawati et al. (2020)	To introduce the utilization of e-learning for mathematics on Resource-Based Learning (RBL) with a scientific approach to increase mathematical creative thinking ability and to develop students’ self-confidence	Seventh graders N = 40)	Indonesia	Open-Ended Problem-Solving Tasks with Multiple Solutions
Yuan (2009)	To compare students’ creativity and mathematical problem-posing abilities in China and the United States	Eleventh and Twelfth Graders (16- and 19-year-old) (N = 123): 55 Jiaozhou, 44 Shanghai, and 30 U.S. students	Jiaozhou, Shanghai, and US	Problem-Posing Tasks or Situations
Yuliardi et al. (2024)	To develop a STEM-based DLS platform that is valid, practical, and effective in enhancing students’ mathematical creativity	Junior High Schoolers (N = 190)	Indonesia	Open-Ended Problem-Solving Tasks with Multiple Solutions
Zainudin et al. (2019)	To prove empirically whether or not all items in each dimension measure constructs, where all items in each dimension match one-factor model, and whether all items in each dimension have a significant effect.	Junior high schoolers (12- to 15-year-old) (N = 313)	Indonesia	Open-Ended Problem-Solving Tasks with Multiple Solutions

Table 2. Overview of Mathematical Creativity Assessments Used in the Studies.

Assessments	Studies Using the Assessment	Target Group	Scoring Types	Components Scored in Assessments	Format
A Creativity Assessment Tool (CAT) (was adapted from the assessment tool for creativity developed by Lucas et al. (2012))	Ariba (2019)	First Grade	No formal scoring	Socio-Emotional and Attitudinal Components	Paper-based
A Mathematical Creativity Scale (MCS) (developed by Akgul and Kahveci (2016))	Akgul and Kahveci (2016)	Fifth to Eighth Graders (10- to 15-year-old) (N = 297)	Criterion & Norm-referenced	Divergent thinking Components	Paper-based
A Mathematical Creativity Instrument (developed by Zainudin et al. (2019))	Zainudin et al. (2019)	(12- to 15-year-old)	Criterion & Norm-referenced	Divergent thinking Components	Paper-based
Analogical Problem Construction Test (APCT) (developed by Kirisci et al. (2020))	Kirisci et al. (2020)	Seventh Grade	Criterion-referenced	Problem-Solving and Thinking Processes Components	Paper-based
A test of Mathematical Creativity (developed by Tubb et al. (2020))	Tubb et al. (2020)	13- to 17-year-old	No formal scoring	Divergent thinking Components	Paper-based
Cartoon Numbers (CN), one of the subtests of the Aurora Battery (developed by Chart et al. (2008))	M. Tan et al. (2013)	10-year-old	Criterion & Norm-referenced	Divergent thinking Components	Paper-based
Creative Ability in the Mathematical Problem-Posing (CAMPP) Test (developed by Sadak et al. (2022) and translated into Turkish)	Sadak et al. (2022)	12- and 13-year-old	Criterion & Norm-referenced	Divergent thinking Components	Paper-based
Creative Ability in the Mathematical Problem-Solving (CAMPS) Test (developed by Sadak et al. (2022) and translated into Turkish)	Sadak et al. (2022)	12- and 13-year-old	Criterion & Norm-referenced	Divergent thinking Components	Paper-based
Discovering Intellectual Strengths and Capabilities while Observing Varied Ethnic Responses (DISCOVER) (developed by Bahar and Maker (2011))	Bahar and Maker (2011, 2020), S. Tan (2015)	First to Fifth Grade, and high school senior	Criterion & Norm-referenced	Divergent thinking Components	Paper-based
Geometrical Figure Apprehension Creative Test (GFACT) (developed by Muzaini et al. (2023))	Muzaini et al. (2023)	14- and 15-year-old	Criterion-referenced	Divergent thinking Components	Paper-based
Mathematics Creative Thinking Ability Scale (developed by Rahyuningsih et al. (2022))	Rahyuningsih et al. (2022)	14-year-old	Criterion-referenced	Divergent thinking Components	Paper-based?
Mathematics Creative Problem-Solving Ability Test (MCPSAT) (developed by Kim et al. (2003) and translated into English and Vietnamese)	Pham (2014) and Teseo (2019)	12- and 13-year-old and Sixth Grade	Criterion & Norm-referenced	Divergent thinking Components	Paper-based
Mathematical Creativity Test (MCT) (developed by Bal-Sezerel and Sak (2022))	Bal-Sezerel and Sak (2022)	Fifth to Eighth Grade	Criterion & Norm-referenced	Divergent thinking Components	Paper-based
Multiple-Solution Task (MST) (developed by R. Leikin (2009))	R. Leikin (2013), R. Leikin and Kloss (2011), R. Leikin and Lev (2013), Lev (2013), and Levav-Waynberg and Leikin (2012), Tabach and Friedlander (2013)	Fourth to ninth, Tenth to Twelfth Grade, and 16- to 18-year-old	Criterion & Norm-referenced	Divergent thinking Components	Paper-based
Observational and Interview-Based tasks developed by the researchers	El-Sahili et al. (2015), Levenson (2011), Riling (2021), Schoevers et al. (2019), Schrauth (2014), and Sengil-Akar and Yetkin-Ozdemir (2022)	Fifth to Eighth Grade and High School, and 9- and 10-year-old	Criterion-referenced & Norm-referenced and No Formal Scoring	Divergent thinking Components, Problem-Solving and Thinking Processes Components, Socio-Emotional and Attitudinal Components	Paper-based
Open-ended Multiple-solution tasks developed by the researchers	Aljarrah (2020), Assmus and Fritzlar (2022), Azaryahu et al. (2025), Barraza-García et al. (2020), Bicer and Bicer (2023), Bishara (2016), Coxbill et al. (2013), El-Sahili et al. (2015), Fatah et al. (2016), Fortes and Andrade (2019), Hall (2009), Haylock (1997), Hu and Wang (2024), Junaedi et al. (2021), Kattou et al. (2013), Kulsum et al. (2019), Kontoyianni et al. (2013), M. Leikin and Tovli (2019), Levenson (2011), Leu and Chiu (2015), Livne and Milgram (2006), Munahefi et al. (2022), Pitta-Pantazi et al. (2011), Sahliawati and Nurlaelah (2020), Sengil-Akar and Yetkin-Ozdemir (2022), Sholihah et al. (2020), Tyagi (2016), Wardani et al. (2011), Yaniawati et al. (2020), and Yuliardi et al. (2024)	1- to 5-year-old, fourth to eighth grade, tenth, eleventh grade, 8- to 16-year-old, and Junior High School	Criterion & Norm-referenced, No formal scoring, and Unclassified Approach	Divergent thinking Components, Problem-Solving and Thinking Processes Components, Socio-Emotional and Attitudinal Components	Paper-based and online
Problem-Posing Tasks/Activities developed by the researchers	Ayvaz and Durmuş (2021), Bicer et al. (2020), Hu and Wang (2024), Jensen (1973), Leu and Chiu (2015), Pelczer and Rodríguez (2011), Shaw et al. (2022), Singer (2012), and Yuan (2009)	First to seventh grade, 11- to 13-year-old, and 16- to 19-year-old	Criterion- & Norm-referenced and No formal scoring	Divergent thinking Components	Paper-based
Self-report or Questionnaire/Inventory generated by researchers	Haavold (2016), Leu and Chiu (2015), Livne and Milgram (2000), and Pelczer and Rodríguez (2011), and Yang et al. (2025)	13- and 14-year-old, fourth grade, eleventh and twelfth grade and 16- and 17-year-old	Criterion & Norm-referenced and No formal scoring	Divergent thinking Components, Problem-Solving and Thinking Processes Components, Socio-Emotional and Attitudinal Components	Paper-based
Test of Creative Problem-Solving Skills in Math (developed by Al-Mayahi and Hassan (2022))	Al-Mayahi and Hassan (2022)	Fourth grade high schoolers	Criterion-referenced	Problem-Solving and Thinking Processes Components	Paper-based
The Creative Ability in Mathematics Test (CAMT) (developed by Balka (1974))	Balka (1974), Haavold (2013, 2016, 2018), and Mann (2005, 2009)	Sixth to Eighth Grade, Eleventh Grade, and 13- and 14-year-old	Criterion & Norm-referenced	Divergent thinking Components	Paper-based
The Creative Problem-Solving Attributes Inventory (CPSAI) (developed by Lin and Cho (2011) and translated into English and Vietnamese)	Pham (2014), and Teseo (2019)	Sixth grade and 12- and 13-year-old	Criterion & Norm-referenced	Divergent thinking Components	Paper-based
The Divergent Production (DP) subtest (developed by Haylock (1987, 1997) and translated into Taiwanese)	Huang et al. (2017)	11- to 14-year-old	Criterion & Norm-referenced	Divergent thinking Components	Paper-based
The Mathematical Creative Thinking based Ethnomathematics Test (MCTTBE) (developed by Suherman and Vidákovich (2022))	Suherman and Vidákovich (2024a)	Average 13-year-old	Criterion & Norm-referenced	Divergent thinking Components	Online
The Mathematical Creative Thinking based Ethnomathematics Test (MCTTBE) (developed by Suherman and Vidákovich (2024a))	Suherman and Vidákovich (2024b, 2025)	11- to 15-year-old	Criterion & Norm-referenced	Divergent thinking Components	Online
The Mathematical Creative Scale (developed by Wei (2023) for Chinese students)	Wang et al. (2025)	Sixth Graders	Criterion & Norm-referenced	Divergent thinking Components	Paper-based
The Mathematical Creativity Test (MCT) (developed by Kattou et al. (2013) and translated into Dutch)	Schoevers et al. (2018)	9-year-old	No formal scoring	Divergent thinking Components	Paper-based
The Mathematical Creativity Test (MCT) (developed by Kattou et al. (2013) and translated by Schoevers et al. (2018) into Dutch)	Stolte et al. (2019)	Third to Fifth Grade	Criterion & Norm-referenced	Divergent thinking Components	Paper-based
The Mathematical Creativity Test (MCT) (developed by Kattou et al. (2013) and translated by Stolte et al. (2020) into Dutch)	Stolte et al. (2020)	8- to 13-year-old	Criterion & Norm-referenced	Divergent thinking Components	Paper-based
The Test for Mathematical Creative Problem-Solving Ability (created by Lee et al. (2003) and adapted by García-García et al. (2024) into Spanish)	García-García et al. (2024)	14- to 15-year-old	Criterion & Norm-referenced	Divergent thinking Components	Paper-based

3. Findings

3.1. Definition of Mathematical Creativity

This section addressed RQ1 by synthesizing the author-provided textual definitions of mathematical creativity (i.e., how each study states what MC means). For RQ1 (How is mathematical creativity defined?), we categorized the definitions of mathematical creativity that were adhered to over the studies we reviewed under three themes: divergent thinking-oriented definitions, problem-solving and problem-posing-oriented definitions, and affective-motivational emphasis. A quick note for the readers is that some studies appeared in more than one category. This overlap occurs because certain definitions and frameworks of mathematical creativity align with multiple conceptual perspectives, which leads to their inclusion in more than one thematic group.

3.1.1. Divergent Thinking-Oriented Definitions (n = 61)

Many studies adopted a divergent-thinking lens to conceptualize mathematical creativity and operationalized it using fluency (number of ideas), flexibility (variety of approaches), originality (novelty), and elaboration (detail and refinement). Authors typically referenced classical frameworks (e.g., Guilford, 1965; Torrance, 1974). Fifteen studies (e.g., Haavold, 2016; Huang et al., 2017; Stolte et al., 2019; Tubb et al., 2020) defined mathematical creativity as the ability for divergent production within mathematical situations. Subsequently, studies such as those by Bicer et al. (2020), Kattou et al. (2013), Kontoyianni et al. (2013), R. Leikin and Lev (2013), Pham (2014), Pitta-Pantazi et al. (2011), and Zainudin et al. (2019) focused on fluency, flexibility, and originality as characteristics of mathematical creativity, while Lev (2013) and Tabach and Friedlander (2013) specifically focused on originality in their definition of mathematical creativity. Junaedi et al. (2021), Levav-Waynberg and Leikin (2012), Sahliawati and Nurlaelah (2020), Yaniawati et al. (2020), and Wang et al. (2025) emphasized one more element: elaboration in addition to fluency, flexibility, and originality.

While many studies explicitly define mathematical creativity through the traditional dimensions of divergent thinking, such as fluency, flexibility, and originality, 24 studies implicitly reflected similar constructs, particularly originality and novelty, but without always using the established terminology. These definitions often describe mathematical creativity as the ability to generate novel, insightful, or unusual ideas. This approach mainly comes from Sriraman’s (2005) widely adopted definition that emphasizes “novel and/or insightful solutions” and/or “view problems from new perspectives”. Many researchers (Aljarrah, 2020; Al-Mayahi & Hassan, 2022; Bahar & Maker, 2020; Bal-Sezerel & Sak, 2022; Barraza-García et al., 2020; El-Sahili et al., 2015; Fatah et al., 2016; García-García et al., 2024; Haavold, 2013, 2018; Hall, 2009; Muzaini et al., 2023; Pelczer & Rodríguez, 2011; Rahyuningsih et al., 2022; Schoevers et al., 2018; Schrauth, 2014; Shaw et al., 2022; Suherman & Vidákovich, 2024a, 2024b, 2025; S. Tan, 2015; Teseo, 2019; Yang et al., 2025; Yuan, 2009) followed this definition. Munahefi et al. (2022), by adopting Chamberlin and Moon’s (2005) definition, Balka (1974), Coxbill et al. (2013), and Mann (2005, 2009) also underscored the ability to generate unusual mathematical ideas. Sadak et al. (2022) and Hu and Wang (2024) also added that creative ability in mathematics is to generate novel mathematical ideas, but they do not have to be new to others. It should be new to that person (Bicer, 2021; Bicer & Bicer, 2023).

3.1.2. Problem-Solving and Problem-Posing-Oriented Definitions (n = 37)

While there is some conceptual overlap with the previous category due to shared elements such as originality and novelty, the studies in this category framed mathematical creativity specifically within problem-solving and problem-posing contexts. Unlike the divergent thinking perspective, which emphasizes idea generation as a cognitive process, this category situated creativity in the mathematical practices of formulating, interpreting, and solving problems directly.

A significant group of studies defined mathematical creativity explicitly within the context of problem-solving and problem-posing. This perspective emphasizes the dynamic process through which individuals engage with mathematical situations by generating, reformulating, or solving problems. Drawing from Krutetskii (1976), Haylock (1997), and Yuan (2009) characterized mathematical creativity as a problem-solving ability marked by problem formulation and inventiveness. Similarly, Ayvaz and Durmuş (2021), R. Leikin and Kloss (2011), and Van Harpen and Sriraman (2013) highlighted problem-solving and problem-posing as central components of mathematical creativity in school settings.

Several studies expanded on this foundation by stressing the importance of solution generation flexibility and logical results within problem contexts. Assmus and Fritzlar (2022), Azaryahu et al. (2025), Bahar and Maker (2011), Jensen (1973), Kirisci et al. (2020), Mann (2005, 2009), Schoevers et al. (2019), Sengil-Akar and Yetkin-Ozdemir (2022), Stolte et al. (2020), S. Tan (2015), and Yuliardi et al. (2024) defined mathematical creativity as the ability to produce novel and multiple solutions and apply mathematical principles in multiple ways to reach valid conclusions. M. Leikin and Tovli (2019) added two more characteristics: reasoning and working memory in the problem-solving process. R. Leikin (2013), Livne and Milgram (2006), and Wardani et al. (2011) characterized mathematical creativity as the intersection of creative thinking with the logical-deductive nature of mathematics, which echoed Silver’s (1997) emphasis on developing mathematical thinking through problem-solving. In a similar vein, Akgul and Kahveci (2016), Huang et al. (2017), Riling (2021), and Tyagi (2016) described mathematical creativity as the ability to apply mathematical knowledge in diverse and original ways, often through generation, testing, and refinement of hypotheses.

Problem-posing also played an important role in the studies. Sriraman’s (2005) widely cited definition emphasized not only the formulation of novel or insightful solutions but also the capacity to reframe problems from new perspectives and to generate new questions. This theme was emphasized in studies by Haavold (2013), Hall (2009), and Pelczer and Rodríguez (2011). This simultaneous emphasis on both problem-solving and posing was reinforced by researchers such as Singer and Voica (2013) and Leu and Chiu (2015). They described mathematical creativity as a continuous cognitive process between problem-posing and solving.

Additionally, studies by Bishara (2016), Fortes and Andrade (2019), Kulsum et al. (2019), Sadak et al. (2022), and M. Tan et al. (2013) positioned solution generation and practical application in the problem-solving process as defining characteristics of mathematical creativity. These definitions often involved the recognition of patterns, flexible use of strategies, and the ability to construct new mathematical knowledge, as seen in Schrauth’s (2014) use of Lithner’s (2008) framework on creative mathematical reasoning and Sengil-Akar and Yetkin-Ozdemir’s (2022) definition. Moreover, Coxbill et al. (2013) and Munahefi et al. (2022) described mathematical creativity as the capacity to produce useful and novel solutions. Taking together, these perspectives conceptualize mathematical creativity not merely as a general cognitive trait but as a situated mathematical competence rooted in the ability to formulate, interpret, and solve mathematical problems in original, diverse, and context-sensitive ways.

3.1.3. Affective–Motivational Emphasis (n = 6)

In the third theme, studies did not solely define mathematical creativity through cognitive traits but instead approached it as an interaction between beliefs, attitudes, self-perceptions, and dispositions that shape learners’ mathematical engagement. For instance, Ariba (2019) and Bicer et al. (2020) conceptualized mathematical creativity by integrating creative self-efficacy, emphasizing students’ confidence and persistence in generating novel mathematical ideas in addition to their divergent thinking ability. Similarly, Levenson (2011), drawing on Silver (1997), framed mathematical creativity as a disposition toward mathematical activity, one that supports original yet personally meaningful contributions within classroom settings.

Sholihah et al. (2020) also underscored the motivational function of mathematical creativity, describing it as a capacity that fuels diverse solutions, grounded in students’ willingness to explore ideas. Extending this view to professional contexts, Livne and Milgram (2000) and Singer (2012) noted that the creativity of expert mathematicians often stems from dispositional factors such as intuition, heuristics, social interaction, and imagination. These components, as also noted by Sriraman (2009), are integral in shaping mathematical insight and innovation. Collectively, these perspectives illustrate that mathematical creativity is rooted in affective and dispositional characteristics that influence how individuals interpret and contribute to mathematical thinking.

3.2. Theoretical Frameworks in the Reviewed Studies

This section addressed RQ2 by mapping the named theories or models that conceptualize mathematical creativity in the included studies (e.g., Guilford’s SOI, Torrance’s divergent thinking). For RQ2 (Which theoretical frameworks are adhered to conceptualize mathematical creativity (MC)?), we categorized the theoretical frameworks that were used to conceptualize MC under three themes: domain-specific, domain-general, and multidimensional frameworks.

3.2.1. Domain-Specific Frameworks (n = 34)

Most studies conceptualized mathematical creativity within the context of mathematical problem-solving and problem-posing, emphasizing students’ ability to approach unfamiliar mathematical situations with originality and flexibility. These frameworks drew on the foundational work of Krutetskii (1976) and Polya (1945). Also, they utilized more recent interpretations generated by Silver (1997) who argued that creativity in mathematics is best revealed when learners engage with non-routine problems, reformulate questions, or explore multiple logically valid solutions. In García-García et al.’s (2024), Pitta-Pantazi et al.’s (2011), and Shaw et al.’s (2022) framing, mathematical creativity is treated as a subcomponent of mathematical competence, specifically, the capacity to produce original and appropriate solutions within mathematical contexts.

Ayvaz and Durmuş (2021), Leu and Chiu (2015), Sadak et al. (2022), Singer (2012), Van Harpen and Sriraman (2013), and Yuan (2009) spotted the importance of problem-posing abilities in the conceptualization of mathematical creativity. In addition to problem-posing, Bal-Sezerel and Sak (2022) added two constructs: making conjectures and proof in framing mathematical creativity. Aljarrah (2020), Barraza-García et al. (2020), Haavold (2013, 2018), Haylock (1997), and El-Sahili et al. (2015), conceptualized mathematical creativity as the ability to overcome cognitive fixations and generate novel approaches to problems. Similarly, Bahar and Maker (2011) and R. Leikin and Kloss (2011) emphasized multiple-solution thinking and model-eliciting activities as tools for surfacing creative problem-solving abilities.

Several studies operationalized creativity through specifically designed open-ended tasks or Multiple Solution Tasks (MSTs) that require learners to generate and evaluate diverse responses (e.g., Assmus & Fritzlar, 2022; Bishara, 2016; Leu & Chiu, 2015; Lev, 2013; Pelczer & Rodríguez, 2011). Coxbill et al. (2013) and Sengil-Akar and Yetkin-Ozdemir (2022) built their frameworks on the interplay between reasoning, pattern recognition, and strategic thinking in problem-solving. Additional studies (e.g., Akgul & Kahveci, 2016; Kirisci et al., 2020; Schoevers et al., 2019; Schrauth, 2014; Stolte et al., 2020; Teseo, 2019) highlighted the dynamic and iterative nature of logical and spatial thinking, mathematical reasoning, often involving hypothesis generation, analogical transfer, or transformation of known strategies. Tyagi (2016) adopted the Theory of Aptitude as the overarching theoretical framework, situating mathematical creativity within the aptitude-creativity relationship. Sholihah et al. (2020) adopted the Creative Problem-Solving (CPS) model as its theoretical framework. The CPS model consists of four main stages: problem clarification, disclosure of opinions, evaluation and selection, and implementation. Through these stages, students are encouraged to actively engage in problem-solving processes, explore multiple solutions, and develop creative thinking skills. Al-Mayahi and Hassan (2022) and Yang et al. (2025) also emphasized a similar process including understanding the problem, idea generation, and planning.

3.2.2. Multidimensional Frameworks (n = 27)

A third group of studies adopts a more integrative approach to conceptualizing mathematical creativity by viewing it as the outcome of a dynamic interaction between cognitive, affective, dispositional, and contextual factors. These frameworks emphasized that creativity in mathematics is not only a function of individual thinking processes but is also shaped by beliefs, motivations, self-perceptions, and social interactions (Bahar & Maker, 2020). For instance, Bicer et al. (2020), Bicer and Bicer (2023), Hu and Wang (2024), Pham (2014), Rahyuningsih et al. (2022); Suherman and Vidákovich (2024a, 2024b, 2025), S. Tan (2015), M. Tan et al. (2013), Yaniawati et al. (2020), and Wang et al. (2025) proposed such a combined framework by incorporating both cognitive outcomes and affective variables such as social interaction, self-awareness, and mathematical creative self-efficacy.

Levenson (2011), by drawing on sociocultural theory and socio-mathematical norms, investigated how classroom discourse and collective meaning-making foster creative mathematical thinking. Likewise, Munahefi et al. (2022) integrated self-regulated learning theory, while Ariba (2019) drew from constructivism and multiple intelligences theory to conceptualize creativity as emerging from personal strengths and active engagement. Fatah et al. (2016) emphasized designing problems that are open in process, product, and development, thereby fostering students’ divergent thinking and creative problem-solving abilities. Several studies adopted multidimensional models of creativity, combining domain-specific and domain-general elements (e.g., Balka, 1974; Mann, 2005, 2009; Muzaini et al., 2023; Tubb et al., 2020). Others, like Hall (2009) and Livne and Milgram (2000, 2006), proposed structured models that categorize mathematical creativity along behavioral and psychological dimensions or as an interaction between individual traits and sociocultural influences.

More recently, Haavold (2016) provided empirical support for such an integrative perspective by validating a five-principal framework originally proposed by Sriraman (2005). This model emphasizes sustained engagement with complex problems (Gestalt), appreciation of mathematical elegance (aesthetic), intellectual risk-taking (free market), tolerance for ambiguity (uncertainty), and independence from authoritative sources such as textbooks and teachers (scholarly). What is more, Riling’s (2021) Creative Mathematical Action Framework and Singer’s (2012) organizational perspective framed mathematical creativity as an emergent and context-sensitive phenomenon that is dependent on students’ dispositions toward inquiry and their willingness to challenge conventions. Collectively, these frameworks reflect a holistic and socially embedded understanding of mathematical creativity. This framework moves beyond cognitive models to consider how learners’ emotional orientations, beliefs, and environments shape their creative engagement with mathematics.

3.2.3. Domain-General Frameworks (n = 25)

The second group investigated mathematical creativity and adopted frameworks rooted in Guilford (1956) and Torrance’s (1974) theories of creativity. These frameworks conceptualized creativity through measurable cognitive components, most specifically fluency (the number of ideas), flexibility (the variety of approaches), originality (the novelty of responses), and elaboration (the level of detail and refinement). Grounded in Guilford’s Structure of Intellect (SOI) model and Torrance’s work on divergent thinking, these studies treated creativity as an individual cognitive capacity that can be quantified and compared across contexts. For example, Aljarrah (2020), Azaryahu et al. (2025), Balka (1974), Haylock (1997), Sengil-Akar and Yetkin-Ozdemir (2022), Tabach and Friedlander (2013), and Yuan (2009) directly followed Guilford’s SOI or Torrance’s structure to frame mathematical creativity. Likewise, more recent works such as Fortes and Andrade (2019), Kattou et al. (2013), Kontoyianni et al. (2013), R. Leikin (2013), M. Leikin and Tovli (2019), R. Leikin and Lev (2013), Levenson (2011), Schoevers et al. (2018), and Zainudin et al. (2019) adapted Torrance’s multiple-factor model specifically to mathematical tasks to assess fluency, flexibility, and originality.

Junaedi et al. (2021), Kulsum et al. (2019), Levav-Waynberg and Leikin (2012), Sahliawati and Nurlaelah (2020), and Wardani et al. (2011) followed this tradition by designing tasks and rubrics explicitly based on these criteria. Additionally, research by Huang et al. (2017), Jensen (1973), Stolte et al. (2019), and Yuliardi et al. (2024) continued to apply these constructs, either through direct testing or conceptual operationalization, to evaluate students’ mathematical creative thinking. Collectively, this stream of studies reflects a tradition in mathematical creativity research that emphasizes divergent thinking as the core construct.

3.3. Assessment of Mathematical Creativity

To answer RQ3 (How is mathematical creativity operationalized and assessed?), we conducted five complementary analyses to synthesize how studies have approached the measurement of mathematical creativity. Specifically, we examined (a) scoring approaches used to evaluate students’ creative responses, (b) the format of assessments to identify whether tasks were delivered in paper-based, online, or alternative modes, (c) the specific components scored to capture different dimensions of creativity, (d) the types of tasks employed to elicit creative thinking in mathematics, and (e) target group context of assessments such as age and grade level.

Here, scoring approaches denote how student work was evaluated (e.g., criterion-referenced, norm-referenced), whereas components scored show what aspects of creativity were judged (e.g., fluency, flexibility, originality, elaboration, socio-emotional factors, or problem-solving processes).

3.3.1. Scoring Approaches in Mathematical Creativity Assessments

Mathematical creativity was evaluated using diverse scoring approaches that reflected different conceptualizations of creativity and varying methodological choices. To synthesize these practices, four main categories were identified: (a) criterion-referenced only, (b) criterion-referenced combined with norm-referenced, (c) norm-referenced only, and (d) no formal scoring framework (qualitative or descriptive). These categories distinguish whether students’ creative performance was judged against predetermined criteria, compared to peers, or evaluated qualitatively without standardized rubrics.

Criterion-referenced Combined with Norm-referenced (n = 48). The majority of studies adopted a hybrid approach, incorporating both criterion-based evaluation and norm-referenced comparisons (see Table 2). This approach applies criterion-based coding (predefined rubrics or task-specific criteria) and then uses norm-referenced scaling to contextualize performance relative to a group. For example, Kattou et al. (2013) considered only correct solutions and defined distinct solution-type families (predetermined criteria for flexibility). They then expressed fluency and flexibility as ratios to the sample maximum and computed originality from within sample frequency.

Criterion-referenced Only (n = 18): The second large subset of studies (see Table 2) employed criterion-referenced scoring in which students’ responses were evaluated against predetermined criteria rather than relative performance to peers. In this group, responses were evaluated against pre-specified descriptors and decision rules that are independent of peer performance. For example, Pelczer and Rodríguez (2011) defined a three-level novelty scheme and rated solutions solely by these descriptors: algebraic novelty (surface changes in expressions while problem structure/type/method remain unchanged), conceptual novelty (a substantial change in the given/requested part or the “form of the question,” with the underlying structure preserved), and methodological novelty (innovation at the level of applicable solution methods). Interpretation relied on these preset categories; no cohort percentiles or norm tables were used.

No Formal Scoring System (n = 14): Third set of studies (e.g., Aljarrah, 2020; Ariba, 2019; Barraza-García et al., 2020) did not apply a standardized scoring rubric (see Table 2). Instead, they used qualitative, descriptive, or holistic evaluations, coding students’ actions, categorizing responses into qualitative levels, or employing binary coding schemes (e.g., “Yes/No” responses). These studies often focused on nature rather than the quantity of creative output. Also, one study (Tubb et al., 2020) employed the Consensual Assessment Technique (Amabile, 1982), in which expert judges rated the overall creativity of students’ mathematical responses on a 1-6 scale. This approach did not rely on predetermined criteria or peer comparisons but instead used expert consensus. Similarly, Bicer and Bicer (2023) did not compute formal creativity scores. They qualitatively analyzed students’ creative processes via eye-tracking and stimulated-recall interviews. Similarly, Bishara (2016) did not use a standardized creativity rubric. Responses were binary-coded (1 = correct, 0 = fail) and summarized as proportion-correct, with analyses based on Cochran’s Q/McNemar and correlations. Likewise, Yang et al. (2025) used a math-adapted creative problem-solving self-report scored dichotomously (0/1) and modeled mastery/non-mastery without a formal mathematical-creativity rubric or component-level (fluency/flexibility/originality/elaboration) scores.

Unclassified Approach (n = 1): In our study, unclassified approach denotes studies that report numerical creativity scores do not yet specify either a norm-referenced or a criterion-referenced interpretive frame (no cut scores/standards or norm tables). It primarily uses scores for within-sample comparisons (e.g., group differences, improvement tests). Only one study, Fatah et al. (2016), reported (see Table 2) a 5-item essay-type MCTA, analyze improvement via t-tests/Mann–Whitney/ANOVA, but provided no rubric levels, performance standards, or norms, hence we classified it as unclassified.

3.3.2. Format of Assessments

The assessment formats identified across the reviewed studies fell into two main categories: paper-based assessments and online assessments which reflected both conventional and new approaches to administering mathematical creativity tasks. In terms of assessment formats, most studies (n = 74) preferred paper-based assessments (see Table 2). Six studies (Kattou et al., 2013; Kontoyianni et al., 2013; Suherman & Vidákovich, 2024a, 2024b, 2025; Yaniawati et al., 2020) used online assessments (see Table 2).

3.3.3. Components Scored in Assessments

To provide a comprehensive synthesis, the components of mathematical creativity scored in the reviewed studies were grouped into three major categories: (a) divergent thinking components, representing the most widely adopted dimensions such as fluency, flexibility, originality, and elaboration; (b) socio-emotional and attitudinal components, encompassing motivational, affective, and interpersonal factors associated with creative engagement; and (c) problem-solving and thinking process components, highlighting the quality and complexity of cognitive processes underlying creative problem-solving.

Divergent Thinking Components (n = 72): The analysis revealed that the components of mathematical creativity scored were predominantly aligned with the classical divergent thinking (see Table 2). Fatah et al. (2016), Livne and Milgram (2000), and Tubb et al. (2020) measured divergent thinking in a general sense. The dimensions of divergent thinking, fluency, flexibility, originality, and elaboration, often come from Torrance’s (1974) framework and were operationalized in various combinations across the studies. 37 studies (Akgul & Kahveci, 2016; Azaryahu et al., 2025; Balka, 1974; Bicer et al., 2020; Bicer & Bicer, 2023; Bishara, 2016; Fortes & Andrade, 2019; García-García et al., 2024; Haavold, 2013, 2016, 2018; Hu & Wang, 2024; Huang et al., 2017; Kattou et al., 2013; Kontoyianni et al., 2013; R. Leikin, 2013; R. Leikin & Kloss, 2011; R. Leikin & Lev, 2013; M. Leikin & Tovli, 2019; Levav-Waynberg & Leikin, 2012; Levenson, 2011; Pitta-Pantazi et al., 2011; Sadak et al., 2022; Schoevers et al., 2018; Stolte et al., 2019, 2020; Mann, 2005, 2009; Pham, 2014; Sengil-Akar & Yetkin-Ozdemir, 2022; Tabach & Friedlander, 2013; Teseo, 2019; Tyagi, 2016; Van Harpen & Sriraman, 2013; Wang et al., 2025; Yuan, 2009; Zainudin et al., 2019) scored fluency, flexibility, and originality.

Thirteen studies (Bahar & Maker, 2011, 2020; Junaedi et al., 2021; Kulsum et al., 2019; Leu & Chiu, 2015; Munahefi et al., 2022; Sahliawati & Nurlaelah, 2020; Sholihah et al., 2020; Suherman & Vidákovich, 2024a, 2024b, 2025; Yaniawati et al., 2020; Wardani et al., 2011) scored the second most common combination of fluency, flexibility, originality, and elaboration.

Researchers scored pairs of components less frequently. For example, Assmus and Fritzlar (2022) measured flexibility and originality while Ayvaz and Durmuş (2021), Bal-Sezerel and Sak (2022), and Jensen (1973) evaluated fluency and flexibility. Other less common combinations also appeared in single studies. Lev (2013) examined correctedness, fluency, flexibility, and originality. Yuliardi et al. (2024) investigated fluency, flexibility, making connections, construction, and originality. M. Tan et al. (2013) assessed appropriateness, fluency, and originality. Haylock (1997) analyzed fluency, flexibility, originality, appropriateness, and overcoming fixation. Shaw et al. (2022) scored fluency and originality.

Some studies examined these elements under revised labels. For example, S. Tan (2015) refined the traditional components of fluency, flexibility, and originality by adding the dimensions of complexity (M. Tan et al., 2013), quantity (Hwang et al., 2007), and quality (Coxbill et al., 2013) to better serve identification and assessment purposes. Livne and Milgram (2006) measured having more than one solution path and/or correct answer, which can be interpreted as fluency. Barraza-García et al. (2020) similarly assessed creativity through four factors: producing unique techniques, optimizing the technique, considering tasks from diverse angles, and adapting a technique. Pelczer and Rodríguez (2011) scored three types of novelty: algebraic, conceptual, and methodological novelty. Along the same lines, Muzaini et al. (2023), Rahyuningsih et al. (2022), and Singer (2012) examined cognitive novelty, cognitive variety, and cognitive framing.

Schoevers et al. (2019) was included under this category because it assessed students’ ability to generate new and original mathematical ideas and to establish connections between multiple concepts, which align with the originality and, to some extent, the flexibility dimensions of divergent thinking. However, it should be noted that fluency and elaboration were not assessed, and the measurement of flexibility was only partial. In this sense, Hall (2009) examined complexity and the number of solution methods in their study. Therefore, these studies represented a limited operationalization of divergent thinking compared to classical frameworks (e.g., Torrance, 1974).

Socio-Emotional and Attitudinal Components (n = 5): Some studies assessed mathematical creativity through socio-emotional and attitudinal dimensions (see Table 2). For instance, El-Sahili et al. (2015) inferred creativity from students’ engagement, reactions, and problem-solving behaviors, focusing on whether they approached problems in nonstandard ways, made insightful or novel connections, and expressed curiosity or surprise when encountering elegant or unexpected solutions. Livne and Milgram (2000) assessed quality of process and product, intrinsic motivation, task commitment, personal initiative, and activity intensity in addition to divergent and convergent thinking. Similarly, Riling (2021) examined four aspects: Context, the mathematical and social setting in which the action occurs; Action, the meaningful mathematical action taken by students; New Possibilities, the emergence of new ways of doing or thinking; and Community, how peers respond to or recognize the new possibilities. Ariba (2019) identified five attributes reflecting creativity: inquisitiveness (wondering, questioning, exploring, investigating, challenging assumptions), persistence (sticking with difficulty, daring to be different, tolerating uncertainty), imagination (playing with possibilities, making connections, using intuition), collaboration (sharing products, giving and receiving feedback, cooperating appropriately), and discipline (developing techniques, reflecting critically, crafting and improving). Likewise, Schrauth (2014) highlighted opportunities for mathematical creativity through making mathematics personally meaningful by creating a safe environment that values students’ voices and effort over perfection and maintaining mathematical practices such as explaining reasoning and applying appropriate terminology.

Problem-Solving and Thinking Processes Components (n = 5): Five studies examined mathematical creativity not through the final product but through the quality of students’ problem-solving and thinking processes (see Table 2). Kirisci et al. (2020) focused on analogical problem-solving, in which students identify, compare, construct, and solve analogical problems, and on selective thinking, which includes selective encoding (filtering out irrelevant information), selective combination (integrating relevant information into a coherent whole), and selective comparison (relating new information to prior knowledge to generate novel solutions). Aljarrah (2020) assessed creativity through summing forces (combining group members’ ideas), expanding possibilities (generating new ideas beyond initial constraints), divergent thinking (seeking unexpected or novel approaches), and assembling things in new ways (reorganizing ideas or representations innovatively). Al-Mayahi and Hassan (2022) assessed the components of understanding the problem, ideation, brainstorming, implementation, and work planning. Sengil-Akar and Yetkin-Ozdemir (2022) scored the ability of making connections in addition to generalizability, usability, and applicability of the solution. Relatedly, Yang et al. (2025) tracked creative problem solving via a math-adapted self-report aligned with four process elements: understanding the challenge, idea generation, preparation for action, and planning approaches.

3.3.4. Types of Tasks Used in Assessments

The tasks identified in the literature were categorized into four main types: (a) open-ended tasks with multiple solutions, (b) problem-posing tasks or situations, and others: (c) self-report or questionnaire-based assessments, and (d) observational and interview-based approaches. Each category reflects a distinct methodological lens for capturing students’ creative potential in mathematics, as described below.

Open-Ended Problem-Solving Tasks with Multiple Solutions (n = 66): 35 studies (e.g., Aljarrah, 2020; Bahar & Maker, 2011, 2020; Balka, 1974) utilized tasks that were both open-ended and allowed for multiple correct solutions (see Table 1). These tasks encouraged students to explore various approaches and generate diverse solution strategies.

In addition, 31 studies (e.g., Assmus & Fritzlar, 2022; Bal-Sezerel & Sak, 2022; El-Sahili et al., 2015; Fatah et al., 2016) employed tasks that did not explicitly use the label of “open-ended multiple-solution tasks,” but nevertheless assessed key elements of divergent mathematical thinking, such as fluency, flexibility, originality, and elaboration. Although these studies varied in terminology and task design, they similarly aimed to capture students’ ability to generate multiple ideas, adopt diverse perspectives, and extend or refine solutions, thereby justifying their inclusion within this category.

Problem-Posing Tasks or Situations (n = 16): These tasks assess students’ ability to create mathematical problems. 14 studies (e.g., Ayvaz & Durmuş, 2021; Bal-Sezerel & Sak, 2022; Bicer et al., 2020; Hu & Wang, 2024) used such tasks (see Table 1).

In addition to performance-based tasks, several studies employed alternative approaches that did not rely on specific mathematical tasks but rather assessed creativity through other means, as described below.

Self-Report or Questionnaire/Inventory (n = 8): Eight studies relied primarily on self-report measures or questionnaires or inventories rather than performance-based tasks (see Table 1). These instruments typically asked students or teachers to reflect on creative dispositions, attitudes, or self-perceived abilities in mathematics. Examples include Ariba (2019), Haavold (2016), Leu and Chiu (2015), Livne and Milgram (2000), Pelczer and Rodríguez (2011), Pham (2014), Teseo (2019), and Yang et al. (2025).

Observational and Interview-Based Task (n = 7): Seven studies employed classroom observations as their primary data source, often complemented by interviews with students, researcher logs, and document analysis (see Table 1). These qualitative approaches enabled a broader understanding of how mathematical creativity emerges in authentic learning environments. Studies using this approach included Ariba (2019), El-Sahili et al. (2015), Levenson (2011), Riling (2021), Schoevers et al. (2019), Schrauth (2014), and Sengil-Akar and Yetkin-Ozdemir (2022).

3.3.5. Target Groups of Studies

Participant information was reported heterogeneously across studies (age, grade, or school stage). To enhance comparability, we used age as the common metric. Table 1 also reports grade and country, and ages originally reported in months were converted to years. Within the age-reported subset, coverage spanned early childhood through late adolescence. At the youngest level, one study focused on 3–5 years (M. Leikin & Tovli, 2019; months converted to years). A group examined younger primary ages around 8–9 years (Hu & Wang, 2024), 8–13 years (Stolte et al., 2020), 9–10 years, (Schoevers et al., 2018, 2019), average 10 years (M. Tan et al., 2013), and a broader 9–12 years window (Kattou et al., 2013). The largest concentration was in early adolescence (10–14 years). Studies included 10–12 years (Barraza-García et al., 2020; Kontoyianni et al., 2013), 11–12 years (Haylock, 1997), 11–13 years (Singer, 2012), 11–14 years (Huang et al., 2017), and 12–13 years (Pham, 2014; Sadak et al., 2022; Sahliawati & Nurlaelah, 2020). Several papers targeted about 13 years (Suherman & Vidákovich, 2024a, 2024b; Tyagi, 2016). 13–14 years were studied in two research (Haavold, 2016, 2018) while 14 year was in only one study (Rahyuningsih et al., 2022). Two broader band, 10–15 years, spanned this cluster (Akgul & Kahveci, 2016; Suherman & Vidákovich, 2025). Older adolescence was less represented. Examples included 12–15 years (Zainudin et al., 2019), 14–15 years (García-García et al., 2024; Muzaini et al., 2023), a wider 13–17 years cohort (Tubb et al., 2020), and ranges of 16–17 years (Pelczer & Rodríguez, 2011), 16–18 years (Lev, 2013; Yang et al., 2025), average 16 years (Livne & Milgram, 2006), and 16–19 years (Van Harpen & Sriraman, 2013; Yuan, 2009).

In summary, age level peaked in early adolescence: 13 years (15 studies), followed by 12 years (13 studies) and 14 years (10 studies). 10 and 11 years were also well represented (9 studies each). Coverage declined thereafter 15 years (6 studies), 16 (7 studies), 17 (6 studies), 18 (4 studies), and 19 (2 studies). It was sparse in early childhood. Ages 3–5 were each represented by one study. 8 years was represented by two studies while 9 years was represented by five studies. There were no studies targeted ages 6–7. (Counts assign each study to all ages included in its reported range.)

For transparency, we also presented studies that reported only grade levels. Grade 1 (Ariba, 2019; Azaryahu et al., 2025; Bahar & Maker, 2011; Bicer & Bicer, 2023; Shaw et al., 2022; S. Tan, 2015), Grade 2 (Azaryahu et al., 2025; Bahar & Maker, 2011; Bicer & Bicer, 2023; Shaw et al., 2022; S. Tan, 2015), Grade 3 (Assmus & Fritzlar, 2022; Bahar & Maker, 2011; Bicer et al., 2020; Bicer & Bicer, 2023; Coxbill et al., 2013; Shaw et al., 2022; Stolte et al., 2019; S. Tan, 2015), Grade 4 (Al-Mayahi & Hassan, 2022; Bahar & Maker, 2011; Bicer et al., 2020; Bicer & Bicer, 2023; Leu & Chiu, 2015; Pitta-Pantazi et al., 2011; Shaw et al., 2022; Stolte et al., 2019; Tabach & Friedlander, 2013; S. Tan, 2015), Grade 5 (Bal-Sezerel & Sak, 2022; Bicer et al., 2020; Bicer & Bicer, 2023; Levenson, 2011; Pitta-Pantazi et al., 2011; Shaw et al., 2022; Stolte et al., 2019; Tabach & Friedlander, 2013; S. Tan, 2015), Grade 6 (Aljarrah, 2020; Balka, 1974; Bal-Sezerel & Sak, 2022; Coxbill et al., 2013; Hall, 2009; Jensen, 1973; Levenson, 2011; Pitta-Pantazi et al., 2011; Tabach & Friedlander, 2013; Teseo, 2019; Wang et al., 2025), Grade 7 (Ayvaz & Durmuş, 2021; Balka, 1974; Bal-Sezerel & Sak, 2022; Bishara, 2016; El-Sahili et al., 2015; Hall, 2009; Kirisci et al., 2020; Mann, 2005, 2009; Schrauth, 2014; Sengil-Akar & Yetkin-Ozdemir, 2022; Sholihah et al., 2020; Tabach & Friedlander, 2013; Yaniawati et al., 2020), Grade 8 (Balka, 1974; Bal-Sezerel & Sak, 2022; Haavold, 2013; Junaedi et al., 2021; R. Leikin & Kloss, 2011; Sengil-Akar & Yetkin-Ozdemir, 2022; Tabach & Friedlander, 2013), Grade 9 (Tabach & Friedlander, 2013), Grade 10 (Fortes & Andrade, 2019; Kulsum et al., 2019; R. Leikin, 2013; R. Leikin & Kloss, 2011; Levav-Waynberg & Leikin, 2012; Wardani et al., 2011), Grade 11 (Fatah et al., 2016; Haavold, 2013; R. Leikin, 2013; R. Leikin & Lev, 2013; Livne & Milgram, 2000; Munahefi et al., 2022), and Grade 12 (R. Leikin & Lev, 2013; Livne & Milgram, 2000). Grades not listed were not explicitly targeted in this grade-reported subset. Because the mapping from grade labels to ages differs by country, we interpret these counts alongside age and country in Table 1. We synthesized patterns primarily by age bands for cross-country comparability.

Within the grade-reported subset, representation peaked at Grade 7 (n = 14) with a big coverage at Grades 6 (n = 11), 4 (n = 10), and 5 (n = 9). Early primary grades were moderately represented (Grade 1, n = 6; Grade 2, n = 5; Grade 3, n = 8). Coverage dropped at the end of secondary schooling. Grade 9 (n = 1) and Grade 12 (n = 2) were underrepresented while Grades 10 and 11 were modest (n = 6 each). Grades not listed were not explicitly targeted in this grade-reported subset. Because the mapping from grade labels to ages differs by country, we interpret these counts alongside age and country in Table 1. We synthesized patterns primarily by age bands for cross-country comparability.

Lastly, a small subset of studies described participants only by school level without specifying grades or ages (Table 1). They were high school seniors (Bahar & Maker, 2020; United States), junior high school (Yuliardi et al., 2024; Indonesia), and high school students (Riling, 2021; United States). In Table 1, country means the country where data were collected or, when applicable, the school system in which participants were enrolled.

4. Discussion

One of the major goals of this review was to synthesize existing research systematically to clarify how mathematical creativity is defined, what theoretical frameworks support it, and how it has been operationalized and measured in educational settings. From its definitions to its assessments, the strong emphasis on divergent thinking shows the influence of classical creativity theories in the conceptualization of mathematical creativity. However, there is a move toward problem-solving and problem-posing highlights in definition of mathematical creativity This shows the need to situate creativity in more mathematic-related activities rather than in abstract cognitive skills alone. This shift may reflect that creativity in mathematics emerges when learners deal with real problems, generate new questions, and explore multiple solutions, rather than when they simply produce many ideas. Together with this, the small but important focus on affective and motivational factors suggests another gap. The most current definitions may overlook the role of students’ beliefs, confidence, and curiosity in supporting creative work. If creativity depends on both cognitive processes and personal dispositions, then assessments and teaching practices that ignore the affective dimensions provide only a partial and potentially misleading view of creativity. Findings that updating (an executive-function process) predict mathematical creativity directly and indirectly in elementary samples further underscore the cognitive support that interact with dispositions and context (Stolte et al., 2020).

Another important finding was the extensive use of domain-specific frameworks. This suggests that the field views mathematical creativity not as a general ability but as an ability linked to nature, problems, and representations of mathematics. This perspective helps us see more authentic mathematical interactions as a way to discover creativity. This also means that assessments and interventions should capture the richness of problem-solving, problem-posing, multiple solution exploration, and mathematical reasoning, rather than relying solely on standardized measures.

Perhaps one of the most significant findings of this study was that literature had a misalignment problem regarding how mathematical creativity has been defined, framed, and assessed. While definitions of mathematical creativity remain largely anchored in domain-general constructs, most notably divergent thinking elements such as fluency, flexibility, and originality, the frameworks guiding empirical studies increasingly emphasize domain-specific perspectives. In our dataset, domain-specific frameworks ranked first with 37 studies; multidimensional approaches ranked second with 27 studies; and domain-general models ranked third with 25 studies (some studies were coded with multiple frameworks). These findings suggest that research designs are increasingly locating creativity within mathematical activities such as problem posing/solving, generating multiple solutions, and justification, but the definitions used do not always reflect this. Our contribution to the literature is to quantitatively reveal this discrepancy and offer practical guidance for future studies: Researchers should clearly map their definition to their adopted framework. Task selection should center on items requiring problem posing, multiple solutions, and justification. Multidimensional studies should standardize the collection of affective indicators such as motivation, interest, and self-efficacy in the same data structure, along with measures of executive function such as updating. Rater reliability, validity evidence, and cross-grade linking should be reported. Rubrics, sample solutions, and codebooks should be made available for public use. These steps bridge the gap between definition and design and enable mathematical creativity to be captured in a more valid, comparable, and transferable form for teaching, with both its domain-specific depth and multidimensional structure.

We also noted that most studies used assessment procedures that combined criterion- and norm-referenced scoring methods. One reason for this pattern appears to be related to how originality was assessed. In many studies, originality was assessed based on how common or rare a response was within a specific group. In other words, originality was rarely seen as a pure quality; instead, its value depended on how unusual an idea was compared to similar ones. However, this practice raises some important methodological and conceptual questions. Relying too heavily on group norms may risk equating creativity with statistical rarity rather than meaningful outcome. In other words, an answer may be rare only because it was compared with small sample sizes, not because it reflects genuine creative thinking. On the other hand, criterion-referenced scoring alone can overlook the social and comparative aspects of creativity, potentially overlooking how creative performance challenges shared expectations. A small group of studies used more qualitative and holistic approaches (e.g., the Consensual Assessment Technique) and further highlighted these tensions. While these approaches capture the richness and context-specific nature of creativity, they lack standardization. This makes cross-study comparisons difficult. Taken together, these models suggest the need for a more balanced framework for assessing mathematical creativity. Future research could combine the strengths of both approaches.

The widespread use of paper-based assessments suggests that mathematical creativity research largely relies on traditional data collection methods. Their low cost and accessibility in educational settings make them convenient and widely applicable. However, this reliance also suggests that measurement practices have not fully embraced technological innovations. The limited but growing use of online assessments points to promising future directions. The rapid development of artificial intelligence (AI) can help us move beyond typical testing formats by offering opportunities to transition to more dynamic and data-rich environments. However, these innovations also present challenges, including the need for technical expertise and ethical considerations. Overall, the findings highlight the need to integrate hybrid models that combine paper-based tools with the flexibility and power of more digital and AI-based systems.

The use of fluency, flexibility, and originality across most studies shows how strongly classical divergent thinking frameworks have shaped mathematical creativity research. This heavy focus reflects the historical influence of Guilford (1956) and others, but it also reveals a conceptual narrowness. That is, creativity is often reduced to producing many varied and novel ideas. However, in mathematics classrooms, creative performance is shaped by students’ dispositions and beliefs (e.g., interest, task value, self-efficacy, mindsets) and by social interactions. These factors operate as motivational and contextual support or constraint on how creativity is enacted, consistent with confluence/componential views that distinguish core creative processes from enabling conditions (e.g., Amabile, 1982; Kaufman & Sternberg, 2010). Less attention to other elements such as complexity and quality suggests that many studies still prioritize idea generation over idea development. However, creative mathematical thinking often requires going beyond generating ideas to develop them in depth by connecting and evaluating them meaningfully. Future assessments could capture a broader picture of creativity by including these underrepresented elements. An even more striking point is the paucity of socioemotional, attitudinal, and process-oriented components. A few studies have examined elements such as motivation, curiosity, and collaboration. However, creativity is shaped not only by cognitive processes but also by students’ dispositions, beliefs, and social interactions. To ignore these elements limits our understanding of the dynamic interactions between personal characteristics and learning environments. Overall, these findings highlight both progress and imbalance. Thus, while measures of divergent thinking have provided a strong foundation, the field now needs broader frameworks that integrate cognitive, affective, and process dimensions.

Our findings also point to a conceptual–operational gap in mathematical creativity research. While the dominant theoretical framework was domain-specific by emphasizing problem-solving, problem-posing, and mathematics-centered reasoning, divergent thinking elements (fluency, flexibility, originality, and elaboration) were frequently scored in the assessments. This misalignment suggests that, although researchers increasingly frame creativity from a mathematical perspective, the actual measurement practices still rely on standardized cognitive indicators, which were originally developed for general creativity assessment. Such a pattern may reflect both the historical dominance of divergent thinking models and the practical appeal of their well-established scoring rubrics. However, it also signals a critical need for theoretical–methodological alignment, where future assessments incorporate components that more fully reflect mathematics-specific conceptions of creativity without relying on the strengths of domain-general measures.

We also would like to interpret the target group pattern we found and what it means for the field. Participant profiles indicate that studies largely focus on early adolescence. The concentration around the age range of 10–14 can be explained by the accelerated transition from pre-algebra to algebra in the curriculum during this period. This concentration may also be related be the feasibility of problem-posing and multiple-solution tasks, the greater manageability of school access, and scoring reliability at this age. Data in early childhood is sparse. There is a particularly significant gap in the 6–7 age range. Representation also declines in late adolescence. Possible reasons can be test and placement pressures, content depth, and sampling difficulties for studies. Because grade level labels vary across countries, we believe it is more valuable to construct the synthesis based on age to provide a more comparable frame. Future research should specifically sample the 6–7 and 16–18 age ranges. They should also explicitly report country information by age and grade and use connectors to facilitate comparison across ages. All of these would significantly increase the validity and generalizability of the findings.

4.1. Implications for Research

This review highlights several critical gaps in the current literature on assessing mathematical creativity. First, the age-level imbalance requires systematic attention. Most studies concentrated on the middle grades, but little is known about how mathematical creativity emerges in early childhood or evolves during the later secondary years when students learn advanced mathematical concepts and make key academic transitions. Future studies should adopt longitudinal designs to trace creativity trajectories across the full K-12 level to identify critical periods for intervention. This is also important to examine how creativity interacts with mathematical knowledge, cognitive growth, and motivational factors over time.

Second, the review exposed a persistent conceptual versus operational gap between how mathematical creativity is defined, framed, and measured. While theoretical frameworks have been increasingly situating creativity within mathematical problem-solving, reasoning, and problem-posing, most assessments continue to rely heavily on domain-general divergent thinking elements such as fluency, flexibility, and originality. Future research should develop more mathematically grounded assessment tools.

4.2. Implications for Practitioners

The findings reveal that most assessments remain domain-general in focus by emphasizing cognitive abilities such as fluency, flexibility, and originality, rather than capturing the mathematics-specific processes central to authentic mathematical creativity. By authentic mathematical creativity, we mean creativity that emerges from mathematics-specific processes, such as problem-posing, reasoning, and proof, rather than only from general divergent thinking tasks. For instance, while generating a list of ideas about the solution to a problem reflects divergent thinking, it is also good to ask students to pose a new problem with multiple valid solutions and to justify their reasoning illustrate authentic mathematical creativity. Classroom teachers and curriculum designers should be aware that while these traditional measures offer accessible ways to evaluate students’ idea generation, they risk overlooking critical dimensions such as problem-posing, mathematical reasoning, and proof construction within real mathematical practices. Developing and using domain-specific tasks that reflect the nature of mathematical thinking will provide teachers with more accurate insights into students’ creative potential and help align instructional practices with how creativity actually manifests in mathematics classrooms.

At the same time, the high use of paper-based assessments and the limited use of AI-based digital tools present practical problems for classrooms. Teachers face time, resource, and training limitations when adopting new creativity assessments. To address this, future work should focus on designing classroom-friendly tools that balance theory and practice by using hybrid assessment models that combine the traditional paper-based approaches and real-time feedback with digital platforms. Such approaches, e.g., NLP-based automated scoring, can provide faster feedback and more consistent ratings to make classroom use more feasible (Marrone et al., 2022). Professional development programs can help teachers interpret creativity assessment data and integrate the results into instructional planning.

4.3. Limitations

We acknowledge a couple of limitations that readers should consider when interpreting our findings. First, the search was restricted to studies published in English and to a set of databases. Second, conference proceedings and other non-peer-reviewed materials were not included. This may have led to the exclusion of relevant research published in other languages or indexed in alternative sources. Together, these limitations suggest that the findings should be interpreted with caution regarding their generalizability across all educational contexts.

5. Conclusions

This systematic review provides a comprehensive synthesis of how mathematical creativity is defined, conceptualized, and assessed in K-12 research. Overall, these findings suggest that research on mathematical creativity has adhered to domain-specific frameworks and relied heavily on divergent thinking measures. At the same time, much less attention has been given to the emotional and social aspects of creativity in mathematics. In addition, most prior studies have concentrated on middle school students, leaving early childhood and high school populations largely overlooked. Addressing these gaps will be possible through theoretically and methodologically strong and diverse approaches that should integrate cognitive, motivational, and contextual factors into creativity assessment. Furthermore, through the development of mathematics-specific and multidimensional tools supported by digital and AI innovations, future research and practice can better capture how creativity emerges in real-world learning environments and design educational experiences that foster mathematical creativity in all students.