Criteria Used by Teachers of Non-Mathematical Subjects to Assess an Interdisciplinary Task That Includes Mathematics
Abstract
1. Introduction
2. Theoretical Framework
2.1. Didactic Suitability Criteria
- Epistemic suitability, which expresses the degree of representativeness of the institutional meanings implemented in relation to a reference meaning;
- Cognitive suitability, referring to the degree to which the institutional meanings implemented are within the students’ zone of potential development, as well as the proximity of the personal meanings achieved to the intended meanings;
- Interactional suitability, which expresses the degree to which the types of didactic configurations implemented and their connection enable identifying and resolving potential semiotic conflicts that arise during the teaching-learning process;
- Mediational suitability, which refers to the degree of availability and suitability of the material and time resources necessary for the development of the teaching-learning process;
- Affective suitability, which expresses the degree of involvement (interest, motivation, etc.) of the students in the teaching-learning process;
- Ecological suitability describes the degree to which the study process fits in with the educational project of the school, the society, and the conditions of the environment in which it is developed.
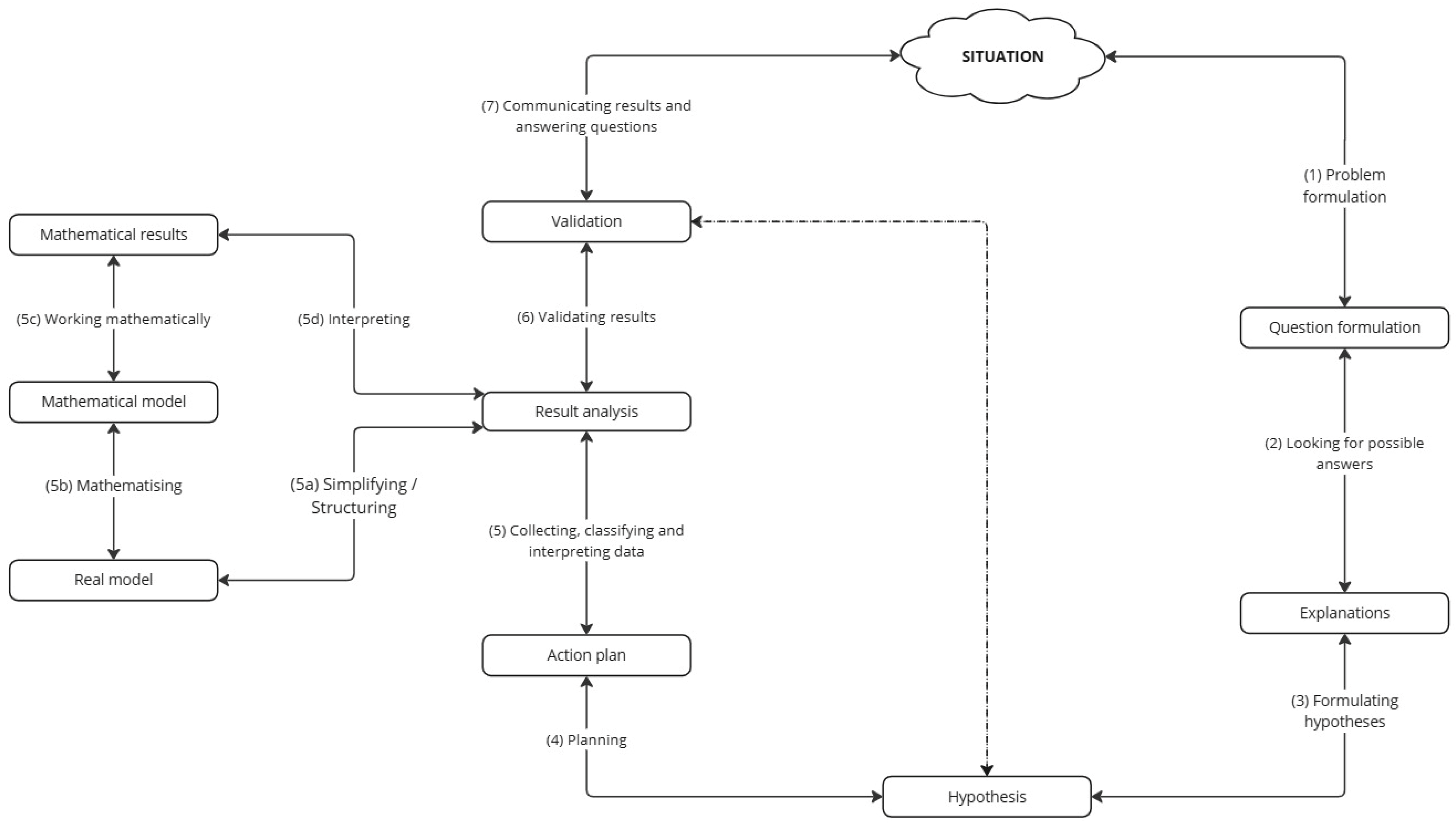
2.2. Inquiry and Mathematical Modelling
3. Methodology
4. Results and Discussion
I think that using GeoGebra for the carbon-14 exercise was difficult for them, but not because of the concept itself. I believe it was because it’s a platform we don’t use much at this school. Perhaps, if they had known it better, they would have found it easier. I think we need to do some preliminary work as a school to become familiar with these types of tools. And I ask myself, could this be the right time to start using it, the excuse to use it? Yes, but then we should be aware that they will have difficulties when doing this activity within the LS, because first they would have to learn how to use it, following a tutorial, going step by step… which, if you already know how it works, you can skip. Perhaps, as part of what made learning difficult, this is, in general terms, the only thing I could interpret that way.
I thought about the students that are struggling the most. In general, they probably showed greater interest because they saw it as something easy, but when it came down to it, they encountered all these difficulties and perhaps they backed out, right? Using the platforms, the new programmes, perhaps they were not able to reach the level. And there are always others who say “leave it, I’ll do it” because the task has to be handed in… But this also happens in other situations.
(…) Several groups that had the same task branched out, and each group worked at a different pace. They had a different learning experience, a different level of depth within a subject that was nonetheless the same.
What I find difficult, and I think it is the hardest, is for them to see the reason for this assessment, what they have done well, what they have done badly, more clearly than we do. I think this is missing in the assessment… It requires feedback, feedback from the teacher to the student.
I found it difficult to convey [the guide during the implementation of the LS] and what they [the students] told me at times was “Are we finished or not? Is this maths, or is it projects?”
I think the timetable this year [referring to the time at which the three class groups of first year CSE students had the subject of projects, in which the LS was implemented] was not favourable. Last year, all the classes were held at the same time [the teacher refers to the fact that during academic year 2022–2023, the projects subject for the three first year CSE class groups took place at the same time, which was not the case for all the sessions of this subject during academic year 2023–2024 because of how the school had organised the timetable. We therefore had more opportunities to share.
This variability in time [referring to the decision to give the students a few more sessions than initially planned for them to be able to delve deeper into their research] made it easier [for the students] to achieve all the learning objectives. Last year, things were more restricted, and although we covered all the learning objectives, we were all clear about that, the students were more pressed for time.
We find it difficult to act in a coordinated manner, and adding an extra teacher [researcher 1, who played the dual role of researcher and teacher] and including extra hours, makes things more difficult in the end. Researcher 1 does not have a specific space for coordination with us that we have [One hour a week in the timetable of the four teachers who teach the projects subject is to meet and coordinate the joint functioning of the subject in the three class groups]. We had to find moments like now, outside of school hours [referring to the teachers’ working hours, not the students’ school hours] to be able to talk, to find the moment, to explain ourselves…
Those of us here [the four teachers] are the ones who have developed the projects together, and therefore all four of us know what we have to do, how we have to do it, when we have to do it… In this case, the person who developed the project was researcher 1, and things were explained to us, and we had a lot of information, and we were all more or less able to look at them [the documents including the development and materials for the LS]. However, in the end, we are not really part of it, are we? We are not the co-creators of all this, and therefore it is no longer just a matter of “ask researcher 1 because I don’t know much about maths,” but rather that I might have to say “draw a graph,” and at that moment they catch me off guard, and I don’t know if it’s a graph or GeoGebra or what, right? That’s what we’ve been talking about: organisation, setting timing, making everything clearer… This will help the students understand it better too. It’s about time and organisation.
One of the things that caught my attention in this activity is that it is about Badalona. I am from Badalona, and I think it is very important to involve students in city matters. It makes them a little more involved because they feel challenged as it is the place where they live, it is related to the things they do, etc. I find this activity interesting, because it is about Badalona… They learn new things they may not have known about Badalona, and I find that interesting.
In the historical context, which is what we are working on, [the LS] fit perfectly [with the curriculum]… We also added a part about mathematics, although we did not know whether what we were working on was in the mathematics curriculum or not because the expert in this area was researcher 1… We were 100% confident that it was… but it did fit because at that moment we were doing things related to the Romans and it could be included there.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LS | Learning situation |
| OSA | Onto-Semiotic Approach |
| DSC | Didactic Suitability Criteria |
| CSE | Compulsory Secondary Education |
References
- Artigue, M., & Blomhøj, M. (2013). Conceptualizing inquiry-based education in mathematics. ZDM, 45(6), 797–810. [Google Scholar] [CrossRef]
- Blum, W. (2002). ICMI Study 14: Applications and modelling in mathematics education—Discussion document. Educational Studies in Mathematics, 51(1–2), 149–171. [Google Scholar] [CrossRef]
- Blum, W. (2011). Can modelling be taught and learnt? Some answers from empirical research. In G. Kaiser, G. Blum, R. B. Ferri, & G. Stillman (Eds.), Trends in teaching and learning of mathematical modelling: ICTMA 14 (pp. 15–30). Springer. [Google Scholar]
- Braun, V., & Clarke, V. (2006). Using thematic analysis in psychology. Qualitative Research in Psychology, 3(2), 77–101. [Google Scholar] [CrossRef]
- Breda, A., Font, V., & Pino-Fan, L. R. (2018). Criterios valorativos y normativos en la Didáctica de las Matemáticas: El caso del constructo idoneidad didáctica. Bolema: Boletim de Educação Matemática, 32(60), 255–278. [Google Scholar] [CrossRef]
- Breda, A., Pino-Fan, L. R., & Font, V. (2017). Meta didactic-mathematical knowledge of teachers: Criteria for the reflection and assessment on teaching practice. EURASIA Journal of Mathematics, Science and Technology Education, 13(6), 1893–1918. [Google Scholar] [CrossRef]
- Capone, R. (2022). Interdisciplinarity in mathematics education: From semiotic to educational processes. EURASIA Journal of Mathematics, Science and Technology Education, 18(2), em2071. [Google Scholar] [CrossRef]
- Ceballos-López, N., Saiz-Linares, Á., Ceballos-López, N., & Saiz-Linares, Á. (2021). Metodologías cualitativas participativas en educación: Photovoice, viñetas y Ketso. Psicoperspectivas, 20(1), 56–69. [Google Scholar] [CrossRef]
- Charalambous, C. Y., & Praetorius, A. K. (2018). Studying instructional quality in mathematics through different lenses: In search of common ground. ZDM–The International Journal on Mathematics Education, 50(3), 355–366. [Google Scholar] [CrossRef]
- Escobar, J., & Bonilla-Jiménez, F. I. (2009). Grupos focales: Una guía conceptual y metodológica. Cuadernos Hispanoamericanos de Psicología, 9(1), 51–67. [Google Scholar]
- Falcó-Solsona, P. J., Ledezma, C., Sala-Sebastià, G., & Font, V. (2024). Inquiry and mathematical modelling with real-archaeological objects in secondary education. Education Sciences, 14(3), 304–331. [Google Scholar] [CrossRef]
- Ferreras, V. M. (Ed.). (2015). La difusión comercial de las ánforas vinarias de Hispania Citerior-Tarraconensis (s. I a.C.—I. d.C.). Archaeopress Publishing Ltd. [Google Scholar] [CrossRef]
- Generalitat de Catalunya. (2022). Decret 175/2022, de 27 de setembre, d’ordenació dels ensenyaments de l’educació bàsica. Diari Oficial de la Generalitat de Catalunya, 8762, 491. [Google Scholar]
- Godino, J., & Burgos, M. (2020). ¿Cómo enseñar las matemáticas y las ciencias experimentales? Resolviendo el dilema entre transmisión e indagación. Paradigma, XLI(e), 80–106. [Google Scholar] [CrossRef]
- Godino, J. D. (2024). Enfoque ontosemiótico en educación matemática. Fundamentos, herramientas y aplicaciones. McGraw Hill-Aula Magna. [Google Scholar]
- Godino, J. D., Batanero, C., & Burgos, M. (2023). Theory of didactical suitability: An enlarged view of the quality of mathematics instruction. EURASIA Journal of Mathematics, Science and Technology Education, 19(6), em2270. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, G. (2020). Mathematical modelling and applications in education. In S. Lerman (Ed.), Encyclopedia of mathematics education (2nd ed., pp. 553–561). Springer. [Google Scholar]
- Klein, J. T. (1990). Interdisciplinarity: History, theory, and practice. Wayne State University Press. [Google Scholar]
- Ledezma, C. (2024). Mathematical modelling from a semiotic-cognitive approach. REDIMAT Journal of Research in Mathematics Education, 13, 268–292. [Google Scholar] [CrossRef]
- Maaß, K., & Doorman, M. (2013). A model for a widespread implementation of inquiry-based learning. ZDM, 45(6), 887–899. [Google Scholar] [CrossRef]
- Macancela-Coronel, G. F., García-Herrera, D. G., Erazo-Álvarez, C. A., & Erazo-Álvarez, J. C. (2020). Comprensión del aprendizaje interdisciplinar desde la educación STEM. Episteme Koinonia, 3(1), 117–139. [Google Scholar] [CrossRef]
- Medina-Nicolalde, M. A., & Tapia-Calvopiña, M. P. (2017). El aprendizaje basado en problemas una estrategia para el trabajo interdisciplinar en el aula. Olimpia. Revista de la Facultad de Cultura Física de la Universidad de Granma, 14(46), 142–153. [Google Scholar]
- Niss, M., Blum, W., & Galbraith, P. L. (2007). Introduction. In W. Blum, P. L. Galbraith, H.-W. Henn, & M. Niss (Eds.), Modelling and applications in mathematics education: The 14thICMI study (pp. 3–32). Springer. [Google Scholar] [CrossRef]
- Pollak, H. (2007). Mathematical modelling—A conversation with Henry Pollak. In W. Blum, P. L. Galbraith, H.-W. Henn, & M. Niss (Eds.), Modelling and applications in mathematics education: The 14th ICMI Study (pp. 109–120). Springer. [Google Scholar]
- Rocard, M., Csermely, P., Jorde, D., Lenzen, D., Walberg-Henriksson, H., & Hemmo, V. (2007). Science education now: A renewed pedagogy for the future of Europe. European Commission, Directorate-General for Research, Science, Economy and Society. [Google Scholar]
- Sala Sebastià, G. (2016). Competència d’Indagació matemàtica en contextos històrics a Primària i Secundària [Ph.D. Thesis, Universitat de Barcelona]. [Google Scholar]
- Sala Sebastià, G., Font, V., & Ledezma, C. (2021). Relaciones entre los procesos de modelización matemática y de indagación desde la perspectiva del aprendizaje de las matemáticas. Quadrante, 30(1), 116–139. [Google Scholar] [CrossRef]
- Silveira Donaduzzi, D. S. d., Colomé Beck, C. L., Heck Weiller, T., Nunes da Silva Fernandes, M., & Viero, V. (2015). Focal group and content analysis in qualitative research. Index de Enfermería, 24(1–2), 71–75. [Google Scholar] [CrossRef]
- Williams, J., Roth, W.-M., Swanson, D., Doig, B., Groves, S., Omuvwie, M., Ferri, R. B., & Mousoulides, N. (2016). Interdisciplinary mathematics education: State of the art. Springer. [Google Scholar] [CrossRef]
- Wittgenstein, L. (2009). Philosophical investigations. Wiley-Blackwell. [Google Scholar]








| Components | Indicators |
|---|---|
| Epistemic suitability | |
| Errors | No practices considered incorrect from a mathematical perspective are observed. |
| Ambiguities | No ambiguities that could lead students to confusion are observed. Definitions and procedures are stated clearly and correctly. They are adapted to the educational level they are aimed at. Explanations, proofs, and demonstrations are adapted to the educational level they are aimed at. |
| Richness of processes | Relevant processes in mathematical activity (modelling, argumentation, problem solving, connections, etc.) are considered in the sequence of tasks. |
| Representativeness of the complexity of the mathematical object | Partial meanings (definitions, properties, procedures, etc.) are a representative sample of the complexity of the mathematical notion to be taught as part of the curriculum. For one or more partial meanings, a representative sample of problems is provided. Students use different ways of expression (verbal, graphic, symbolic, etc.). for one or several partial meanings. |
| Cognitive suitability | |
| Prior knowledge | Students have the necessary prior knowledge to study the topic (they have either previously studied it, or they are familiar with it). The intended meanings (of reasonable difficulty) can be taught through their different components. |
| Curricular adaptation to meet students’ individual needs | Extension and support activities are included. |
| Learning | The different assessment methods show internalisation of the intended or implemented knowledge/competencies. |
| High cognitive demand | Important cognitive processes are activated (generalisation, intra-mathematical connections, changes of representation, assumptions, etc.). Metacognitive processes are promoted. |
| Interactional suitability | |
| Teacher-student interaction | The teacher introduces the topic properly (clear and well-organised presentation, not speaking too fast, emphasis on the key concepts of the topic, etc.) Students’ conflicts of meaning are identified and resolved (proper interpretation of students’ silence, facial expressions, questions, question-answer games, etc.) The aim is to reach consensus based on the best argument. Several rhetorical and argumentative resources are used to involve and capture the students’ attention. Student engagement in the classroom dynamics is encouraged. Exclusion is discouraged. |
| Student interaction | Dialogue and communication between students are encouraged. Inclusion in the group is promoted and exclusion is discouraged. |
| Autonomy | Moments in which students assume responsibility for their study (exploration, formulation, and validation) are observed. |
| Formative assessment | The students’ cognitive progress is observed systematically. |
| Mediational suitability | |
| Material resources (manipulatives, calculators, computers) | The use of manipulatives and technology lead to favourable conditions, language, procedures, and arguments adapted to the intended meaning. Definitions and properties are contextualised and encouraged using specific situations, models, and visuals. |
| Class size, timetable, and classroom conditions | The number of students and student grouping enable intended teaching to take place. The time of day the subject is taught is appropriate (e.g., not all the sessions are taught late in the day). Classroom seating arrangements are appropriate for developing the intended teaching method. |
| Time (for collective teaching/tutoring, for learning) | The intended meanings are adapted to the time available. Time is spent on the most important or central aspects of the topic. Time is spent on the content students find the most difficult. |
| Affective suitability | |
| Interests and needs | Tasks that are of interest to the students are chosen. Learning situations that enable students to assess the usefulness of mathematics both in everyday life and in professional life are proposed. |
| Attitudes | Student engagement, commitment, responsibility, etc., in activities is promoted. Argumentation is fostered in a context of equality. The arguments themselves are evaluated, not the person presenting them. |
| Emotions | Self-esteem is nurtured, hence avoiding a negative attitude towards mathematics and/or fear of mathematics. Aesthetic qualities and accuracy of mathematics are stressed. |
| Ecological suitability | |
| Curricular adaptation | The content, its implementation and assessment are in accordance with the curriculum guidelines. |
| Intra- and interdisciplinary connections | The content is related to other mathematical topics (connecting advanced mathematics with mathematics in the curriculum, and different mathematics content included in the curriculum), or to the content of other disciplines (in an extra-mathematical context or in connection with other subjects in the same educational stage). |
| Socio-professional usefulness | The content is useful for integration into the workforce and society. |
| Didactic innovation | Innovation is based on research and reflexive practice (introduction of new content, technological resources, assessment methods, classroom organisation, etc.) |
| Phase | Process | Description |
|---|---|---|
| 1 | Familiarising yourself with your data | Transcribe the data (if necessary), read and re-read them, and start taking notes for coding. |
| 2 | Generating initial codes | Code the interesting aspects of the data, working systematically through the entire data set, matching up the codes with data extracts that demonstrate that code. |
| 3 | Searching for themes | Sort the different codes into potential themes, collating all the relevant coded data extracts in each potential theme within the identified themes. |
| 4 | Reviewing themes | Check whether the themes ‘work’ in relation to the coded excerpts (phase 1) and the entire data set (phase 2), generating a thematic map for each theme. |
| 5 | Defining and naming themes | Conduct an analysis to define and refine the essence of what each theme is about and the broader overall story you are telling about your data, providing clear definitions and names for each theme. |
| 6 | Producing the report | This is the final opportunity for analysis. Select vivid and compelling excerpts as examples. Carry out a final analysis of the selected excerpts, relating the analysis to the research question and literature. Write an academic report of the analysis. |
| Epistemic Suitability | Cognitive Suitability | Interactional Suitability | Mediational Suitability | Affective Suitability | Ecological Suitability | |
|---|---|---|---|---|---|---|
| Teacher 1 (technology) 34 times | 1 | 4 | 1 | 5 | 3 | 2 |
| Teacher 2 (natural sciences) 35 times | 0 | 5 | 5 | 5 | 2 | 1 |
| Teacher 3 (counselling) 33 times | 0 | 3 | 4 | 4 | 1 | 2 |
| Teacher 4 (social sciences) 14 times | 0 | 4 | 1 | 3 | 3 | 2 |
| Total | 1 | 14 | 10 | 17 | 8 | 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Falcó-Solsona, P.J.; Sala-Sebastià, G.; Breda, A.; Font, V. Criteria Used by Teachers of Non-Mathematical Subjects to Assess an Interdisciplinary Task That Includes Mathematics. Educ. Sci. 2025, 15, 1284. https://doi.org/10.3390/educsci15101284
Falcó-Solsona PJ, Sala-Sebastià G, Breda A, Font V. Criteria Used by Teachers of Non-Mathematical Subjects to Assess an Interdisciplinary Task That Includes Mathematics. Education Sciences. 2025; 15(10):1284. https://doi.org/10.3390/educsci15101284
Chicago/Turabian StyleFalcó-Solsona, Pere Joan, Gemma Sala-Sebastià, Adriana Breda, and Vicenç Font. 2025. "Criteria Used by Teachers of Non-Mathematical Subjects to Assess an Interdisciplinary Task That Includes Mathematics" Education Sciences 15, no. 10: 1284. https://doi.org/10.3390/educsci15101284
APA StyleFalcó-Solsona, P. J., Sala-Sebastià, G., Breda, A., & Font, V. (2025). Criteria Used by Teachers of Non-Mathematical Subjects to Assess an Interdisciplinary Task That Includes Mathematics. Education Sciences, 15(10), 1284. https://doi.org/10.3390/educsci15101284










