1. Introduction
College physics education is essential for developing theoretical and practical knowledge and higher-order thinking skills necessary to specialize in different science, technology, engineering, and mathematics (STEM) fields. Research on student-centered curricula and teaching strategies in physics education in the USA and many countries (such as Japan) have created active learning environments where students are responsible for their learning processes [
1,
2]. These innovative methods have increased students’ conceptual understanding and provided positive evidence in learning outcomes [
3]. However, in many countries such as Turkey, university physics education is supported by rote learning in crowded classrooms without sufficient student-teacher and student-student communication.
Traditional physics courses passively focus on transferring knowledge, memorizing formulas, and solving standard problems. With this method, even if students can develop subject knowledge, they need help acquiring deep conceptual understanding and applying knowledge in new contexts using scientific practices [
4]. The fact that teachers focus on rote learning by repetition causes many students to learn in shallower ways and with limited retention of knowledge.
Another critical factor in physics education is students’ prejudices about physics concepts. Students’ biases about physics significantly affect how they assimilate, interpret, and integrate or accommodate new information with their previous knowledge during physics learning [
5]. Research in this area shows that students may develop wrong approaches to physics concepts in advance, and teachers should recognize these prejudices during the lesson to turn them into more scientific conceptions [
6]. For this purpose, instead of rote teaching methods that do not value the students’ misconceptions, teachers should plan systematic physics teaching and learning environments to address student alternative conceptions via different strategies and curricula.
Active learning can contribute to physics education and increase learning outcomes by adapting to innovative teaching strategies such as problem- or experiment-based learning. Thanks to these approaches, students’ scientific interaction with the teacher and other students increases, and research-based strategies aimed at helping students realize and actively revise misconceptions through inquiry [
7]. For example, during active learning, students can conduct group experiments and collaboratively discuss experimental setup, data collection, and analysis [
8]. In this way, students enter the process of defining problems, asking questions, explaining, designing models, and solving problems by creating arguments. Students actively engage in the solution of the problem instead of passively understanding the solution of the problem; they use conceptual knowledge in problem-solving by integrating it with scientific practices. Taking an active role in problem-solving using scientific practices enables students to learn concepts by constructing them during application.
Research on science education has shown the positive results of innovative approaches. However, is it possible and easy to adopt research-oriented methods in university physics education? Adoption necessitates understanding the factors influencing the development and use of innovative and research-oriented methods. These factors were investigated in the study of Henderson and colleagues (2012) [
9]. Approaches such as physics teachers’ preference to use the existing curriculum verbatim, their failure to make appropriate modifications for the needs of students, and professional development needs in applying innovative methods were among these factors. At the same time, teachers needed to learn how to use the curriculum suitable for the student-centered method since the physics teachers took an isolated culture that affected the validity of innovative strategies.
Research on science education focuses on students’ understanding of science topics, their knowledge, and their approach to science learning. Researching students’ difficulties in understanding science learning and science concepts and models is one of the research topics of science education [
8,
10]. Therefore, it is essential to find and implement instructional strategies and new ways to improve students’ science learning in the classroom [
11]. In recent years, there have been many visible attempts to improve teaching and learning in university science courses at different institutions [
12]. Many studies show that students learn better in classrooms where they interact with instructors and peers, participate in group discussions, and exchange ideas [
13,
14]. Researchers developed active learning environments and innovative curricular materials to encourage scientific research and increase student engagement and conceptual understanding of science courses. These new materials developed through science laboratory experiments should target helping students gain a qualitative and quantitative understanding of basic scientific principles and develop their problem-solving strategies in a qualitative way that differs from traditional practice [
15]. Recent studies also reported the effectiveness of such techniques as life cycle assessment teaching [
16]. Pozuelo-Munoz et al. (2023) highlighted the science skills development through problem-based learning that learners engaged in the inquiry process to look for solutions to the problem, develop experimentation protocols, collect and analyze data, and communicate the results [
17].
In this study, we want to understand how innovative course materials prepared in contrast to traditional methods develop students’ conceptual understanding. This study aims to quantitatively investigate the results of using research-oriented curricula targeting innovative teaching strategies in an environment where instructors enact traditional teaching methods in college science education. In particular, the study is conducted with university physics and engineering students, focusing on approaches to solving two kinematic problems selected from research-based curriculum materials. This study investigates how the concepts developed by students with traditional methods affect the effectiveness of dealing with different teaching approaches. It also offers suggestions to facilitate the integration of innovative pedagogies into the physics curriculum.
This study is essential to understand the state of physics education at a research university in a metropolitan province in Turkey, the innovative approach of students accustomed to the traditional method, and to make suggestions. Developing physics education through methods that enable students to develop scientific concepts guides students to take an active role in their learning and to be able to use them in different contexts. This work will contribute to the ongoing dialogue on curriculum, pedagogy, and teaching in higher education and ultimately aims to develop a more effective and engaging learning environment for future physicists and engineers.
4. Results
In this section, we answered questions to address the purpose of the study.
4.1. How Do Frequencies for Knowledge Level Differ across Gender, Grade, and Department?
Table 2 shows the distribution of students’ knowledge levels across genders (female and male), departments (PHYS, PEDU, ENG), and grade levels (sophomore, junior, senior) for the first and second questions. Raw data is provided as
Supplementary Materials. Generally, physics (PHYS) students had the highest participation, and engineering (ENG) students had the male dominance for deep and procedural knowledge approaches. For question 1, most male and physics students approached the solution with deep knowledge. Sophomore male students responded to the question with a procedural approach, and junior students (both female and male) had a surface approach.
From the physics education department (PEDU), most sophomore male students showed a deep approach, senior students had a procedural approach, and most junior students had a surface approach. In the engineering department (ENG), mostly sophomore male students solved the problem with a deep approach, but junior male students showed a procedural approach. For question 2, a few students from three departments used a deep approach. Mostly, senior PHYS students displayed a deep approach, and juniors from the PHYS department had a procedural and surface approach. From PEDU, most junior students had a surface approach to solving the problem. From ENG, most male sophomore (22) students presented a surface approach, whereas sophomore (11) and junior (10) male students presented procedural knowledge.
As a result, primarily male students from the PHYS and ENG departments tended to have deep or procedural knowledge, but female PEDU students displayed procedural knowledge. Some dominant male students solved the problems with surface approach among physics and engineering students. Females were dominant on a balanced surface and procedural approach. The difference between males and females showed that male and engineering students presented a deep knowledge.
4.2. How Does the Distribution of Knowledge Level, Skill Type, and Logical Progression Level Differ across Grades?
Table 3 provides data on questions 1 and 2 on knowledge, skill, and logical progression levels for students from physics (PHYS), physics education (PEDU), and engineering (ENG) departments at different grade levels. Raw data is provided as
Supplementary Materials. There is variability in knowledge, skills, and logical progression across majors and grades. Results for question 1 showed that a sophomore student from the PEDU department showed the highest (3.00) or deep knowledge; senior students from the PEDU department presented the lowest (1.27) or surface knowledge. Besides, engineering (ENG) students generally reported higher knowledge on average than physics (PHYS) students. For the skill type, most sophomore ENG students reported high engagement in intuitive (INT [
21]) and mathematical (MATH [
26]) skills, whereas most junior PHYS students reported high engagement in INT (12) and MATH (19) skills. Sophomore PHYS students focused only on MATH (13) skills in solving the first question. PEDU students presented minimal engagement skills, and senior PEDU students (8) focused on making predictions through INT skills. For the logical progression level, only one sophomore PEDU student showed good progress on average (4), but senior PEDU students showed the lowest scores (1.73). Junior ENG students reported the highest logical progression scores (3.29) among all groups.
These results presented that for question 1, ENG majors, especially juniors, focused on INT and MATH skills, but PHYS students, particularly juniors, reported a balanced engagement across multiple skills. One sophomore PEDU student displayed high knowledge and learning progression levels with a blended skill approach. Junior and senior PEDU students showed the lowest knowledge and learning progression, mostly with intuitive or mathematical skills. For question 2, senior ENG students showed the highest (2) procedural knowledge across all groups; sophomore PEDU students had the lowest (1) surface knowledge. Knowledge scores tended to increase from sophomore to senior levels across majors. For the skill type, in this question, most majors engaged in qualitative (QUAL) or mathematical (MATH) skills. Junior and senior PHYS and sophomore ENG students utilized QUAL and MATH skills in a balanced approach. Junior ENG students displayed QUAL skills; senior ENG students showed low engagement skills. Sophomore and senior PEDU students presented minimal engagement skills. For the logical progression level, senior engineering students displayed the highest logical progression in the neutral level (3); senior physics students also showed high logical progression (2.66). These results reported that physics students had a balanced range of skills in solving the question, while physics education students had a gap or limited skill development. For logical progression, engineering students showed clear solutions, accuracy, and connection between the steps.
4.3. Do Knowledge Scores of Male and Female Students Differ Significantly?
We aimed to compare the knowledge scores of male and female students for two questions by using non-parametric methods since the data is not normally distributed. The Mann-Whitney U test was appropriate when comparing two independent samples for non-normal distributions.
Table 4 shows the results for questions 1 and 2.
In this analysis, a Mann-Whitney U test was conducted to examine whether there was a significant difference in knowledge scores between male and female students in solving question 1. Descriptive statistics showed that the mean score for knowledge was very close to procedural knowledge. For gender, males participated the most, indicating that there might be gender differences. The test showed a significant difference between males and females on knowledge scores, U = 2656.5, z = −2.29, p = 0.022 (p < 0.05). This result suggested that females had higher knowledge scores than male students, indicating a negative z score. Gender influenced the knowledge scores in the sample, and one group had a higher knowledge approach (deep or procedural) than the other.
In this analysis for question 2, a Mann-Whitney U test was conducted to examine whether there was a significant difference in knowledge scores between male and female students. Descriptive statistics showed that the mean score for knowledge was not very high between the surface and procedural approaches. The test indicated no significant difference between males and females on knowledge scores, U = 2998, z = −1.12, p = 0.26. This result suggested that gender did not play a role in knowledge scores.
4.4. Is Being in the Physics, Physics Education, and Engineering Department Significantly Different across Logical Progression Levels?
To determine if there were significant differences in logical progression scores across students in physics, physics education, and engineering departments, the researcher conducted a non-parametric test, the Kruskal–Wallis Test, as an alternative to ANOVA to compare scores across departments. We obtained the evidence in
Table 5 for questions 1 and 2.
There was a significant difference in logical progression scores among the departments. PHYS department had the highest mean rank, suggesting that most PHYS students displayed higher logical progression scores. PEDU had the lowest logical progression score, whereas ENG students’ scores were higher than PEDU and lower than PHYS. For the first question, the results of the Kruskal–Wallis test showed statistically different scores (KWH = 17.51, p < 0.001) across the departments. For the second question, the results of the Kruskal–Wallis test also showed statistically different scores (KWH = 7.12, p < 0.05). It was clear that there was a higher difference in the distribution of logical progression scores for the first question than for the second question.
4.5. Do Knowledge Level and Skill Types Have Significant Correlations?
The question asked about the correlation between surface (1), procedural (2), and deep (3) knowledge scores and intuitive (1), qualitative (2), visual (3), mathematical (4), and blended (5) skill categories. Knowledge was an ordinal variable, whereas skill types were nominal variables. A Chi-Square test was performed to compare knowledge levels with skill types for two questions. The results are shown in
Table 6.
For question 1, this result showed a significant difference (p < 0.001) between knowledge level and skill type. For example, students with surface knowledge mainly used intuitive skills to make predictions; students with deep knowledge used mathematical skills to do numerical solutions. Students are less likely to engage in other skill types, including qualitative, visual, and blended types; a small proportion (4%) of students employed blended skills. Additionally, there was a significant difference (p < 0.001) between knowledge level and skill type for the second question. For example, students with surface or procedural knowledge mostly used qualitative skills and made explanations. Students were less likely to engage in other skill types, including visual, intuitive, or blended types, even though students also utilized mathematical skills at the surface knowledge level. Students with procedural and deep knowledge preferred qualitative skills in solving the second question.
4.6. Is There a Significant Correlation between Knowledge Level and Logical Progression Level?
In this analysis, the researcher used Spearman Rho’s rank correlation test to correlate ordinal and non-normally distributed data. The investigation of the first question reported a strong correlation between knowledge levels and logical progression levels with
ρ = 0.94,
p < 0.001. The analysis of the second question also displayed a strong correlation between knowledge levels and logical progression levels with
ρ = 0.91,
p < 0.001. This finding indicated that students with profound knowledge tended to show high-quality (excellent or good) logical progression. This statistically significant correlation suggests that the observed relationship is improbable due to chance.
Table 7 presents the results.
4.7. How Do Knowledge and Skill Types Predict Logical Progression?
A structural equation modeling analysis was utilized to determine whether knowledge level and skill type could predict the logical progression process, as shown in
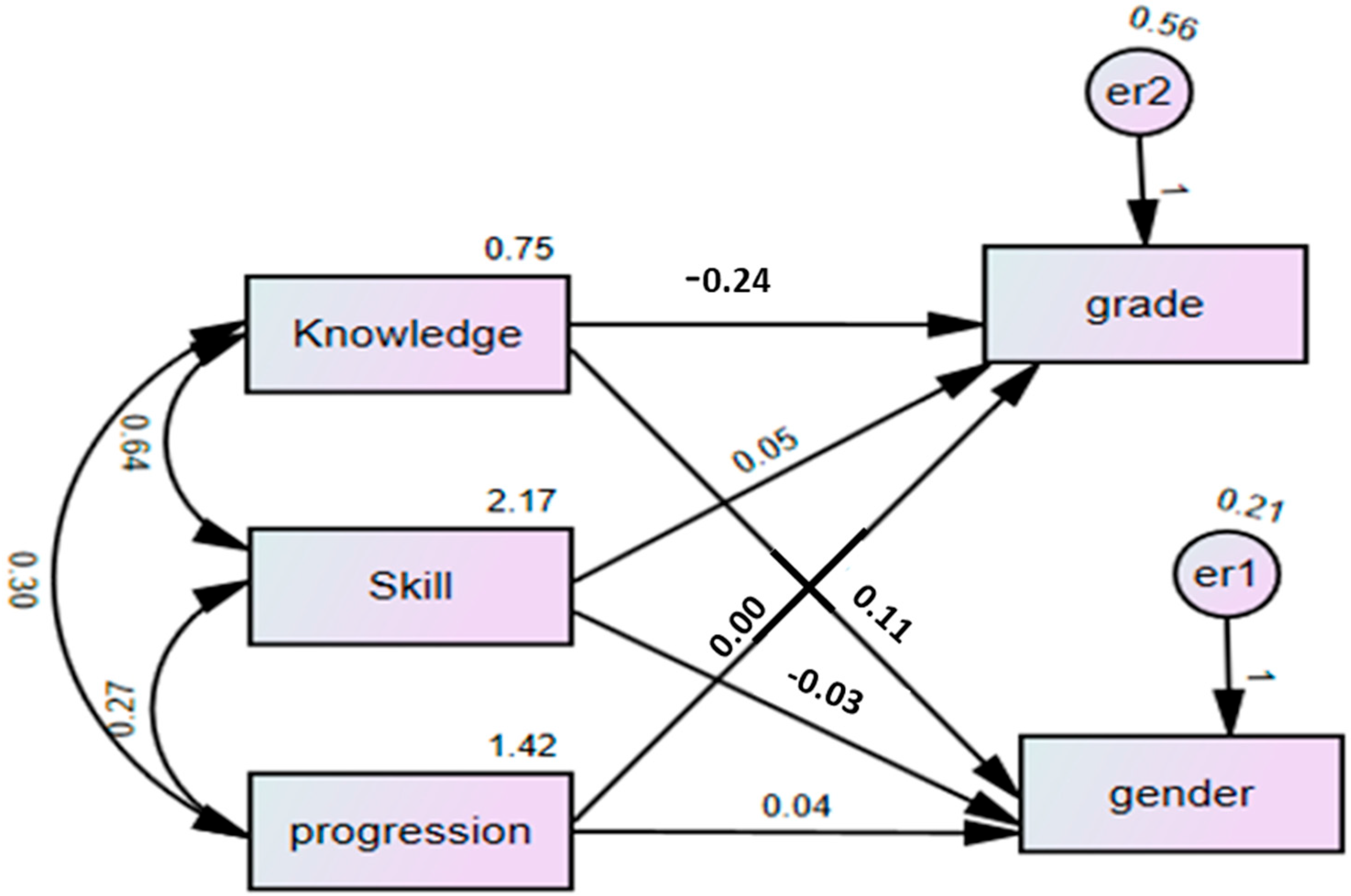
Figure 2 for question 1. The chi-square test of the model fit the data perfectly with comparative fit index (CFI) values above 0.95 and root mean square error of approximation (RMSEA) values below 0.05. The suggested model showed a statistically significant result that knowledge level was a predictor of logical progression level, with an estimate of β = 1.39 and
p < 0.001. This result indicated the positive relationship between knowledge and logical progression level. However, there was a statistically insignificant result between skill type and logical progression level with an estimate of β = −0.001 and
p > 0.1 (
p = 0.979). Specifically, it is reported that skill type is significantly related to knowledge with an estimate of β = 0.64 and
p < 0.01. This result displayed a positive correlation between knowledge level and skill type, indicating that higher levels of knowledge tend to be associated with mathematical or blended skill type. There was an error term for the progression level with a variance of 0.19, showing a variance in progression that was not explained by the model.
The model in
Figure 3 was also utilized to determine whether knowledge level and skill type could predict the logical progression process for question 2. The chi-square test of the model fit the data perfectly with comparative fit index (CFI) values above 0.95 and root mean square error of approximation (RMSEA) values below 0.05. The suggested model showed a statistically significant result that knowledge level was a predictor of logical progression level, with an estimate of β = 1.32 and
p < 0.001. This result indicated the positive relationship between knowledge and logical progression level. However, there was not a statistically significant result between skill type and logical progression level with an estimate of β = −0.039 and
p > 0.1 (
p = 0.205). Specifically, skill type did not have a significant relationship to knowledge level with an estimate of β = −0.11 and
p > 0.01 (
p = 0.082). This result displayed the negative correlation between knowledge and skill type, indicating that higher levels of knowledge level tend to be associated with intuitive and qualitative skill types. There was an error term for the progression level with a variance of 0.21, showing a variance in progression that was not explained by the model.
4.8. How Do Knowledge, Skill, and Logical Progression Scores Predict Gender and Grade Separately in Problem-Solving in Physics?
A structural equation modeling was utilized to determine whether knowledge level, skill type, and logical progression process predicted the gender and grade, as shown in
Figure 4 for question 1. The chi-square test of the model fit the data perfectly with comparative fit index (CFI) values above 0.95 and root mean square error of approximation (RMSEA) values below 0.05. The model showed a statistically significant result that knowledge level was a predictor of grade level, with an estimate of β = −0.239 and
p < 0.01. This result indicated a negative relationship between knowledge and grade level. Lower grades, such as sophomore and junior, tended to have a deep or procedural-level approach. There was also a statistically significant result between knowledge level and gender with an estimate of β = 0.11 and
p < 0.05 (
p = 0.022). This result indicated that gender was the indicator of knowledge approach, especially with male dominance. However, skill type was not significantly related to grade on an estimate of β = 0.049 and
p > 0.01 (
p = 0.269) and to gender on an estimate of β = −0.030 and
p > 0.01 (
p = 0.278). However, gender negatively correlated with the skill that females tended to use qualitative or intuitive skill types, and males tended to use mathematical or blended skills. Logical progression did not show a significant relationship for gender with β = 0.035 and
p > 0.01 (
p = 0.25) and grade β = 0.003 and
p > 0.01 (
p = 0.955). The covariances between skill and knowledge (β = 0.64), between progression and skill (β = 0.27), and between progression and knowledge (β = 0.30) showed a significant relationship (
p ≤ 0.05) with the optimistic estimates. There was an error term for progression level with a variance of 0.21 for gender and 0.56 for grade, showing a variance in progression that was not explained by the model.
For question 2, another model in
Figure 5 was utilized to determine whether knowledge level, skill type, and logical progression level predicted the grade and gender separately. The chi-square test of the model fit the data perfectly with comparative fit index (CFI) values above 0.95 and root mean square error of approximation (RMSEA) values below 0.05. The model below was conducted and did not show a statistically significant result between grade or gender and knowledge, skill, or learning progression. The results showed that knowledge level was not a predictor of grade level, with an estimate of β = 0.186 and
p > 0.01 (
p = 0.321). This result indicated that the positive relationship between knowledge and grade level did not show the actual relationship. There was also no statistically significant result between knowledge level and gender, with an estimate of β = 0.144 and
p > 0.05 (
p = 0.213). This result indicated that gender was not the indicator of knowledge approach. It is also reported that skill type was not significantly related to grade and gender with an estimate of β = 0.044 and
p > 0.01 (
p = 0.381) and β = −0.018 and
p > 0.01 (
p = 0.572), respectively. This result displayed a positive correlation between skill type and grade; higher grades are associated with mathematical skills. However, gender had a negative correlation with the skill that males tended to utilize qualitative skills. Logical progression did not show a significant relationship for gender with β = −0.077 and
p > 0.01 (
p = 0.32) and grade β = −0.029 and
p > 0.01 (
p = 0.818). The covariances between progression and skill type (β = −0.19) and between progression and knowledge (β = 0.62) showed a significant relationship (
p ≤ 0.05). Logical progression and skill type had negative estimates, meaning that students could complete the question accurately while using intuitive or qualitative skills. Logical progression and knowledge approach had a positive relationship, meaning that surface knowledge was related to poor or fair progression. Additionally, the relationship between skill and knowledge (β = −0.11) with (
p = 0.082) was not significant at
p < 0.05 level, meaning that skill type did not relate to the knowledge approach. There was an error term for progression level with a variance of 0.22 for gender and 0.58 for grade, showing a variance in progression that was not explained by the model.
5. Discussion
This study aimed to investigate the variables that played a role in the problem-solving process in physics. The systematic analysis examined the relationship between knowledge approach, skill type, and logical progression level with demographic variables, including gender, grade, and department. These findings contribute to the knowledge base to improve the teaching and learning practices in science fields. To answer the research questions, we utilized two physics questions from a research-based curriculum material developed by McDermott et al. (1996) [
24]. The analysis of college science students’ responses yielded the following results:
More PHYS and PEDU students had surface knowledge, but more ENG students indicated deep knowledge for question 1. For question 2, a more significant proportion of ENG students displayed surface knowledge. Junior and senior male PHYS students tended to have surface knowledge in both questions; however, sophomore ENG male students approached with surface knowledge. Sophomore and Junior male ENG students tended to have procedural knowledge when the purpose was to design an experiment.
The sophomore PEDU students tended to show profound knowledge associated with mathematical skills accurately for question 1. However, there were fewer sophomore PEDU students in the sample. Sophomore PHYS students and junior and sophomore ENG students presented a procedural approach with intuitive and mathematical skills at a nearly good level of accuracy. For question 2, students from three departments presented surface and procedural knowledge approaches associated with qualitative and mathematical skills at neutral accuracy.
There were differences in knowledge approach for male and female students in two questions. Question 1 was a graphical question requiring the interpretation of position versus time graphs. The responses showed a significant difference in knowledge approaches for males and females. In contrast, a negative z score meant that females tended to have a higher level- deep or procedural approach. In the second question, the design included three ramps to measure the speed of balls on the ramps. Data involved the second and third ramps to find the speed of the ball on the first ramp. The question asked students to design an experiment to find the speed of ball one at different time points. The results showed statistically insignificant differences between males and females in knowledge approaches. This result suggested that gender did not contribute to knowledge scores when college science students participated in designing an experiment.
Logical progression addressed how students appropriately and accurately solved the question. The study investigated whether students’ logical progression scores differed across departments, PHYS, PEDU, and ENG. For question 1, there was a significant difference across the departments: the differences between the departments were high for highly sampled PHYS and ENG departments. For question 2, the results showed statistically significant differences, but the difference across the departments was less than in question 1.
Both questions showed a significant difference between knowledge level and skill type. Students utilized consistent skills, for example, intuitive and mathematical for the first question and qualitative and mathematical for the second question.
The knowledge approach and logical progression level had a direct positive correlation. For example, the deep approach displayed a good or excellent-level progression, but the surface approach indicated a fair or poor-level progression.
There was a positive and significant relationship between knowledge and progression levels, but skill type was not an indicator of logical progression. This result showed that even though students preferred mathematical or blended skills, they might have a poor logical progression.
Gender was likely to contribute to knowledge and logical progression levels, but grades might not show a positive relationship with knowledge level. For example, for question 2, senior students displayed a surface approach to solving physics problems.
5.1. Scientific Significance of the Study
This study aimed to understand how sophomore and higher-level college science students approached kinematics problems at a research university in Turkey. The first question focused on examining students’ approach to graphs and interpretation of graphs. With this question, we found that college students tended to use intuitive or prediction and mathematical skills to solve the question. They made predictions on the graph to define approximate speed values from the position versus time graph. The logical progression levels for mathematical skill types were higher than intuitive skill types. The second question required students to define a problem and design a solution. Students defined the data and used them to solve the problem, so they generally engaged in qualitative and mathematical skill types. There was no difference in the logical progression for these skill types in this question. In a former study, Walsh et al. (1993) studied college students’ conceptions of kinematics through interviews [
26]. The study had a qualitative approach to conceptualizing how students related kinematics to everyday experiences and underscored mathematical formalism. Our study employed qualitative and quantitative data collection for quantitative data analysis. Like the results from Testa et al. (2002), college science students tended to read graphs, make predictions, and show deep knowledge to apply mathematical formalism [
27]. Their approach to graphs was to find the slope and derivative of the values without considering a physics context [
28]. Temiz (2014) also presented an experimental apparatus to measure the position and speed of an object [
29]. In this study, for question 2, students needed extensive time to design the experiment. With the given 30 min, they were less likely to explain a comprehensive experiment. Long-term studies should be conducted with college science students to investigate their conceptions.
We also investigated how knowledge approach, skill type, and logical progression level were related to each other and related to gender, department, and grade variables. As Maries & Singh (2023) suggested, students needed to engage in higher-order thinking at more than the application level with synthesis and evaluation levels [
19]. However, in traditional classrooms, students tended to engage in rote memorization or shallower learning experiences. This study aimed to investigate whether students who passed first-year science courses can engage in higher-level knowledge, skill type, and logical progression. The grade less likely served as an indicator to predict students’ knowledge, skill type, and logical progression. For example, sophomore students tended to have deep content knowledge and high-quality logical progression. This result raised the question: If students newly passed the first-year courses, did they tend to remember more? Or did senior students tend to solve the problems with a complex mathematical or Lagrange approach? Our study was new in exploring knowledge, skill type, and logical progression together. Knowledge and logical progression levels had a positive correlation, but skill type did not indicate the logical progression or accuracy of the problem-solving. Although the study aimed for students to engage in scientific practices systematically [
18], most students approached the problems without considering a physics context to reach the solution or product. Therefore, science classrooms should aim to move beyond learning science to promote learning about characteristics of science through engaging in investigation, constructing explanations, and argumentation in an active process [
20,
30].
5.2. Limitations
The results were limited to students from three departments, PHYS, ENG, and PEDU, and a larger sample could be recruited for better statistical analysis. Specifically, we had 23 PEDU students because the PEDU department included fewer students than the PHYS and ENG departments. Secondly, we could increase the number of females in the sample. Thirdly, we provided 30 min to solve two problems. We could design further studies so that students would have more time individually. They might need to discuss their conceptions with peers, so focus group discussion sessions could be added to the study. Fourthly, the methodological approach could be improved to collect qualitative and quantitative data with a mixed-method design. Fifth, we did not have any interaction with college science instructors. We could design a professional development program for college instructors on innovative pedagogies and assess students’ knowledge, skill type, and logical progression before and after the instruction.
5.3. Implications
This study showed that college students tended to solve familiar problems and had difficulty with context-based problems. For example, question 1 was a typical graphical problem, and students had consistent knowledge and logical progression levels. However, question 2 required students to think about the context of a ramp. Students tended to use mathematical skills without any explanation of the question. Therefore, we need to focus on teaching physics in a context that guides students in understanding how a phenomenon occurs in everyday life. In these two problems, we assumed that students would approach them differently. We found different knowledge levels, skill types, and logical progression levels. The same students might have different knowledge approaches, skill types, and logical progression levels based on separate questions. We need to examine how students develop knowledge approach (Is it related to introductory course grade?), skill type (does context matter in skill type?), logical progression level (how accurately can students approach the problem?), and how teachers promote students’ scientific conceptions. Therefore, college science education should emphasize innovative pedagogies and curriculum materials. Systematic longitudinal studies should investigate how students’ knowledge level, skill type, and logical progression level change during their college years. The current study focused on two problems in kinematics. Further research should focus on other physics contents with a larger sample size and long diagnostic questions.