A Review of Research on Mathematics Teacher Educator Knowledge: Mapping the Terrain
Abstract
1. Introduction
2. Conceptualizing MTE Knowledge
3. Method
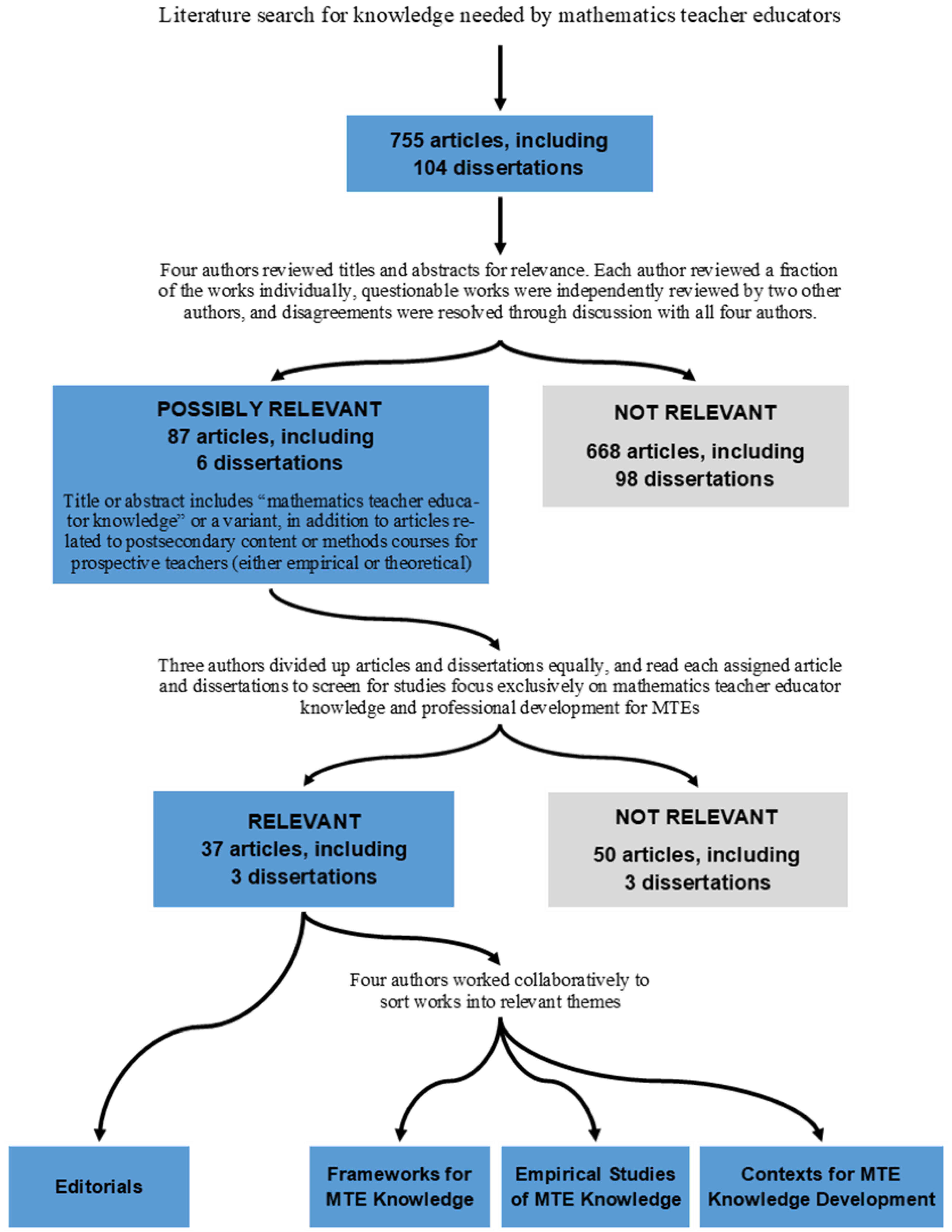
Literature Search
4. Selection of Articles
5. Review of Articles
6. Results
Summary of the State of Research on MTE Knowledge
7. Frameworks for MTE Knowledge
7.1. Comprehensive Frameworks for MTE Knowledge
7.2. Components of a Framework for MTE Knowledge
8. Empirical Studies of MTE Knowledge
8.1. Studies of How MTE Knowledge Is Leveraged in Teaching PTs
8.2. Self-Studies of MTE Knowledge in Practice
9. Contexts for MTE Knowledge Development
9.1. Conducting Research to Develop MTE Knowledge
9.2. Professional Learning Experiences to Develop MTE Knowledge
9.3. Developing MTE Knowledge through Self-Study
10. Discussion
11. Conceptual and Structural Similarities across MTE Knowledge Frameworks
12. Expanding the Contexts for MTE Knowledge Development
13. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Brown, C.; Borko, H. Becoming a math teacher. In Handbook of Research on Math Teaching and Learning: A Project of the National Council of Teachers of Mathematics; Grouws, D.A., Ed.; Macmillan Publishing Co., Inc.: New York, NY, USA, 1992; pp. 209–239. [Google Scholar]
- Even, R.; Ball, D. The Professional Education and Development of Teachers of Mathematics: The 15th ICMI Study; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Association of Mathematics Teacher Educators. Standards for Preparing Teachers of Mathematics. 2017. Available online: http://amte.net/standards (accessed on 18 June 2018).
- Ball, D.; Thames, M.; Phelps, G. Content knowledge for teaching: What makes it special? J. Teach. Educ. 2008, 59, 389–407. [Google Scholar] [CrossRef]
- Conference Board of the Mathematical Sciences. The Mathematical Education of Teachers II; American Mathematical Society and Mathematical Association of America: Providence, RI, USA; Washington, DC, USA, 2012. [Google Scholar]
- Adler, J. Professional knowledge matters in mathematics teaching. In Proceedings of the International Congress of Mathematicians, Hyderabad, India, 19–27 August 2010. [Google Scholar]
- Dinham, S. The quality teaching movement in Australia encounters difficult terrain: A personal perspective. Aust. J. Educ. 2013, 57, 91–106. [Google Scholar] [CrossRef]
- Greenberg, J.; Walsh, K. No Common Denominator: The Preparation of Elementary Teachers in Mathematics by America’s Education Schools; National Council on Teacher Quality: Washington, DC, USA, 2008. [Google Scholar]
- Jaworski, B. Mathematics teacher educator learning and development: An introduction. In The International Handbook of Mathematics Teacher Education: The Mathematics Teacher Educator as a Developing Professional; Jaworski, B., Wood, T., Eds.; Sense Publishers: Rotterdam, The Netherlands, 2008; pp. 1–17. [Google Scholar]
- Beswick, K.; Chapman, O. Mathematics teacher educators’ knowledge for teaching. In Proceedings of the 12th International Congress on Mathematical Education, Seoul, Republic of Korea, 8–15 July 2012; Cho, S.J., Ed.; Springer: Cham, Switzerland, 2015; pp. 629–632. [Google Scholar]
- Goos, M.; Beswick, K. (Eds.) The Learning and Development of Mathematics Teacher Educators: International Perspectives and Challenges; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Welder, R.; Appova, A.; Olanoff, D.; Taylor, C.; Kulow, T. Improving preservice elementary teacher education through the preparation and support of elementary mathematics teacher educators. In Proceedings of the 38th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Tucson, AZ, USA, 3–6 November 2016; Wood, M.B., Turner, E.E., Civil, M., Eli, J.A., Eds.; University of Arizona: Tucson, AZ, USA, 2016; pp. 1713–1722. [Google Scholar]
- Appova, A.; Welder, R.; Feldman, Z. (Eds.) Supporting Mathematics Teacher Educators’ Knowledge and Practices for Teaching Content to Prospective (Grades K-8) Teachers; Special Issue: The Mathematics Enthusiast; ScholarWorks; University of Montana: Missoula, MT, USA, 2020; Volume 17, Issues 2 and 3. [Google Scholar]
- Beswick, K.; Goos, M. Mathematics teacher educator knowledge: What do we know and where to from here? J. Math. Teach. Educ. 2018, 21, 417–427. [Google Scholar] [CrossRef]
- Beswick, K.; Chapman, O. (Eds.) International Handbook of Mathematics Teacher Education: Vol. 4. The Mathematics Teacher Educator as a Developing Professional, 2nd ed.; Brill Sense: Leiden, The Netherlands, 2020. [Google Scholar]
- Alderton, J. Exploring self-study to improve my practice as a mathematics teacher educator. Stud. Teach. Educ. 2008, 4, 95–104. [Google Scholar] [CrossRef]
- Taylan, R.; da Ponte, J. Investigating PCK-in-action. REDIMAT-J. Res. Math. Educ. 2016, 5, 212–234. [Google Scholar] [CrossRef][Green Version]
- Chauvot, J. Grounding practice in scholarship, grounding scholarship in practice: Knowledge of a mathematics teacher educator-researcher. Teach. Teach. Educ. 2009, 25, 357–370. [Google Scholar]
- Zaslavsky, O. Meeting the challenges of math teacher education through design and use of tasks that facilitate teacher learning. In The International Handbook of Mathematics Teacher Education: The Mathematics Teacher Educator as a Developing Professional; Jaworski, B., Wood, T., Eds.; Sense Publishers: Rotterdam, The Netherlands, 2008; Volume 4, pp. 93–114. [Google Scholar]
- Li, W.; Castro Superfine, A. Mathematics teacher educators’ perspectives on the design of content courses for elementary preservice teachers. J. Math. Teach. Educ. 2016, 21, 179–201. [Google Scholar]
- Veselovsky, A. Knowledge Base of Math Teacher Educators: A Goals-Knowledge-Practice Approach. Ph.D. Thesis, University of Illinois at Chicago, Chicago, IL, USA, 2017. [Google Scholar]
- Mullis, I.; Martin, M.; Goh, S.; Cotter, K. (Eds.) TIMSS 2015 Encyclopedia: Education Policy and Curriculum in Mathematics and Science; Boston College: Chestnut Hill, MA, USA, 2016; Available online: http://timssandpirls.bc.edu/timss2015/encyclopedia/ (accessed on 9 September 2018).
- Coggshall, J.; Bivona, L.; Reschly, D. Evaluating the Effectiveness of Teacher Preparation Programs for Support and Accountability; National Comprehensive Center for Teacher Quality: Washington, DC, USA, 2012. [Google Scholar]
- Masingila, J.O.; Olanoff, D.E.; Kwaka, D.K. Who teaches mathematics content courses for prospective elementary teachers in the United States? Results of a national survey. J. Math. Teach. Educ. 2012, 15, 347–358. [Google Scholar]
- Leinhardt, G.; Putnam, R.; Stein, M.; Baxter, J. Where subject matter knowledge matters. In Advances in Research on Teaching; Brophy, J., Ed.; JAI Press: Greenwich, CT, USA, 1991; Volume 2, pp. 87–113. [Google Scholar]
- Shulman, L. Those who understand: Knowledge growth in teaching. Educ. Res. 1986, 15, 4–14. [Google Scholar]
- Hiebert, J.; Morris, A. Building a knowledge base for teacher education: An experience in K-8 mathematics teacher preparation. Elem. Sch. J. 2009, 109, 475–490. [Google Scholar]
- Ball, D.; Bass, H. Interweaving content and pedagogy in teaching and learning to teach: Knowing and using mathematics. In Multiple Perspectives on Mathematics of Teaching and Learning; Boaler, J., Ed.; Ablex Publishing: Westport, CT, USA, 2000; pp. 83–104. [Google Scholar]
- Cochran-Smith, M.; Lytle, S. Relationships of knowledge and practice: Teacher learning in communities. Rev. Res. Educ. 1999, 24, 249–305. [Google Scholar]
- Jaworski, B.; Huang, R. Teachers and didacticians: Key stakeholders in the process of developing mathematics teaching. ZDM Math. Educ. 2014, 46, 173–188. [Google Scholar] [CrossRef]
- Rogoff, B. Evaluating developing in the process of participation: Theory, methods, and practice build on each other. In Change and Development; Amsel, E., Renninger, A., Eds.; Lawrence Erlbaum: Hillsdale, NJ, USA, 1997; pp. 265–285. [Google Scholar]
- Bergsten, C.; Grëvholm, B. Knowledgeable teacher educators and linking practices. In The Mathematics Teacher Educator as a Developing Professional; Wood, T., Jaworski, B., Eds.; Sense Publishers: Rotterdam, The Netherlands, 2008; pp. 223–246. [Google Scholar]
- Zopf, D. Mathematical Knowledge for Teaching Teachers: The Mathematical Work of and Knowledge Entailed by Teacher Education. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2010. Available online: http://deepblue.lib.umich.edu/bitstream/2027.42/77702/1/dzopf_1.pdf (accessed on 26 May 2018).
- Creswell, J. Qualitative Inquiry and Research Design: Choosing among Five Approaches; SAGE Publications: Newbury Park, CA, USA, 2012. [Google Scholar]
- Shaughnessy, M.; Garcia, N.; Selling, S.; Ball, D. What knowledge and skill do math teacher educators need and (how) can we support its development? In Proceedings of the 38th Annual Conference of the North American Chapter of the International Group for the Psychology of Mathematics Education, Tucson, AZ, USA, 3–6 November 2016; Wood, M.B., Turner, E.E., Civil, M., Eli, J.A., Eds.; University of Arizona: Tucson, AZ, USA, 2016; pp. 813–820. [Google Scholar]
- Selmer, S.; Bernstein, M.; Bolyard, J. Multilayered knowledge: Understanding the structure and enactment of teacher educators’ specialized knowledge base. Teach. Dev. 2016, 20, 437–457. [Google Scholar] [CrossRef]
- Prestage, S.; Perks, P. Towards a pedagogy of initial teacher education. In Proceedings of the BSRLM Day Conference, Coventry, UK, 3 November 1999; Bills, L., Ed.; University of Warwick: Coventry, UK, 1999; pp. 91–96. [Google Scholar]
- Cohen, D.; Raudenbush, S.; Ball, D. Resources, instruction, and research. Educ. Eval. Policy Anal. 2003, 25, 119–142. [Google Scholar] [CrossRef]
- Jaworski, B. Mathematics teaching: What is it? Learn. Math. 1992, 12, 8–14. [Google Scholar]
- Mason, J. Enabling teachers to be real teachers: Necessary levels of awareness and structure of attention. J. Math. Teach. Educ. 1998, 1, 243–267. [Google Scholar]
- Zaslavsky, O.; Leikin, R. Professional development of math teacher educators: Growth through practice. J. Math. Teach. Educ. 2004, 7, 5–32. [Google Scholar] [CrossRef]
- Perks, P.; Prestage, S. Tools for learning about teaching and learning. In The International Handbook of Mathematics Teacher Education: The Mathematics Teacher Educator as a Developing Professional; Jaworski, B., Wood, T., Eds.; Sense Publishers: Rotterdam, The Netherlands, 2008; Volume 4, pp. 31–56. [Google Scholar]
- Castro Superfine, A.; Prasad, P.V.; Welder, R.M.; Olanoff, D.; Eubanks-Turner, C. Exploring mathematical knowledge for teaching teachers: Supporting prospective teachers’ relearning of mathematics. In Supporting Mathematics Teacher Educators’ Knowledge and Practices for Teaching Content to Prospective (Grades K-8) Teachers; Special Issue: The Mathematics Enthusiast; Appova, A., Welder, R.M., Feldman, Z., Eds.; ScholarWorks; University of Montana: Missoula, MT, USA, 2020; Volume 17, pp. 367–402. ISSN 1551-3440. [Google Scholar]
- Olanoff, D.; Welder, R.M.; Prasad, P.V.; Castro Superfine, A. Fractalization as a metaphor for mathematical knowledge for teaching teachers: Synthesizing the frameworks and exploring the consequences. In Proceedings of the 40th Annual Conference of the North American Chapter of the International Group for the Psychology of Mathematics Education, Greenville, SC, USA, 15–18 November 2018; Hodges, T.E., Roy, G.J., Tyminski, A.M., Eds.; University of South Carolina: Greenville, SC, USA; Clemson University: Clemson, SC, USA, 2018; pp. 500–503. [Google Scholar]
- Hauk, S.; Jackson, B.; Tsay, J. Those who teach the teachers: Knowledge growth in teaching for math teacher educators. In Proceedings of the 20th Annual Conference on Research in Undergraduate Mathematics Education, San Diego, CA, USA, 23–25 February 2017; Weinberg, A., Rasmussen, C., Rabin, J., Wawro, M., Brown, S., Eds.; pp. 428–439. [Google Scholar]
- Hauk, S.; Toney, A.; Jackson, B.; Nair, R.; Tsay, J.-J. Developing a model of pedagogical content knowledge for secondary and post-secondary mathematics instruction. Dialogic Pedagog. Int. Online J. 2014, 2, 16–40. [Google Scholar]
- Escudero-Avila, D.; Montes, M.; Contreras, L.C. What do mathematics teacher educators need to know? Reflections emerging from the content of mathematics teacher education. In The Learning and Development of Mathematics Teacher Educators: International Perspectives and Challenges; Goos, M., Beswick, K., Eds.; Springer: Cham, Switzerland, 2021; pp. 23–40. [Google Scholar]
- Chick, H.; Beswick, K. Educating Boris: An examination of PCK for mathematics teacher educators. In Mathematics Education: Yesterday, Today and Tomorrow, Proceedings of the 36th Annual Conference of the Math Education Research Group of Australasia, Melbourne, Australia, 7–11 July 2013; Steinle, V., Ball, L., Bardini, C., Eds.; MERGA: Melbourne, Australia, 2013; pp. 170–177. [Google Scholar]
- Chick, H.; Beswick, K. Teaching teachers to teach Boris: A framework for mathematics teacher educator PCK. J. Math. Teach. Educ. 2017, 21, 475–499. [Google Scholar] [CrossRef]
- Chauvot, J. Curricular knowledge and the work of mathematics teacher educators. Issues Teach. Educ. 2008, 17, 83. [Google Scholar]
- Olanoff, D. Mathematical Knowledge for Teaching Teachers: The Case of Multiplication and Division of Fractions. Ph.D. Thesis, Syracuse University, Syracuse, NY, USA, 2011. [Google Scholar]
- Felton-Koestler, M. Teaching sociopolitical issues in math teacher preparation: What do mathematics teacher educators need to know? In Supporting Mathematics Teacher Educators’ Knowledge and Practices for Teaching Content to Prospective (Grades K-8) Teachers; Special Issue: The Mathematics Enthusiast; Appova, A., Welder, R., Feldman, Z., Eds.; ScholarWorks: Missoula, MT, USA, 2020; Volume 17, pp. 435–468. ISSN 1551-3440. [Google Scholar]
- Ball, D.L.; Bass, H. With an eye on the mathematical horizon: Knowing mathematics for teaching to learners’ mathematical futures. In Proceedings of the 43rd Jahrestagung für Didaktik der Mathematik, Oldenburg, Germany, 1–4 March 2009; Available online: https://eldorado.tu-dortmund.de/bitstream/2003/31305/1/003.pdf (accessed on 14 June 2018).
- Rowland, T.; Huckstep, P.; Thwaites, A. Elementary teachers’ math subject knowledge: The knowledge quartet and the case of Naomi. J. Math. Teach. Educ. 2005, 8, 255–281. [Google Scholar] [CrossRef]
- Castro Superfine, A.; Li, W. Developing mathematical knowledge for teaching teachers: A model for the professional development of teacher educators. Issues Teach. Educ. 2014, 23, 113–132. [Google Scholar]
- Jankvist, U.; Clark, K.; Mosvold, R. Developing mathematical knowledge for teaching teachers: Potentials of history of mathematics in teacher educator training. J. Math. Teach. Educ. 2020, 23, 311–332. [Google Scholar] [CrossRef]
- John, P. The teacher educator’s experience: Case studies of practical professional knowledge. Teach. Teach. Educ. 2002, 18, 323–341. [Google Scholar] [CrossRef][Green Version]
- Zazkis, R.; Mamolo, A. From disturbance to task design, or a story of a rectangular lake. J. Math. Teach. Educ. 2018, 21, 501–516. [Google Scholar] [CrossRef]
- Muir, T.; Wells, J.; Chick, H. Developing an understanding of what constitutes mathematics teacher educator PCK: A case study of a collaboration between two teacher educators. Aust. J. Teach. Educ. 2017, 42, 60–79. [Google Scholar] [CrossRef]
- Masingila, J.; Olanoff, D.; Kimani, P. Mathematical knowledge for teaching teachers: Knowledge used and developed by math teacher educators in learning to teach via problem solving. J. Math. Teach. Educ. 2018, 21, 429–450. [Google Scholar] [CrossRef]
- Mendoza Álverez, J.; Rhoads, K.; Jorgensen, T. Mathematics teacher educators learning from efforts to facilitate the learning of key mathematics concepts while modelling evidence-based teaching practice. In The Learning and Development of Mathematics Teacher Educators: International Perspectives and Challenges; Goos, M., Beswick, K., Eds.; Springer: Cham, Switzerland, 2020; pp. 305–341. [Google Scholar]
- Rowland, T.; Turner, F.; Thwaites, A. Research into teacher knowledge: A stimulus for development in MTE practice. ZDM Math. Educ. 2014, 46, 317–328. [Google Scholar] [CrossRef]
- Peled, I.; Hershkovitz, S. Evolving research of math teacher educators: The case of non-standard issues in solving standard problems. J. Math. Teach. Educ. 2004, 7, 299–327. [Google Scholar] [CrossRef]
- Jaworski, B. The plurality of knowledge growth in mathematics teaching. In Mathematics Teacher Education: Critical International Perspectives; Jaworski, B., Wood, T., Dawson, A., Eds.; Falmer Press: London, UK, 1999. [Google Scholar]
- Sztajn, P.; Ball, D.; McMahon, T. Designing learning opportunities for math teacher developers. In The Work of Mathematics Teacher Educators: Continuing the Conversations; Lynch-Davis, K., Rider, R., Eds.; Association of Mathematics Teacher Educators Monograph Series 2006; Information Age Publishing: Charlotte, NC, USA, 2015; Volume 3, pp. 149–162. [Google Scholar]
- Castro Superfine, A.; Li, W. Exploring the mathematical knowledge needed for teaching. J. Teach. Educ. 2014, 65, 303–314. [Google Scholar] [CrossRef]
- Van, L.; Mao, S.; Cnudde, V. Improving pedagogical knowledge on rational numbers of Cambodian teacher trainers. Glob. Educ. Rev. 2018, 5, 196–211. [Google Scholar]
- Golding, J.; Batiibwe, M. A design approach to mathematics teacher educator development in East Africa. J. Res. Adv. Math. Educ. 2021, 6, 1–16. [Google Scholar] [CrossRef]
- Roesken-Winter, B.; Schüler, S.; Stahnke, R.; Blömeke, S. Effective CPD on a large scale: Examining the development of multipliers. ZDM Math. Educ. 2015, 47, 13–25. [Google Scholar] [CrossRef]
- Welder, R.M.; Prasad, P.V.; Castro Superfine, A.; Olanoff, D. Developing a framework for mathematical knowledge for improving the content preparation of elementary teachers. In Proceedings of the 39th Annual Conference of the North American Chapter of the International Group for the Psychology of Mathematics Education, Indianapolis, IN, USA, 5–8 October 2017; Galindo, E., Newton, J., Eds.; Purdue University: Indianapolis, IN, USA, 2017; p. 637. [Google Scholar]
- Zazkis, R. Relearning Mathematics: A Challenge for Prospective Elementary School Teachers; Information Age Publishing: Charlotte, NC, USA, 2011. [Google Scholar]
- Goos, M. Investigating the professional learning and development of math teacher educators: A theoretical discussion and research agenda. In Crossing Divides: Proceedings of the 32nd Annual Conference of the Mathematics Education Research Group of Australasia, Palmerston North, New Zealand, 5–9 July 2009; Hunter, R., Bicknell, B., Burgess, T., Eds.; MERGA: Palmerston, NZ, USA, 2009; pp. 209–216. [Google Scholar]
- Adler, J.; Ball, D.; Krainer, K.; Lin, F.; Novotna, J. Reflections on an emerging field: Researching mathematics teacher education. Educ. Stud. Math. 2005, 60, 359–381. [Google Scholar] [CrossRef]
- Goodwin, A.; Smith, L.; Souto-Manning, M.; Cheruvu, R.; Tan, M.; Reed, R.; Taveras, L. What should teacher educators know and be able to do? Perspectives from practicing teacher educators. J. Teach. Educ. 2014, 65, 284–302. [Google Scholar] [CrossRef]
- Lovin, L.; Sanchez, W.; Leatham, K.; Chauvot, J.; Kastberg, S.; Norton, A. Examining beliefs and practices of self and others: Pivotal points for change and growth for mathematics teacher educators. Stud. Teach. Educ. 2012, 8, 51–68. [Google Scholar] [CrossRef]
- Schuck, S.; Pereira, P. (Eds.) What Counts in Teaching Mathematics: Adding Value to Self and Content; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Lampert, M.; Graziani, F. Instructional activities as a tool for teachers’ and teacher educators’ learning. Elem. Sch. J. 2009, 109, 491–509. [Google Scholar] [CrossRef]
- Chapman, O. Mathematics teacher educator knowledge for teaching teachers. In The Learning and Development of Mathematics Teacher Educators: International Perspectives and Challenges; Goos, M., Beswick, K., Eds.; Springer: Cham, Switzerland, 2021; pp. 403–417. [Google Scholar]
| Category | Subcategory | Description |
|---|---|---|
| Frameworks for MTE Knowledge (n = 14) | Complete Frameworks for MTE Knowledge (n = 9) | Proposes a complete framework for MTE knowledge; most articles are theoretical |
| Components of a Framework for MTE Knowledge (n = 5) | Proposes different components of a framework for MTE knowledge | |
| Empirical Studies of MTE Knowledge (n = 10) | Studies of MTE Knowledge (n = 6) | Focuses on the knowledge MTEs use when teaching PTs |
| Studies of Relationship Between MTE Knowledge and Practice (n = 4) | Describes different aspects of MTE instructional practice and decision making | |
| Contexts for MTE Knowledge Development (n = 9) | Conducting Research to Develop MTE Knowledge (n = 2) | Describes how MTEs conducting research in math teacher education enhances MTE knowledge |
| Professional Learning to Develop MTE Knowledge (n = 6) | Describes PL workshops, experiences, and coursework for MTEs designed to further develop their knowledge | |
| Developing MTE Knowledge Through Self-Study (n = 1) | Focuses on MTEs’ conducting self-studies of their own teaching practice and describes it as a means by which MTEs can further develop their knowledge |
| Author(s) | Year | Origin | Research Purpose |
|---|---|---|---|
| Comprehensive Frameworks for MTE Knowledge (n = 9) | |||
| Castro Superfine, Prasad, Welder, Olanoff, and Eubanks-Turner | 2020 | USA | Proposes a conceptualization of MKTT that extends from and contains analogous domains of MKT [4] |
| Chavout | 2009 | USA | Proposes a conceptualization of MTE knowledge that builds on the MKT framework [4]; suggests an “MTE as researcher” knowledge subdomain |
| Escudero-Avila, Montes, and Contreres | 2021 | Mexico and Spain | Proposes a conceptualization of MTE knowledge with seven subdomains based on a review of research with and about mathematics teachers |
| Hauk, Jackson, and Tsay | 2017 | USA | Builds on Ball et al.’s MKT framework [4] to propose a framework for the “mathematical knowledge for teaching future teachers” |
| Mason | 1998 | UK | Conceptualizes MTE knowledge as including different levels of awareness |
| Olanoff, Welder, Prasad, and Castro Superfine | 2018 | USA | Proposes a conceptualization of MKTT that extends from and contains analogous domains of MKT [4] |
| Perks and Prestage | 2008 | UK | Proposes an MTE knowledge “tetrahedron” based on their teacher knowledge “tetrahedron” [37] |
| Shaughnessy, Garcia, Selling, and Ball | 2016 | USA | Builds on Ball et al.’s MKT framework [4] and Cohen et al.’s instructional triangle [38] |
| Zaslavsky and Leikin | 2004 | Israel | Builds on Jaworski’s “teaching triad model” for teacher knowledge [39] |
| Components of a Framework for MTE Knowledge (n = 5) | |||
| Chavout | 2008 | USA | Proposes curricular knowledge for MTEs: knowledge of programs and materials, lateral and vertical curriculum knowledge, indications and contraindications of curricula |
| Chick and Beswick | 2013 | Australia | Proposes PCK for MTEs: knowledge of examples, curricula, student thinking, common misconceptions |
| Chick and Beswick | 2017 | Australia | Proposes PCK for MTEs |
| Felton-Koestler | 2020 | USA | Proposes MTE knowledge for sociopolitical mathematics teaching: knowledge of sociopolitical issues and sociopolitical curriculum |
| Olanoff | 2011 | USA | Proposes components of MTE knowledge for teaching multiplication and division: multiple representations of topics, how topics relate, how to identify student learning goals in relation to topics, and how to design and use topic assessments |
| Author(s) | Year | Origin | Research Question(s) |
|---|---|---|---|
| How MTE Knowledge is Leveraged in Teaching PTs (n = 6) | |||
| Castro Superfine and Li | 2014a | USA | What forms of knowledge do MTEs use, and how is this knowledge different from that of teachers? |
| Jankvist, Clark, and Mosvold | 2020 | Denmark, USA, and Norway | What knowledge do MTEs leverage when describing how they would engage in certain tasks of teaching with PTs? |
| John | 2002 | UK | What are the knowledge and expertise that teacher educators hold and use? |
| Veselovsky | 2017 | USA | What goals for teaching and learning do MTEs develop in their teaching of content courses? What practices do they foster and why do they draw on particular forms of knowledge? |
| Zazkis and Mamolo | 2016 | Canada | How can the work of an MTE be explained in terms of levels of awareness [40] and knowledge of the mathematical horizon [53]? |
| Zopf | 2010 | USA | What is the work of teaching math to teachers, and what are the knowledge demands entailed by this work? |
| Self-Studies of MTE Knowledge in Practice (n = 4) | |||
| Masingila, Olanoff, and Kimani | 2018 | USA | When MTEs reflect on their teaching in a community of practice, what types of MKTT do they use and develop? |
| Mendoza Álverez, Rhoads, and Jorgensen | 2020 | USA | How is MTEs’ knowledge developed as they implement and revise tasks in math courses for PTs? |
| Muir, Wells, and Chick | 2017 | Australia | What aspects of MTE PCK are evident when MTEs observe each other’s practice? In what ways do MTEs make their teaching practice explicit to PTs? |
| Muir, Livy, and Downton | 2021 | Australia | How does the knowledge needed by MTEs differ from that required by schoolteachers? To what extent is the Knowledge Quartet [54] applicable to MTEs? |
| Author(s) | Year | Origin | Research Question(s) |
|---|---|---|---|
| Conducting Research to Develop MTE Knowledge (n = 2) | |||
| Peled and Hershkovitz | 2004 | Israel | In what ways do various phases of research conducted by MTEs afford them learning opportunities, and what conditions contribute to their learning? |
| Rowland, Turner, and Thwaites | 2014 | UK | In what ways do MTEs experience changes in their awareness and practice as a consequence of conducting research in math education? |
| Professional Learning Experiences to Develop MTE Knowledge (n = 6) | |||
| Castro Superfine and Li | 2014b | USA | What are MTEs’ design decisions and goals for their math content courses? How do MTEs achieve these goals? What challenges do MTEs encounter as they carry out these goals? |
| Golding and Batiibwe | 2021 | UK and Uganda | What are the affordances and constraints in the design of a Mathematical Thinking and Instructional Technology course for MTEs? What impact did the course have on MTE knowledge? |
| Roesken-Winter, Schüler, Stahnke and Blömeke | 2015 | Germany and Norway | What was the impact of a year-long course for MTEs on MTE content knowledge and pedagogical content knowledge? To what extent did the design principles applied in the course become relevant for MTEs’ work? |
| Shaughnessy, Garcia, Selling, and Ball | 2016 | USA | What knowledge/skills are demanded of MTEs to engage in practice-based teacher education? What structures are useful for supporting novice MTEs’ learning of such knowledge/skills? |
| Szatjn, Ball, and McMahon | 2006 | USA | How can researchers design professional learning models for MTEs focused on developing their understanding of MKT for PTs? |
| Van, Mao, and Cnudde | 2018 | Cambodia | What is the impact of a professional development intervention on MTEs’ PCK and content knowledge of rational numbers? |
| Developing MTE Knowledge Through Self-Study (n = 1) | |||
| Taylan and da Ponte | 2016 | Turkey and Portugal | How does teaching and researching students support MTEs in developing MKTT? |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castro Superfine, A.; Olanoff, D.; Welder, R.M.; Prasad, P.V. A Review of Research on Mathematics Teacher Educator Knowledge: Mapping the Terrain. Educ. Sci. 2024, 14, 810. https://doi.org/10.3390/educsci14080810
Castro Superfine A, Olanoff D, Welder RM, Prasad PV. A Review of Research on Mathematics Teacher Educator Knowledge: Mapping the Terrain. Education Sciences. 2024; 14(8):810. https://doi.org/10.3390/educsci14080810
Chicago/Turabian StyleCastro Superfine, Alison, Dana Olanoff, Rachael M. Welder, and Priya V. Prasad. 2024. "A Review of Research on Mathematics Teacher Educator Knowledge: Mapping the Terrain" Education Sciences 14, no. 8: 810. https://doi.org/10.3390/educsci14080810
APA StyleCastro Superfine, A., Olanoff, D., Welder, R. M., & Prasad, P. V. (2024). A Review of Research on Mathematics Teacher Educator Knowledge: Mapping the Terrain. Education Sciences, 14(8), 810. https://doi.org/10.3390/educsci14080810







