Professional Support in Teaching Mathematics through Guided Discovery: The Role of Agency on Multiple Levels
Abstract
1. Introduction
- What are the challenges and the process of growth of a novice teacher while being immersed in using guided discovery in their classroom with mentoring support in planning and reflection?
- What aspects of the mentoring structure are effective for giving support in guided discovery, and how can it be improved and adapted to involve a larger number of teachers?
2. Background
2.1. Guided Discovery
- Students’ creativity and responsibility in learning.
- Teachers’ creativity and responsibility in teaching.
- Aptitude to utilize students’ ideas in classroom dialogue.
- Problem- and activity-centered.
- The unity of mathematics; topics interlocked during instruction.
- Elongated, spiral buildup from concrete to abstract.
- Conveyance of real mathematics towards a broader student population.
- Enhancing students’ competency from their individual level.
2.2. Mentoring Framework
- Mentors designed tasks to be adapted and used by the teacher.
- Mentors and the teacher co-planned lessons.
- The teacher reflected on her lessons in writing and during mentoring sessions. Mentors gave feedback on these reflections.
- The mentors observed lessons and gave feedback to the teacher.
3. Methods
- Pre- and post-unit interviews with Hanna (semi-structured interviews about Hanna’s former experience, beliefs, aims, challenges, progress).
- Video recordings of classes.
- Voice recordings of mentoring sessions.
- Emails exchanged between Hanna and the mentors.
- Written post-lesson reflections by Hanna.
- Post-unit questionnaire for students (with open-ended questions about their experiences during the intervention and Likert scale questions about their backgrounds and experiences).
- Voice recordings of post-unit interviews with three students.
- A.
- Lesson considered a failure by Hanna (students did not have a negative perception of any particular lesson, but Hanna perceived students to be passive during this one).
- B.
- Lesson considered an outstanding success by Hanna and the students.
- C.
- Lesson where Hanna piloted tasks she designed herself (which she identified as a main aim during the unit).
4. Results
- Student affect and growth: students’ view.
- Student affect and growth: teacher’s view.
- Teacher affect and growth.
- Teacher agency.
- What helped teacher learning.
4.1. Sample Tasks
4.1.1. Lesson A (with “Paper-Slip Task”)
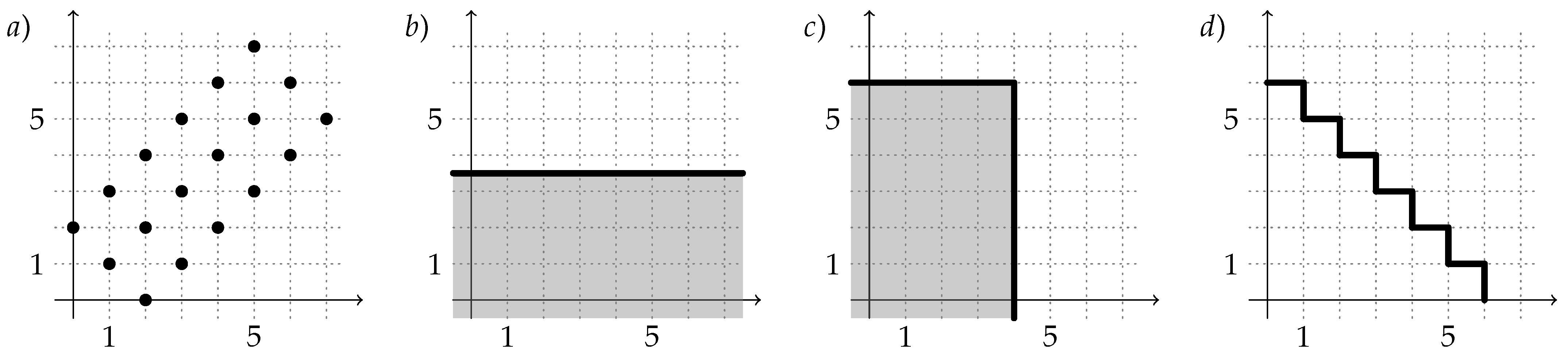
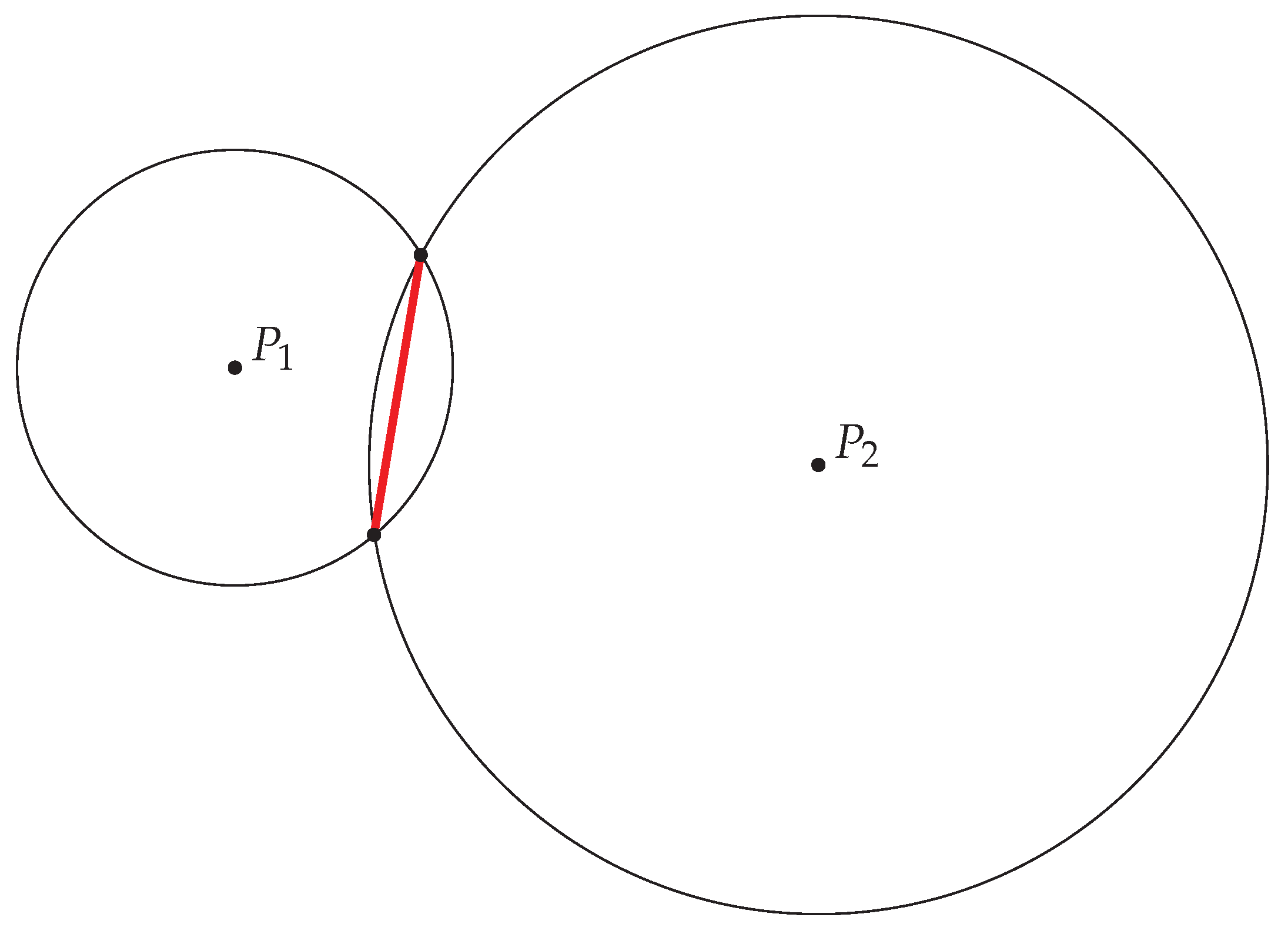
4.1.2. Lesson B (Distance Guessing and Circle Equation)
- Let us speak about what distance means. We tried , and the software said its distance from is . What does this mean?
- Let us look at a specific example. How could we get ?
- How many points are there with distance ?
- So we have eight possibilities. What if we include points where coordinates are not integers? Brigi already said it; what shape will this be?
- Let us try looking at it in this way: we are here at , and we are looking for points at distance. How could we describe them algebraically?
4.1.3. Lesson C (with Tasks Designed by Hanna)
4.2. Student Affect and Growth: Students’ View
Balázs: I could feel that the main point of the experiment was that she does not say what this is about, but we need to find it out ourselves. […] So we basically figured out for ourselves what is written in the Big Book.
Brigi: It’s more interesting and more useful if we make discoveries on our own, because like that I don’t need to revise the material, I will remember it well enough.
Balázs: I think this way we can understand more what is why in math, because if we are given a formula, then maybe we know what the formula is for, and maybe we can even use it, but we don’t see the logical connections behind, and what the formula expresses. And I think this is exactly why this worked, so we found out faster what we should do than if we were told what to do.
4.3. Student Affect and Growth: Teacher’s View
Hanna: What specifically improved is their creativity and their courage in using things. So they gave beautiful solutions and I felt that they not only learned a formula but they tried […] so when the task was to simply apply a formula, if a student did not know the formula, they transformed [the problem] in a way that they could solve it.
4.4. Teacher Affect and Growth—Teacher’s View
Hanna: it is a wonderful feeling that they discovered the circle equation […] even after days, weeks, and now months it feels great that this is possible to achieve, possible to do, they could discover this, and I had something to do with it.
4.5. Teacher Agency
Hanna: In the future it would help me to get involved in task design on some level, how this works, how you design a task, because this is very comfortable for me and very helpful, but I don’t think that in ten years they will stand by me and design tasks for me.
Panka: and there were more fun tasks like that, […] it’s nice that it’s more interesting, and I don’t know, it’s more exciting, and it makes you feel better, because I’m not calculating two circles, but where the lambs meet.
Hanna: I dare to dream big, I never thought before that it was possible to come up with such tasks. Since then, I’ve been trying to look at the topics with an eye to how the students can be engaged, what tools could be used, what they can discover on their own, through interesting tasks.
4.6. What Helped Teacher Learning
- Professional development workshop on guided discovery helped her build awareness of its main components and set these components as aims for growth in her own teaching.
- Tasks provided by mentors gave her stability; sometimes she asked mentors to give her a task with a specific aim.
- Joint planning with mentors helped her think more about her lessons and have access to an external point of view. Specifically, this helped in thinking more about aims, timing, amount and difficulty of tasks, long term planning, and assessment.
- Reflection helped her see more clearly and adjust accordingly. Specifically, what worked and what did not, what students understood and what was difficult for them, what was left out and what can be let go, what went faster or slower than expected.
- Mentor feedback on lessons helped her make sense of students’ understanding, and difficulties, teacher strategies concerning math content, and timing. They also strengthened her self-confidence by confirming that she was on the right track.
- Observing mentors teaching lessons, and telling her the story with application as if she were a student.
5. Discussion
5.1. Agency and Affect (Further Theoretical Background)
5.2. Levels of Agency
- Student agency in the classroom.
- Teacher agency in the classroom.
- Teacher agency within the mentoring framework.
- Teacher agency over the mentoring framework.
5.2.1. Student Agency in the Guided Discovery Classroom
Panka: Well, at first it was so bad, because we didn’t really know what to start out from, but then we scaled it down to one degree, and then we examined how high one degree was, and then we multiplied, and then we could calculate quite close results, and then we could guess, and that felt good.
5.2.2. Teacher Agency in the Guided Discovery Classroom
5.2.3. Teacher Agency within the Guided Discovery Mentoring Framework
5.2.4. Teacher Agency over the Guided Discovery Mentoring Framework
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pedaste, M.; Mäeots, M.; Siiman, L.A.; de Jong, T.; van Riesen, S.A.; Kamp, E.T.; Manoli, C.C.; Zacharia, Z.C.; Tsourlidaki, E. Phases of inquiry-based learning: Definitions and the inquiry cycle. Educ. Res. Rev. 2015, 14, 47–61. [Google Scholar] [CrossRef]
- Gosztonyi, K. Mathematical Culture and Mathematics Education in Hungary in the XXth Century. In Trends in the History of Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 71–89. [Google Scholar] [CrossRef]
- Wenger, E. Communities of Practice: Learning, Meaning, and Identity; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar] [CrossRef]
- Loewenberg Ball, D.; Thames, M.H.; Phelps, G. Content Knowledge for Teaching: What Makes It Special? J. Teach. Educ. 2008, 59, 389–407. [Google Scholar] [CrossRef]
- Lesh, R. Research design in mathematics education: Focusing on design experiments. In Handbook of International Research in Mathematics Education; Routledge: London, UK, 2002; pp. 39–62. [Google Scholar]
- Polya, G. How to Solve It: A New Aspect of Mathematical Method; Number 246; Princeton University Press: Princeton, NJ, USA, 2004. [Google Scholar]
- Gosztonyi, K.; Kosztolányi, J.; Pintér, K.; Vancsó, Ö. Varga’s «complex mathematics education» reform: At the crossroad of the new math and Hungarian traditions. ICMI Study 2018, 24, 133–140. [Google Scholar]
- Gosztonyi, K. Tamás Varga’s reform movement and the Hungarian Guided Discovery approach. Teach. Math. Comput. Sci. 2020, 18, 11–28. [Google Scholar] [CrossRef]
- Juhász, P. Talent nurturing in Hungary: The Pósa weekend camps. Not. Am. Math. Soc. 2019, 66, 898–900. [Google Scholar]
- Pósa, L.; Juhász, P.; Matsuura, R.; Szász, R. Problem Posing in Pósa Problem Threads. In Problem Posing and Problem Solving in Mathematics Education; Springer Nature: Singapore, 2023; pp. 233–246. [Google Scholar] [CrossRef]
- Győri, J.G.; Juhász, P. An extra-curricular gifted support programme in Hungary for exceptional students in mathematics. In Teaching Gifted Learners in STEM Subjects; Routledge: London, UK, 2017; pp. 89–106. [Google Scholar] [CrossRef][Green Version]
- Matzal, C.; Manahan, K.; Galaty, B.; Wang, H.; Barbarics, M. Guided Discovery in Hungarian Education Using Problem Threads: The Pósa Method in Secondary Mathematics Classrooms. Teach. Math. Comput. Sci. 2020, 18, 51–67. [Google Scholar] [CrossRef]
- Gosztonyi, K. Conceiving teaching trajectories in the form of series of problems: A step for the theoretical reconstruction of the Hungarian Guided Discovery approach. In Proceedings of the Eleventh Congress of the European Society for Research in Mathematics Education, Utrecht, The Netherlands, 6–10 February 2019. Number 17. [Google Scholar]
- Gosztonyi, K.; Varga, E. Teachers’ practices and resources in the Hungarian “Guided Discovery” approach to teaching mathematics: Presenting and representing “series of problems”. ZDM Math. Educ. 2023, 55, 641–656. [Google Scholar] [CrossRef]
- Tamas, V. Mathematics education in Hungary today. Educ. Stud. Math. 1988, 19, 291–298. [Google Scholar] [CrossRef]
- Gueudet, G.; Trouche, L. Teachers’ Work with Resources: Documentational Geneses and Professional Geneses. In From Text to “Lived” Resources; Springer: Dordrecht, The Netherlands, 2011; pp. 23–41. [Google Scholar] [CrossRef]
- Pepin, B.; Gueudet, G.; Trouche, L. Refining teacher design capacity: Mathematics teachers’ interactions with digital curriculum resources. ZDM 2017, 49, 799–812. [Google Scholar] [CrossRef]
- Brown, M.W. The teacher-tool relationship: Theorizing the design and use of curriculum materials. In Mathematics Teachers at Work: Connecting Curriculum Materials and Classroom Instruction; Remillard, J.T., Herbel-Eisenmann, B.A., Lloyd, G.M., Eds.; Routledge: New York, NY, USA, 2009; Chapter 2; pp. 17–36. [Google Scholar] [CrossRef]
- Matusov, E.; Bell, N.; Rogoff, B. Situated Learning: Legitimate Peripheral Participation. JEAN Lave and ETIENNE Wenger. Am. Ethnol. 1994, 21, 918–919. [Google Scholar] [CrossRef]
- Putnam, R.T.; Borko, H. What Do New Views of Knowledge and Thinking Have to Say About Research on Teacher Learning? Educ. Res. 2000, 29, 4–15. [Google Scholar] [CrossRef]
- Nam, J.; Seung, E.; Go, M. The Effect of a Collaborative Mentoring Program on Beginning Science Teachers’ Inquiry-based Teaching Practice. Int. J. Sci. Educ. 2013, 35, 815–836. [Google Scholar] [CrossRef]
- Winsløw, C.; Bergsten, C.; Butlen, D.; David, M.; Gómez, P.; Grevholm, B.; Wood, T. First years of teaching. In The Professional Education and Development of Teachers of Mathematics; Springer: Boston, MA, USA, 2009; pp. 93–101. [Google Scholar]
- Schön, D.A. Educating the Reflective Practitioner; Jossey-Bass: San Francisco, CA, USA, 1987. [Google Scholar]
- Chapman, O. Educators reflecting on (researching) their own practice. In The Professional Education and Development of Teachers of Mathematics: The 15th ICMI Study; Springer: New York, NY, USA, 2009; pp. 121–126. [Google Scholar]
- Matos, J.F.; Powell, A.; Sztajn, P.; Ejersbø, L.; Hovermill, J.; Matos, J.F. Mathematics Teachers’ Professional Development: Processes of Learning in and from Practice. In The Professional Education and Development of Teachers of Mathematics; New ICMI Study Series; Springer: New York, NY, USA, 2009; pp. 167–183. [Google Scholar] [CrossRef]
- Braun, V.; Clarke, V. Thematic analysis. In APA Handbook of Research Methods in Psychology, Vol 2: Research Designs: Quantitative, Qualitative, Neuropsychological, and Biological; American Psychological Association: Washington, DC, USA, 2012; pp. 57–71. [Google Scholar] [CrossRef]
- Buchholtz, N. Planning and Conducting Mixed Methods Studies in Mathematics Educational Research. In Compendium for Early Career Researchers in Mathematics Education; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 131–152. [Google Scholar] [CrossRef]
- Sang, G. Teacher Agency. In Encyclopedia of Teacher Education; Springer: Singapore, 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Biesta, G.; Priestley, M.; Robinson, S. The role of beliefs in teacher agency. Teach. Teach. 2015, 21, 624–640. [Google Scholar] [CrossRef]
- Boaler, J.; Greeno, J.G. Identity, agency, and knowing in mathematics worlds. In Multiple Perspectives on Mathematics Teaching and Learning (International Perspectives on Mathematics Education, V. 1); Ablex Publishring: Westport, CT, USA, 2000; pp. 171–200. [Google Scholar]
- Orland-barak, L. Introductory Chapter III: Learning Teacher Agency in Teacher Education. In The SAGE Handbook of Research on Teacher Education, 1st ed.; Jean Clandinin, D., Husu, J., Eds.; SAGE Publications Ltd.: London, UK, 2017; Volume 2, pp. 247–250. [Google Scholar]
- Priestley, M.; Biesta, G.; Robinson, S. Teacher agency: What is it and why does it matter? In Flip the System; Routledge: London, UK, 2015; pp. 134–148. [Google Scholar] [CrossRef]
- Hannula, M.S. Affect in Mathematics Education. In Encyclopedia of Mathematics Education; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 32–36. [Google Scholar] [CrossRef]
- Vygotsky, L.S. Mind in Society: Development of Higher Psychological Processes; Harvard University Press: Cambridge, MA, USA, 1980. [Google Scholar] [CrossRef]
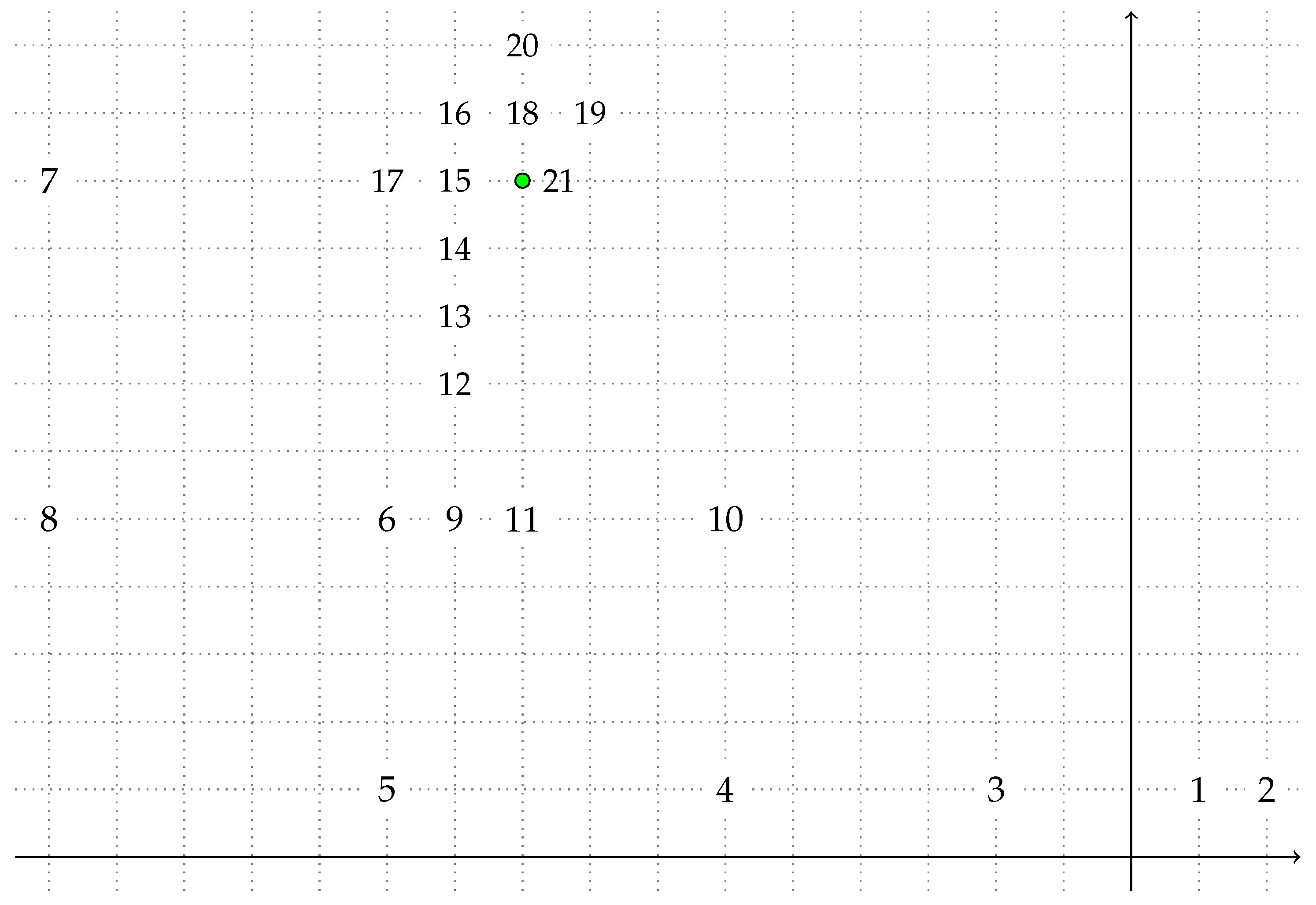
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Juhász, P.; Szász, R.; Szűcs, G.; Varga, E. Professional Support in Teaching Mathematics through Guided Discovery: The Role of Agency on Multiple Levels. Educ. Sci. 2024, 14, 769. https://doi.org/10.3390/educsci14070769
Juhász P, Szász R, Szűcs G, Varga E. Professional Support in Teaching Mathematics through Guided Discovery: The Role of Agency on Multiple Levels. Education Sciences. 2024; 14(7):769. https://doi.org/10.3390/educsci14070769
Chicago/Turabian StyleJuhász, Péter, Réka Szász, Gábor Szűcs, and Eszter Varga. 2024. "Professional Support in Teaching Mathematics through Guided Discovery: The Role of Agency on Multiple Levels" Education Sciences 14, no. 7: 769. https://doi.org/10.3390/educsci14070769
APA StyleJuhász, P., Szász, R., Szűcs, G., & Varga, E. (2024). Professional Support in Teaching Mathematics through Guided Discovery: The Role of Agency on Multiple Levels. Education Sciences, 14(7), 769. https://doi.org/10.3390/educsci14070769




