Abstract
Teaching vector addition seems challenging in secondary-level mathematics education. Vector addition requires both geometric and algebraic understandings, and the overreliance on abstract representations causes students difficulties in learning this complex mathematics skill. The concreteness fading framework is promising for effectively teaching complex mathematical topics in a progressive way. This study explores the contribution of concreteness fading to learning by implementing an instructional intervention for eighth graders on vector addition. Through a grounded theory method, this research reveals key concreteness fading mechanisms: (1) consistent design elements establish inter-task connections; (2) the fading task facilitates the co-building of operational and procedural knowledge; and (3) unfamiliar symbols within tasks promote mathematical sense-making. These findings suggest the potential for future studies to incorporate concreteness fading as a valuable strategy for enhancing the learning experience on complex mathematical subjects.
1. Introduction
Secondary-level mathematics education often faces the challenge of teaching abstract concepts in a comprehensible and engaging way due to the overreliance on abstract concepts and symbols in the current secondary mathematics education, which is criticized as “formalisms first” by Nathan [1]. Vector addition, as a fundamental topic in both mathematics and science curricula [2,3], exemplifies this challenge. Students frequently encounter difficulties with vector addition because it requires a robust understanding of both geometric and algebraic representations [4].
To address these learning difficulties, we propose that concreteness fading (CF) can be a promising instructional design framework for teaching vector addition. CF involves transitioning from concrete, tangible representations of a concept to more abstract, symbolic representations [5]. Grounded in cognitive science theories, CF suggests that starting with concrete materials can help anchor students’ understanding before moving to abstract representations that are more generalizable [6].
This study aims to explore how the CF framework can be effectively applied to teach vector addition to eighth-grade students. Previous CF research has demonstrated the effectiveness of concreteness fading in various mathematical domains [7,8,9]. However, there is a paucity of studies specifically examining its application in vector addition. Thus, we seek to explore how CF tasks influence students’ engagement, understanding, and problem-solving strategies in the context of vector addition. In this context, understanding is conceptualized as the ability to recognize and apply vector addition principles across various representations and problem contexts. Also, by implementing a CF intervention, we expect to produce some design principles that can inspire future CF intervention design.
This study is guided by two primary research questions. RQ1: How do students engage with and adapt to concreteness fading tasks in learning vector addition? RQ2: What design principles can be derived for incorporating the concreteness fading framework in teaching complex mathematical topics that involve both geometric and algebraic representations?
To answer these questions, we designed a three-stage CF intervention to teach eighth graders vector addition. The intervention involves a series of activities that progress from concrete (physical manipulatives) to abstract (symbolic representations) tasks. Since this study is exploratory, we employed a grounded theory method [10] to analyze how our participants interacted with CF tasks designed for learning vector addition from classroom recordings and student work samples.
We believe that by elucidating the mechanisms through which CF tasks facilitate learning, this study can provide actionable insights for educators seeking to improve instruction in complex mathematical topics. The findings are expected to contribute to the broader field of mathematics education by offering evidence-based design principles for integrating CF into teaching practices.
2. Difficulties in Learning Vector Addition
Understanding the challenges inherent in vector addition learning is crucial before introducing the CF intervention. Vector addition is a complex skill that requires both geometric and arithmetic understandings. Unlike the straightforward addition of integers, vector addition involves considering both magnitudes and directions. In secondary mathematics classrooms, there are three vector addition approaches: the “tip-to-tail” method (refer to Figure 1), the parallelogram addition rule (refer to Figure 2), and the vector component method (refer to Figure 3). Among these three methods, the vector component method is often perceived as the most intricate. This approach requires the integration of knowledge of the Cartesian coordinate plane with their understanding of vectors, adding an extra layer of complexity to the learning process. In this study, we focus on the third vector component method.
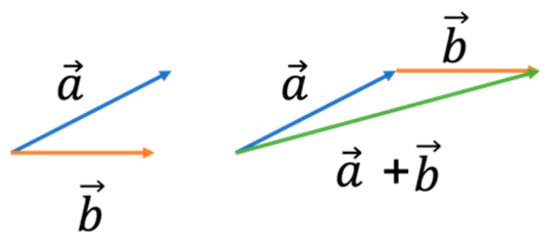
Figure 1.
“Tip-to-tail” method.
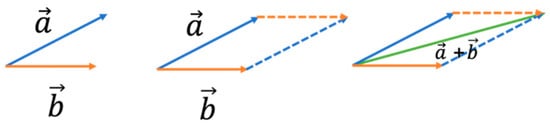
Figure 2.
Parallelogram addition rule.
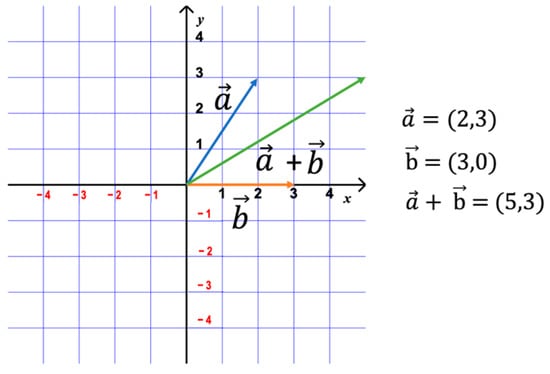
Figure 3.
Vector component method.
There are three major difficulties in learning vector addition identified by previous studies. The first difficulty is the rigid reliance on vector addition rules. Nguyen and Meltzer’s study revealed that students often mechanically apply the “tip-to-tail” method and the parallelogram addition rule and often have an erroneous application of the Pythagorean theorem to deal with vector addition problems [11]. Similarly, Knight’s research discovered that students struggle with comprehending vector components and face difficulties in linking a vector’s algebraic representations with its geometric content during vector addition problem-solving [12]. Consequently, a lack of a solid understanding of vector addition can cause students ample challenges in learning advanced college-level mathematics and physics [13]. The second difficulty comes from the representations of vectors. Latifa et al. discovered that both the graphical representation itself and the switching between graphical and algebraic representations of vectors cause difficulties to students in operating vector addition [14]. Also, Heckler and Scaife found that students feel that it is hard to comprehend the graphical representation of vectors and fail to connect with the symbolic algebraic expressions that allow them to conduct arithmetic and algebraic calculations [4]. The third difficulty is caused by the disconnection between students’ prior knowledge and the concept of vector addition. By researching the performance on vector addition at secondary level, Gubrud and Novak noted that these novice learners encounter challenges in associating vector addition with their previous knowledge [15]. Another study also discovered that students face challenges in generalizing the concept of vector addition from concrete contexts [13].
These existing studies underscore the difficulty of vector addition as a complex mathematical skill. To address these difficulties and create learning activities that allow students to ground the vector component method, comprehend different forms of vector representations, and establish connections with their prior knowledge and experience, we will utilize CF as an instructional design framework.
3. Concreteness Fading as an Instructional Design Framework
To comprehend why CF holds promise as an instructional design framework for vector addition learning, it is essential to explore the advantages and disadvantages of both abstract and concrete learning. Additionally, understanding the rationale and necessity of integrating these two modes of learning is essential.
In the current secondary-level mathematics classes, the primary approach for teaching abstract mathematical concepts involves learning through abstract materials; abstract learning has its advantages but risks unproductive learning. Abstract learning typically requires students to construct representations of the concepts they are supposed to learn. This abstraction-based approach avoids the unnecessary perceptual details of an object [5] and enables students to focus more on underlying structural and representational aspects rather than superficial characteristics [16,17] to generalize knowledge for its application in new contexts [16]. However, abstract-based learning exhibits similar drawbacks to information-processing-based learning. These drawbacks include the following: (1) regarding learning as a passive, atomistic, and mechanical process; (2) neglecting the contexts in which actual learning, as a cognitive process, takes place; and (3) researching learning in an artificial laboratory setting and ignoring the learner’s affective, social, biological, and metacognitive aspects of cognition [18]. Moreover, Nathan challenges the effectiveness of abstract learning and argues that abstraction often involves a notational system lacking meaning for those unfamiliar with the convention [1]. The absence of personal meaning may hinder students from connecting the content to familiar concepts, impeding the usefulness of the learning experience and diminishing self-motivated learning [19]. In addition, research indicates that overreliance on abstract representations can lead to ineffective and more error-prone problem-solving [20] and the rigid application of learned procedures [21]. In mathematics classes, teachers often face a dilemma in that students with abstract knowledge are able to identify a similar problem and select the apt procedures, yet they lack comprehension of how the procedure works and often make illogical mistakes [22].
Recognizing the drawbacks of abstract learning, some advocate for the incorporation of concrete materials as an alternative in mathematics education. The term “concreteness” is clarified by Koedinger et al. as “grounded” representations, which relate to physical objects and everyday events [23]. Fyfe and Nathan expand on this by defining four types of information to determine the level of concreteness: physicality (whether the object is two-dimensional or three-dimensional), perceptual richness (the visual surface features of an object), dependency on existing knowledge (how conceptual familiarity can help with understanding a representation), and the narrative context to which the representation belongs (how linguistic familiarity can help with understanding a representation) [22]. Incorporating these four types of information, concrete learning materials offer four potential benefits in mathematics learning: activating a learner’s real-world knowledge [24], facilitating the construction of abstract concepts with a learner’s prior knowledge [25], encouraging physical actions for enhanced understanding [26], and preventing disengagement due to lengthy procedural instruction [1]. However, concrete materials may present challenges, such as distractions from irrelevant perceptual details [27], attraction to materials themselves rather than their referents [17], and difficulties in transferring knowledge to new contexts [28].
Given the inherent advantages and disadvantages of both abstract and concrete learning, the instructional approach of concreteness fading (CF) emerges as a strategy that harnesses the strengths and mitigates the limitations of each. Inspired by Bruner’s three progressive forms of understanding new concepts—enactive form, iconic form, and symbolic—CF has a multi-stage process to facilitate learning [29]. Bruner’s model suggests that learners initially establish representations through actions, progress to recognize and utilize visual patterns, and ultimately form generative language representations. Reflecting on Bruner’s notion of three forms, Goldstone and Son define CF as “the process of successively decreasing the concreteness of a simulation with the intent of eventually attaining a relatively idealized and decontextualized representation that is still clearly connected to the physical situation that it models” [6] (p. 70). However, considering that the initial enactive form may not always be a simulation, Fyfe and Nathan propose a broader definition, defining CF as “the three-step progression by which a concrete representation of a concept is explicitly faded into a generic and idealized representation of that same concept” [22]. According to this definition, CF always initiates with a concrete representation, which can be a physical manipulative or a simulation in rich contextual information. The CF process then involves transforming this representation into more idealized and transferrable forms through a fading process. This process gradually removes extraneous perceptual details and irrelevant conceptual information from the learning context, establishing mutual references across different representations. It is vital to note that CF encourages learners to consider each representation as an instantiation of the concept at one time, rather than holding all representations in mind simultaneously. CF aims to maintain an idealized representation of the target concept with an invariant relationship across various learning contexts [22]. By guiding learners through a sequence of representations with decreasing concreteness, CF strives to optimize the learning process and enhance the transferability of knowledge.
CF offers distinct advantages at each stage of its progression, as well as cumulative benefits throughout the entire process. In the initial concrete stage, learners engage with familiar concrete objects, leveraging their prior knowledge [6,30]. This stage fosters embodied learning experiences and establishes connections between abstract representations and perceptual physical processes [22]. Such connections help learners construct conceptual metaphors from motor–sensory experiences, facilitating the comprehension of unfamiliar mathematical ideas [31]. Moreover, since people often think about past experiences and imaginatively reconstruct a perceptual simulation that grounds their comprehension [32], the concrete stage enables the formation of mental images of the target concept, which can be accessed when learners encounter unfamiliar symbols that represent that concept in later stages, enhancing their understanding of the concept and related symbols [5].
Recognizing the limitations of sole concrete learning, the following CF stages are equally important. In the second stage, learners are introduced to some formal symbols in a concrete context with unrelated perceptual information gradually removed. This process prevents learners from fixating on the material itself [27] and serves as scaffolding that guides learners through their zone of proximal development [33]. This stage also facilitates a smooth transition from familiar concepts to those less familiar and creates explicit links between the first and final stages through mutual referents [34]. In the last stage, abstract representations are presented, and learning content becomes decontextualized, allowing learners to focus on the structural patterns and representational features. This stage promotes the generation of portable knowledge and the development of alternative representations for the same concept, preparing students for future learning [5].
In essence, CF optimally combines the advantages of both concrete and abstract learning while mitigating the drawbacks and provides learners with opportunities to reference established representations and construct new knowledge progressively. Previous studies have explored the effectiveness of CF in teaching various concepts, such as the equal sign [8], basic circuits [35], and complex systems thinking [6]. While there are no previous studies applying CF to teach vector addition, the method holds the potential.
Sfard’s two ways of conceiving abstract mathematical concepts—structurally and operationally—align well with the CF framework [36]. A structural conception views mathematical objects as static structures, akin to entities in space and time. Conversely, an operational conception treats mathematical concepts as processes, algorithms, and actions [36]. Sfard illustrated these two types of mathematical conceptions with the following example (see Figure 4). The left parabola graph represents the structural representation of the middle algebraic expression, while the right computer program illustrates the operational representation of the same algebraic expression.

Figure 4.
Different types of mathematical conceptions [36].
Sfard’s argument that operational conceptions often precede structural conceptions in the formation of mathematical concepts [36] parallels with the principles of CF. In the context of Sfard’s example, students may find it more accessible to understand the procedures of a computer program step by step, which represents operational knowledge. On the other hand, grasping the graphical representation, such as the left parabola, requires a deeper understanding involving both geometry and algebra. Furthermore, Sfard challenges the notion that geometric ideas are primarily conceived structurally, using the idea of a circle as an example and contending that mathematicians often first observe and interact with objects that are proximately round, which leads to the conceptualization of the law of roundness before expressing it formally. Therefore, students often initiate their understanding of a new mathematical concept by engaging with it in operational processes and experimenting with it in concrete contexts, rather than immediately recognizing it as an abstract mathematical object with various properties.
This perspective seamlessly aligns with the philosophy of CF. As mentioned beforehand, a CF intervention commences with concrete learning materials linked to learners’ prior knowledge and experiences and allows learners to interact with the concept using their naïve operational knowledge, gradually transitioning to more structural mathematical conceptions, such as symbols and formal mathematical language. Therefore, investigating the learning process in a CF intervention sheds light on the learners’ progression from an operational representation of a mathematical concept to a more structured understanding of the same concept.
4. Method
4.1. Participants
For this study, a total of 9 eighth-grade students (4 female and 5 male students) were recruited from a charter school (in the United States, a charter school is a public school that is funded by the government but operates independently from the local public school system) located in a large Midwestern city in the United States. The students’ math performance in this school was reported to be below the state’s average, according to U.S. News & World Report. This school was chosen because there was collaboration established between the school administrators and the researcher.
As told by the participants’ mathematics teacher, all participants had been exposed to the coordinate plane during their 7th-grade mathematics class but had not been taught about vector concepts before. A pre-study screening confirmed that none of the students could correctly perform vector addition. The participants were randomly assigned to three groups of three (Group Cardinal, Group Jay, and Group Dove). Each group was balanced in terms of gender: Group Cardinal had 1 female and 2 males, Group Jay had 2 females and 1 male, and Group Dove had 1 female and 2 males. Given the exploratory nature of this study and the absence of prior research on vector addition learning in a CF intervention, the choice of a relatively small number of participants was deemed acceptable due to resource constraints.
4.2. Study Design
Aligning with the three stages (enactive, iconic, and abstract) proposed in the CF literature [5,6], in the CF intervention of this study, there are three distinctive tasks: enactive physicality (EP), iconic depiction (ID), and abstract representation (AR), following the sequence of EP-ID-AR. We incorporate an American football (referred to as football below) context in our design for two reasons: First, there is a renowned university nearby with a top-tier college football team, and most students at this middle school are fans of that team. Second, a sports context can connect the learning experience to students’ personal experiences, making it more culturally relevant for them [37].
In the first EP task, participants engage in a physical activity. They tile the floor with 48 pieces of 2 feet by 2 feet cardboard tiles in two colors (light green and dark green, 24 pieces each). Two participants step onto the tiles and randomly select two points to stand on. Subsequently, participants are asked to describe their positions on the tiles. Once participants know their positions on the tile, one participant is handed a foam football and walks along the tiles to deliver the football to the other participant. Upon receiving the football, the second participant measures the tiles walked to their left/right and front/back. Simultaneously, a third participant uses red and blue sticks to mark the distance walked. Following this, the participant who delivers the football passes the football directly to the other participant, and the third participant measures the passing distance using yellow sticks (see Figure 5). This task comprises two rounds, with participants switching roles in each round.

Figure 5.
Enactive physicality task.
In the second ID task, participants play a football passing simulation game developed by the researcher (see Figure 6). In this game, participants need to determine the units to add along the X and Y axes (indicated by red and blue arrows) to make the quarterback (red dot) successfully pass the ball to the wide receiver (blue dot) on a football field with a grid. A successful pass will result in the wide receiver moving to a random position towards the end zone and the quarterback relocating to the wide receiver’s previous position. In the case of a failed pass, the ball will be returned to the quarterback, and participants have to redetermine the units along the X and Y axes. Additionally, there is a button allowing participants to view the projected trajectory of the football (yellow arrow). The ultimate objective of the simulation game is to achieve a passing touchdown, characterized by the quarterback successfully passing the ball to the wide receiver in the end zone. Participants play the simulation game collaboratively for three rounds: the first round serves as a familiarization phase, the second round introduces the yellow arrow representing the trajectory, and the third round conceals the yellow arrow.
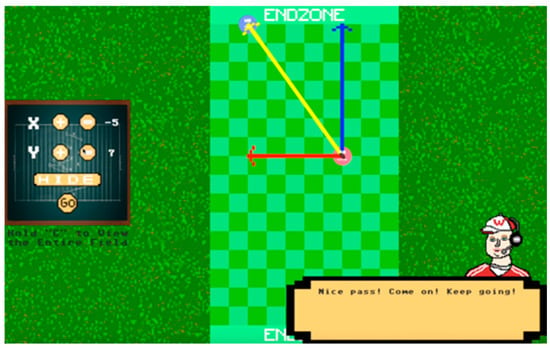
Figure 6.
The football simulation game in the iconic depiction task.
In the third AR task, participants need to solve two questions within a football context (see Figure 7) that feature formal vector notations and the Cartesian coordinate plane. Participants will attempt to solve these questions individually and then engage in a group discussion to exchange their answers and thoughts. The researcher emphasizes that there are no definitive correct answers to these questions; rather, participants are encouraged to articulate and share their perspectives freely.
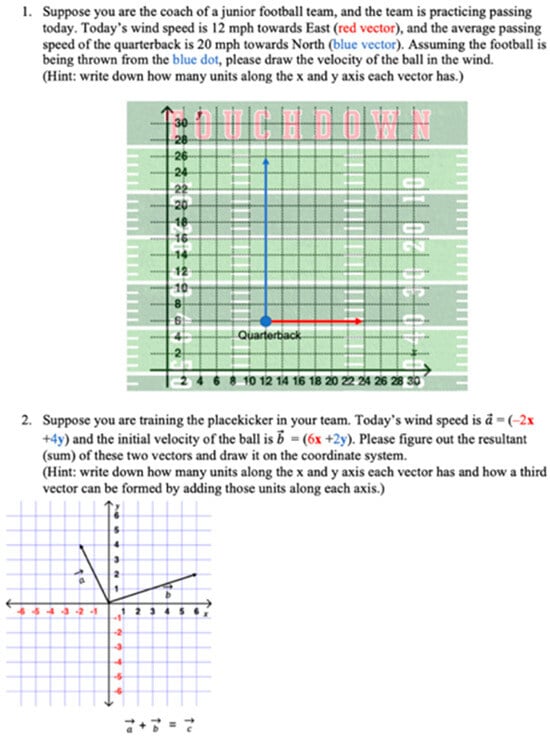
Figure 7.
Questions in the abstract representation task.
4.3. Data Collection
Three sessions were conducted between February and March 2022 at this charter school, with each session lasting approximately 2 h after regular school hours. Prior to each session, parental consent and participant assent were obtained. Each task within the session required approximately 20 min to complete.
At the beginning of each task, the researcher initiated a discussion by prompting participants to propose rough problem-solving ideas. The participants then collaborated as a group to work on the task, with the researcher providing necessary guidance and facilitation to clarify the tasks during the study session. To capture observational data, two video recorders were positioned at different angles, recording both video and audio throughout the sessions.
4.4. Data Analysis
Since the research questions in this study adopt a process lens and focus on the procedure of the intervention, the goal is not to produce sample-to-population generalization but to reveal important generalizations of relationships among theoretical constructs [38]. In this case, the goal of our analysis is not to examine students’ performance on vector addition after the intervention but to understand how different elements of the CF intervention influence their learning of vector addition. Considering this goal, all audio data were transcribed, and a grounded theory method was applied to analyze the transcripts. The NVivo 12 software was utilized for coding the dataset. Given the limited existing research on vector addition learning, particularly focusing on the learner’s process during a CF intervention and the post-intervention learning demonstration, a deductive coding approach was not feasible. Instead, a grounded theory method was chosen to analyze the discursive data. As a qualitative research method, grounded theory method involves using data to generate theories, with a preference for rich and detailed data placed within relevant situational contexts [10]. Emphasizing theory construction through an iterative analysis process, grounded theory method seeks to uncover actions and processes inherent in the data [39]. The chart below (see Figure 8) shows the process of applying grounded theory method to analyze the qualitative data in this study. Since students worked as a group during the intervention, the unit of analysis is a group.
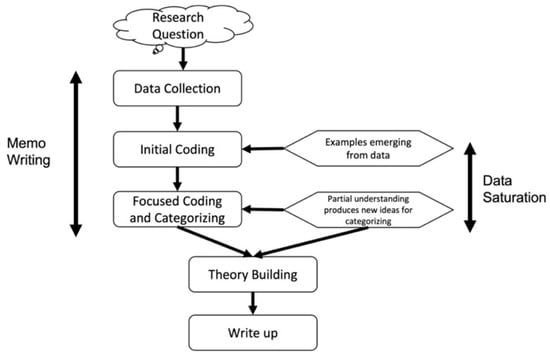
Figure 8.
The workflow of the grounded theory method (adapted from [40]).
The discursive data collected from the three learning tasks were organized based on the researcher’s prompt questions (see Appendix A). Following the introduction of each task by the researcher, participants engaged with the learning materials and responded to the instructions and questions. The collaborative nature of the group work required unanimous agreement within each group before proceeding with the task, making the unit of analysis one group. The conversations between participants and the researcher were structured around these prompt questions. Thus, the discursive data were segmented by the researcher’s prompt questions. Each instance where the researcher posed a question or a follow-up question constituted a distinct segment of discourse. To aid in coding, three colors were used—yellow, blue, and grey—to distinguish between different segments for subsequent analysis (see Figure 9).

Figure 9.
An example of using colors to differentiate segments.
Following the data segmentation, the subsequent steps in the grounded theory method involved inductive coding, iterative coding processes to identify connections among codes, and the eventual formation of categories for theory building. The inductive coding process encompassed three levels: open coding, focused coding, and theoretical coding [39,41]. Open coding, beginning from the start of data collection, involved creating open, short, and precise codes closely tied to the data. Focused coding, more conceptual than open coding, aimed to synthesize the codes from the open coding [42]. With a set of focused codes, the final step was to explore relationships between those codes, analytically integrate them, and elevate the abstract level of those codes to construct theories [43].
5. Results
5.1. Connections across Tasks
Establishing connections between different learning tasks is an essential aspect of a CF intervention; learners benefit from a progressive learning experience when they recognize the interrelated nature of the tasks [22]. The analysis of the inter-task connections involved fourteen open codes, five focused codes, and two categories. Figure 10 shows the connections established by the participants across the three learning tasks.
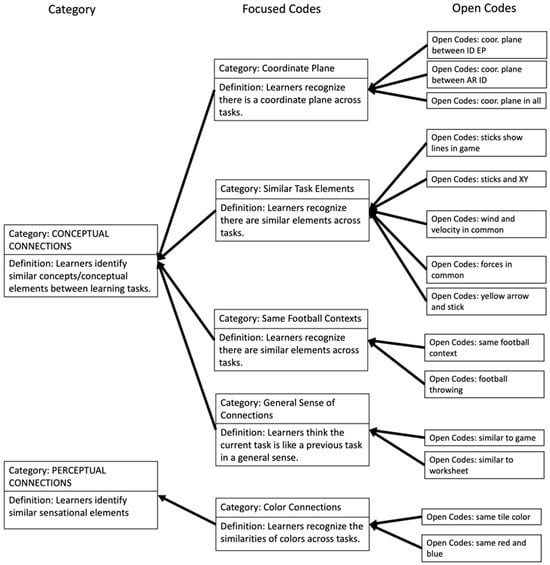
Figure 10.
Codes for connections.
As presented in Figure 10, the identified connections can be categorized into two types: CONCEPTUAL CONNECTIONS and PERCEPTUAL CONNECTIONS. These connections contribute to the participants’ ability to understand the interrelated nature of the learning tasks in the CF intervention. The majority of connections fall under the conceptual category. There are four types of conceptual connections. First, the recognition of the coordinate plane: Participants from Group Dove recognized a coordinate plane across all three tasks, even though the tasks ID and EP did not explicitly include coordinate planes. Design elements like grids or X/Y symbols in these tasks might have contributed to this perception. Second, the identification of similar elements: Participants noticed similarities among sticks (EP task), arrows (ID task), and X/Y values (ID task). They also connected the yellow stick in the EP task to the yellow arrow in the ID task, both representing the distance between the original and final points. Third, the claimed forces and contextual elements: participants from Group Jay claimed the presence of wind speed, initial velocity, and forces in all tasks, even though these concepts only appeared in the AR task. Fourth, the football context: All groups identified a football context in all three tasks. Only one type of connection was identified as a perceptual connection, which was color connections. Groups Jay and Dove recognized consistent color use (dark green, light green, red, and blue) across all three tasks. Color served not only to perceptually connect tasks but also had broader affordances.
5.2. The Affordances of Color
In the context of this CF intervention, color played a pivotal role with distinct affordances to assist in comprehending vector addition. The analysis of the color affordances encompassed eight open codes and three focused codes, and three affordances were discovered. Figure 11 shows those affordances.
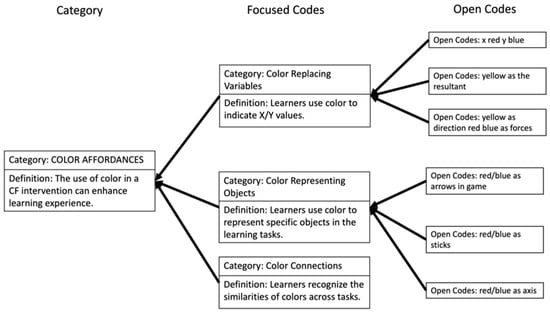
Figure 11.
Codes for color affordances.
Firstly, participants harnessed color to establish perceptual connections across tasks by recognizing consistent elements and maintaining symbolic meanings such as dark green and light green for the field as well as red and blue for distance along X and Y, which facilitated transitions across tasks. Secondly, color served as a tool to replace variables, with participants frequently using red and blue to symbolize X and Y variables in the ID task (e.g., “the red is X. And then subtract one more…”) and creating a tangible representation of abstract mathematical concepts. Lastly, color was used to represent objects, such as sticks or arrows, providing participants with visual cues and enhancing their understanding of specific elements within the learning context. For example, in the EP task, the red and blue colors referred to the sticks that the participants placed on the tiles (e.g., “the blue and red is the distance [on the tile]”.); similarly, in the ID task, the red and blue colors represented the arrows or the axes in the simulation game (e.g., “take some off the blue”).
5.3. Direction and Magnitude
The process of the intervention provided participants with ample opportunities to engage with and apply their knowledge of direction and magnitude across the three learning tasks. Since the two defining characteristics of a vector are direction and magnitude, the way that the participants contemplated the concepts of direction and magnitude could evince their understanding of a vector. Their comprehension of vector direction and magnitude was multifaceted, as depicted in Figure 12 and Figure 13, respectively. There were nine open codes and three focused codes related to the participants’ comprehension of the direction of a vector in the intervention and six open codes and three focused codes about the understanding of a vector’s magnitude.
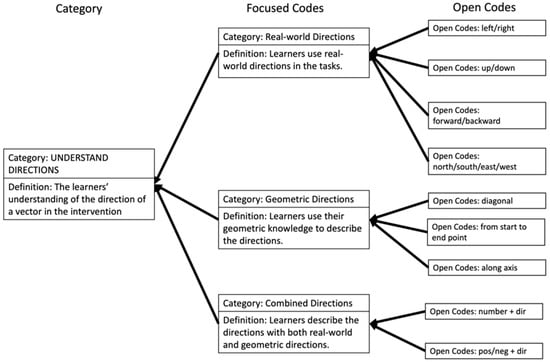
Figure 12.
Codes for understanding directions.
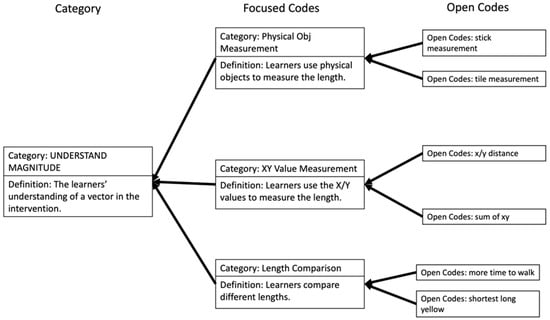
Figure 13.
Codes for understanding magnitude.
Regarding the directions, real-world directions were commonly utilized, including left/right (e.g., “it’s going right”), up/down (e.g., “Red is facing up”.), forward/backward (e.g., “I think one is like the friction because it’s holding it back the A. And then the B is like how far we’ll go forward”.), and north/south/east/west (e.g., “She’s facing north”.). Geometric directions, incorporating participants’ geometric knowledge, were less frequent but involved concepts like diagonal (e.g., “Researcher: Is there any direction the yellow arrow is facing? P1: Yeah. It’s facing diagonal”.), from start to end point (e.g., “P3: I counted the tiles of how far it was and it was 10. 10 being the tiles from the start to the point”.), and along axes (e.g., “P1: It is down along the X”.). Combined directions integrated both real-world and geometric aspects, including number plus direction (e.g., “P1: I think the red vector is 12 miles to the right. And the blue vector is 20 miles, 20 units up”.) and positive/negative plus direction (e.g., “P3: Yeah, that would be positive. Then downwards and left would be negative”.). Participants consistently employed real-world and geometric directions in both EP and ID tasks, while combined directions were only employed in the AR task. The rationale behind the observed pattern of different directions utilized will be further explored in the ensuing Section 6.
As for the magnitude, participants used physical objects as measures including the sticks and tiles in the EP task. Participants used these physical measures to quantify walked distances (red and blue sticks) and estimate the ball’s flying path (yellow sticks or the number of tiles beneath the yellow sticks). In the subsequent ID task, the X/Y values in the game became the primary metric for magnitude. Participants employed two main approaches for using those values: (1) interpreting the Y value as the height the result arrow could reach and the X value as the degree that the result arrow bent and (2) using the sum of X and Y values as the result arrow’s length. Notably, participants in Group Dove compared the lengths in EP, stating that the length of yellow sticks was physically longest but conceptually shortest. Their explanation was that the red and blue represented the walk distances and the yellow represented the flying path, so the yellow was shorter because tossing the ball to the other participant was faster than walking to deliver the ball.
5.4. Operations in the Intervention
The process of the intervention facilitated the application of operational knowledge in problem-solving, aligning with Sfard’s notion about structural and operational knowledge: Operational knowledge often precedes structural understanding when encountering a new mathematical concept, and practical operational knowledge allows students to generate solutions to problems before comprehending the underlying rationale. Hence, the operations across tasks were examined, with ten open codes and three focused codes for the operations in EP, two open codes and one focused code for the operations in ID, and eleven open codes and six focused codes for the operations in AR.
As shown in Figure 14, operations in EP involved three focused codes—body movement, define coordinate plane, and relative positions. When asked to describe positions on the tiled floor, participants in all groups recognized the tiled floor as a coordinate plane, defining the origin and axes. They then employed relative positions to locate themselves, showcasing their understanding of the spatial relationship between individuals (e.g., “my position is six right and five down of his”.), rows and dots (e.g., “my position is like in the fifth row. I’m on the third dot in this way”.), and distances from sides (e.g., “two tiles away from that side”), as well as tiles of different colors (e.g., “I’m sitting like between light green tiles and dark green tiles”.). In addition, the operational actions included alignment (stepping to the same line to easily measure the distance), turn requests (participants asking if they could have a turn while delivering the football), and recognition of right angles (e.g., “Oh, like 1, 2, 3, 4, 5, and then turn. And then always in the right angle. There’s not always that far, but this is always right there”.). These actions reflected participants’ emerging operational knowledge in the EP task, and some even implied their application of prior knowledge in the current context, such as defining a coordinate plane on the tiled floor.
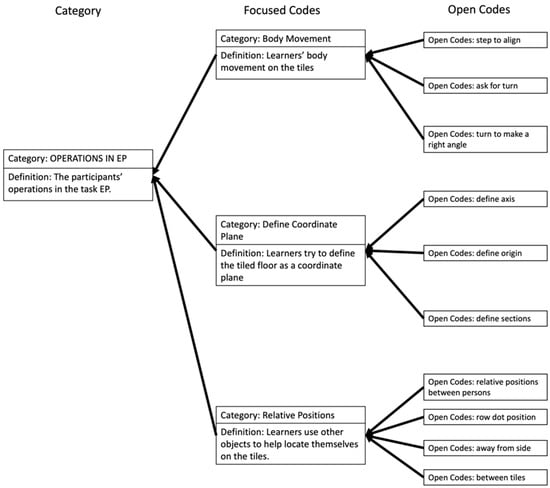
Figure 14.
Codes for operations in EP task.
In contrast, the iconic depiction (ID) task predominantly entailed operations related to adding or subtracting X/Y values within the football passing simulation game. As shown in Figure 15, participants referred directly to X/Y values (e.g., “Try to add one more to X”.) or used the red/blue colors to denote these values (e.g., “Add more to the blue one”.).

Figure 15.
Codes for operations in ID task.
The AR task, with two questions, involved multiple operational strategies, as shown in Figure 16. For Question 1, participants in both conditions engaged with counting blocks to obtain lengths on the coordinate plane by counting the tiles on the grid (e.g., “I counted the tiles of how far it was and it was 10”.) or the units on the axes (e.g., “I am counting the units”.). All the participants demonstrated additional operations. First, participants either traced the line to find a dot at the end of the line they drew or a dot that connected to that line, which indicated their belief that the answer was a dot. The second operation was to use a “copy-and-paste” approach. Taking one participant in Group Cardinal as an example, she moved the red vector to the tip of the blue vector and the blue vector to the tip of the red vector to form a rectangle on the coordinate plane (see Figure 17) and named her method as “copy-and-paste”. This approach was also observed in Group Jay: one participant in Group Jay told the researcher that there was a “square” on the coordinate plane and used his fingers to trace the possible sides of his square on the coordinate plane. In addition, another participant in Group Cardinal told the researcher that the origins (one was the blue dot that represented the quarterback and the other was the point (24, 26)) matched up, which showcased his intuition of a type of motion in the form of a vector.
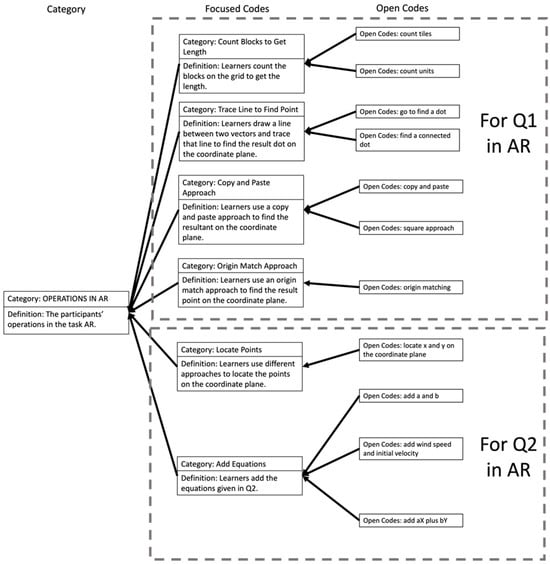
Figure 16.
Codes for operations in AR task.
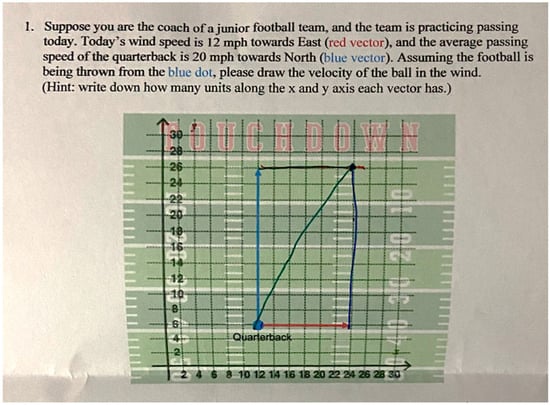
Figure 17.
Copy-and-paste approach for Q1.
For Question 2 in the AR task, participants from both conditions employed similar operations: locating points on the coordinate plane and adding up the given equations. To locate the points on the coordinate plane, participants found the number on the X/Y axis first and then traced the gridline to find the exact points on the coordinate plane. While adding the two “equations (the algebraic expressions in the question)”, participants performed the same calculation but expressed differently—adding a and b, adding wind speed and initial velocity, and adding aX + bY—reflecting that the context of the AR task allowed various ways of articulating the same operational process.
Overall, the intervention process provided participants with diverse opportunities to apply operational knowledge, from dynamic physical interactions to numerical manipulations. By applying the emerging operational knowledge, participants started to understand those unfamiliar mathematical symbols and construct more structural knowledge of vector addition.
5.5. Interpreting Symbols in AR
The AR task posed challenges for participants in interpreting symbols on the worksheet. Figure 18 revealed three main focused codes: arrow meaning (with six open codes), Q1 result format (with three open codes), and Q2 result format (with four open codes).
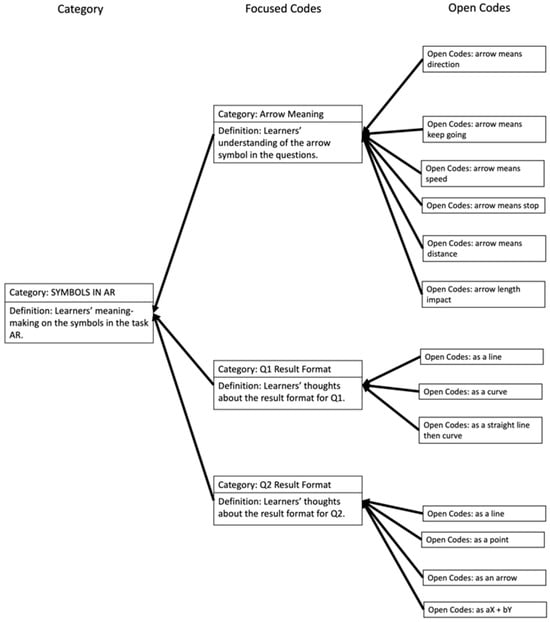
Figure 18.
Codes for meaning of symbols in AR task.
In response to the question about the meaning of arrows, none of those participants correctly identified that arrows represented direction, aligning with the definition of vectors. Instead, participants had various interpretations, considering arrows as an indicator to keep going (e.g., “You can’t change your mid arrow, so it’s gonna keep you going this way”.), stop (e.g., “I think that it would be stopping out like the arrow where it stops”.), represent speed (e.g., “I think the arrow means how many miles per hour are going right now”.), or symbolize distance (e.g., “Because it’s showing the distance”.). Moreover, comparisons among arrow lengths led to beliefs that longer arrows indicated a stronger impact on movement.
Besides the arrow symbol, participants also exhibited variations in the symbols they used for their answers to both questions. For Q1, participants depicted a straight line, reminiscent of their experiences in the EP (placing sticks to measure distance) and ID (adding units along axes to obtain a straight yellow arrow) tasks.
Regarding Q2, participants had unique interpretations. Participants in Group Jay were distinctive in perceiving the answer as an arrow. Others speculated that the answer could be a dot as 4x + 6y was similar to the coordinate (4,6), a line connecting the origin and the point (4, 6), or even the equation “4x + 6y”. The diversity in Q2’s answer formats likely stemmed from the abstract nature of the question, and the escalated level of complexity even impeded participants from connecting this question with previous learning tasks.
5.6. Structural Understanding
In accordance with Sfard’s (1991) assertion that procedural knowledge often precedes structural knowledge, the participants in the intervention exhibited a richer understanding of operational aspects for emergent problem-solving, with comparatively less emphasis on structural understanding [36]. Figure 19 categorizes structural understanding across the learning tasks, involving six focused codes (two per category) and a total of sixteen open codes.
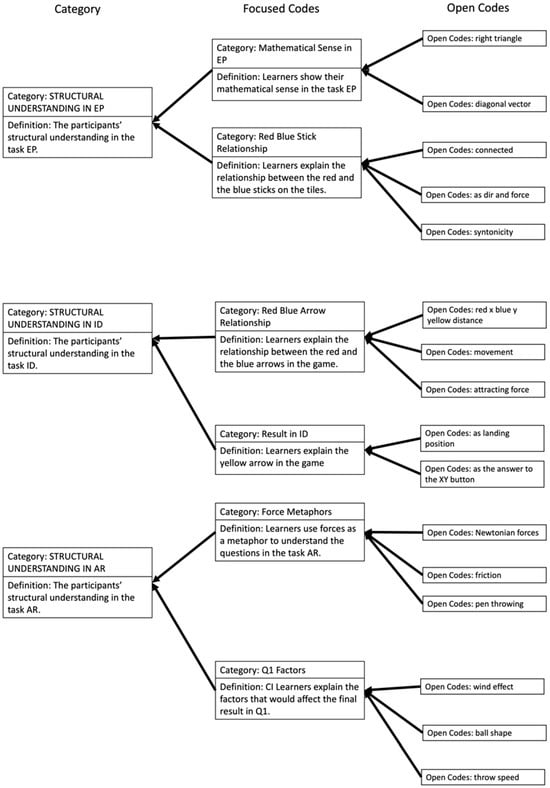
Figure 19.
Codes for other structural understanding.
In the EP task, all the participants exhibited “mathematical sense”, which refers to an uncertain and informal feeling about a mathematical concept, recognizing patterns formed by sticks on tiles as resembling right triangles (e.g., “It looks like a right triangle”.) and associating diagonal yellow sticks with vectors (e.g., “Because I don’t remember vectors, but I think vectors are like this”.). Connectivity is also identified as the relationship between red and blue sticks.
Within the iconic depiction task (ID), participants responded to the question about the relationship between red and blue arrows in the simulation game. Group Dove considered these arrows as X/Y values, while Group Jay envisioned the red and blue arrows working together to make a movement or assumed that one arrow was the force attracting the other.
In the AR task, Group Cardinal employed a “force metaphor” to explain the questions. They analytically compared two opposing forces with varying magnitudes. Group Dove participants vaguely perceived one vector holding back another akin to friction, while one participant from Group Jay embodied the force metaphor by simulating throwing a pen whose trajectory was influenced by wind. In addition, participants proposed wind, the football’s spiral shape, and the quarterback’s throw speed as factors influencing the ball trajectory in Q1. This highlights the tendency to employ concrete ideas as part of their procedural knowledge construct when grappling with abstract structural problems.
6. Discussion
In response to the research question, this section synthesizes the results to construct preliminary theories. The focus is on delineating how the CF process engages students in the learning of vector addition. To answer RQ 1, the preliminary theories are elucidated from three perspectives: the connections across tasks, the relationship between operational and structural knowledge, and the use of symbols. To answer RQ 2, based on the three preliminary theories, three design suggestions for a successful CF intervention are proposed. Also, the limitations of this study are examined at the end of this section.
6.1. Preliminary Theories
Preliminary Theory I: the CF process that incorporates the same question contexts, identical colors, and similar problems can activate prior knowledge and establish meaningful connections across learning tasks.
In designing a successful concreteness fading (CF) intervention, it is imperative to incorporate mutual referents that enable learners to discern explicit connections and comprehend the interconnectedness of representations at each stage [22,44]. Unlike previous CF studies that primarily focused on the similarity of questions across tasks, such as the equal sign questions in McNeil and Fyfe’s study (2012), with a more complex mathematical topic—vector addition—this study advocates for the utilization of the same question context to assist students in offloading [21]. The intricacy of the vector addition topic renders the consistency of questions across tasks challenging, especially when striving to exclude formalisms in the enactive task. However, opting to solely maintain the question context is a more manageable approach, which ensures the desired interconnectedness between tasks. As elaborated in the part of the inter-task connection above (refer to Figure 10), the participants recognized the overarching football contexts across the three learning tasks, establishing it as a mutual referent. Moreover, maintaining consistent colors for key elements like sticks, arrows, and vectors facilitated the quick recognition of connections and the exploration of different representations of the same concept. The strategic use of color to reduce visual search and support rapid information access [45] served as a valuable clue for information retrieval [46]. In this study, participants’ recognition of color was a cue across tasks, where the red and blue colors consistently represented sticks, arrows, and vectors, forming another mutual referent (refer to Figure 11). Additionally, the activation of participants’ prior knowledge, encompassing the coordinate plane and algebraic arithmetic, across diverse learning tasks facilitated their engagement in those tasks and reduced cognitive load, aligning with Myhill and Brackley’s findings [47]. Setting up similar contexts across all three learning tasks aimed not only to assist students in offloading when transitioning between tasks but also to leverage their prior knowledge, including both prior mathematical knowledge and knowledge constructed in the early tasks of this intervention, effectively. For instance, in Figure 10, participants identified a coordinate plane across tasks, even in the absence of a clear indication in tasks EP and ID. Their familiarity with the coordinate plane prompted recognition when encountering a tiled floor and the grid field in the simulation game. Regarding participants’ knowledge developed in the process of the intervention, their application of operational knowledge across tasks (refer to Figure 14, Figure 15 and Figure 16) and development of vector magnitude understanding (refer to Figure 13), which was implied by using sticks to measure distance on the tiles, determining the arrow length by the X/Y values, and counting blocks or units to find vector lengths, indicated that similar task settings leveraged their knowledge constructed in the intervention and helped them establish inter-task connections. Furthermore, these connections align with variation theory [48]; the process of CF learning allows students to form the idea of vector addition step by step and in different formats.
Preliminary Theory II: the in-between fading task of the CF process facilitates the intertwining of structural knowledge building with operational knowledge construction.
In mathematics education, there is always a fundamental dichotomy between procedures and concepts, delineating the distinction between tasks to perform and knowledge to acquire [49], but procedural operations have the potential to transform into objects that serve as units of a higher-level theory [50]. In the context of this study, the operational knowledge oriented towards problem-solving, constructed during the intervention, played a role, to some extent, in fostering the development of structural knowledge related to vector addition. Specifically, in the ID task, the operational knowledge encompassed the utilization of X/Y values to manipulate arrows within the simulation game, while the structural knowledge revolved around understanding the impact of X/Y values, which was derived from the operations performed on those values (refer to Figure 15 and Figure 19). An illustrative instance from Group Jay emerged when they inquired about the correlation between the red and blue stick/arrow in the ID task.
In the EP task, the participant P3 in this group told the researcher, “Well, there’s a relationship with the red and blue one, cuz they connect. But the yellow one, they go in the straight”. Then, in the ID task, P3 said, “We have to use the sticks to make, to show what we’re going, like the X and Y integers”.
In this instance, P3 noticed that the relationship between the red and blue arrows (though he used the term “sticks”) in the simulation was associated with the X and Y integers. Consequently, as P3 engaged in the simulation game by manipulating X/Y values, he realized that the relationship between the red and blue arrows was more intricate than the connection between the red and blue sticks in the EP task. This realization propelled him into the final AR task, where he proposed the “square” approach that was analogous to the formal “parallelogram method” for vector addition. Therefore, the simplicity of the ID task characterized by operational knowledge focused on manipulating X/Y values to determine arrow lengths, integrated with some formal symbols like X/Y values and arrows, facilitates the concurrent development of both operational and structural knowledge. Therefore, the fading stage avoids sudden change in representations and provides students with a smooth transition from operational knowledge application to structural knowledge construction.
Preliminary Theory III: the inclusion of unfamiliar symbols in the CF process may initially result in a naïve understanding but provides an avenue for mathematical sense-making.
The examination of arrow meaning and answer formats for the abstract questions in this study uncovered participants’ struggle with unfamiliar symbols (see the codes in Figure 18). This struggle is understandable, given that symbols often originate from a heavily regulated notational system that lacks inherent meaning for those unfamiliar with it [1]. Consequently, participants developed diverse interpretations of the symbols, which led to different answer formats for the two questions in the AR task (see Figure 18). However, from a mathematical sense-making perspective, participants were still making progress. When explaining these symbols, they engaged in a process of reasoning through their problem-solving rationale and attempted to articulate unfamiliar mathematical ideas in their own words. Encouraging students to reflect on their problem-solving processes and embracing diverse problem-solving strategies contributes to a student-centered mathematical learning experience and fosters a supportive learning environment [51]. By presenting different representations of the same mathematical concept across tasks (e.g., sticks, arrows, and vector symbols), the CF process empowers learners to interpret the meaning of symbols in multiple ways and thereby facilitates mathematical sense-making.
6.2. Design Principles
Based on the preliminary theories, three design principles are formulated for future CF intervention design for complex mathematical topics:
- Maintain consistency in design elements: When designing and implementing a CF intervention for a complex mathematical topic, ensure that design elements, such as colors and question contexts, remain consistent. This consistency offers a space for leveraging prior knowledge in the learning process.
- Monitor knowledge development in the mediate fading task: Track the progression of similar ideas during the mediate fading task to identify moments when operational and structural knowledge intertwine. Recognizing these instances is crucial as they represent key learning moments.
- Embrace naïve understanding of unfamiliar symbols: Allow for a naïve understanding of unfamiliar symbols to encourage mathematical sense-making. Provide timely lectures to teach these symbols afterward to enhance the learning experience.
6.3. Limitations
Three limitations were identified in this study. The first pertains to the sample size, comprising only three groups. Some students may feel more comfortable with this format of learning, while others may not. Future studies may consider replicating this design with a larger group of students. Also, due to scheduling issues, this study used convenience samples, which might prevent the researcher from incorporating culturally responsive instruction during the intervention as there was limited time for the researcher to know the participants better.
The second limitation is possibly associated with the first one. The choice of football as the context for the intervention may introduce biases in student responses due to varying degrees of enthusiasm or emotional engagement with the topic. For future studies, it might be better to know the participants better and design/develop the corresponding context for better engagement.
The third limitation relates to the exploration of learning at a group level, which deviates from the conventional approach in CF studies that typically focus on individual learning. Due to constraints in resources and scheduling, this study adopted a group-oriented approach. Nevertheless, future investigations could provide valuable insights by exploring the individual learning processes within a CF intervention.
7. Conclusions
In this study, a CF intervention was designed and implemented to teach eighth graders a complex mathematical topic, vector addition. In response to the research question about how the CF process contributes to learning vector addition, through a grounded theory method, this study discovers that the inter-task connectedness can be established through design elements, the fading task can be a good space to intertwine operational and structural knowledge, and the unfamiliar symbols embodied in the task can promote mathematical sense-making. Theoretically, in this study, the innovative instructional design that incorporates the framework of concreteness fading extends the topic of CF studies to more complex mathematical topics, like vector addition, and the findings present how the connections between tasks establish, the operational and structural knowledge intertwine, and the unfamiliar symbols promote mathematical sense-making. Practically, this study provides design suggestions for designing and implementing CF interventions to teach complex mathematical topics. This study is an exploratory study with a small sample size, so future studies may implement this design with a larger sample size to teach this or other complex mathematical tasks and probe the effects of the sequence of tasks.
Addressing the research questions concerning the contribution of the CF process to learning vector addition, this study, using a grounded theory method, uncovers key findings that highlight that inter-task connectedness can be effectively established through thoughtful design elements, the fading task serves as a space for intertwining operational and structural knowledge, and the incorporation of unfamiliar symbols within tasks promotes valuable mathematical sense-making.
The theoretical contributions of this study extend beyond the scope of traditional CF research by innovatively applying the instructional design framework to complex mathematical topics, such as vector addition. This research elucidates the mechanisms through which connections between tasks are established, operational and structural knowledge are developed concurrently, and unfamiliar symbols foster mathematical sense-making. Practically, this study offers valuable design suggestions for crafting and implementing CF interventions aimed at teaching complex mathematical subjects. Recognizing the exploratory nature of this study and its limited sample size, future research may consider implementing the proposed design with a larger cohort. This extension could further explore the efficacy of the sequence of tasks in teaching not only vector addition but also other complex mathematical concepts.
Funding
This research received no external funding.
Institutional Review Board Statement
This study was reviewed and approved by the Institutional Review Board (IRB) of University of Wisconsin–Madison, under approval number 2021-1514 (Approval Date: 13 December 2021). All procedures performed in this study involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki Declaration and its later amendments or comparable ethical standards. Informed consent was obtained from all individual participants included in this study.
Informed Consent Statement
All subjects gave their informed consent for inclusion before they participated in this study. This study was conducted in accordance with the Declaration of Helsinki, and the protocol was approved by the Institutional Review Board (IRB) of University of Wisconsin–Madison, under approval number 2021-1514 (Approval Date: 13 December 2021).
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to restrictions stated in the informed consent form signed by the study participants.
Acknowledgments
I would like to extend my gratitude to Matthew Berland and Mitchell J. Nathan for their invaluable guidance and support throughout this study. Special thanks to Jaime Gibson, the principal of Horizon Science Academy Columbus Middle School, who provided me with ample support for this study.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A. Researcher’s Prompt Questions
- EP task:
- Could you explain to your teammates how you describe your position? And why do you think your position should be XXX?
- [After placing blue and red sticks, for the stick placing student] Could you explain to your teammates why you put sticks in this way?
- Do you agree with him/her? Why do you think it is a good way to connect points like this?
- How would you describe the directions of these red and blue sticks?
- [After placing yellow sticks] How long do you think this line is in terms of sticks you have placed?
- How would you like to describe the direction of these yellow sticks?
- Could you explain to [NEXT STUDENT] what you think the relationship is between those yellow sticks and those red and blue sticks in terms of their lengths and directions?
- ID task:
- 8.
- Could you explain how you get the x and y units to your teammates?
- 9.
- Do you agree with him/her? Why do you think this is the correct answer?
- 10.
- Could you explain to [NEXT STUDENT] what you think the relationship is between the red and blue arrows and the yellow arrow in terms of their lengths and directions?
- 11.
- Did you find any connections between this simulation and our previous activity? What are they?
- AR task:
- 12.
- Do you have any rough ideas about how to solve this?
- 13.
- Did you find anything in this question that relates to what we have done before? What is it?
- 14.
- Could you explain to [NEXT STUDENT] how you got your answer?
- 15.
- Could you explain to [Next STUDENT] what kind of connections you find between the questions you solved and the previous activities we have done?
References
- Nathan, M.J. Rethinking Formalisms in Formal Education. Educ. Psychol. 2012, 47, 125–148. [Google Scholar] [CrossRef]
- National Council of Teachers of Mathematics. Principles and Standards for School Mathematics: An Overview, 3rd ed.; NCTM, Ed.; National Council of Teachers of Mathematics: Reston, VA, USA, 2000; ISBN 978-0-87353-484-0. [Google Scholar]
- National Research Council. Next Generation Science Standards: For States, By States; National Academies Press: Washington, DC, USA, 2013; ISBN 978-0-309-27227-8. [Google Scholar]
- Heckler, A.F.; Scaife, T.M. Adding and Subtracting Vectors: The Problem with the Arrow Representation. Phys. Rev. Spec. Top.-Phys. Educ. Res. 2015, 11, 010101. [Google Scholar] [CrossRef]
- Fyfe, E.R.; McNeil, N.M.; Son, J.Y.; Goldstone, R.L. Concreteness Fading in Mathematics and Science Instruction: A Systematic Review. Educ. Psychol. Rev. 2014, 26, 9–25. [Google Scholar] [CrossRef]
- Goldstone, R.L.; Son, J.Y. The Transfer of Scientific Principles Using Concrete and Idealized Simulations. J. Learn. Sci. 2005, 14, 69–110. [Google Scholar] [CrossRef]
- Kim, H. Concreteness Fading Strategy: A Promising and Sustainable Instructional Model in Mathematics Classrooms. Sustainability 2020, 12, 2211. [Google Scholar] [CrossRef]
- McNeil, N.M.; Fyfe, E.R. “Concreteness Fading” Promotes Transfer of Mathematical Knowledge. Learn. Instr. 2012, 22, 440–448. [Google Scholar] [CrossRef]
- Ottmar, E.; Landy, D. Concreteness Fading of Algebraic Instruction: Effects on Learning. J. Learn. Sci. 2017, 26, 51–78. [Google Scholar] [CrossRef]
- Glaser, B.G.; Strauss, A.L. The Discovery of Grounded Theory: Strategies for Qualitative Research; Aldine Transaction: Piscataway, NJ, USA, 1967; ISBN 978-0-202-30260-7. [Google Scholar]
- Nguyen, N.-L.; Meltzer, D.E. Initial Understanding of Vector Concepts among Students in Introductory Physics Courses. Am. J. Phys. 2003, 71, 630–638. [Google Scholar] [CrossRef]
- Knight, R.D. The Vector Knowledge of Beginning Physics Students. Phys. Teach. 1995, 33, 74–77. [Google Scholar] [CrossRef]
- Aguirre, J.; Erickson, G. Students’ Conceptions about the Vector Characteristics of Three Physics Concepts. J. Res. Sci. Teach. 1984, 21, 439–457. [Google Scholar] [CrossRef]
- Latifa, B.R.A.; Purwaningsih, E.; Sutopo, S. Identification of Students’ Difficulties in Understanding of Vector Concepts Using Test of Understanding of Vector. J. Phys. Conf. Ser. 2021, 2098, 012018. [Google Scholar] [CrossRef]
- Gubrud, A.R.; Novak, J.D. Learning Achievement and the Efficiency of Learning the Concept of Vector Addition at Three Different Grade Levels. Sci. Educ. 1973, 57, 179–191. [Google Scholar] [CrossRef]
- Kaminski, J.A.; Sloutsky, V.M.; Heckler, A. Transfer of Mathematical Knowledge: The Portability of Generic Instantiations. Child Dev. Perspect. 2009, 3, 151–155. [Google Scholar] [CrossRef]
- Uttal, D.H.; Scudder, K.V.; DeLoache, J.S. Manipulatives as Symbols: A New Perspective on the Use of Concrete Objects to Teach Mathematics. J. Appl. Dev. Psychol. 1997, 18, 37–54. [Google Scholar] [CrossRef]
- Mayer, R.E. Learners as Information Processors: Legacies and Limitations of Educational Psychology’s Second. Educ. Psychol. 1996, 31, 151–161. [Google Scholar] [CrossRef]
- Priniski, S.J.; Hecht, C.A.; Harackiewicz, J.M. Making Learning Personally Meaningful: A New Framework for Relevance Research. J. Exp. Educ. 2018, 86, 11–29. [Google Scholar] [CrossRef] [PubMed]
- Koedinger, K.R.; Nathan, M.J. The Real Story Behind Story Problems: Effects of Representations on Quantitative Reasoning. J. Learn. Sci. 2004, 13, 129–164. [Google Scholar] [CrossRef]
- McNeil, N.M.; Alibali, M.W. Why Won’t You Change Your Mind? Knowledge of Operational Patterns Hinders Learning and Performance on Equations. Child Dev. 2005, 76, 883–899. [Google Scholar] [CrossRef]
- Fyfe, E.R.; Nathan, M.J. Making “Concreteness Fading” More Concrete as a Theory of Instruction for Promoting Transfer. Educ. Rev. 2019, 71, 403–422. [Google Scholar] [CrossRef]
- Koedinger, K.R.; Alibali, M.W.; Nathan, M.J. Trade-Offs Between Grounded and Abstract Representations: Evidence from Algebra Problem Solving. Cogn. Sci. 2008, 32, 366–397. [Google Scholar] [CrossRef]
- Schliemann, A.D.; Carraher, D.W. The Evolution of Mathematical Reasoning: Everyday versus Idealized Understandings. Dev. Rev. 2002, 22, 242–266. [Google Scholar] [CrossRef]
- Brown, M.C.; McNeil, N.M.; Glenberg, A.M. Using Concreteness in Education: Real Problems, Potential Solutions. Child Dev. Perspect. 2009, 3, 160–164. [Google Scholar] [CrossRef]
- Martin, T.; Schwartz, D.L. Physically Distributed Learning: Adapting and Reinterpreting Physical Environments in the Development of Fraction Concepts. Cogn. Sci. 2005, 29, 587–625. [Google Scholar] [CrossRef] [PubMed]
- Kaminski, J.A.; Sloutsky, V.M.; Heckler, A.F. The Advantage of Abstract Examples in Learning Math. Science 2008, 320, 454–455. [Google Scholar] [CrossRef]
- Goldstone, R.L.; Sakamoto, Y. The Transfer of Abstract Principles Governing Complex Adaptive Systems. Cognit. Psychol. 2003, 46, 414–466. [Google Scholar] [CrossRef]
- Bruner, J.S. Toward a Theory of Instruction. In Toward a Theory of Instruction; Harvard University Press: Cambridge, MA, USA, 1966. [Google Scholar]
- Son, J.Y.; Smith, L.B.; Goldstone, R.L.; Leslie, M. The Importance of Being Interpreted: Grounded Words and Children’s Relational Reasoning. Front. Psychol. 2012, 3, 45. [Google Scholar] [CrossRef]
- Lakoff, G.; Núñez, R.E. Where Mathematics Comes from: How the Embodied Mind Brings Mathematics into Being. In Where Mathematics Comes from: How the Embodied Mind Brings Mathematics into Being; Basic Books: New York, NY, USA, 2000; ISBN 0-465-03770-4. [Google Scholar]
- Barsalou, L.W. Grounded Cognition. Annu. Rev. Psychol. 2008, 59, 617–645. [Google Scholar] [CrossRef] [PubMed]
- Vygotsky, L.S. Mind in Society: The Development of Higher Psychological Processes; Harvard University Press: Cambridge, MA, USA, 1980; ISBN 0-674-07668-0. [Google Scholar]
- Fyfe, E.R.; McNeil, N.M.; Borjas, S. Benefits of “Concreteness Fading” for Children’s Mathematics Understanding. Learn. Instr. 2015, 35, 104–120. [Google Scholar] [CrossRef]
- Jaakkola, T.; Veermans, K. Exploring the Effects of Concreteness Fading across Grades in Elementary School Science Education. Instr. Sci. 2018, 46, 185–207. [Google Scholar] [CrossRef]
- Sfard, A. On the Dual Nature of Mathematical Conceptions: Reflections on Processes and Objects as Different Sides of the Same Coin. Educ. Stud. Math. 1991, 22, 1–36. [Google Scholar] [CrossRef]
- Borgerding, L.A.; Kaya, F.; Librea-Carden, M.R.; Pantuso, D.; Maybin, J. Sports Experiences as Funds of Knowledge for Science: College Students’ Ideas about Science in American Football. Electron. J. Res. Sci. Math. Educ. 2018, 22, 1–18. [Google Scholar]
- Czocher, J.A.; Melhuish, K. Attending to Coherence Among Research Questions, Methods, and Claims in Coding Studies. J. Res. Math. Educ. 2024, 55, 148–155. [Google Scholar] [CrossRef]
- Charmaz, K. Constructing Grounded Theory. In Introducing Qualitative Methods, 2nd ed.; Sage: London, UK; Thousand Oaks, CA, USA, 2014; ISBN 978-0-85702-913-3. [Google Scholar]
- Tweed, A.; Charmaz, K. Grounded Theory Methods for Mental Health Practitioners. In Qualitative Research Methods in Mental Health and Psychotherapy: A Guide for Students and Practitioners; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 131–146. [Google Scholar]
- Strauss, A.; Corbin, J.M. Basics of Qualitative Research: Grounded Theory Procedures and Techniques. In Basics of qualitative research: Grounded Theory Procedures and Techniques; Sage Publications, Inc.: Thousand Oaks, CA, USA, 1990; p. 270. ISBN 0-8039-3250-2. [Google Scholar]
- Glaser, B.G. Theoretical Sensitivity: Advances in the Methodology of Grounded Theory; Sociology Press: Mill Valley, CA, USA, 1978; ISBN 978-1-884156-01-4. [Google Scholar]
- Glaser, B.G. Doing Quantitative Grounded Theory; Sociology Press: Mill Valley, CA, USA, 2008; ISBN 978-1-884156-17-5. [Google Scholar]
- Suh, S.; Lee, M.; Law, E. How Do We Design for Concreteness Fading? Survey, General Framework, and Design Dimensions. In Proceedings of the Interaction Design and Children Conference, New York, NY, USA, 21 June 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 581–588. [Google Scholar]
- Keller, T.; Grimm, M. The Impact of Dimensionality and Color Coding of Information Visualizations on Knowledge Acquisition. In Knowledge and Information Visualization: Searching for Synergies; Tergan, S.-O., Keller, T., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; pp. 167–182. ISBN 978-3-540-31962-7. [Google Scholar]
- Hanna, A.; Remington, R. The Representation of Color and Form in Long-Term Memory. Mem. Cognit. 1996, 24, 322–330. [Google Scholar] [CrossRef] [PubMed]
- Myhill, D.; Brackley, M. Making Connections: Teachers’ Use of Children’s Prior Knowledge in Whole Class Discourse. Br. J. Educ. Stud. 2004, 52, 263–275. [Google Scholar] [CrossRef]
- Kullberg, A.; Runesson Kempe, U.; Marton, F. What Is Made Possible to Learn When Using the Variation Theory of Learning in Teaching Mathematics? ZDM 2017, 49, 559–569. [Google Scholar] [CrossRef]
- Gray, E.M.; Tall, D.O. Duality, Ambiguity, and Flexibility: A “Proceptual” View of Simple Arithmetic. J. Res. Math. Educ. 1994, 25, 116–140. [Google Scholar] [CrossRef]
- Sfard, A. Transition from Operational to Structural Conception: The Notion of Function Revisited. Proc. PME XIII 1989, 3, 151–158. [Google Scholar]
- Schoenfeld, A.H. Learning to Think Mathematically: Problem Solving, Metacognition, and Sense Making in Mathematics. In Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics; Macmillan Publishing Co., Inc.: New York, NY, USA, 1992; pp. 334–370. ISBN 978-0-02-922381-9. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).