A Study on the Influence of the Affective Domain on the Attitudes of Middle School Students toward Mathematics from a Gender Perspective
Abstract
1. Introduction
- Comprehend the association between gender stereotypes and attitudes toward mathematics.
- Understand how the affective domain impacts attitudes toward mathematics.
- Analyze the effect on middle school students to being exposed to content from videos of STEM professionals regarding their perspectives on gender equity and attitudes toward mathematics.
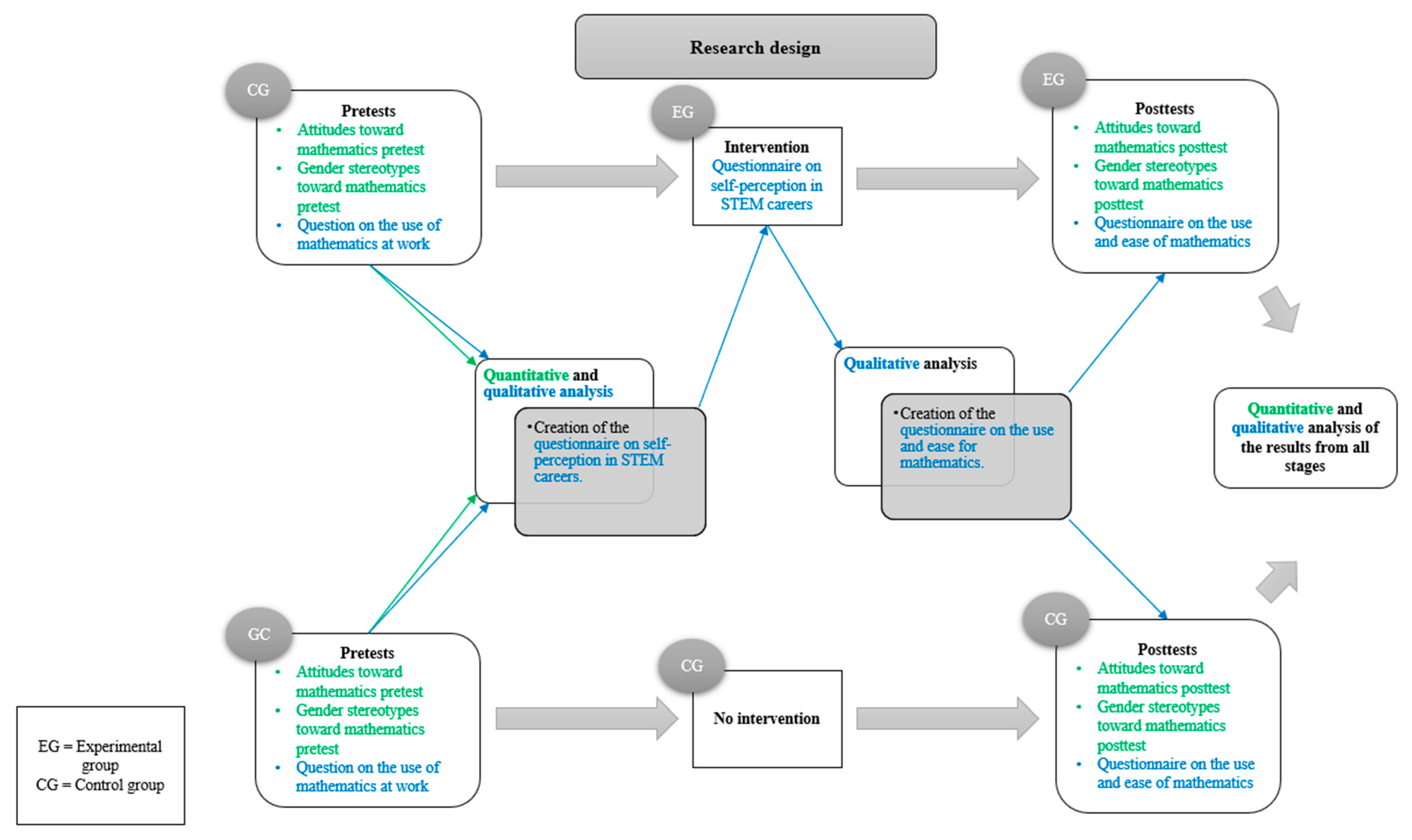
2. Methods
2.1. Participants
2.2. Instruments
2.3. Analysis Strategy
- Gender is associated with the affective domain toward mathematics in middle school students (SA.1).
- Gender is associated with gender stereotypes toward mathematics in middle school students (SB.1).
3. Results and Discussion
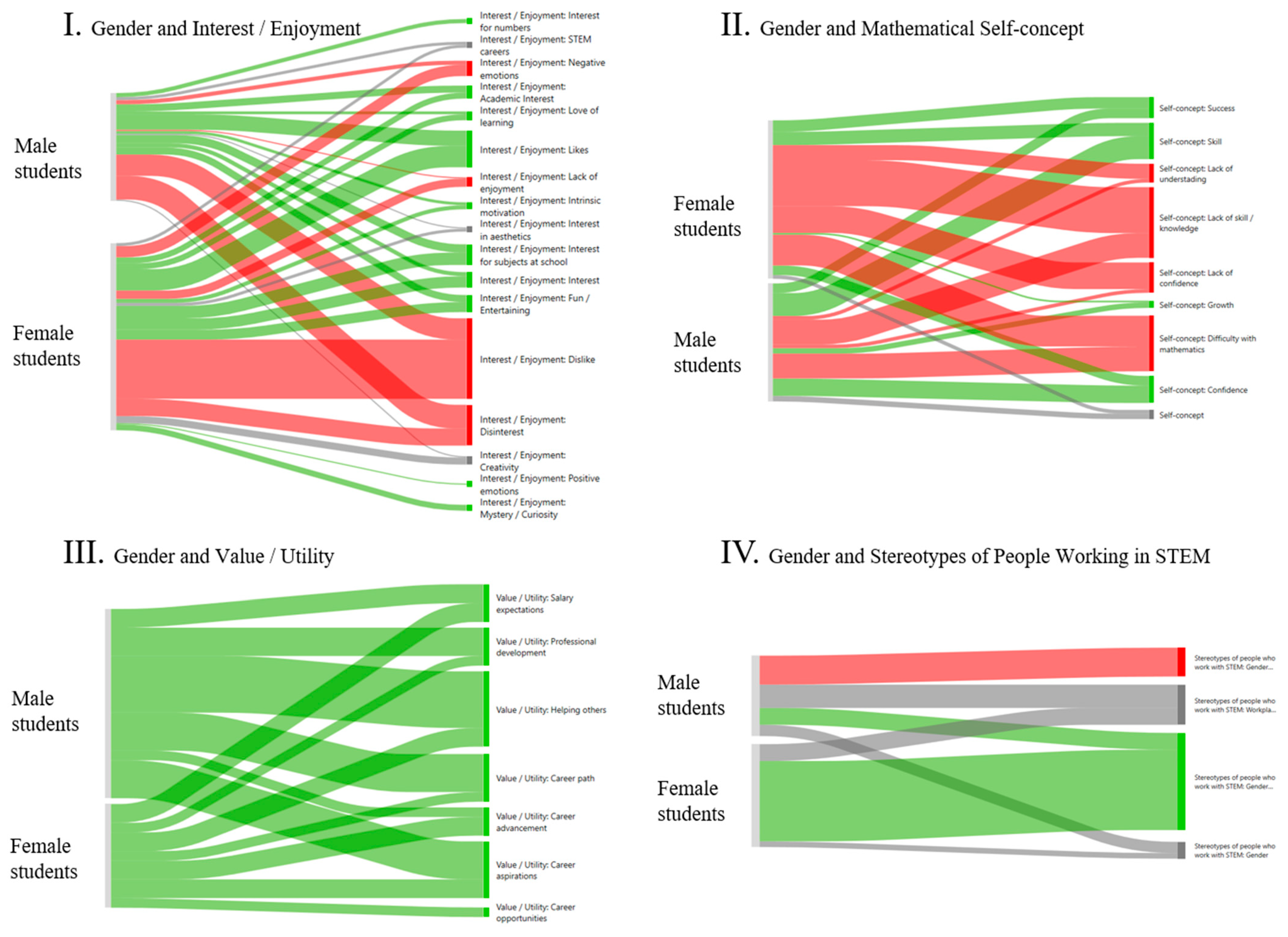
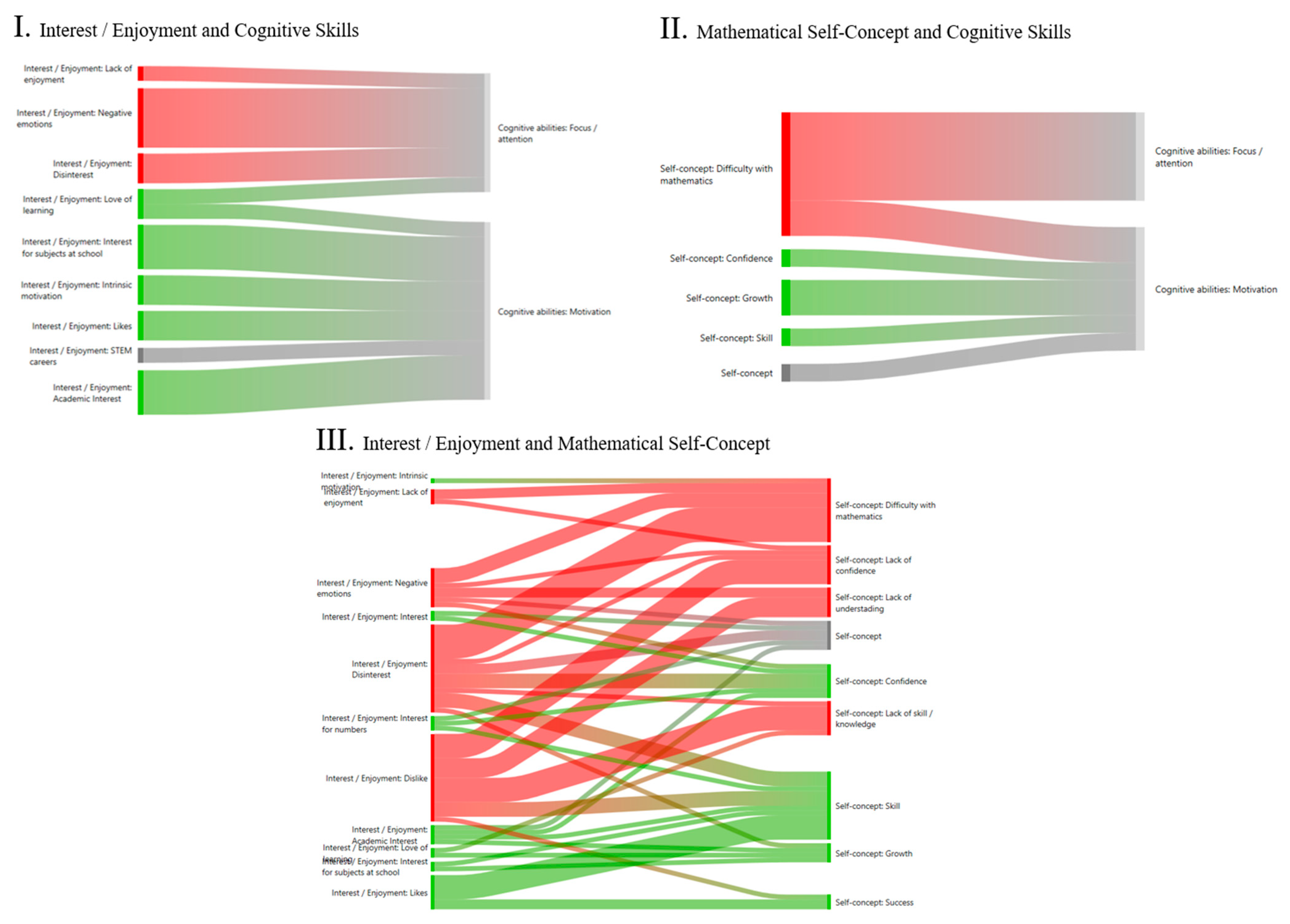
3.1. Qualitative Analysis
3.1.1. Coding Strategy
3.1.2. Pretest: Question about the Use of Mathematics in the Workspace
3.1.3. Intervention: Questionnaire about Self-Perception in STEM Careers
3.1.4. Post-Test: Questionnaire about the Use and Ease of Mathematics
3.2. Quantitative Analysis
3.2.1. Pretest
3.2.2. Post-Test
3.2.3. Pretest vs. Post-Test
3.3. General Contrast of Results
4. Conclusions and Lessons Learned
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B
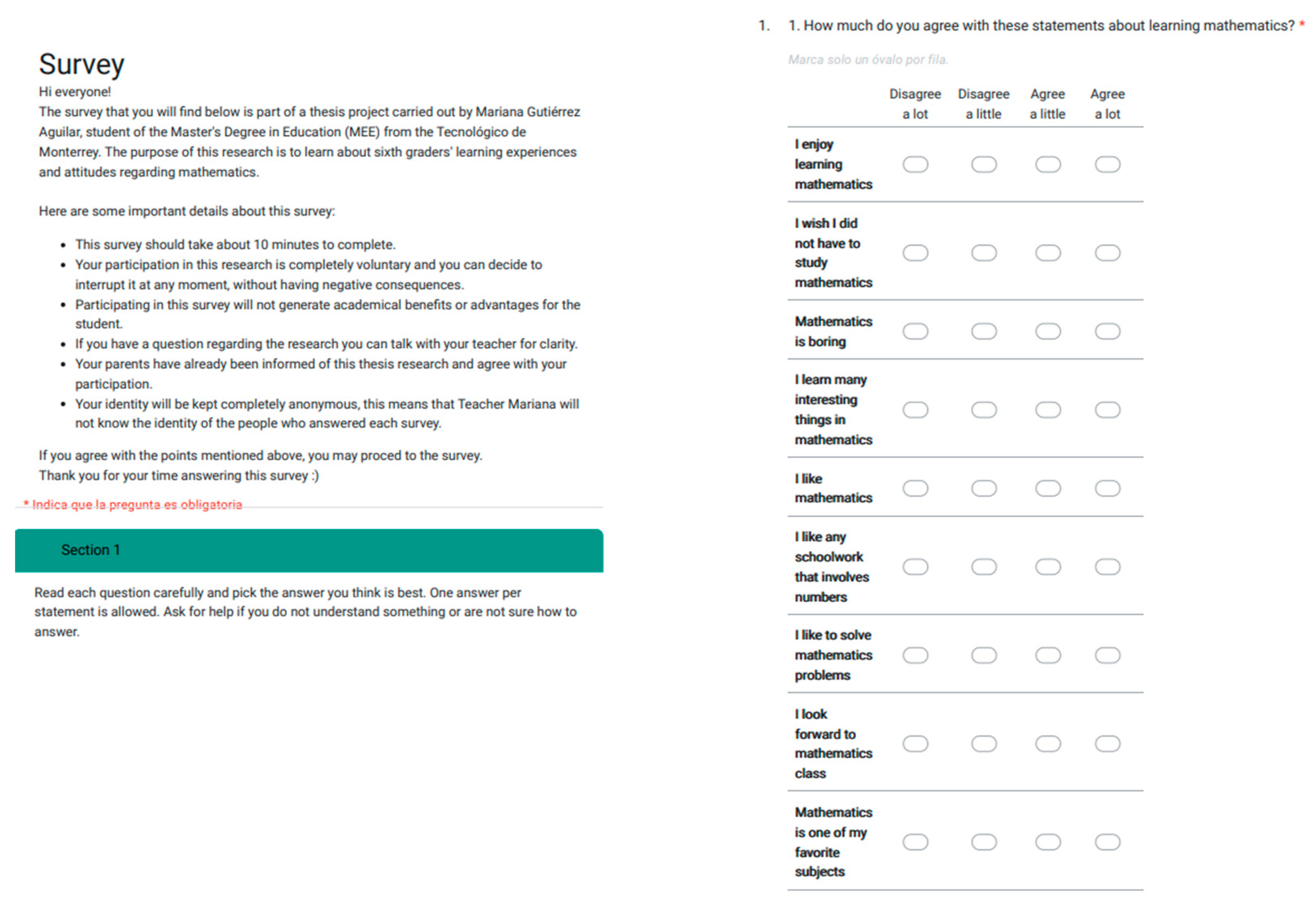

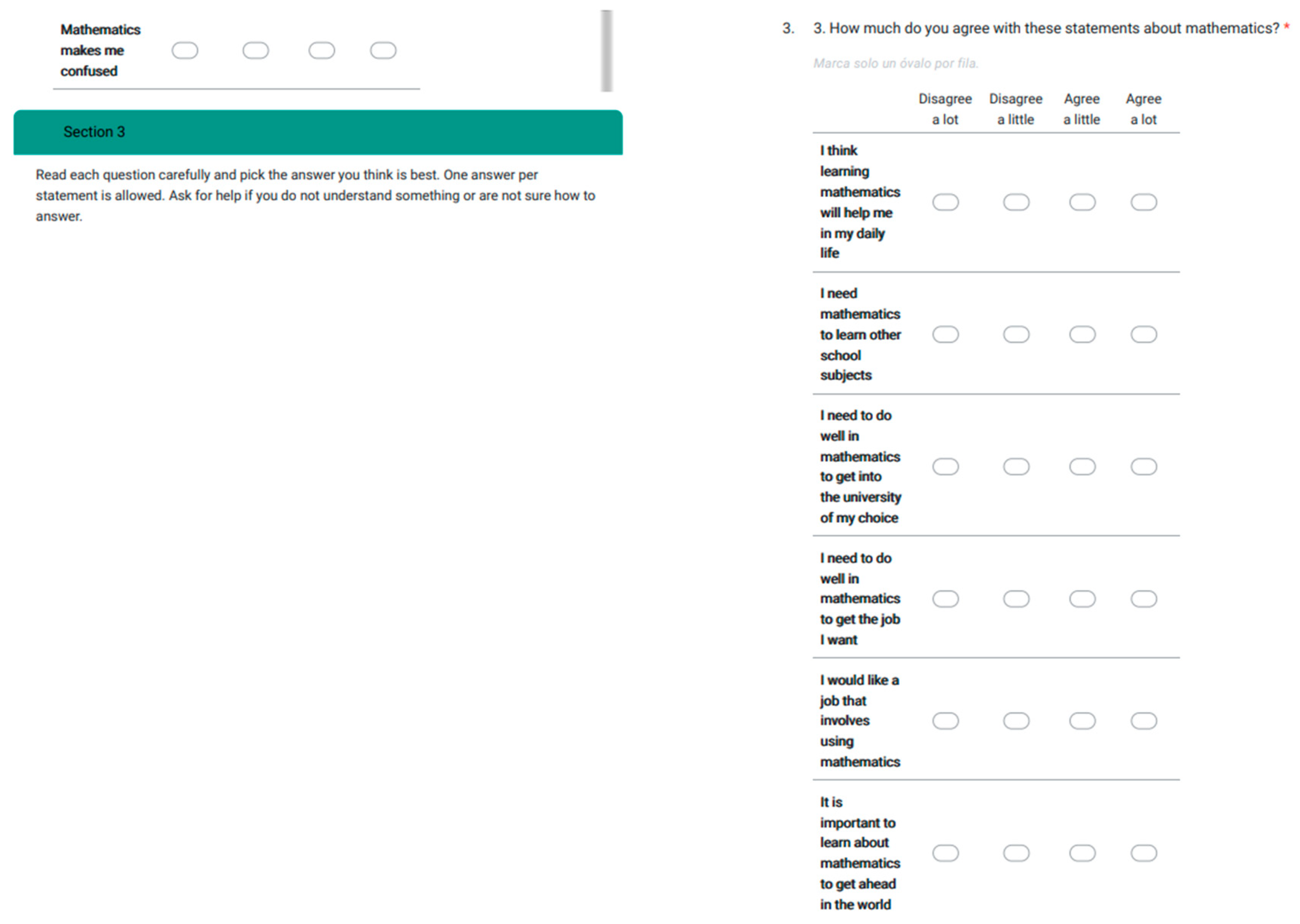
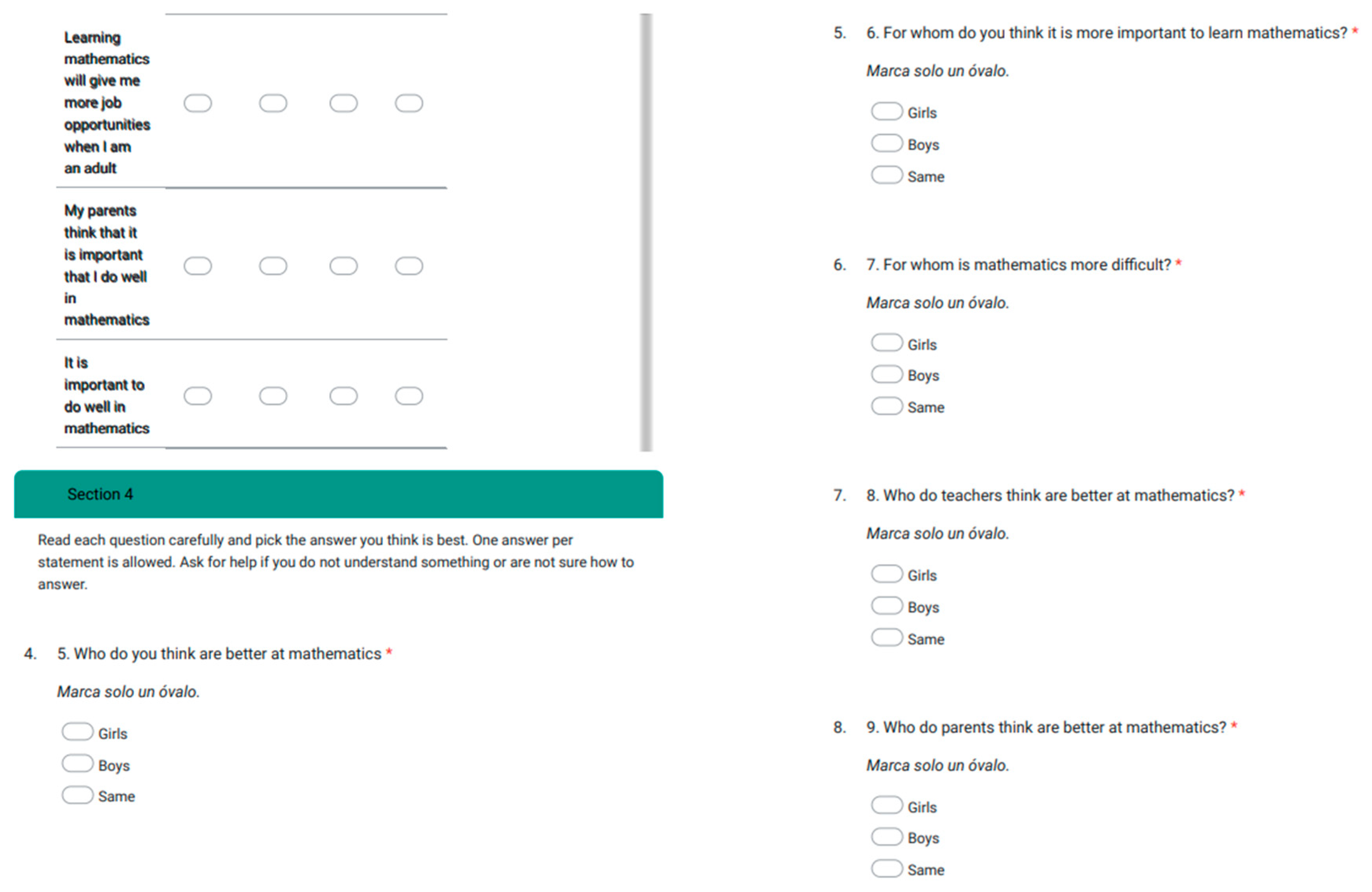
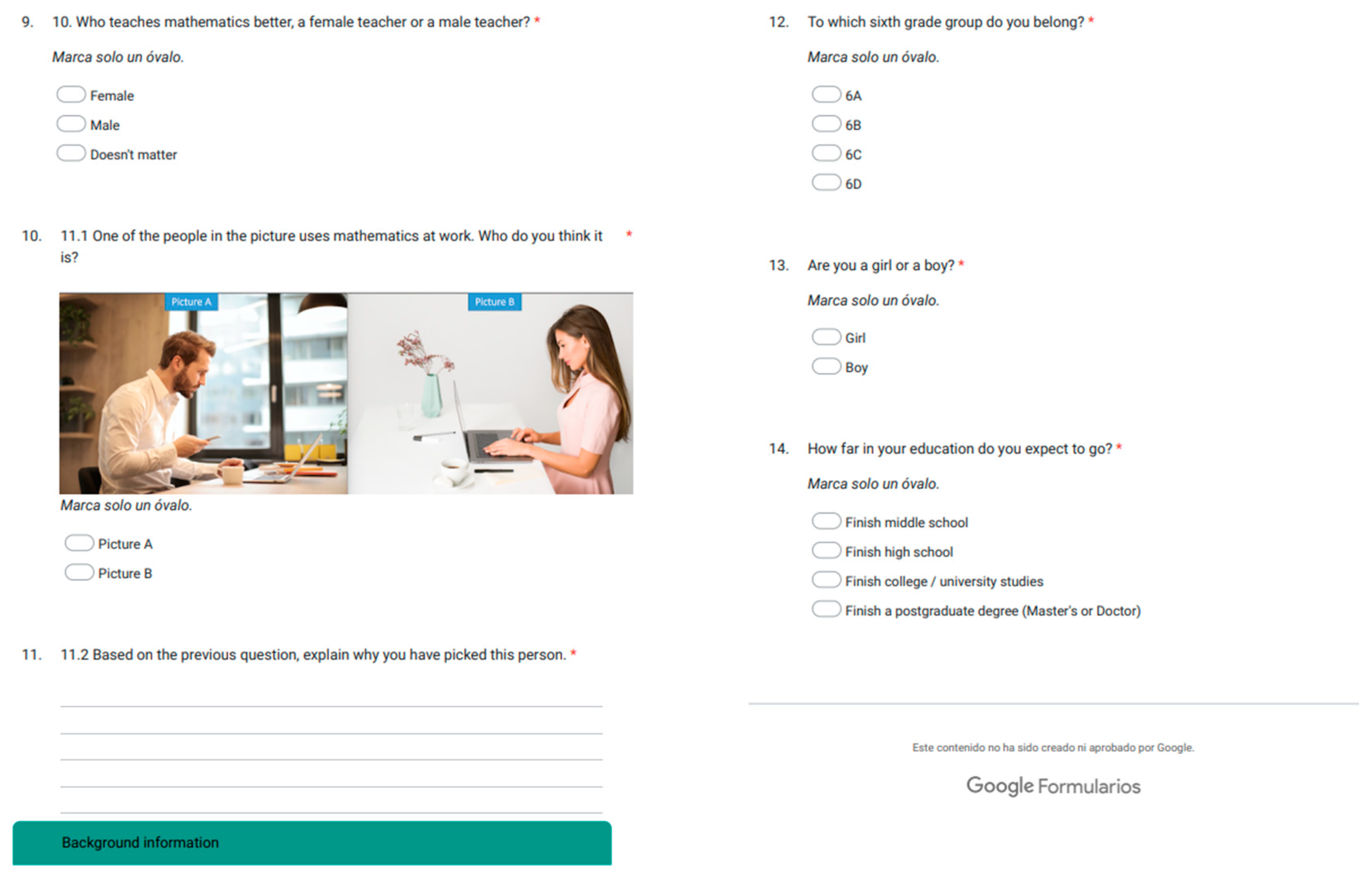
Appendix C


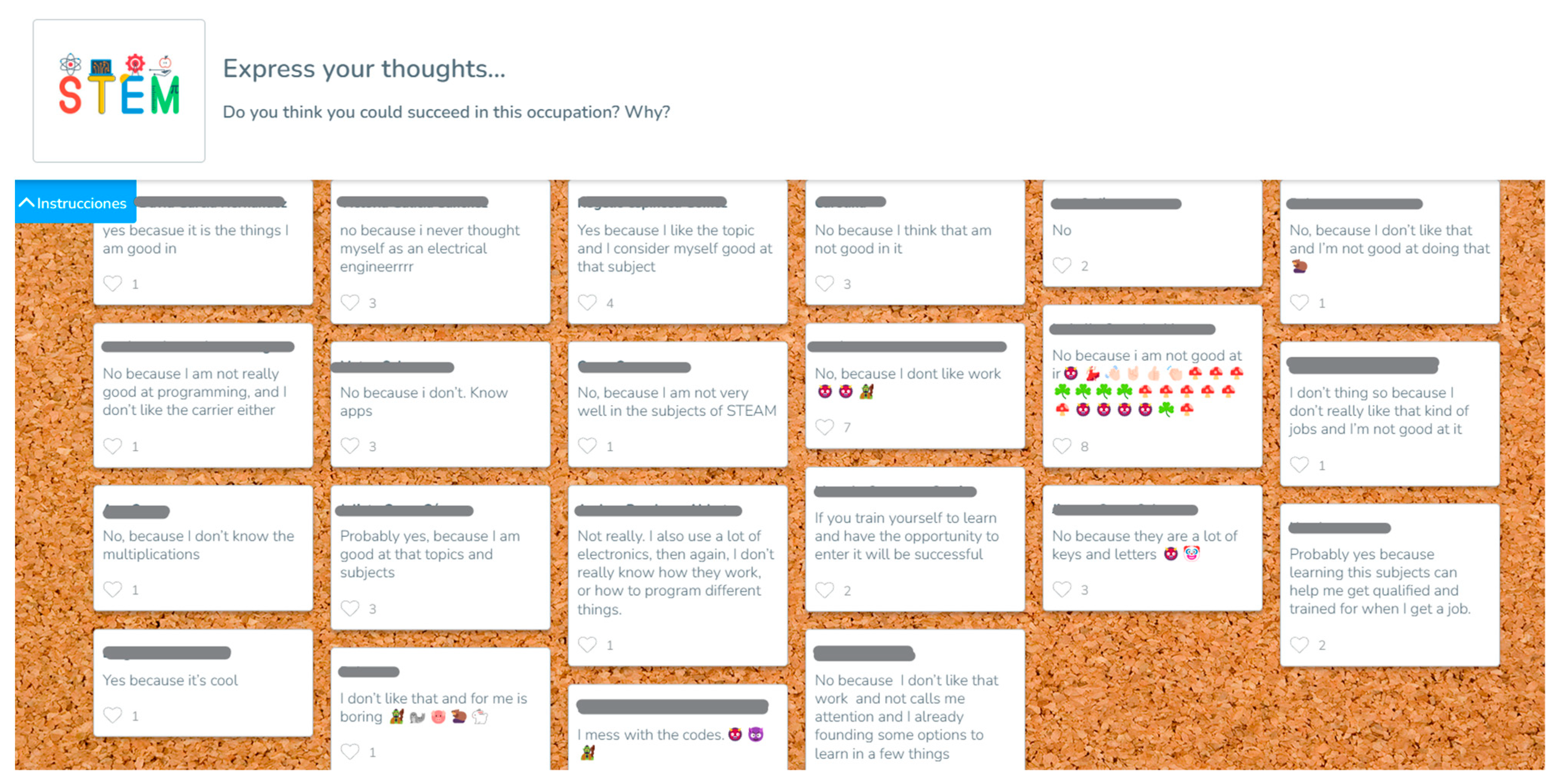
Appendix D


References
- Galende, N.; Arrivillaga, A.R.; Madariaga, J.M. Attitudes towards Mathematics in Secondary School Students. Personal and Family Factors. Cult. Educ. 2020, 32, 529–555. [Google Scholar] [CrossRef]
- Christensen, R.; Knezek, G. Indicators of Middle School Students’ Mathematics Enjoyment and Confidence. Sch. Sci. Math. 2020, 120, 491–503. [Google Scholar] [CrossRef]
- Amemiya, J.; Wang, M. Transactional Relations between Motivational Beliefs and Help Seeking from Teachers and Peers across Adolescence. J. Youth Adolesc. 2017, 46, 1743–1757. [Google Scholar] [CrossRef]
- Dare, E.A.; Roehrig, G.H. “If I Had to Do It, Then I Would”: Understanding Early Middle School Students’ Perceptions of Physics and Physics-Related Careers by Gender. Phys. Rev. Phys. Educ. Res. 2016, 12, 020117. [Google Scholar] [CrossRef]
- Steinke, J.; Applegate, B.; Penny, J.R.; Merlino, S. Effects of Diverse STEM Role Model Videos in Promoting Adolescents’ Identification. Int. J. Sci. Math. Educ. 2022, 20, 255–276. [Google Scholar] [CrossRef]
- Bond, B.J. Fairy Godmothers > Robots. Bull. Sci. Technol. Soc. 2016, 36, 91–97. [Google Scholar] [CrossRef]
- Dominguez, A.; Tejeda, S.; Ruiz, B. Influencing Factors to Choose STEM Areas: The Case of Strongly STEM-Oriented High School Students. In Proceedings of the 2020 IEEE Integrated STEM Education Conference (ISEC), Princeton, NJ, USA, 1 August 2020. [Google Scholar] [CrossRef]
- González-Jiménez, R.M. Evaluation of Training Strategies to Improve Attitudes towards Mathematics in Secondary. Educ. Mat. 2019, 31, 176–203. [Google Scholar] [CrossRef]
- Ursini, S.; Ramírez Mercado, M. Equidad, Género y Matemáticas En La Escuela Mexicana. Rev. Colomb. Educ. 2017, 211, 213–233. [Google Scholar] [CrossRef]
- Ergün, A. Identification of the Interest of Turkish Middle-School Students in Stem Careers: Gender and Grade Level Differences. J. Balt. Sci. Educ. 2019, 18, 90–104. [Google Scholar] [CrossRef]
- Riegle-Crumb, C.; Morton, K.; Nguyen, U.; Dasgupta, N. Inquiry-Based Instruction in Science and Mathematics in Middle School Classrooms: Examining Its Association With Students’ Attitudes by Gender and Race/Ethnicity. AERA Open 2019, 5, 1–17. [Google Scholar] [CrossRef]
- Aikman, S.; Halai, A.; Rubagiza, J. Conceptualising Gender Equality in Research on Education Quality. Comp. Educ. 2011, 47, 45–60. [Google Scholar] [CrossRef]
- Chan, R.C.H. A Social Cognitive Perspective on Gender Disparities in Self-Efficacy, Interest, and Aspirations in Science, Technology, Engineering, and Mathematics (STEM): The Influence of Cultural and Gender Norms. Int. J. STEM Educ. 2022, 9, 37. [Google Scholar] [CrossRef]
- Levy, H.E.; Fares, L.; Rubinsten, O. Math Anxiety Affects Females’ Vocational Interests. J. Exp. Child Psychol. 2021, 210, 105214. [Google Scholar] [CrossRef] [PubMed]
- Kaur, T.; McLoughlin, E.; Grimes, P. Mathematics and Science across the Transition from Primary to Secondary School: A Systematic Literature Review. Int. J. STEM Educ. 2022, 9, 13. [Google Scholar] [CrossRef]
- O’Rourke, I.; Prendergast, M. Mathematics as a Gendered Subject: A Deeper Insight into Students’ Attitudes in Irish Post-Primary Schools. Ir. Educ. Stud. 2021, 40, 627–646. [Google Scholar] [CrossRef]
- International Association for the Evaluation of Educational Achievement (IEA). Student Questionnaire, Grade 8: Trends in International Mathematics and Science Study; IEA: Boston, MA, USA, 2018. Available online: https://nces.ed.gov/timss/pdf/T19_GR8_StudentQ_USA_Questionnaire.pdf (accessed on 14 April 2023).
- Forgasz, H.; Markovits, Z. Elementary Students’ Views on the Gendering of Mathematics. Eur. J. Educ. Res. 2018, 7, 867–876. [Google Scholar] [CrossRef]
- Hernández-Sampieri, R.; Mendoza Torres, C.P. Metodología De La Investigación—Las Rutas Cuantitativa, Cualitativa y Mixta, 7th ed.; McGraw-Hill Intereamericana Editores: Ciudad de México, Mexico, 2018. [Google Scholar]
- Taylor, S.; Bogdan, R. Introducción a Los Métodos Cualitativos de Investigación, 2nd ed.; Paidós: Buenos Aires, Argentina, 1994; ISBN 84-7509-816-9. [Google Scholar]
- Ikkatai, Y.; Inoue, A.; Minamizaki, A.; Kano, K.; McKay, E.; Yokoyama, H.M. Effect of Providing Gender Equality Information on Students’ Motivations to Choose STEM. PLoS ONE 2021, 16, e0252710. [Google Scholar] [CrossRef] [PubMed]
- Flore, P.C.; Wicherts, J.M. Does Stereotype Threat Influence Performance of Girls in Stereotyped Domains? A Meta-Analysis. J. Sch. Psychol. 2015, 53, 25–44. [Google Scholar] [CrossRef] [PubMed]
- Master, A. Gender Stereotypes Influence Children’s STEM Motivation. Child Dev. Perspect. 2021, 15, 203–210. [Google Scholar] [CrossRef]
- Cohen, S.M.; Hazari, Z.; Mahadeo, J.; Sonnert, G.; Sadler, P.M. Examining the Effect of Early STEM Experiences as a Form of STEM Capital and Identity Capital on STEM Identity: A Gender Study. Sci. Educ. 2021, 105, 1126–1150. [Google Scholar] [CrossRef]
- García-Holgado, A.; Verdugo-Castro, S.; Dominguez, A.; Hernández-Armenta, I.; García-Peñalvo, F.J.; Vázquez-Ingelmo, A.; Sánchez-Gómez, M.C. The Experience of Women Students in Engineering and Mathematics Careers: A Focus Group Study. In Proceedings of the 2021 IEEE Global Engineering Education Conference, Vienna, Austria, 21–23 April 2021; pp. 50–56. [Google Scholar]
- Mendoza Cazarez, D.C. Exploring Influences on the Choice of Fields of Study in Higher Education: Evidence from Mexico. Int. J. Educ. Dev. 2022, 93, 102643. [Google Scholar] [CrossRef]
- Wieselmann, J.R.; Dare, E.A.; Ring-Whalen, E.A.; Roehrig, G.H. “I Just Do What the Boys Tell Me”: Exploring Small Group Student Interactions in an Integrated STEM Unit. J. Res. Sci. Teach. 2020, 57, 112–144. [Google Scholar] [CrossRef]
- Klee, H.L.; Miller, A.D.; Buehl, M.M. Mathematics Anxiety, Self-Concept, and Self-Efficacy: A Multidimensional Scaling Consideration of Measures. J. Exp. Educ. 2022, 91, 494–516. [Google Scholar] [CrossRef]
- Sáinz, M.; Fàbregues, S.; Rodó-de-Zárate, M.; Martínez-Cantos, J.L.; Arroyo, L.; Romano, M.J. Gendered Motivations to Pursue Male-Dominated STEM Careers Among Spanish Young People: A Qualitative Study. J. Career Dev. 2020, 47, 408–423. [Google Scholar] [CrossRef]
- Cheryan, S.; Plaut, V.C.; Handron, C.; Hudson, L. The Stereotypical Computer Scientist: Gendered Media Representations as a Barrier to Inclusion for Women. Sex Roles 2013, 69, 58–71. [Google Scholar] [CrossRef]
- Gladstone, J.R.; Cimpian, A. Which Role Models Are Effective for Which Students? A Systematic Review and Four Recommendations for Maximizing the Effectiveness of Role Models in STEM. Int. J. STEM Educ. 2021, 8, 59. [Google Scholar] [CrossRef]

| Category | Pretest Question about the Use of Mathematics in the Workspace | Post-Test Questionnaire about the Use and Ease of Mathematics | Intervention Questionnaire about Self-Perception in STEM Careers | Total |
|---|---|---|---|---|
| Interest/enjoyment | 3 | 26 | 180 | 209 |
| Self-concept | 3 | 26 | 116 | 145 |
| Perceived value/utility | 0 | 0 | 31 | 31 |
| Peer influence | 0 | 1 | 2 | 3 |
| Adult influence | 0 | 1 | 10 | 11 |
| Stereotypes of people that work in STEM | 9 | 23 | 0 | 32 |
| Contextual elements and events | 21 | 15 | 12 | 48 |
| Cognitive skills | 6 | 15 | 15 | 36 |
| Study areas | 1 | 1 | 48 | 50 |
| Attitudes | 0 | 5 | 4 | 9 |
| Total | 43 | 113 | 418 | 574 |
| Category | Statement | Male Students | Female Students | ||
|---|---|---|---|---|---|
| Mean | σ 1 | Mean | σ 1 | ||
| Interest/Enjoyment | 4. I learn many interesting things in mathematics | 4 | 0.57 | 3 | 0.84 |
| 6. I like any schoolwork that involves numbers | 3 | 1.05 | 2 | 1.00 | |
| Self-concept | 6. I am good at working out difficult mathematics problems | 3 | 1.00 | 2 | 1.07 |
| 9. Mathematics makes me confused | 2 | 1.03 | 3 | 0.68 | |
| Value/Utility | 3. I need to do well in mathematics to get into the university of my choice | 3 | 0.75 | 4 | 0.44 |
| 5. I would like a job that involves using mathematics. | 3 | 0.92 | 2 | 1.02 | |
| Category | Statement | Male Students | Female Students | ||
|---|---|---|---|---|---|
| Mean | σ 1 | Mean | σ 1 | ||
| Interest/Enjoyment | 6. I like any schoolwork that involves numbers | 3 | 1.03 | 2 | 0.73 |
| Self-concept | 6. I am good at working out difficult mathematics problems | 2 | 1.19 | 3 | 0.98 |
| 9. Mathematics makes me confused | 3 | 1.03 | 2 | 1.04 | |
| Value/Utility | 3. I need to do well in mathematics to get into the university of my choice | 3 | 0.73 | 4 | 0.40 |
| 5. I would like a job that involves using mathematics. | 4 | 0.56 | 3 | 0.55 | |
| Statements | Pretest: interest/enjoyment results | Post-test: interest/enjoyment results | ||||||||||||||
| Control group | Experimental group | Control group | Experimental group | |||||||||||||
| Males | Females | Males | Females | Males | Females | Males | Females | |||||||||
| Interest/Enjoyment | Mean | σ 1 | Mean | Σ | Mean | σ | Mean | σ | Mean | σ | Mean | σ | Mean | σ | Mean | σ |
| 4. I learn many interesting things in mathematics | 4 | 0.62 | 3 | 0.69 | 4 | 0.52 | 3 | 0.99 | 4 | 0.68 | 4 | 0.55 | 3 | 0.82 | 3 | 0.67 |
| 6. I like any schoolwork that involves numbers | 2 | 0.98 | 2 | 0.87 | 3 | 1.13 | 2 | 1.14 | 3 | 0.85 | 2 | 0.76 | 2 | 1.21 | 2 | 0.71 |
| Pretest: self-concept results | Post-test: self-concept results | |||||||||||||||
| Control group | Experimental group | Control group | Experimental group | |||||||||||||
| Males | Females | Males | Females | Males | Females | Males | Females | |||||||||
| Mathematical Self-Concept | Mean | σ | Mean | Σ | Mean | σ | Mean | σ | Mean | σ | Mean | σ | Mean | σ | Mean | σ |
| 3. Mathematics is not one of my strengths | 2 | 1.06 | 3 | 1.08 | 2 | 1.16 | 2 | 1.10 | 2 | 1.06 | 3 | 0.95 | 2 | 1.33 | 3 | 1.01 |
| 6. I am good at working out difficult mathematics problems | 3 | 0.87 | 2 | 0.96 | 3 | 1.13 | 2 | 1.17 | 3 | 0.97 | 2 | 0.75 | 3 | 1.10 | 3 | 1.33 |
| 9. Mathematics makes me confused | 3 | 1.03 | 3 | 0.73 | 2 | 1.04 | 3 | 0.63 | 3 | 1.15 | 3 | 0.95 | 3 | 1.05 | 3 | 1.00 |
| Pretest: value/utility results | Post-test: value/utility results | |||||||||||||||
| Control group | Experimental group | Control group | Experimental group | |||||||||||||
| Males | Females | Males | Females | Males | Females | Males | Females | |||||||||
| Value/Utility | Mean | σ | Mean | σ | Mean | σ | Mean | σ | Mean | σ | Mean | σ | Mean | σ | Mean | σ |
| 3. I need to do well in mathematics to get into the university of my choice | 4 | 0.76 | 4 | 0.55 | 3 | 0.74 | 4 | 0.32 | 3 | 0.63 | 4 | 0.47 | 3 | 0.82 | 4 | 0.33 |
| 5. I would like a job that involves using mathematics | 2 | 1.19 | 2 | 1.07 | 3 | 0.64 | 3 | 0.97 | 2 | 1.01 | 2 | 0.92 | 3 | 1.22 | 2 | 0.97 |
| 6. It is important to learn about mathematics to get ahead in the world | 3 | 0.69 | 3 | 0.64 | 3 | 1.06 | 3 | 0.67 | 4 | 0.57 | 4 | 0.58 | 4 | 0.55 | 3 | 0.53 |
| # | Word | Total Frequency | # | Word | Total Frequency |
|---|---|---|---|---|---|
| 1 | Students/boys | 96 | 16 | Computer | 19 |
| 2 | Students/girls | 83 | 17 | Notebook | 19 |
| 3 | Good | 82 | 18 | Engineer | 18 |
| 4 | Think | 80 | 19 | STEM | 17 |
| 5 | Mathematics | 71 | 20 | Cars | 16 |
| 6 | Work/job | 64 | 21 | Problems | 15 |
| 7 | Calculator | 51 | 22 | Sciences | 13 |
| 8 | Career/studies | 51 | 23 | Courses | 13 |
| 9 | Difficult | 51 | 24 | Fun | 12 |
| 10 | Focus/concentrate | 35 | 25 | Nature | 12 |
| 11 | Know | 35 | 26 | Create | 11 |
| 12 | Image/picture | 30 | 27 | Stress | 11 |
| 13 | Women | 29 | 28 | Success | 11 |
| 14 | Motivate | 27 | 29 | Process | 11 |
| 15 | Numbers | 26 | 30 | Cellphone | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutierrez-Aguilar, M.; Tejeda, S. A Study on the Influence of the Affective Domain on the Attitudes of Middle School Students toward Mathematics from a Gender Perspective. Educ. Sci. 2024, 14, 594. https://doi.org/10.3390/educsci14060594
Gutierrez-Aguilar M, Tejeda S. A Study on the Influence of the Affective Domain on the Attitudes of Middle School Students toward Mathematics from a Gender Perspective. Education Sciences. 2024; 14(6):594. https://doi.org/10.3390/educsci14060594
Chicago/Turabian StyleGutierrez-Aguilar, Mariana, and Santa Tejeda. 2024. "A Study on the Influence of the Affective Domain on the Attitudes of Middle School Students toward Mathematics from a Gender Perspective" Education Sciences 14, no. 6: 594. https://doi.org/10.3390/educsci14060594
APA StyleGutierrez-Aguilar, M., & Tejeda, S. (2024). A Study on the Influence of the Affective Domain on the Attitudes of Middle School Students toward Mathematics from a Gender Perspective. Education Sciences, 14(6), 594. https://doi.org/10.3390/educsci14060594






