The Promise of AI Object-Recognition in Learning Mathematics: An Explorative Study of 6-Year-Old Children’s Interactions with Cuisenaire Rods and the Blockplay.ai App

Abstract

We developed and trained a prototype AI-based object-recognition app, blockplay.ai, to recognise Cuisenaire rods placed on a tabletop, and speak the rods’ lengths. We challenged 6-year-olds in a primary school in England to play a ‘game’: can you make the app say the two times table? Drawing methodologically on theories of embodiment, we analyse two videoclips, each of a child interacting with rods, the app and the task set by the researchers, as a dynamic, complex child-rods-app-task body-artefact system. Theoretically we draw on Davydovian concepts of learning as a concrete-to-abstract-to-new-concrete cycle, using abstract artefacts such as mathematical language to coordinate new perceptually-guided actions on concrete objects. In one videoclip the child’s pattern of actions are consistent with a change, within a few minutes, from perceiving and acting on rods as counters, to perceiving and acting on rods as lengths; in the other videoclip, this does not happen. We analyse the changes in patterns of interactions as shifts to new stable attractors in a dynamic child-rods-app-task body-artefact system, driven by tensions generated by unexpected concrete-to-abstract relationships. We end by looking forward to the range of possible uses of object-recognition technology in the learning of mathematics, for example, provoking algebraic awareness.

1. Introduction

This paper describes a trial of an app (blockplay.ai, see Supplementary Materials) that uses an artificial neural network (ANN) object-recognition algorithm to recognise Cuisenaire rods placed on a tabletop under a webcam and speaks their lengths. Cuisenaire rods are coloured cuboids of different lengths, with a consistent cross-section (see Figure 1, right), which can be used in primary mathematics, e.g., forming one of the key representations of number promoted by the UK’s National Centre for Excellence in the Teaching of Mathematics [1]. Our interest in Cuisenaire rods comes from our engagement in the work of Gattegno [2] and Davydov [3], who both (and independently, as far as we can tell) proposed a curriculum structure in which algebra is taught before arithmetic, via mobilising the metaphor of number as a measure of length.

Given the novelty of the object-recognition technology used, our research is exploratory, not driven by questions as much as by curiosity and open-ness as to what working with an object-recognition app may provoke. We anticipate that specific research questions will emerge in later iterations of our work. Rapid advances in software and hardware, and recent releases of apps such as ChatGPT-4o, suggest that stable and accurate recognition of many real-world objects, including mathematical manipulatives, is now feasible on standard laptops and phones. We will be arguing that object-recognition opens up vast possibilities for innovation in education and that our exploratory study hints at the promise of such developments.

The novelty of the technology prompts us to structure this paper in a non-standard manner. In the next section, we describe the development of the app itself, given its likely unfamiliarity to readers, both our theoretical inspirations and more technical aspects. In Section 3, we then set out the view of learning which has informed our approach, since this is central to how we interpret what took place when trialing the app. As part of Section 3, we detail how we have come to think about “concrete” and “abstract” in relation to learning. Section 4 details our methodology where we make a novel proposal for how it is possible to study affective flows during interactions with the app. In Section 5, we lay out the methods used in our exploratory study, leading to Section 6 where we present and analyse results of two children’s interactions with the app. In Section 7 we draw out conclusions and implications for the future.

2. Background to the Development of the App

The original stimulus for this research was a problem one of the authors, Michael, faced in his doctoral study, in wishing to study young children’s mathematical block play in Kindergarten: how to gather data on young children’s arrangements of wooden blocks? The problem was accentuated by general restrictions on researchers’ gathering data in person in England at the time due to the COVID pandemic. The starting point was to consider how to collect data on children’s block play in a way that might not require the close presence of a researcher. In other words, our starting point was a methodological challenge, and we view one of the key contributions of this paper as the proposal of a role for object-recognition in researching mathematics education, as well as in teaching and learning mathematics. We have one specific example (our study on block play) but our larger argument is that object-recognition opens up possibilities for creative engagement with concepts through manipulating real-world objects, in a manner that is hard to achieve without such technology.

Children’s block play can be traced back almost 200 years to the central focus on creative block play by Friedrich Froebel (1782–1852) in his Kindergarten pedagogy [4]. And there is a corresponding long history of educational research studies of children’s block play [5,6]. However, technically, many of the previous studies relied on in-person adult observation and categorisation of block constructions through notetaking and sketching ‘live’, or reviewing video recordings [7], or using specially-built cubes containing electronic devices to record and transmit their own positions and orientations [8].

At the same time there was emerging evidence from computer vision research that ANN algorithms could recognise objects in a video stream in near real-time, for example the ARMath project drew on the open-source COCO database of images of everyday objects to train an app to detect some of these objects (e.g., batteries and coins) from a webcam and count them [9]. The Beatblocks app recognises Lego bricks on a Lego baseboard and translates their positions into music [10]. Commercially available educational apps, albeit with bespoke add-on hardware, such as Osmo [11], could recognise proprietary plastic objects placed in front of a camera. And rapid advances in 3D object detection and tracking technology apparent from, for instance, face detection in mobile phone cameras, and augmented reality apps detecting the environment—including some supporting 3D mathematical modelling [12]—suggested that there might be object-recognition technology available, able to assist in identifying blocks in a video.

Unsure when researchers would next be permitted to observe children in person, we decided to explore whether software might be able to detect, from a webcam video stream, the positions and orientations of Froebelian wooden cubes placed on a table, for example as 3D coordinates, to facilitate both anonymised—and potentially remote—data gathering, as well as statistical analysis.

Not finding any suitable apps commercially available, we contacted a computer vision programmer, Pysource, and we began collaborating on exploring technical options for an app, which, after some false starts with procedural edge-detection algorithms, led us to making use of rapidly evolving ANN-based object-recognition algorithms, such as PyTorch, Mask-RCNN, and YOLO. After initial unsuccessful trials in recognising the three-dimensional constructions of plain Froebelian wooden cubes common in play, complicated not least by the challenge of how to see blocks hidden underneath other blocks, we felt we needed to try a new approach. We decided to radically refocus on recognising two-dimensional arrangements of Cuisenaire rods on a tabletop.

Cuisenaire rods, because of their different colours and lengths, offered more affordances for an ANN-based app to distinguish between them. This choice also by necessity shifted our research focus from free play 3D block constructions common in pre-school settings, to mathematical contexts supported by Cuisenaire rods more common in primary classrooms. Whilst this change was expeditious from a technical object-recognition perspective for us to develop a functional prototype to explore the technology, it also meant a significant shift in context, from pre-school settings, where creative free play with blocks is culturally established, to primary school settings, where Cuisenaire rods are typically used in the specific context of supporting progress in a structured mathematics curriculum. Though this meant abandoning (at least temporarily) the original aspiration of a research tool to capture free-play block construction by preschoolers, it opened up the possibility of engaging with primary school mathematics pedagogy.

Pedagogically, since their invention by Georges Cuisenaire in the 1950s, there has always been an ambiguity around the use of Cuisenaire rods, key to their use in relation to teaching number, in that they can be viewed as objects (e.g., allowing cardinal counting) or as lengths (e.g., allowing a focus on relationships such as greater than, less than, equal). This ambiguity becomes central to the empirical work we describe later. As we noted at the start of the paper, the rods are recommended for use in the UK [3], precisely in order to facilitate simultaneous development of the concept of numbers as objects, with numbers as lengths (or measures), in the primary curriculum. We view the ambiguity inherent in the rods as one that, while it can cause confusion, allows children the opportunity to develop vital awarenesses about the different ways in which number is invoked and used, and how different concepts can lead to different descriptions of the same situation (e.g., by focusing on the number of objects or their lengths). We follow Gattegno [2] in assuming children have ample capacity to handle such ambiguities of description (as they show in recognising, e.g., that “my aunt” and “my mother’s sister” are the same person), and indeed that this capacity is key to algebraic thinking.

After five months of iterative development, by summer 2021 we had a prototype “blockplay.ai” app, trained to recognise Cuisenaire rods, which, though not 100% reliable, we felt was sufficiently usable to test with children (see Figure 2). When a child places one or more rods on the table within view of the webcam, and removes their hands so no movement is detected, the app takes a snapshot which the ANN algorithm processes in near-real-time to identify the lengths and positions of the rods, and the app then speaks the lengths of the rods, in the order of their detected positions left to right. The snapshots, as well as statistical data on the number and colours of the rods in each snapshotted image, are also stored for subsequent analysis.

At the time indoor research visits to schools were highly restricted because of the pandemic, however we were fortunate to find a school willing to participate who had an outdoor courtyard play area we were able to use to conduct our first trial. A year later, in 2022, with a new iteration of the app, we were able to return to the school and conducted a second trial indoors.

The Blockplay.ai App

In this section, we share aspects of what we have learnt through working with computer vision tools based on ANNs. Over the 18 months of development described, new more accurate and more efficient open-source object-recognition algorithms were becoming available, for example the first iterations required specialist hardware optimised for processing AI tasks (such as the NVIDIA Jetson Xavier NX), whereas later iterations achieved similar recognition accuracy and speeds, running on standard Windows laptops. We anticipate this is a pattern which will continue, to the point where accurate, near-real-time object-recognition will soon become ubiquitous on mobile phones.

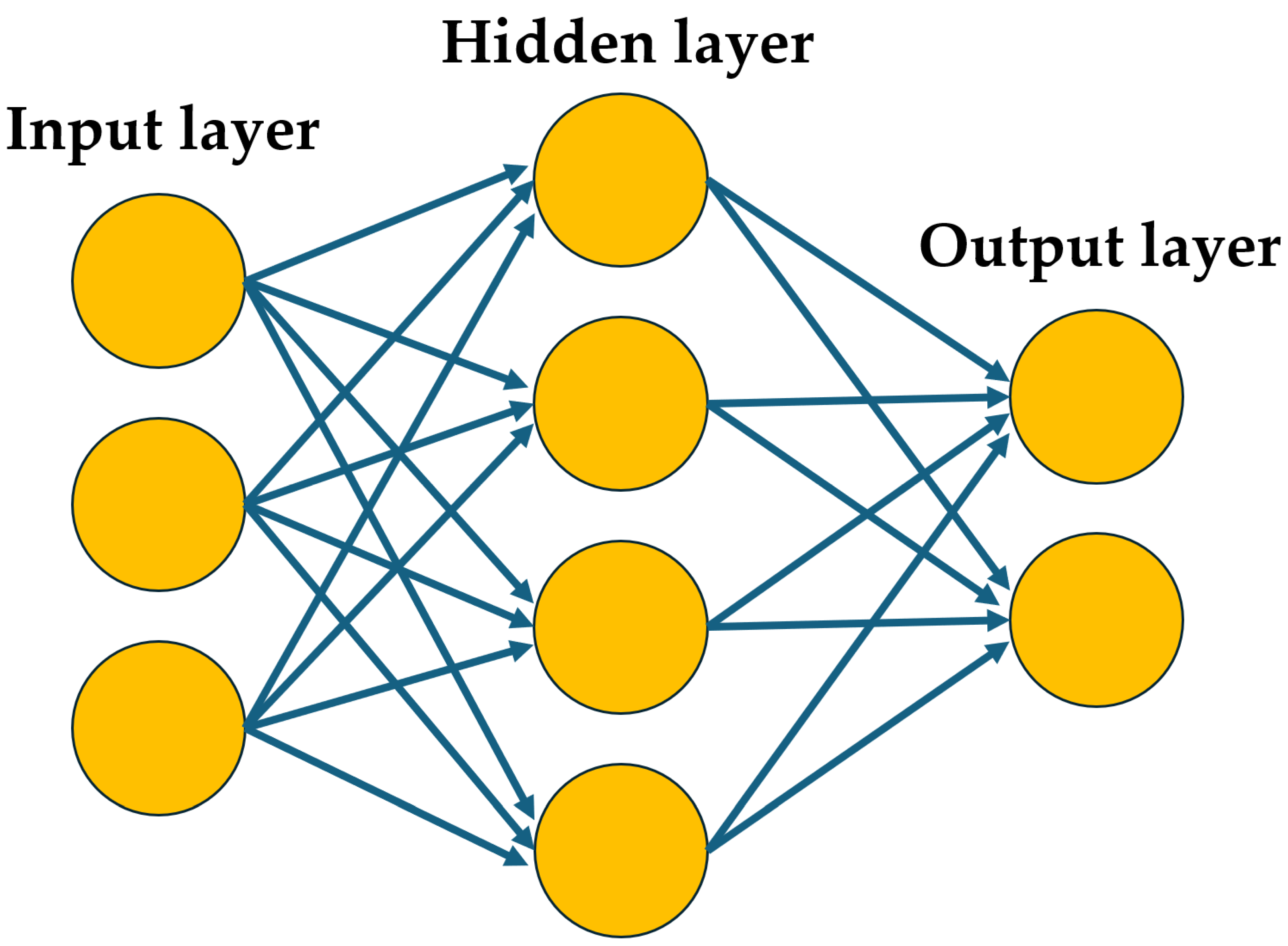
The key challenge in making the app was the development and training of the object-recognition algorithm. ‘Deep learning’ algorithms based on ‘feed-forward’ ANNs typically consist of a set of input nodes connecting to a set of output nodes, via a network of connections many layers ‘deep’ (see Figure 3). For example, to recognise handwritten numbers, the inputs may consist of pixels in an image of a handwritten digit, and the outputs the numbers 0 to 9. During training, the weightings of these multi-layered connections are amplified or dampened depending how closely a given input matches a desired output. This process may be repeated many thousands of times, varying the inputs, until the algorithm achieves an acceptable level of accuracy. Once trained, the system—though complex—is static, in the sense that the connection weightings no longer change, and the ANN should generate the same output from a given input.

In practice, in the field, the inputs, for example pixels in a live image from a webcam, may vary constantly, reflecting the complexity of environmental systems such as the weather affecting light levels and the direction and depth of shadows changing over time. This may lead to apparently chaotic behaviour, such as rods not being recognised, and then suddenly being recognised as light levels change slightly.

A key factor in the reliability of recognition is training on a wide range of images taken with diverse lighting conditions, angles and backgrounds. These are then ‘annotated’—for example in the case of the app the Cuisenaire rods in the images are outlined manually by a human—so that they can be used to train the ANN, by iteratively adjusting the weightings of the connections so the input image generates the shapes outlined in the annotated images with increasing accuracy. For the version of the app used in this trial, a relatively small set of around 300 images of various Cuisenaire rods on tabletops were used to train it, taken with the same webcam as was to be used in the trial.

In contrast to feed-forward networks such as the one used in the app, ‘recurrent’ networks are dynamic, in that outputs from one layer may feed back as inputs to previous layers, creating complex, dynamic patterns and potentially chaotic loops, with changing outputs. As we describe below, introducing a human participant in a system with a feed-forward ANN may create a dynamic, recurrent network.

Having set out some of the technical challenges around the app development, we now move to consider the theoretical commitments which guided both our aims for the app itself and how we interpret what took place when we used the blockplay.ai app with children in the field.

3. Theoretical Framework: Complex Dynamic Systems of Action-Perception Loops

Driven by our interest in human-technology interaction and the learning that ensues, we have come to view such interactions as complex, dynamic systems [13]. We are influenced by enactivist insights that perception and action are ultimately inseparable [14]. Organisms do not receive the world passively, through perception, rather, to perceive is to reach out, to engage actively with the world and to receive the world reaching back [15].

Taking a radical embodiment perspective (which shares many assumptions of enactivism), Shvarts et al. suggest knowledge cannot be separated from the body of the learner: “Knowledge emerges as part of a complex dynamic system of behavior, which is constituted through multiple perception-action loops” [16] (p. 448). In addition, cultural tools, or artefacts—which may be objects such as blocks, or words or symbols—may extend and participate in these bodily action-perception loops: “When a functional system is extended by an artifact, this artifact takes part in perception-action loops.” [16] (p. 465). Tools such as our app, therefore, enter into complex dynamic systems with children and teachers and researchers (and much more).

One implication of taking interactions to exist in dynamic systems is a shift away from the Piagetian idea of equilibrium [17] as the base state of a system, or organism. Complex, dynamic systems never reach states of equilibrium (they are too complex for that), rather they move between “attractor states”, which can be interpreted as patterns of interaction which are locally stable, for a while [18]. The concept of an attractor of a system has been used by, for instance, Jacobson and Degotardi in analysing shifting patterns of shared attention between young children and their carers [19]. An object and shared attention on that object, can be interpreted as an attractor in the complex system involving observers and objects. There is an attractor, for the duration of the shared attention, which then fades as attention moves somewhere else (potentially creating a new attractor for the system).

Shvarts et al. [16] highlight the key role of intentionality in driving shifts to new attractor states, for example if a student is engaged in a task to align two graphical objects on a screen, each with a separate controller, after initially struggling they may learn eventually to repeat the task successfully, a temporary attractor state. We use the word “flow”, to describe times when intentionality is realised relatively smoothly in a system, e.g., when an organism wants something and is able to act to bring that thing about in the system, or when a technological tool responds as anticipated. Of course, in any complex system, there is rarely a direct link between intention and outcome, and we do not assume intentions are always known (even to the organism with an intention). An attractor state, then, describes a time in a complex system when, from an enactivist perspective, we could say there are effective actions taking place [14]. In other words, the sequence of actions taking place are adequate for the maintenance of relationships within the system, which we characterise as a flow of actions. We can say, therefore, that actions flow, in an attractor state, and that tensions, frustrations or disruptions which break up that flow imply there is no stable attractor state present.

Davydov’s (Concrete-to-)Abstract-to-New-Concrete Cycle

Having set out our broad commitments to knowledge and interaction, we need to set up two key concepts for our work and analysis, namely, concrete and abstract. For the last decade or so in primary schools in England the government has been promoting so-called mastery approaches for teaching mathematics, which make use of concrete manipulatives such as multilink cubes, Dienes blocks and Cuisenaire rods etc., as part of a Concrete-Pictorial-Abstract framework based on Jerome Bruner’s theories of Enactive, Iconic and Symbolic learning [20]. While Bruner was nuanced about how these three types of learning interacted, in English schools the practice is often to see them as sequential from Concrete to Abstract [21], in line with Piaget’s stages of development. And the pedagogy of mastery approaches in England, for example the professional development materials for the White Rose mathematics resources used by almost 90% of English primaries [22,23] tends to support a gradual progression, from handling of physical concrete objects, to drawings of them, to drawings bounded by boxes, to empty boxes, to annotated rectangles as ‘bar’ models, i.e., lengths labeled with numbers—an incremental ‘small steps’ process that may take months or years to master [24,25].

This sequence is sometimes contrasted with Davydov’s theories of learning as proceeding from Abstract to Concrete [3]. However, as Coles and Sinclair highlight [26], the concepts of abstract and concrete have different connotations for Davydov—coming from a Vygotskian socio-cultural perspective—compared to Bruner, coming from a Piagetian tradition. These differences, even leaving aside the nuances of translation, and the distinct Soviet context of the Vygotskyian tradition, can make direct comparison problematic.

We draw on two interpretations of what it might mean to move from abstract to concrete in learning. Wilensky [27] points to a re-interpretation of the words concrete and abstract, which can help make sense of how greater sophistication might lead away from the abstract towards the concrete. For Wilensky, what makes something abstract is its lack of connections to what is familiar and what makes something concrete is the presence of connections. So, fractions or numbers might indeed seem abstract to children on first encounter, if they are reduced to symbolic rules, but over time, as they become linked to more and different experiences, these concepts can become more intimate and more concrete.

A second interpretation comes from Shvarts et al. [28], where the words “concrete” and “abstract” have relatively standard meanings (e.g., concrete referring to tangible objects and abstract referring to intangible conceptual models and symbols, such as the number ‘2’). They take Davydov’s notion of the ascent from abstract to concrete as suggesting learning involves both the concrete and the abstract, where abstract thinking offers a lens with which to perceive and act on concrete objects in new ways. We could take a Rubik’s cube as an example. In an initial “concrete” phase, children might play with a Rubik’s cube as a toy. Later engagement with group theory (“abstract” ideas) leads to being able to see the Rubik’s cube as an instantiation of group theoretic ideas (“new concrete”). A concrete object becomes a “new concrete” when it is overlain with an abstract structure (such as group theory), both instantiating and illuminating the abstract and potentially influencing those abstract ideas in turn (e.g., allowing new insights and developments).

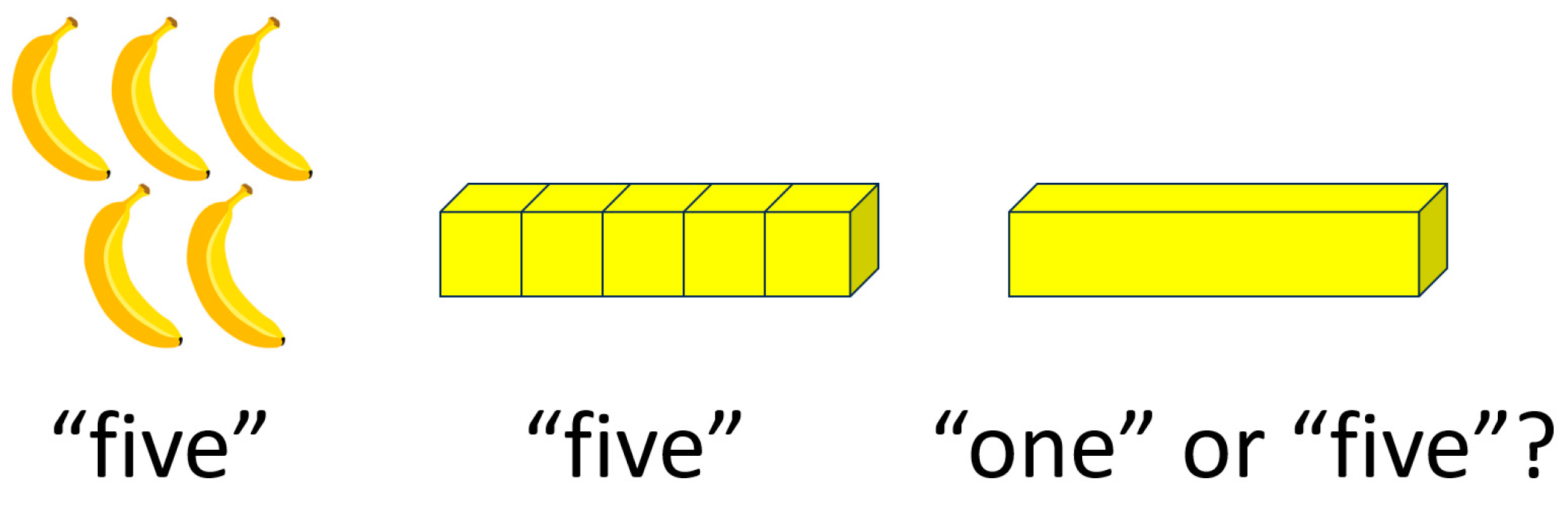
We are sympathetic to both interpretations and while, in what follows, we use Shvarts et al. [28]’s interpretation (i.e., retaining the meanings, broadly, of concrete as tangible and abstract as conceptual), we also point to places where Wilensky’s [27] interpretation offers us insight. To offer an example of what we mean by concrete and abstract, relating more to the levels of mathematics we move on to discuss, bananas, and block manipulatives (see Figure 4), may both be understood as ‘concrete’ objects. Both may be also associated with abstract artefacts such as number words, which may be overlain—through verbal labelling for example—and affect children’s perceptions of and actions on the objects, and vice versa (the objects newly associated with abstract artefacts becoming a new concrete). Often concrete objects may be seen through multiple lenses of abstraction, for example rods as counters, or lengths. Overlaying of abstract number words, for instance, can engender a switch from one lens to another.

In the example of the blockplay.ai app trial presented below, the children were already familiar with the abstract memorised sequence of number words denoted by the two times table (perhaps also relatively abstract in Wilensky’s sense [27]). However, they were not familiar with the concrete Cuisenaire rods. The app, by uttering associated number words in the order Cuisenaire rods are placed left to right on the tabletop, enables children to iteratively coordinate placements of rods by using the known order of the number words. Thus, they may begin to see and act on the rods in new ways. They may or may not also apply abstract artefacts such as the concept of ‘length’, as we will explore. Having set out our relevant theoretical commitments, we now move to the methodology we used in exploring some of the dynamic systems we observed, involving the tool of the blockplay.ai app.

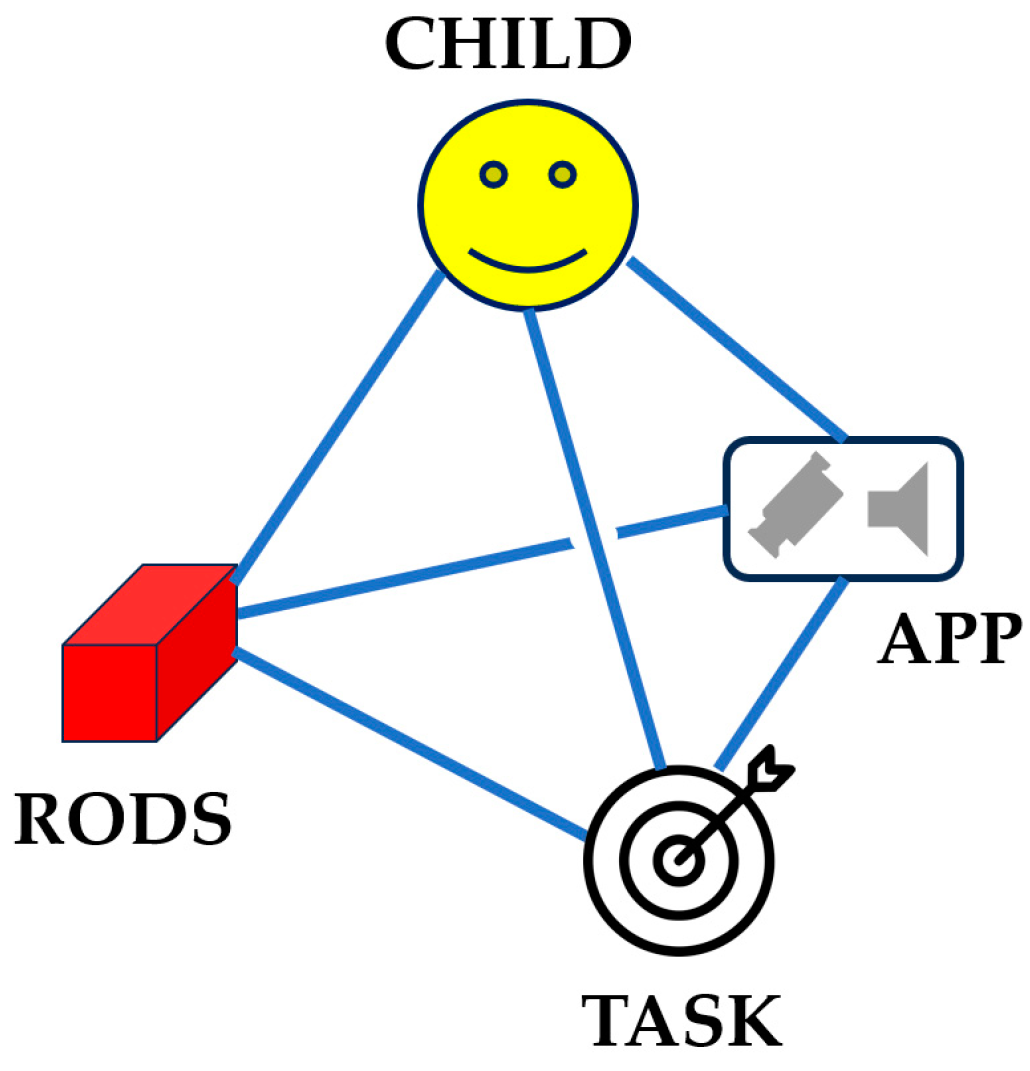
4. Methodology for Analysing a Dynamic Child-Rods-App-Task System and Its Attractors

Adapting Shvarts’ body-artefact system, with the intentionality of an engaging task, we have chosen to view the child interacting with rods and the app as a child-rods-app-task system (see Figure 5). We do not want to downplay the role of the researcher or teacher, but are simply recognising in this Figure that their role is not the focus of the current writing, which is attending to the technology. Figure 5 could therefore be seen as an adaptation of Rezat & Sträßer’s socio-didactical tetrahedron [29], where we have ignored a “teacher” node and separated an “artefact” node into rods and app.

While the blockplay.ai app enables children’s arrangements of manipulatives to be augmented, for instance adding computer-generated audio and/or imagery, at the same time the app imposes constraints, such as the requirement for the child to remove their hands from the webcam’s field of view, before the app speaks. The child can thus be seen as participating in a system of app and rods, with its own affordances, some of which may be restrictive. These restrictions can be seen as a form of gamification [30].

For example just as a trivial task (for many), such as ‘walk from one side of a room to the other’, may be ‘gamified’ by imposing a constraint, such as ‘without touching the floor’, so a trivial mathematical challenge for a given child, such as counting up to five, may be gamified by requiring the child to make the app do the counting by placing rods such that it speaks the lengths one to five in order. Thus, the child is invited to participate in a child-rods-app-task system. The theoretical aim is that this temporary participation in an artificially constrained dynamic system may engender new ways of coordinating actions on objects which are of enduring educational value to the child in learning mathematics, for example a new perception that numbers may be acted on as lengths. In terms of attractor states, the deliberate destabilisation of the system (and resulting tension), for example by placing a constraint such as requiring the child to speak ‘via’ the app, can pedagogically open up paths to new attractor states.

Abrahamson and Sánchez-García [18] give the example of a piano teacher, who wishes to teach a student to play with straight rather than curled fingers. The teacher could demonstrate and invite the student to copy them, or they could use a constraining artefact (placing a book on the student’s hand as they play), arguably (if done in a playful spirit) a form of gamification. The artefact (with the constraint that it must not fall) changes the dynamic system involving the child-keyboard-music, and “[i]n response, the student must adapt her situated motor-action schemes […] Thus, via the mediation of the book constraint, the piano comes to afford a new way of acting on it. At this point, the book may no longer be necessary and could thus be removed.” (p. 213). As researchers, we made the choice not to be explicit to the children in the trial how we would describe the app’s interpretations of the rods (e.g., that the app speaks their lengths) in allowing dynamic interactions to unfold. The object-recognition app therefore acts as a constraining artefact, inviting new actions without a requirement for children to copy what a teacher/researcher says or to follow detailed instructions.

In our analysis of the child-rods-app-task system over the period of the videoclips we aim to identify stable attractor states, as well as constraints—physical, technical, affective or cognitive—which may be destabilising the system and triggering shifts to new attractors. For instance, if the child places a rod expecting blockplay.ai to utter the number ‘6’, and it says ‘5’, the child may change their expectation—the perception that guides the action—and be motivated to act anew to replace the rod.

Methodologically, we are also influenced by de Freitas and Sinclair’s [31] work to disrupt an overly cognitive, disembodied and individualistic bias in interpretations of teaching and learning. De Freitas and Sinclair invoke notions of intensities and flows of affect and argue for the material agency of mathematical concepts and other artefacts. Building on that work, Sinclair and Coles [32] developed the notion of an affective aligning and misaligning across participants in a sequence of interactions (interpreted through actions such as mirroring, or features such as proximity and gaze). Thus, attractor states can be seen as moments of affective aligning over time.

4.1. Simplifying the Model

In designing a method for working with a novel—and still error-prone—object recognition app we are conscious that there is a risk of overload for participants—both the children playing with the app, and the researchers analysing the data.

In particular for a participating child, we recognise that interacting with three other dynamic elements at once, i.e., the rods, app and task, represents considerable complexity. However, in practice we have found this appears to be mitigated by (a) the task being simply stated and not changing until it is completed, (b) the app being inactive during hands-on activity with the rods and vice versa, so that attention can be safely switched from rods to app and back, and (c) the use of distinct sensory channels, i.e., primarily tactile and visual interactions with the rods, and auditory interaction with the blockplay.ai app.

From our own perspective as researchers, the six-dimensional relationship between the four elements of the system represents a methodological challenge to track over time. To simplify analysis, given the task is a constant of the main phase of ‘Can you make it say the two times table?’, and the relationships between the task and the rods and the task and the app—the task-rods-app sub-triad—are often passive, we may optionally ‘fade’ the task component of the system, for analysis, i.e., to focus on the sub-triad of child-rods-app interactions (see Figure 6). This halves the number of potential relationships in the original tetrahedral 6-dimensional relationship system to the three relationships in the child-rods-app sub-triad, facilitating analysis.

4.2. Diagramming the Child-Rods-App Triad

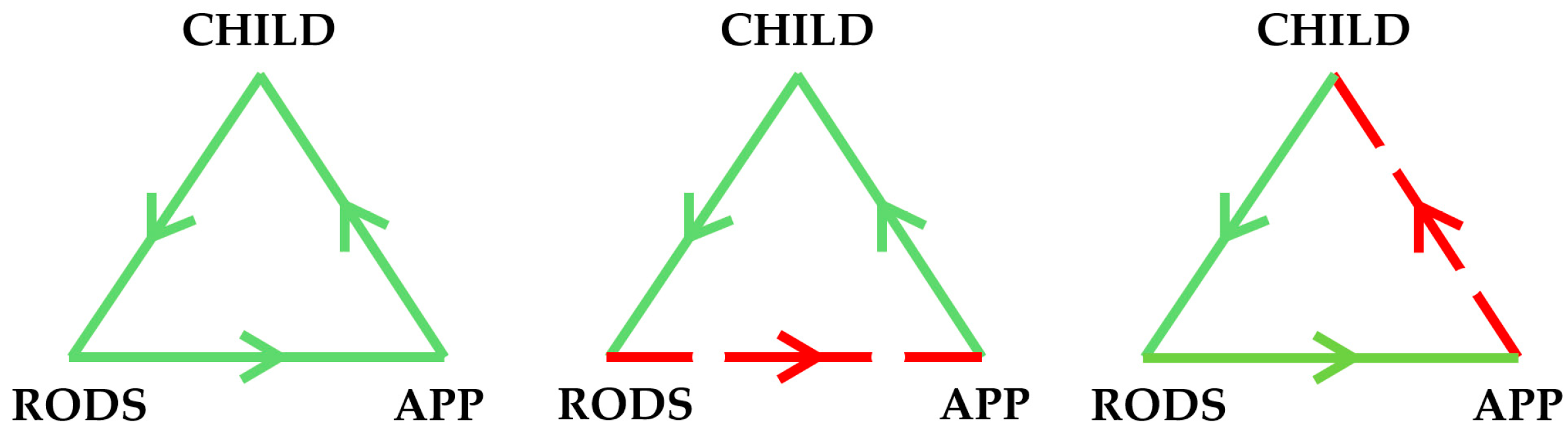
De Freitas et al. [33] demonstrate the power of diagramming to provoke new thinking, particularly around exploring the presence and flow of forces such as affect. As stated above, we are particularly interested, in our data, to analyse what is happening when such flows become visible, either through a stable pattern occurring for a while, or through the expression of tensions and frustrations. We have developed diagrammatic notation of the child-rods-app triad, with the child at the top, and activity flowing anti-clockwise, with placement of the rods represented by the left side of the triangle, the recognition of the app by the bottom side, and the app’s speaking of the rods’ lengths by the right-hand side (Figure 7). If the flow of placement, recognition and length-speaking appear to align with the intentionality of the child—so the app speaks numbers the child intended to hear—these sides are coloured green. A positively self-reinforcing flow of activity matching the child’s intentionality to engage with the task represents a potential attractor state, if stable over time.

Where intentional flow is disrupted, either by the app’s failure to recognise the rods correctly (Figure 7, centre) or the app does not speak the numbers predicted by the child (Figure 7, right), this destabilises the flow, creating a tension between the child’s actions and perceptions. Broken red lines indicate a tension, or frustration, in the system.

5. Methods

The app version we used for initial trialing corresponded to iteration 2, using the Mask-RCNN artificial neural network algorithm, running on a laptop with a GPU (enabling faster image processing), to recognise Cuisenaire rods from an image from a webcam video feed and generate pre-programmed sound files accordingly. An apparatus incorporating a webcam connected to a speaker-equipped laptop running the app was designed to be set up easily on a standard school desk for safe, supervised use by young primary school children (Figure 8).

Twelve 5–6-year-olds in year 1 of a local primary school in south-west England (by the summer of Year 1 most would be already or nearly six years old) were recruited in 2021. The primary school served a catchment area with a relatively high level of socio-economic, ethnic and gender diversity and children with special educational needs and disabilities. Informed consent was obtained from all participants in the study, including parents—for their children to participate—and the teachers involved in facilitating the sessions. All subjects, and their parents, gave their informed consent for inclusion before they participated in the study. The study was conducted in accordance with the Declaration of Helsinki, and the protocol was approved by the Faculty of Social Sciences and Law Research Ethics Committee, University of Bristol (ref 118381).

Over the period of two, 90-min sessions in July 2021, closely supervised by a researcher, the children were invited singly or in pairs, for 10–15 min at a time, to try out a ‘game’ which involved making the computer say words suggested by the researcher, such as the number three, or the two times table, by placing rods on the desk, and taking their hands away to make it speak. A similar session with an updated version of the app was repeated in July 2022 with a new group of year 1s.

The app captured snapshots of the rod arrangements, and a video camera trained on the blocks also captured the audio generated. All video was edited to anonymise it. These sessions were the first time the prototype app had been trialed in the field, so were also an early technical trial of the technology. In this paper we focus on a ~7-min video clip from 2021 of one 5–6-year-old interacting with the blockplay.ai app, and a set of Cuisenaire rods, and a ~7-min clip from 2022 of another 5–6-year-old. These were chosen as the clearest comparable examples of two different attractor states, with children engaged in similar tasks.

None of the participants had used Cuisenaire rods, or the blockplay.ai app, previously. During the sessions, the app was set to speak the lengths of the rods, relative to the smallest white rod, so for example if the ten rods were placed in ascending order of length, left to right, the app would say ‘1, 2, 3, 4, 5, 6, 7, 8, 9, 10’.

After a few minutes of free play to familiarise themselves with the interaction dynamic of the app (i.e., placing rods on the table in view of the webcam, then removing their hands to trigger the app to speak), the children were set a preliminary task: ‘Can you make it say [a number chosen by the child]?’, and then a longer challenge: ‘Can you make it say the two times table?’, and the resulting interactions were video recorded and analysed.

To re-iterate, our purpose in this paper is to argue for the potential of object-recognition beyond a research tool, to provoke new and powerful teaching and learning opportunities in mathematics (and other subject areas). The results and analysis which follow offer the first small step, i.e., just one illustration of possibilities.

6. Results

In practice there were many technical challenges to running the prototype object-detection app in the field for the first time, for example varying lighting conditions when the sun came out affecting recognition—especially in the session held outdoors—movement of the table as children leant on it, and the app struggling to recognise unexpectedly large piles of rods sometimes made by the children, which were all valuable learnings to feed into technical development of future iterations. The researchers were often not only providing prompts for the game as planned but also troubleshooting technical object recognition issues while attempting to keep the ‘game’ going.

Nevertheless, there were sessions which ran relatively smoothly technically, from which we have chosen the two we present below. The 2021 episode includes two tasks—an initial phase of the researcher asking the participant Child A ‘Can you make the app say…’ a number, e.g., ‘1?’, ‘3?’ etc. The researcher then asks Child A ‘Can you make it say the two times table?’ In the 2022 episode with Child B the researcher similarly initially asks if they can make the app say a number, but the child seems too absorbed in the activity to reply and only responds to the main task, ‘Can you make it say the two times table?’.

The dialogue with Child A and B, including the Child’s observed actions and the Researcher’s and the App’s utterances, are included to the left of each screengrab, in Table 1, Table 2 and Table 3, for Child A, and Table 4 and Table 5 for Child B, with an ordinal identifier #1 etc. for the snapshots for each child. For the two-times table task there was no dialogue with either child other than a short final exchange with Child A. The blockplay.ai app utterances are presented alongside screenshots of the block arrangements which triggered them throughout.

The transcripts in Table 1, Table 2, Table 3, Table 4 and Table 5 below were analysed as a dynamic child-rods-app-task system. As described in Section 4 above, where the task was stable for the period of the activity and seemed to be a constant, this task element of the system was assumed, and ‘faded’ from the diagrammatic analysis in order to focus on the child-rods-app triadic sub-system (see “triad” columns). The exception to this was the introductory task for Child A of making the app say a given number, which was adjusted and supported by the researcher, described in Table 1 below.

If there is a disruption to the flow, the triad is coloured red. There are therefore three possibilities (remembering the child is at the top, the rods to the left and app to the right):

• The bottom rods-app side of the triangle is red if the app fails to recognise the rods placed.
• The right-hand app-child side of the triangle being red implies the app does not speak the numbers the child expects. This disruption may create a tension between the child’s actions and perceptions, potentially motivating the child to adjust their actions and/or perceptions to resolve the tension in order to complete the task as intended. for example when the rod was replaced immediately, such as in A#14 when the child places a black rod and the app says ‘2, 4, 6, 7’, then replaces the black (‘7’) with a brown rod (‘8’), we believe the child intended to make the app say ‘8’ in line with the two times table task, so this counts as unintended. Where the intention of the child was not clear to us in relation to the task we have placed a question mark.
• In practice the left-hand child-rods side of the triangle—the placement of the rods as intended by the child—always seemed successful so this is always green, though it is conceivable that this might not always be the case, for example for children with less developed fine-motor skills.

All children were informed beforehand that they could stop and leave the table whenever they wished, and if the tension is too uncomfortable over time the child may plausibly relieve it by disengaging from the task, however both Child A and Child B persisted with and ultimately succeeded in the main task given. We have split the transcripts, for analysis, into sections which share a similar “attractor”.

6.1. Videoclip 1: Child A

In the first four snapshots, A#1 to A#4 in Table 1 below, the rods appear to act as counters (the attractor of the system). There are tensions, shown in the triad as broken red lines, between rods and app (in the misrecognition in A#2, A#3 and A#4) and also between the app and child. Initially three rods are placed, with the intention to make the app say “3” (A#2), then two rods to make it say “2”, and four rods to try to make it say “5”.

Table 1. Snapshots A#1–A#4 of Child A’s rod placements with dialogue and triadic flow diagrams.

A#	Transcript	Rods on Table	Triad
1	Res: “Can you make it say the number one?” Child A: [places white rod as shown] App: “1”
2	Res: “Well done, yeah! Now if you take that out of the way, can you make it say the number three?” Child A: [removes white rod and places black dark green and yellow rods] App: “6, 6, 5, 7, 5” Res: “What numbers is it saying?” Child: “Five…?”
3	Res: “Now can you make it say just the number two?” Child A: [removes black rod] App: “5, 8, 5, 5, 5” Res: “Now which one isn’t it seeing? Can you see it puts a little green line on when it sees it? Which one isn’t it seeing?” Child A: “This one?” [pointing to green rod] Res: “And which one is it seeing?” Child A: “This one” [pointing to yellow rod] Res: “And what’s it saying when it sees that one?” Child A: “Five?” Res: “Yep.”
4	Res: “So, can you make it just say the number five do you think?” Child A: “Er yeah” [adds light green and red rods] App: “6, 3, 2” Res: “Oh it’s seeing the green one now. OK I think it’s actually when you’re wobbling the table slightly it sort of starts again when it sees a movement.”

Table 1. Snapshots A#1–A#4 of Child A’s rod placements with dialogue and triadic flow diagrams.

A#	Transcript	Rods on Table	Triad
1	Res: “Can you make it say the number one?” Child A: [places white rod as shown] App: “1”
2	Res: “Well done, yeah! Now if you take that out of the way, can you make it say the number three?” Child A: [removes white rod and places black dark green and yellow rods] App: “6, 6, 5, 7, 5” Res: “What numbers is it saying?” Child: “Five…?”
3	Res: “Now can you make it say just the number two?” Child A: [removes black rod] App: “5, 8, 5, 5, 5” Res: “Now which one isn’t it seeing? Can you see it puts a little green line on when it sees it? Which one isn’t it seeing?” Child A: “This one?” [pointing to green rod] Res: “And which one is it seeing?” Child A: “This one” [pointing to yellow rod] Res: “And what’s it saying when it sees that one?” Child A: “Five?” Res: “Yep.”
4	Res: “So, can you make it just say the number five do you think?” Child A: “Er yeah” [adds light green and red rods] App: “6, 3, 2” Res: “Oh it’s seeing the green one now. OK I think it’s actually when you’re wobbling the table slightly it sort of starts again when it sees a movement.”

In rows A#5 to A#14, shown in Table 2 below, tensions are worked through to reach a point of relative stability (from A#12), denoted by the green triads. There appears to be some trial and error going on, instigated by the child and a mix of seeing rods as counters and as lengths, although it is hard to interpret with any certainty.

Table 2. Snapshots A#5–A#14 of Child A’s rod placements with dialogue and triadic flow diagrams.

5	Res: “So how about—you’re doing really well—how about… do you think you can make it say the number… What number do you think you can make it say?” Child A: “Ten?” Res: “Ok do you want to try to make it say ten?” Child A: [adds orange rod] App: “5, 3, 2, 10” Res: “Can you hear it?” Child A: “Yeah” Res: “Ten, yeah well done!”
6	Res: “Now how about if you wanted to make it say just the number ten?” Child A: [removes dark green, yellow, light green and red rods leaving orange rod] App: “10”
7	Res: “Well done yeah! Now how about if you wanted to make it say… two numbers, what two numbers would you make it say?” Child A: “Two?” Res: “And any other number?” Child A: “Four?” Res: “Two and four, OK do you want to try that? Take the ten out of the way and see if you can make it say two and four.” Child A: [removes orange rod and places white and red rods] App: “2, 1” Res: “What’s it say?” Child A: “Three?”
8	Res: “Oh yeah maybe move it, that’s it if you move it in the middle maybe it helps it see it…” Child A: [removes white rod leaving red rod] App: “2” Res: “Well done, you got two.”
9	Res: “Now how about—what was the other one you wanted to do?” Child A: “Four” Res: “How do you get that one?” Child A: [adds green rod] App: “2, 3” Res: “What did it say?” Child A: “Three and a two?”
10	Res: “So how are you going to get it to say four do you think?” Child A: [removes light green rod and adds white rod] App: “2, 1”
11	Child A: [removes red and white rods and places yellow and pink rods] App: “5, 4” Res: “Ooh! What’s is saying now?” Child A: “Five and a four?” Res: “That’s great. What did you want it to say?”
12	Child A: [removes yellow rod leaving pink] App: “4” Res: “Fantastic, is that what you wanted it to say?” Child A: “Yeah” Res: “And, OK, now have you been doing times tables just now—did I hear you doing times tables?” Child A: “Er yeah… the ten times table” Res: “Gosh that’s a big one.” Child A: “…the five times table Res: “How about the two times table?” Child A: “Yeah” Res: “Do you know it?” Child A: “Yeah” Res: “How does it go?” Child A: “Good” Res: “How does it go?” Child A: “Good” Res: “Two…?” Child A: “Er two, four, six, eight, ten” Res: “Fantastic!” Child A: “…twelve” Res: “It goes on and on, yeah that’s brilliant!”
13	Res: “And now do you think you could get this to say the two times table?” Child A: “Er yeah?” [clears block]
14	Child A: [places red and pink blocks] App: “2, 4”

Table 2. Snapshots A#5–A#14 of Child A’s rod placements with dialogue and triadic flow diagrams.

5	Res: “So how about—you’re doing really well—how about… do you think you can make it say the number… What number do you think you can make it say?” Child A: “Ten?” Res: “Ok do you want to try to make it say ten?” Child A: [adds orange rod] App: “5, 3, 2, 10” Res: “Can you hear it?” Child A: “Yeah” Res: “Ten, yeah well done!”
6	Res: “Now how about if you wanted to make it say just the number ten?” Child A: [removes dark green, yellow, light green and red rods leaving orange rod] App: “10”
7	Res: “Well done yeah! Now how about if you wanted to make it say… two numbers, what two numbers would you make it say?” Child A: “Two?” Res: “And any other number?” Child A: “Four?” Res: “Two and four, OK do you want to try that? Take the ten out of the way and see if you can make it say two and four.” Child A: [removes orange rod and places white and red rods] App: “2, 1” Res: “What’s it say?” Child A: “Three?”
8	Res: “Oh yeah maybe move it, that’s it if you move it in the middle maybe it helps it see it…” Child A: [removes white rod leaving red rod] App: “2” Res: “Well done, you got two.”
9	Res: “Now how about—what was the other one you wanted to do?” Child A: “Four” Res: “How do you get that one?” Child A: [adds green rod] App: “2, 3” Res: “What did it say?” Child A: “Three and a two?”
10	Res: “So how are you going to get it to say four do you think?” Child A: [removes light green rod and adds white rod] App: “2, 1”
11	Child A: [removes red and white rods and places yellow and pink rods] App: “5, 4” Res: “Ooh! What’s is saying now?” Child A: “Five and a four?” Res: “That’s great. What did you want it to say?”
12	Child A: [removes yellow rod leaving pink] App: “4” Res: “Fantastic, is that what you wanted it to say?” Child A: “Yeah” Res: “And, OK, now have you been doing times tables just now—did I hear you doing times tables?” Child A: “Er yeah… the ten times table” Res: “Gosh that’s a big one.” Child A: “…the five times table Res: “How about the two times table?” Child A: “Yeah” Res: “Do you know it?” Child A: “Yeah” Res: “How does it go?” Child A: “Good” Res: “How does it go?” Child A: “Good” Res: “Two…?” Child A: “Er two, four, six, eight, ten” Res: “Fantastic!” Child A: “…twelve” Res: “It goes on and on, yeah that’s brilliant!”
13	Res: “And now do you think you could get this to say the two times table?” Child A: “Er yeah?” [clears block]
14	Child A: [places red and pink blocks] App: “2, 4”

From snapshot A#15 to the end, shown in Table 3 below, we see a consistent interpretation of rods as lengths, within the child-rods-app system, which we interpret as an “attractor” of the system in this section of transcript. There are tensions (row A#16, A#18) when a different length is intended than the one chosen, but these are resolved as the attractor stabilises. We see potential evidence in this transcript of the rods appearing as a “new-concrete” artefact over the course of interactions. The app provokes what we take to be a “scientific” interpretation of the rods, which is that they represent numbers not in an iconic manner (as tokens) but in the more abstract manner of their length.

Table 3. Snapshots A#15–A#20 of Child A’s rod placements with dialogue and triadic flow diagrams.

15	Child A: [adds dark green rod as shown] App: “2, 4, 6”
16	Child A: [adds black rod] App: “2, 4, 6, 7”
17	Child A: [removes black rod] App: “2, 4, 6”
18	Child A: [adds blue rod] App: “2, 4, 6, 9”
19	Child A: [removes blue rod and adds brown rod—researcher attempts to mitigate a brief pause in recognition] Res: “Maybe put it a little further down, do you want to try that? Because the sun’s gone behind a cloud… Maybe the other one a bit further down…” App: “2, 4, 6, 8” Res: “Any more?” Child A: “Ten?”
20	Child A: [adds orange rod] Res: “OK maybe let it go [referring to leaning on table interrupting recognition] because I think when it wobbles it starts again maybe.” App: “2, 4, 6, 8, 10”

Table 3. Snapshots A#15–A#20 of Child A’s rod placements with dialogue and triadic flow diagrams.

15	Child A: [adds dark green rod as shown] App: “2, 4, 6”
16	Child A: [adds black rod] App: “2, 4, 6, 7”
17	Child A: [removes black rod] App: “2, 4, 6”
18	Child A: [adds blue rod] App: “2, 4, 6, 9”
19	Child A: [removes blue rod and adds brown rod—researcher attempts to mitigate a brief pause in recognition] Res: “Maybe put it a little further down, do you want to try that? Because the sun’s gone behind a cloud… Maybe the other one a bit further down…” App: “2, 4, 6, 8” Res: “Any more?” Child A: “Ten?”
20	Child A: [adds orange rod] Res: “OK maybe let it go [referring to leaning on table interrupting recognition] because I think when it wobbles it starts again maybe.” App: “2, 4, 6, 8, 10”

6.2. Videoclip 2: Child B

In the snapshots of Child B’s rod placements in Table 4 below, there is no obvious attractor which emerges in the first five turns B#1 to B#5. We observe the rods spaced in two dimensions. The “3” and “9” rods were placed close enough to each other to trigger the app to speak a “plus” audio routine. Initially, with no task, there is no tension we can analyse as a triadic flow. In row B#5, the intention to get the two times table emerges and there is a possibly systematic trial and error attempt, in the use of the smallest white rod.

Table 4. Snapshots B#1–B#5 of Child B’s rod placements with dialogue and triadic flow diagrams.

B#	Transcript	Rods on Table	Triad
1	Res: “You want to try numbers?” Child B: [places green and blue rods as shown] App: “3, 9”		?
2	Child B: [adds red and two white rods] App: “1, 2, 1, 3, 9”		?
3	Child B: [replaces one white rod with a pink rod] App: “2, 4, 1, 3, 9” Res: “Now how about, do you think you can make… what number do you think you can make? Make it say…” [Child B continues to place rods without responding to prompt]		?
4	Child B: [removes pink rod] Res: “Do you know the two times table?” Child B: “Yeah” Res: “How does the two times table go?” App: “2, 1, 3 plus 9” Res: “Do you know the two times table? How does it go?” Child B: “2, 4, 6, 8” Res: “OK, do you want to see if you can make it say that?”		?
5	Child B: [clears rods, places white rod] App: “1”

Table 4. Snapshots B#1–B#5 of Child B’s rod placements with dialogue and triadic flow diagrams.

B#	Transcript	Rods on Table	Triad
1	Res: “You want to try numbers?” Child B: [places green and blue rods as shown] App: “3, 9”		?
2	Child B: [adds red and two white rods] App: “1, 2, 1, 3, 9”		?
3	Child B: [replaces one white rod with a pink rod] App: “2, 4, 1, 3, 9” Res: “Now how about, do you think you can make… what number do you think you can make? Make it say…” [Child B continues to place rods without responding to prompt]		?
4	Child B: [removes pink rod] Res: “Do you know the two times table?” Child B: “Yeah” Res: “How does the two times table go?” App: “2, 1, 3 plus 9” Res: “Do you know the two times table? How does it go?” Child B: “2, 4, 6, 8” Res: “OK, do you want to see if you can make it say that?”		?
5	Child B: [clears rods, places white rod] App: “1”

In snapshots B#6 to B#18, in Table 5 below, we observe a continued use of trial and error (e.g., using a smaller rod than 4, to try to get 6, in turn B#8). Tensions appear between the app and child and, the attractor of trial and error seems to persist until the end. The child is successful on the task of getting the app to say the two times table. We do not observe evidence of a shift to a “new-concrete” interpretation of the rods in this transcript. The app offers the abstract interpretation of rods as lengths, but it does not appear as though any new perception of the rods is reached.

Table 5. Snapshots B#6–B#18 of Child B’s rod placements with dialogue and triadic flow diagrams.

6	Child B: [removes white rod and places red rod as shown] App: “2”
7	Child B: [adds pink rod] App: “2, 4”
8	Child B: [adds green rod] App: “2, 4, 3”
9	Child B: [removes green rod and adds blue rod] App: “2, 4, 9”
10	Child B: [removes blue rod] App: “2, 4”
11	Child B: [adds orange rod] App: “2, 4, 10”
12	Child B: [moves orange rod a distance to right] App: “2, 4, 10”
13	Child B: [adds green rod to right of pink rod] App: “2, 4, 3, 10”
14	Child B: [replaces green rod with dark green rod] App: “2, 4, 6, 10”
15	Child B: [removes orange rod, adds yellow rod] App: “2, 4, 6, 5”
16	Child B: [removes yellow rod] App: “2, 4, 6”
17	Child B: [adds brown rod] App: “2, 4, 6, 8”
18	Child B: [adds orange rod] App: “2, 4, 6, 8, 10”

Table 5. Snapshots B#6–B#18 of Child B’s rod placements with dialogue and triadic flow diagrams.

6	Child B: [removes white rod and places red rod as shown] App: “2”
7	Child B: [adds pink rod] App: “2, 4”
8	Child B: [adds green rod] App: “2, 4, 3”
9	Child B: [removes green rod and adds blue rod] App: “2, 4, 9”
10	Child B: [removes blue rod] App: “2, 4”
11	Child B: [adds orange rod] App: “2, 4, 10”
12	Child B: [moves orange rod a distance to right] App: “2, 4, 10”
13	Child B: [adds green rod to right of pink rod] App: “2, 4, 3, 10”
14	Child B: [replaces green rod with dark green rod] App: “2, 4, 6, 10”
15	Child B: [removes orange rod, adds yellow rod] App: “2, 4, 6, 5”
16	Child B: [removes yellow rod] App: “2, 4, 6”
17	Child B: [adds brown rod] App: “2, 4, 6, 8”
18	Child B: [adds orange rod] App: “2, 4, 6, 8, 10”

6.3. Similarities and Differences

It is first perhaps worth highlighting some overarching similarities and differences between Child A and Child B’s sessions. For example, Child A’s session took place outdoors, with an earlier, less extensively trained version of the blockaplay.ai app, and the changes in sunlight meant that object recognition was sometimes less reliable than with Child B, whose session took place indoors. Child A lined her rods up vertically, facilitating direct length comparison, whereas Child B lined his up horizontally, eventually curling the row upwards to fit it into the field of view. And Child B seemed so engrossed in the activity that he seemed to ignore the preliminary task of making the app say a number, whereas for Child A this provided a significant challenge, which may have focused her attention, early on, on the tension between her expectations and how the app worked in practice.

In our analysis of Child A’s actions on the rods we identified three distinct phases:

• An initial phase, when the actions generated app utterances which only occasionally matched the prompting task (to make it say a single number)—with the initial placement of ‘1’ an exceptional positive reinforcement. In this phase multiple rods were arranged, apparently intended to generate utterance of a single number word implied in the task, but generating multiple utterances—in tension with this expectation.
• An intermediate phase when there was some consistent placing of a rod that generated the expected utterance, alongside other rods. And some returning to reiterate previous placements. In this phase it was hard to discern a consistent pattern of action.
• A third final phase in which rods were placed which mostly generated the expected utterances. Where there was a discrepancy noticed, a single rod—the last placed—was replaced with one longer or shorter according to the perceived error until the expected utterance was made.

We found the initial and final phases consistent with two temporarily stable patterns—the first one of perceiving and acting on rods as counters, for example placing three rods to generate the uttered number ‘3’, and the final one of perceiving and acting on rods as lengths. In terms of the dynamic child-rods-app-task system, we propose that these can be understood as stable attractors—a ‘rods as counters’ attractor and a ‘rods as lengths’ stable attractor. Thus, we see the intermediate phase as a transition phase of unstable behaviour—a mixture of treating rods as counters and as lengths. This unstable phase coincides with the expectations of the initial rods as counters attractor being disrupted by the unexpected responses of the app to the preliminary task of making it say a number.

In Child B’s interactions we did not find such clearly distinct phases. It took child B longer (and more moves) to make the app say the two times table, and they did not appear to use the correlation of lengths with uttered numbers to inform choices of the next rod in the sequence. Rods appeared to be chosen effectively at random, and then kept if they matched the known next numbers in the times table. We characterise this as a pattern, or attractor, of ‘Trial and error’. It served Child B to complete the task, albeit more slowly than Child A.

7. Discussion

The ANN algorithm used in blockplay.ai’s object-recognition, as well as the child-rods-app-task system, are both examples of complex, dynamic systems, that may behave in unpredictable ways, for example small changes in inputs may cause large changes in behaviour—such as the sun going behind a cloud causing the app to stop, or start, recognising a given rod. At the same time, they may show stability over time, which we characterise as an attractor in the dynamic system.

A key difference between the two systems is that the object recognition algorithm is a feed-forward network, i.e., it takes inputs—pixels from the snapshotted image-and after processing through a many-layered network, with connections weighted through training on hundreds of images, produces the output of the colour and position of the rods. Whereas the child-rods-app-task system is a recurrent network—with information on what the app said fed back ‘live’ into the system, making it dynamic over time. Thus, states in the child-rods-app-task system do not arrive at a ‘final output’ but tend to shift over time, anticipating and perceiving new information, such as a new task or app utterance, and acting accordingly. Nevertheless, the system appears to settle into stable patterns of interactions—such as placing rods in a row of increasing lengths left to right.

It is through the capacity of the child-rods-app dynamic system to shift from one attractor state to another that we interpret the app as offering children an abstract interpretation of the concrete artefacts at play (i.e., the rods). To resolve the tension between the app’s utterances and the child’s predictions, the system ‘tips’ into a new attractor consistent with seeing and acting on “rods as lengths”—which we equate in our examples with a move to a “new-concrete” perception of the same rods, coordinating actions, in the concrete-abstract-new-concrete, proposal of Shvarts et al. [28].

We are struck by the speed with which, for Child A, the system changed from a “rods as counters” attractor, to a “rods as lengths” attractor. The transcript of Child B is a demonstration that “rods as lengths” is by no means an obvious or easy interpretation of the sounds from the app. And in Concrete-Pictorial-Abstract pedagogies—for example in introducing bar-modelling—this shift is typically introduced incrementally in a highly structured progression over several months if not years.

While conscious that this was an early experimental functional trial of a prototype app, rather than a contextualised pedagogical intervention, we are particularly interested that the interpretation of Cuisenaire rods as lengths, that it highlights, is potentially an important insight when children are learning mathematics. Davydov [3] who inspired our view of learning, proposed a curriculum based on number as a measure of length (shown, recently, to be a mathematically consistent interpretation of number [34]). The use of “bars” to represent number is a recurrent feature of curricula in Singapore and China, a practice that has now spread to England and several other countries. Effective use of “bar models” of number depends on interpreting rods or bars as lengths, something Child A comes to do over the course of the transcript offered above. We view the changes in the system involving Child A, especially, as a form of existence proof that powerful new attractors may develop, in dynamic systems involving ANN algorithms, attractors which may potentially be significant for future mathematics learning.

Finally, as a curious and unexpected instance of the ANN system literally transforming the perception of fingers—commonly used as embodied counters — into rods or numbers-as-lengths, we include an image captured shortly after the first session described above (see Figure 9). Here a child had, apparently unintentionally, rested their hand in shot, very still, such that no movement was detected, and the app had then snapshotted their fingers and recognised them as rods, much to the delight of the child, who then attempted to repeat the process intentionally. Entirely unpredicted shifts in a dynamic system’s attractor states such as this—stemming from its open-ended non-linear behaviour—may provoke fresh perceptions on the relationship between number-as-counting and number-as-measure, in a playful way.

8. Conclusions

In this article we set out to explore the potential of a deep learning algorithm trained to recognise placements of physical manipulatives, in the context of a child-app-rods-task dynamic system, learning mathematics and a novel methodology for analysing that system. By way of conclusion, we reflect on what we have learnt.

We have spent most space in this article describing the trial of the app, and offered details of observations of two children, and the child-rods-app dynamic systems which emerged through their interactions. Our approach to analysis involved mapping the recurrent dynamically looping interactions of child to rods to app to child and tracing the tensions and stabilities which emerged. The role of tensions, or disrupted intentions, in the system appears significant. It is the tensions in the system which appear to provoke change out of one attractor and into another (e.g., with Child A, out of a “rods as counters” attractor and into the more generative “rods as lengths” attractor). As Abrahamson and Sánchez-García [18] point out, from an ecological dynamics systemic perspective, changes are relativistic: “it does not make sense to say that the student per se has changed, because what the student learned is intrinsically situated and mutually adaptive […] As far as the student is concerned, the world has changed—it now bears new opportunities for action” (p. 213). Our interpretation of the system involving Child A demonstrates, for us, just this idea of the world (in the form of ‘concrete’ rods) coming to bear new opportunities for action (via perceiving rods as lengths).

As we analysed above, we have taken learning to mean a movement from concrete to abstract to a “new concrete” in which perception is through the lens of abstraction [28]. We believe the object-recognition app we trialed offers access to abstraction—via the app’s utterances of number words—and precisely the kind of new perception and action on the concrete—the placement of rods-through the lens of the abstract—that was proposed by Davydov [3]. As we stated at the outset, this research was curiosity driven, we initially wanted to observe what took place when children engaged with the app, with little idea of what would happen. We were surprised by the way that “rods as counters” shifted to “rods as lengths” for Child A—we had not anticipated that we would be able to observe such shifts, nor that the interactions could exhibit such swift change, and towards an attractor that is so significant a starting point for engaging in curricular proposals making use of the notion of number as measure or length.

However, our aim in this paper is broader than just a focus on the particular exploratory research that we report here. We want to use the example of this research to point to the further possibilities opened up by object-recognition. The significant technological challenge is to achieve quick and reliable recognition of the positioning of common objects such as mathematical manipulatives, in real-world contexts such as tabletops in classrooms or homes, on standard, widely available devices. Once objects have been recognised, it is relatively easy to programme an app to offer learners any kind of aural and visual feedback. The aural feedback is particularly straightforward to change on apps such as blockplay.ai, since these are simply audio files. So, for instance, instead of associating the words one to ten with Cuisenaire rods, these could be “ten, twenty, thirty… etc.”, or “a tenth, two tenths etc.”. We mentioned that one interest we have in Cuisenaire rods relates to proposals of a curriculum sequence in which algebra is offered before arithmetic [3]. We can associate rods with colour names, or letters (as suggested by Gattegno [2]) and the app can offer feedback comparing the lengths of rods recognised, such as saying “y[ellow] is greater than r[ed]”, or, in the form of equations, e.g., “y[ellow] plus p[ink] equals b[lue]”. Object-recognition, however, does not need to be associated with the particular curriculum sequencing which interests us. It would be possible to develop more standard cardinal awareness of number by offering aural feedback in relation to the number of objects placed under a camera. The point is that object-recognition technology generates the potential for children to become engaged in hands-on creative activity with concrete manipulatives directly (rather than via already-abstracted clickable graphics on a screen, for instance), gaining feedback which can be carefully designed to support particular curriculum intentions. Tools such as blockplay.ai may offer new ways of realising ‘Concrete-Pictorial-Abstract’ pedagogies, not just as a linear sequence, but as a cycle. And the use of tangible real-world objects as an interface also offers to liberate this learning activity from screens (and the necessity of a ‘Pictorial’ stage), via audio-driven interactions, opening up access, for example to visually-impaired users.

The potential for object-recognition, of course, is not limited to mathematics. We have experimented with associating rods with musical frequencies proportional to the lengths, to allow for the creation of tunes. Gattegno associated rods with phonemes to facilitate learning to read, and with vocabulary for learning languages. And, we have experimented with a mode in which rods become molecules (carbon, oxygen, hydrogen), to allow a modelling of chemical processes involved in climate change. Though outside the scope of the present study, in principle these varied uses offer possibilities of further “abstract-new-concrete” changes in patterns of perceptions and actions to be studied and compared in future. And similarly, with additional training, other concrete objects could be used, for example in later iterations we trained the app to recognise multilink cubes. And recently researchers have begun experimenting with combining machine learning and augmented reality to enable users to train ANNs themselves to recognise their own gestures with familiar objects to them [35,36].

It also seems to us potentially powerful that the abstraction inherent in object recognition (i.e., in our case, the app’s recognition of rod length) is something not made explicit (either by the app, or, in this case, by the researchers). In other words, children, in a child-rods-app system can come to act effectively, within the system, without necessarily needing to go through a process of conscious recognition, deliberate action and subsequent habitualisation. Much like the piano teacher and the book (mentioned in Section 4) the app can destabilise in order to open up new possibilities for action. And, we assume, attractors such as “rods as lengths” might, in time, be able to be invoked without the need for the blockplay.ai app.

As a last comment, we also recognise a movement for ourselves from concrete to abstract to new concrete, in relation to object-recognition. We began with the concrete tools of a camera, app software and rods, unsure what they might afford. Through trial and engagement with abstract ideas from enactivism and complex, dynamic systems theory, we have come to view those same concrete tools in a new way, with the potential to afford attractor states that could be powerful for children’s future learning. We hope we have pointed to the myriad possibilities of object-recognition, in an educational context, possibilities which we and others have only just started to explore.