Abstract
This study focuses on interdisciplinary approaches within mathematics and physics education. Secondary schools, particularly those specialized in scientific curricula, have opportunities to explore common topics between mathematics and physics; however, creating a coherent interdisciplinary educational experience is challenging. Adopting an interdisciplinary perspective when designing learning sequences becomes imperative. The proposed approach harnesses the power of storytelling to engage students, emphasizing the interconnectedness of subjects and humanizing the evolution of scientific ideas. This study investigates the adaptation of the Digital Interactive Storytelling in Mathematics (DIST-M) model for interdisciplinary storytelling learning sequences. It aims to explore how this model, initially developed for mathematics activities in a virtual environment, can be enriched with elements from inquiry-based learning models to integrate the experimental aspects of physics. The research presents a theoretical discussion grounded in the design of a learning sequence centered around the study of light, taking place in a non-virtual environment and approached from an interdisciplinary standpoint. It introduces hypotheses for adapting the DIST-M model to accommodate interdisciplinary storytelling sequences. One involves the incorporation of an additional phase within the DIST-M cycle, dedicated to consolidating, transferring to other contexts, and addressing variations in the concepts explored, proved, and refined in earlier phases.
1. Introduction
Interdisciplinarity is becoming increasingly prominent in educational, research, political, and institutional contexts [1].
In particular, interdisciplinarity in mathematics education refers to an approach that integrates concepts, methods, and perspectives from multiple disciplines within the realm of education to enhance the teaching and learning of mathematics in different contexts. Rather than treating mathematics in an isolated manner, interdisciplinary mathematics education recognizes the interconnectedness of mathematics with other subjects and real-world contexts. This approach aims to provide a more holistic and meaningful learning experience for students [2].
Interdisciplinarity can be implemented in various ways; some characteristics of interdisciplinary mathematics education may include real-world applications or problem-solving scenarios, but also a deeper integration of different subjects to see the interconnected nature of knowledge and deepen students’ understanding [3].
With this approach, it is also possible to make mathematics more engaging, relevant, and accessible to students while preparing them for the complexities of the real world [4].
In the context of science education, the family resemblance approach (FRA) [5,6] is a useful framework for characterizing disciplinary identities and, at the same time, connecting disciplines by fostering mechanisms of crossing and transgressing boundaries. In the family resemblance approach applied to science, the emphasis is on recognizing the diverse and interconnected nature of scientific practices, methods, and knowledge. This perspective encourages educators to present science as a dynamic and evolving enterprise with different branches, methods, and approaches, thus integrating a reflection on the nature of science in education. It also emphasizes the importance of understanding the relationships and connections between the various scientific disciplines, promoting a more holistic view of science in education. Irzik and Nola’s work [7] suggests that adopting a family resemblance approach in science education can contribute to a more complete and realistic portrayal of the nature of science, fostering a deeper appreciation for the interconnectedness and diversity inherent in scientific practices.
In our work, we focus on the theme of interdisciplinarity between mathematics and physics in science education. The relation between the two subjects is often underestimated: mathematics is seen as a tool in physics education, and physics is viewed as a context for applying mathematical concepts, but recent approaches and models are explored to overcome this dichotomy and emphasize the interplay between mathematics and physics [8,9,10,11,12,13], from a cognitive point of view [8] and also regarding a historical-epistemological perspective that sees them intertwined [13].
Particularly in secondary schools, the challenge of interdisciplinary education involving mathematics and physics is of main concern. In these school grades, especially within schools that address a curriculum focused on scientific subjects, these two subjects have several aspects that intersect and overlap. However, often the discussion of topics relevant to both subjects may occur in a non-cohesive manner within the two, potentially affecting the opportunity to respect the interplay of the two disciplines from an interdisciplinary perspective. For this reason, designing educational sequences from an interdisciplinary perspective appears to be necessary.
A context that allows working on the strong interplay between mathematics and physics is that of modelling [14]. A modelling cycle explicitly framed to effectively incorporate mathematics into physics education is the one proposed by Uhden et al. [15]. The cycle consists of a series of steps that, starting from the real world, involve simplification, mathematization, interpretation, technical mathematical operations, and, finally, validation of the model thus created to describe a real-world phenomenon or problem. The peculiarity of this model lies in the distinction between the technical and structural role of mathematics in physics and, consequently, the related competencies, technical and structural. Technical competencies are related to computational manipulations in a purely mathematical context and concern purely mathematical skills, while structural competencies are related to the ways of reasoning that mathematics provides for understanding physical situations. The key processes that the model describes are mathematization, which consists of formalizing a physical problem with gradually increasing degrees of mathematization; interpretation, which allows physical meaning to be deduced from equations, identifying special cases or making physical predictions from the formalism; and technical-mathematical operations related to purely technical skills.
Since modelling is a relevant competence to be developed in education [16], we can consider it an appropriate context for designing interdisciplinary activities in classroom practice also in secondary school.
Furthermore, to actively engage students in and navigate the challenges of interdisciplinary work, argumentation is seen as an essential competence that enables them to collaborate effectively across disciplinary lines and contribute innovative solutions to challenging problems, as in modelling contexts. Indeed, argumentation facilitates an aware integration of disciplinary and interdisciplinary perspectives through the promotion of critical thinking and the encouragement of communication across different fields of study [5,17]. For the design of interdisciplinary inquiry-based learning sequences that focus on promoting argumentation, employing storytelling could be a promising approach. Indeed, storytelling can be a useful educational tool for emphasizing the interrelationships among various subjects, tracing their historical evolution, and fostering students’ engagement and active participation [18]. Since narrative thinking [19] is a powerful method for infusing meaning into our experience, the process of creating stories is an effective means of conveying the meaning of concepts, models and theories in the scientific domain, especially when the scientific process becomes the direct experience of the character within the story [20]. This approach helps to draw parallels between the art of storytelling and the practice of systems modelling in science, as noted by [21]. In particular, in the realm of mathematics, storytelling takes on added significance when narrative thinking is developed in synergy with logical thinking [22].
As an emergent field of research, there is no explicit reference model to design interdisciplinary activity between mathematics and physics framed upon storytelling. On the contrary, to develop a storytelling mathematics-related activity centered on the argumentative competence, a reference model for instructional design is Digital Interactive Storytelling in Mathematics (DIST-M) [23,24,25]. This model was originally created for developing mathematics activities in a virtual environment. However, more generally, it is possible to consider it a tool for designing storytelling mathematics learning sequences, even if the digital component is not included. Then, DIST-M can be considered as a starting model to frame the learning sequence. Nevertheless, to foster an interdisciplinary approach between mathematics and physics that upholds the significance of both disciplines, it is essential also to consider the experimental features inherent to physics [5]. Specifically, research shows that it is particularly effective to introduce laboratories in education with objectives aimed at developing scientific practices/skills [26,27]. Moreover, in the 2012 Framework for K-12 Science Education [28] we can find ‘Planning and carrying out a systematic investigation’ as a major practice of scientists that should be strengthened throughout the K-12 curriculum.
Looking at the experimental aspect, an Inquiry-based learning approach [29], to which, for example, Kolb’s model [30,31], 5E [32], and the Investigative Science Learning Environment (ISLE) refer [33,34,35], can guide the design choice to give relevance to these core components of physics. Thus, the following research question emerges: How and to what extent can the experimental features emphasized by design models of inquiry-based learning be integrated within the storytelling model proposed by DIST-M?
This study aims to explore how to effectively integrate an interdisciplinary approach between mathematics and physics within the realm of storytelling. In particular, what adaptations the DIST-M model, originally intended to develop mathematics activity, may require to be a design model for a storytelling interdisciplinary learning sequence? In this contribution, we will present a theoretical dissertation derived from the example of the design of a learning sequence concerning the study of light, from an interdisciplinary perspective. This learning sequence emerges from the collaborative efforts of educators and researchers within the paradigm of action research, aiming to design an interdisciplinary instructional path focused on developing modelling and argumentation skills [36]. Subsequently, we will propose hypotheses for the adaptation of the DIST-M model for developing interdisciplinary activities from this initial example. This adaptation will be based on the design models for Inquiry-based learning, considered in the development of the sequence to enhance the experimental component that distinguishes the field of physics. This learning sequence is provided exclusively as an example for theoretical discussion purposes. This contribution will not deepen the aspects related to its implementation in school contexts and justifications of the decision in this direction (e.g., students’ participation, group work, assessment) will be not illustrated here. However, future research will move in the direction of examining the outcomes of the learning sequence implementations.
2. Models for Instructional Design
In this paragraph, we will present the fundamental models we refer to in our dissertation. The models were chosen with reference to our target objectives: to work in an interdisciplinary manner through modelling by promoting argumentation. To develop an interdisciplinary teaching–learning sequence on storytelling, we start framing with the reference model for designing storytelling activities in mathematics DIST-M [23,24,25]. From this starting point, to integrate other guides to encompass the physical dimension, from an experimental perspective, we consider Kolb’s model [30,31]. What resulted was not a simple overlap of approaches, but involved careful reflection on the role of each model for the individual discipline and the interconnection between disciplines. This reflection was guided by the Family Resemblance Approach (FRA), for keeping in mind the core features of the involved disciplines, and the work of Uhden et al. for the attention on modeling between mathematics and physics.
2.1. The DIST-M Model
DIST-M guided us to design a compelling narrative structure that seamlessly integrates disciplinary concepts.
As general directions, according to the model, the story must provide context and relevance to the content, creating a cohesive and engaging learning experience. At the same time, the narrative must allow students to actively participate by encountering problem-solving included in the storyline and relevant to its progression. This encourages critical thinking and reinforces the use of mathematics in real contexts. The model highlights that the experience must, as far as possible, be customizable to different learning rhythms and assessment must also be integrated into the storytelling experience. On the one hand, design choices must promote collaborative learning, fostering shared work and argumentation skills. On the other hand, providing feedback to students within the storytelling environment is considered essential. Feedback helps guide students, reinforcing deep and meaningful understanding of concepts.
Concerning the structure of a storytelling learning sequence framed upon the DIST-M model, the following steps are identified [23,24]:
- Phase 1—inquiry: students begin to explore the problem, investigate the hypothesis leading to an initial and personal conjecture (even if only verbal).
- Phase 2—conjecture and formalization: students discuss and manipulate the initial statements to achieve a formalized one.
- Phase 3—arguing and proof: students, then, attempt to prove the conjecture, justifying each step of the deduction.
- Phase 4 and 5—summing up and refining: students, when retelling a story, reflect on the entire process that led to the solution of the problem. This step helps to evaluate the work done and the role played (self-assessment, metacognitive, and affective level).
Other descriptions of the cycle have emerged in previous works related to the DIST-M model [25], focusing on the articulation stages of five episodes within the story, aiming to support the argumentative process: Exploration, Conjecture, Formalization, Proof, and Reflection. Apart from a re-arrangement of the phases, the overall structure of the cycle remains identical to the previous one. Specifically, we can observe that phases 4 and 5 have been further condensed into the final phase. It justifies the grouping we made in the previous list, considering them within a single step.
2.2. The Inquiry-Based Learning Models
In the field of inquiry-based learning, some planning structures help teachers develop student-centered inquiry-based lessons and units, such as the Kolb [30,31] or 5E [32] model. We have chosen the former to create a more complete and experiential learning environment that suits different students with their different learning preferences. The cyclical nature of the Kolb model emphasizes the importance of continuous reflection and application in the learning process. To summarize, Kolb’s model is a cyclic process involving four stages (Figure 1):
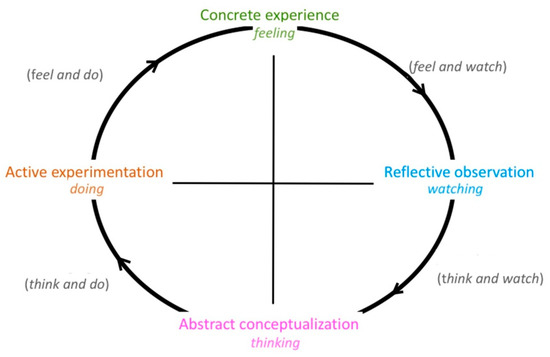
Figure 1.
Schema of the Kolb cycle.
- Concrete experience, which involves direct, practical experiences as the starting point of the learning process.
- Reflective observation, which promotes a reflective attitude on what has been observed to encourage the formulation of questions and the search for answers.
- Abstract conceptualization, in which students analyze their observations and reflections to generalize, move towards abstract concepts and finally develop laws and theories.
- Active experimentation, which involves applying concepts and theories to new situations or actively testing what has been learned. This practical experimentation completes the learning cycle and prepares the learner for the next concrete experience.
Especially focusing on the role of experimental experience, a particularly useful approach for didactic implementation is the Investigative Science Learning Environment (ISLE) because it has an emphasis on aspects of didactic meta-reflection, while also providing a range of validated teaching materials, including assessment rubrics that encourage the development of scientific practices. It can be used to support students in learning physics by involving them in processes that reflect scientific practice. The ISLE model can inspire the use of different kinds of experiments (observational, testing, application), the structure of the laboratory worksheets, and the assessment rubrics (in addition to what has already been stated in the previous paragraph) as in [33,34,35].
3. Research Design
For discussing the adaptation of the DIST-M model for a storytelling interdisciplinary mathematics–physics learning sequence, we make use of a first example: the design of a learning sequence concerning the study of light, aimed at developing argumentative and modeling competence.
As a reference to pinpoint the core characteristics of an interdisciplinary learning sequence, the FRA appears effective in respecting the epistemological complexity of interdisciplinarity and in providing categories (aims and values, practices, methods, and methodological rules, knowledge organized between cognitive-epistemic and a social-institutional system) to reason about disciplinary identities and their dialogue. The FRA framework thus allows reflection on what characterizes the scientific disciplines and, at the same time, promotes explicit disciplinary meta-reflections on the epistemologies of mathematics and physics. Under its guidance, we can, therefore employ Uhden’s model, which delves into the role of mathematics in physics, providing a model for emphasizing the translation process between physics and mathematics. In particular, simplification and validation connect the world with the physical model, while mathematization and interpretation connect the physical model with mathematics. Indeed, Uhden’s model can be seen as potentially asymmetrical, since the focus is more on physics and the role of mathematics in physics [37]. We thus consider its involvement appropriate to balance the fact that our starting point on interdisciplinarity is from the mathematical field. Even though it is usually considered as a framework to model a problem, in this work, it is conceived as a framework guiding the design of the learning unit itself, further than being taken into account to structure the various activities.
In particular, the theoretical characterization of Uhden et al.’s work highlights the need for integrating a supplementary framework to design the learning unit, further than the DIST-M reference. Indeed, we start conceiving the DIST-M model, which fits since the activity also involves mathematics, but we further need to integrate aspects of Kolb’s design, to address the characterization of physics as having an experimental nature.
The activity is designed as described in the following section. Starting from the example provided, a possible adaptation of the DIST-M model to the interdisciplinary learning sequence will be discussed in Section 4, looking back to the design of the unit from the perspective of Kolb and the DIST-M cycle.
The Learning Sequence
The developed learning sequence aims to study light, a central topic in physics that lends itself to interdisciplinary reading, particularly with mathematics, and also promotes awareness of the nature of science. The unit revolves around three core questions about light: What is the nature of light? How does it propagate? How does it interact with matter? To address these questions, specific topics covered are the models of light—rays, particles, and waves models—and the first phenomena concerning the interaction of light and matter: reflection and refraction.
The learning objectives of the learning sequence are inherently interdisciplinary. The students are expected to have a comprehensive understanding of the models of light and should be able to explain various phenomena involving light-matter interaction and predict the outcome of experiments. It includes using mathematics to identify, compare and generalize, formulate laws (geometry, sine function, and basic algebra), and solve problems in optics. Other objectives align with the choice of making use of storytelling in the learning sequence: the students should be able to collaborate with peers to find solutions to problems, and actively participate in discussions being responsible for expressing their own thinking and contributing to the problem-solving process.
The learning sequence has been implemented in a class of 14/15-year-old students (grade 9) in a scientific-oriented high school with an experimentation involving four hours per week for 6 weeks. Adapted to the specific context of the class, including the students’ interests and dynamics, the intervention employs a narrative approach inspired by “Lord of the Rings”. The class comprises 18 students and, although they show interest, few actively engage in discussions. To solve this problem, it was decided to implement storytelling and role-playing in order to increase participation and feedback to improve learning and attitude.
The unit has been developed starting from the DIST-M model, organizing the narratives in multiple cycles: a macro-cycle concerning an overall view on the main questions, which starts in the introductory phase and continues in the concluding part of the sequence, and two other DIST-M cycle in between, the first explicitly referring to reflection and the second to refraction (Figure 2).
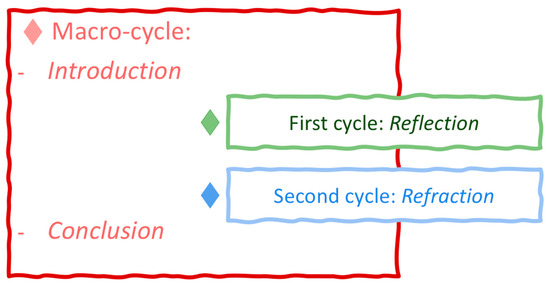
Figure 2.
Schema of the three DIST-M cycles in the learning sequence.
Each cycle begins with the Inquiry and Conjecture activities (points 1 and 2 of the above list), continues with the tasks and discussion on Arguing and Proof (point 3), and ends with the Summing up and Refining section (points 4 and 5). More precisely, a lesson explicitly aimed at phases 4 and 5 has been included in the concluding part of the macro-cycle, which involves the overall contents of the sequence. However, a partial Summing up and Refining phase has been integrated into each cycle.
Apart from the narrative script and didactic structure that follows the DIST-M cycle, as mentioned above, the overall design of the learning sequence was developed according to the characteristics of the DIST-M model as well, except for the digital aspect. We start the learning sequence with an explorative problem, which has to be solved dealing with several activities. The focus of the entire sequence is on the collaboration, and the students (divided into groups) and the expert (teacher or researcher) playing clearly defined roles integrated into the narrative. The story evolves precisely according to the interactions between the characters and the stimuli coming from the expert. Furthermore, evaluation takes place through both collective and individual feedback, which is constant within the story. Other formative assessment strategies were included, such as self-evaluation, often related to the partial Summing up and Refining phases. Traces can be found in the quest provided in Appendix A (Figure A4, Figure A5, Figure A7 and Figure A10).
The narration upon which the story is articulated is inspired by “The Fellowship of the Ring” by Tolkien. To prioritize the engagement, the narrative framework is chosen according to teachers and students’ interest. Thus, in a different context, another background might be a better choice. Through the narration, students start a journey and delve into a series of adventures. The experience will give them the expertise and knowledge necessary to reach the final goal of the story, which is aligned with the learning objects of the learning sequence.
The story begins with Galadriel giving Frodo a crystal vial containing the light of the star of Eärendil to help him in his important task. A new group of characters arrive in Lórien and are asked to help the Fellowship against the dark forces of Sauron, gaining experience through quests. These are the students, who become the characters of the story with unique abilities based on Tolkien’s races. During their journey, they encounter various challenges related to light and its interaction with matter, exploring concepts such as reflection and refraction and trying to understand the nature of light through multiple models (ray, wave, particle). This knowledge will be needed to solve the problems they encounter, for example, to repel orcs and detect poison in the blood of elves using light, and will enable them to really help the Fellowship.
Without going into too much detail, but in order to illustrate the overall structure of the learning sequence, in Table 1 we explain the modules that make it up through the learning objectives and questions that guided its development. In Table 1, the refraction cycle is not included because we will analyze the cycle in detail later, showing illustratively how the cycles were created.

Table 1.
The learning sequence described through the objectives and the guiding questions.
In the following, we will illustrate how the refraction cycle has been designed, starting from the narrative framed upon the DIST-M model, after having identified the core theme and learning objective to be addressed. This provides an example of how the whole learning sequence has been created upon the selected models, under the guidance of Uhden’s directions.
In Table 2, the script of the narration upon which the refraction cycle is articulated, framed on the DIST-M model phases, is briefly described. In the last column on the right, there are indicated the didactic modules related to the specific narrative phases. A short description of each didactic module is provided in Table 4.

Table 2.
Refraction cycle: Narration articulated on the DIST-M phases.
Having reached phase 4 and 5, the DIST-M cycle would be concluded. However, in order to emphasize the inherent aspects of physics within the interdisciplinary learning sequence, recourse is again made to FRA and Uhden’s model, and the essential role of the experimental and applied nature of physics. Putting attention on this component, to help us guide the analysis of how the experimental components fit in the sequence, we will refer to Kolb’s model.
Adopting DIST-M, which is a framework for developing mathematics activities, the cycle is structured around phases that correspond to the mathematical components of the unit. However, with adaptation concerning how physics is taken into consideration, the sequence also aligns with part of Kolb’s cycle. Indeed, the first three phases of the Kolb cycle could be traced back to the designed modules, in parallel with the DIST-M cycle: the concrete experience in Module 1 and in the school trip, as well as the reflective observation in Module 2 and part of Module 1, and abstract conceptualization in Module 3. However, the last phase of the Kolb cycle, corresponding to active experimentation, cannot find a place within the planned didactic modules. This phase involves the application of the concepts and laws derived to new situations or the active verification of what has been learned.
Therefore, in line with the Kolb cycle, we expand the narrative and didactic sequence with a further phase, which we refer to as Phase 6, in which we incorporate didactic modules regarding the reflection concerning the re-interpretation within the physical models of what has been discovered in terms of mathematical laws, and the applications, and the verifications of these laws in further problematic and experimental situations (Table 3).

Table 3.
Refraction cycle: The additional phase.
In Table 4, the whole structure of the Refraction cycle, articulated in didactic modules, is illustrated. Each module has been associated with the specific learning objective addressed, the questions that guide the module, the typology of activities involved in the module, and features concerning how the module is planned to be implemented in class. The worksheets guided the requests encountered by the students in the development of the story, as quests to be completed. The quests related to the cycle here described are illustrated in Appendix A.

Table 4.
Refraction cycle: Descriptions of didactic modules.
4. An Exemplary Integration of Models from an Interdisciplinary Perspective
By using DIST-M to develop an interdisciplinary learning sequence between mathematics and physics with an experimental connotation, it becomes evident from the example presented in the previous paragraph (Table 2 and Table 3) that it is necessary to add a phase. Indeed, in the experimental domain, it is essential to repeat experiments by applying them to new situations in order to continue testing their validity [33,34].
What was presented in the exemplar cycle occurred for the entire sequence, in each of its cycles. In the previous section, we showed it for the refraction cycle, but, as can be seen in the summary table below (Table 5), it occurs systematically within all cycles and thus for the entire learning sequence.

Table 5.
The learning sequence declined in modules and analyzed according to DIST-M and Kolb model, with reference to the guidance of Uhden’s framework.
In the DIST-M model, the last phase is intended as a form of evaluation. After the students have formalized the proof, organizing and justifying the deductive steps, we then move on to a reflection phase that is useful both as a form of collective and self-assessment, while remaining on a cognitive, metacognitive, and affective level. Instead, in the field of experimental physics, we need a further moment in which to apply the concepts to new situations, experimentally and actively verifying what we have learnt. This is, for example, what Kolb’s model’s ‘Active Experimentation’ phase provides for. On the other hand, DIST-M helps us to integrate the structural role of mathematics into physics, focusing on reasoning, formalization, and proof.
Intending to follow Uhden’s suggestions as a design guide, integrating DIST-M and Kolb models could generate a complete model for designing experimental interdisciplinary activity. Then, we propose to adapt the DIST-M model, adding the phase called Consolidation, Transfer, and Variation. It serves to consolidate what has been learned, apply it in a new context, and understand how it can be enriched by this, and what changes it can undergo. This phase thus encompasses problem-solving of various kinds and new experiments (e.g., tests or applications according to ISLE approach [33,34,35]) that validate or modify what has been theorized.
The DIST-M integrated with the new phase at the end becomes consistent with Kolb’s model and with what Uhden advocates. We can trace back the steps of the Uhden model, adapted to be read as design guidance, in all the cycles that make up our learning sequence, as well as within a single module. For example, looking at the macro-cycle, we can find in the Introduction a simplification phase followed by mathematization, when we start using geometry, and then return to physics by interpreting what we have obtained mathematically. Analyzing the wave and particle models, we start again with simplification, mathematization, and interpretation. Then, the macro-cycle concludes with the validation phase and, when applied to the solution of the game, all the phases of Uhden’s model return. This is true also for internal cycles. For instance, looking at the refraction cycle, we can find in the Module 1 a simplification phase followed by mathematization in Module 2, when we start searching mathematical relations and formalizing, doing also some technical mathematical operations to find a law (with the highest degree of mathematization) in Module 3, and then return to physics by interpreting what we have obtained mathematically. In Module 4 applying the law to new different situations involves the validation phase, but also inside the various proposed activities the Uhden cycle is retraced again. In Module 5 checking if the models are consistent with the rule for specular refraction is also a validation stage. Finally, the solution of the contextualized open problem serves both as the validation phase of the entire process, but also internally requires all steps of the Uhden cycle again.
5. Discussion and Conclusions
To adopt an interdisciplinary approach that integrates mathematics and physics, first of all, we considered the Family Resemblance Approach [5,6,7] to always keep in mind aims and values, practices, and knowledge that distinguish one disciplinary domain from another, particularly for what characterizes science [5].
In parallel, to treat the relationship between mathematics and physics and find the right way to integrate and interlace them, we propose to draw on the theoretical guidelines provided by Uhden and colleagues [15]. We view their theorization as a valuable resource for guiding the design of a learning sequence that originates from an interdisciplinary perspective. It incorporates the intertwining of mathematics and physics and also allows us to distinguish between technical and structural skills, bearing in mind that the role of pure mathematics and pure qualitative reasoning should not be neglected, but resolving the translation process between physics and mathematics in more detail. This model is also useful in highlighting different ways of reasoning, highlighting some possible sources of difficulty, and suggesting more appropriate approaches. In contrast to the common reference to Uhden et al.’s theorization for analyzing students’ thinking or for planning individual math-physics activities, the perspective adopted in the research goes further. We see this perspective as a framework to be considered when planning an entire learning sequence. However, it is important to note that Uhden’s work, while offering guidance for the planning of specific activities, does not by itself constitute a truly comprehensive instructional design model. For this reason, we believe that it is necessary to supplement these guidelines with models explicitly created for the design of learning sequences.
In the specific case of designing an interdisciplinary math-physics learning sequence centered around storytelling, we found it essential to refer to a specific design model suited for this type of activity. In the absence of an interdisciplinary model specifically directed at designing mathematics and physics storytelling sequences, we turned to the well-established DIST-M model [23,24,25] within the field of mathematics. This model is considered suitable for creating argumentative mathematics learning sequences, and, even if it originates in virtual contexts, it is enough feasible to be extended in non-digital environments. Indeed, DIST-M provides a structured framework with specific characteristics, such as the focus on Inquiry–Conjecture–Proof progression, collaborative, role-driven work, continuous feedback for monitoring learning, and guided reflection aspects for developing metacognitive skills, that can be adapted for use outside of digital contexts.
However, following the indications of the FRA and Uhden, it became evident that the DIST-M model, being designed for the mathematical domain only, did not incorporate the necessary components to comply with the aims and values of physics. In particular, the experimental aspect was underestimated within this model, and the reinterpretation of mathematical results within the physical context and applications, as well as the interpretation phase of the physical meaning of mathematical expressions and the possibility of making physical predictions from the formalism was lacking. Consequently, the need arose to supplement this model with a design framework highlighting the fundamental steps of an experimental teaching unit focusing on inquiry-based learning.
In this context, we chose to incorporate Kolb’s model [30,31] for designing experimental activities as an integral part of the learning sequence and, consequently, the narrative script. This adaptation forced us to extend the DIST-M model by adding a phase beyond the existing model, emphasizing the features highlighted by Uhden which we recall consists of the attention to the structural role of mathematics in physics, expressed by the phases of mathematization, which consists of formalizing a physical problem with different degrees of mathematization, and interpretation, which allows the physical meaning to be deduced from the formal mathematical language.
In this contribution, we illustrated an exemplary case to support our argument that an integrated design model should be considered when designing interdisciplinary teaching sequences based on storytelling. We highlight, starting from this case, the necessity of adapting the DIST-M model by revisiting the design structure, revaluating Uhden’s model as a guiding framework for the didactic sequence, and comparing the cycles with those proposed by Kolb.
As one possible adaptation, we suggest extending the DIST-M cycle with an additional phase focused on consolidation, transfer, and variation in what has been learned in the previous phases. This adaptation leads to the creation of an integrated model, which we propose to call “Interdisciplinary Interactive Storytelling in Mathematics and Physics” (IIST-MP). This model envisions a design script for storytelling in interdisciplinary activities comprising five phases: those outlined by DIST-M, along with the new sixth phase aimed at consolidation, transfer, and variation (Figure 3).
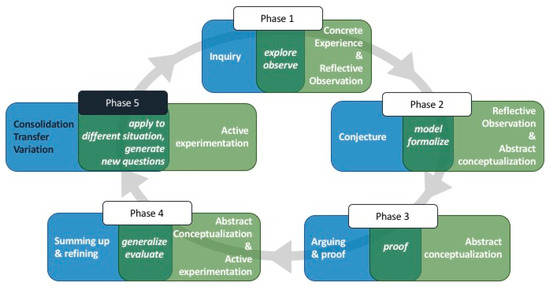
Figure 3.
Schema of the IIST-MP cycle.
Furthermore, it is essential to emphasize that the adaptation goes beyond surface changes. Within each phase, we should also expand the perspective to include relevant aspects of experimental characterization, as outlined in the Kolb model, following Uhden’s guidance. This entails revisiting the steps of DIST-M by incorporating a physics reinterpretation and considering each phase from Uhden’s perspective.
6. Limitation and Further Directions
In this article, we discussed the need to adapt the DIST-M model to design interdisciplinary experimental activities in mathematics and physics, with a focus on storytelling. We achieved this by examining the necessity of integrating experimental design models, especially the one proposed by Kolb. To illustrate this, we used a specific example related to an argumentative and modeling activity centered around light. We found this example particularly valuable as it showcased how the Kolb model required adjustments through multiple cycles. However, we specifically detailed the educational design process in relation to one cycle, that of refraction. The other cycles are exclusively briefly illustrated in Table 1 showing the didactic modules.
While our discussion was based on a specific context, which we considered significant, it necessitates further investigation to validate the hypotheses of adaptations derived from our study. Additionally, for the development of an interdisciplinary storytelling activity in the realm of mathematics and physics, we should attempt to apply the IIST-MP design model here outlined to a different topic, narrative and context. A further direction may be to investigate if this model can be considered to design interdisciplinary activities involving mathematics and other experimental sciences within the STEM field further than physics. This reflection also extends to our choice of Uhden as a guiding framework for interdisciplinary design. Indeed, in our work, we adopted Uhden’s theorization as a design guide, because it appears to provide a solid perspective from an interdisciplinary standpoint, aligning with the FRA framework, as advocated by Satanassi et al. [37]. Nevertheless, utilizing this theoretical model as a guide for designing interdisciplinary activities warrants further exploration.
Our reflection on the integration of models also raises questions about whether selecting the Kolb model for the design of experimental activity is the most suitable approach. Specifically, we ponder if adopting a different model, such as the 5E model [32], would yield similar requirements for adapting DIST-M or result in different outcomes.
Finally, in our contribution, we used the DIST-M model, although we did not consider its original feature of being designed for virtual activities. A possible future direction could be to explore the integration of the DIST-M model from an interdisciplinary perspective, in cases where it is employed for an activity developed in a digital environment, as originally conceived.
Author Contributions
Conceptualization, S.L. and A.B.; Methodology, S.L. and A.B.; Validation, S.L. and A.B.; Formal analysis, S.L. and A.B.; Investigation, S.L. and A.B.; Data curation, S.L. and A.B.; Writing—original draft preparation, S.L. and A.B.; Writing—review and editing, S.L. and A.B.; Visualization, S.L. and A.B.; Supervision, S.L. and A.B.; Project administration, S.L. and A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding. The APC was funded by the MDPI Editorial Office.
Institutional Review Board Statement
This study was approved by the Ethics Committee of the University of Genova (Comitato etico per la ricerca di Ateneo, CERA, protocol code n. 2023.66 and date of approval 29 September 2023).
Informed Consent Statement
Informed consent was obtained from all subjects involved in this study.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The research developed from a collaboration formed during the BrEW Math 01 (Brixen Education Workshop on Storytelling in STEM disciplines at the crossroads of science and humanities) held at the MultiLab of the Faculty of Education, Free University of Bozen-Bolzano, 8–10 November 2022.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Below are reported worksheets given to students for quest 6 (Figure A1, Figure A2, Figure A3, Figure A4 and Figure A5), quest 7 (Figure A6 and Figure A7), quest 8 (Figure A8), and quest 9 (Figure A9 and Figure A10).

Figure A1.
Quest 6_Part 1.

Figure A2.
Quest 6_Part 2.

Figure A3.
Quest 6_Part 3.
Figure A4.
Quest 6_Part 4.

Figure A5.
Quest 6_Part 5.

Figure A6.
Quest 7_Part 1.

Figure A7.
Quest 7_Part 2.

Figure A8.
Quest 8.

Figure A9.
Quest 9_Part 1.

Figure A10.
Quest 9_Part 2.
References
- Williams, J.; Roth, W.M.; Swanson, D.; Doig, B.; Groves, S.; Omuvwie, M.; Borromeo Ferri, R.; Mousoulides, N. Interdisciplinary Mathematics Education: A State of the Art; ICME-13 Topical Surveys; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Roth, W.-M. Interdisciplinary approaches in mathematics education. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 647–650. [Google Scholar]
- Nikitina, S. Three strategies for interdisciplinary teaching: Contextualizing, conceptualizing, and problem—Centring. J. Curric. Stud. 2006, 38, 251–271. [Google Scholar] [CrossRef]
- Tonnetti, B.; Lentillon-Kaestner, V. Teaching interdisciplinarity in secondary school: A systematic review. Cogent Educ. 2023, 10, 2216038. [Google Scholar] [CrossRef]
- Erduran, S.; Dagher, Z.R. Reconceptualizing the Nature of Science for Science Education: Scientific Knowledge, Practices and Other Family Categories; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Erduran, S.; Dagher, Z.R. Regaining focus in Irish junior cycle science: Potential new directions for curriculum and assessment on nature of science. Ir. Educ. Stud. 2014, 33, 335–350. [Google Scholar] [CrossRef]
- Irzik, G.; Nola, R. A family resemblance approach to the nature of science. Sci. Educ. 2011, 20, 591–607. [Google Scholar] [CrossRef]
- Tuminaro, J.; Redish, E.F. Elements of a cognitive model of physics problem solving: Epistemic games. Phys. Rev. Spec. Top. Phys. Educ. Res. 2007, 3, 020101. [Google Scholar] [CrossRef]
- Redish, E.F.; Bing, T.J. Using math in physics: Warrants and epistemological frames. In Physics Community and Cooperation, Proceedings of the GIREP-EPEC & PHEC 2009 International Conference, Leicester, UK, 17–21 August 2009; Raine, D., Hurkett, C., Rogers, L., Eds.; University of Leicester: Leicester, UK, 2009; Volume 2, p. 2. [Google Scholar]
- Redish, E.F.; Kuo, E. Language of physics, language of math: Disciplinary culture and dynamic epistemology. Sci. Educ. 2015, 24, 561–590. [Google Scholar] [CrossRef]
- Redish, E.F. Problem solving and the use of math in physics courses. arXiv 2006, arXiv:physics/0608268. [Google Scholar]
- Karam, R. Introduction of the thematic issue on the interplay of physics and mathematics. Sci. Educ. 2015, 24, 487–494. [Google Scholar] [CrossRef]
- Tzanakis, C. Mathematics & physics: An innermost relationship. Didactical implications for their teaching & learning. In History and Pedagogy of Mathematics; HAL: Montpellier, France, 2016; p. hal-01349231. [Google Scholar]
- Hestenes, D. Notes for a Modeling Theory of Science, Cognition and Instruction. In Proceedings of the 2006 GIREP Conference: Modelling in Physics and Physics Education, Amsterdam, The Netherlands, 20–25 August 2006. [Google Scholar]
- Uhden, O.; Karam, R.; Pietrocola, M.; Pospiech, G. Modelling mathematical reasoning in physics education. Sci. Educ. 2012, 21, 485–506. [Google Scholar] [CrossRef]
- Blum, W.; Borromeo Ferri, R. Mathematical modelling: Can it be taught and learnt? J. Math. Model. Appl. 2009, 1, 45–58. [Google Scholar]
- Jiménez-Aleixandre, M.P.; Erduran, S. Argumentation in Science Education: An Overview. In Argumentation in Science Education; Erduran, S., Jiménez-Aleixandre, M.P., Eds.; Science & Technology Education Library, 35; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar] [CrossRef]
- Engel, A.; Lucido, K.; Cook, K. Rethinking Narrative: Leveraging storytelling for science learning. Child. Educ. 2018, 94, 4–12. [Google Scholar] [CrossRef]
- Bruner, J. Actual Minds, Possible Words; Harvard University Press: Cambridge, UK, 1986. [Google Scholar]
- Dahlstrom, M.F.; Scheufele, D.A. (Escaping) the paradox of scientific storytelling. PLoS Biol. 2018, 16, e2006720. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, H.U. From Stories to Scientific Models and Back: Narrative framing in modern macroscopic physics. Int. J. Sci. Educ. 2015, 37, 934–957. [Google Scholar] [CrossRef]
- Zan, R. La dimensione narrativa di un problema: Il modello C&D per l’analisi e la (ri)formulazione del testo. In L’Insegnamento della Matematica e delle Scienze Integrate; Centro Ricerche Didattiche Morin: Paderno del Grappa, Italy, 2012; Volume 35. [Google Scholar]
- Albano, G.; Pierri, A. Digital storytelling in mathematics: A competence-based methodology. J. Ambient Intell. Human Comput. 2017, 8, 301–312. [Google Scholar] [CrossRef]
- Polo, M.; Dello Iacono, U.; Fiorentino, G.; Pierri, A. A Social Network Analysis approach to a Digital Interactive Storytelling in Mathematics. Je-LKS 2019, 15, 239–250. [Google Scholar]
- Albano, G.; Coppola, C.; Dello Iacono, U. What does Inside Out mean in problem solving? Learn. Math. 2021, 41, 32–36. [Google Scholar]
- Smith, E.M.; Holmes, N.G. Best practice for instructional labs. Nat. Phys. 2021, 17, 662–663. [Google Scholar] [CrossRef]
- Wilcox, B.R.; Lewandowski, H.J. Developing skills versus reinforcing concepts in physics labs: Insight from a survey of students’ beliefs about experimental physics. Phys. Rev. Phys. Educ. Res. 2017, 13, 010108. [Google Scholar] [CrossRef]
- National Research Council. A Framework for K-12 Science Education: Practices, Crosscutting Concepts, and Core Ideas; The National Academies Press: Washington, DC, USA, 2012. [Google Scholar]
- Rocard, M.; Csermely, P.; Jorde, D.; Lenzen, D.; Walberg-Henriksson, H.; Hemmo, V. Science Education Now: A Renewed Pedagogy for the Future of Europe; European Commission: Brussels, Belgium, 2007. [Google Scholar]
- Kolb, D. Experiential Learning: Experience as the Source of Learning and Development; Prentice Hall: Englewood Cliffs, NJ, USA, 1984. [Google Scholar]
- Kolb, D.; Kolb, A. The Kolb Learning Style Inventory 4.0: Guide to Theory, Psychometrics, Research & Applications; Experience Based Learning Systems: Kaunakakai, HI, USA, 2013. [Google Scholar]
- Bybee, R.W.; Taylor, J.A.; Gardner, A.; Van Scotter, P.; Powell, J.C.; Westbrook, A.; Landes, N. The BSCS 5E Instructional Model: Origins and Effectiveness. BSCS 2006, 5, 88–98. [Google Scholar]
- Etkina, E.; Van Heuvelen, A.; Brookes, D.T.; Mills, D. Role of experiments in physics instruction—A process approach. Phys. Teach. 2002, 40, 351–355. [Google Scholar] [CrossRef]
- Etkina, E.; Van Heuvelen, A.; White-Brahmia, S.; Brookes, D.T.; Gentile, M.; Murthy, S.; Rosengrant, D.; Warren, A. Scientific abilities and their assessment. Phys Rev. Spec. Top. Phys. Edu. Res. 2006, 2, 020103. [Google Scholar] [CrossRef]
- Etkina, E.; Planinsic, G.; Van Heuvelen, A. College Explore and Apply, 2nd ed.; Pearson Education, Inc.: New York, NY, USA, 2019. [Google Scholar]
- Lewin, K. La Teoria, la Ricerca, L'Intervento; Il Mulino: Bologna, Italy, 2005. [Google Scholar]
- Satanassi, S.; Branchetti, L.; Fantini, P.; Casarotto, R.; Caramaschi, M.; Barelli, E.; Levrini, O. Exploring the boundaries in an interdisciplinary context through the Family Resemblance Approach: The Dialogue Between Physics and Mathematics. Sci. Educ. 2023, 32, 1287–1320. [Google Scholar] [CrossRef]
- Thogersen, J.; Simpson, A.; Hammond, G.; Janiszewski, L.; Guerry, E. Creating curriculum connections: A university museum object-based learning project. Educ. Inf. 2018, 34, 113–120. [Google Scholar] [CrossRef]
- Einstein, A.; Infeld, L. The Evolution of Physics: The Growth of Ideas from Early Concepts to Relativity and Quanta; Cambridge University Press: Cambridge, UK, 1938. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).