Abstract
Numerical analysis is a unique combination of mathematical and computing skills. It facilitates a deeper understanding of data analytics and machine learning software libraries, which are exploding in use and importance. However, it is a topic that continues to challenge students because it requires a confluence of conceptual, procedural, and computational skills and associated pedagogies. Therefore, it is valuable to identify effective pedagogies and tools to enhance and assess student numerical analysis skills. Despite the proliferation of mobile technology in postsecondary education, its role in the context of numerical analysis is largely unknown. This quasi-experimental pilot study used Practi, an educational mobile app designed to assess numerical analysis performance and promote both retrieval practice and deliberate practice, which have been shown to help improve performance and develop expertise. Participants were 32 undergraduate students enrolled in a second-year introductory Numerical Analysis course at a large North American university. They were prompted to use Practi to solve quizzes on a regular basis throughout the course, before and after each lecture, to promote deliberate practice and spaced retrieval. Results of a paired t-test analysis showed that Practi was able to detect improvement in student quiz performance after the lectures compared to before the lectures. Additionally, performance on the Practi quizzes after the lectures was positively associated with the overall course performance. This suggests that mobile apps supporting deliberate and retrieval practice can complement more traditional means of instruction and assessment of numerical analysis in postsecondary mathematics education.
1. Introduction
New trends in higher education have emerged due to workforce, cultural, and technological shifts in the wake of the COVID-19 pandemic [1]. These trends include data security and protection, hybrid and remote work options, data-informed decision-making, well-being and mental health, equitable and inclusive environments, digital transformation and institutional resilience, and hybrid and online learning. Thus, members of the campus community are expected more than ever to be able to connect from anywhere, anytime, using any device [1].
Smartphones and tablets have increasingly become ubiquitous in learning environments. In 2014, a report sampling 75,306 undergraduate students from 213 higher education institutions across 45 U.S. states and 15 countries, including Canada, found that 86% of undergraduate students owned a smartphone and 47% owned a tablet [2]. Similarly, in 2015, a Pearson survey of U.S. college student mobile device use found that 85% of college students owned a smartphone and that 52% owned a tablet [3]. In 2017, a study sampling 43,559 undergraduate students and 13,451 faculty members from 157 institutions across seven countries, including the U.S. and Canada, found that over 97% of undergraduate students owned a smartphone, whereas 93% of faculty members owned a smartphone [4]. In 2018, the results of a multiyear study (i.e., 2012–2016) with University of Central Florida students highlighted a need for enhanced mobile integration strategies in the classroom and institutions [5]. By 2018, nearly every student (98%) and faculty member (96%) sampled from several countries, including U.S. and Canada, had access to a smartphone or a tablet [6]. Students use these devices for most of their courses and view them as important to their academic success [6]. These percentages of mobile technology use have increased exponentially [7], especially since 2014. By 2020, more than 93% of the world’s population had access to at least a 3G mobile network [8]. Moreover, many studies have highlighted the effectiveness of mobile learning (m-learning) in higher education [9,10]. Responses from 2668 European and U.S. university students and staff revealed that students with a great university experience reported having easy online access to data and resources, services available via mobile, positive digital experiences, and personalized learning experiences [11]. By 2023, one of the key technologies and practices advanced in response to several social, technological, economic, environmental, and political trends in higher education was supporting student connection and access to readily available technologies [12]. Recently, in the general population, 90% of Americans [13] and 84% of Canadians [14] reported owning a smartphone.
These findings suggest that mobile technologies constitute important opportunities for education. There is a tremendous potential for both students and instructors to integrate mobile devices (e.g., smartphones, tablets) into their learning environments because device ownership is prevalent in postsecondary education [15,16], especially as students and instructors alike already use mobile technology in their daily activities, including their learning and teaching experiences. Mobile learning is a good way for students to learn and become proficient in various subject areas because mobile devices have improved availability, convenience, and accessibility, being readily integrated into students’ lives. Moreover, students have come to expect learning experiences to be mobile-accessible [17]. It was found that 79% of U.S. students access online courses through a mobile device [18]. Since the COVID-19 pandemic, this percentage has continued to increase. Importantly, mobile devices have the potential to foster innovation and improve access to digital materials and tailored learning and assessment [19] in the postdigital age [20,21]. Moreover, targeted training resources have positively impacted students’ mobile learning practices [15]. A meta-analysis of the effects of integrated mobile devices in teaching and learning analyzed 110 journal articles published during 1993 and 2013 and found a moderate mean effect size of 0.52 for the application of mobile devices to education [22]. Another meta-analysis examined 22 research studies published between 2010 and 2020 to compare mobile to traditional learning of mathematics in K–16, and it revealed that mobile learning yielded a medium-level positive effect (Hedges’ g = 0.48; p < 0.001) on student mathematics achievement, with content area being a significant moderator [23]. More recently, a meta-analysis examining 5575 participants across 70 studies revealed that pedagogical approaches for mobile learning had a large effect on student learning (Hedges’ g = 0.93, p < 0.001) but that the effect was moderated by the field of education, the level of education, the learning setting, the sample size, and the mobile device [24].
2. Challenges
Although mobile technology is ubiquitous in postsecondary education, more research is needed to determine its potential in supporting or assessing numerical analysis. For example, several systematic reviews emphasized that most studies tended to focus on the technological rather than the pedagogical aspects of mobile learning, with much of the mobile learning research not being grounded in pedagogical theory [25,26,27]. Thus, mobile learning studies have largely been concerned with trends, advantages and disadvantages, as well as affordances of mobile learning in teacher education [26]. In particular, a systematic review of mobile learning pedagogy recommended researchers to focus on the pedagogy of subjects traditionally taught in formal settings such as science, given the importance of such subjects and the paucity of investigations of mobile technology in these settings [26]. In general, findings revealed that mobile technologies tend to be underutilized in mathematics and science education at both secondary and postsecondary levels [25,26].
Also, conventional classroom teaching methods of numerical analysis that use numerical solutions have not been sufficient to help students identify numerical solutions [28,29]. More recently, computational tools have become pervasive in higher education and researchers have started to take note. For instance, an experimental study employed GPT and Colab to enable 52 undergraduate students to explore numerical solutions while solving difference equations and measured their self-efficacy in finding numerical solutions [29]. They found that students displayed high levels of self-efficacy after using these learning tools.
3. Practi
One way to leverage student learning with technology is to support students in developing deliberate practice and retrieval practice behaviors by integrating such behaviors (e.g., periodic self-quizzing) into technology-rich learning environments. For example, a math game was used to support middle-school students’ deliberate practice [30]. Also, voluntary e-learning exercises were designed to support university students’ retrieval practice to learn statistics [31]. These behaviors leverage the retrieval practice (or testing) effect, which is a phenomenon studied in cognitive psychology, whereby taking a memory test has a dual role: it assesses what the learner knows, and it also enhances later retention [32,33]. Thus, the proposed research leverages the ubiquity of mobile devices in university students’ lives, at school, at home, and on the road. The present study employs Practi [34], a domain-independent educational mobile platform that draws on deliberate practice and retrieval practice (e.g., self-quizzing) for acquisition of knowledge-based expertise through regularly solving quizzes. Practi applies a competency-based active learning approach to content delivery. This mobile application provides immediate feedback to students, an essential ingredient in deliberate practice for acquiring expertise, and helps instructors identify student misconceptions.
4. Study Objectives
The overarching goal of this research was to assess the usability and effectiveness of the Practi mobile app in detecting changes in undergraduate student numerical analysis performance and to ascertain student metacognitive assessments of Practi. Thus, the following research questions were posed:
- Was there a difference in student numerical analysis performance between Practi pre-lecture and post-lecture quizzes?
- Were Practi quizzes associated with student achievement in the course?
- Were student metacognitive assessments associated with the Practi quiz performance?
5. Theoretical Framework
This study draws on the deliberate practice theoretical framework [35,36] and on temporally spaced retrieval practice [37,38]. These theories are blended in this study with the aim of supporting students in their transition from routine to adaptive expertise [39], which will ultimately help students transfer their numerical analysis knowledge beyond the classroom.
6. Deliberate Practice
Deliberate practice is defined as “effortful activities designed to optimize improvement” [35]. It is considered to be crucial in improving performance and developing expertise as well as a catalyst that leads to the disparity in proficiency levels between novices and experts in many domains [40]. Deliberate practice posits that, to become an expert in a field, one needs to devote time and sustained intense effort to practice behaviors that improve performance, typically for a minimum of ten years [35]. A crucial aspect of deliberate practice is the presence of feedback that is assigned immediately by an expert, such as an instructor [41]. Thus, developing tools that scale up to a large number of students to provide individualized feedback is an important step in supporting deliberate practice. Reimann and Markauskaite [42] have highlighted the importance of blending cognitive with sociocultural and situated theoretical perspectives to better understand the development of expert competence and performance.
7. Retrieval Practice
Retrieval practice consists of attempting to recall facts, concepts, or events from memory through active retrieval or testing [37]. Empirical research revealed that practicing retrieval makes learning stick far better than re-exposure to the original material [32,33,37,43]. Specifically, when testing is temporally spaced, it tends to be a more effective learning strategy than review by re-reading [37]. Retrieving information from memory via regular testing increases the probability of that information being remembered [44]. For instance, even a simple quiz administered after attending a lecture or reading a piece of text can generate better learning and retention than revisiting the text or reviewing the lecture notes [37]. Additionally, one tends to build better mastery when using testing as a tool to identify and bring up areas of weakness [37]. It was found that most students do not quiz themselves, thus, they tend to overestimate their mastery of the class material [37]. Collectively, these phenomena are known in the field of cognitive psychology as the retrieval practice (or testing) effect. Compared to other approaches, it was found that retrieval practice outperformed elaborative studying with concept mapping [45].
8. Literature Review
Several researchers have explored the effect of teaching the behaviors and strategies of expert mathematicians to students as a way of supporting their mathematical development and provided problem-solving frameworks to better understand these processes [46,47]. Also, the importance of practice for learning has been emphasized through several meta-analyses that revealed a large 0.49 effect size [48]. It is important to note that the structure of practice rather than the repetition of practice is essential for performance improvement in mathematics [49]. Specifically, deliberate practice, with its three main characteristics (challenging, varied, and regular), was found to be the most effective, with a focus on spaced-out deliberate practice [48]. The mathematics education literature has also positioned the act of teaching as deliberate practice with the goal of ultimately improving students’ mathematics performance [50].
8.1. K–12 Education
In the context of K–12 education, a mixed-methods research approach was proposed in which mathematics teachers modeled expert knowledge, skills, and strategies drawing on a relational reasoning paradigm to support their Grade 2 students’ problem solving [51]. Their experimental study revealed that students who were taught additive word problem solving through relational thinking and modeling of expert strategies (n = 216) significantly outperformed their control group peers who received traditional instruction and used personal strategies in problem solving (n = 196). A naturalistic experimental case study compared middle-school students who demonstrated the characteristics of the Zen concept of beginner’s mind (treatment condition) to those who did not (control condition) when solving the same mathematical task [52]. They found that the modeling of beginner’s mind behaviors, which involves a deeper exploration of the task and a more open attitude towards considering several different solutions, may support the development of habits that endorse a deeper understanding of the underlying problem. Another study sampled 214 Grade 6 Finnish students to investigate whether playing Number Navigation Game, a game that taught complex arithmetic relations, could promote deliberate practice [30]. Their findings showed that students who engaged more in deliberate practice behaviors during the game consistently improved their performance on the more challenging aspects of the game.
8.2. Postsecondary Education
In the context of postsecondary education, researchers explored the effect of instructors modeling expert mathematicians’ flexible procedural knowledge and skills in teaching several subjects (e.g., calculus, statistics) and whether such skills could be taught. For example, an experimental research study compared undergraduate students who were given a list of functions to differentiate (control condition) to their peers who were given the same task but asked to use alternative methods and to compare the two resulting solutions (treatment condition) when finding the derivatives of functions [53]. They found that students in the treatment condition spontaneously used more methods, which also resembled expert solutions more often, to complete the task than the students in the control condition, showing that expert skills and strategies could be taught. A different study provided 67 German social science university students with weekly e-learning exercises to supplement the face-to-face lectures in a statistics class [31]. The e-learning exercises promoted retrieval practice and spacing, providing corrective feedback. The study findings revealed that working on the e-learning exercises increased students’ final exam performance and that students who spaced out the exercises throughout the semester gained additional benefits.
9. Methods
9.1. Participants
This study sampled all n = 32 undergraduate students enrolled in an introductory second-year Numerical Analysis course at a large, research-intensive North American university. Table 1 presents the participant demographic information.

Table 1.
Demographic information of the participants.
The course introduces students to numerical analysis and scientific computing using Matlab. Course topics include floating-point arithmetic, solutions of linear and non-linear equations, interpolation, numerical integration, and solutions of ordinary differential equations. The prerequisites of this class were two first-year mathematics courses, Calculus I and Calculus II. The course also provided a weekly 50 min laboratory. The final grade in the class was composed of marks on the following assignments: class contribution (10%), guided notes (5%), post-lecture quizzes (5%), 5 assignments due every 2–3 weeks (20%), 2 in-class midterm exams (20%), and a final exam (40%); further details are provided below.
9.2. Research Design
The study employed a quasi-experimental design as depicted in Figure 1 to compare numerical analysis performance captured by Practi quizzes before and after each lecture. This repeated-measures design is also appropriate to detect possible effects for small sample sizes, where the same participants are measured twice. Power calculation using the pwr.t.test R package [54] to compute the sample size needed for a power of 0.80, and the estimation for a large effect size (Cohen’s d = 1 for a paired-samples t-test with alpha = 0.05 and a two-sided hypothesis) yielded n = 10 pairs. In contrast, we employ 26 pairs in our analysis.
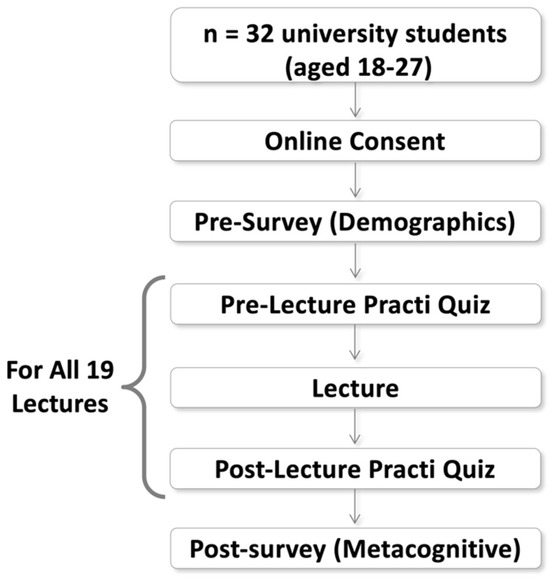
Figure 1.
Study design.
9.3. Procedure
At the beginning of the term, students completed an online consent form followed by an online pre-survey of demographic information items, according to the University’s ethics protocol Pro00068349. Lectures were 1 h and 20 min long and were delivered twice a week in a flipped classroom format, with the first 20–30 min spent taking up guided notes (fill-in-the-blank style notes on the lecture material presented in video format) and the remaining time spent on problem solving in small groups. Every week, before and after each lecture, students were prompted to solve quizzes via the Practi mobile application, created by Mathtoons Media Inc., for the duration of the term to promote spaced retrieval and enhance long-term knowledge retention, which is important in acquiring numerical analysis knowledge. Students were instructed to download the Practi app on their mobile devices and use it to practice their numerical analysis knowledge throughout the term. Thus, during the term, students were prompted to solve 19 pre-lecture quizzes to test student knowledge before exposure to a chapter in the course syllabus through the lecture and 19 post-lecture quizzes to test their knowledge after exposure to that chapter. This procedure aimed to encourage students to space out their practice throughout the term rather than cram at the end of the term. The pre-lecture and post-lecture quizzes were identical. Each quiz consisted of 10–15 multiple-choice items. Not all students completed the pre- and post-lecture quizzes. Participant averages of the Practi pre-lecture quiz and post-lecture quiz scores were computed across the 19 items, yielding the measures Practi Pre-Lecture Quiz and Practi Post-Lecture Quiz.
The Class Contribution mark took into account student participation in, but not correctness of, the pre-lecture quizzes, class attendance, and active involvement in the problem-solving groups.
At the end of the term, participants completed a post-survey regarding their metacognitive assessment of their Practi experience. The post-survey included two metacognitive measures: Satisfaction with as well as Relevance and effectiveness of Practi for learning, each measured on a 5-point Likert scale.
Finally, the Midterm 1, Midterm 2, and Final Exam are measures of student numerical analysis performance on the first midterm, second midterm, and final exam, respectively, without using Practi.
Of the 32 students who agreed to participate in this study, 31 completed the pre-survey providing demographic information, 24 completed the post-survey, and 26 completed the Practi quizzes. Specifically, 23 participants completed both the pre- and post-surveys, while 22 participants completed the pre-survey, post-survey, and the Practi quizzes.
10. The Measurement Instruments
The pre-survey employed in the present study included demographic information questions (see Table 1). The post-survey included two 5-point Likert scale questions on the relevance and effectiveness of Practi for learning as well as the satisfaction with Practi (see Table 2).

Table 2.
Description of the post-survey items related to Practi.
This study also collected quiz scores via the Practi mobile application that supports the development of courses on several subjects.
The pre-lecture quizzes provided immediate feedback in the form of verification or knowledge of results (KR) feedback (i.e., participants were told whether their choice was correct or not) as well as hints (upon request) of increased specificity, which acted as elaboration feedback [55,56]. Appendix A provides several examples of Practi items.
The post-lecture quizzes provided knowledge of correct response (KCR) feedback (i.e., participants were told which was the correct response if they made a mistake). Only the first attempt of each pre-/post-lecture quiz was considered in the current analyses.
11. Statistical Analyses
All analyses were conducted in the R programming language version 4.3.3 [57].
11.1. Descriptive Statistics and Bivariate Correlations
Participant averages of the Practi pre-lecture quiz and post-lecture quiz scores were computed. Bivariate Pearson correlations were conducted between the Practi quizzes and the course achievement measures. Then, bivariate Spearman correlations using the built-in cor R function [57] were performed to ascertain the associations between the non-normally distributed post-survey items and the rest of the measures.
11.2. Test of Outcome Differences
A paired-samples t-test was performed in R [57] between the pre- and post-lecture quiz performance, as assessed using the Practi mobile app, to examine whether participants improved their quiz performance during the term because these variables were not normally distributed.
12. Results
12.1. Descriptive Statistics
Table 3 shows the participant average Practi quiz scores before and after each of the 19 lectures covered in the course together with their standard deviations. It also shows these statistics for the course performance measures: the scores on the two midterms (Midterm 1 and Midterm 2), Final Exam, Class Contribution, Final Grade (excluding the post-lecture Practi quiz scores, to obtain a clearer understanding of its relationship with Practi), and Final Grade Including the Post-Lecture Practi Quizzes (i.e., the final grade in the course). The Shapiro–Wilk normality tests were not significant for the Practi Pre-Lecture Quiz (W = 0.98, p = 0.85) and for the Practi Post-Lecture Quiz (W = 0.98, p = 0.93). Thus, both variables are normally distributed. The Bartlett’s test of homogeneity of variances was not significant: K2 = 1.136, df = 1, p = 0.29; thus, we cannot reject the null hypothesis of homogeneity of variances. Therefore, we can conduct a parametric paired t-test to compare the Practi quiz performance before and after the lectures.

Table 3.
Descriptive statistics and correlations between the variables of interest (Practi quiz scores and the achievement variables).
The findings suggest that student performance on the quizzes improved from the pre-lecture to the post-lecture quizzes, with the central portion of the pre-lecture quiz data as measured by the interquartile range (IQR) being slightly more spread out than the central portion of the post-lecture quiz data. Concomitantly, the performance on the exams slightly decreased from the first midterm to the final exam, likely because of the increased difficulty of these subsequent tests.
Table 4 shows the descriptive statistics of the post-survey items. A higher item response average indicates a higher level of endorsement for that item statement. Overall, students tended to report low satisfaction and relevance regarding Practi.

Table 4.
Correlations of the post-survey with the Practi quizzes and course achievement (*** p < 0.001).
12.2. Was There a Difference in Student Numerical Analysis Performance between Practi Pre-Lecture and Post-Lecture Quizzes?
Participant performance scores on the Practi pre-lecture and post-lecture quizzes were compared using a paired-samples t-test because both the pre-lecture and post-lecture quizzes were normally distributed. The findings indicate that participants improved their mean Practi quiz performance significantly after the lecture compared to before the lecture: t(25) = 5.19, p < 0.001, mean difference = 0.16, 95% CI [0.10, 0.23]. A large effect size was detected: Cohen’s d = 0.84, 95% CI [0.26, 1.41]. Figure 2 shows the Practi pre- and post-lecture quiz performance mean values.
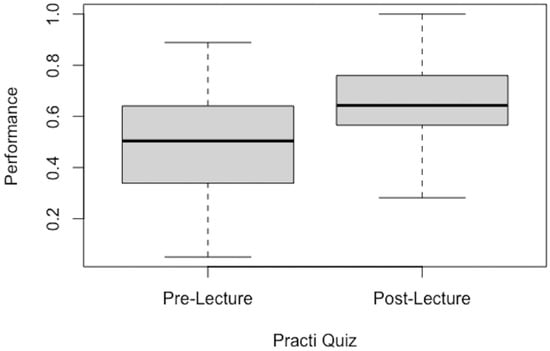
Figure 2.
The median pre- and post-lecture quiz performance.
12.3. Were Practi Quizzes Associated with Student Achievement in the Course?
The results of the Pearson correlation analyses among all the normally distributed variables are shown in Table 3. Because the variable Class Contribution was not normally distributed, its Spearman correlation with the rest of the variables was conducted instead and shown in Table 3. Most relationships were significant, with the exception of the association between the pre-lecture quizzes and the second midterm (p = 0.22), as well as the association between the post-lecture quizzes and the final exam, which was marginally significant (p = 0.059). We also employed a Spearman correlation to assess the non-linear association between the post-lecture Practi quizzes and the final exam, and we found a significant strong association rho = 0.42, p < 0.04.
12.4. Were Student Metacognitive Assessments Associated with the Practi Quiz Performance?
Table 4 shows the descriptive statistics for the post-survey responses related to Practi. Analyses to examine the associations between the Practi quiz scores and metacognitive assessments were conducted. A Spearman correlation analysis revealed no significant associations of Satisfaction and Relevance with the Practi pre- and post-lecture quizzes, as shown in Table 4. However, Satisfaction and Relevance were strongly and positively associated with each other.
13. Discussion
13.1. Was There a Difference in Student Numerical Analysis Performance between Practi Pre-Lecture and Post-Lecture Quizzes?
The results indicate that students improved their numerical analysis performance with a large effect, as measured by the Practi mobile app during the term before and after each chapter of the course. There can be many reasons behind this result. It is possible that the performance improvement was due to the Practi use alongside the more traditional face-to-face lectures, guided notes, assignments, midterm exams, weekly labs, or a combination of these aspects. Students may have proactively accessed the other materials provided as part of the course before each lecture. However, the retrieval practice effect may have prompted this behavior. Thus, another possibility is that periodic testing could facilitate concept understanding because it offers opportunities to study the material, so this result could underscore benefits accruing to retrieval practice. The act of retrieval may prompt learners to restudy the material and distribute their study over a longer period of time rather than engaging in massed practice (i.e., cramming) at the end of an assessment unit. Spacing out the quizzes relatively equally during the course, rather than at the end of the course, seems to be associated with improvement on the quiz scores. According to retrieval practice theory, retrieval must be repeated in temporally spaced-out sessions to be most effective because the act of recall requires some cognitive effort to differ from mere recitation [37]. This result is concordant with other research showing that multiple sessions of retrieval practice seemed to work better than a single session, especially when spacing out the test sessions. It was found that learners who temporally spread out their study of a topic and return to it periodically also remember it better [37]. This is likely because when learners space out practice and forget some of the material, retrieval becomes more difficult and, although this retrieval act feels less productive, the effort of retrieval produces long-lasting learning and tends to be easier to transfer to a new situation at a later point [37].
The effect of the pre-lecture quizzes could also be beneficial to student quiz performance after the lecture because research shows that attempts to solve a problem before being taught the solution tend to lead to better learning, especially when the learner makes mistakes [37]. In the present study, it may be that the retrieval effect is at work: perhaps the act of retrieval makes it easier to remember that material again later and thus improve performance. Additionally, frequent low-stakes testing such as that offered by the pre-lecture quizzes that were not part of the final grade may help decrease test anxiety and stress among learners because students become familiar with the format of the quiz. The post-lecture quizzes were equally spread across the term (instead of massed at the end of the term) and were only worth 5% of the final grade, likely contributing to diminishing the stress associated with this assignment. For instance, an experimental study showed that retrieval practice (i.e., taking tests) strengthens memory against the negative effects of acute stress relative to restudying [58]. Another advantage of using Practi is that, in general, mobile apps can also be used offline (e.g., on the bus or subway as part of the daily commute), fitting better into students’ daily lives and extending their learning space.
This result also echoes similar findings in the related literature. For instance, a meta-analysis of the effects of integrated mobile devices in teaching and learning found a moderate mean effect size of 0.52 for the application of mobile devices to education [22]. Overall, the results are in concordance with studies showing that spaced retrieval of learned information through assessments improves information retention in many domains of postsecondary education, including mathematics [59,60], science [32], biology [61], and physiology [62]. Similar to the present study, Schwerter and Brahm [31] found that voluntarily working on e-learning statistics exercises that promoted retrieval practice improved students’ learning performance and that students who also spaced out their practice throughout the semester gained additional benefits.
Given that the present study is quasi-experimental, future experimental studies need to be conducted to isolate the role of Practi in student quiz performance improvement and to explore learner motivation to use the guided notes, lecture notes, videos, and other materials available in the course before each quiz. In the present study, the course instructor provided anecdotal evidence that all students who finished the Practi quizzes also passed the course. In contrast, in past traditional course offerings that did not use Practi, some students did not pass the course, even after completing all the requirements of the course. Future studies may investigate whether students learn more in a traditional versus a mobile environment, so other researchers and instructors may find ways of integrating tools such as Practi into their research and practice to improve course completion rates and measure student performance. Meanwhile, whether Practi’s guided deliberate practice and retrieval practice before and after each lecture throughout the term is associated or not with more frequency of such self-regulatory behaviors and, hence, with better performance, Practi was able to detect changes in numerical analysis performance from the beginning to the end of the semester. Thus, Practi could be used as an alternative assessment of numerical analysis.
Considering the current findings and those of other researchers [31], we recommend spacing out self-quizzes over an entire semester to reap and maximize the benefits of deliberate practice and retrieval practice.
13.2. Were Practi Quizzes Associated with Student Achievement in the Course?
The post-lecture Practi quizzes were positively and significantly associated with the course measures of achievement: the two midterms and the final exam. Also, the course achievement measures were all strongly and positively correlated with each other, indicating the internal consistency of the course measures. Taken together, these results indicate that the Practi quizzes measure important numerical analysis knowledge that is evaluated by the two midterms and the final exam, which are measures external to the mobile app environment. The marginally significant Pearson correlation between the post-lecture quizzes and the final exam may be due to either the small sample size or the non-linear nature of the relationship between the post-lecture quizzes and the final exam. More data will be collected in future studies to clarify this. In the meantime, this pilot study brings initial evidence to support the external validity of Practi in measuring numerical analysis knowledge. Also, the power of the paired-samples t-test with an effect size of Cohen’s d = 1, alpha = 0.05, two-sided hypothesis, and n = 26 in this study is 0.98.
Thus, the results show that the post-lecture Practi quizzes are able to detect similar information about student performance as course midterms and final exams that may weigh more with respect to the final grade, take more time and effort to administer, produce more anxiety, and require a fixed day, time, and place for the examination. Thus, one recommendation based on these preliminary results is to embed tools like Practi as a frequent, shorter activity in a numerical analysis class for university students with the aim to replace more traditional assessments. Tools such as Practi can prompt students to engage in deliberate practice and to space out their retrieval practice.
13.3. Were Student Metacognitive Assessments Associated with the Practi Quiz Performance?
Finally, metacognitive measures (Satisfaction and Relevance) provided results suggesting that participants were not aware of the beneficial effects of testing with Practi. The results also suggest no association between the metacognitive student assessments and their course achievement measures. This is not surprising, and it is echoed in the retrieval practice literature. Specifically, surveys showed that students prefer to use the re-read strategy when studying and are largely unaware of the effectiveness of retrieval practice to improve their performance [63,64,65]. Students may perceive self-testing as less productive than restudying the material and also less appealing because it elicits more effort than re-reading. More research is needed to ascertain whether mobile learning could help increase engagement and enrollment in subjects such as mathematics and science.
One of the reasons for these results could be that students may have been negatively influenced by Practi’s occasional technical glitches (this was the first time that the Practi mobile app was used in a numerical analysis course), by the fact that the pre-lecture quizzes were not part of the course grade (i.e., they were optional), or by the small sample size. More data need to be collected to better understand these results.
Regarding relevance, Practi was introduced at the beginning of the class to the students as a way to promote self-regulated learning behaviors (e.g., self-assessment) and to provide more engaging formative (quizzes assigned before each lecture that are not part of the final grade) and summative (quizzes assigned after each lecture that are part of the final grade) assessments. Given that Practi post-lecture quizzes were positively associated with a higher performance on other class metrics, future studies will provide more details to inform students about this relationship as a way to highlight the relevance of Practi for the course in prompting them to space out their deliberate practice and in detecting their potential improvement of numerical analysis knowledge. Thus, one recommendation stemming from this study is to provide students with more information about educational theories and how they inform the learning of numerical analysis to increase student engagement in deliberate practice as well as in retrieval and spaced practice.
Finally, future work will examine the long-term effect of using Practi because the related literature shows long-term benefits of retrieval practice in middle-school social studies and science classrooms [66,67]. Even small interventions that taught students how to perform repeated retrieval practice over restudying showed positive long-term effects in both the use or retrieval practice and performance [68]. More research is warranted into the best ways to deliver materials and assess performance so students learn complex concepts more deeply. Future studies may also examine whether students are able to transfer their problem-solving skills and attitudes from the mobile app environment to the classroom and beyond. A limitation of this study is that the analyses considered only the first attempt for each of the pre-lecture and the post-lecture quizzes. Future studies will examine the relationship between the overall frequency of Practi use and the variables used in this study.
14. Scholarly Significance
14.1. Theoretical Significance
This study highlights the use of testing as a tool for learning in a naturalistic setting: an actual university classroom. Principles and practical strategies like these may be implemented easily in many learning environments [69]. The current findings can be used to improve research into better ways of delivering instruction and conducting assessment in online environments of mathematics courses because this study brings ecological validity evidence from a real classroom setting. Numerical analysis is a subject area at the intersection of mathematics and computing science. Thus, it is relevant for students in science, technology, engineering, and mathematics (STEM), and it opens up numerous other learning opportunities in more specialized areas such as machine learning and data analytics.
Another advantage of this mobile learning approach is that retrieval practice does not have to be initiated by the instructor. Students can practice retrieval in both formal and informal learning environments. The Practi mobile app could be used to reach a wider population of postsecondary students and to promote deliberate practice and retrieval practice in learning numerical analysis concepts, both inside and outside the classroom. Generally, through deliberate practice and temporally spaced retrieval practice, learners can remember concepts better and use them more effectively. Practice at retrieving numerical analysis knowledge from memory has the potential to help learners solidify the material and facilitate long-term retention, which are necessary steps in applying knowledge creatively to solve problems and in developing expertise. For instance, expert problem solvers often apply problem-solving strategies that are domain-specific, so extensive knowledge of the problem domain is crucial in efficient problem solving and deep thinking [70], especially in the field of mathematics [71]. Moreover, one of the mechanisms through which the transfer of specific skills and knowledge takes place is low-road transfer [72,73], which relies on the extensive, deliberate, and necessarily varied practice of a skill until it almost becomes automatic. The teaching of thinking skills requires solid factual knowledge in order to promote problem solving and support transfer [71].
In addition to the factors mentioned above, performance gains from the pre-lecture quiz to the post-lecture quiz may also be due to students’ ability to learn from the feedback provided by the Practi app. Additionally, heeding feedback is an important indication of student learning potential because it provides a glimpse into how students go about learning on their own. It is possible that students learn during the pre-lecture quizzes via the feedback and hints; thus, the Practi assessment has the potential to both measure and improve learning along with measuring student learning potential. In essence, the processes involved in retrieving learning from memory prompted by repeated quizzing have the benefits of both helping learners identify their misconceptions and, concomitantly, giving them an opportunity to improve in those areas and consolidate their memory by making that information easily retrievable at a later point. More research is needed to tease out the effect of Practi and, more generally, deliberate practice and retrieval practice, in the learning of numerical analysis concepts.
14.2. Practical and Methodological Significance
This study emphasizes the potential of mobile teaching and learning to afford innovative paths to access knowledge and to learn, without overlooking the effort it may take the instructor to develop good content for such platforms. The present study aligns with the findings of a report that emphasized the need to provide students and instructors with technological, logistical, and pedagogical support before mobile apps are meaningfully integrated in their learning environments, in both formal and informal settings [15]. With a mobile app such as Practi, instructors may influence their student retrieval practice and support them in determining when and how much they should practice to improve their performance, especially in domains such as mathematics, where long-term retention of foundational skills and knowledge is integral to learning. The practice of testing as a generator of feedback to instructors and students may help guide subsequent classroom practices. Given the expansion of mobile learning to smartwatches or augmented and virtual reality headsets, this approach seems a promising prospect for higher education.
Moreover, the final exam in the course consisted of selected-response items. This is a format with which students are familiarized by solving Practi quizzes throughout the term. Thus, the present study is aligned with the principles of transfer-appropriate processing, which emphasize selecting practice methods for knowledge acquisition that are consistent with the means of testing that knowledge [74].
15. Conclusions
This study piloted an innovative approach to use Practi, a mobile app designed to facilitate both the learning and assessment of undergraduate student knowledge, in a numerical analysis course. Findings show that students improved their Practi quiz performance significantly after the lectures compared to their quiz performance before the lectures. Moreover, performance on Practi post-lecture quizzes was positively associated with all the measures of course performance, in particular the final grade, thus supporting the external validity of this mobile app in the context of numerical analysis. Additional experimental studies are needed to further explore the potential of mobile apps such as Practi in conjunction with more traditional means of instruction to optimize knowledge acquisition, retention, and assessment.
Author Contributions
Conceptualization, M.C., K.G. and R.J.S.; methodology, M.C., K.G. and R.J.S.; Practi software, K.G.; validation, M.C., K.G. and R.J.S.; formal analysis, M.C.; investigation, M.C., K.G. and R.J.S.; resources, K.G. and R.J.S.; data curation, M.C., K.G. and R.J.S.; writing—original draft preparation, M.C.; writing—review and editing, M.C., K.G. and R.J.S.; visualization, M.C.; funding, M.C., K.G. and R.J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the University of Alberta Kule Institute for Advanced Study Dialogue Grant, Social Sciences and Humanities Research Council of Canada—Insight Development Grant (SSHRC IDG) RES0062310, the Social Sciences and Humanities Research Council of Canada—Insight Grant (SSHRC IG) RES0048110, Mitacs, the Natural Sciences and Engineering Research Council Discovery Grant (NSERC DG) (RES0043209, M.C.; RGPN-2020-04467, R.J.S.), and the Natural Sciences and Engineering Research Council Engage Grant.
Institutional Review Board Statement
This study has secured ethics approval with protocol Pro00068349 from the Research Ethics Board 2 of the University of Alberta, Edmonton, Alberta, Canada and University of Saskatchewan, Saskatoon, Saskatchewan, Canada. The study was presented to the participants by the research team at the beginning of the term and students subsequently completed an online consent form prior to participating in this study.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data set presented in this study is not available due to its small size and risk of de-anonymization.
Acknowledgments
We are grateful to the students who participated in this study, to the editor and anonymous reviewers, and to the funding agencies that supported this work.
Conflicts of Interest
Although Kristin Garn is the founder of Mathtoons Media Inc., the company that created the Practi math app used in this study, this company no longer exists. The other authors have no financial ties or other business arrangements with the Practi product featured in the manuscript.
Appendix A
Appendix A.1. Which of the following Is the Triangle Inequality?
- Hint 1:
- Hint 2: In a triangle, the sum of any two sides is greater than the other side.
Appendix A.2. The Thomas Algorithm Is Equivalent to
- An algorithm that Thomas wrote.
- decomposition of full matrices.
- decomposition of tridiagonal matrices.
- None of these options.
- Hint 1: The Thomas algorithm is applied to a special case of banded systems.
- Hint 2: Remember that the Thomas algorithm is applied to tridiagonal systems.
Appendix A.3. What Is the Standard Form of Gaussian Elimination with Partial Pivoting?
- None of these options.
- Hint 1: Recall that factorization is an interpretation of Gaussian elimination.
- Hint 2: Remember that sometimes you have to reorder the equations to be able to factor them in terms of upper- and lower-triangular matrices.
Appendix A.4. What Are the Two Famous Measures of the Quality of the Approximate Solution?
- Residual and error.
- Residue and efficacy.
- Absolute and relative conditioning.
- None of these options.
- Hint 1: Gauss elimination with partial pivoting guarantees this to be small but does not necessarily directly correlate to accuracy.
- Hint 2: Do not forget that the residual is a measure of the self-consistency of an approximate solution.
Appendix A.5. The Process of Gaussian Elimination for a Specific System Ends Up with the Augmented Matrix
This means that our system has:
- No solutions.
- Complex solutions.
- Exactly one solution.
- An infinite number of solutions.
- Hint 1: Look at the last row.
- Hint 2: Do not forget to first consider the last row and write in the form of an equation. Does your equation make sense?
Appendix A.6. When Solving a Linear System Numerically, a Small Residual Implies
- A small error.
- The matrix has a small condition number.
- The numerical solution is close to the true solution.
- None of these options.
- Hint 1: Small residual does not imply small error.
- Hint 2: Small residual is dependent on the size of the matrix, its elements, and the elements in our solution. If any of these are “large”, the residual will not be “small” in an absolute sense.
Appendix A.7. What Is the Leading Coefficient of ?
- −2
- 0
- 1
- 5
- Hint 1: The leading coefficient is on the term that determines the degree of the polynomial.
- Hint 2: Remember that the leading coefficient is the coefficient of the highest degree.
Appendix A.8. If We Want to Determine the Smallest Positive Root of Using IQI, Which of the following Is Likely to Work Best as Initialization?
- ,
- Hint 1: Recall IQI is short for inverse quadratic interpolation.
- Hint 2: Recall inverse quadratic interpolation requires three points to compute the next iterate.
Appendix A.9. If , the Fixed Point of Which Function Is not the Solution to the Equation ?
- Hint 1: Assume that is a fixed point of the function if and only if .
- Hint 2: Start with and rearrange to get zero on one side. The other side leaves you with
Appendix A.10. What Is for ?
- Hint 1:
- Hint 2: Remember that you need to compute the derivatives of each function with respect to each variable.
References
- Muscanell, N. Higher Education Trend Watch; EDUCAUSE: Boulder, CO, USA, 2024. [Google Scholar]
- Dahlstrom, E.; Bichsel, J. ECAR Study of Undergraduate Students and Information Technology; Research Report; EDUCAUSE Center for Analysis and Research: Louisville, CO, USA, 2014; Research Report; Available online: http://www.educause.edu/ecar (accessed on 10 April 2024).
- Poll, H. Pearson Student Mobile Device Survey; Pearson: London, UK, 2015. [Google Scholar]
- Pomerantz, J.; Brooks, D.C. ECAR Study of Undergraduate Students and Information Technology; Research Report; EDUCAUSE Center for Analysis and Research: Louisville, CO, USA, 2017. [Google Scholar]
- Chen, B.; Bauer, S.; Salter, A.; Bennett, L.; Seilhamer, R. Changing Mobile Learning Practices: A Multiyear Study 2012–2016. 2018. Available online: https://er.educause.edu/articles/2018/4/changing-mobile-learning-practices-a-multiyear-study-2012-2016#fn2 (accessed on 10 April 2024).
- Grajek, S.; Grama, J.L. Higher Education’s 2018 Trend Watch and Top 10 Strategic Technologies; Research Report; EDUCAUSE Center for Analysis and Research: Louisville, CO, USA, 2018. [Google Scholar]
- Qureshi, M.I.; Khan, N.; Hassan Gillani, S.M.A.; Raza, H. A systematic review of past decade of mobile learning: What we learned and where to go. Int. J. Interact. Mob. Technol. 2020, 14, 67–81. [Google Scholar] [CrossRef]
- ITU. International Telecommunication Union. Measuring Digital Development: Facts and Figures. 2020. Available online: https://www.itu.int/en/ITU-D/Statistics/Documents/facts/FactsFigures2020.pdf (accessed on 10 April 2024).
- Crompton, H.; Burke, D. Mobile learning and pedagogical opportunities: A configurative systematic review of PreK-12 research using the SAMR framework. Comput. Educ. 2020, 156, 103945. [Google Scholar] [CrossRef]
- El-Sofany, H.F.; El-Haggar, N. The effectiveness of using mobile learning techniques to improve learning outcomes in higher education. Int. J. Interact. Mob. Technol. 2020, 14, 4–18. [Google Scholar] [CrossRef]
- Salesforce. Connected Student Report: Insights into Global Higher Education Trends from over 2600 Students and Staff, 3rd ed.; Salesforce, Inc.: San Francisco, CA, USA, 2022. [Google Scholar]
- Pelletier, K.; Robert, J.; Arbino, N.; Muscanell, N.; McCormack, M.; Reeves, J.; McDonald, B.; Grajek, S. 2023 EDUCAUSE Horizon Report: Holistic Student Experience Edition; Research Report; EDUCAUSE Center for Analysis and Research: Boulder, CO, USA, 2023. [Google Scholar]
- Pew Research Center. Mobile Fact Sheet. 2023. Available online: https://www.pewresearch.org/internet/fact-sheet/mobile/?tabId=tab-428a8f10-3b74-4b36-ad2d-183a4ba27180 (accessed on 11 April 2024).
- Statistics Canada. So Long Landline, Hello Smartphone. 2023. Available online: https://www.statcan.gc.ca/o1/en/plus/3582-so-long-landline-hello-smartphone (accessed on 10 April 2024).
- Chen, B.; Seilhamer, R.; Bennett, L.; Bauer, S. Students’ Mobile Learning Practices in Higher Education: A Multi-Year Study. Educause Review. 2015. Available online: http://er.educause.edu/articles/2015/6/students-mobile-learning-practices-in-higher-education-a-multiyear-study (accessed on 10 April 2024).
- Chen, B.; Denoyelles, A.; Brown, T.; Seilhamer, R. The Evolving Landscape of Students’ Mobile Learning Practices in Higher Education. 2023. Available online: https://er.educause.edu/articles/2023/1/the-evolving-landscape-of-students-mobile-learning-practices-in-higher-education (accessed on 10 April 2024).
- Alexander, B.; Ashford-Rowe, K.; Barajas-Murphy, N.; Dobbin, G.; Knott, J.; McCormack, M.; Pomerantz, J.; Seilhamer, R.; Weber, N. EDUCAUSE Horizon Report: 2019 Higher Education Edition; EDUCAUSE: Louisville, CO, USA, 2019. [Google Scholar]
- Magda, A.J.; Aslanian, C.B. Online College Students 2018: Comprehensive Data on Demands and Preferences; The Learning House, Inc.: Louisville, KY, USA, 2018. [Google Scholar]
- West, D.M. Mobile learning: Transforming education, engaging students, and improving outcomes. Brook. Policy Rep. 2013, 9, 1–7. [Google Scholar]
- Jandrić, P.; Hayes, S. Postdigital Critical Pedagogy. In The Palgrave Handbook on Critical Theories of Education; Abdi, A.A., Misiaszek, G.W., Eds.; Palgrave Macmillan: Cham, Switzerland, 2022. [Google Scholar]
- Jandrić, P.; Knox, J.; Besley, T.; Ryberg, T.; Suoranta, J.; Hayes, S. Postdigital science and education. Educ. Philos. Theory 2018, 50, 893–899. [Google Scholar] [CrossRef]
- Sung, Y.T.; Chang, K.E.; Liu, T.C. The effects of integrating mobile devices with teaching and learning on students’ learning performance: A meta-analysis and research synthesis. Comput. Educ. 2016, 94, 252–275. [Google Scholar] [CrossRef]
- Güler, M.; Bütüner, S.Ö.; Danişman, Ş.; Gürsoy, K. A meta-analysis of the impact of mobile learning on mathematics achievement. Educ. Inf. Technol. 2022, 27, 1725–1745. [Google Scholar] [CrossRef]
- Tlili, A.; Salha, S.; Garzón, J.; Denden, M.; Kinshuk; Affouneh, S.; Burgos, D. Which pedagogical approaches are more effective in mobile learning? A meta-analysis and research synthesis. J. Comput. Assist. Learn. 2024, 1–26. [Google Scholar] [CrossRef]
- Bano, M.; Zowghi, D.; Kearney, M.; Schuck, S.; Aubusson, P. Mobile learning for science and mathematics school education: A systematic review of empirical evidence. Comput. Educ. 2018, 121, 30–58. [Google Scholar] [CrossRef]
- Tlili, A.; Padilla-Zea, N.; Garzón, J.; Wang, Y.; Kinshuk; Burgos, D. The changing landscape of mobile learning pedagogy: A systematic literature review. Interact. Learn. Environ. 2023, 31, 6462–6479. [Google Scholar] [CrossRef]
- Wu, W.-H.; Wu, Y.-C.J.; Chen, C.-Y.; Kao, H.-Y.; Lin, C.-H.; Huang, S.-H. Review of trends from mobile learning studies: A meta-analysis. Comput. Educ. 2012, 59, 817–827. [Google Scholar] [CrossRef]
- Eyrikh, N.V.; Bazhenov, R.I.; Markova, N.V.; Putkina, L.V. Applying Maple computing environment in teaching mathematics to university students majoring in technical. In Proceedings of the IEEE International Conference Quality Management, Transport and Information Security, Information Technologies (IT&QM&IS), St. Petersburg, Russia, 24–28 September 2018; pp. 623–628. [Google Scholar]
- Seebut, S.; Wongsason, P.; Kim, D. Combining GPT and Colab as learning tools for students to explore the numerical solutions of difference equations. Eurasia J. Math. Sci. Technol. Educ. 2024, 20, em2377. [Google Scholar] [CrossRef] [PubMed]
- McMullen, J.; Bui, P.; Brezovszky, B.; Lehtinen, E.; Hannula-Sormunen, M. Mathematical game performance as an indicator of deliberate practice. Int. J. Serious Games 2023, 10, 113–130. [Google Scholar] [CrossRef]
- Schwerter, J.; Brahm, T. Voluntary e-learning exercises support students in mastering statistics. Technol. Knowl. Learn. 2024, 1–38. [Google Scholar] [CrossRef]
- Roediger, H.L., III; Karpicke, J.D. Test-enhanced learning: Taking memory tests improves long-term retention. Psychol. Sci. 2006, 17, 249–255. [Google Scholar] [CrossRef] [PubMed]
- Roediger, H.L., III; Karpicke, J.D. The power of testing memory: Basic research and implications for educational practice. Perspect. Psychol. Sci. 2006, 1, 181–210. [Google Scholar] [CrossRef] [PubMed]
- Bahreman, V.; Chang, M.; Amistad, I.; Garn, K. Design and Implementation of Self-regulated Learning Achievement: Attracting Students to Perform More Practice with Educational Mobile Apps. In State-of-the-Art and Future Directions of Smart Learning; Springer: Singapore, 2016; pp. 263–267. [Google Scholar]
- Ericsson, K.A.; Krampe, R.T.; Tesch-Römer, C. The role of deliberate practice in the acquisition of expert performance. Psychol. Rev. 1993, 100, 363–406. [Google Scholar] [CrossRef]
- Litzinger, T.; Lattuca, L.R.; Hadgraft, R.; Newstetter, W. Engineering education and the development of expertise. J. Eng. Educ. Wash. 2011, 100, 123. [Google Scholar] [CrossRef]
- Brown, P.C.; Roediger, H.L., III; McDaniel, M.A. Make It Stick: The Science of Successful Learning; Belknap Press of Harvard University Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Karpicke, J.D. Retrieval-based learning: A decade of progress. In Cognitive Psychology of Memory, Vol. 2 of Learning and Memory: A Comprehensive Reference; Byrne, J.H., Ed.; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar] [CrossRef]
- Hatano, G.; Inagaki, K. Two courses of expertise. In Child Development and Education in Japan; Stevenson, H.A.H., Hakuta, K., Eds.; Freeman: New York, NY, USA, 1986; pp. 262–272. [Google Scholar]
- Lajoie, S.P.; Gube, M. Adaptive expertise in medical education: Accelerating learning trajectories by fostering self-regulated learning. Med. Teach. 2018, 40, 809–812. [Google Scholar] [CrossRef] [PubMed]
- Ericsson, K. The Differential Influence of Experience, Practice, and Deliberate Practice on the Development of Superior Individual Performance of Experts. In The Cambridge Handbook of Expertise and Expert Performance; Ericsson, K., Hoffman, R., Kozbelt, A., Williams, A., Eds.; Cambridge Handbooks in Psychology; Cambridge University Press: Cambridge, UK, 2018; pp. 745–769. [Google Scholar] [CrossRef]
- Reimann, P.; Markauskaite, L. Expertise. In The International Handbook of the Learning Sciences; Fischer, F., Hmelo-Silver, C., Goldman, S., Reimann, P., Eds.; Routledge Press: New York, NY, USA, 2018; pp. 54–63. [Google Scholar]
- Karpicke, J.D.; Lehman, M.; Aue, W.R. Retrieval-based learning: An episodic context account. In Psychology of Learning and Motivation; Academic Press: Cambridge, MA, USA, 2014; Volume 61, pp. 237–284. [Google Scholar] [CrossRef]
- Latimier, A.; Peyre, H.; Ramus, F. A meta-analytic review of the benefit of spacing out retrieval practice episodes on retention. Educ. Psychol. Rev. 2021, 33, 959–987. [Google Scholar] [CrossRef]
- Karpicke, J.D.; Blunt, J.R. Retrieval practice produces more learning than elaborative studying with concept mapping. Science 2011, 331, 772–775. [Google Scholar] [CrossRef] [PubMed]
- Carlson, M.P.; Bloom, I. The cyclic nature of problem solving: An emergent multidimensional problem-solving framework. Educ. Stud. Math. 2005, 58, 45–75. [Google Scholar] [CrossRef]
- Clark, K.; James, A.; Montelle, C. We definitely wouldn’t be able to solve it all by ourselves, but together…: Group synergy in tertiary students’ problem-solving. Res. Math. Educ. 2014, 16, 306–323. [Google Scholar] [CrossRef]
- Hattie, J.; Zierer, K. Visible Learning Insights, 1st ed.; Routledge: New York, NY, USA, 2019. [Google Scholar]
- Wong, M.; Evans, D. Improving basic multiplication fact recall for primary school students. Math. Educ. Res. J. 2007, 19, 89–106. [Google Scholar] [CrossRef]
- Choy, B.H. Snapshots of mathematics teacher noticing during task design. Math. Educ. Res. J. 2016, 28, 421–440. [Google Scholar] [CrossRef]
- Polotskaia, E.; Savard, A. Using the relational paradigm: Effects on pupils’ reasoning in solving additive word problems. Res. Math. Educ. 2018, 20, 70–90. [Google Scholar] [CrossRef]
- Armstrong, A. Beginner’s mind and the middle years mathematics student. Res. Math. Educ. 2020, 22, 48–66. [Google Scholar] [CrossRef]
- Maciejewski, W.; Star, J.R. Developing flexible procedural knowledge in undergraduate calculus. Res. Math. Educ. 2016, 18, 299–316. [Google Scholar] [CrossRef]
- Champely, S. pwr: Basic Functions for Power Analysis. R Package Version 1.3-0. 2020. Available online: https://CRAN.R-project.org/package=pwr (accessed on 10 April 2024).
- Kulhavy, R.W.; Stock, W. Feedback in written instruction: The place of response certitude. Educ. Psychol. Rev. 1989, 1, 279–308. [Google Scholar] [CrossRef]
- Shute, V.J. Focus on formative feedback. Rev. Educ. Res. 2008, 78, 153–189. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024; Available online: https://www.R-project.org/ (accessed on 10 April 2024).
- Smith, A.M.; Floerke, V.A.; Thomas, A.K. Retrieval practice protects memory against acute stress. Science 2016, 354, 1046–1048. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, R.F.; Lyle, K.B.; Hieb, J.L.; Ralston, P.A. Spaced retrieval practice increases college students’ short-and long-term retention of mathematics knowledge. Educ. Psychol. Rev. 2016, 28, 853–873. [Google Scholar] [CrossRef]
- Lyle, K.B.; Bego, C.R.; Hopkins, R.F.; Hieb, J.L.; Ralston, P.A. How the amount and spacing of retrieval practice affect the short-and long-term retention of mathematics knowledge. Educ. Psychol. Rev. 2020, 32, 277–295. [Google Scholar] [CrossRef]
- Jeno, L.M.; Adachi, P.J.; Grytnes, J.A.; Vandvik, V.; Deci, E.L. The effects of m-learning on motivation, achievement and well-being: A Self-Determination Theory approach. Br. J. Educ. Technol. 2019, 50, 669–683. [Google Scholar] [CrossRef]
- Cadaret, C.N.; Yates, D.T. Retrieval practice in the form of online homework improved information retention more when spaced 5 days rather than 1 day after class in two physiology courses. Adv. Physiol. Educ. 2018, 42, 305–310. [Google Scholar] [CrossRef] [PubMed]
- Karpicke, J.D.; Butler, A.C.; Roediger, H.L., III. Metacognitive strategies in student learning: Do students practise retrieval when they study on their own? Memory 2009, 17, 471–479. [Google Scholar] [CrossRef] [PubMed]
- Kornell, N.; Bjork, R.A. The promise and perils of self-regulated study. Psychon. Bull. Rev. 2007, 14, 219–224. [Google Scholar] [CrossRef] [PubMed]
- McCabe, J. Metacognitive awareness of learning strategies in undergraduates. Mem. Cogn. 2011, 39, 462–476. [Google Scholar] [CrossRef] [PubMed]
- McDaniel, M.A.; Agarwal, P.K.; Huelser, B.J.; McDermott, K.B.; Roediger, H.L., III. Test-enhanced learning in a middle school science classroom: The effects of quiz frequency and placement. J. Educ. Psychol. 2011, 103, 399–414. [Google Scholar] [CrossRef]
- Roediger III, H.L.; Agarwal, P.K.; McDaniel, M.A.; McDermott, K.B. Test-enhanced learning in the classroom: Long-term improvements from quizzing. J. Exp. Psychol. Appl. 2011, 17, 382. [Google Scholar] [CrossRef] [PubMed]
- Ariel, R.; Karpicke, J.D. Improving self-regulated learning with a retrieval practice intervention. J. Exp. Psychol. Appl. 2018, 24, 43–56. [Google Scholar] [CrossRef] [PubMed]
- Dunlosky, J.; Rawson, K.A.; Marsh, E.J.; Nathan, M.J.; Willingham, D.T. Improving students’ learning with effective learning techniques: Promising directions from cognitive and educational psychology. Psychol. Sci. Public Interest 2013, 14, 4–58. [Google Scholar] [CrossRef] [PubMed]
- Jonassen, D.H. Toward a design theory of problem solving. Educ. Technol. Res. Dev. 2000, 48, 63–85. [Google Scholar] [CrossRef]
- Bransford, J.D.; Brown, A.L.; Cocking, R.R. How People Learn: Brain, Mind, Experience, and School; National Academy Press: Washington, DC, USA, 2000. [Google Scholar]
- Garrett, M. Developing Knowledge for Real World Problem Scenarios: Using 3D Gaming Technology within a Problem-Based Learning Framework. Ph.D. Dissertation, Edith Cowan University, Joondalup, Australia, 2012. Available online: https://ro.ecu.edu.au/theses/527 (accessed on 10 April 2024).
- Salomon, G.; Perkins, D.N. Rocky roads to transfer: Rethinking mechanisms of a neglected phenomenon. Educ. Psychol. 1989, 24, 113–142. [Google Scholar] [CrossRef]
- Roediger, H.L., III; Gallo, D.A.; Geraci, L. Processing approaches to cognition: The impetus from the levels-of-processing framework. Memory 2002, 10, 319–332. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).