A Novel Influence Analysis-Based University Major Similarity Study
Abstract
1. Introduction
2. Overview of Data Model
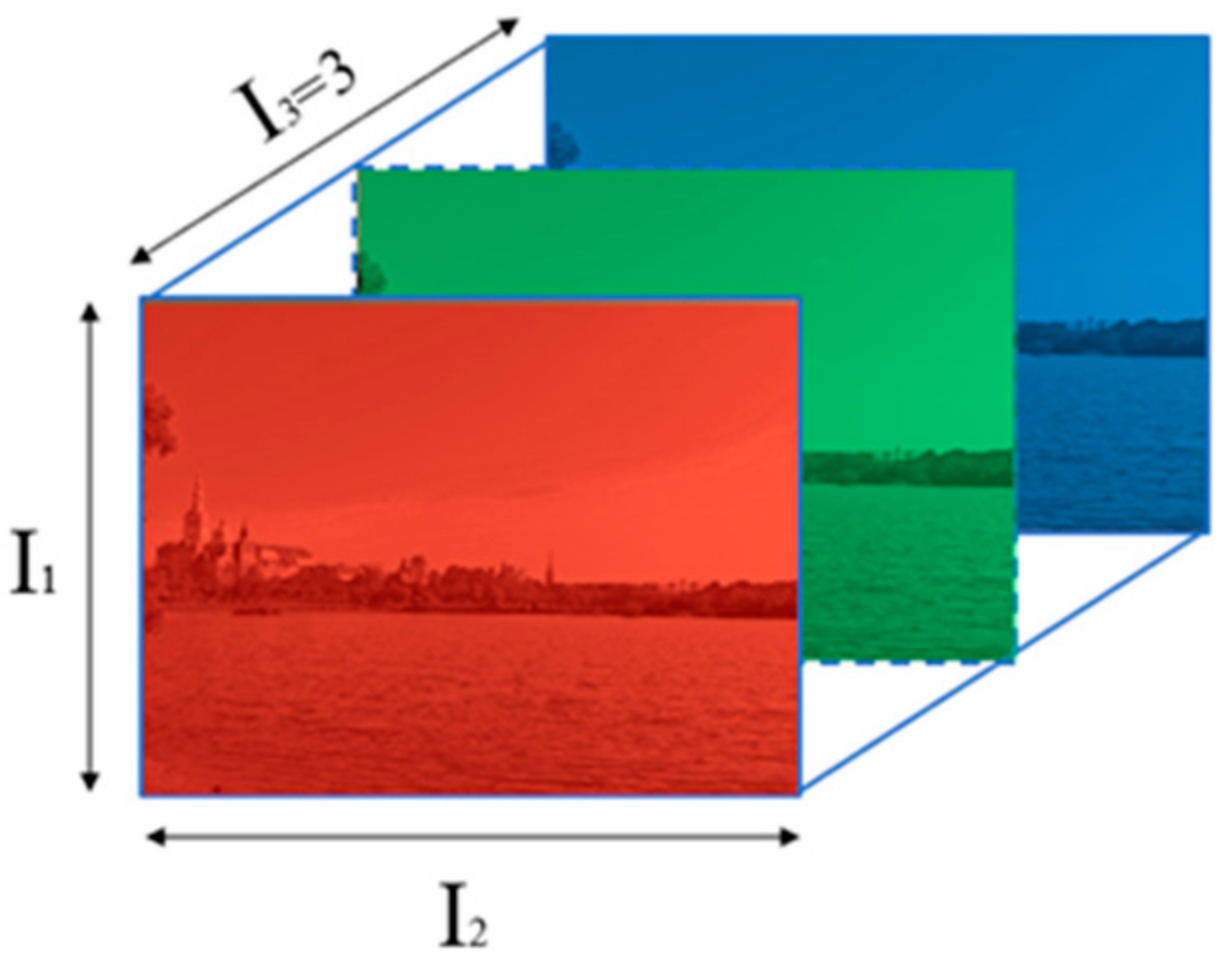
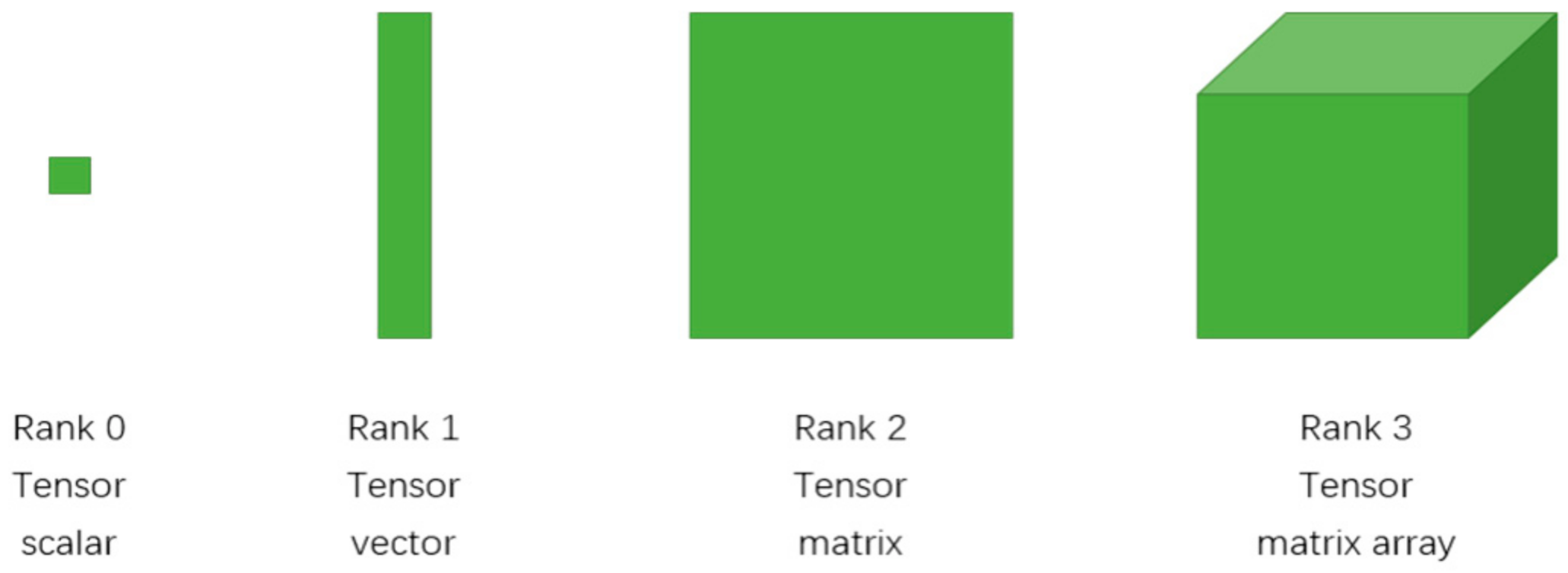
2.1. Tensor
2.2. Opinion Dynamic Model
3. Material and Methods
- Level of importance of different skills and competencies obtained at the Univeristy for the alumni in the working environment.
- Level of satisfaction with the education the Univeristy provided in terms of nurturing different skills and competencies of students.
- Alumni’s learning and living experiences at school, and views on supporting staff.
- Alumni’s anonymous job information and their engagement with the Univeristy after graduation.
3.1. Data Preprocessing
3.2. Selection of the Leader Major
3.3. Extraction of Majors’ Opinion Vector
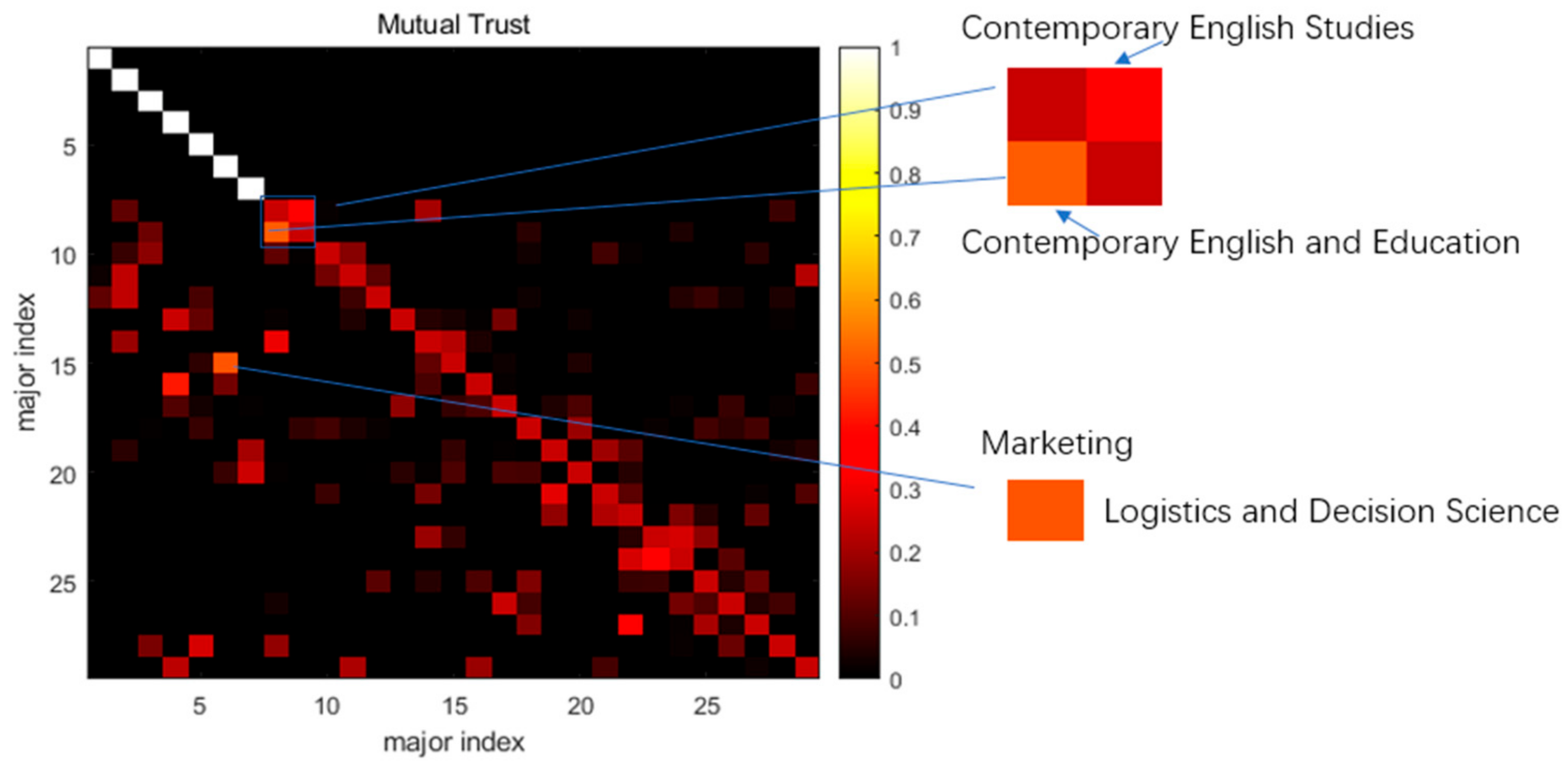
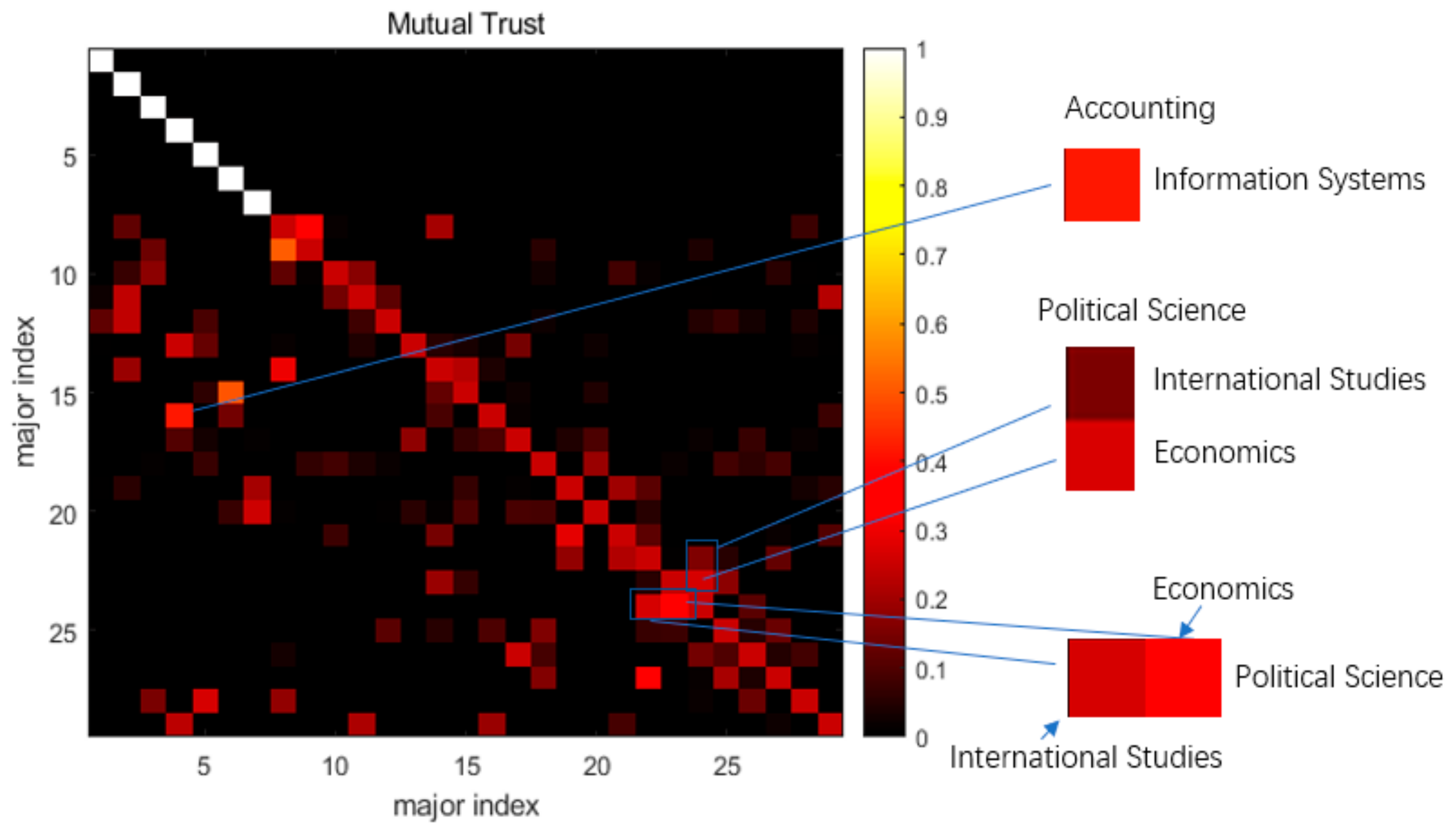
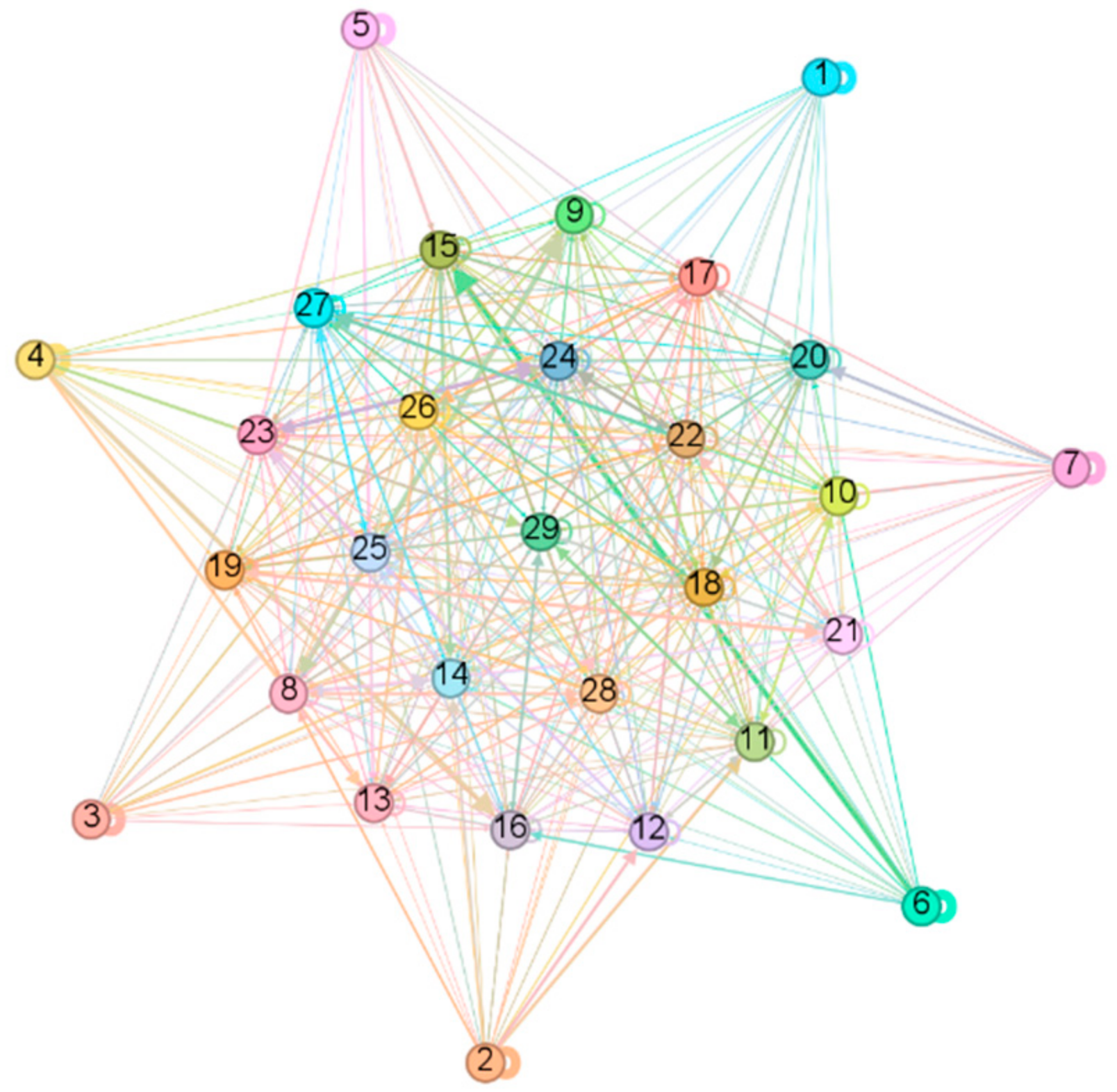
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
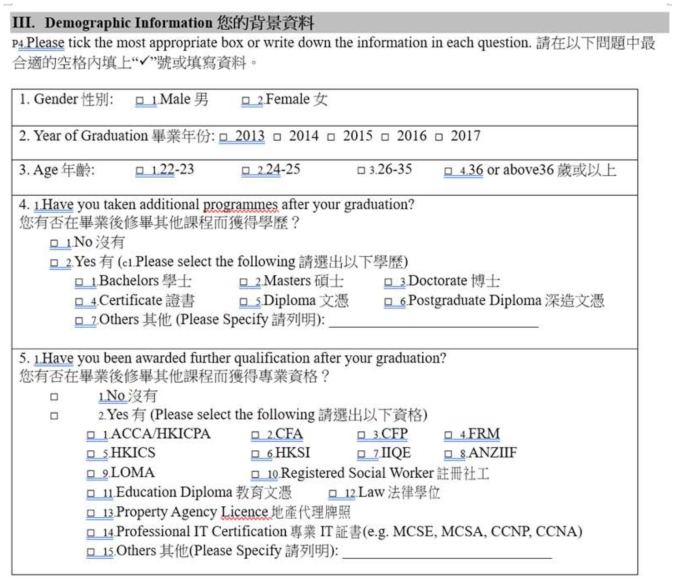
Appendix A. The Questionnaire from the Alumni Survey







References
- Gordon, V.N.; Steele, G.E. The Undecided College Student: An Academic and Career Advising Challenge; Charles C Thomas Publisher: Springfield, IL, USA, 2015. [Google Scholar]
- Neumann, R. Disciplinary Differences and University Teaching. Stud. High. Educ. 2001, 26, 135–146. [Google Scholar] [CrossRef]
- Hsu, Y.; Chi, Y. Academic major satisfaction and regret of students in different majors: Perspectives from Self-Determination Theory. Psychol. Sch. 2022, 59, 2287–2299. [Google Scholar] [CrossRef]
- Peffer, M.; Renken, M. Practical strategies for collaboration across discipline-based education research and the learning sciences. CBE—Life Sci. Educ. 2016, 15, es11. [Google Scholar] [CrossRef]
- Denice, P.A. Choosing and Changing Course: Postsecondary Students and the Process of Selecting a Major Field of Study. Sociol. Perspect. 2021, 64, 82–108. [Google Scholar] [CrossRef]
- Pinxten, M.; De Fraine, B.; Van Den Noortgate, W.; Van Damme, J.; Boonen, T.; Vanlaar, G. ‘I choose so I am’: A logistic analysis of major selection in university and successful completion of the first year. Stud. High. Educ. 2015, 40, 1919–1946. [Google Scholar] [CrossRef]
- Glynn, S.M.; Brickman, P.; Armstrong, N.; Taasoobshirazi, G. Science motivation questionnaire II: Validation with science majors and nonscience majors. J. Res. Sci. Teach. 2011, 48, 1159–1176. [Google Scholar] [CrossRef]
- Balsamo, M.; Lauriola, M.; Saggino, A. Work values and college major choice. Learn. Individ. Differ. 2013, 24, 110–116. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, P.-C.; Wang, M.-N.; Chen, N.-Y. Big Data Mining and Analysis of Hot Issues in International Education—Based on K-means algorithm of cluster analysis. In Proceedings of the 2020 International Conference on Information Science and Education (ICISE-IE), Sanya, China, 4–6 December 2020; pp. 1–4. [Google Scholar] [CrossRef]
- De Paula Santos, F.; Lechugo, C.P.; Silveira-Mackenzie, I.F. “Speak well” or “complain” about your teacher: A contribution of education data mining in the evaluation of teaching practices. In Proceedings of the 2016 International Symposium on Computers in Education (SIIE), Salamanca, Spain, 13–15 September 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Yanrong, P. Research on Intelligent Education Method Based on Data Mining of Distance Education System. In Proceedings of the 2021 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), Xi’an, China, 27–28 March 2021; pp. 586–589. [Google Scholar] [CrossRef]
- Tang, R.; Zou, J.; Chen, S.; Li, L. Research on Quality Modeling of Information Education in Colleges and Universities Based on Web Data Mining. In Proceedings of the 2019 International Conference on Smart Grid and Electrical Automation (ICSGEA), Xiangtan, China, 10–11 August 2019; pp. 576–582. [Google Scholar] [CrossRef]
- Mastoory, Y.; Rajaee Harandi, S.; Abdolvand, N. The effects of communication networks on students’ academic performance: The synthetic approach of social network analysis and data mining for education. Int. J. Integr. Technol. Educ. 2016, 5, 23–34. [Google Scholar] [CrossRef]
- Peng, S.; Zhou, Y.; Cao, L.; Yu, S.; Niu, J.; Jia, W. Influence analysis in social networks: A survey. J. Netw. Comput. Appl. 2018, 106, 17–32. [Google Scholar] [CrossRef]
- Wasserman, S. Social Network Analysis: Methods and Applications; Cambridge University Press: Cambridge, UK, 1994; Volume 2, pp. 1–22. [Google Scholar]
- Abdul-Rahman, A.; Hailes, S. Supporting trust in virtual communities. In Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, Maui, HI, USA, 7 January 2000; Volume 1, p. 9. [Google Scholar] [CrossRef]
- DeGroot, M.H. Reaching a consensus. J. Am. Stat. Assoc. 1974, 69, 118–121. [Google Scholar] [CrossRef]
- Altafini, C. Consensus Problems on Networks with Antagonistic Interactions. IEEE Trans. Autom. Control 2013, 58, 935–946. [Google Scholar] [CrossRef]
- Altafini, C. Dynamics of opinion forming in structurally balanced social networks. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 5876–5881. [Google Scholar] [CrossRef]
- Wu, S.X.; Wai, H.-T.; Scaglione, A. Estimating Social Opinion Dynamics Models from Voting Records. IEEE Trans. Signal Process. 2018, 66, 4193–4206. [Google Scholar] [CrossRef]
- Acemoglu, D.; Ozdaglar, A. Opinion dynamics and learning in social networks. Dyn. Games Appl. 2011, 1, 3–49. [Google Scholar] [CrossRef]
- Wai, H.T.; Scaglione, A.; Leshem, A. Active sensing of social networks. IEEE Trans. Signal Inf. Process. Netw. 2016, 2, 406–419. [Google Scholar] [CrossRef]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Wang, H.; Ahuja, N. A Tensor Approximation Approach to Dimensionality Reduction. Int. J. Comput. Vis. 2008, 76, 217–229. [Google Scholar] [CrossRef]
- Gerstner, T.; Griebel, M. Dimension–Adaptive Tensor–Product Quadrature. Computing 2003, 71, 65–87. [Google Scholar] [CrossRef]
- Li, X.; Ng, M.K.; Cong, G.; Ye, Y.; Wu, Q. MR-NTD: Manifold Regularization Nonnegative Tucker Decomposition for Tensor Data Dimension Reduction and Representation. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 1787–1800. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Guo, Y.; Tropp, J.A.; Udell, M. Tensor random projection for low memory dimension reduction. arXiv 2021, arXiv:2105.00105. [Google Scholar]
- Sahafizadeh, E.; Ladani, B.T. The impact of group propagation on rumor spreading in mobile social networks. Phys. A Stat. Mech. Appl. 2018, 506, 412–423. [Google Scholar] [CrossRef]
- Dong, Y.; Ding, Z.; Chiclana, F.; Herrera-Viedma, E. Dynamics of public opinions in an online and offline social network. IEEE Trans. Big Data 2017, 7, 610–618. [Google Scholar] [CrossRef]
- CVX Research, Inc. CVX: Matlab Software for Disciplined Convex Programming, Version 2.0. April 2011. Available online: http://cvxr.com/cvx (accessed on 31 August 2012).
- Bastian, M.; Heymann, S.; Jacomy, M. Gephi: An open source software for exploring and manipulating networks. In Proceedings of the Third International AAAI Conference on Web and Social Media, San Jose, CA, USA, 17–20 May 2009; Volume 3, pp. 361–362. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, N.; Li, Q.; Wu, S.X.; Zhu, J.; Han, J. A Novel Influence Analysis-Based University Major Similarity Study. Educ. Sci. 2024, 14, 337. https://doi.org/10.3390/educsci14030337
Zhang N, Li Q, Wu SX, Zhu J, Han J. A Novel Influence Analysis-Based University Major Similarity Study. Education Sciences. 2024; 14(3):337. https://doi.org/10.3390/educsci14030337
Chicago/Turabian StyleZhang, Ningqi, Qingyun Li, Sissi Xiaoxiao Wu, Junjie Zhu, and Jie Han. 2024. "A Novel Influence Analysis-Based University Major Similarity Study" Education Sciences 14, no. 3: 337. https://doi.org/10.3390/educsci14030337
APA StyleZhang, N., Li, Q., Wu, S. X., Zhu, J., & Han, J. (2024). A Novel Influence Analysis-Based University Major Similarity Study. Education Sciences, 14(3), 337. https://doi.org/10.3390/educsci14030337





