How Multiple Representations Using Cyber–Physical System to Teach Rectilinear Motion Improves Learning and Creativity
Abstract
1. Introduction
2. Materials and Methods
2.1. Domain
2.2. Sample
2.3. Experimental Design
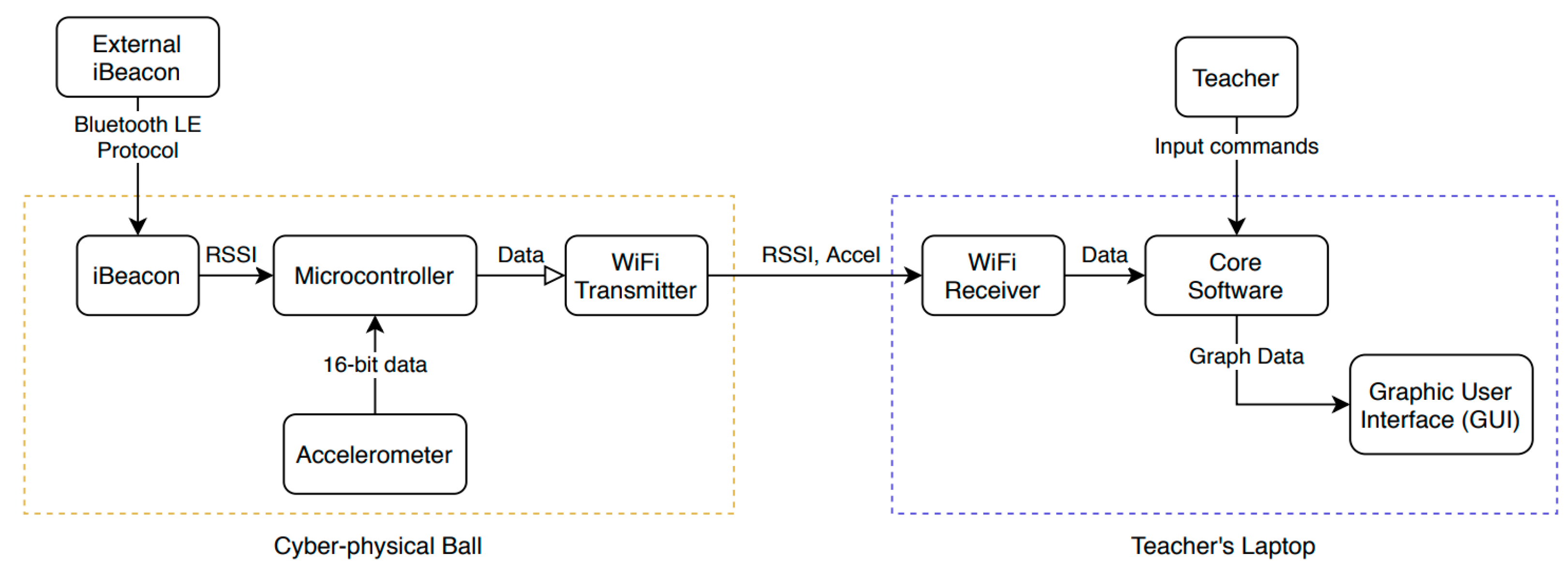
2.4. Cyber–Physical Systems for Teaching Rectilinear Motion
2.5. Teacher Software
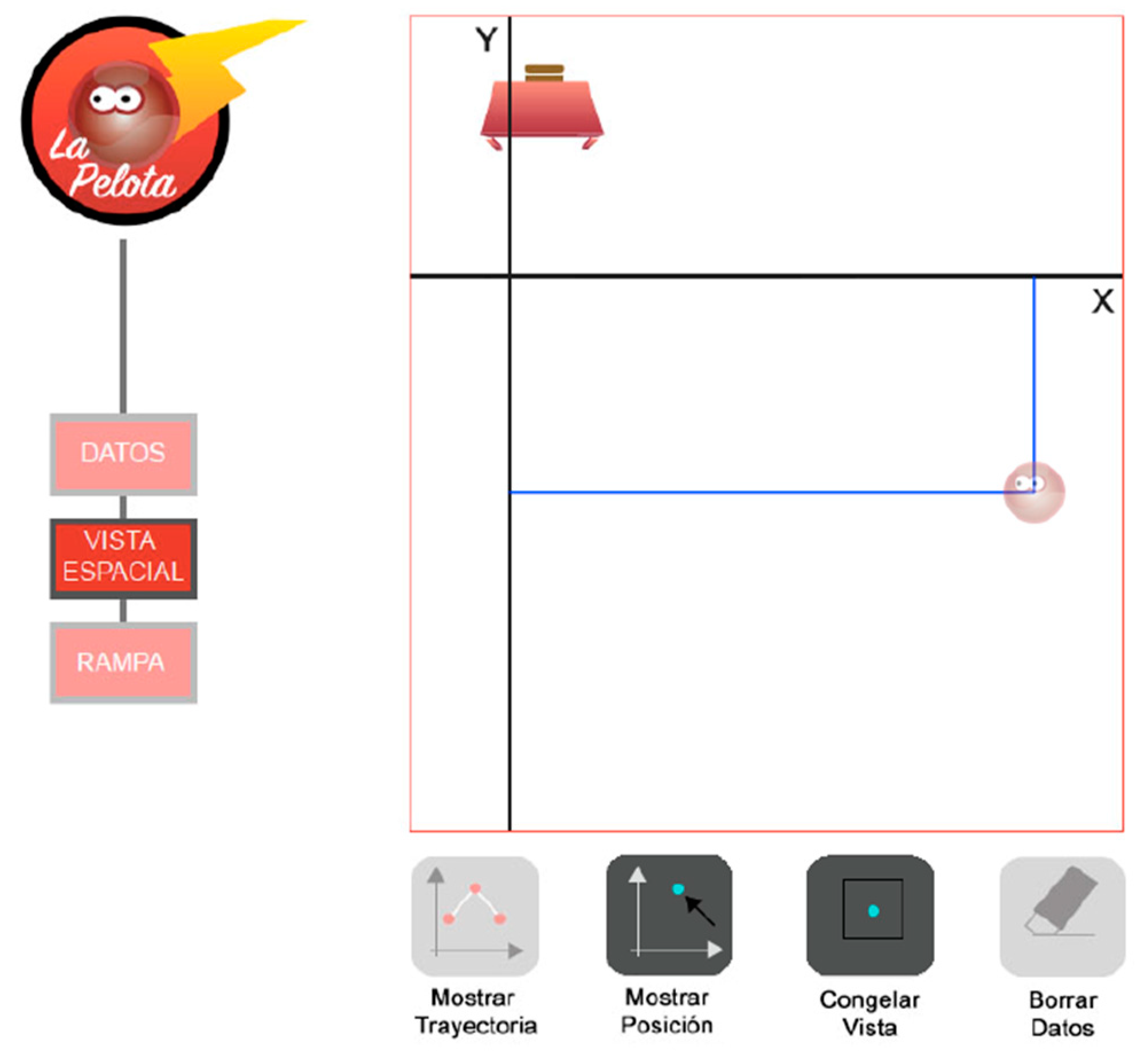
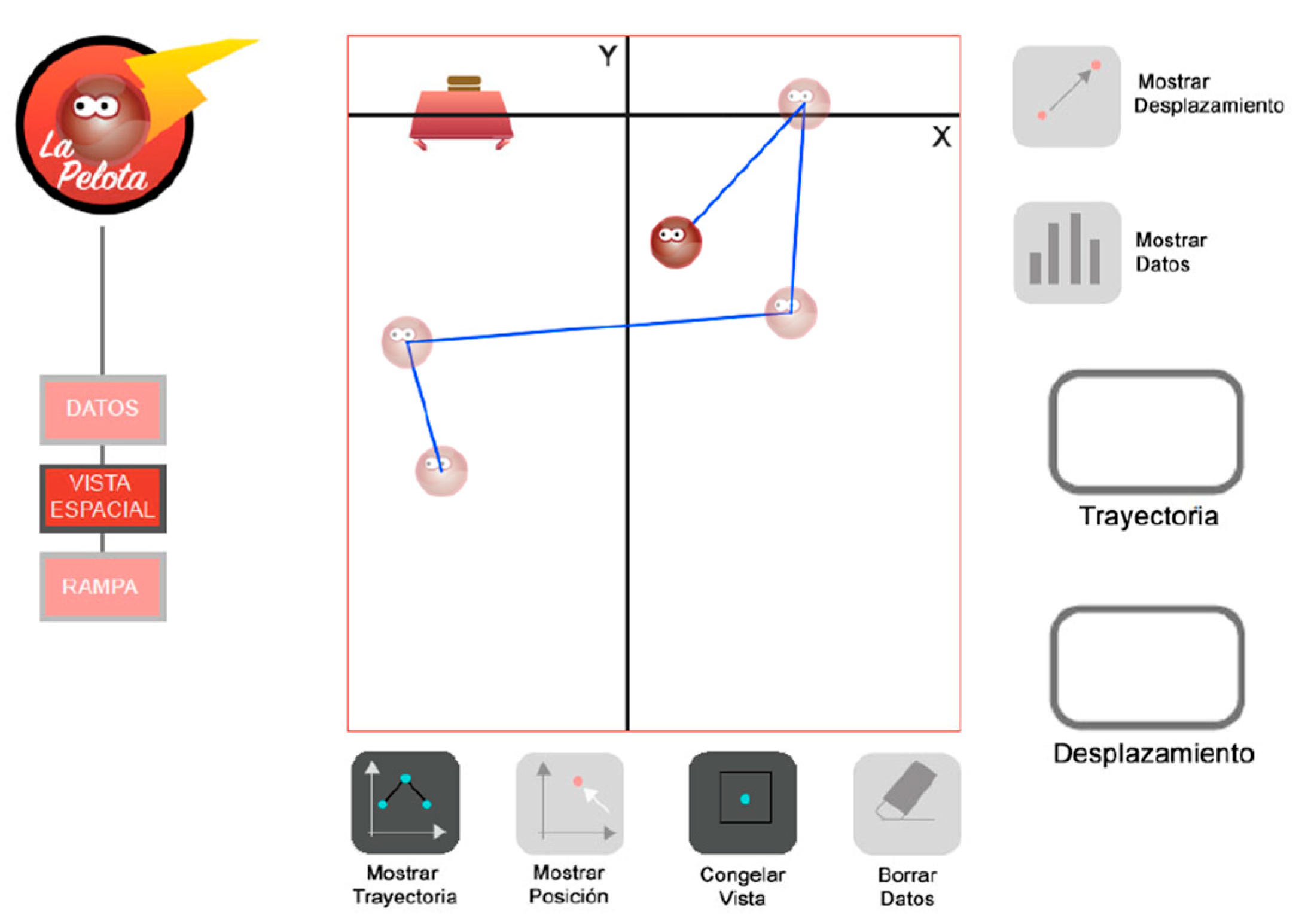
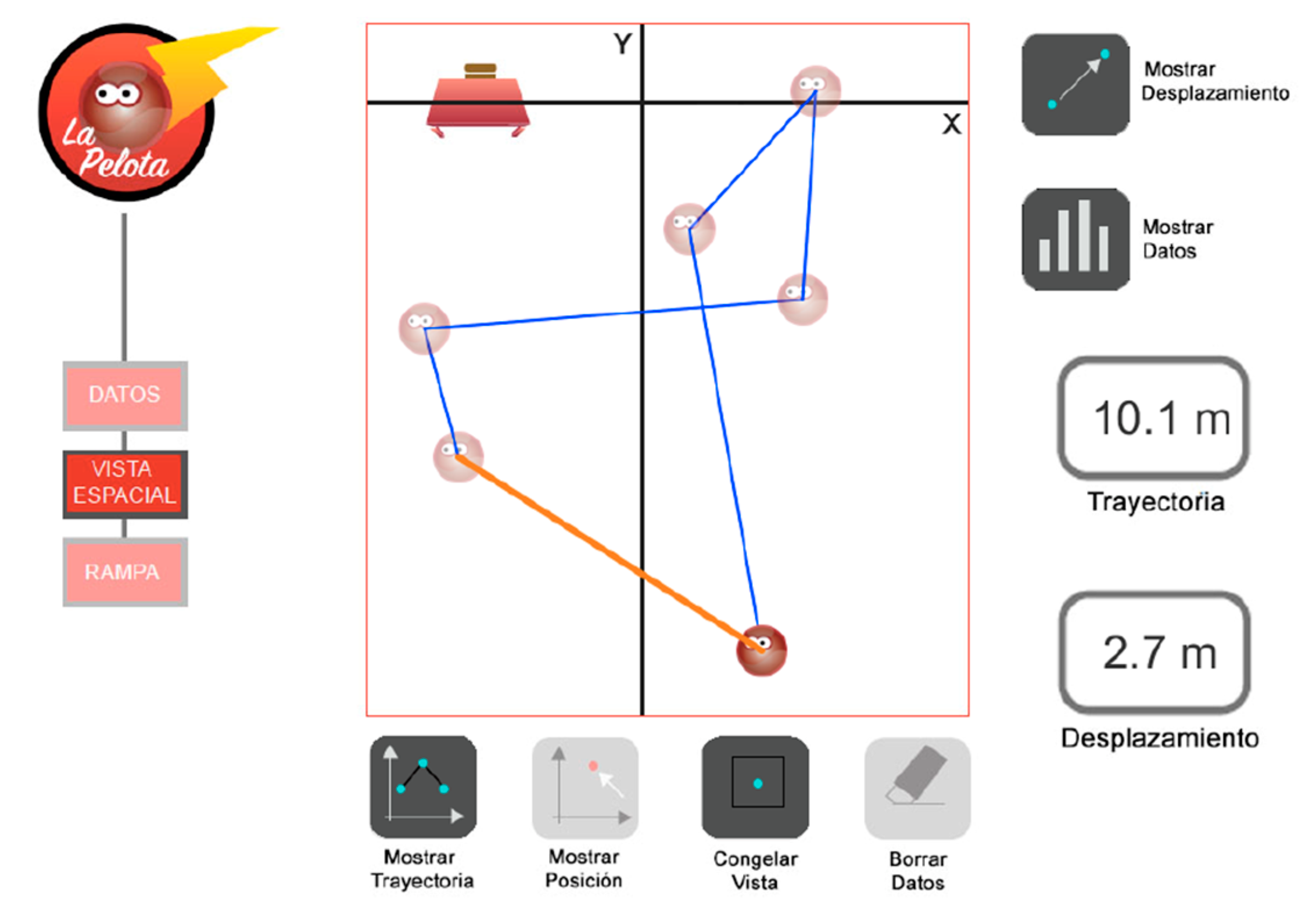
2.5.1. Spatial View
- Show a vertical representation of the classroom space;
- Show the ball’s position inside the classroom in real time;
- Show an XY axis representing the current reference frame;
- Display lines to represent the projection of the ball’s current position on the actual reference frame;
- Set the origin for each of the axes from the XY reference frame;
- Freeze the screen so that no new positions would be updated;
- Plot the trajectory of the ball around the classroom;
- Erase the previous positions from the trajectory;
- Plot the displacement made by the ball and toggle its visibility when necessary;
- Display numerical values of the total trajectory and total displacement after the interface had been paused.
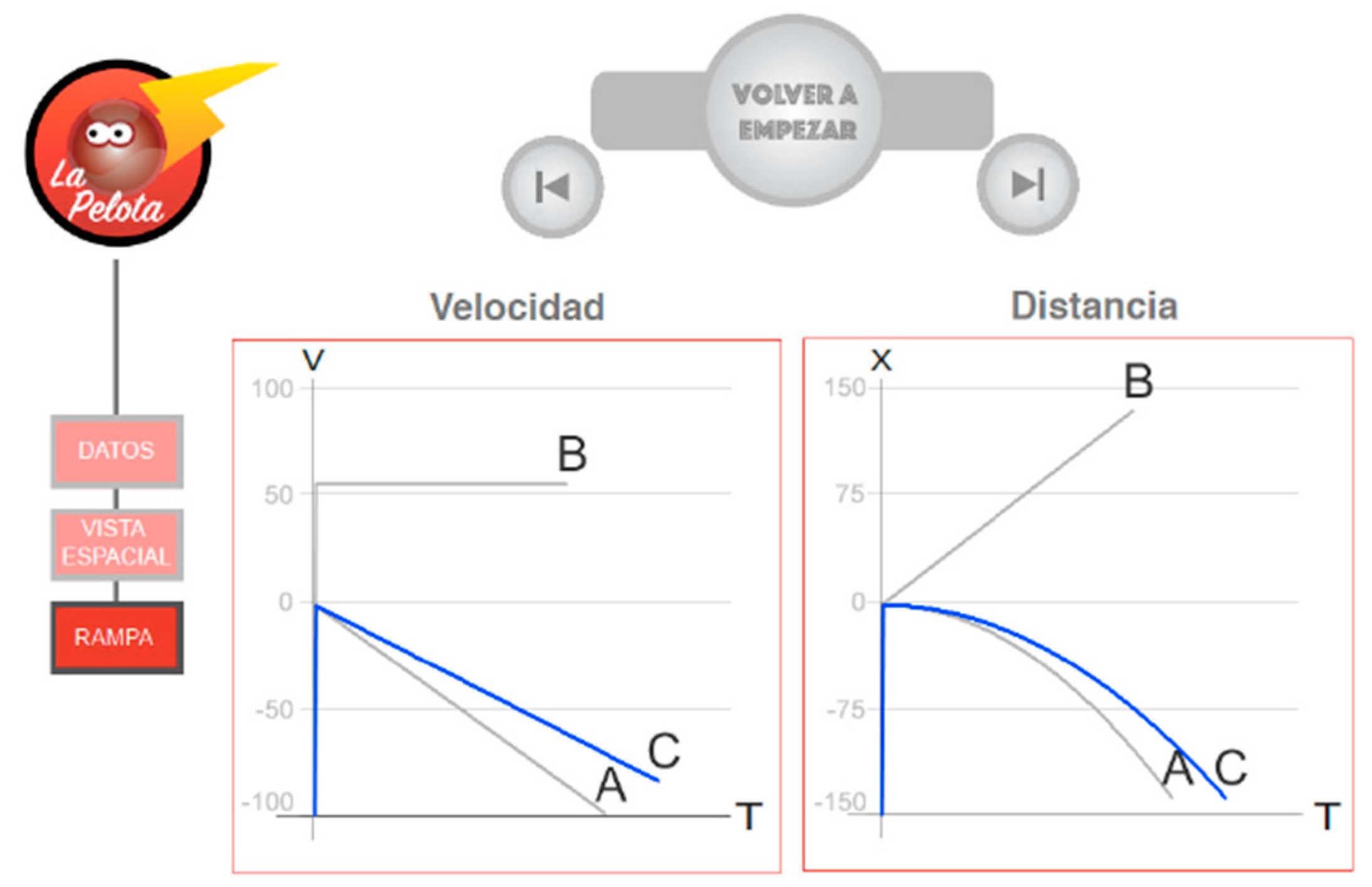
2.5.2. Ramp View
- Plot the data for velocity vs. time for each experiment;
- Plot the data for distance vs. time for each experiment;
- Plot the three experiments on the same graph so as to easily compare them;
- Show an animation of each plot being drawn, with the time taken to draw the line proportional to the time the action took in real life;
- Simultaneously show the animations for all three experiments;
- Change which plots are being shown;
- Reset the saved data and draw the plots from scratch;
- Show referential values on the Y axis of the graph.
2.5.3. Data View
- Show plots of the accelerations measured by the ball;
- Show a plot of the magnitude of the ball’s acceleration vs. time;
- Select between viewing the plot of the magnitude or the detail for each direction (X,Y,Z);
- Pause and resume the program to control when it receives new data;
- Show a timeline to use as a reference for the graphs;
- Display average values for each interval when needed.
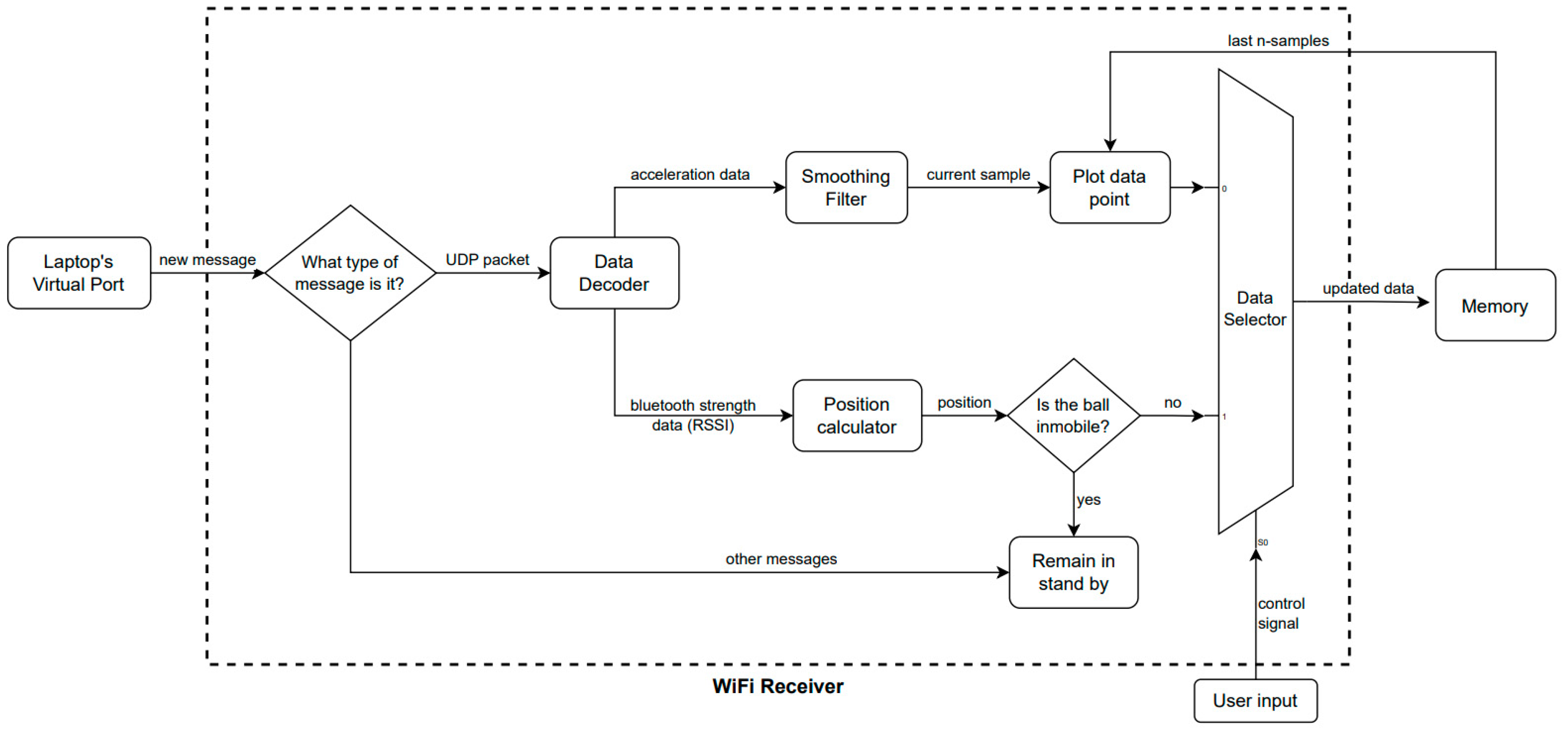
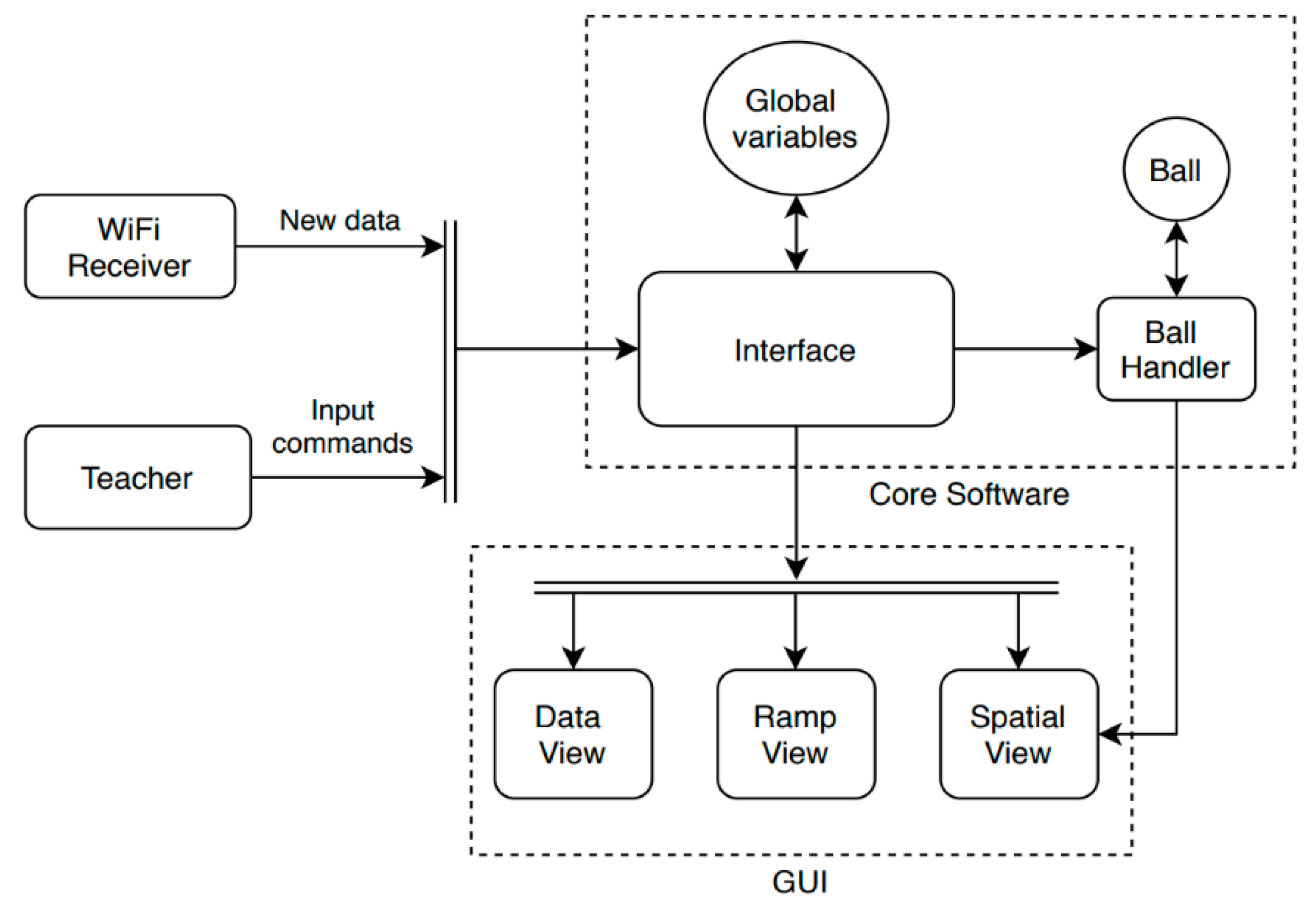
2.6. Hardware/Software Architecture
- STORE system’s images used in the different views of the GUI;
- ADD graphic elements to each view of the GUI;
- SET the parameters at the start of the system and when a soft restart is issued;
- DRAW the plot data on the corresponding graphs from the Data and Ramp Views;
- HANDLE mouse triggers when the teacher interacts with the GUI;
- CONTROL the current state of the system and which view is active;
- ENABLE the operation of the ball handler and the display of the active view.
- Plot data generated from the outputs from the Wi-Fi receiver;
- Static parameters for the classroom dimensions, size of the ball, and sampling frequency;
- Parameters for the GUI design dimensions;
- Auxiliary variables for the program control flow.
- STORE an array of ball objects with the current and previous coordinates of the ball’s position inside the classroom since the last reset;
- UPDATE the visibility of each ball within the array based on the state of the current program;
- DRAW a line with the trajectory travelled by the ball based on the array of coordinates saved previously;
- DRAW a line with the displacement based on the ball’s initial position after reset and its current position;
- DISPLAY numerical data on the total distance traveled and displacement, in meters.
- UPDATE its visual properties depending on the behavior of each subclass;
- DETECT whether the mouse is currently above it;
- TRIGGER a mouse-pressed event for the core software’s interface, if clicked;
- DISPLAY or HIDE itself on the GUI if required by the core software’s interface.
2.7. Measurement Instruments
2.7.1. Physics Grades
2.7.2. Creativity Test
- Fluency: the ability to generate many ideas. The student is awarded 1 point for every idea they produce;
- Flexibility: the ability to move between domains. The student is awarded 1 point for each (different) category or domain they produce;
- Originality: the ability to produce novel and unusual ideas. The student is awarded 2 points for every idea that was generated by less than 2% of the class and 1 point for every idea generated by less than 5% of the class.
2.8. Quantitative Analysis
2.9. Quantitative Analysis
- (1)
- In terms of motivation: Were you happy to go to class, knowing that you were going to watch videos? Or play with the ball? During class, were you keen to comment on the videos/activities with the ball?
- (2)
- In terms of the content: In what way were the videos useful to you? And the activities with the ball? Did the way in which the teacher linked the content with the videos make sense to you? And what about the activities with the ball? If it were up to you, would you add more videos, more ball activities, or more examples on the board?
- (3)
- In terms of the context used to frame the videos and activities: Can you remember any of the videos or activities you did with the ball in class? Which ones? What was the topic, and what could you take away from the videos/activities with the ball? Did the content of the videos or ball activities make sense to you?
- (4)
- In terms of knowledge transfer: Was the content you studied in class in any way use-ful? What for?
- (5)
- Finally, in terms of the activities with the ball in particular: Would you have liked to have done more activities with the ball? What would you have done differently?
3. Results
3.1. Quantitative Results
3.2. Qualitative Results
4. Discussion
- S3:
- “(the classes) switched things up.”
- S6:
- “The ball allowed us to look at things from another angle, not just the theory.”
- S5:
- “The experiments had an impact on our learning, I mean we learned quicker.”
- S3:
- “I like it because it’s more practical”.
- S4:
- “The ball was more practical than theoretical”.
- S1:
- “use a towel as a medical supply to stop bleeding, reduce fever or as a sling”.
- S2:
- “using a towel as a filter”.
- S1:
- “it had a pulse”.
- S2:
- “you could revive it, or make it die…”
- S1:
- “What I liked most was that the teacher made the classes dynamic”.
- S2:
- “The classes were fun”.
- S1:
- “I find that it’s better when the teacher makes us part of the class, when it’s not just them talking, when we also get to say what we think, what we understand and what we’re struggling with”.
- S2:
- “I think that maybe all of the teachers could, like, maybe learn from their colleagues, because there are teachers who, like… talk all class and the class is more boring, but if they could maybe look elsewhere and say: OK, I like how she teaches her classes… Like, more dynamic, where the students participate, I think that would be better”.
- S1:
- “What I liked most was that the teacher made the classes dynamic”.
- S2:
- “Everything made sense”.
- S1:
- “With the ball, you could draw on everything you’d seen before, like you could confirm what you knew”.
5. Conclusions, Limitations, and Future Work
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Lesson Topics | Learning Objectives | Activities |
|---|---|---|
| Lesson 1: Reference frames—trajectory and displacement |
|
|
| Lesson 2: Speed and velocity |
|
|
| Lesson 3: Addition of velocities |
|
|
| Lesson 4: Uniform rectilinear motion |
|
|
| Lesson 5: Uniformly accelerated rectilinear motion |
|
|
Appendix B


Appendix C
| Component | Price ($USD) |
|---|---|
| FLORA Accelerometer LSM9DS0 | $ 19.95 |
| Feather Huzzah ESP8266 (Micontroller + WiFi) | $ 16.95 |
| 3.7 V 3700 mAh Lithium-Ion Polymer Battery | $ 14.95 |
| HM-10 Bluetooth 4.0 | $ 7.99 |
| 6” Foam Ball | $ 12.99 |
| 100 g of PLA (3D printed block) | $ 2.5 |
| Total Cost | $ 75.33 |
Appendix D
| Category | Finding | Quote |
|---|---|---|
| (1) Assessment of the class: shows what the students valued about the classes in general | The students appreciate it when the classes are fun and dynamic. | S1: “What I liked most was that the teacher made the classes dynamic” S2: “The classes were fun” S3: “(the classes) switched things up” |
| (2) Assessment of the use of the ball in class | The students appreciate it when teachers use different resources in class. They have a positive opinion of practical activities in class and believe that they improve learning. All of the students in the focus group suggested that the ball activities were their favorite part of class. | S1: “(The ball) is totally different from the classes that the other teachers do” S2: (The ball) is, like, different, but at the same time I think it helps us understand more” S3: “I like it because it’s more hands-on” S4: “The ball is more practical than theoretical” S5: “The experiments had an impact on our learning, I mean we learned quicker.” S6: “The ball allowed us to look at things from another angle, not just the theory.” |
| (3) Relationship between the activities and content | The students managed to relate the practical activities with the theory. | S1: “With the ball, you could draw on everything you’d seen before, like you could confirm what you knew” S2: “Everything made sense” |
| (4) Role of the students | The students want their teachers to involve them and have them play an active role in class. | S1: “I find that it’s better when the teacher makes us part of the class, when it’s not just them talking, when we also get to say what we think, what we understand and what we’re struggling with” S2: “I think that maybe all of the teachers could, like, maybe learn from their colleagues, because there are teachers who, like… talk all class and the class is more boring, but if they could maybe look elsewhere and say: OK, I like how she teaches her classes… Like, more dynamic, where the students participate, I think that would be better” |
| (5) Importance of innovation and technology | The students want their teachers to use technology in the classroom. | S1: “because you’re more used to technology” S2: “with technology it’s easier to understand” S3: “because you just see a volleyball ball, but it sent a signal to other devices through Bluetooth, so it was cool” |
| (6) Perception of how the ball can be related to real life | The students acknowledged the ball as a real-life object that they could interact with directly. | S1: “it had a pulse” S2: “you could revive it, or make it die…” |
References
- Maghfiroh, A.; Kuswanto, H.; Susetyo, B. The development of android-based physics comic on optical devices for high school students. J. Phys. Conf. Ser. 2020, 1440, 012023. [Google Scholar] [CrossRef]
- Cromley, J.G. Learning from Multiple Representations. In Handbook of Learning from Multiple Representations and Perspective, 1st ed.; Routledge: New York, NY, USA, 2020; pp. 62–75. [Google Scholar]
- Hahn, L.; Klein, P. The impact of multiple representations on students’ understanding of vector field concepts: Implementation of simulations and sketching activities into lecture-based recitations in undergraduate physics. Front. Psychol. 2023, 13, 1012787. [Google Scholar] [CrossRef]
- Wilson, B.G. Constructivism for Active, Authentic Learning. In Trends and Issues in Instructional Design and Technology, 4th ed.; Reiser, B., Dempsey, J., Eds.; Pearson: New York, NY, USA, 2017; pp. 61–67. [Google Scholar]
- van Gog, T.; Paas, F.; Sweller, J. Cognitive Load Theory: Advances in Research on Worked Examples, Animations, and Cognitive Load Measurement. Educ. Psychol. Rev. 2010, 22, 375–378. [Google Scholar] [CrossRef]
- Murshed, M.; Phang, F.A.; Bunyamin, M.A.H. Transformation of multiple representation in real world physics problem solving. J. Phys. Conf. Ser. 2021, 1760, 012004. [Google Scholar] [CrossRef]
- Becker, S.; Klein, P.; Gößling, A.; Kuhn, J. Investigating Dynamic Visualizations of Multiple Representations Using Mobile Video Analysis in Physics Lessons. ZfDN 2020, 26, 123–142. [Google Scholar] [CrossRef]
- Clements, D.H.; Vinh, M.; Lim, C.I.; Sarama, J. STEM for Inclusive Excellence and Equity. Early Educ. Dev. 2020, 32, 148–171. [Google Scholar] [CrossRef]
- Hugues, J.; Hristosov, A.; Hudak, J.J.; Yankel, J. TwinOps-DevOps meets model-based engineering and digital twins for the engineering of CPS. In Proceedings of the 23rd ACM/IEEE International Conference on Model Driven Engineering Languages and Systems: Companion Proceedings, New York, NY, USA, 18–23 October 2020. [Google Scholar] [CrossRef]
- Opfermann, M.; Schmeck, A.; Fischer, H.E. Multiple Representations in Physics and Science Education—Why Should We Use Them? In Multiple Representations in Physics Education; 2017; pp. 1–22. Available online: http://www.springer.com/series/6931 (accessed on 14 February 2024).
- Munfaridah, N.; Avraamidou, L.; Goedhart, M. The Use of Multiple Representations in Undergraduate Physics Education: What Do we Know and Where Do we Go from Here? Eurasia J. Math. Sci. Technol. Educ. 2021, 17, em1934. [Google Scholar] [CrossRef] [PubMed]
- Radanliev, P.; De Roure, D.; Van Kleek, M.; Santos, O.; Ani, U. Artificial intelligence in cyber physical systems. AI Soc. 2020, 36, 783–796. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.D.; Duan, L. Big data for cyber physical systems in industry 4.0: A survey. Enterp. Inf. Syst. 2018, 13, 148–169. [Google Scholar] [CrossRef]
- Liu, Y.; Peng, Y.; Wang, B.; Yao, S.; Liu, Z. Review on cyber-physical systems. IEEE/CAA J. Autom. Sin. 2017, 4, 27–40. [Google Scholar] [CrossRef]
- Kurde, S.; Shimpi, J.; Pawar, R.; Tingare, B. Cyber Physical Systems (CPS) and Design Automation for healthcare System: A new Era of Cyber Computation for Healthcare System. IRJET 2019, 6, 1472–1475. [Google Scholar]
- Tilbury, D.M. Cyber-Physical Manufacturing Systems. Annu. Rev. Control 2019, 2, 427–443. [Google Scholar] [CrossRef]
- Tao, W.; Lai, Z.H.; Leu, M.C.; Yin, Z.; Qin, R. A self-aware and active-guiding training & assistant system for worker-centered intelligent manufacturing. Manuf. Lett. 2019, 21, 45–49. [Google Scholar] [CrossRef]
- Cecil, J.; Ramanathan, J.; Huynh, J. A shape modification app and cyber-physical framework for collaborative manufacturing. Procedia Manuf. 2019, 34, 932–939. [Google Scholar] [CrossRef]
- White, T.; Pea, R. Distributed by design: On the promises and pitfalls of collaborative learning with multiple representations. J. Learn. Sci. 2011, 20, 489–547. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, J.; Cheng, L.; Cheng, X.; Ma, X.; Chen, Y. Improving the Students’ Creativity in Chinese Mathematics Classrooms. Creat. Educ. 2020, 11, 1645–1665. [Google Scholar] [CrossRef]
- Munfaridah, N.; Goedhart, M. Multiple representations (MR) based instructional approach in support of physics identity and physics teachers’ identity development: Design considerations. Momentum Phys. Educ. J. 2023, 7, 1–16. [Google Scholar] [CrossRef]
- Marange, I.; Alex, J.; Kariyana, I. Gender Differences on Impact of Geogebra as a Manipulative Tool Among Grade 11 Geometry Learners in South Africa. In Proceedings of the 29th Annual Conference of the Southern African Association for Research in Mathematics, Science and Technology Education, Maseru & Roma, Lesotho, 12–15 January 2021; pp. 80–88. [Google Scholar]
- Puryear, J.S.; Lamb, K.N. Defining Creativity: How Far Have We Come Since Plucker, Beghetto, and Dow? Creat. Res. J. 2020, 32, 206–2014. [Google Scholar] [CrossRef]
- Glăveanu, V.P.; Beghetto, R.A. Creative Experience: A Non-Standard Definition of Creativity. Creativity Res. J. 2020, 33, 75–80. [Google Scholar] [CrossRef]
- Bonetto, E.; Pichot, N.; Pavani, J.B.; Adam-Troïan, J. The paradox of creativity. Paradox Creat. 2021, 60, 100820. [Google Scholar] [CrossRef]
- Venckutė, M.; Mulvik, I.B.; Lucas, B. Creativity—A transversal skill for lifelong learning. In An Overview of Existing Concepts and Practices: Final Report; Publications Office of the European Union: Luxembourg, 2020. [Google Scholar] [CrossRef]
- Martins, D.; McCauley, V. Creativity in science: A dilemma for informal and formal education. Sci. Educ. 2021, 105, 498–520. [Google Scholar] [CrossRef]
- Ministerio de Educación. Programa de Estudio Segundo medio: Ciencias Naturales. 2016. Available online: https://curriculumnacional.mineduc.cl/614/articles-34453_programa.pdf (accessed on 24 April 2021).
- Agencia de Calidad de la Educación. Resultados Categoría de Desempeño. 2019. Available online: https://agenciaorienta.gob.cl/inicio (accessed on 24 April 2021).
- Junta Nacional de Auxilio Escolar y Becas. Prioridades 2020 con IVE SINAE Básica Media y Comunal. 2020. Available online: https://www.junaeb.cl/ive (accessed on 14 February 2024).
- Demirci, C. The effect of active learning approach on attitudes of 7th grade students. Int. J. Instr. 2017, 10, 129–144. [Google Scholar] [CrossRef]
- Ayop, S.K.; Ismail, A.T. Students’ Understanding in Kinematics: Assessments, Conceptual Difficulties and Teaching Strategies. Int. J. Acad. Res. Bus. Soc. Sci. 2019, 9, 1278–1285. [Google Scholar] [CrossRef]
- Redish, E.F.; Saul, J.M.; Steinberg, R.N. On the effectiveness of active-engagement microcomputer-based laboratories. Am. J. Phys. 1998, 65, 45–54. [Google Scholar] [CrossRef]
- Ye, J.; Lu, S.; Bi, H. The effects of microcomputer-based laboratories on students macro, micro, and symbolic representations when learning about net ionic reactions. Chem. Educ. Res. Pract. 2018, 20, 288–301. [Google Scholar] [CrossRef]
- Bernhard, J. What matters for students’ learning in the laboratory? Do not neglect the role of experimental equipment! Instr. Sci. 2018, 46, 819–846. [Google Scholar] [CrossRef]
- Instituto Nacional de Deporte. Encuesta Nacional de Hábitos de Actividad Física y Deportes en la Población de 18 Años y Más. Informe Final. 2016. Available online: https://www.mindep.cl/secciones/151 (accessed on 14 February 2024).
- Sandoval, P.; García, I. Cultura deportiva en Chile: Desarrollo histórico, institucionalidad actual e implicancias para la política pública. Polis 2014, 39, 441–462. [Google Scholar] [CrossRef]
- Cruz, E.S. Fútbol y nacionalismo de mercado en el Chile actual. In Futbologias: Futbol, Identidad y Violencia en America Latina; CLACSO: Buenos Aires, Argentina, 2003; pp. 199–244. Available online: https://core.ac.uk/download/pdf/35172223.pdf (accessed on 24 April 2021).
- Müter, L.; Deoskar, T.; Mathijssen, M.; Brinkkemper, S.; Dalpiaz, F. Refinement of User Stories into Backlog Items: Linguistic Structure and Action Verbs: Research Preview. In Requirements Engineering: Foundation for Software Quality; Springer: Cham, Switzerland, 2019; pp. 109–116. [Google Scholar] [CrossRef]
- Sha, L.; Lucey, P.; Yue, Y.; Wei, X.; Hobbs, J.; Rohlf, C.; Sridharan, S. Interactive sports analytics: An intelligent interface for utilizing trajectories for interactive sports play retrieval and analytics. ACM Trans. Comput. Hum. Interact. 2018, 25, 1–32. [Google Scholar] [CrossRef]
- Mclaren F1 Race Dashboard. Available online: http://naimagon.com/sap-mclaren-race-dashboard/ (accessed on 24 April 2021).
- Guilford, J.P. Creativity. Am. Psychol. 1950, 5, 444–454. [Google Scholar] [CrossRef]
- Oltețeanu, A.M. Two Types of Evaluation: Human Creativity, Computational Creativity. In Cognition and the Creative Machine; Springer: Cham, Switzerland, 2020; pp. 41–54. [Google Scholar]
- Kaufman, J.C.; Plucker, J.; Baer, J. Essentials of Creativity Assessment; John Wiley & Sons: Hoboken, NJ, USA, 2008; Volume 53. [Google Scholar]
- Streiner, D.L. Starting at the Beginning: An introduction to Coefficient Alpha and Internal Consistency. J. Personal. Assess. 2003, 80, 99–103. [Google Scholar] [CrossRef] [PubMed]
- López, X.; Valenzuela, J.; Nussbaum, M.; Tsai, C.C. Some recommendations for the reporting of quantitative studies. Comput. Educ. 2015, 91, 106–110. [Google Scholar] [CrossRef]
- Clark, V.L.P. Meaningful integration within mixed methods studies: Identifying why, what, when, and how. Contemp. Educ. Psychol. 2019, 57, 106–111. [Google Scholar] [CrossRef]
- Hsieh, H.F.; Shannon, S.E. Three approaches to qualitative content analysis. Qual. Health Res. 2005, 15, 1277–1288. [Google Scholar] [CrossRef] [PubMed]
- Mahardika, I.K.; Delftana, R.E.; Rasagama, I.G.; Suprianto; Rasyid, A.N.; Sugiartana, I.W. Practicality of physics module based on contextual learning accompanied by multiple representations in physics learning on senior high school. J. Phys. Conf. Ser. 2020, 1521, 0222064. [Google Scholar] [CrossRef]
- Kandemir, M.A.; Karadeniz, I. Pre-Service Teachers’ Cognitive and Metacognitive Processes in Integrated STEM Modeling Activity. J. Educ. Sci. Environ. Health 2021, 7, 104–127. [Google Scholar] [CrossRef]
- Zepeda, C.D.; Hlutkowsky, C.O.; Partika, A.C.; Nokes-Malach, T.J. Identifying teachers’ supports of metacognition through classroom talk and its relation to growth in conceptual learning. J. Educ. Psychol. 2019, 111, 522–541. [Google Scholar] [CrossRef]
- Alsaleh, N.J. Teaching Critical Thinking Skills: Literature Review. TOJET Turk. Online J. Educ. Technol. 2020, 19, 21–35. [Google Scholar]
- Hargrove, R.A.; Nietfeld, J.L. The impact of metacognitive instruction on creative problem solving. J. Exp. Educ. 2014, 83, 291–318. [Google Scholar] [CrossRef]
- Haigh, M. Can investigative practical work in high school biology foster creativity? Res. Sci. Educ. 2006, 37, 123–140. [Google Scholar] [CrossRef]
- Abrahams, I.; Reiss, M.J. Practical work: Its effectiveness in primary and secondary schools in England. J. Res. Sci. Teach. 2012, 49, 1035–1055. [Google Scholar] [CrossRef]
- Greenyer, J.; Lochau, M.; Vogel, T. Explainable Software for Cyber-Physical Systems (ES4CPS). In GI Dagstuhl Seminar 19023; Leibniz Universität Hannover: Hannover, Germany, 2019; Available online: https://arxiv.org/pdf/1904.11851.pdf (accessed on 14 February 2024).
- Raza, A. Intelligent Tutoring Systems and Metacognitive Learning Strategies: A Survey. Educ. Res. Highlights Math. Sci. Technol. 2020, 2020, 47–63. [Google Scholar]
- Forehand, M. Bloom’s Taxonomy: Original and Revised. Emerg. Perspect. Learn. Teach. Technol. 2005, 8, 41–44. [Google Scholar]
- Shechtman, N.; Roschelle, J.; Feng, M.; Singleton, C. An Efficacy Study of a Digital Core Curriculum for Grade 5 Mathematics. AERA Open 2019, 5, 1–20. [Google Scholar] [CrossRef]
- Freeman, S.; Eddy, S.L.; McDonough, M.; Smith, M.K.; Okoroafor, N.; Jordt, H.; Wenderoth, M.P. Active learning increases student performance in science, engineering, and mathematics. Proc. Natl. Acad. Sci. USA 2014, 111, 8410–8415. [Google Scholar] [CrossRef] [PubMed]
- Dehe, B.; Bamford, D.; Olaniyan, O. Sport Analytics Utilization in The Sport Industry: A Structured Literature Review. In Proceedings of the POMS 2017, 28th Annual Conference, Seattle, WA, USA, 5–8 May 2017. [Google Scholar]
- Hughes, M.; Franks, I.; Dancs, H. Essentials of Performance Analysis in Sport; Routledge: Abingdon, UK, 2015. [Google Scholar] [CrossRef]
- Odball. Available online: https://www.kickstarter.com/projects/1535627339/oddball-the-drum-machine-crammed-in-a-ball (accessed on 24 April 2021).
- Drazan, J.F. Biomechanists can revolutionize the STEM Pipeline by engaging youth athletes in sport-science based STEM outreach. J. Biomech. 2020, 99, 109511. [Google Scholar] [CrossRef]




| Pre-Intervention Grades | |
|---|---|
| Control Group (n = 23) | |
| M | 5.34 |
| SD | 1.23 |
| Experimental Group (n = 27) | |
| M | 5.23 |
| SD | 1.25 |
| Fluency Pre | Fluency Post | Flex. Pre | Flex. Post | Original. Pre | Original. Post | |
|---|---|---|---|---|---|---|
| Control Group (n = 12) | ||||||
| M | 4.92 | 4.33 | 4.33 | 3.83 | 0.17 | 1.33 |
| SD | 2.75 | 2.42 | 2.39 | 1.64 | 0.58 | 1.30 |
| Experimental Group (n = 16) | ||||||
| M | 5.00 | 5.63 | 4.19 | 4.31 | 0.80 | 0.67 |
| SD | 2.22 | 3.73 | 1.52 | 2.09 | 1.47 | 0.90 |
| Exit Tickets (Post) | |
|---|---|
| Control Group (n = 23) | |
| M | 5.02 |
| SD | 0.85 |
| Experimental Group (n = 25) | |
| M | 5.56 |
| SD | 0.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guentulle, V.; Muñoz, R.; Nussbaum, M.; Madariaga, L. How Multiple Representations Using Cyber–Physical System to Teach Rectilinear Motion Improves Learning and Creativity. Educ. Sci. 2024, 14, 293. https://doi.org/10.3390/educsci14030293
Guentulle V, Muñoz R, Nussbaum M, Madariaga L. How Multiple Representations Using Cyber–Physical System to Teach Rectilinear Motion Improves Learning and Creativity. Education Sciences. 2024; 14(3):293. https://doi.org/10.3390/educsci14030293
Chicago/Turabian StyleGuentulle, Victoria, Rodolfo Muñoz, Miguel Nussbaum, and Leonardo Madariaga. 2024. "How Multiple Representations Using Cyber–Physical System to Teach Rectilinear Motion Improves Learning and Creativity" Education Sciences 14, no. 3: 293. https://doi.org/10.3390/educsci14030293
APA StyleGuentulle, V., Muñoz, R., Nussbaum, M., & Madariaga, L. (2024). How Multiple Representations Using Cyber–Physical System to Teach Rectilinear Motion Improves Learning and Creativity. Education Sciences, 14(3), 293. https://doi.org/10.3390/educsci14030293







