Assessing Disparities in Predictive Modeling Outcomes for College Student Success: The Impact of Imputation Techniques on Model Performance and Fairness
Abstract
1. Introduction
2. Bias in Education
3. Fairness in Predictive Modeling
4. Handling Missing Values in Education
5. Experiments
5.1. The Student Success Prediction Case Study
5.2. Experimental Setup
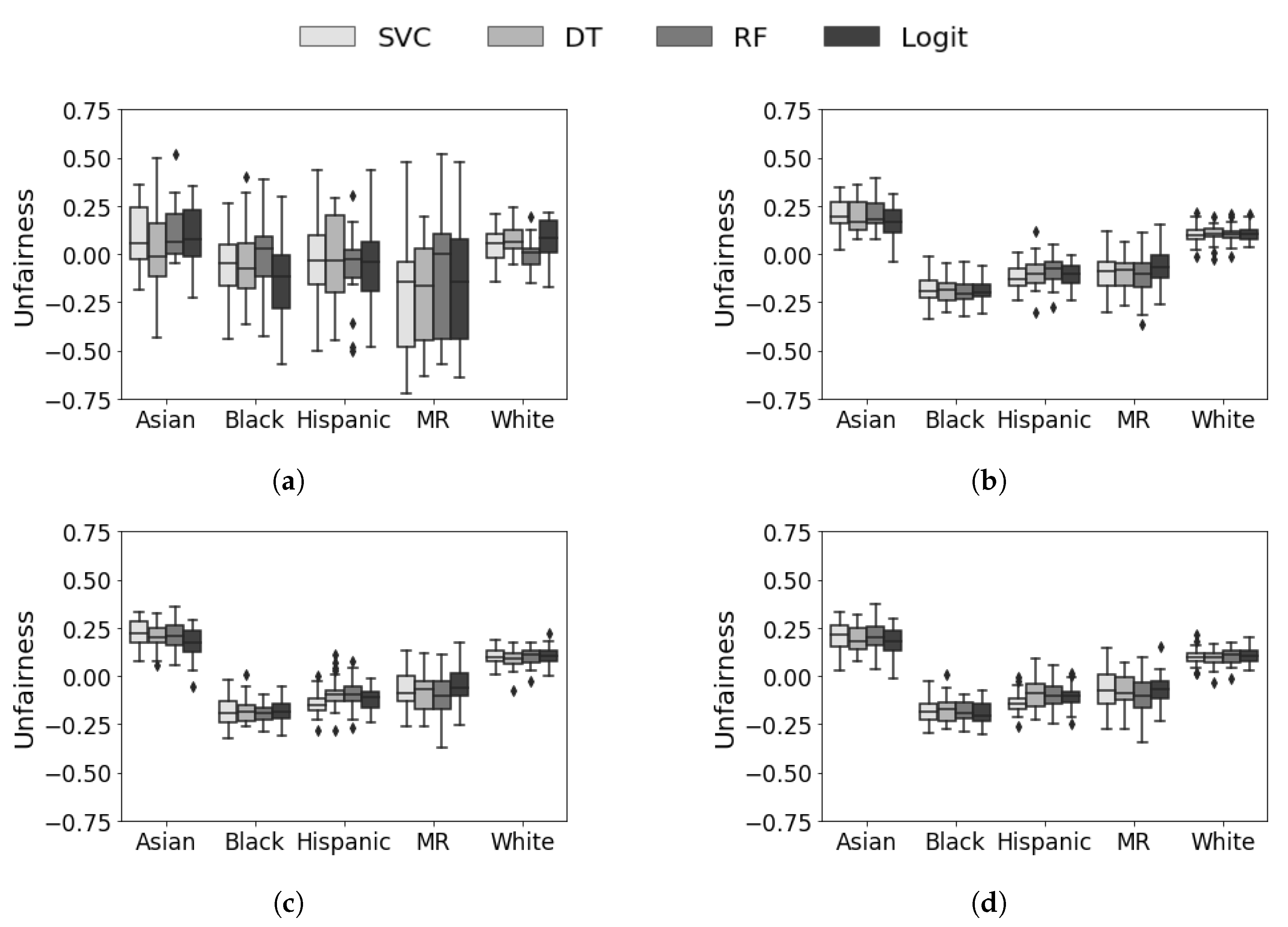
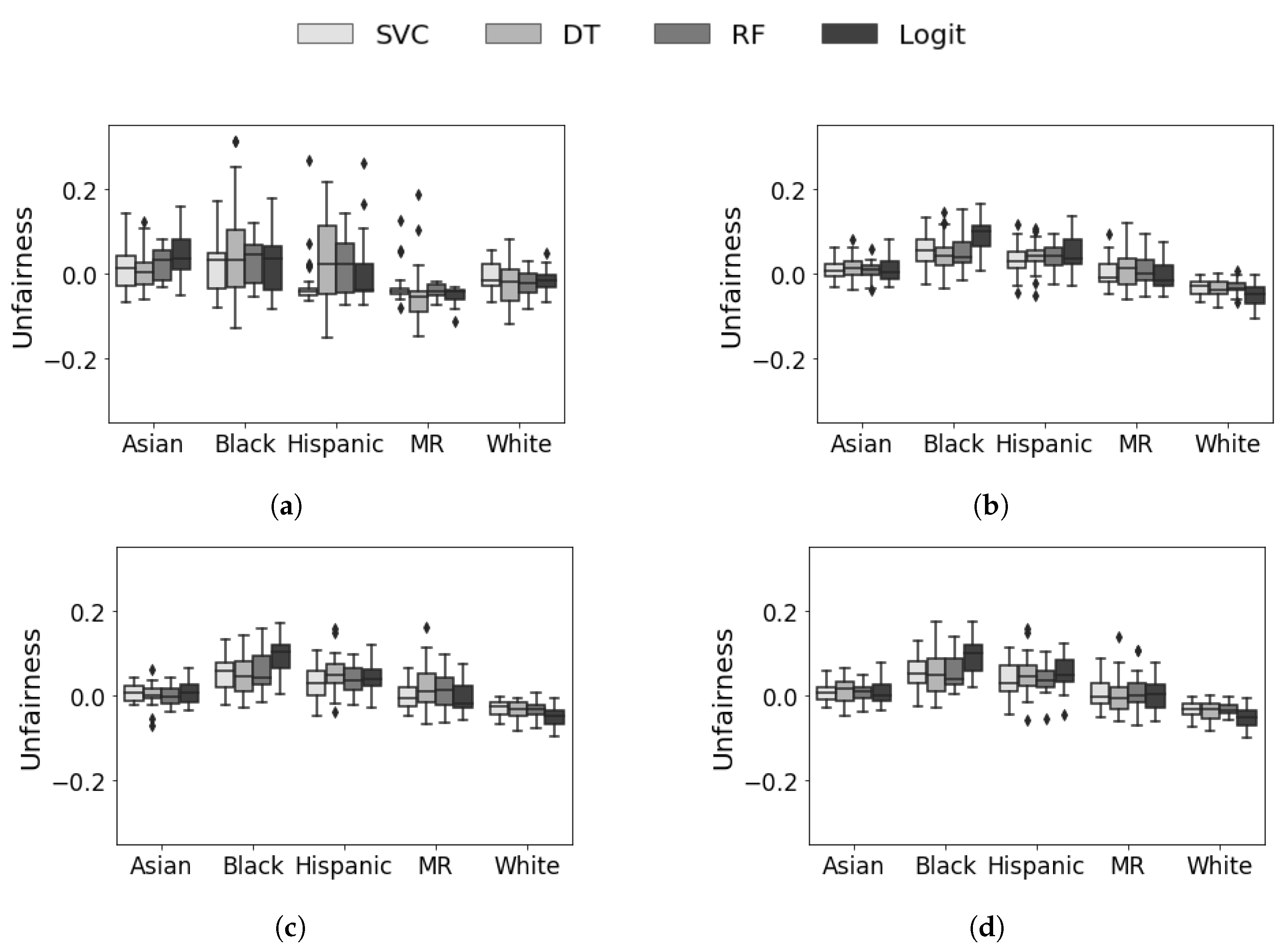
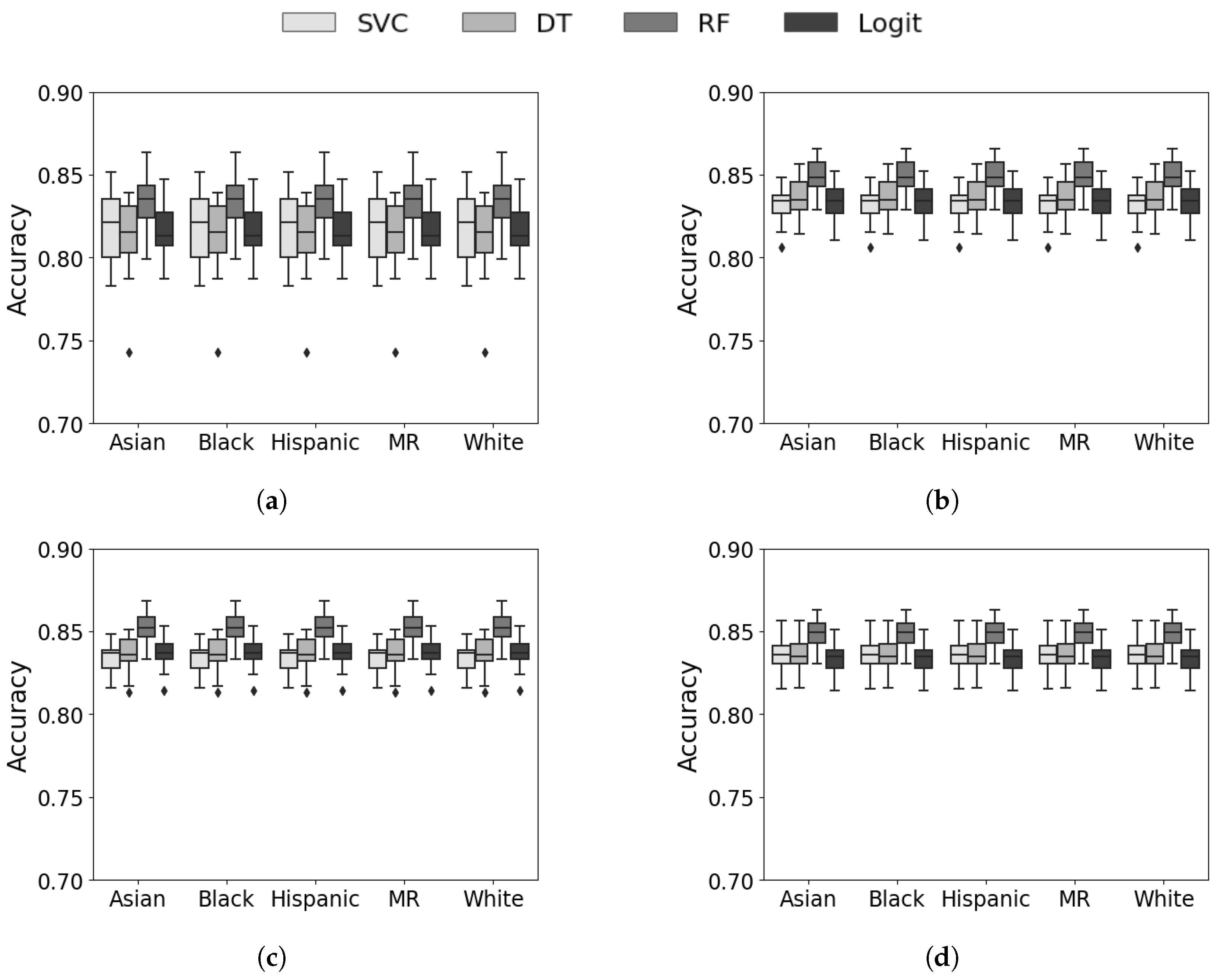
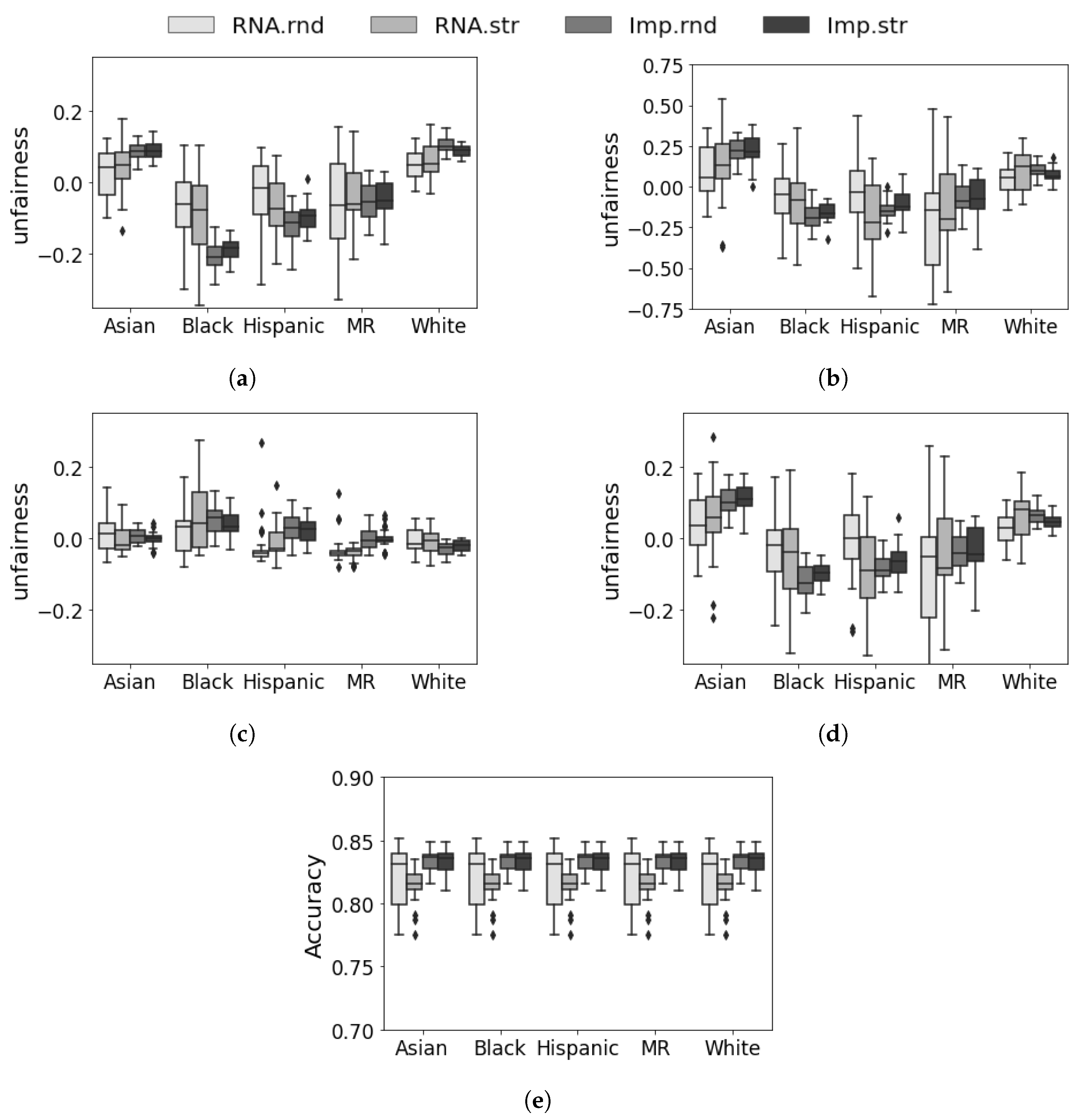
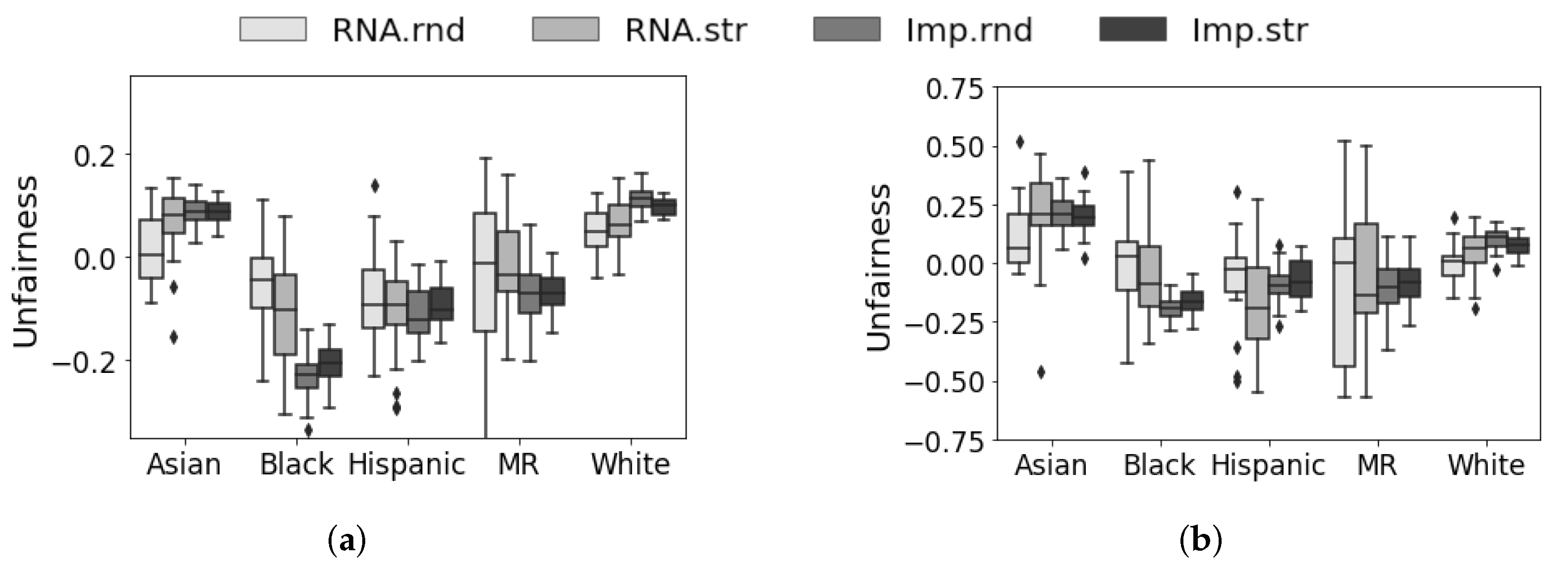
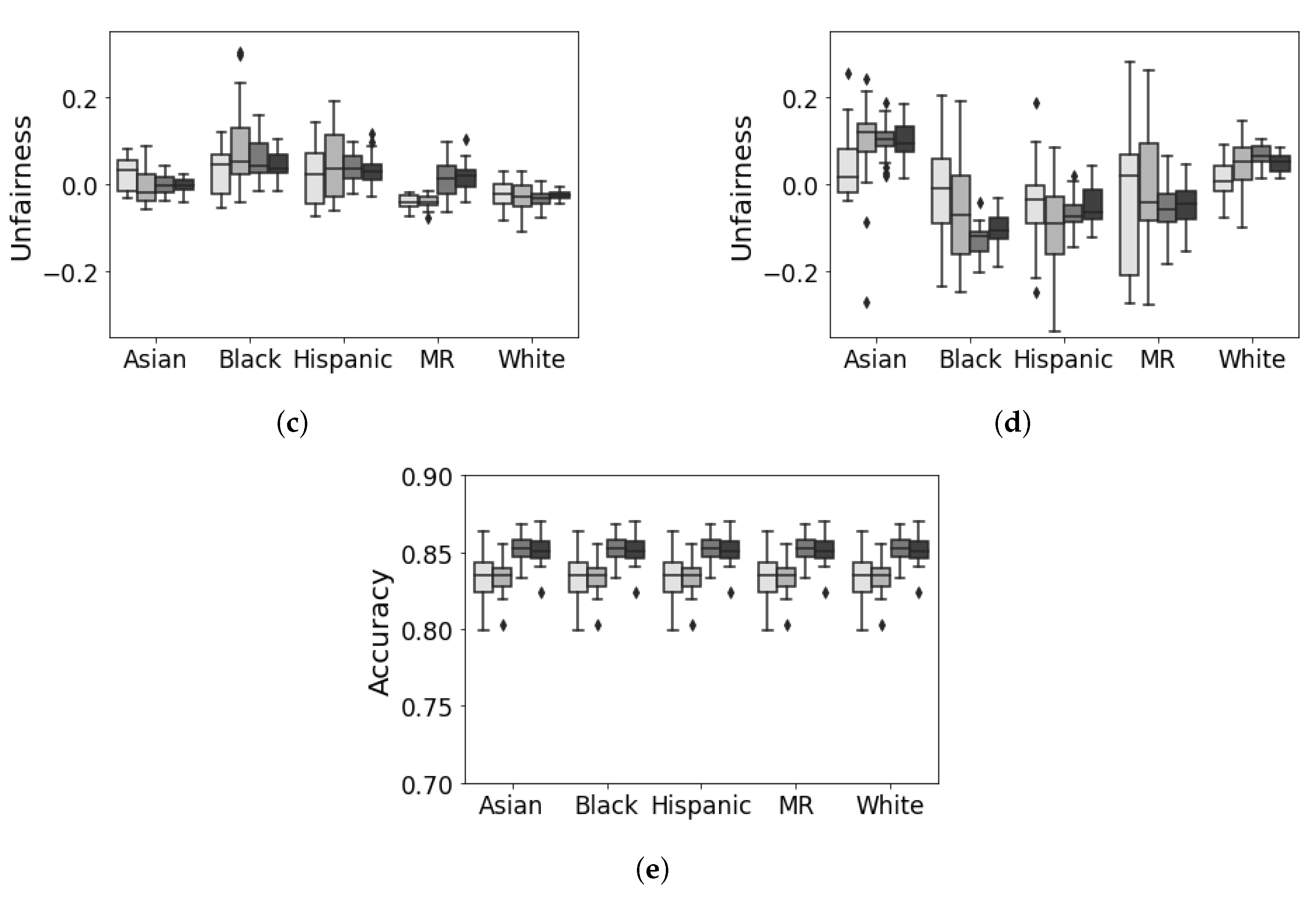
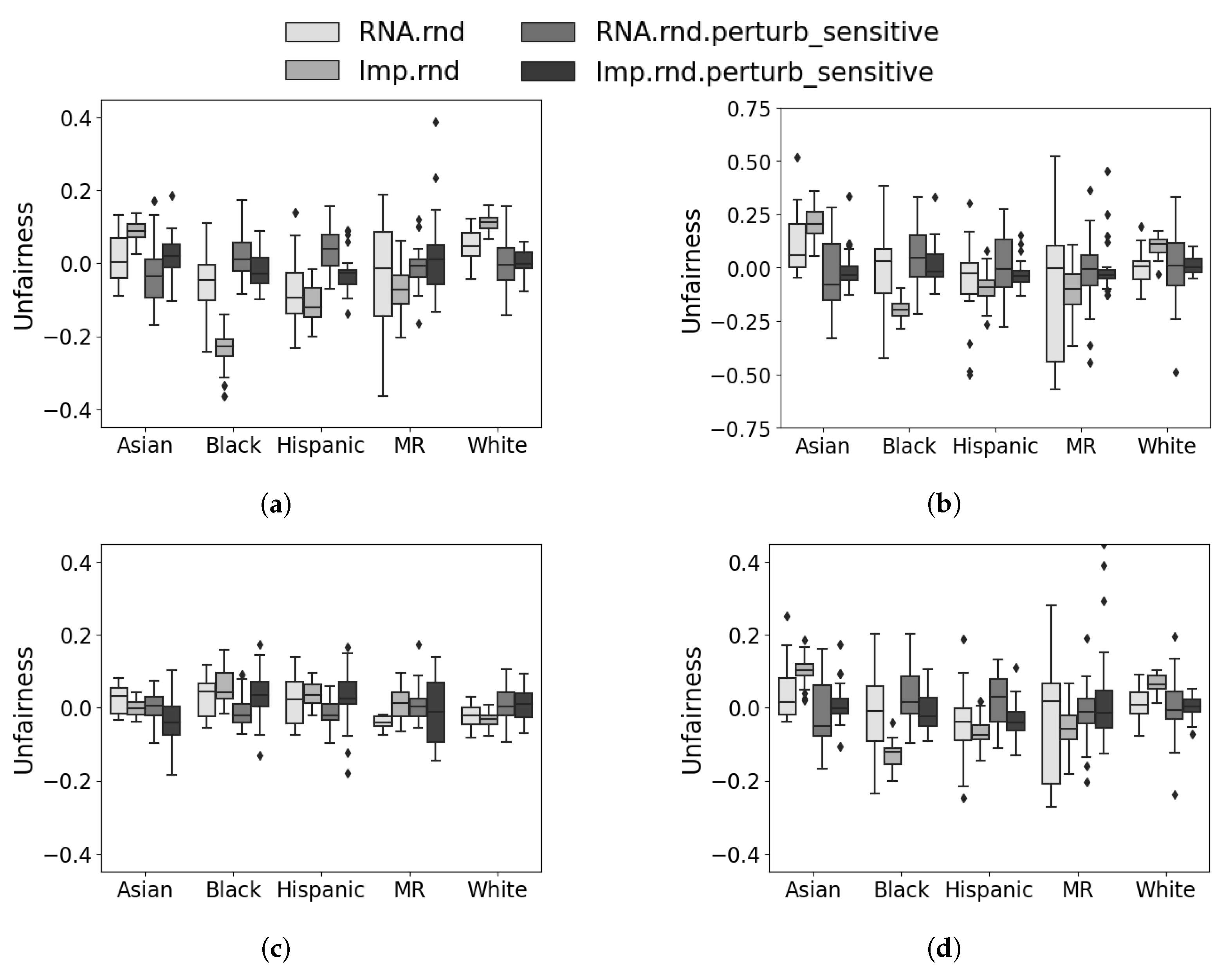
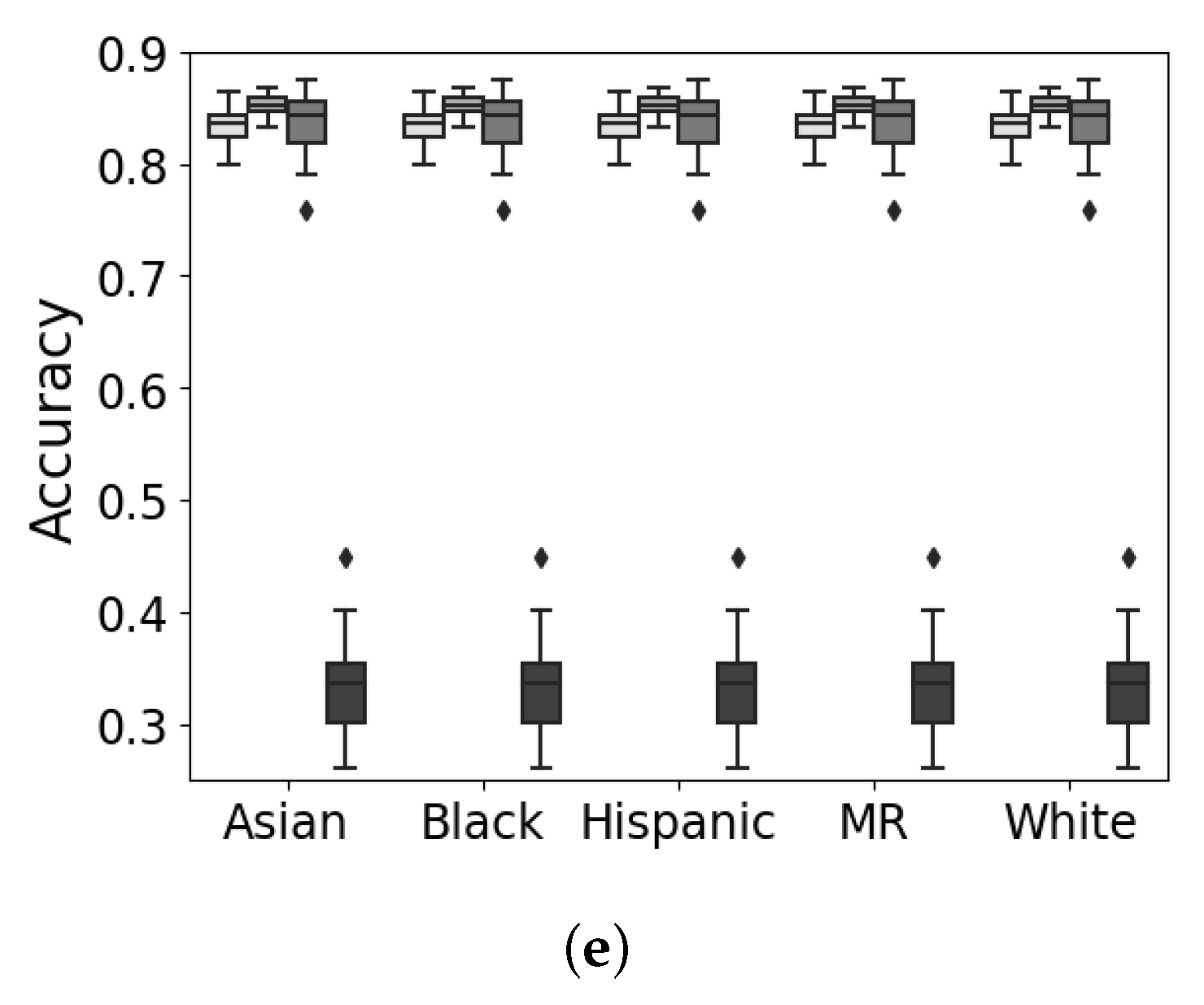
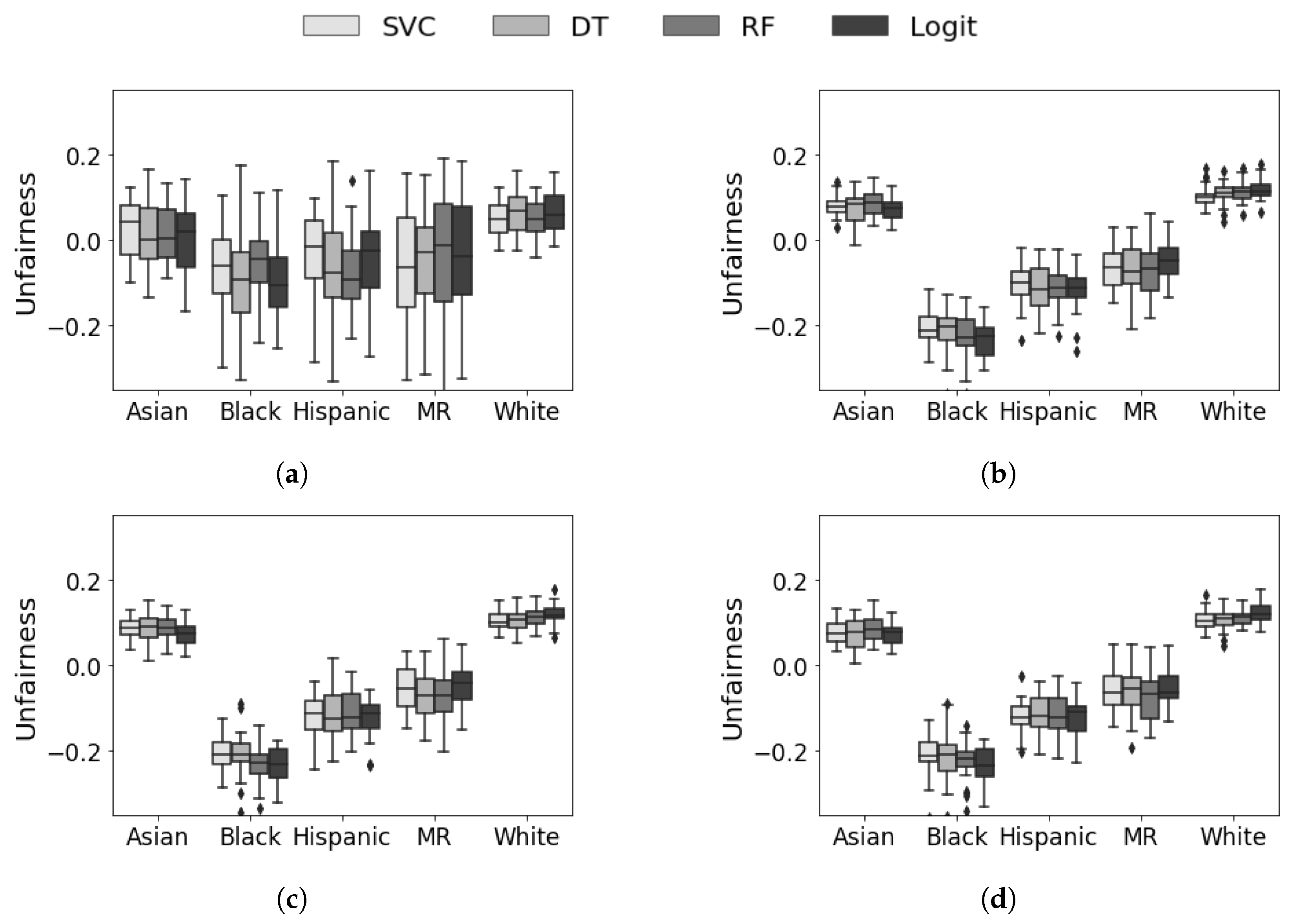
5.3. Prospective Evaluation
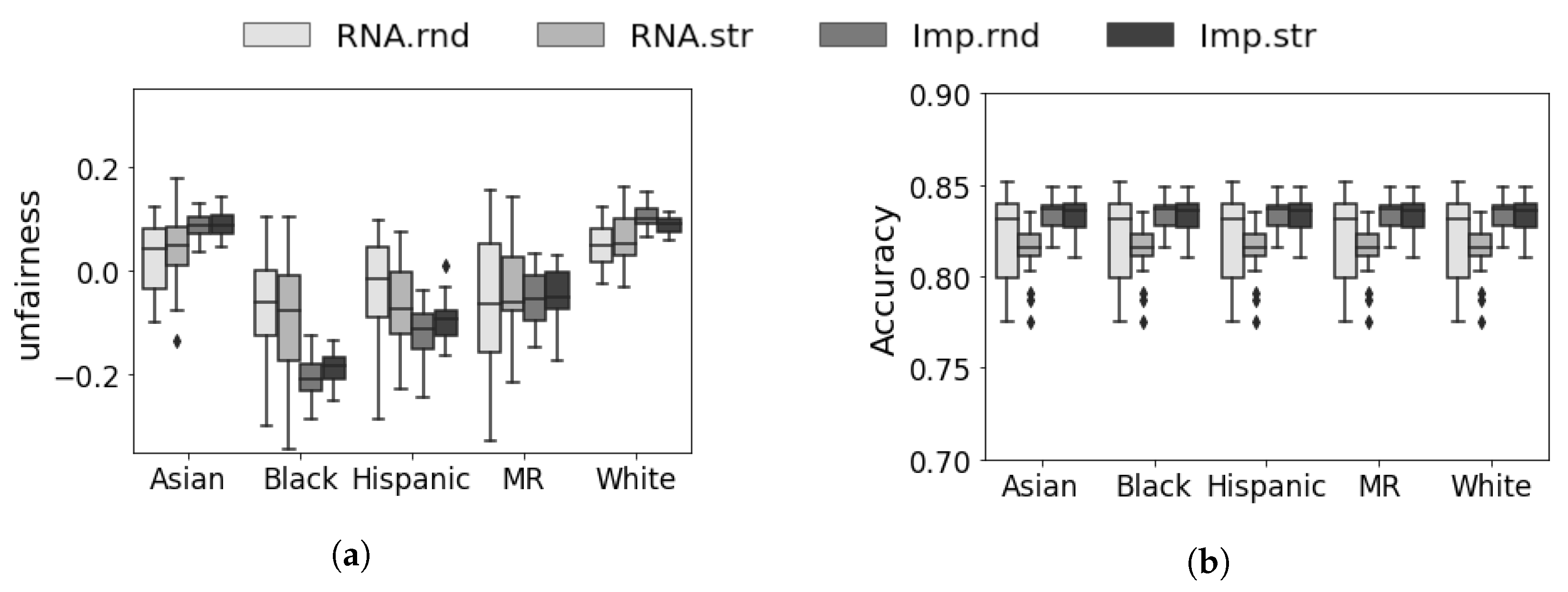
- RNA.rnd scenario: In this scenario, we follow the common practice in the ML literature and remove all rows with missing values before performing a train/test split. This ensures that the testing data follows the same distribution as the training data and serves as a baseline for comparison.
- RNA.str scenario: In this scenario, we remove missing values while ensuring stratification on both the “race” and “response” variables. This guarantees that each racial subgroup and success outcomes are well-represented in both the training and testing datasets, addressing potential biases introduced by missing data.
- Imp.rnd scenario: In this scenario, we split the entire dataset into train/test sets, perform an imputation technique on the training set to replace missing values, and transfer the trained imputer to replace missing values in the testing set. The imputation technique allows us to retain more data and potentially improve predictive performance.
- Imp.str scenario: Similar to the Imp.rnd scenario, we perform imputation on the training set and transfer the imputer to replace missing values in the testing set. However, we also consider stratification on the “race” and “response” variables to generate representative training and testing datasets, addressing potential biases related to imputation and ensuring fair evaluation.
- Imp.prop scenario: In this scenario, we aim to maintain the distribution of different racial groups in the train/test splits. We fix the fraction of observations from each racial group in the splits to match the fractions observed in the entire available dataset. This scenario helps assess the impact of imputation on fairness by preserving the representation of different racial subgroups.
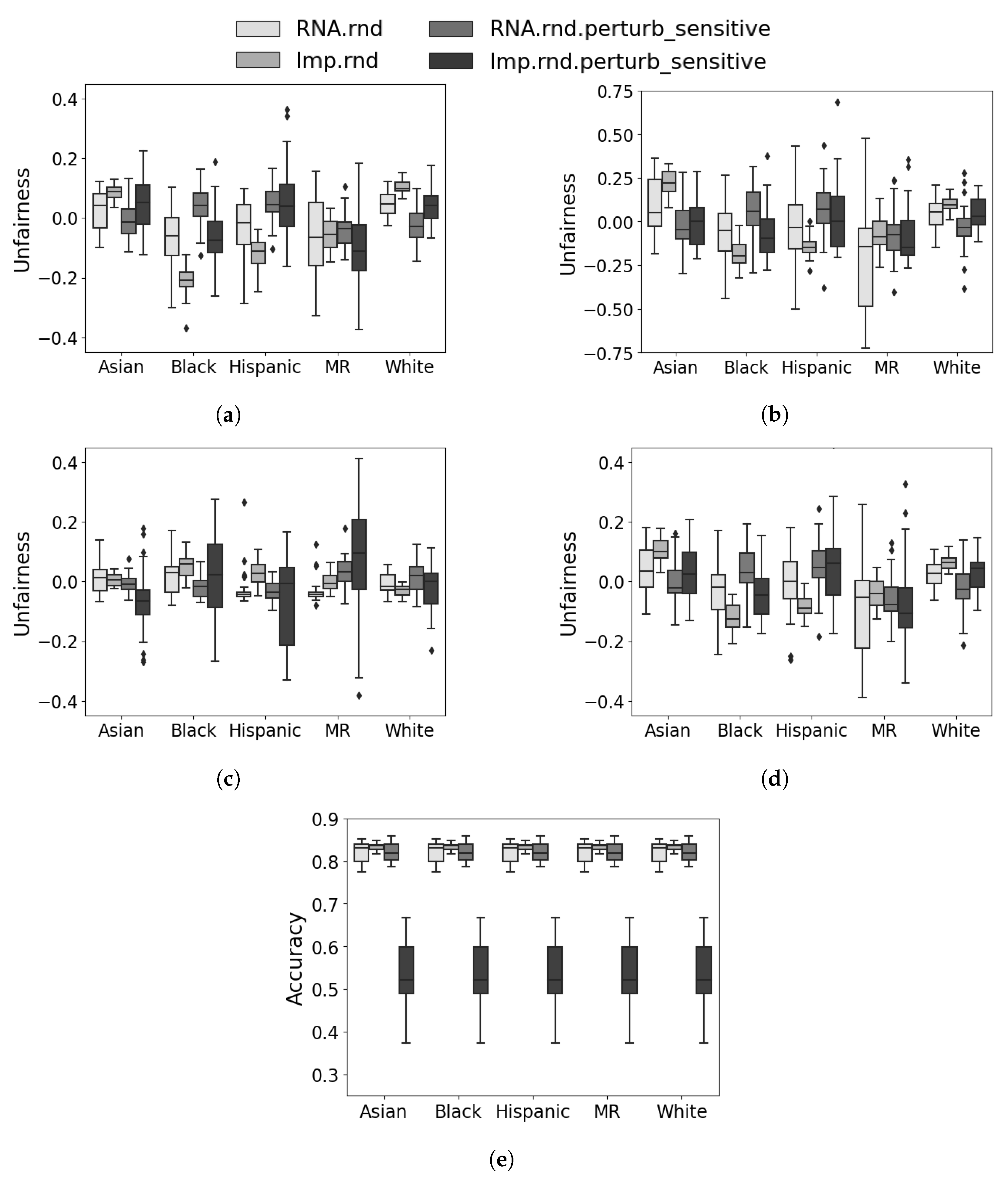
5.4. Discussion and Analysis
5.5. Summary of Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Ekowo, M.; Palmer, I. The Promise and Peril of Predictive Analytics in Higher Education: A Landscape Analysis. New America, 24 October 2016. [Google Scholar]
- Barocas, S.; Selbst, A.D. Big data’s disparate impact. Calif. Law Rev. 2016, 104, 671. [Google Scholar] [CrossRef]
- Cheema, J.R. A review of missing data handling methods in education research. Rev. Educ. Res. 2014, 84, 487–508. [Google Scholar] [CrossRef]
- Manly, C.A.; Wells, R.S. Reporting the use of multiple imputation for missing data in higher education research. Res. High. Educ. 2015, 56, 397–409. [Google Scholar] [CrossRef]
- Kwak, S.K.; Kim, J.H. Statistical data preparation: Management of missing values and outliers. Korean J. Anesthesiol. 2017, 70, 407. [Google Scholar] [CrossRef] [PubMed]
- Valentim, I.; Lourenço, N.; Antunes, N. The Impact of Data Preparation on the Fairness of Software Systems. In Proceedings of the 2019 IEEE 30th International Symposium on Software Reliability Engineering (ISSRE), Berlin, Germany, 28–31 October 2019; pp. 391–401. [Google Scholar]
- Fernando, M.P.; Cèsar, F.; David, N.; José, H.O. Missing the missing values: The ugly duckling of fairness in machine learning. J. Intell. Syst. 2021, 36, 3217–3258. [Google Scholar] [CrossRef]
- Kizilcec, R.F.; Lee, H. Algorithmic Fairness in Education. arXiv 2020, arXiv:2007.05443. [Google Scholar]
- Angwin, J.; Larson, J.; Mattu, S.; Kirchner, L. Machine Bias: Risk Assessments in Criminal Sentencing. ProPublica 2016. Available online: https://www.propublica.org/article/machine-bias-risk-assessments-in-criminal-sentencing (accessed on 5 January 2024).
- Feathers, T. Major Universities Are Using Race as a “High Impact Predictor” of Student Success. 2021. Available online: https://themarkup.org/news/2021/03/02/major-universities-are-using-race-as-a-high-impact-predictor-of-student-success (accessed on 5 January 2024).
- Marcinkowski, F.; Kieslich, K.; Starke, C.; Lünich, M. Implications of AI (un-) fairness in higher education admissions: The effects of perceived AI (un-) fairness on exit, voice and organizational reputation. In Proceedings of the ACM FAccT, Barcelona, Spain, 27–30 January 2020. [Google Scholar]
- Yu, R.; Li, Q.; Fischer, C.; Doroudi, S.; Xu, D. Towards accurate and fair prediction of college success: Evaluating different sources of student data. In Proceedings of the 13th International Conference on Educational Data Mining (EDM 2020), Virtual, 10–13 July 2020; pp. 292–301. [Google Scholar]
- Kondmann, L.; Zhu, X.X. Under the Radar—Auditing Fairness in ML for Humanitarian Mapping. arXiv 2021, arXiv:2108.02137. [Google Scholar]
- Kearns, M.; Neel, S.; Roth, A.; Wu, Z.S. Preventing fairness gerrymandering: Auditing and learning for subgroup fairness. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 2564–2572. [Google Scholar]
- Kleinberg, J.; Ludwig, J.; Mullainathan, S.; Rambachan, A. Algorithmic fairness. In AEA Papers and Proceedings; American Economic Association: Nashville, TN, USA, 2018; Volume 108, pp. 22–27. [Google Scholar]
- Kusner, M.J.; Loftus, J.R.; Russell, C.; Silva, R. Counterfactual fairness. arXiv 2017, arXiv:1703.06856. [Google Scholar]
- Cole, G.W.; Williamson, S.A. Avoiding resentment via monotonic fairness. arXiv 2019, arXiv:1909.01251. [Google Scholar]
- Olteanu, A.; Castillo, C.; Diaz, F.; Kiciman, E. Social data: Biases, methodological pitfalls, and ethical boundaries. Front. Big Data 2019, 2, 13. [Google Scholar] [CrossRef]
- Barocas, S.; Hardt, M.; Narayanan, A. Fairness and Machine Learning: Limitations and Opportunities. 2019. Available online: http://fairmlbook.org (accessed on 5 January 2024).
- Asudeh, A.; Jin, Z.; Jagadish, H. Assessing and remedying coverage for a given dataset. In Proceedings of the ICDE, Macao, China, 8–11 April 2019; pp. 554–565. [Google Scholar]
- Dwork, C.; Hardt, M.; Pitassi, T.; Reingold, O.; Zemel, R. Fairness through awareness. In Proceedings of the ITSC, Anchorage, AK, USA, 16–19 September 2012; pp. 214–226. [Google Scholar]
- Zafar, M.B.; Valera, I.; Rogriguez, M.G.; Gummadi, K.P. Fairness constraints: Mechanisms for fair classification. In Proceedings of the Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 20–22 April 2017; pp. 962–970. [Google Scholar]
- Feldman, M.; Friedler, S.A.; Moeller, J.; Scheidegger, C.; Venkatasubramanian, S. Certifying and removing disparate impact. In Proceedings of the SIGKDD, Sydney, Australia, 10–13 August 2015; ACM: New York, NY, USA, 2015; pp. 259–268. [Google Scholar]
- Kamiran, F.; Calders, T. Data preprocessing techniques for classification without discrimination. Knowl. Inf. Syst. 2012, 33, 1–33. [Google Scholar] [CrossRef]
- Calmon, F.; Wei, D.; Vinzamuri, B.; Ramamurthy, K.N.; Varshney, K.R. Optimized pre-processing for discrimination prevention. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 3992–4001. [Google Scholar]
- Zafar, M.B.; Valera, I.; Rodriguez, M.G.; Gummadi, K.P. Fairness constraints: Mechanisms for fair classification. arXiv 2015, arXiv:1507.05259. [Google Scholar]
- Zhang, H.; Chu, X.; Asudeh, A.; Navathe, S.B. OmniFair: A Declarative System for Model-Agnostic Group Fairness in Machine Learning. In Proceedings of the SIGMOD, Xi’an, China, 20–25 June 2021; pp. 2076–2088. [Google Scholar]
- Anahideh, H.; Asudeh, A.; Thirumuruganathan, S. Fair active learning. arXiv 2020, arXiv:2001.01796. [Google Scholar] [CrossRef]
- Pleiss, G.; Raghavan, M.; Wu, F.; Kleinberg, J.; Weinberger, K.Q. On fairness and calibration. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5680–5689. [Google Scholar]
- Zehlike, M.; Bonchi, F.; Castillo, C.; Hajian, S.; Megahed, M.; Baeza-Yates, R. Fa* ir: A fair top-k ranking algorithm. In Proceedings of the CIKM, Singapore, 6–10 November 2017; pp. 1569–1578. [Google Scholar]
- Žliobaitė, I. Measuring discrimination in algorithmic decision making. Data Min. Knowl. Discov. 2017, 31, 1060–1089. [Google Scholar] [CrossRef]
- Narayanan, A. Translation tutorial: 21 fairness definitions and their politics. In Proceedings of the ACM FAT*, New York, NY, USA, 23 August 2018. [Google Scholar]
- Gardner, J.; Brooks, C.; Baker, R. Evaluating the fairness of predictive student models through slicing analysis. In Proceedings of the 9th International Conference on Learning Analytics & Knowledge, Tempe, AZ, USA, 4–8 March 2019; pp. 225–234. [Google Scholar]
- Hardt, M.; Price, E.; Srebro, N. Equality of opportunity in supervised learning. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 3315–3323. [Google Scholar]
- Corbett-Davies, S.; Pierson, E.; Feller, A.; Goel, S.; Huq, A. Algorithmic decision making and the cost of fairness. In Proceedings of the SIGKDD, Halifax, NS, Canada, 13–17 August 2017; ACM: New York, NY, USA, 2017; pp. 797–806. [Google Scholar]
- Madras, D.; Creager, E.; Pitassi, T.; Zemel, R. Fairness through causal awareness: Learning causal latent-variable models for biased data. In Proceedings of the ACM FAT*, New York, NY, USA, 17 January 2019; pp. 349–358. [Google Scholar]
- Makhlouf, K.; Zhioua, S.; Palamidessi, C. On the applicability of machine learning fairness notions. ACM SIGKDD Explor. Newsl. 2021, 23, 14–23. [Google Scholar] [CrossRef]
- Anahideh, H.; Nezami, N.; Asudeh, A. On the choice of fairness: Finding representative fairness metrics for a given context. arXiv 2021, arXiv:2109.05697. [Google Scholar]
- Veale, M.; Van Kleek, M.; Binns, R. Fairness and accountability design needs for algorithmic support in high-stakes public sector decision-making. In Proceedings of the ACM CHI, Montreal, QC, Canada, 21–26 April 2018; pp. 1–14. [Google Scholar]
- Holstein, K.; Wortman Vaughan, J.; Daumé III, H.; Dudik, M.; Wallach, H. Improving fairness in machine learning systems: What do industry practitioners need? In Proceedings of the ACM CHI, Glasgow, UK, 4–9 May 2019; pp. 1–16. [Google Scholar]
- Chouldechova, A.; Benavides-Prado, D.; Fialko, O.; Vaithianathan, R. A case study of algorithm-assisted decision making in child maltreatment hotline screening decisions. In Proceedings of the ACM FAT*, New York, NY, USA, 23–24 February 2018; pp. 134–148. [Google Scholar]
- Mokander, J.; Floridi, L. Ethics-based auditing to develop trustworthy AI. arXiv 2021, arXiv:2105.00002. [Google Scholar] [CrossRef]
- Raji, I.D.; Smart, A.; White, R.N.; Mitchell, M.; Gebru, T.; Hutchinson, B.; Smith-Loud, J.; Theron, D.; Barnes, P. Closing the AI accountability gap: Defining an end-to-end framework for internal algorithmic auditing. In Proceedings of the ACM FAccT, Barcelona, Spain, 27–30 January 2020; pp. 33–44. [Google Scholar]
- Wilson, C.; Ghosh, A.; Jiang, S.; Mislove, A.; Baker, L.; Szary, J.; Trindel, K.; Polli, F. Building and auditing fair algorithms: A case study in candidate screening. In Proceedings of the ACM FAccT, Online, 3–10 March 2021; pp. 666–677. [Google Scholar]
- Allison, P.D. Missing Data; Sage Publications: New York, NY, USA, 2001. [Google Scholar]
- Rubin, D.B. Multiple imputation after 18+ years. J. Am. Stat. Assoc. 1996, 91, 473–489. [Google Scholar] [CrossRef]
- Troyanskaya, O.; Cantor, M.; Sherlock, G.; Brown, P.; Hastie, T.; Tibshirani, R.; Botstein, D.; Altman, R.B. Missing value estimation methods for DNA microarrays. Bioinformatics 2001, 17, 520–525. [Google Scholar] [CrossRef]
- Somasundaram, R.; Nedunchezhian, R. Evaluation of three simple imputation methods for enhancing preprocessing of data with missing values. Int. J. Comput. Appl. 2011, 21, 14–19. [Google Scholar] [CrossRef]
- Stephan, J.L.; Davis, E.; Lindsay, J.; Miller, S. Who Will Succeed and Who Will Struggle? Predicting Early College Success with Indiana’s Student Information System; REL 2015-078; Regional Educational Laboratory Midwest: Washington, DC, USA, 2015. [Google Scholar]
- Voyer, D.; Voyer, S.D. Gender differences in scholastic achievement: A meta-analysis. Psychol. Bull. 2014, 140, 1174. [Google Scholar] [CrossRef] [PubMed]
- Ramaswami, M.; Bhaskaran, R. A study on feature selection techniques in educational data mining. arXiv 2009, arXiv:0912.3924. [Google Scholar]
- Chamorro-Premuzic, T.; Furnham, A. Personality, intelligence and approaches to learning as predictors of academic performance. Personal. Individ. Differ. 2008, 44, 1596–1603. [Google Scholar] [CrossRef]
- Zlatkin-Troitschanskaia, O.; Schlax, J.; Jitomirski, J.; Happ, R.; Kühling-Thees, C.; Brückner, S.; Pant, H. Ethics and fairness in assessing learning outcomes in higher education. High. Educ. Policy 2019, 32, 537–556. [Google Scholar] [CrossRef]
- Filmer, D. The Structure of Social Disparities in Education: Gender and Wealth; The World Bank: Washington, DC, USA, 2000. [Google Scholar]
- Avdic, D.; Gartell, M. Working while studying? Student aid design and socioeconomic achievement disparities in higher education. Labour Econ. 2015, 33, 26–40. [Google Scholar] [CrossRef]
- Heitjan, D.F.; Basu, S. Distinguishing “missing at random” and “missing completely at random”. Am. Stat. 1996, 50, 207–213. [Google Scholar]
- Hamoud, A.; Hashim, A.S.; Awadh, W.A. Predicting student performance in higher education institutions using decision tree analysis. Int. J. Interact. Multimed. Artif. Intell. 2018, 5, 26–31. [Google Scholar] [CrossRef]
- Pelaez, K. Latent Class Analysis and Random Forest Ensemble to Identify At-Risk Students in Higher Education. Ph.D. Thesis, San Diego State University, San Diego, CA, USA, 2018. [Google Scholar]
- Agaoglu, M. Predicting instructor performance using data mining techniques in higher education. IEEE Access 2016, 4, 2379–2387. [Google Scholar] [CrossRef]
- Thompson, E.D.; Bowling, B.V.; Markle, R.E. Predicting student success in a major’s introductory biology course via logistic regression analysis of scientific reasoning ability and mathematics scores. Res. Sci. Educ. 2018, 48, 151–163. [Google Scholar] [CrossRef]
 race for: (a) Total credits earned; (b) Std Math/Reading score; (c) GPA.
race for: (a) Total credits earned; (b) Std Math/Reading score; (c) GPA.
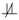 race for: (a) Total credits earned; (b) Std Math/Reading score; (c) GPA.
race for: (a) Total credits earned; (b) Std Math/Reading score; (c) GPA.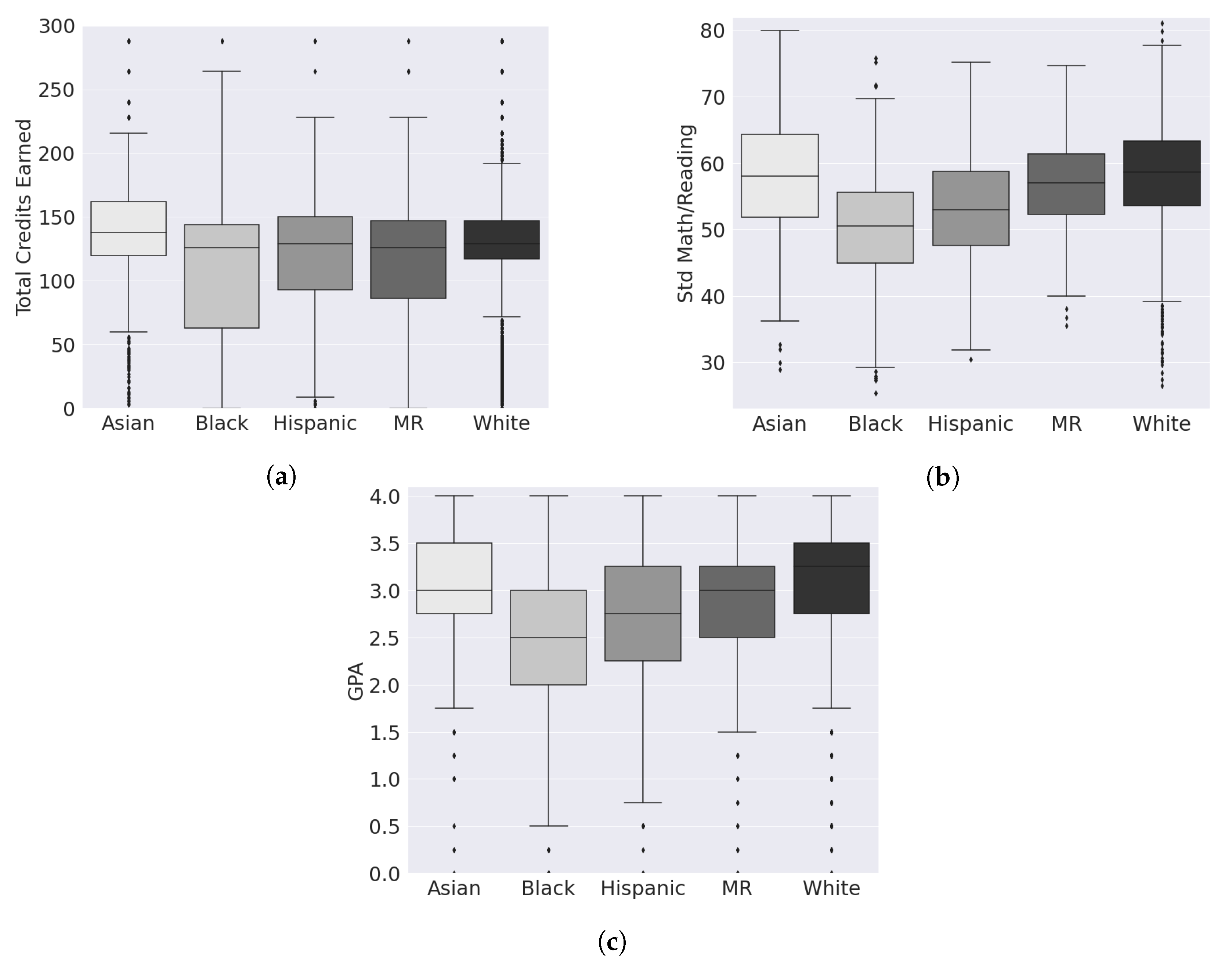

| Race | Percent of the Population |
|---|---|
| Asian | 11.13% |
| Black | 10.21% |
| Hispanic | 8.13% |
| Multiracial | 4.27% |
| White | 65.83% |
| Fairness Notion | Formulation |
|---|---|
| Statistical Parity (SP) | |
| Equalized Odds (EO) | |
| Equal Opportunity (EOP) | |
| Predictive Equality (PE) |
| Variables | % Missing | Variables | % Missing |
|---|---|---|---|
| Student-Teacher relationship | 33.32 | Std Math/Reading | 0.02 |
| F3-loan-owed | 25.33 | F3_Employment | 0 |
| %white teacher | 23.69 | F3_Highest level of education | 0 |
| %Black teacher | 19.85 | High school attendance | 0 |
| %Hispanic teacher | 17.72 | Family Composition | 0 |
| TV/video (h/day) | 14.87 | Race_Hispanic, race specified | 0 |
| Work (h/week) | 12.06 | F3_Separated no partner | 0 |
| F2_College entrance | 9.75 | F3_Never Married w partner | 0 |
| Generation | 7.06 | F3_Never Married no partner | 0 |
| F3_GPA (first attended) | 6.79 | F3_Married | 0 |
| F3_GPA (first year) | 6.78 | F3_Divorced/Widowed w partner | 0 |
| F1_TV/video (h/day) | 6.76 | F3_Divorced/Widowed no partner | 0 |
| F1_units in math | 6.13 | Race_White | 0 |
| Athletic level | 5.39 | Race_More than one race | 0 |
| F1_frequency of computer use | 4.27 | Race_Hispanic, no race specified | 0 |
| Total credits earned | 4.04 | School Urbanicity | 0 |
| F1_Std Math | 3.64 | Race_Black or African Amer | 0 |
| First-year credits earned | 3.48 | Race_Asian, Hawaii/Pac. Isl | 0 |
| F3_GPA (all) | 3.33 | Race_Amer. Indian/Alaska | 0 |
| F3_ total credits earned in Math | 3.01 | Gender_Male | 0 |
| F3_total credits earned in Science | 2.90 | Gender_Female | 0 |
| F1_Work (h/week) | 2.77 | Parents education | 0 |
| Homework (h/week) | 1.85 | Family income level | 0 |
| Number of school activities | 0.84 | F1_Drop out status | 0 |
| Native English speaker | 0.02 | F3_Separated w partner | 0 |
| Scenario | Missing Values | Train Test Data |
|---|---|---|
| RNA.rnd | Removed | 80:20 split, iid |
| RNA.str | Removed | 80:20 split, stratified on race and response variable, iid |
| Imp.rnd | Imputed | 80:20 split, iid |
| Imp.str | Imputed | 80:20 split, stratified on race and response variable, iid |
| Imp.prop | Imputed | 80:20 split and fixing the fraction of observations within each group to match the entire dataset, iid |
| RNA.rnd.perturb | Imputed | RNA.rnd scenario but the testing data is perturbed for non-sensitive attributes, non-iid |
| Imp.rnd.perturb | Imputed | Imp.rnd scenario but the testing data is perturbed for non-sensitive attributes, non-iid |
| Imp.prop.perturb | Imputed | Imp.prop scenario but the testing data is perturbed for non-sensitive attributes, non-iid |
| RNA.rnd.perturb.sensitive | Imputed | RNA.rnd scenario but the testing data is perturbed for the sensitive attributes, non-iid |
| Imp.rnd.perturb.sensitive | Imputed | Imp.rnd scenario but the testing data is perturbed for the sensitive attributes, non-iid |
| Scenario | Race | Pop. | Pop. | ||
|---|---|---|---|---|---|
| RNA.rnd | Asian | 95 | 26 | 20 | 22 |
| Black | 75 | 19 | 13 | 15 | |
| Hispanic | 75 | 17 | 13 | 14 | |
| Multiracial | 32 | 9 | 7 | 8 | |
| White | 712 | 175 | 128 | 145 | |
| Imp.rnd | Asian | 494 | 123 | 90 | 108 |
| Black | 452 | 114 | 62 | 77 | |
| Hispanic | 357 | 94 | 58 | 67 | |
| Multiracial | 190 | 47 | 30 | 35 | |
| White | 2923 | 727 | 526 | 598 | |
| Imp.prop | Asian | 494 | 123 | 90 | 100 |
| Black | 452 | 114 | 58 | 66 | |
| Hispanic | 361 | 90 | 55 | 65 | |
| Multiracial | 190 | 47 | 30 | 36 | |
| White | 2920 | 730 | 525 | 614 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nezami, N.; Haghighat, P.; Gándara, D.; Anahideh, H. Assessing Disparities in Predictive Modeling Outcomes for College Student Success: The Impact of Imputation Techniques on Model Performance and Fairness. Educ. Sci. 2024, 14, 136. https://doi.org/10.3390/educsci14020136
Nezami N, Haghighat P, Gándara D, Anahideh H. Assessing Disparities in Predictive Modeling Outcomes for College Student Success: The Impact of Imputation Techniques on Model Performance and Fairness. Education Sciences. 2024; 14(2):136. https://doi.org/10.3390/educsci14020136
Chicago/Turabian StyleNezami, Nazanin, Parian Haghighat, Denisa Gándara, and Hadis Anahideh. 2024. "Assessing Disparities in Predictive Modeling Outcomes for College Student Success: The Impact of Imputation Techniques on Model Performance and Fairness" Education Sciences 14, no. 2: 136. https://doi.org/10.3390/educsci14020136
APA StyleNezami, N., Haghighat, P., Gándara, D., & Anahideh, H. (2024). Assessing Disparities in Predictive Modeling Outcomes for College Student Success: The Impact of Imputation Techniques on Model Performance and Fairness. Education Sciences, 14(2), 136. https://doi.org/10.3390/educsci14020136





