Teachers’, Researchers’, and Educators’ Partnerships: The Effect of Co-Creation on Pupils’ Problem-Solving Performance in Mathematics
Abstract
1. Introduction
- (a)
- What is the status of primary school pupils’ mathematics problem-solving performance?
- (b)
- How did co-creation affect primary school pupils’ mathematics problem-solving performance?
- (c)
- How do the effects of co-creation on primary school pupils’ mathematics problem-solving performance vary across gender, school level, and school location?
2. Theoretical Framework
2.1. The Concept of Co-Creation
2.2. Effect of Co-Creation on Teachers’ Practices
2.3. Effect of Co-Creation on Pupils’ Learning and Performance
2.4. The Effects of Teachers and Researchers’ Partnerships on Students’ Learning
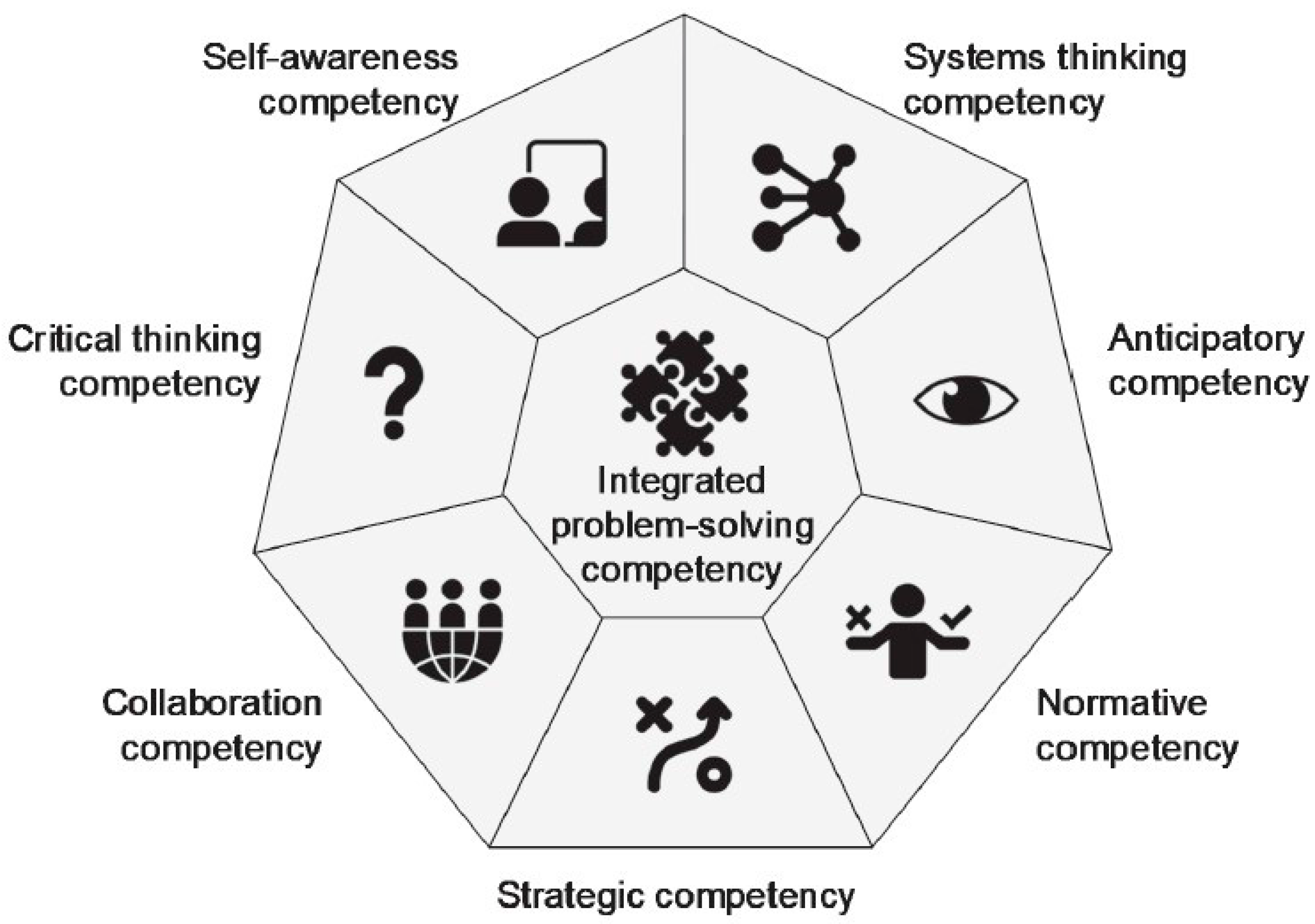
2.5. Conceptual and Theoretical Framework
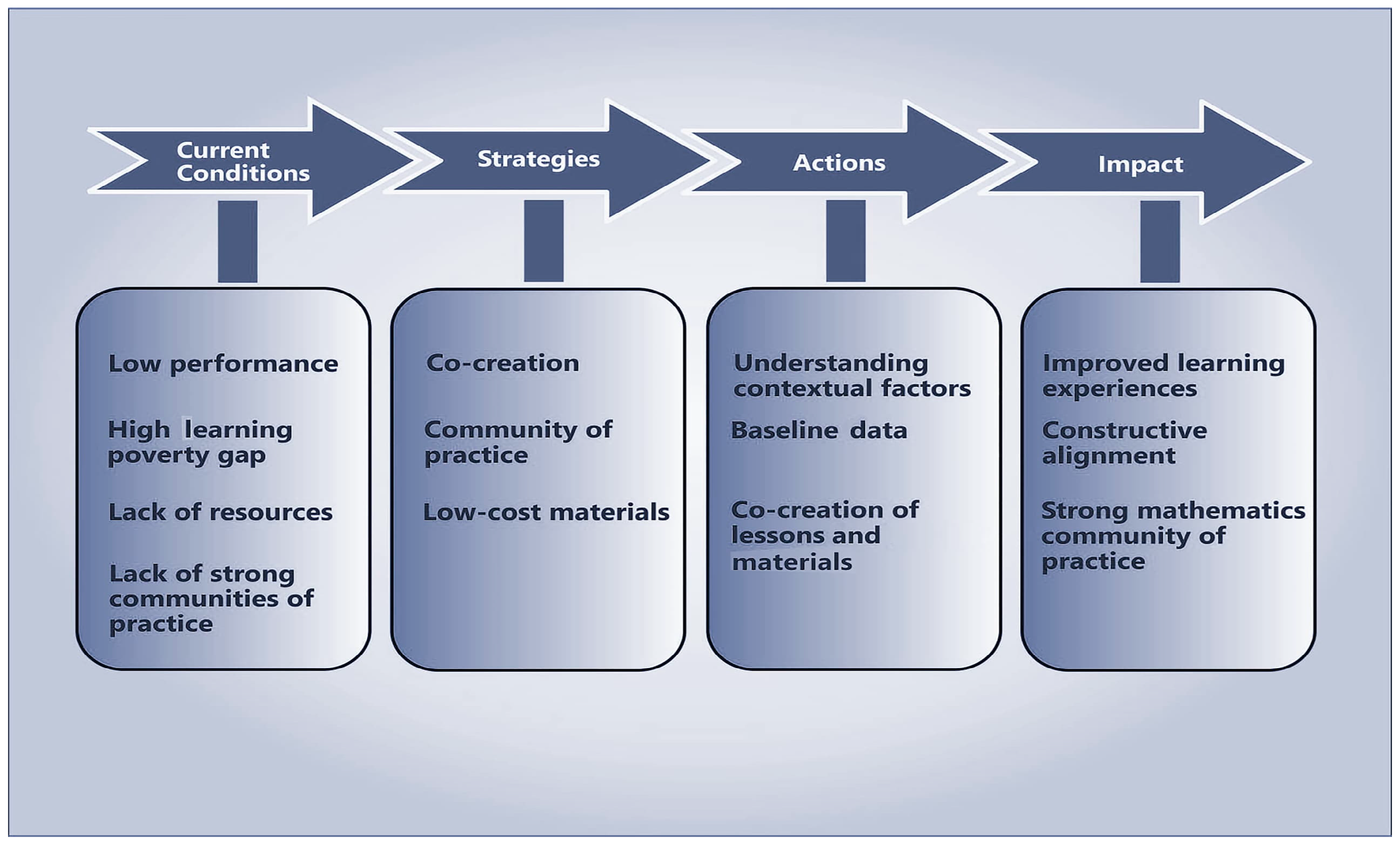
2.6. Theory of Change
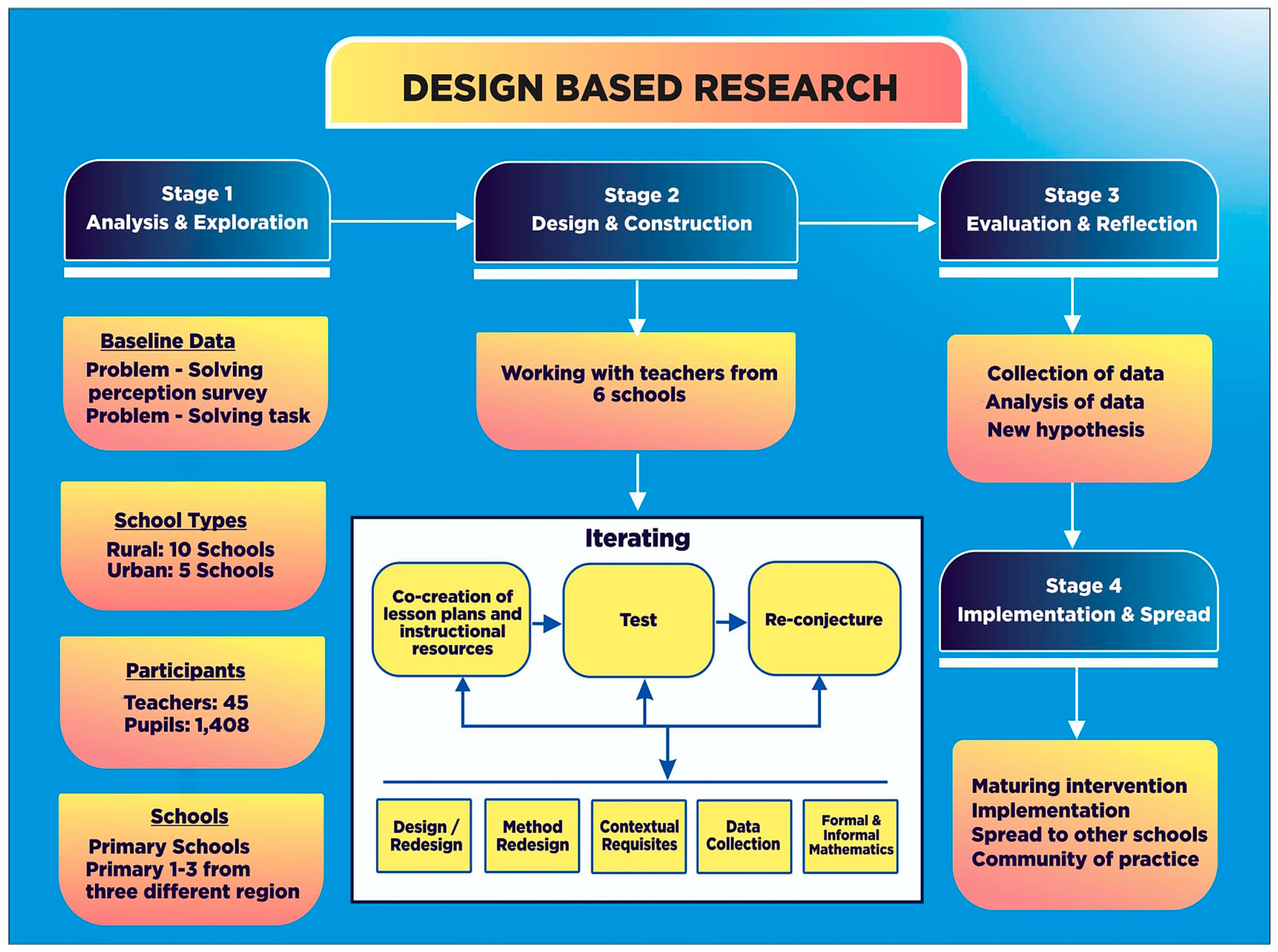
3. Materials and Methods
4. Results
4.1. Pupils’ Performance by Strand
4.2. Pupils’ Problem-Solving Performance and Gender
4.3. Pupils’ Problem-Solving Performance and School Location
4.4. Pupils’ Problem-Solving Performance and Class Level
4.5. Factorial ANOVA Composite Results
5. Discussion and Implication
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chou, B.K.P. The paradox of educational quality and education policy in Hong Kong and Macau: A postcolonial perspective. Chin. Educ. Soc. 2012, 45, 96–110. [Google Scholar] [CrossRef]
- Azevedo, J.P.; Goldember, D. “Learning for All: Within-Country Learning Inequality”. Published at Education for Global Development Series of the World Bank Blogs. 2020. Available online: https://blogs.worldbank.org/education/learning-all-within-country-learning-inequality (accessed on 12 November 2020).
- Azevedo, J.P. Learning Poverty in the Time of COVID-19: A Crisis Within a Crisis. 2020. Available online: https://openknowledge.worldbank.org/handle/10986/34850 (accessed on 12 November 2020).
- Crouch, L.; Rolleston, C.; Gustafsson, M. Eliminating global learning poverty: The importance of equalities and equity. Int. J. Educ. Dev. 2021, 82, 102250. [Google Scholar] [CrossRef]
- UNESCO. Education for All in Sub-Saharan Africa Assessment Report 2014; UNESCO: Paris, France, 2014; Available online: https://unesdoc.unesco.org/ark:/48223/pf0000232658 (accessed on 18 September 2023).
- UNESCO. Education for Sustainable Development Goals: Learning Objectives; UNESCO Publishing: Paris, France, 2017. [Google Scholar]
- Liljedahl, P.; Santos-Trigo, M.; Malaspina, U.; Bruder, R. Problem-solving in mathematics education. Int. Conf. Humanit. Soc. Sci. 2022, 2, 742–750. [Google Scholar] [CrossRef]
- Abidin, Z.; Ansari, B.I. Improving students’ mathematical communication skills and learning interest through problem-based learning model. J. Phys. Conf. Ser. 2020, 1460, 012047. [Google Scholar] [CrossRef]
- Mevarech, Z.; Bracha, K. Mathematics education and problem-solving skills in innovative societies. In Critical Maths for Innovative Societies: The Role of Metacognitive Pedagogies; OECD Publishing: Paris, France, 2014. [Google Scholar] [CrossRef]
- National Council for Curriculum and Assessment. Mathematics Core Programme; MoE: Accra, Ghana, 2020. [Google Scholar]
- Mereku, D.K. Sixty years of teacher education in Ghana: Successes, challenges and the way forward. Afr. J. Educ. Stud. Math. Sci. 2019, 15, 69–74. [Google Scholar] [CrossRef]
- Ampadu, E. Mathematics teachers’ perceptions about problem-solving: The case of Ghana. Oguaa Educ. 2019, 13, 1–18. [Google Scholar] [CrossRef]
- Brehmer, D.; Ryve, A.; Van Steenbrugge, H. Problem-solving in Swedish mathematics textbooks for upper secondary school. Scand. J. Educ. Res. 2016, 60, 577–593. [Google Scholar] [CrossRef]
- Aisy, N.M.R.; Mulyono; Walid. Analysis of students’ difficulties in mathematics problem-solving ability on number pattern material. J. Pijar Mipa 2022, 17, 706–711. [Google Scholar] [CrossRef]
- Lotz-Sisitka, H.; Wals, A.E.; Kronlid, D.; McGarry, D. Transformative, transgressive social learning: Rethinking higher education pedagogy in times of systemic global dysfunction. Curr. Opin. Environ. Sustain. 2015, 16, 73–80. [Google Scholar] [CrossRef]
- Klang, N.; Karlsson, N.; Kilborn, W.; Eriksson, P.; Karlberg, M. Mathematical problem-solving through cooperative learning—The importance of peer acceptance and friendships. In Frontiers in Education; Frontiers: Lausanne, Switzerland, 2021; p. 324. [Google Scholar]
- Kamp, A. CDIO: Can we continue the way we are? In Proceedings of the 17th International CDIO Conference, Hosted Online by Chulalongkom University & Rajamangala University of Technology Thanyaburi, Bangkok, Thailand, 21–23 June 2021.
- Bovill, C. Co-creation in learning and teaching: The case for a whole-class approach in higher education. High. Educ. 2019, 79, 1023–1037. [Google Scholar] [CrossRef]
- Cook-Sather, A.; Bovill, C.; Felten, P. Engaging Students as Partners in Learning and Teaching: A Guide for Faculty; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Prahalad, C.; Ramaswamy, V. Co-creating unique value with customers. Strategy Leadersh. 2004, 32, 4–9. [Google Scholar] [CrossRef]
- Bovill, C.; Cook-Sather, A.; Felten, P. Students as co-creators of teaching approaches, course design, and curricula: Implications for academic developers. Int. J. Acad. Dev. 2011, 16, 133–145. [Google Scholar] [CrossRef]
- Vygotsky, L.S. Mind in Society: The Development of Higher Psychological Processes; Harvard UP: Cambridge, MA, USA, 1978. [Google Scholar]
- Ryan, R.M.; Deci, E.L. Self-Determination Theory: Basic Psychological Needs in Motivation, Development, and Wellness; The Guilford Press: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Cambaya, E.J.; Tan, D.A. Enhancing students’ problem-solving skills and engagement in mathematics learning through contextualized instruction. Sci. Int. 2022, 34, 101–109. [Google Scholar]
- Hetmanenko, L. The role of interactive learning in mathematics education: Fostering student engagement and interest. Multidiscip. Sci. J. 2024, 6, e2024ss0733. [Google Scholar] [CrossRef]
- Sanders, E.B.; Stappers, P.J. Co-creation and the new landscapes of design. CoDesign 2008, 4, 5–18. [Google Scholar] [CrossRef]
- Matthews, K. Students as partners as the future of student engagement. Stud. Engagem. High. Educ. J. 2016, 1. Available online: https://sehej.raise-network.com/raise/article/view/380 (accessed on 10 May 2024).
- Bovill, C.; Woolmer, C. How conceptualisations of curriculum in higher education influence student-staff co-creation in and of the curriculum. High. Educ. 2018, 78, 407–422. [Google Scholar] [CrossRef]
- Könings, K.D.; Mordang, S.; Smeenk, F.; Stassen, L.; Ramani, S. Learner involvement in the co-creation of teaching and learning: AMEE Guide No. 138. Med. Teach. 2020, 43, 924–936. [Google Scholar] [CrossRef]
- Mercer-Mapstone, L.; Bovill, C. Equity and diversity in institutional approaches to student–staff partnership schemes in higher education. Stud. High. Educ. 2019, 45, 2541–2557. [Google Scholar] [CrossRef]
- Godbold, N.; Hung, T.Y.; Matthews, K.E. Exploring the role of conflict in co-creation of curriculum through engaging students as partners in the classroom. High. Educ. Res. Dev. 2021, 41, 1104–1118. [Google Scholar] [CrossRef]
- Vescio, V.; Ross, D.; Adams, A. A review of research on the impact of professional learning communities on teaching practice and student learning. Teach. Teach. Educ. 2008, 24, 80–91. [Google Scholar] [CrossRef]
- Cook-Sather, A. Student-faculty partnership in explorations of pedagogical practice: A threshold concept in academic development. Int. J. Acad. Dev. 2013, 19, 186–198. [Google Scholar] [CrossRef]
- Cordingley, P.; Bell, M.; Thomason, S.; Firth, A. The Impact of Collaborative CPD on Classroom Teaching and Learning. CUREE. 2005. Available online: http://www.curee.co.uk/resources/publications/impact-collaborative-cpd-classroom-teaching-and-learning (accessed on 14 August 2024).
- Nelson, J.; O’Beirne, C. Using Evidence in the Classroom: What Works and Why? Report; National Foundation for Educational Research: Slough, UK, 2014. [Google Scholar]
- Hennessy, S.; Mercer, N.; Warwick, P. A dialogic inquiry approach to working with teachers in developing classroom dialogue. Teach. Coll. Rec. 2011, 113, 1906–1959. [Google Scholar] [CrossRef]
- National Research Council (NRC). Standards for K-12 Engineering Education? National Academies Press: Washington, DC, USA, 2010. [Google Scholar]
- Assaraf, O.B.Z.; Orion, N. Development of system thinking skills in the context of earth system education. J. Res. Sci. Teach. 2005, 42, 518–560. [Google Scholar] [CrossRef]
- Main, P. Theory of Change. 2023. Available online: https://www.structural-learning.com/post/theory-of-change (accessed on 5 July 2024).
- Weiss, C.H. Nothing as practical as good theory: Exploring theory-based evaluation or comprehensive community initiatives for children and families. In New Approaches to Evaluating Community Initiatives: Concepts, Methods, and Contexts; Aspen Institute: Washington, DC, USA, 1995; Volume 1, pp. 65–92. [Google Scholar]
- Vogel, I. Review of the use of Theory of Change in International Development: Review report. 2012. Available online: www.theoryofchange.org/pdf/DFID_ToC_Review_VogelV7.pdf (accessed on 26 November 2024).
- UNDG. Theory of Change: UNDAF Companion Guidance. 2017. Available online: https://unsdg.un.org/sites/default/files/UNDG-UNDAF-Companion-Pieces-7-Theory-of-Change.pdf (accessed on 4 July 2024).
- White, H. Theory-based systematic reviews. J. Dev. Eff. 2018, 10, 17–38. [Google Scholar] [CrossRef]
- Anderson, T.; Shattuck, J. Design-based research: A decade of progress in education research? Educ. Res. 2012, 41, 16–25. [Google Scholar] [CrossRef]
- Major, L.; Watson, S.; Kimber, E. Developing instructional and pedagogical design for the Cambridge mathematics education project: A design-based research approach. Proc. Br. Soc. Res. Into Learn. Math. 2015, 35, 43–47. [Google Scholar]
- Doyle, E.; Buckley, P.; McCarthy, B. The impact of content co-creation on academic achievement. Assess. Eval. High. Educ. 2020, 46, 494–507. [Google Scholar] [CrossRef]

| Number | Percentage (%) | ||
|---|---|---|---|
| Gender | Male Female | 283 247 | 53.4 46.6 |
| Total | 530 | 100 | |
| Class | Primary 1 | 158 | 29.8 |
| Primary 2 | 177 | 33.4 | |
| Primary 3 | 195 | 36.8 | |
| Total | 530 | 100 | |
| School Location | Urban | 280 | 52.8 |
| Rural | 250 | 47.2 | |
| Total | 530 | 100 |
| Strands | Class/Level | ||
|---|---|---|---|
| Primary 1 | Primary 2 | Primary 3 | |
| Numbers and Algebra | Questions 1, 2, 5 | Questions 1, 2, 4 | Questions 1, 2, 3 |
| Measurement and Geometry | Questions 3a, b, c, d, e | Questions 5a, b, c, d | Questions 5a, b |
| Data | Question 4 | Questions 3a, b | Questions 4a, b, c, d |
| Baseline Data Results | Endline Data Results | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Strands | No. | Mean | SD | No. | Mean | SD | df | t | p |
| Numbers and Algebra | 530 | 2.62 | 1.34 | 530 | 3.05 | 1.41 | 528 | 5.09 | <0.001 |
| Geometry and Measurement | 530 | 2.60 | 2.07 | 530 | 3.63 | 1.73 | 528 | 8.73 | <0.001 |
| Data | 530 | 2.28 | 2.08 | 530 | 3.30 | 2.00 | 528 | 8.11 | <0.001 |
| Baseline Data Results | Endline Data Results | |||||||
|---|---|---|---|---|---|---|---|---|
| Strands | Gender | Mean | SD | Mean | SD | df | t | p |
| Numbers and Algebra | Male | 2.63 | 1.38 | 3.11 | 1.36 | 528 | 1.24 | 0.22 |
| Female | 2.60 | 1.32 | 2.98 | 1.47 | ||||
| Geometry and Measurement | Male | 2.65 | 2.06 | 3.58 | 1.74 | 528 | 0.41 | 0.68 |
| Female | 2.55 | 2.09 | 3.68 | 1.72 | ||||
| Data | Male | 2.29 | 2.10 | 3.27 | 2.01 | 528 | 0.24 | 0.84 |
| Female | 2.29 | 2.06 | 3.32 | 1.99 | ||||
| Baseline Data Results | Endline Data Results | |||||||
|---|---|---|---|---|---|---|---|---|
| Strands | School | Mean | SD | Mean | SD | df | t | p |
| Numbers and Algebra | Urban | 2.76 | 1.30 | 3.13 | 1.30 | 528 | 2.79 | 0.004 |
| Rural | 2.51 | 1.38 | 2.97 | 1.53 | ||||
| Geometry and Measurement | Urban | 2.95 | 2.07 | 3.64 | 1.79 | 528 | 3.30 | 0.001 |
| Rural | 2.33 | 2.04 | 3.62 | 1.68 | ||||
| Data | Urban | 1.93 | 2.01 | 3.15 | 2.01 | 528 | 2.98 | 0.003 |
| Rural | 2.58 | 2.09 | 3.46 | 1.99 | ||||
| Strand | Sum of Squares | df | Mean Square | F | p | |
|---|---|---|---|---|---|---|
| Numbers and Algebra | Between Groups | 64.26 | 2 | 32.12 | 16.93 | <0.001 |
| Within Groups | 2005.1 | 528 | 1.89 | |||
| Geometry and Measurement | Between Groups | 694.4 | 2 | 347.20 | 106.41 | <0.001 |
| Within Groups | 3448.8 | 528 | 3.26 | |||
| Data | Between Groups | 536.49 | 2 | 268.24 | 68.40 | <0.001 |
| Within Groups | 4145.33 | 528 | 3.92 |
| Source | Dependent Variables | Type III Sum of Squares | df | Mean Square | F | p |
|---|---|---|---|---|---|---|
| Corrected Model | Numbers and Algebra | 89.890 | 11 | 8.172 | 4.33 | <0.001 |
| Geometry and Measurement | 857.299 | 11 | 77.936 | 24.86 | <0.001 | |
| Data | 691.245 | 11 | 62.840 | 16.50 | <0.001 | |
| Intercept | Numbers and Algebra | 8518.78 | 1 | 8518.78 | 4510.1 | <0.001 |
| Geometry and Measurement | 10,122.23 | 1 | 10,122.23 | 3228.4 | <0.001 | |
| Data | 7758.08 | 1 | 7758.08 | 2037.4 | <0.001 | |
| Class | Numbers and Algebra | 66.42 | 2 | 33.21 | 17.58 | <0.001 |
| Geometry and Measurement | 734.44 | 2 | 367.22 | 117.12 | <0.001 | |
| Data | 536.22 | 2 | 268.10 | 70.41 | <0.001 | |
| Gender | Numbers and Algebra | 2.209 | 1 | 2.209 | 1.169 | 0.280 |
| Geometry and Measurement | 1.654 | 1 | 1.654 | 0.527 | 0.468 | |
| Data | 1.559 | 1 | 1.559 | 0.409 | 0.522 | |
| School Location | Numbers and Algebra | 16.62 | 1 | 16.62 | 8.80 | 0.003 |
| Geometry and Measurement | 72.04 | 1 | 72.04 | 22.98 | <0.001 | |
| Data | 56.27 | 1 | 56.27 | 14.78 | <0.001 | |
| Class and gender | Numbers and Algebra | 0.125 | 2 | 0.062 | 0.033 | 0.968 |
| Geometry and Measurement | 1.551 | 2 | 0.775 | 0.247 | 0.781 | |
| Data | 3.884 | 2 | 1.942 | 0.510 | 0.601 | |
| Gender, school and location | Numbers and Algebra | 0.731 | 1 | 0.731 | 0.387 | 0.534 |
| Geometry and Measurement | 0.177 | 1 | 0.177 | 0.057 | 0.812 | |
| Data | 0.953 | 1 | 0.953 | 0.250 | 0.617 | |
| Class andschool location | Numbers and Algebra | 4.054 | 2 | 2.027 | 1.073 | 0.342 |
| Geometry and Measurement | 94.992 | 2 | 47.49 | 15.15 | <0.001 | |
| Data | 93.551 | 2 | 46.78 | 12.28 | <0.001 | |
| Class, gender, and school Location | Numbers and Algebra | 1.064 | 2 | 0.532 | 0.282 | 0.755 |
| Geometry and Measurement | 1.886 | 2 | 0.943 | 0.301 | 0.740 | |
| Data | 6.519 | 2 | 3.259 | 0.856 | 0.425 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ampadu, E.; Narh-Kert, M.; Yeboah, R. Teachers’, Researchers’, and Educators’ Partnerships: The Effect of Co-Creation on Pupils’ Problem-Solving Performance in Mathematics. Educ. Sci. 2024, 14, 1328. https://doi.org/10.3390/educsci14121328
Ampadu E, Narh-Kert M, Yeboah R. Teachers’, Researchers’, and Educators’ Partnerships: The Effect of Co-Creation on Pupils’ Problem-Solving Performance in Mathematics. Education Sciences. 2024; 14(12):1328. https://doi.org/10.3390/educsci14121328
Chicago/Turabian StyleAmpadu, Ernest, Millicent Narh-Kert, and Rita Yeboah. 2024. "Teachers’, Researchers’, and Educators’ Partnerships: The Effect of Co-Creation on Pupils’ Problem-Solving Performance in Mathematics" Education Sciences 14, no. 12: 1328. https://doi.org/10.3390/educsci14121328
APA StyleAmpadu, E., Narh-Kert, M., & Yeboah, R. (2024). Teachers’, Researchers’, and Educators’ Partnerships: The Effect of Co-Creation on Pupils’ Problem-Solving Performance in Mathematics. Education Sciences, 14(12), 1328. https://doi.org/10.3390/educsci14121328





