Mastery of the Concept of Percentage and Its Representations in Finnish Comprehensive School Grades 7–9
Abstract
1. Introduction
- How did Finnish students in grades 7–9 perform on the problems related to the concepts of percentage and ratio?
- How did Finnish students in grades 7–9 express their mathematical thinking in solving the problems?
2. Theoretical Framework
2.1. Concepts of Percent and Ratio in the Finnish Core Curriculum (FCC)
2.2. Multimodal Expressions of Student’s Mathematical Thinking
3. Methods
3.1. Research Tasks
3.2. Participants and Data Collection
3.3. Analysis
4. Results
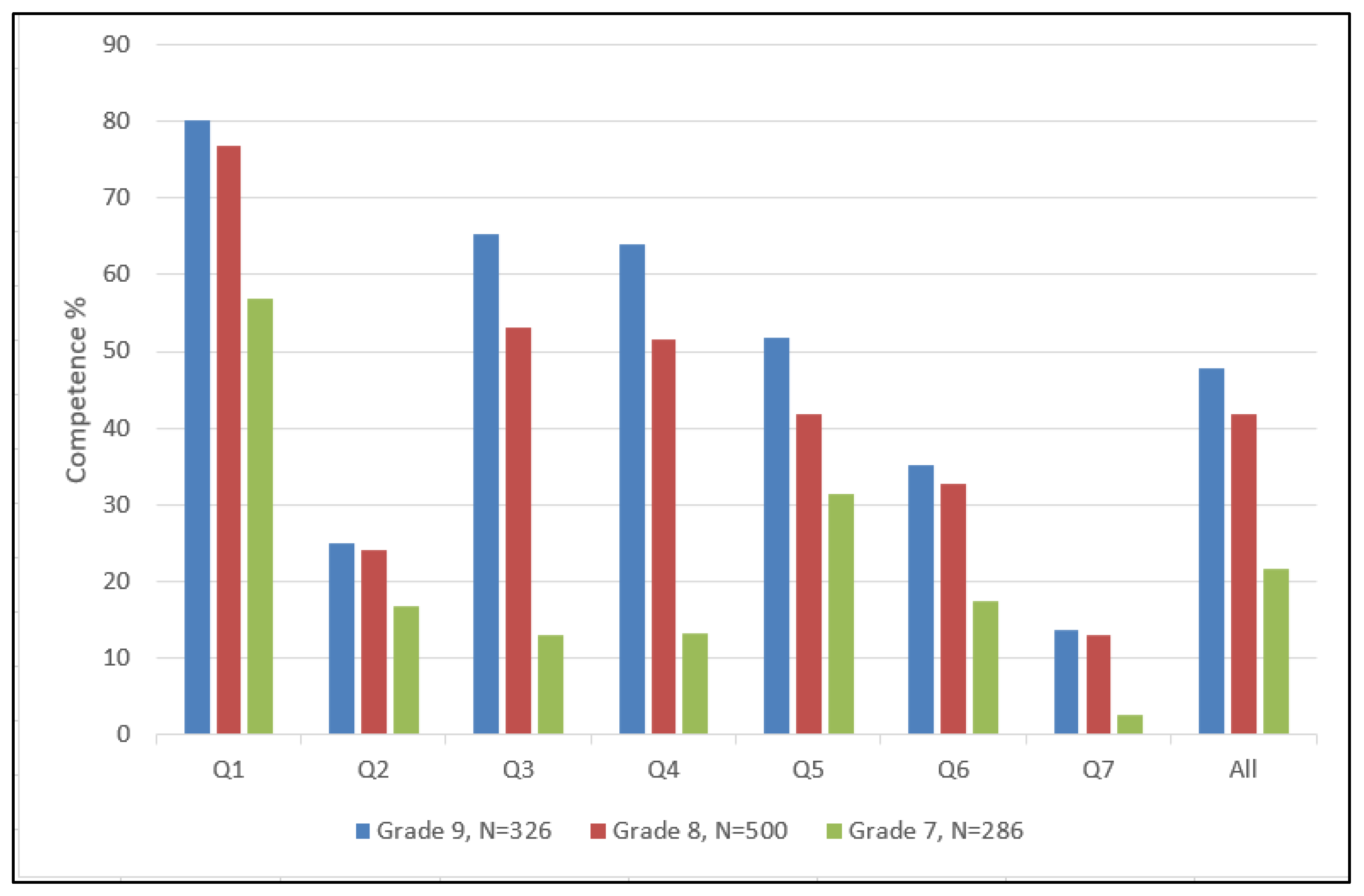
4.1. Students’ Understanding of Percentage and Ratio in the Questionnaire
4.2. Students’ Mathematical Thinking Processes in Solving Task Q2
5. Discussion
5.1. The Concept of Percentage
5.2. Multimodal Expressions in Students’ Solutions of the Task
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Code of Question | Question |
|---|---|
| Q1 | If a cake with a price of EUR 20 is sold at a 30% discount, what is the price after the discount? Write down the method and the answer. |
| Q2 | A company is selling 180 g of canned salmon; the weight of the salmon is 20% more than that sold in the previous year. What was the weight of the canned salmon sold in the previous year? (a) Write down the answers to the problem. (b) If you were to explain to a friend who does not understand how to find (a), how would you explain it in a way that is easy to understand using diagrams, tables, pictures, etc.? Write it down below. It is not necessary to use all the figures, tables, pictures, etc. |
| Q3 | The approximate land areas of Finland and Japan are shown in the table below. Country Land area Finland 340,000 km2 Japan 380,000 km2 (a) Write an equation to find the approximate percentage of Finnish land area based on the Japanese land area. It is not necessary to find the answer. |
| Q4 | The approximate land areas of Finland and Japan are shown in the table below. Country Land area Finland 340,000 km2 Japan 380,000 km2 (b) Write an equation to find the approximate percentage of the Japanese land area based on the Finnish land area. It is not necessary to find the answer. |
| Q5 | In lower secondary school A, 30% of the students commute to school by bicycle, 60% of which are boys. What percentage of boys commute to school by bicycle? Write the answer and how to find it. |
| Q6 | It is checked the annual number of visitors at the zoo from 2015 to 2017. The number of visitors in 2016 increased by 10% compared to the number of visitors in 2015. Conversely, the number of visitors in 2017 decreased by 10% compared to the number of visitors in 2016. How did the number of visitors in 2017 compare to the number of visitors in 2015? Check one correct answer from the following, (a) to (c), and write the reason for the answer. (a) Increased, (b) remained the same, or (c) decreased |
| Q7 | The ratio of the area of forest to the total area of town A was 50% ten years ago, but it was 30% this year. Write the answer and how to find it. The total area of town A has not changed between 10 years ago and this year. |
References
- Perkkilä, P.; Joutsenlahti, J. Academic Literacy Supporting Sustainability for Mathematics Education—A Case: Collaborative Working as a Meaning Making for “2/3”? In Transitioning to Quality Education; Jeronen, E., Ed.; Transitioning to Sustainability; MDPI: Basel, Switzerland, 2021; Volume 4, pp. 163–188. [Google Scholar] [CrossRef]
- Joutsenlahti, J.; Perkkilä, P. Sustainability Development in Mathematics Education—A Case Study of What Kind of Meanings Do Prospective Class Teachers Find for the Mathematical Symbol “”? Sustainability 2019, 11, 457. [Google Scholar] [CrossRef]
- Mullis, I.V.S.; Martin, M.O.; Foy, P. TIMSS 2007 International Mathematics Report: Findings from IEA’s Trends in International Mathematics and Science Study at the Fourth and Eighth Grades; Chestnut Hill: Boston College, MA, USA, 2008. [Google Scholar]
- Morgan, C. The place of pupil writing in learning, teaching and assessing mathematics. In Issues in Mathematics Teaching; Gates, P., Ed.; Routledge: London, UK, 2001; pp. 234–244. [Google Scholar]
- Perkkilä, P. Oppikirja ja uskomukset alkuopettajien matematiikan opetuksessa (Textbook and beliefs in the teaching of mathematics by primary teachers). In Tutkimus Kouluopetuksen Kehittämisessä; Ahtineva, A., Ed.; Faculty of Education, University of Turku: Turku, Finland, 2001; Volume 17, pp. 112–125. (In Finnish) [Google Scholar]
- Vosniadou, S. Capturing and modelling the process of conceptual change. Learn. Instr. 1994, 4, 45–69. [Google Scholar] [CrossRef]
- Adjiage, R.; Pluvinage, F. An Experiment in Teaching Ratio and Proportion. Educ. Stud. Math. 2002, 65, 149–175. [Google Scholar] [CrossRef]
- Joutsenlahti, J.; Kulju, P. Multimodal Languaging as a Pedagogical Model—A Case Study of the Concept of Division in School Mathematics. Educ. Sci. 2017, 7, 9. [Google Scholar] [CrossRef]
- Siegler, R.S.; Fazio, L.K.; Bailey, D.H.; Zhou, X. Fractions: The new frontier for theories for numerical development. Trends Cogn. Sci. 2013, 17, 13–19. [Google Scholar] [CrossRef] [PubMed]
- Fuson, K.C. Overcoming Errors in Fraction Computation by Emphasizing Unit Fractions, Length Drawings, and Student Explanations. Univers. J. Educ. Res. 2019, 7, 1663–1678. [Google Scholar] [CrossRef]
- Zhou, X.; Zeng, J. Three-component mathematics for students. Infant Child Dev. 2022, 31, e2283. [Google Scholar] [CrossRef]
- Brooks, C. Making Maths useful: How two teachers prepare adult learners to apply their numeracy skills in their lives outside the classroom. Adults Learn. Math. 2015, 10, 24–39. [Google Scholar]
- Freudenthal, H. Mathematics as An Educational Task; Springer Science & Business Media: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Zhou, X.; Li, M.; Li, L.; Zhang, Y.; Cui, J.; Liu, J.; Chen, C. The semantic system is involved in mathematical problem solving. NeuroImage 2018, 166, 360–370. [Google Scholar] [CrossRef] [PubMed]
- Swain, J.; Baker, E.; Holder, D.; Newmarch, B.; Coben, D. ‘Beyond the Daily Application’: Making Numeracy Teaching Meaningful to Adult Learners; National Research and Development Council (NRDC): London, UK, 2005. [Google Scholar]
- Díez-Palomar, J.; Flecha, A.; de Sanmamed, F.; García-Carrión, R.; Molina-Roldán, S. Pathways to equitable and sustainable education through the inclusion of roma students in learning mathematics. Sustainability 2018, 10, 2191. [Google Scholar] [CrossRef]
- FCC. Finnish Core Curriculum for Basic Education 2014. 2016. Available online: https://www.oph.fi/sites/default/files/documents/perusopetuksen_opetussuunnitelman_perusteet_2014.pdf (accessed on 5 August 2023).
- Park, J.; Guҫler, B.; McGrory, R. Teaching prospective teachers about fractions: Historical and pedagogical perspectives. Educ. Stud. Math. 2013, 82, 455–479. [Google Scholar] [CrossRef]
- Pantziara, M.; Philippou, G. Levels of students’ conception of fractions. Educ. Stud. Math. 2012, 79, 61–68. [Google Scholar] [CrossRef]
- Joutsenlahti, J. Lukiolaisen Tehtäväorientoituneen Matemaattisen Ajattelun Piirteitä: 1990-Luvun Pitkän Matematiikan Opiskelijoiden Matemaattisen Osaamisen Ja Uskomusten Ilmentämänä (Characteristics of Upper-Secondary Students’ Task-Oriented Mathematical Thinking: As Reflected in the Mathematical Knowledge and Beliefs of 1990’ s Long Mathematics Students). Doctoral Thesis, University Tampere, Tampere, Finland, 2005. Acta Universitatis Tamperensis 1061. Available online: https://trepo.tuni.fi/handle/10024/67453 (accessed on 8 August 2023).
- Kilpatrick, J.; Swaford, J.; Findell, B. Adding It Up: Helping Children Learn Mathematics; National Academy Press: Washington, DC, USA, 2001. [Google Scholar]
- Moschkovich, J.N. A sociocultural approach to academic literacy in mathematics for adolescent English learners: Integrating mathematical proficiency, practices, and discourse. In Multilingual Learners and Academic Literacies: Sociocultural Contexts of Literacy Development in Adolescents; Molle, D., Sato, E., Boals, T., Hedgspeth, C.A., Eds.; Routledge: New York, NY, USA, 2015; pp. 75–104. [Google Scholar]
- Moschkovich, J.N. Codeswitching and mathematics learners: How hybrid language practices provide resources for student participation in mathematical practices. In Codeswitching in the Classroom. Critical Perspectives on Teaching, Learning, Policy, and Ideology. Language Education Tensions in Global and Local Contexts; Swan, J.M., Faltis, C.J., Eds.; Routledge: New York, NY, USA; Center for Applied Linguistics: Washington, DC, USA, 2019. [Google Scholar]
- Moschkovich, J.N.; Zahner, W. Using the academic literacy in mathematics framework to uncover multiple aspects of activity during peer mathematical discussions. ZBM 2018, 50, 999–1011. [Google Scholar] [CrossRef]
- Joutsenlahti, J.; Rättyä., K. Kielentämisen käsite ainedidaktisissa tutkimuksissa (The concept of languaging in didactic studies). In Rajaton Tulevaisuus. Kohti Kokonaisvaltaista Oppimista. Proceedings of the Didactics Symposium, Jyväskylässä, Finland, 13–14 February 2014; Kauppinen, M., Rautiainen, M., Tarnanen, M., Eds.; Ainedidaktisia Tutkimuksia 8; University of Jyväskylä: Jyväskylä, Finland, 2014; pp. 45–61. [Google Scholar]
- FPEC. The Finnish Pre-Primary Education Curriculum 2014. 2016. Available online: https://www.oph.fi/sites/default/files/documents/esiopetuksen_opetussuunnitelman_perusteet_2014.pdf (accessed on 5 August 2023).
- NCC. National Core Curriculum for Education. 2019. Available online: https://www.oph.fi/sites/default/files/documents/lukion_opetussuunnitelman_perusteet_2019.pdf (accessed on 5 August 2023).
- Kumakura, K.; Kunimune, S.; Matsumoto, S. A survey study on the understanding of proportion among junior and senior high school students. Bull. Cent. Educ. Pract. 2019, 29, 80–89. [Google Scholar]
- Kambara, K. Understanding “proportion” and mathematical identity: A study of Japanese elementary school teachers. LUMAT Int. J. Math Sci. Technol. Educ. 2022, 10, 239–255. [Google Scholar] [CrossRef]
- Guideline of the Board on Research Integrity TENK 2019. Available online: https://tenk.fi/en/research-integrity-ri (accessed on 15 August 2023).
- Tuomi, J.; Sarajärvi, A. Laadullinen Tutkimus ja Sisällönanalyysi (Qualitative Research and Content Analysis); Tammi: Helsinki, Finland, 2018. [Google Scholar]
- Schreier, M. Qualitative Content Analysis in Practice, 1st ed.; SAGE Publications, Inc.: London, UK, 2012. [Google Scholar] [CrossRef]
- Lepik, M.; Grevholm, B.; Viholainen, A. Using textbooks in the mathematics classroom—The teachers’ view. Nord. Stud. Math. Educ. 2015, 20, 129–156. [Google Scholar]
- Hargreaves, A.; Fink, D. Sustaining leadership. Phi Delta Kappan 2003, 84, 693–700. [Google Scholar] [CrossRef]
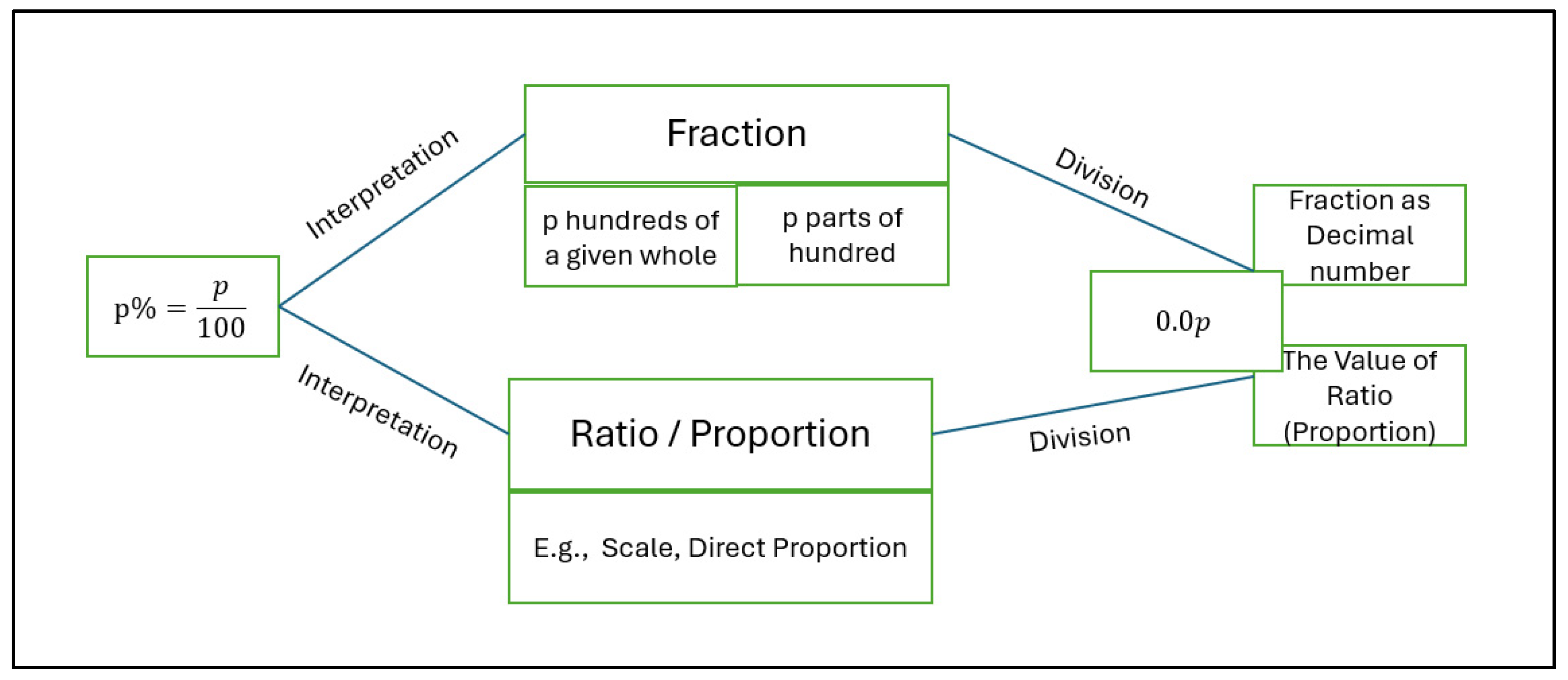
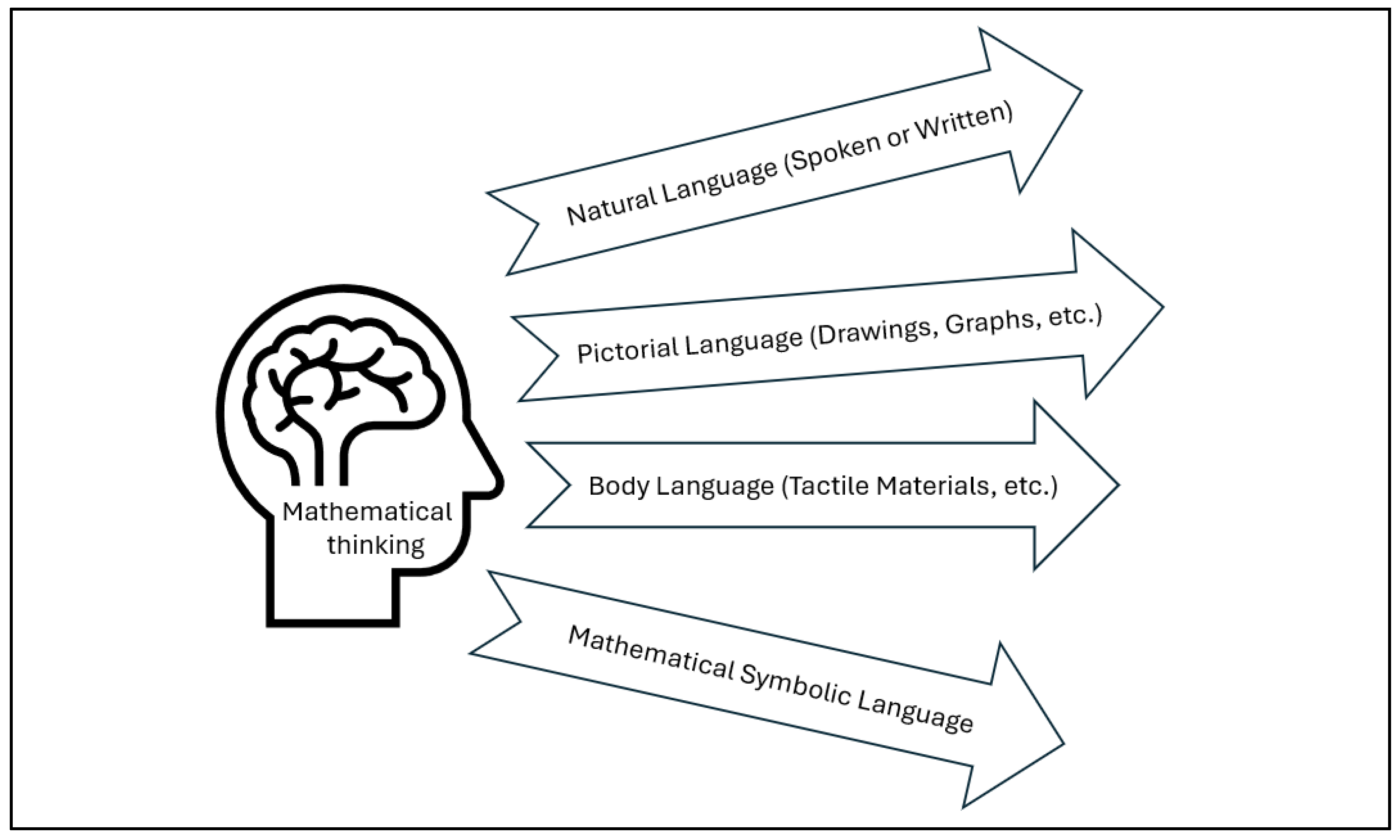
| Grades | Percentage | Ratio |
|---|---|---|
| 3–6 | Understanding the percentage and its value and practice calculating them in simple cases. Connections between the concepts of fractions, decimals, and percentages. | Scale Enlargement Reduction |
| 7–9 | Ensure understanding of the concept of the percentage. Practice calculating the percentage and counting the amount of a whole number indicated by the percentage. Learn to calculate the changed value, the base value, the percentage of change, and the reference percentage. | Proportion Direct proportionality Inverse proportion |
| Grade Level/ Type of Expression | Grade 7 (N = 9) | Grade 8 (N = 69) | Grade 9 (N = 45) | Sum (N = 123) |
|---|---|---|---|---|
| Pictures, etc. | 4 | 9 | 9 | 22 |
| Rectangle diagram | 0 | 7 | 5 | 12 |
| Line segment diagram | 0 | 5 | 0 | 5 |
| Tables | 0 | 9 | 11 | 20 |
| Pie chart | 1 | 2 | 0 | 3 |
| Arrows | 1 | 7 | 1 | 9 |
| Expressions only | 0 | 18 | 14 | 32 |
| Other (including no answer | 3 | 12 | 5 | 20 |
| Halfway through) |
| Student’s Response Number and Grade Level | Mathematical Symbolic Language | Pictorial Language | Natural Language |
|---|---|---|---|
| Student 142 Grade 7 | 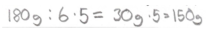 | Last year 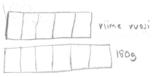 (A rectangle diagram) | “20% is , so you have to divide by six, because that is , of last year’s weight, and then multiply by five to get last year’s weight.” |
| Student 38 Grade 8 | 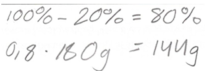 | The starting point  (Picture) | |
| Student 71 Grade 8 | 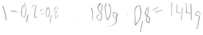 | Year Last year (Arrows) | |
| Student 228 Grade 9 | x = original weight | 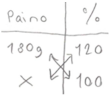 Note! Uses the concepts of proportion and ratio. (Table) | “I used a table to form the equation. I cross multiplied the quantities. An equation was created, and the solution gave me the answer.” |
| Answer (g) | N | % |
|---|---|---|
| 36.00 | 7 | 1 |
| 144.00 | 279 | 48 |
| 150.00 | 174 | 30 |
| 160.00 | 13 | 2 |
| 171.00 | 7 | 1 |
| 179.80 | 10 | 2 |
| 216.00 | 12 | 2 |
| Others | 78 | 13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joutsenlahti, J.; Perkkilä, P. Mastery of the Concept of Percentage and Its Representations in Finnish Comprehensive School Grades 7–9. Educ. Sci. 2024, 14, 1043. https://doi.org/10.3390/educsci14101043
Joutsenlahti J, Perkkilä P. Mastery of the Concept of Percentage and Its Representations in Finnish Comprehensive School Grades 7–9. Education Sciences. 2024; 14(10):1043. https://doi.org/10.3390/educsci14101043
Chicago/Turabian StyleJoutsenlahti, Jorma, and Päivi Perkkilä. 2024. "Mastery of the Concept of Percentage and Its Representations in Finnish Comprehensive School Grades 7–9" Education Sciences 14, no. 10: 1043. https://doi.org/10.3390/educsci14101043
APA StyleJoutsenlahti, J., & Perkkilä, P. (2024). Mastery of the Concept of Percentage and Its Representations in Finnish Comprehensive School Grades 7–9. Education Sciences, 14(10), 1043. https://doi.org/10.3390/educsci14101043









