Problem Posing and Problem Solving in Primary School: Opportunities for the Development of Different Literacies

Abstract

Problem posing and problem solving, involving significant situations for students, encourage effective learning, mathematical reasoning, communication, and connections in/with mathematics, enhancing the emergence of different literacies. Although problem solving is more frequently present in teaching practices, the ability to formulate them must also be developed, since it requires other skills, such as writing a problem statement, establishing connections between reality and mathematical knowledge, and creating and idealizing problematic situations, among others. Financial Literacy and Consumer Literacy promote contexts related to the student’s daily life and are promising in the development of problem posing. These literacies are also relevant to the development of a healthy, balanced, and responsible relationship with money and to raising awareness of the student regarding the importance of their actions in society, the economy, and the environment. This text presents part of a qualitative, descriptive, and interpretive research, developed by a teacher of children in the third year of a Portuguese primary school, involving problem posing and problem solving in Financial and Consumer Education contexts, with the following research question: How does posing and solving problems, in contexts close to the students’ reality, influence the development of different literacies? The results point out the mobilization of different mathematical concepts, in articulation with other areas of knowledge, and the development of skills and knowledge innate to different literacies, namely Mathematical Literacy, Financial Literacy and Consumer Literacy.

1. Introduction

The development of different literacies enhances the expansion of young people’s knowledge and understanding as future citizens, as it improves social interaction and encourages critical thinking and abstract communication. Thus, it is up to teachers to create learning environments in the classroom that familiarize students with ways to question their work and functions [1].

Throughout life, financial decisions increasingly require in-depth knowledge of information, based on the increasing complexity of the financial products and services available [2]. Linked to Financial Education is Consumer Education [3], as it enables young people to become more participatory and responsible consumers in society. In this sense, it is important that the different areas of the curriculum establish connections with Financial Education (FE) and Consumer Education (CE). One of the areas where this connection is an asset is in mathematics.

Providing students with moments of Mathematical Education with real contexts involving Financial Education and Consumer Education stimulates naturally rich learning moments. In mathematics, the formulation of problems by students depends on their conception of the problem, so students must first understand that concept [4]. On the other hand, problem solving involves a set of actions, and consists of an activity of extreme complexity, since it integrates the way that the problem is presented, the mathematical experience and interest, and the motivation to solve it [5]. In addition, it is important to emphasize that the relationship between the formulation of problems and the real or close contexts of the students supports them in attributing meaning to problems [6,7].

The presented work corresponds to part of a broader investigation, developed by a trainee teacher and involving students from the third year of a Portuguese primary school, and aims to promote the posing and solving of mathematical problems in FE contexts. This text focuses on the formulation and resolution of problems to promote opportunities for the development of different literacies, such as Mathematical, Financial and Consumer Literacies, and has the following research question: How does posing and solving problems, in contexts close to the students’ reality, influence the development of different literacies?

2. Theoretical Framework

The theoretical support of this study is based on research and readings carried out on knowledge and skills that a future citizen must develop, considering the characteristics and requirements of the 21st century. Social, technological, and emotional developments have highlighted the relevance of educating children to solve and formulate everyday problems. In this sense, the theoretical foundation of this study is based on problem solving and detaching the relevance of training good problem posers; it highlights the importance of developing different literacies in future citizens in an articulated way.

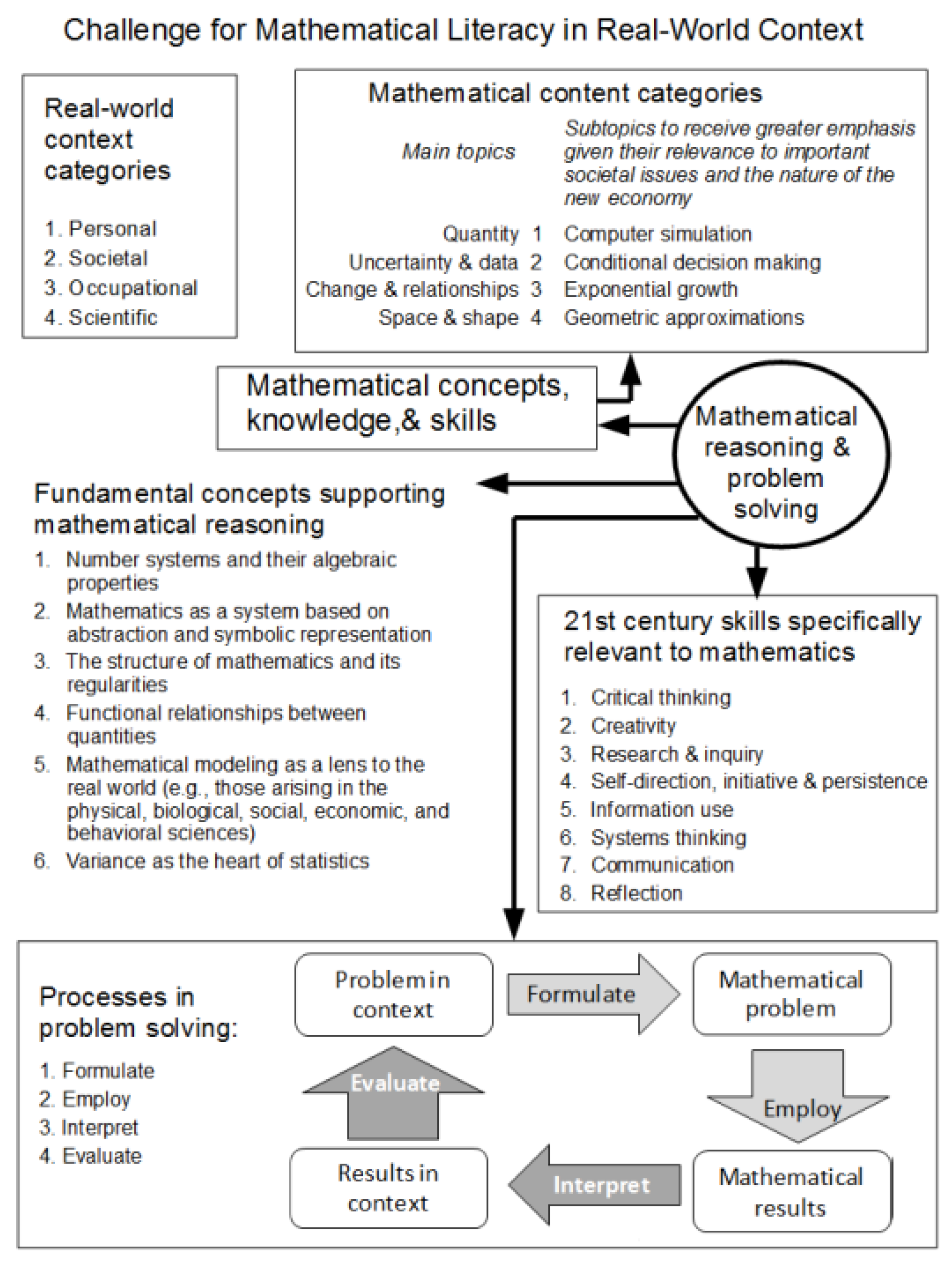
2.1. Mathematical Literacy

Mathematics, as a purely academic discipline, taught and learned in a context absent from its relationship with reality, has long since dissipated from educational environments. Researchers such as Skovsmose [8] have highlighted the relevance of developing a critical mathematical education, known as Mathemacy. According to Skovsmose, Mathemacy refers not only to mathematical skills but also to the ability to “interpret and act in a social and political situation structured by mathematics” [8] (p. 2). Students’ fluency in the application of mathematical knowledge in everyday situations makes them mathematically literate. According to the Programme for International Student Assessment [9], Mathematical Literacy (ML) means:

“An individual’s capacity to formulate, employ and interpret mathematics in a variety of contexts. It includes reasoning mathematically and using mathematical concepts, procedures, facts, and tools to describe, explain and predict phenomena. It assists individuals to recognize the role that mathematics plays in the world and to make the well-founded judgments and decisions needed by constructive, engaged, and reflective citizens” [9].

(pp. 4–5)

Thus, for students to be considered mathematically literate, they must be able to use their knowledge of mathematical content and processes to recognize the nature of a real-life situation and then formulate it in a mathematical context [9].

The 21st century brought out changes in personal, social, and scientific domains, requiring the development of other skills. In the document “PISA 2021 Mathematics: A Broadened Perspective”, a model of ML is presented (Figure 1) representing the influence that the characteristics of real-world context have on the type of problems that societies pose and the demands and changes in terms of reasoning, concepts, mathematical knowledge and skills required in the problem-solving process, which are detached the following skills pointed out as specifically relevant to mathematics in the 21st century: critical thinking; creativity; research and inquiry; self-direction, initiative, and persistence; information use; systems thinking; communication; reflection [9].

In Portugal, the curricular guidelines for mathematics teaching and learning show intentionality in developing mathematically literate citizens from the early years. In “Novas Aprendizagens Essenciais de Matemática para o Ensino Básico” [10], the most recent curriculum document that guides the teaching of mathematics in Portugal in the early years, the idea of ML, defended by the Organisation for Economic Co-operation and Development (OECD), is embodied in its guiding principles: mathematics for all; mathematics is unique, but it is not the only one; and mathematics for the 21st century.

2.2. Problem Posing and Problem Solving

Posing and solving problems is associated with fundamental capabilities of mathematical activity. However, research in mathematics education has not emphasized the importance of problem posing in educational contexts as much as it has in relation to problem solving [11]. Sometimes, posing a problem is more important than obtaining a solution, which can only result from the application of mathematical or experimental processes. Problem posing marks advances in science and, furthermore, requires the formulation of new questions or reformulation of problems from other perspectives; it requires imagination, creativity, and innovation [11].

Mathematical Literacy (ML) presupposes the application of knowledge in recognizing the mathematical nature of a real-life problematic situation and in formulating the problem from a mathematical point of view [9]. In this sense, students must be able not only to solve problems but also to formulate them. Problem posing should be considered in curricula and in educational practices [12] because, in addition to being related to and contributing to successful problem solving, it promotes essential skills and attitudes in mathematics education [13]. The formulation of new questions promotes the establishment of relationships with other proposed problems, creativity, and imagination [11].

2.2.1. Problem Posing

Kilpatrick [14] marked the research into problem posing, arguing that students, during their academic training, should have the opportunity to experience the discovery of new problems and formulate their own problems. According to Ellerton, success in solving mathematical problems has long been considered and emphasized as the objective, however, the time has come for problem posing has a prominent and natural place in curricula and in educational practices [12]. Some authors relate the problem posing with mathematics education in general, highlighting the skills and attitudes that the process involves, and interrelating it with problem solving [13,15,16]. Problem posing, in addition to facilitating students’ understanding of mathematical concepts and processes, influences positively their skills, attitudes, and confidence in problem solving [17].

Stoyanova and Ellerton categorized three types of situations in problem posing: free situations, in which students are challenged to create a problem, without restrictions or information given; semi-structured situations, in which students are provided with an open situation, that is, photographs, figures, diagrams, inequalities, equations, in relation to which students are invited to formulate a problem; structured situations, in which students reformulate specific problems, varying only some conditions or questions [18]. In problem posing from semi-structured situations, it is essential to define the characteristics of the information given to students to assist in the process of constructing their own problems. The relationship between problem posing and students’ real or close contexts supports them in attributing meaning to the problematic situations [6,19].

Problem solving has had a more pronounced emphasis in curricular guidelines; however, its relationship with problem posing is close and has been highlighted for a long time by several educators and researchers. Einstein and Infeld emphasized the importance of formulating problems when they stated that “the formulation of problems is often more essential than their resolution” [20] (p. 15). Despite not using the expression “problem posing”, Polya highlights the relevance of encouraging students to analyze problems they have solved and to create new problems based on them, arguing that this practice helps them to consolidate their knowledge, develop their skills, improve the solving process, and understand the problems posed to them [21,22]. Students should be provided with opportunities to discover and formulate new problems. In fact, problem posing positively influences students’ learning, skills, attitudes, and confidence when solving this type of task [14,17,23].

There are different categories for problem posing based on their intentionality or context: only with the intention of creating new problems (students’ experiences, in or outside of school, are contexts that favor the formulation of new problems, both to respond to everyday needs and to interpret real-life phenomena); only with the intention of reformulating existing or proposed problems (it may occur on the initiative of students, when faced with a problem they find interesting, or be proposed to them by someone, such as the teacher); with both intentions, creating new problems and reformulating problems; with the intention of proposing questions and viewing already known issues from another angle (although it may seem similar to reformulating problems, in this case, the focus is on the questions posed in a problem and not on the problem as a whole, that is, creating new problems from questions of a problem); as an act of modeling (when approached as an opportunity to interpret and analyze reality through its mathematization) [20]. The authors emphasize that the previously mentioned categories are not necessarily disjoint, and the formulation of problems can be approached in contexts in which more than one of them prevails. There are several strategies that a teacher can use when implementing problem posing in the classroom.

2.2.2. Problem Solving

Problem solving has been investigated from an educational point of view for decades. Problem solving in mathematics teaching and learning processes is constantly reinforced in curricular guidelines from the early years, being considered one of the mathematical skills to be developed in students [10]. In addition to being a skill to develop in students, problem solving is also an important teaching tool [24], since in this process, the concepts gain meaning, and the internal and external connections are established in and to mathematics.

Polya, in his work “How to solve it”, marked a turning point in the “art” of solving problems and its approach in educational contexts. In solving mathematical problems there is a line of demarcation between two eras, problem solving before and after Polya, respectively [25]. Faced with the question “What is a problem?”, Polya considers that it is a task without an initially obvious way to reach its solution [24], distinguishing the problems of discovering (the results of the discovery can be theoretical and practical, concrete or abstract) the problems of providing proof (demonstrating the veracity of a statement) [26]. According to the definition of a problem presented by Polya, what for someone is a problem, for others will not be, since, faced with the same task, someone will be able to immediately see its solution and others will not. In the mathematics education context, the following question often arises: How to solve a problem? It is not easy, or even impossible, to present an answer that is valid for any type of problem; however, several models on the process of solving a problem have been presented. In “How to solve it: A new aspect of mathematical method”, Polya presented a model composed of four steps: understand the problem; outline a plan; execute the plan; verify the solution. However, other models have emerged developed by different authors [27].

The nature of mathematical tasks can be classified into two dimensions: degree of challenge, varying between reduced and high, and degree of structure, varying between closed (what is given and requested is explicit) and open (there is some indeterminacy in what is given, what is requested, or both). Crossing these two dimensions, Ponte classifies tasks into: (i) exercise (closed and low-challenge task); (ii) problem (closed and highly challenging task); (iii) exploration (open and low-challenge task); (iv) investigation (open and highly challenging task). This author also states that these tasks can emerge in real, semi-real (apparently real, but which may be slightly deviated from reality or that may have no meaning for students) or purely mathematical contexts [28].

Charles and Lester propose a typology of problems for the context of the first Cycle of Basic Education (CBE): (i) one-step problems (can be solved through the direct application of one of the four basic arithmetic operations); (ii) two or more step problems (can be solved through the direct application of two or more of the four basic arithmetic operations); (iii) process problems (are solved through non-routine and non-mechanized processes); (iv) application problems (typically involve data collection and decision making about real-life situations); (v) puzzle-type problems (involve students in potentially enriching situations, raising their interest and getting them used to looking at problems from different points of view) [29,30].

2.3. Mathematical Connections

In recent decades, mathematical connections have been highlighted more prominently. The National Council of Teachers of Mathematics [31] states that, when students have the possibility of connecting mathematical ideas, their understanding is deeper. One of the connections mentioned is related to the recognition and application of mathematical ideas in non-mathematical contexts. Canavarro states that “the main purpose of connections is to broaden the understanding of the ideas and the concepts involved in them and, consequently, allow students to give meaning to mathematics and understanding this discipline as coherent, articulated, and powerful” [32] (p. 38).

Different authors state that the difficulties experienced by students in learning mathematics can be overcome by establishing appropriate connections between the informal and intuitive mathematical experience that they bring to the classroom and the formal and abstract mathematics that they are expected to learn [33].

Regarding Portuguese curricular documents, the mathematics program [34] presented the interpretation of society as one of the purposes for teaching mathematics, stating that mathematics is “indispensable to the study of different areas of human activity (…), or even sales and promotion campaigns for consumer products” (p. 2). Currently, the new curricular mathematics program for elementary school [10] supports the importance of mathematics having a privileged place in the curriculum due to the need to mobilize multiple literacies to respond to the demands of the current times characterized by unpredictability and accelerated changes. In this sense, is possible to promote the development of different literacies establishing connections between mathematics and many other discipline areas, Financial Literacy and Consumer Literacy being examples of such literacies. In fact, Financial Education (FE) and Consumer Education (CE) are promising contexts for approaching mathematical concepts articulated with the themes listed in the Financial Education Referential [2] and in the Consumer Education Referential [3].

2.3.1. Financial Education

Over the last two decades, the OECD has reinforced the need to educate the population financially, stating that Financial Literacy is one of the essential skills for life [35], since it adds knowledge and understanding of financial concepts and risks and the ability, motivation and confidence to apply them, which is necessary for citizens to become competent in the use of their financial resources, make effective decisions and improve their financial and societal well-being.

In 2013, a guiding document for the implementation of FE in educational and training contexts was published in Portugal the Financial Education Referential [2]. Not being a prescribed document, it gives freedom to educators and teachers to implement its ideas in different ways, and is one of the possibilities in articulation with different disciplines, such as mathematics. For the first CBE context, the document refers to the approach of five of its six themes, from which we highlight, in the scope of our research, the following: Budget Planning and Management; Basic Financial Systems and Products; and Savings. In the Profile of Students Leaving Compulsory Schooling [36], one of the values to work on is citizenship and participation, where the FE is also inserted.

Research carried out on different levels of education, involving FE tasks in mathematics class, states that at these moments students are involved in carrying out the tasks, discussing the topics with their colleagues and teachers, questioning teachers about the themes worked on, taking the topic outside the classroom, and discussing it both with colleagues and within the family, mobilizing different concepts [37,38,39]. These contexts promote the approach of different concepts, both in mathematics and financial education [37], being the natural link between them [40].

2.3.2. Consumer Education

Consumer Education (CE), like Financial Education, has also proven to be increasingly important due to the hermetic nature of markets being crucial to empowering consumers with the knowledge to face challenges in terms of consumption, to better understand market mechanisms, and to make more informed decisions, with a view to improving their well-being [3].

In 2019, the Consumer Education Referential, a guiding document for the implementation of CE in educational and training contexts was published in Portugal, defending that educating for consumption is promoting responsibility, but also defending the well-being of each person [3]. For the first CBE, this document states the approach of eight themes that we highlight in the scope of our study: Consumption Framework and Evolution; Consumption of Goods and Services; Marketing and Advertising; and Families, Financial Management and Consumption.

3. Purpose and Research Question

In this study, a part of a broader investigation developed in the 2020/2021 academic year in the context of a pedagogical internship in a Portuguese primary school is presented. The study involved a trainee teacher, 1 of the researchers, and 17 students in the third school year, aged between 8 and 9 years old. Having an intention of promoting different literacies through problem posing and problem solving, a research question that guides this work was considered: Can the posing and solving problem, in contexts close to the students’ reality, influence the development of different literacies? Keeping this question in mind, this study aimed to evaluate the possible influence that posing and solving problems in contexts familiar to students could have on the students’ performance and, consequently, on the development of literacies, identify opportunities to develop Mathematical, Financial and Consumer Literacy in problems formulated by students and in its resolutions, recognize opportunities to establish internal/external connections in and to mathematics, and develop skills and competencies related to the mentioned literacies.

To infer a possible answer to the research question, a qualitative case study [41] was developed, supported by a descriptive and interpretative approach [42].

4. Method and Materials

4.1. Participants

The students from the class in which the study was implemented came from lower-middle-class families. Six students had educational support and three required universal and selective measures. Most students usually respected the classroom’s rules and were involved in proposed tasks. The students had very different learning rhythms, some of which required constant monitoring. However, despite the difficulties experienced by some students, they were, overall, interested and participative children, presenting a predisposition to learn. In general, students had some weaknesses regarding problem solving, namely problems involving mathematical concepts. Although the students had already experienced posing problems, this was not a common practice in that class. Considering Financial and Consumer Literacy, most students had not developed it yet.

4.2. Intervention Phases

The intervention phases were influenced by the ideas of Cheng and Ling [43], in which planning, implementing, evaluating, and reflecting are involved. Regarding the conception of the didactical proposal to be implemented, in its planning phase, the main skills and content to be developed in students were selected, and the learning objectives were identified, namely formulating and solving problems, developing Financial Literacy, and establishing internal and external connections within and to mathematics. The didactical proposal involved problem posing in a semi-structured situation [18], being implemented in three sessions. In the first session, the trainee teacher took a promotions leaflet from a hypothetical hypermarket (Figure A1) to the class and asked students to analyze the leaflet and formulate, in pairs, possible problems from it. In the second session, after the trainee teacher had evaluated and analyzed the formulated problems, ensuring that, as well as being well formulated, they had solutions, distributed them among students who had not been their authors, to be solved by the work pairs of the previous session. In the last session, the formulated problems, and respective presented resolutions, were discussed in a large group.

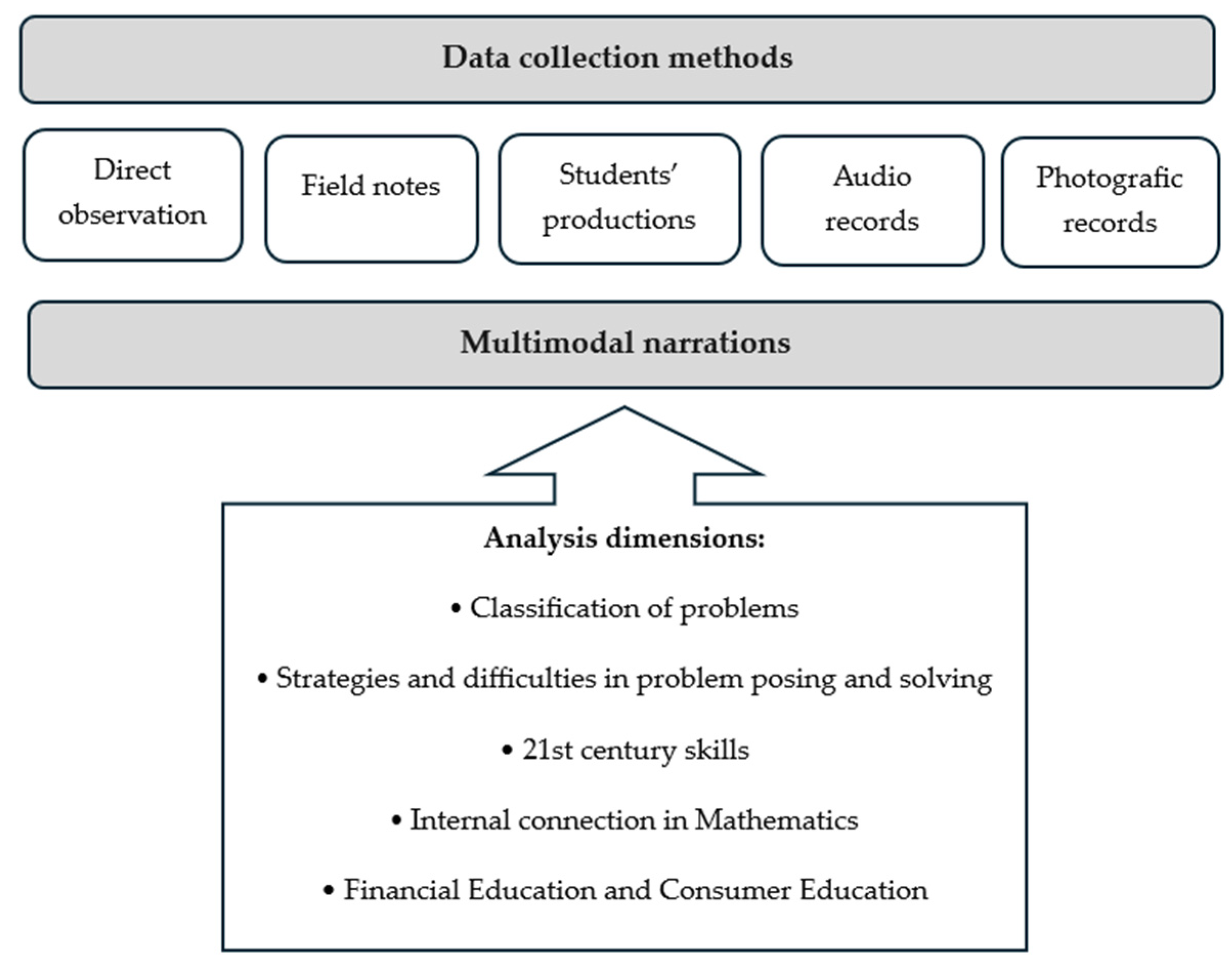
4.3. Data Collection

The data were collected in different ways from sessions developed by students, namely from direct observations, field notes from the trainee teacher, who was also a researcher, students’ productions, and audio and photographic records. From the collected data, multimodal narrations were created in accordance with the protocol described in [44], being validated by a research team independent of this study. The multimodal narrations allowed us to describe, in the most complete and multimodal way, what happened inside the classroom, such as its contextualization, the teacher’s intentions and actions, and students’ reactions and actions. The data were collected under the authorization of the students’ guardians who were aware of the research and its characteristics through an informative document. The confidentiality of the collected data was guaranteed, being accessed only by researchers. The anonymity of each student was also guaranteed, being designated in this study by a letter of the alphabet.

5. Results

In this section, the data arising from the sessions developed with students are presented and analyzed. Data analysis consisted of content analysis, following the principles of Bogdan and Biklen [45], in which the following dimensions were considered: type of problem (formulated and solved) according to the classification of Charles and Lester [29]; strategies or difficulties felt by students in problems posing or solving; 21st-century skills involved, considering the Mathematical Literacy Model [9] in Figure 1; internal connections in mathematics, in accordance with the Basic Education Mathematics Curricular Program and Goals [34]; external connections to mathematics promoting different literacies, namely the development of Financial Education, whose analysis was based on the Financial Education Referential [2], and Consumer Education, whose analysis was sustained on the Consumer Education Referential [3].

The use of different data collection methods and the access to information of different natures allowed researchers, with a view to analyzing the previously mentioned dimensions, to compare the data obtained and develop different perspectives on the same situation, making it possible to carry out a triangulation of the information obtained, according to the following scheme (Figure 2).

Next are presented five problems formulated by students accompanied by respective resolutions proposed by their authors (developed during their formulation) and by pairs of students to whom they were proposed. As in previous classes, students had been solving problems in a context involving a birthday; formulating problems related to that context was suggested to them. The presented problems were selected according to the representativeness of the data. The analysis of each problem is accompanied by students’ productions as well as excerpts from the large group discussion about them, led by the trainee teacher, with the intention of highlighting situations in which opportunities to answer the research question stand out.

For confidentiality reasons, students will be designated by capital letters of the alphabet and the trainee teacher by TT. Since the problems formulated by the students were written in the Portuguese language, they were translated into English, keeping the translation faithful to the vocabulary and sentence construction presented by the students. In students’ resolutions, according to the Portuguese education system, in numbers, decimal places are separated by a comma instead of a period.

5.1. Analysis of Problem 1

Problem 1, proposed by Students A and K, consists of three questions, with questions 1 and 2 corresponding to, according to the classification of Charles and Lester [29], a two-or-more-step problem. In turn, question 3 corresponds, according to the same classification, to a process problem.

Problem 1:

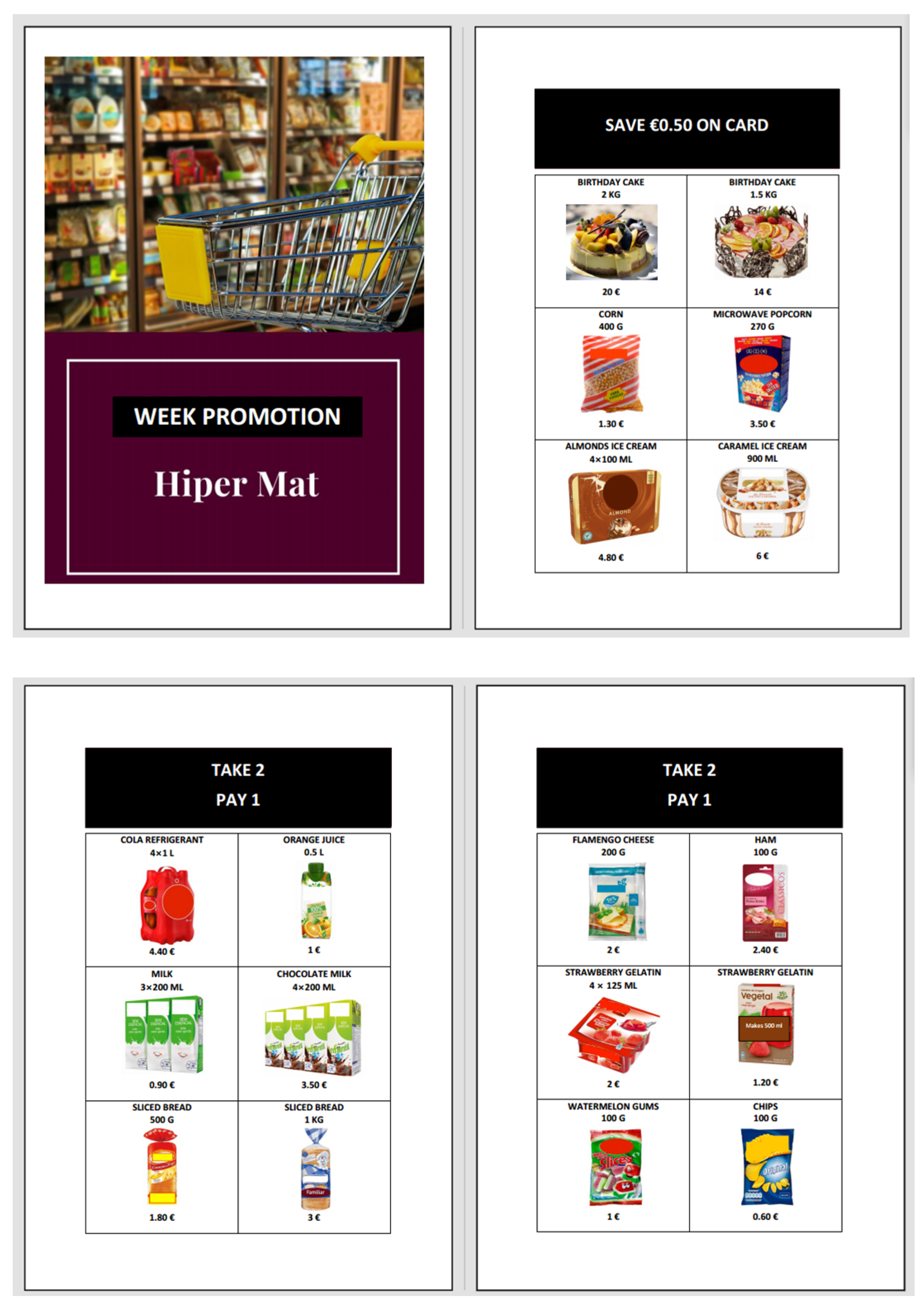
• Gabriel’s parents have €68.37, if they buy one of each type cake, how many euros will they end up with? (Explain how you thought.)
• With the money left, will Gabriel’s parents be able to buy three packages of popcorn? (Explain how you thought.)
• With €30.47, Gabriel’s parents still wanted to buy two more products, and had €21.27 left. How many products did they buy? (Explain how you thought.)

The use of values such as EUR 68.37 and EUR 21.27 reveals the intention of students to approximate the problem with what happens in a real context, that is, the values we have in the coin purse are not “round” numbers. The next excerpt, from the large group discussion, demonstrates this.

TT:

Before we start our discussion, I want to ask Student A and Student K two questions. You, you chose a value that is not at all round, €68.37… Which is a common value, it is a value of reality, because we have one cent, we have two-cent coins in our wallet. So, my question to you is the following: did you choose this value because it is a common value in our reality, we have cents in our wallet, or, because you wanted to make it difficult for your colleagues to resolve?

Student K:

Because…

TT:

Student K can start, and Student A helps next.

Student K:

SI think we put that in because it is… because it is reality. We don’t have sixty euros. We have sixty euros and a few cents.

This problem was proposed to two pairs of students: B and W; C and G. Next, for each question of the problem, we present the resolutions proposed by these pairs of students and by the authors of the problem, respectively.

• Analysis of the resolution of Question 1

In the resolutions presented, Students B and W did not reveal any difficulties in interpreting and resolving the question (Figure 3). However, Students C and G showed errors in interpreting the leaflet, having obtained an incorrect result (Figure 4). Students A and K, who proposed the problem, solved Question 1 correctly (Figure 5).

In Figure 4, Students C and G used incorrect values, that is, EUR 19.50 instead of EUR 20, and EUR 13.50 instead of EUR 14. During the discussion of this resolution, it is possible to verify that the students did not understand the meaning of “Save €0.50 on card” presented in the hypermarket’s hypothetical leaflet (Figure A1), as we can see through the following excerpt.

TT:

So, Student C, how did you think? Because you have €19.50 + €13.50 here. You didn’t add up the value of the cake… why? What were you confused about? Why did you put €19.50, Student C and Student G?

Student C:

Because it says save fifty euros… cents! (Student C refers to the hypothetical hypermarket’s leaflet).

In the excerpt below, the trainee teacher explains to students what the expression “Save €0.50 on card” means, reinforcing that it is not an immediate discount upon purchase, but rather an amount that is accumulated on the card and that can be used for later purchases.

TT:

Student C said that took away fifty cents, because in the leaflet’s header says “save fifty cents on card”. So, we’re going to start a discussion here… When it says “save fifty cents on your card”, do you think the money is deducted right away? Or, it will remain on the card so that it can be deducted from the next purchase? Who think in this way? Or, who has anything to say to me? In the leaflet you have “save fifty cents on card”. (TT insists on the expression).

Student C:

At the time…

TT:

So why would it say on a card? The card is not an ATM card. It’s the hypermarket card.

Student E:

In this case it was Hiper Mat.

TT:

In this case it is the Hiper Mat. Therefore, in this case you could not have deducted the fifty cents right away. They would stay on the card…

As can be seen in Figure 5, Students A and K, the authors of this problem, solved the question correctly.

• Analysis of the resolution of Question 2

Students B and W, despite mentioning that it was possible to buy three packages of popcorn, made a mistake in the calculations, since they obtained a higher value than the initial one (Figure 6), not revealing a critical spirit.

During the discussion of this question, TT questioned the class about why Students B and W made a mistake in solving this question to clarify their reasoning, as we can see in the following excerpt.

Student K:

Do you know why, teacher?

TT:

Why?

Student K:

Because in the previous exercise, they had done the calculation wrong, and it gave them €48.37.

TT:

Exactly…

Student K:

Therefore, they wouldn’t obtain the right value!

TT:

Very well! As they already had a wrong value in the previous question, this one would be incorrect. Very good!

In turn, like what happened when solving question 1, Students C and G made a mistake in interpreting the leaflet, resulting in a wrong result (Figure 7).

As can be seen in Figure 8, Students A and K solved the question correctly.

• Analysis of the resolution of Question 3

Although this question can be classified as an open structure problem [28], allowing several response options, Students C and G did not present any possible resolution. However, Students B and W presented a resolution (Figure 9) different from the resolution proposed by the authors of this question (Figure 10).

5.2. Analysis of Problem 2

Problem 2 was formulated by Students D and E and consists of three questions classified, respectively, according to Charles and Lester [29] as follows: Question 1 (marked “1”) is a problem with two or more steps; Question 2 (marked “1.1”) is a process problem; and Question 3 (marked “1.2”) is a one-step problem.

Problem 2:

• If we bought 1 cake costing €20 plus 2 packets of chips costing €0.60, how much money would we spend?

  1.1.

  Gabriel and his parents invited 28 Gabriel’s friends, from his class 13 classmates liked gummies and 5 liked gelatins, how many people liked both?

  1.2.

  If Gabriel’s parents had €30, with how much money would they stay?

• Analysis of the resolution of Question 2

Although Students D and E were unable to express the idea they had in mind, in the problem formulation, they intended to formulate a problem involving the Venn diagram (Figure 11), although the information presented was insufficient to carry this out.

This question was also proposed to Student L and, through its resolution, it was possible to see that she resorted to another resolution strategy (Figure 12).

During the discussion, Student K explained to the class her perspective on the most correct strategy to resolve this issue. However, the presented strategy did not correspond to the proposed resolution by the students who proposed the problem, as we can verify in the following excerpt.

TT:

Now, we have Student L, here. Student L also said that four friends liked them both. So, also got your result, right? Despite having used another strategy, since he used an addition and then, finally, a subtraction.

Student K:

But that was the right strategy.

TT:

This? Yes, it was.

Student C:

Yes.

TT:

And why, Student K? Do you want to explain?

Student K:

Because we, first… we had to add the classmates who liked gummies and those who liked gelatin, which gave us 18, like Student L did.

TT:

Very good!

Student K:

And then, we had to subtract the eighteen. The eighteen colleagues who liked gelatin and… and who liked gummies, we had to subtract from the twenty-two. And the rest that were left were those who liked both!

Comparing the two resolutions presented, the trainee teacher highlights the importance of explaining the reasoning when students are solving a problem, as can be seen in the following excerpt.

TT:

Did you think so, Student L?

Student L:

Yes!

TT:

So, what can we conclude here? That Student L, through what she did, made the way she thought clearly clear, because a colleague who had not even proposed the problem and to whom the problem was not even proposed to be solved, understand the Student L’s reasoning. This means that Student L discriminated the way she thought very well, right? Did you understand too?

All students:

Yes.

This question was also proposed to the pair formed by Students O and P; however, they were unable to understand what was asked, solving it incorrectly (Figure 13).

5.3. Analysis of Problem 3

Problem 3, proposed by Students C and G, corresponds, according to the classification of Charles and Lester [29], to a process problem.

Problem 3:

It’s Gabriel’s birthday and he wants to buy a cake and some sweets, but he can only spend €24, justify your calculations.

The problem formulated by Students C and G admits several resolution proposals, being classified, according to Ponte [28], as an open structure problem. The problem was proposed to the pair formed by Students A and K, who presented a resolution (Figure 14) different from that proposed by the pair that formulated it (Figure 15).

During the discussion of this problem, it was noted, once again, that Students C and G failed in the interpretation of the hypermarket leaflet, as we can see in the following excerpt.

TT:

So, here we have €4.50 for an almond ice cream plus €13.50 for the second birthday cake. Afterwards, they also bought a cola, an orange juice… And now, I have a question, Student C. We’re back to the same thing, that is, you discount your €0.50, since it was said “save €0.50 on your card”. Then, the obtained value could never work out…

Furthermore, from the resolution proposed by the pair who formulated the problem (Figure 15), it was possible verify that the students were confused with the term “sweets”, which is verified also in the following excerpt.

TT:

…But I have one more question to ask Student C. The fries are a sweet?

Student C:

No…

TT:

No, they are savory.

Student K:

Not even Coca-Cola.

TT:

Coca-Cola is a soft drink.

Student C:

Yeah, so the question was…

TT:

The question is completely correct, but to answer this question, you could only use the sweets and cake mentioned in the leaflet, because there are certain things that are drinks, some are savory… right? Right, Student C?

Student C:

Right!

5.4. Analysis of Problem 4

Problem 4, proposed by Students N and S, corresponds to, according to the classification of Charles and Lester [29], a problem with two or more steps. The classification can be inferred through the resolution (Figure 16) presented by the students, although information is missing in the statement.

Problem 4:

Gabriel’s parents wanted to buy food for the party. But they want to spend a low price, calculate the prices of the cheapest foods that Gabriel’s parents could buy?

Figure 16. Resolution presented by Students N and S to Problem 4. [Answer’s translation of Problem 4, presented in Figure 16: Gabriel’s parents could buy corn, cake, 2 juices, 2 packets of gummies and chips, which in total will give EUR 19.90.]

Figure 16. Resolution presented by Students N and S to Problem 4. [Answer’s translation of Problem 4, presented in Figure 16: Gabriel’s parents could buy corn, cake, 2 juices, 2 packets of gummies and chips, which in total will give EUR 19.90.]

The teacher begins by asking the problem’s authors to clarify some aspects that were not mentioned in the statement, such as the lack of information regarding the quantities of products to be purchased or what they mean by “a low price”, and that can condition the interpretation and resolution of the problem.

TT:

So, Student S, come here next to me. Tell me, what do you mean by “lower prices”?

Student S:

Like the prices of one euro… (The student refers one euro as an example of a low price).

TT:

So, do you think your colleagues could know which… how many products you wanted to buy?

Student S:

No.

TT:

No… so how could you have asked the question? Student N, you ask us to calculate the lowest prices and what advantage could we consider? I don’t know if you…

Student N:

Giving a price.

TT

Giving a price… But we must know how many products you want to buy, so we know which… which ones have a lower price.

In the presented resolution in Figure 16, the students indicate two packages of juice corresponding to a cost of EUR 2. In the leaflet, there are two options for juice: a pack of four bottles of Cola-Cola, one liter each, for EUR 4.40; a 0.5 L of orange juice for EUR 1. Since the condition presented in the problem is to buy what is cheapest, the students only paid attention to the price values and did not consider the price/quantity relationship which, from this perspective, would lead them to consider the pack as the best solution.

During the discussion in a large group, it was clarified what the authors of the problem intended with it, and the meaning of the expression “Take 2, pay 1”, presented in the hypothetical hypermarket leaflet (Figure A1) was clarified, as shown in the following excerpt.

TT:

(…) And if you see, your colleagues did something very important, that we can pick up on, since were mentioned lower prices. Nowadays, and more and more, we must pay attention to the money we spend and if we can save it, should we or shouldn’t we, do it?

All students:

Yes.

TT:

We should. In this hypermarket leaflet, you had in the headers “save fifty cents on card” and “take two, pay one”. Can anyone explain to me what “take two, pay one” is?

Student N:

I know.

TT:

Student N.

Student N:

I can take two packs of gum and only pay one of them.

TT:

Exactly! For example, she could take two packs of gum and only pay for one. So, is this a promotion or not?

All students:

Yes.

5.5. Analysis of Problem 5

Problem 5, proposed by Students J and V, corresponds to, according to the classification of Charles and Lester [29], a problem with two or more steps.

Problem 5:

How much money did parents spend knowing that they bought 10 cakes weighing 2 kg, 4 multi-fruit cakes weighing 1.5 kg, 6 caramel ice creams of 900 mL, 6 orange juice of 0.5 L, 6 strawberry jellies costing €2, 16 watermelon gummies of €1, and cheese fries, knowing that they bought 2 packages of it, but the parents have €1000?

The formulation of this problem reveals that students are not aware of what responsible consumption is, with the remaining students showing astonishment during the discussion of the problem, as is shown in the following excerpt.

All students:

One thousand euros!

TT:

Exactly, €1000.

Student D:

A thousand euros…

Since the problem statement does not specify an issue, during the discussion, it was proposed to reformulate it, as we can see below.

TT:

Very good. So, look, but the parents have €1000. What is it here, what do you want to know in this issue? You know you want to buy that and that your parents have a thousand euros. What will be the question we have to ask? Here, you are not asking any question. You say how much money they spent and that the parents have a thousand euros.

Student J:

A subtraction operation.

TT:

Ah… so what Student J wanted to know was how much money his parents ended up with!

All students:

Ah…

TT:

Very good, Student J, but you didn’t ask that, did you?

Student J:

No.

TT:

No… very well, you can sit down. So, tell me, now, that we have a specific question, we know that the parents have a thousand euros. We know what they want to buy. So, we can or cannot ask how much money the parents ended up with?

All students:

Yes.

TT:

And so, we were able or unable to solve the problem proposed by our colleagues?

All students:

Yes.

Considering the typology of the proposed problems, in general, in terms of applied strategies, the students solved the problems using elementary arithmetic operations. From the presented results, is possible to verify the emergence of several mathematical skills, according to the 21st-century skills relevant to mathematics [9], creativity, critical thinking, thinking systems and communication involved. According to the problem types, considering the Charles and Lester classification [29], conclusions surrounding difficulties in posing and solving problems, respectively, are presented in

Table 1. Synthesis of information on problem posing and solving.

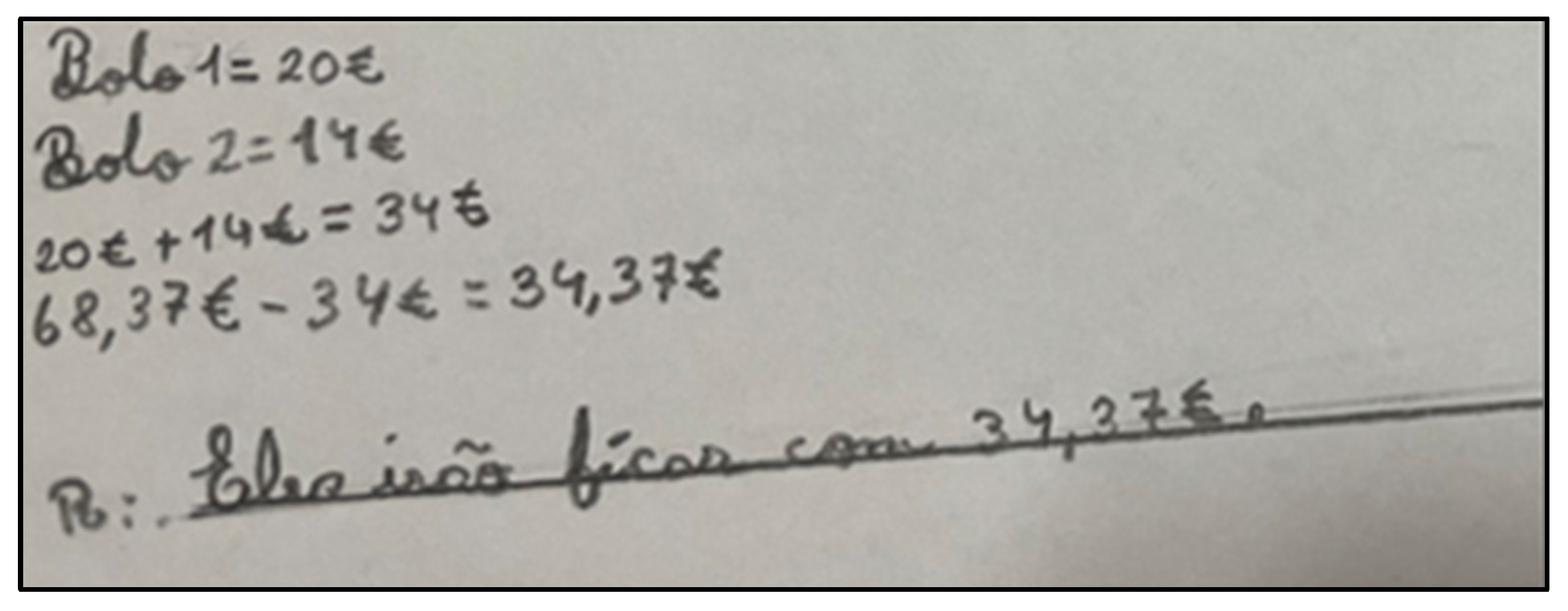
Problems	Problem Classification	Posing Problem	Difficulties in Solving
1	Two-or-more-step problem Process problem	The problem is clear considering what is given and requested	Use of elementary arithmetic operations Leaflet’s interpretation The meaning of “Save €0.50 on card” Lack of critical reasoning
2	One-step problem Two-or-more-step problem Process problem	One of the questions is not clear, although is possible to infer the students’ idea, the given data are not sufficient to solve it	In the question which is not clear
3	Process problem	Open structure problem, admitting several resolution proposals	Language difficulties The meaning of “Save €0.50 on card”
4	Two-or-more-step problem	The problem is not clear and the given data are not sufficient to solve it	Relationship price/quantity The meaning of “Take 2, pay 1”
5	Two-or-more-step problem	The problem is not clear as to what is requested and reveals a lack of sensibility for responsible consumption	Related to the unclear problem intention

.

From the analysis and discussion of the results, internal connections in mathematics can be seen, involving the domains of Numbers and Operations and Measurement (money and uses of money; mass; capacity). From the results, it is also possible to identify external connections to mathematics, promoting the development of Financial Education and Consumer Education. In

Table 2. Financial Education and Consumer Education guidelines involved in the study.

Education Referential	Guidelines
Financial Education	Budget Planning and Management-Needs and Desires: establish the difference between “need” and “want”; distinguish between necessary and superfluous expenditure; Understand that spending more than is necessary may compromise one’s ability to meet future needs. Budget Planning and ManagementExpenditure and Income: establish the relationship between income and expenditure, and understand the concept of balance; make decisions considering that income is limited. Financial System and Basic Financial Products-Means of Payment: Understand money as a means of payment. Savings-The Goals of Savings: understand the role of savings as a precaution against risk, to address predicted and unpredicted fluctuations in income or expenditure.
Consumer Education	Consumption: Framework and Evolution-The Consumer Society: understanding that publicity motivates consumption. Consumption: Framework and Evolution-The Dimensions of the Consumer Concept: understanding that consumer choices can have consequences; have the notion of responsible consumption. The Consumption of Goods and Services-Consumption and Satisfaction of Needs: distinguishing necessary goods and superfluous goods. The Consumption of Goods and Services-The Act of Consumption: exemplify some criteria for choosing the act of consumption. The Consumption of Goods and Services-The Safety and Quality of Food Products: recognizing the importance of consuming healthy foods. The Consumption of Goods and Services-The Relationship between Advertising and Marketing and Consumption: understanding that marketing encourages attitudes and behaviors. Marketing and Advertising-The Relationship between Advertising and Marketing and Consumption: understanding that marketing encourages attitudes and behaviors. Families, Financial Management and Consumption-Planning and financial management: identify consumption priorities in relation to the money we have; know that a budget provides a perspective on what you can consume. Families, Financial Management and Consumption-The consumption of financial products and services: recognizing that there are different means of payment.

, are presented guidelines of the Financial Education Referential [2] and Consumer Education Referential [3], respectively, involved in the study.

6. Conclusions

6.1. Summary of Key Findings

The presented study focuses on posing and solving problems in contexts close to the students’ reality involving Financial Education and Consumer Education. When formulated problems, students were asked, based on a familiar scenario [20] and through a semi-structured situation [18] involving a hypothetical hypermarket leaflet, to formulate their own questions. In general, students carried out what had been asked of them without many difficulties. Most of the problems formulated by students are of two or more steps, and application problems have also been presented [29]. Although most of the formulated problems have a closed structure, some revealed some indeterminacy in the data presented or requests, being considered as open structure problems. The difficulties experienced by the students are related to communication, mathematical concepts, or otherwise, being evident in terms of interpreting the information in the leaflet and in writing the problem statement. Some students also revealed difficulties in identifying the necessary information (to be included in the statement) to answer the proposed problems. The fact that this type of task is not performed with any regularity may be the justification for such difficulties [46].

Regarding external connections to mathematics, in many of the formulated problems, evidence of skills or opportunities to develop Mathematical Literacy, Financial Literacy and Consumer Literacy emerged. Considering Financial Education, savings as well as budget planning and management stood out above all. Also present are the following: Budget Planning and Management—Needs and Desires and Expenses and Income; Basic Financial System and Products-Payment Methods; and Savings-Savings Objectives. In relation to Consumer Education, the consumption of goods and services as well as the influence that marketing and advertising have on consumer choices were present: Consumption—Framework and Evolution; Consumption of Goods and Services; Marketing and Advertising-The Relationship between Advertising and Marketing and Consumption; Families, Financial Management and Consumption-Financial Planning and Management, Consumption of Financial Products and Services. In general, students highlighted, when formulating their problems, conditions related to the ideas “cheaper”, “spend less”, among others [37,38,40]. Some problems also revealed a lack of awareness of responsible consumption on the part of students, resulting in an opportunity to work on this topic [46].

Considering the internal connections in mathematics, connections between the themes of Numbers and Operations-decimal numerals and Measurement-use of money, mass, and capacity were identified [34]. This challenge involved several mathematical skills, in particular, problem posing, problem solving, connections, reasoning, representations, and communication. Considering the 21st-century skills relevant to mathematics [9], creativity, critical thinking, thinking systems and communication stood out.

Regarding the research question “can posing and solving problems, in contexts close to the students’ reality, contribute to the development of different literacies?”, from the data analysis presented, it is evident that there is a need to mobilize skills within the scope of Mathematical, Financial and Consumer Literacy on the part of students, as well as a need to develop other emerging ones. Thus, it can be inferred that the moments implemented promoted the use of skills related to different literacies, by students, and allowed the identification of some skills to be developed. However, it must be said that the contexts involved in the challenge, in themselves, were in connection to the literacies considered within the scope of this study.

6.2. Limitations of Research

One limitation of the study was the time available for the trainee teacher to implement the planned sessions with the class since the trainee teacher did not have her own class. This fact conditioned, in a certain way, the large group discussion of the problems formulated by students and respective resolutions, since the trainee teacher had to manage time very well, sometimes taking on a more incisive role in moderating the discussion. Since the trainee teacher is not the titular teacher of the class, she did not have the opportunity to continue the work carried out with the students, that is, to continue promoting the formulation and resolution of problems in meaningful contexts and the development of different literacies, which would reinforce the conclusions presented.

Considering the materials and resources, to make the context more real, instead of a leaflet from a hypothetical hypermarket, a real leaflet from a hypermarket could have been used.