An Approach to the Teacher Educator’s Pedagogical Content Knowledge for the Development of Professional Noticing in Pre-Service Teacher Education

Abstract

This study endeavors to illustrate how research on the professional development of mathematics teachers can help to enhance and nurture the professional knowledge of mathematics teacher educators (MTEs), thus becoming a potential source of professional growth for MTEs. To achieve this, a professional task was administered to 38 prospective secondary teachers from two Spanish public universities to explore their level of development in professional noticing. Specifically, the study focused on their skill of attending to children’s strategies in relation to transformations between semiotic representations as well as their awareness of the role of the semiotic register in task design. Drawing from the responses provided for the task, we offer a range of insights regarding expected or desirable Pedagogical Content Knowledge (MTEPCK) aimed at fostering the development of professional noticing, such as several challenges to be overcome by pre-service teachers or the identification of three potential levels of progression in their skill to attend to children’s strategies.

1. Introduction

Characterizing the professional knowledge of mathematics teacher educators is a complex problem due to the diverse range of tasks they undertake, including teaching in schools, preparing prospective teachers, participating in professional development programs for practicing teachers, conducting research, and attending professional development programs as trainers [1]. Furthermore, teacher education takes place in a wide variety of contexts, such as universities, teacher training schools, and private entities, among others. Therefore, in this article, we use the term “mathematics teacher educator” (MTE) in the same sense as Escudero-Ávila et al. [2], “because it encapsulates a multiplicity of approaches that teacher training can take, from the various roles the trainer might play to the different elements that can become the object of construction during these vital early stages of training” (p. 23). This allows us to conceive of a MTE as a multifaceted agent within a professional community [3] who assumes various roles in the practice of their profession.

As MTEs ourselves, we understand that MTEs are facilitators who guide the professional development of teachers and require specific professional knowledge to do so. As noted by Ponte [4], pre-service and ongoing teacher education constitute a potential context for professional development, which is a continuous process of evolution oriented toward enabling teachers to exercise their profession autonomously in the face of problems that emerge from practice. This involves considering theory and practice as interdependent elements, with a dialectic constructed based on reflection on and in practice. From this perspective, Bossio et al. [5] suggest that teacher training focused on professional development should mainly focus on the transformation and evolution of professional knowledge necessary for the practice of teaching mathematics, the core activity of the teacher. In this process of developing professional knowledge, professional noticing is an important aspect to consider in the practice of teaching mathematics, as noted by Jacobs et al. [6]. When a person tries to understand a mathematical topic, they incorporate part of the meaning into the representation they interact with or construct. Additionally, when a teacher is able to identify representations developed by students, they can access valuable information about their understanding [7] and thus construct powerful pedagogical reasoning from a professional perspective, which allows them to support the student.

However, despite the efforts of the research community to understand the nature, organization, and development of the professional knowledge of MTEs for teaching to teach, the literature remains limited. In this sense, Zaslavsky and Leikin [8] proposed a three layer model that explains how MTEs can develop professional knowledge through subjective reflection on the professional tasks they provide to their students during their education, among other possibilities. For instance, these authors demonstrated how an MTE could enhance their sensitivity to teachers’ cognitive processes and develop an understanding of the expectations placed upon them through classroom observation and reflective analysis of sessions and professional tasks. Additionally, Ozmantar and Agac [9] highlight that academic research on teacher professional development plays a crucial role in generating valuable professional knowledge for MTEs. In this regard, we must not forget that the research literature on mathematics teacher professional development systematically captures the reflections and insights of the research community regarding how teachers learn.

Aligned with these ideas, the objective of this article is to illustrate how reflecting on a professional task administered in a pre-service teacher education context can provide insights into different aspects of the desirable or required MTE’s Pedagogical Content Knowledge (MTEPCK) to facilitate the development of skill to attend to children’s strategies. Therefore, the research question that guides our study is: how does reflecting on the results obtained from a professional task contribute to understanding the desirable MTEPCK necessary for fostering the development of skill, of attending to children’s strategies, as part of professional noticing in pre-service teacher education?

To address this question and accomplish our objective, we initiated this study by presenting the theoretical underpinnings of our research. Subsequently, we provide an overview of the methodology, including the context and the specific professional task that was administered. Following that, we detail the obtained results and engage in a discussion regarding their potential implications for the MTE. Finally, in the concluding section, we synthesize multiple facets that enable us to characterize and comprehend the desirable MTEPCK necessary for fostering the development of professional noticing in pre-service teacher education.

2. Theoretical Framework

In this section, we present the theoretical foundations of our research. First, we reflect on the role of the MTE in teacher education and on the professional knowledge required to facilitate the professional development of teachers. Next, we draw on the model proposed by Escudero-Ávila et al. [2] and focus on the development of professional noticing competence in mathematics teaching and learning as part of teacher education. Finally, we provide some theoretical notes on the role of the cognitive functions of semiotic registers in mathematics teaching and learning, which constitute reference knowledge for the development of professional noticing by teachers with the help of the MTE.

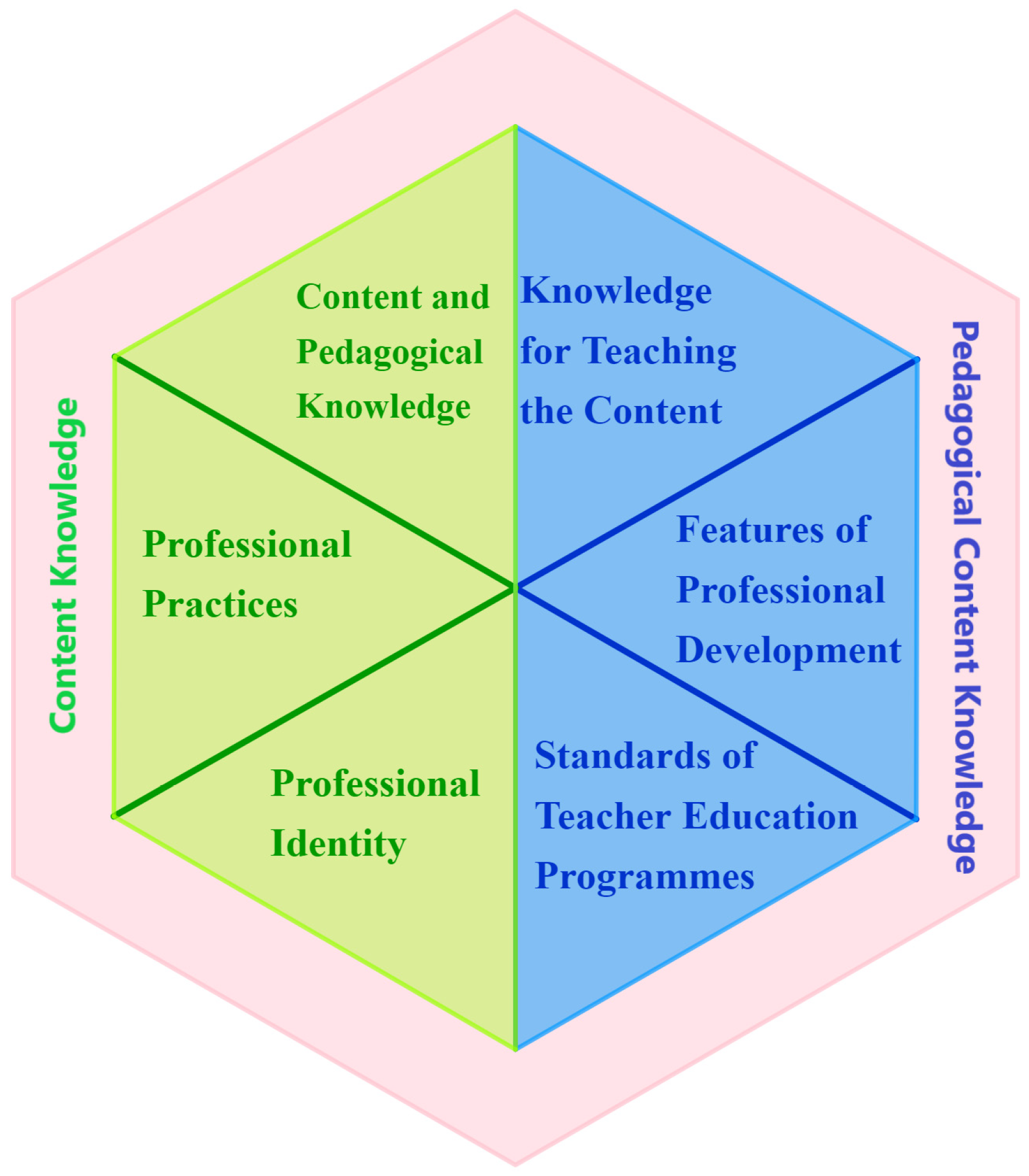
2.1. Professional Knowledge of Mathematics Teacher Educators in Pre-Service Teacher Education

From our perspective, pre-service teacher education represents a first stage in the process of professional development (hereafter PD). In this sense, one of the main objectives of PD is to facilitate the development of professional knowledge by prospective teachers, understood as practical knowledge [10], since its validity is not governed by academic criteria but by its effectiveness and efficiency in practice. It is critical knowledge, as it guides and directs the teacher’s decisions, and it is elaborated since it results from the integration of various types of knowledge. Therefore, problem-solving and reflection on and about practice [4] are two of the main ways of constructing professional knowledge and, consequently, PD.

In this sense, the MTE, as a facilitator of the PD of prospective and in-service teachers, requires specific professional knowledge that is also practical [11], as it arises from the integration of various types of information, with research in mathematics education being one of the main ones. One of its purposes is to respond to professional problems related to the PD of teachers, a characteristic that distinguishes it from the teacher, whose goal is to facilitate the development of their students in order to prepare them for critical citizenship.

Regarding the organization of the professional knowledge required by an MTE, there are several existing theoretical approaches [12,13,14], although, as Chapman [15] points out, the professional knowledge that the teacher must develop is an important dimension of the MTE’s knowledge. From our perspective, we consider that the model proposed by Escudero-Ávila et al. [2] (see Figure 1) represents a potential tool for describing some relevant elements of the professional knowledge required by an MTE in their activity of educating prospective teachers.

Regarding the content of teacher education, Ponte and Chapman [16] point out that teacher education is a complex process in which numerous elements interact, such as knowledge of mathematics, knowledge of mathematics teaching, and teachers’ professional identity. Researchers have attempted to approach and understand these elements, providing a plausible starting point for structuring the content of teacher education. Ponte [17] identifies three areas: knowledge, practices and skills, and professional identity.

The first area refers to the development of teachers’ subject matter knowledge (SMK) and pedagogical content knowledge (PCK) [18] during teacher education.

Regarding professional practices, teacher educators must have knowledge of teachers’ routines and how they enact them, emphasizing the connections between theoretical-academic knowledge and that which comes from practical or phenomenological contexts [10]. Competencies and skills for teaching, such as professional noticing [6], can be included in this sub-domain.

Finally, MTE’s knowledge of teachers’ professional identities is aimed at promoting awareness among prospective teachers of the different perspectives that exist regarding their being and feeling like teachers within a professional community and at an individual level.

In turn, the pedagogical content knowledge of mathematics teacher educators (MTEPCK) can be considered a meta-knowledge of teachers’ PCK [13], as it guides MTEs’ decisions on how to design and implement contexts that facilitate PD within the teacher education classroom. It is organized into three sub-domains: knowledge of teaching the content of teacher education; knowledge of the characteristics of the professional development of prospective teachers; and knowledge of the standards of teacher education programs [19].

Knowledge of teaching the content of teacher education includes knowledge of different strategies or resources to facilitate PD. As for knowledge of teacher education program standards, MTEs must be familiar with documents such as the Standards for Preparing Teachers of Mathematics [20] and the structure and sequencing of content in the programs they teach.

Finally, knowledge of the features of the professional development of prospective teachers includes knowledge of the strengths and weaknesses linked to the PD process, theories that explain how professional knowledge, practices, or their identity evolve, and knowledge of how prospective teachers reason or think [13], considering their ways of thinking as a manifestation of the degree of development of their professional knowledge and, therefore, of their PD.

In this work, we mainly focus on the MTEPCK. For the purposes of this research, we investigate how prospective teachers use their professional noticing to attend to children’s strategies, specifically how they identify relevant mathematical elements, such as transformations between semiotic representations, and moreover, their level of knowledge about the role of the semiotic register of representation in the task. Understanding these aspects of the MTEPCK can inform the design of effective teacher education programs that enable prospective teachers to develop the knowledge and skills necessary for facilitating their own professional growth and the growth of their future students.

2.2. Development of Professional Noticing in Initial Teacher Education

As we have pointed out, teacher education must impact different facets of a teacher’s PD, one of which is professional practices. Specifically, an important aspect of this process is to help prospective and in-service teachers integrate and transform their professional knowledge of reference in order to interpret professional practice. In line with Llinares [21], “the idea of learning to teach involves learning to use and generate new knowledge from teaching” (p. 55). Therefore, facilitating the development of professional noticing competence requires helping the teacher to be able to identify and interpret their own practice, i.e., make sense of the phenomenological information that nourishes their professional knowledge, using theoretical and technical knowledge from disciplinary and metadisciplinary sources [10]. From this dialectic, an interaction emerges that generates professional knowledge, so the teacher educator must be aware of the characteristics of how teachers use knowledge when faced with a specific practice in order to facilitate the construction of professional knowledge. Therefore, professional noticing could be integrated into the content of teacher education in the subdomain of professional practices. That is, developing a professional perspective on mathematics teaching involves making connections between specific classroom events and more general ideas [22], i.e., knowing and being able to use knowledge in a specific way [23], with the role of MTE being to help establish these connections in teacher education.

In this work, we focus on the professional noticing of children’s mathematical thinking described by Jacobs et al. [6], who point out three interdependent skills: (1) attending to children’s strategies; (2) interpreting children’s mathematical understandings as evidenced by these strategies; and (3) deciding how to respond on the basis of children’s understandings to help students progress.

Of the three skills, we focus exclusively on attending to children’s strategies. Regarding this skill, for Jacobs et al. [6], paying attention to student strategies is not only about being able to focus on their most important characteristics but also about focusing on what may be mathematically significant for the student, as well as being able to find these indicators of significant mathematical elements in disordered and/or incomplete responses [6].

2.3. The Semiotic Registers of Representation and Their Importance in the Teaching/Learning of Mathematics

Regarding the professional knowledge needed by a teacher to use their professional noticing to analyze children’s mathematical thinking and specifically attend to their strategies, Dreher and Kuntze [24] noted that there is a scarcity of representational transformations by teachers in their teaching. This fact, according to the aforementioned authors, could pose an obstacle for the student while highlighting the importance of the MTE possessing professional knowledge that helps teachers understand the role of multiple representations in the teaching and learning of mathematics. Therefore, paying attention to changes between representations in specific didactic situations and evaluating whether they are useful for student learning can be considered evidence of professional noticing [25]. However, when the teacher changes the representation system, they often perform these transformations tacitly and automatically [26,27], without paying attention to the demand that this poses for the student and the need to help them link and integrate these representations [24]. Therefore, it is fundamental for the teaching and learning of mathematics that in student-teacher interactions, attention is paid to the choice of the register and the changes between them [24].

For all of the above, the representations that students use when solving tasks are a relevant mathematical element that must be considered by the teacher. The mathematics education research community has extensively reflected on the role of representations in the teaching and learning of mathematics, information that can well be part of the teacher education content, especially circumscribed to the knowledge of content and pedagogical content knowledge that must be elaborated. Therefore, these contributions must be known to the MTE. Specifically, Duval [26] states that a semiotic representation is a construction that presents a mathematical object and is constituted of three elements: the object of the representation, the content, and the form (register) [28]. In general, when a student tries to understand a mathematical object, they incorporate part of the meaning of said object into the representation with which they interact or elaborate, which is why it is essential to differentiate the mathematical object from its representation. In turn, this collection of representations that students use or elaborate on—graphics, verbal expressions, algebraic ones, etc.—has great pedagogical importance since they constitute an indicator of the mathematical knowledge they are developing.

Regarding the role of mathematical object representations in the teaching of mathematics, Duval [29] identifies two fundamental activities: semiosis and noesis. Semiosis refers to the elaboration and understanding of representations, while noesis emphasizes the conceptual apprehension of the mathematical object to be represented. In this sense, for this author, a semiotic system can be considered a semiotic representation register if it allows three cognitive activities related to semiosis:

• The presence of an identifiable representation;
• The treatment of a representation consists of transforming the representation within the same register where it was formulated. For example, transforming 2(x + 1) = 3 into 2x = 1, as both are symbolic representations of the same equation (object);
• The conversion of a representation consists of transforming the representation into another one in another register while preserving part or all of the initial meaning. For example, converting the verbal representation “an odd number” to the symbolic expression 2n + 1.

Therefore, knowing the complexity of the cognitive processes related to semiosis [26], their strengths, weaknesses, and obstacles, is part of the PCK that a teacher must develop during their training. Additionally, this knowledge serves as a reference to understand the role of the semiotic register of the task and how it conditions the way students use one resolution strategy or another [26], which is known as the problem of the first threshold of understanding. Similarly, it provides the teacher with theoretical elements to identify transformations made by the student and therefore interpret their reasoning.

3. Methodology

3.1. Study Design and Participants

This study adopts a qualitative methodology with a descriptive and interpretive approach [30]. The study included 38 participants who were pre-service teachers (referred to as PST) who were enrolled in the master’s degree program in secondary education at two Spanish public universities. These universities were selected because they were affiliated with the research team. It is important to note that the MTEs were not involved in the research, nor were they the authors of this work. Furthermore, it is worth mentioning that the concept of professional noticing had not been previously addressed, neither theoretically nor practically, in any of the groups at these two universities. In fact, it was not part of either curriculum at the time. Consequently, the aim of this paper is to explore and gather evidence on the level of development of professional noticing, which can be subsequently analyzed to profile and characterize the expected MTEPCK.

3.2. Instrument

A scenario (see Appendix A) was designed in which a fictitious dialogue was presented in which a mathematics teacher asks a student, Juan David, to reason about the existence or non-existence of asymptotes of a function presented graphically. Specifically, the discussion focuses on the existence or non-existence of horizontal asymptotes (HA) and slant asymptotes (SA). The task design is based on the contributions made by Spangler and Hallman-Trasher [31] to the task dialogue. The task was completed individually by the PSTs in the training classroom without any assistance or intervention from the MTE. Each PST was assigned the following two instructions:

• Identify and describe the strategy or strategies used by the student to solve the task (what has been performed);
• Characterize the ideas or meanings about the asymptote that you believe the student possesses. What information do you rely on as a teacher? (What the teacher understands and where they observe it).

We anticipate that the responses to the first prompt will provide evidence of the development of the first skill, which is attending to children’s strategies. Similarly, the responses to the second prompt will shed light on the second skill, which involves interpreting children’s mathematical understandings. Given the limitations in terms of length and the specific focus of this study, our analysis exclusively focuses on the responses provided by the PSTs in relation to the first prompt of the task. It is important to clarify that the decision to not explicitly instruct the PSTs to identify transformations between semiotic representations or pay attention to the task’s register in the first prompt was deliberate. We aimed to avoid influencing the specific aspects that should be identified by the participants. This decision was primarily based on their lack of prior exposure to such concepts during their initial education. Additionally, our objective was to analyze which mathematical elements of the strategy prevailed and which ones were disregarded in their responses. With the information gathered from the written responses and subsequent reflection, we hope to obtain insights that will allow us to characterize a desirable MTEPCK for fostering professional noticing in pre-service teacher education.

3.3. Data Analysis

The variables analyzed in this study, which we believe can help characterize the potential level of development of the skill of attending to children’s strategies achieve within professional noticing, are: (1) knowledge of the first threshold problem, (2) treatments, and (3) conversions.

• Knowledge of the first threshold problem [26]: This variable takes the values yes or no. Yes, if the PST demonstrates an awareness of how the semiotic register of the task conditions the strategy used by the student; no, otherwise. Reasoning like “since the function is given by a graph, Juan David couldn’t use the algebraic expression of the function to find the limit as it approaches infinity. Therefore, he analyzes the behavior graphically by observing if the graph seems to stabilize around a specific value”, which would be evidence of knowledge of the first threshold problem;
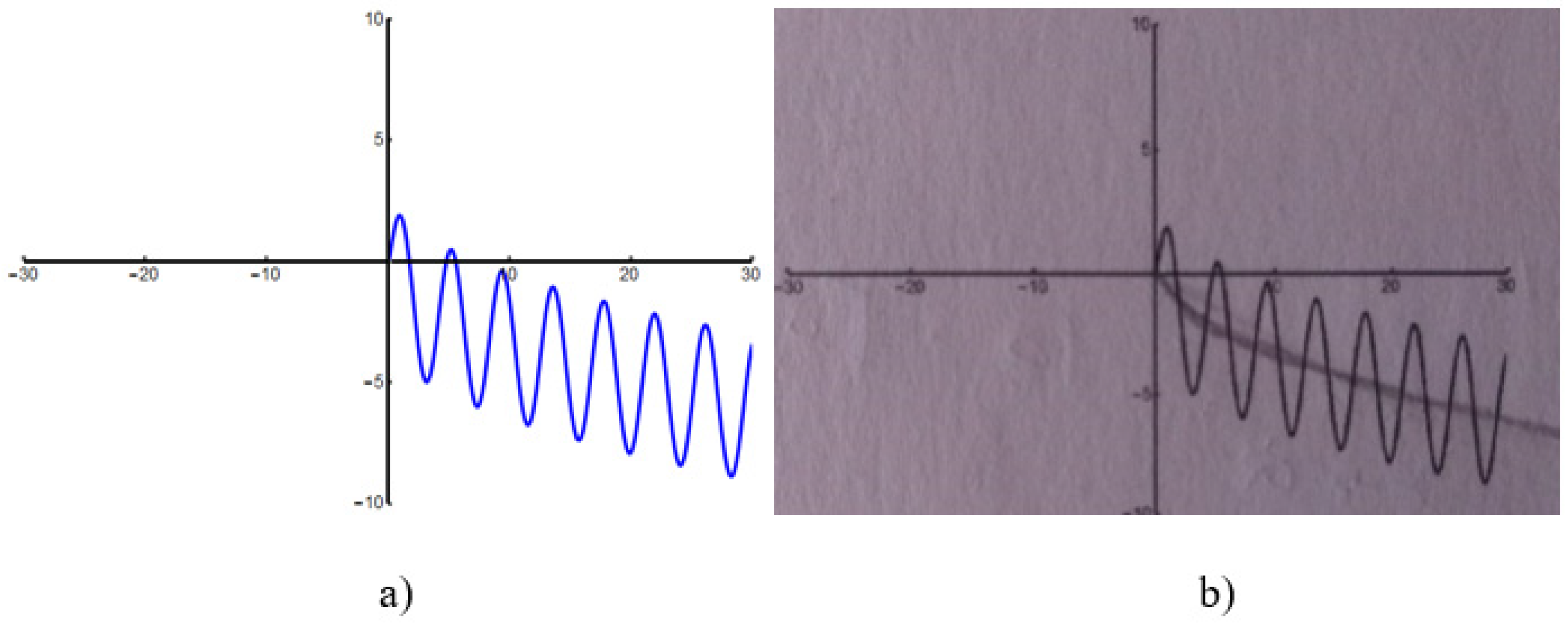
• Treatments: As previously mentioned, we aim to describe the transformations identified by the PSTs in the dialogue within the same register. To do so, the PST must indicate which registers of representation they believe Juan David uses during the fragment. Possible evidence of treatment can be found when Juan David says: “As seen in the image, it seems that it is not defined for negative values of x, so I will focus on the positive values. I would say that it looks like some kind of sine or cosine, and those functions are oscillating.” As we noted before, the student is using a graphical representation of the limit all the time;
• Conversions: This variable considers the transformations identified by the PST in Juan David’s reasoning between different registers. To do so, the PST must indicate which registers of representation they believe Juan David uses during the fragment. Possible evidence of conversion can be found when Juan David says: “the maxima (marked with dots) are becoming more negative each time, so if the larger values are getting smaller and smaller, the function tends to negative infinity.” Now, Juan David changes from a graphical idea of maxima (dots) to a numerical representation (their numerical y coordinates).

To ensure reliability in the analysis of each of these categories, there was double coding, meaning each of the authors analyzed and followed independent coding. Subsequently, each of the discrepancies was discussed until reaching full consensus, in line with the approach taken by Jacobs et al. [6] in their study.

Finally, regarding the potential level of development of the skill, we have established three potential levels: initial, intermediate, and advanced. The criteria for assigning a level to a PST were agreed upon based on the results. In this case, a PST will present an initial level when they can identify at most one transformation; they will be at an intermediate level if they detect two, and advanced for three or more. We must clarify that the purpose of distinguishing these three clusters is to group individuals with comparable behaviors in their responses, and given the small number of participants, they are intended only as a reference for the MTE on the ways in which PSTs reason about the task.

4. Results

Firstly, 13 PSTs (34.2%) of 38 demonstrate an awareness of how the task’s semiotic register, in this case, graphical, influences Juan David’s strategy and reasoning, known as the problem of the first threshold [26]. For example, when PST24 (see Figure 2) says, “as a teacher, it can be observed that depending on the type of exercise…” it can be noticed that they show awareness. Other expressions used by PSTs were “observing the limit of the function visually. Since the function is given by its graph” (PST14).

Therefore, 25 PSTs (65.8%) of 38 do not demonstrate an awareness of how the task’s semiotic register influences Juan David’s strategy. In the case of Figure 3, it is observed that the PST4 evaluates and lists some of the mathematical notions involved in the situation presented: domain, range, function, maximum, minimum, and limit, but does not mention anything about the task’s register.

Regarding the different degrees of potential development in the skill of attending to Juan David’s strategy and specifically to identify both treatments and conversions, we describe below the three levels detected: initial, intermediate, and advanced, as follows:

• Initial level

Firstly, it should be noted that 23 participants (60.5%) in total were able to extract from Juan David’s reasoning one (11 PST) or zero (12 PST) transformations between registers, such as PST34 (Figure 4), who does not identify any transformation. Therefore, it is the largest group in our pre-service teacher education program. Regarding the type of transformation, in total, nine treatments (81%) are observed compared to two conversions (19%).

However, a distinctive characteristic of these individuals is that in their descriptions, they tend to not specify whether the transformation refers to the segment of reasoning about the horizontal or slant asymptote, which makes it difficult to assign them. In total, eight (72%) treatments in the graphic register were identified where it was not possible to discern whether they corresponded to the HA or SA. Only three transformations (28%) that we describe explicitly mentioned a specific type of asymptote and were linked to a specific fragment of the dialogue.

In this regard, only PST30 detected a transformation in Juan David’s exposition when reasoning about the existence of HA, specifically stating, “Juan David interprets the graph trying, even, to define it with a formula (sine or cosine) and with the graph and the limit definition, concludes that there is no horizontal asymptote”. It is, therefore, a conversion between the graphic and symbolic registers, as he observes that the student tries to resort to an algebraic expression linked to the graph that allows him to calculate a limit.

Regarding the SA, there is one conversion and one treatment from two different PSTs. The conversion described by PST16 (Figure 5) shows how he focuses on Juan David’s appreciation of the decreasing numerical value of the maximum coordinates, which is shown in the graph, and thus realizes that for the student there is no SA as the limit is negative infinity.

On the other hand, in Figure 6, PST14 identifies a treatment for the SA as they extract a piece of the dialogue, and from their response, we deduce that they were able to recognize that Juan David is trying to calculate a limit using the graphical representation of the function;

• Intermediate level

In total, eight PSTs (21.1%) of thirty-eight extracted two transformations between representations of Juan David’s reasoning. Therefore, they present an intermediate level of development in their skill to identify transformations when they attend to Juan David’s strategy.

In these PSTs, it was possible to recognize a total of four conversions (25%), all of them between the graphic and numerical registers, and twelve treatments (75%), all of them in the graphic register. At this intermediate level, two PSTs (25%) establish the existence of a conversion without making explicit reference to when Juan David reasons about HA or SA; that is, they establish them in a generic way. On the other hand, three PSTs (37.5%) at this level observe some treatment in the graphic register without explicitly attending to either HA or SA, so they do it with vague descriptions, making it impossible to determine if they referred to reasoning related to HA or SA carried out by Juan David.

Regarding those transformations where the HA is explicitly mentioned, no conversion is observed, while there are three PSTs (37.5%) that identify some treatment, all of them in the graphic register. In the analyzed responses, they resort to aspects such as the oscillation of the graph and its similarity to sine and cosine functions: “it looks like a sine or cosine, that is, the graph oscillates” (PST15); “he sees an oscillating function (sine and cosine type)” (PST37); while others refer to Juan David seeming to focus on some points on the graph itself, that is, he focuses on more local aspects than general ones.

Regarding the slant asymptote, two PSTs (25%) identified some conversion, all between the graphic and numerical registers. The PSTs focus on aspects of Juan David’s reasoning such as the decrease of the ordinate values of the maxima of the graph: “he thinks that since the function is decreasing and oscillating, obviously its maxima will have more negative y-values and go to −∞” (PST25). In addition, six PSTs (75%) recognize some treatment in the dialogue: “he tries to find an slant asymptote by responding that the function doesn’t seem to approach any line” (PST15), “he understands that it cannot intersect the function and always has to have a positive slope” (PST37), among others. In both the cases of PST25 and PST37, the identified treatments focus on how the PSTs observe the graph of the function and relate it to not approaching or intersecting a line, attending to two meanings of the slant asymptote itself.

The identified treatments focus especially on aspects such as the shape that the graph of the function should have (a line) or the fact that the graph intersects the asymptote infinitely many times.

Next, an excerpt of the response of PST27 is shown, which reflects a conversion (Figure 7 above) between graphical and numerical registers and a treatment (Figure 7. below) on the slant asymptote using a graphical representation;

• Advanced Level

The group of PSTs with the highest potential development degree in this skill was composed of seven individuals (18.4% of the total of PSTs) who were able to detect three transformations. Compared to their group, these pre-service teachers detected a total of thirteen treatments (61.9%) and eight conversions (38.1%) in total, with the smallest difference observed in this group. In their descriptions, these participants identified the type of asymptote that Juan David reasoned about and explicitly indicated it. Therefore, there were only two generic register shifts (9.5%).

In the dialogue excerpt where Juan David reasoned about the existence of a HA, a total of six PSTs (86%) detected at least one treatment, and four individuals (57%) detected some conversion. All treatments were within the graphical register, and the behavior of the function or its oscillating character was highlighted with expressions like “observe the graph and how it behaves at positive and negative infinity” (PST8). Regarding the conversion, Figure 8 shows how PST29 perceives the domain of the graph when the student observes it with the goal of finding a limit. Additionally, this PST realizes that the student uses the oscillating character of the function to conclude that the limit does not exist (conversion).

In the SA, six participants in this group (86%) were able to detect at least one treatment and three PSTs (43%) a conversion. The identified treatments particularly focus on aspects such as the shape that the function graph should have (a straight line) or the fact that the graph intersects the slant asymptote infinitely many times. On the other hand, the conversions identified in the dialogue start from the graphical register towards the numerical register and focus on the maximums and minimums of the function or on the tendency towards negative infinity of the graph, such as: “they look at possible maximums and minimums of the function and deduce that they would go towards negative infinity” (PST8). Finally,

Table 1. Summary of results for the different levels of development.

Level of Development	Semiosis Activities	Categories	Perc. of PSTs (Per Level)	Perc. of PSTs (Total)
Initial	Knowledge of the first threshold problem	Yes	6 (26.1%)
		No	17 (73.9%)	23 (60.5%)
	Treatments	HA	0 (0%)
		SA	1 (4.3%)
		No asymptote type specified	8 (34.8%)
	Conversions	HA	1 (4.3%)
		SA	1 (4.3%)
		No asymptote type specified	0 (0%)
Intermediate	Knowledge of the first threshold problem	Yes	4 (50%)	8 (21.1%)
		No	4 (50%)
	Treatments	HA	3 (37.5%)
		SA	6 (75%)
		No asymptote type specified	3 (37.5%)
	Conversions	HA	0 (0%)
		SA	2 (25%)
		No asymptote type specified	2 (25%)
Advanced	Knowledge of the first threshold problem	Yes	3 (42.9%)	7 (18.4%)
		No	4 (57.1%)
	Treatments	HA	6 (85.7%)
		SA	6 (85.7%)
		No asymptote type specified	1 (14.3%)
	Conversions	HA	4 (57.1%)
		SA	3 (42.9%)
		No asymptote type specified	1 (14.3%)

summarizes the percentages presented above.

5. Discussion

Regarding the understanding of the problem of the first threshold [26], generally, prospective teachers do not seem to show awareness of how the task representation—in this case, the graph—conditions the strategy used by the fictitious student. We could attribute this low percentage to the fact that the graphical representation is not predominant in teaching limits at the end of secondary education and pre-university education [32], where the algebraic representation predominates due to various types of social beliefs and practices that consider it less formal [33]. In this sense, Arnal-Palacián et al. [34] suggest that PSTs tend to use other representations, such as symbolic ones. This may be due to the fact that, due to their training, they privilege certain representations over others, mainly for reasons of efficiency when successfully carrying out certain algorithmic procedures [35]. This motivates them to work with a limited set of representations, and, therefore, transformations between representations are scarce. Therefore, these findings emphasize two critical points. Firstly, MTEs must recognize that PSTs commonly overlook the significance of the task’s semiotic register when analyzing students’ strategies. This can be interpreted as a weakness in their learning process that MTEs should help them overcome. Secondly, the existing research literature offers valuable insights to assist MTEs in understanding the underlying causes of this phenomenon.

Regarding the potential expectation of progress that we observe in the participants with regard to their skill to identify transformations between semiotic representations, PSTs in an initial phase of development do not seem to be aware of how the task representation influences Juan David’s reasoning, as only six PSTs (26.1%) of this group made any reference to it in their analysis. In addition, their descriptions are generally vague, comments on the validity and relevance of Juan David’s argumentation or proof abound, and they have difficulties identifying some key elements with which to interpret and understand the student’s thinking, such as the type of asymptote. This data is in line with the results provided by van Es and Sherin [36], according to which most participants, at the beginning, mainly focused on evaluating whether the student’s reasoning was correct or incorrect. However, some do focus on other mathematical elements such as the shape of the graph, limits, or maximum and minimum values, but not so much on transformations between representations. Nevertheless, these students have more ease in detecting treatments than conversions, which are very scarce.

At the intermediate level, four PSTs (50%) in this group made some mention of how the task’s representation conditions were part of the student’s strategy. In line with the results of van Es and Sherin [36], there is a greater tendency for PSTs in this cluster to describe what the student does, resulting in a higher number of treatments compared to conversions between representations. There are fewer unassigned generic transformations than at the initial level. Notably, the recognition of transformations related to reasoning about the existence of HA is low, while for SA, it is higher. Therefore, it seems that the PSTs in this group pay more attention to the reasoning about slant asymptotes than to that about horizontal asymptotes. We believe that this may be due to the design of the dialogue itself and to the difficulty that pre-service teachers have in detecting two differentiated reasonings on two different types of asymptotes.

At the advanced level, three PSTs (43%) in this group show awareness of the problem of the first threshold. In their descriptions, which are more detailed, they indicate how the task’s representation conditions the strategy of the fictitious student. Additionally, and in general, they can identify dialogue excerpts where reasoning about each type of asymptote occurs, offering a more organized analysis. That is, they tend to interpret and make inferences about what the student does and why they do it [36]. Regarding transformations between representations, although they identify more treatments than conversions, the differences are smaller compared to the previous levels. These PSTs tend to recognize two differentiated reasonings in the dialogue, one on horizontal asymptotes and the other on slant asymptotes, and therefore observe both conversions and treatments in both.

The three potential levels of progression described above offer valuable information that could help MTEs gain sensitivity regarding the ways PSTs attend to students’ strategies. At the initial level, evaluative reasoning appears to be predominant, while as a higher level of development is reached, the description and interpretation of the student’s thinking become more significant. Despite the limited number of participants, the referenced research literature provides support for this thesis, underscoring the importance of PSTs’ thinking as a valuable indicator or descriptor in fostering the development of this competence. Another notable aspect to consider is whether they demonstrate the skill to differentiate between types of asymptotes or not.

In summary, the results suggest that PSTs pay little attention to the semiotic register of representation of the task and the transformations between representations. In this sense, attending to a student’s strategy not only involves identifying what is relevant but also ignoring what is not [36]. These two actions, paying attention to certain aspects and ignoring others, indicate that there is a subjective element in the teacher that guides their decisions regarding what is relevant and what aspects should be ignored. Authors such as López and Zakaryan [37] point to beliefs. Based on our findings, it can be inferred that a great number of our participants do not consider transformations between representations or the semiotic register of the task as significant focal points. Therefore, MTEs should be aware that this potential weakness among PSTs is a common feature of their initial stage of professional development.

6. Conclusions

This article described the developmental level of the skill of attending to students’ answers within professional noticing in the context of pre-service teacher education. The study identified three potential levels of development. The findings revealed that most PSTs (60.5%) are at an initial level of development. Consequently, at this stage of their professional growth, they have not yet developed an awareness of the significance of semiotic representations. López and Zakaryan [37] (p. 350) affirm that “professional noticing is a fundamental aspect of the professional competence of mathematics teachers in relation to the different practices carried out in the classroom”, thereby highlighting its inclusion as part of the content covered in teacher education.

Firstly, we want to emphasize the importance for MTEs to possess extensive and in-depth theoretical knowledge of professional noticing, given its status as a topic of ongoing research and continuous updates [6,21,36]. Additionally, MTEs should strive for a high level of competency development in order to explicitly show PSTs their own ways of perceiving, understanding, and addressing professional issues that arise in the mathematics classroom. By doing so, they can create a space for reflection and debate, contrasting different approaches and generating valuable insights. This approach holds significant power, as it not only aims to enhance the skills and competencies of teachers but also aims to acknowledge the theoretical contributions offered by the research community in various aspects of mathematics teaching and learning, fostering a strong connection between theory and practice. As an example, the contributions of Duval, as described in our theoretical framework, exemplify a potential source of Pedagogical Content Knowledge (PCK), which could be developed by PSTs as they learn to professionally notice.

In relation to the objective of the article and based on the reflection of the results obtained in the professional task as well as from our perspective as MTEs, we now proceed to present some of the most relevant contributions that we believe have aided us in delving deeper and characterizing the desired or necessary MTEPCK for fostering professional noticing in pre-service teacher education. Initially, the use of dialogue-type tasks can effectively encourage the utilization of this competence. These professional tasks, serving as potential training tools, may help facilitate the restructuring of ideas among teachers [10], fostering their awareness of decision-making and actions in practice. Additionally, the research literature offers valuable insights into other viable strategies for cultivating professional noticing, such as group analysis of videos showcasing classroom excerpts [36] or the modeling of teaching practices [38]. Therefore, we would like to emphasize how research literature on teacher professional development can provide the MTE with valuable information regarding potential tools, tasks, and resources to elicit and facilitate the development of the skills of professional noticing. Towards the end of this section, we will address some limitations encountered when using task-dialogue-type tasks. Thus, the tasks, resources, teaching strategies, and examples employed by the MTE serve as evidence of their MTEPCK, specifically related to the subdomain of knowledge of teaching the content of teacher education, as outlined in the model presented by Escudero-Ávila et al. [2], and more specifically categorized as knowledge of teaching strategies and resources with prospective teachers [13]. Considering this fact, it would be desirable for an MTE to possess a broad repertoire of teaching strategies, tasks, and resources, as well as an awareness of their limitations and strengths, in order to optimize the opportunities for professional development of the PSTs.

Secondly, our observations of the results of the professional task indicate that a significant majority of prospective teachers do not recognize the significance of the semiotic register of the task as a relevant mathematical element that deserves consideration. Consequently, they tend to disregard it, resulting in a constrained comprehension of students’ actions. This last finding allows us to expose a weakness of the PSTs in relation to the development of their skill of attending to children’s strategies. Therefore, when an MTE shows sensitivity to the main advantages and limitations of the PSTs in acquiring professional noticing, for example, anticipating answers or ways of thinking, they are revealing their knowledge concerning the strengths and weaknesses of the PSTs, which falls within the subdomain of the features of professional development. On a different note, our investigation has also revealed a robust mathematical foundation, which represents a notable strength. Thirdly, literature provides information to MTEs about which teacher’s knowledge supports each skill of professional noticing [37], and these insights can be regarded as further substantiation within this category.

Considering these recent insights, we would like to suggest that it would be advisable for the MTE to support PSTs in eliciting and discussing the aspects they consider significant or insignificant while providing them with the underlying justifications. By engaging in this process, the MTE can help PSTs become aware of their own beliefs and guide them towards a progression from less critical perspectives to more deliberate ones [10,36].

On the other hand, the selected excerpts in the analysis provide evidence of the level of development in the skill of attending to students’ strategies by the PSTs. Thus, the expressions they employ, the prevailing mathematical elements, and those that are disregarded, as well as their modes of reasoning [13], could be regarded as indicators or evidence of professional development, a category within the domain of knowledge concerning the features of professional development. Similarly, within the domain of knowledge regarding the features of professional development, we postulate that the three potential levels of development described in this study could serve as the foundation for a prospective learning trajectory that elucidates the progression of professional noticing (knowledge about learning theories in teacher education contexts). Nonetheless, the task’s specificity and the limited number of participants render such generalizations unattainable.

Lastly, we would like to highlight a limitation of this study: the instrument utilized requires supplementation with additional data collection tools, such as interviews or small group discussions, to acquire more precise and comprehensive descriptions of the pedagogical reasoning of the prospective secondary teachers. It is worth noting that in this context, we have observed instances where certain participants tended to conflate the descriptions of the strategy (the first prompt) with the characterization of the meanings (the second prompt). Consequently, this prompts us to contemplate the necessity of revising the wording of the prompts.

In conclusion, significant efforts are still required to enhance our comprehension of the nature and structure of the professional knowledge held by MTEs. This study represents an initial stride in that trajectory, underscoring the potential of research within the domain of mathematics teacher professional development as a potent catalyst for professional advancement among teacher educators. We earnestly encourage the entire research community to embark on this pursuit. Furthermore, certain facets, including the professional noticing of MTEs [39], have remained unexplored and hold promise for yielding valuable insights into the professional practice of MTEs in future endeavors.