Outcomes of a Teaching Learning Sequence on Modelling Surface Phenomena in Liquids
Abstract
1. Introduction
2. The Mesoscopic Model of Surface Tension
3. Some Examples of Simulation Activities
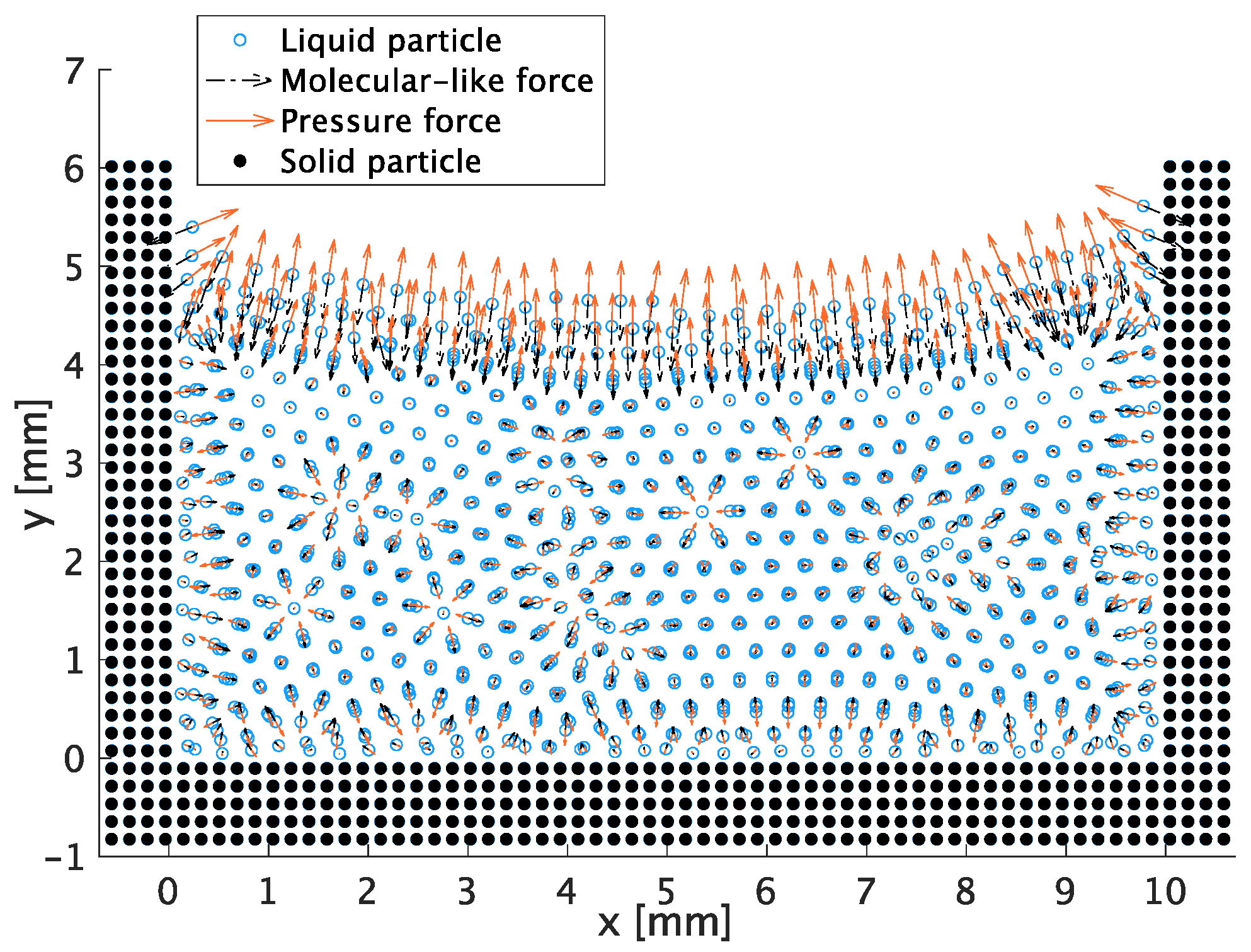
3.1. Menisci Formation
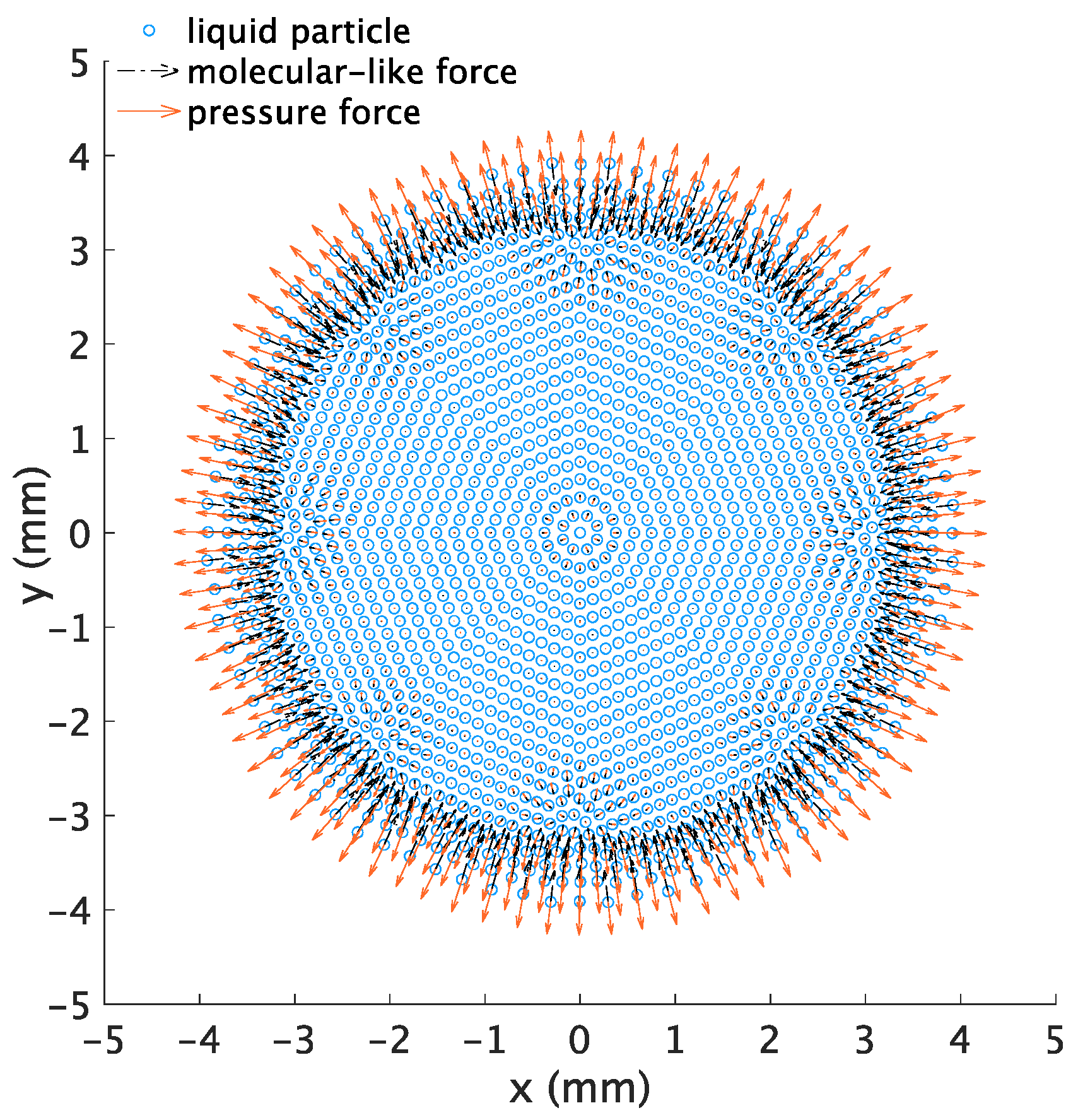
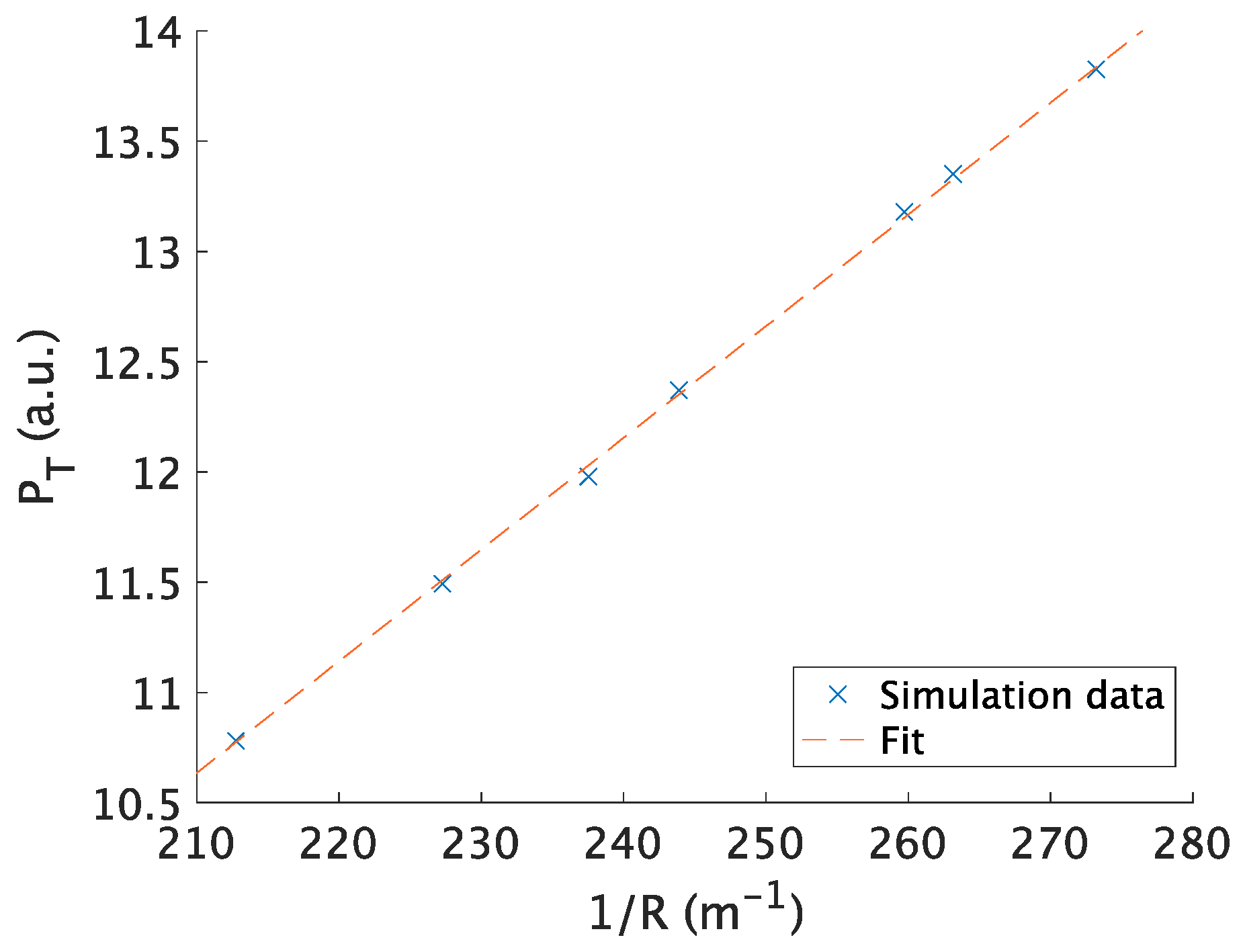
3.2. The Pressure inside a Droplet
4. The Student Sample and the Teaching/Learning Sequence
4.1. The Student Sample
4.2. The TLS
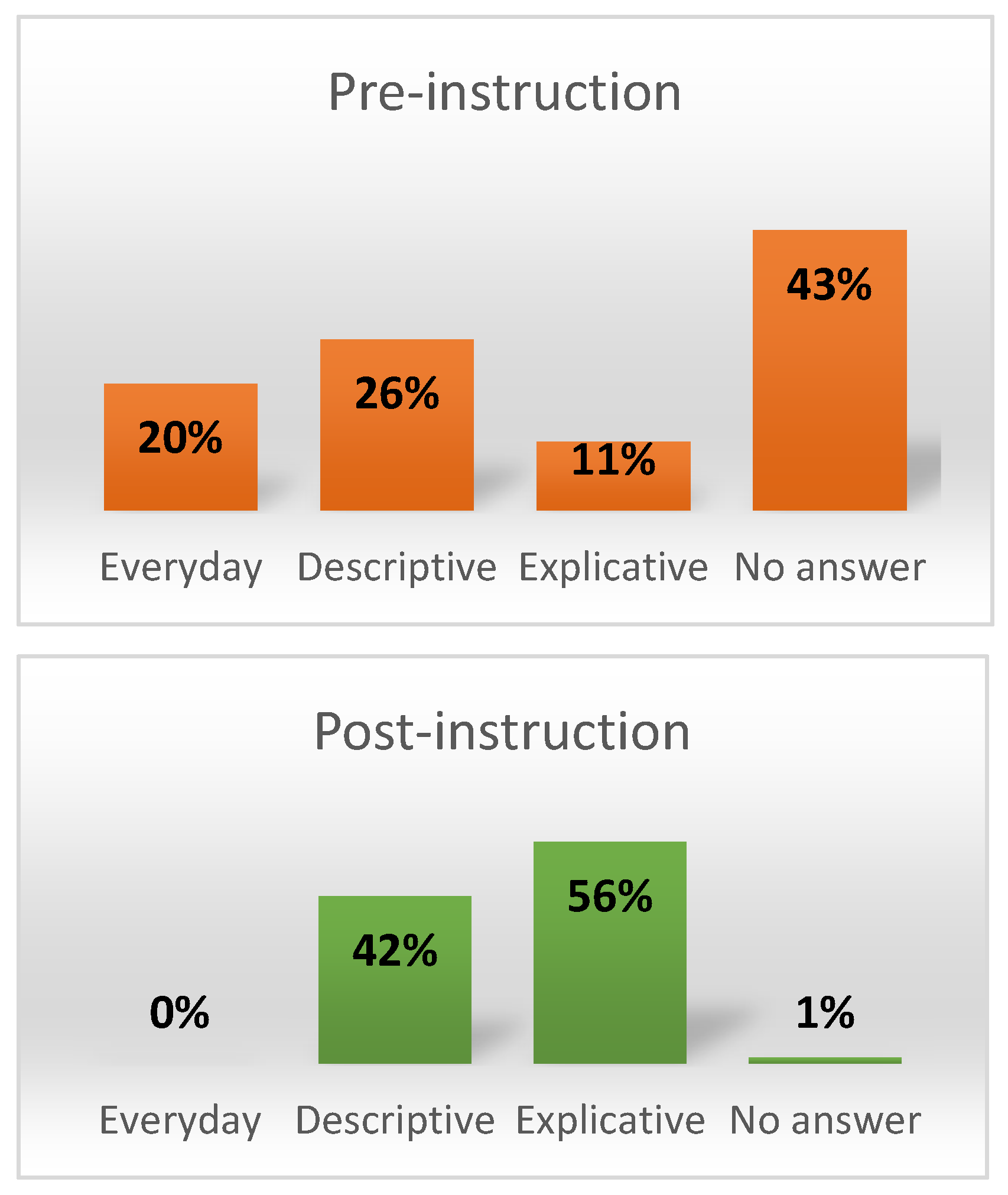
5. The Results
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- Questionnaire and student typical responses
- Question 1: The liquid inside a glass capillary tube has a concave meniscus (see the figure). Why? Explain in terms of forces.
- (1)
- The student explains in terms of equilibrium of the adhesive and cohesive forces in the liquid
- (2)
- The student describes in terms of cohesive forces and adhesive forces between liquid and glass. The student does not go into detail
- (3)
- The student explains in terms of adhesive forces between liquid and glass
- (4)
- The student describes in terms of forces acting among liquid molecules
- (5)
- The student explains in terms of inter-molecular forces. The student introduces the adhesive forces between liquid and the walls of the capillary tube
- (6)
- The student explains in terms of adhesive forces between liquid and solid and cohesive forces of the liquid
- (7)
- The student describes the observed phenomenon by introducing the surface tension concept in a general sense
- (8)
- The student explains in terms of surface tension of the liquid
- (9)
- No response
- Question 2: A liquid does not wet the glass it is in contact with. Why? Explain in terms of forces.
- (1)
- The student describes in terms of general properties of the molecules
- (2)
- The student describes in terms of cohesive forces and adhesive forces with the glass. The student does not go into detail
- (3)
- The student explains in terms of adhesive force with the glass
- (4)
- The student describes in terms of properties of material
- (5)
- The student describes in terms of liquid inter-molecular forces
- (6)
- The student explains in terms of inter-molecular forces
- (7)
- The student explains in terms of adhesive forces between liquid and solid and cohesive forces of the liquid
- (8)
- The student explains in terms of surface tension of the liquid
- (9)
- The student describes in terms of general forces (repulsive forces, capillary forces, etc.)
- (10)
- No response
- Question 3: Consider a toy boat floating on the surface of the water contained in a tank. After dropping a few drops of soap in the water with a dropper, it is observed that the boat starts to move. Why? Explain in terms of the forces acting on the boat.
- (1)
- The student explains in terms of physical-chemical properties of the soap
- (2)
- The student describes in terms of interaction forces between water and soap
- (3)
- The student describes in terms of general forces (elastic force for example)
- (4)
- The student explains in terms of formation/breaking of inter-molecular bonds
- (5)
- The student explains the phenomenon indicating the surfactant as the agent that cause surface tension breaking
- (6)
- The student describes in terms of surfactant properties
- (7)
- The student explains the cause of the boat’s motion with a change in the structure and/or bonds of the liquid
- (8)
- The student introduces (describes) surface tension as the cause of the boat’s motion
- (9)
- No response
- Question 4: What are the units of measurement of surface tension? How is it possible to obtain them?
- (1)
- The student indicates the units but does not explain how to derive them
- (2)
- The student indicates the units and explains how to derive them
- (3)
- The student indicates the units and derives them through a mathematical relation
- (4)
- The student indicates the physical quantities but not the relationship between them (units)
- (5)
- The student indicates the physical quantities and explains how to derive them
- (6)
- No response
- Question 5: The number of water droplets required to completely cover the surface of a coin is greater than the number of seed oil droplets required to cover the surface of a coin identical to the first one. Explain what this phenomenon might be related to.
- (1)
- The student describes in terms of liquid properties (density, surface tension etc.)
- (2)
- The student describes in terms of adhesive and/or cohesive forces in the liquid
- (3)
- The student explains in terms of adhesive and/or cohesive forces in the liquid
- (4)
- The student describes macroscopically
- (5)
- The student explains in terms of surface tension of the liquid
- (6)
- The student explains in terms of liquid inter-molecular interactions
- (7)
- The student describes in terms of surface properties
- (8)
- No response
- Question 6: Consider three capillary tubes of the same material and of the same diameter each dipped in three tanks containing water, mercury and oil, respectively. Represent how each liquid will be arranged inside the capillary tubes graphically. Explain in terms of forces.
- (1)
- The student describes in terms of liquid properties (density, capillarity, surface tension etc.)
- (2)
- The student describes in terms of general forces
- (3)
- The student describes in terms of adhesive and/or cohesive forces in the liquid
- (4)
- The student explains in terms of adhesive and/or cohesive forces in the liquid
- (5)
- The student describes in terms of liquid inter-molecular interactions
- (6)
- The student explains in terms of liquid inter-molecular interactions
- (7)
- No response
- Question 7: What do you think are the “adhesive forces” and “cohesive forces”? Give some examples of contexts in which these forces are present.
- (1)
- The student explains among whom the forces act. The student does not give examples
- (2)
- The student explains among whom the forces act and gives examples
- (3)
- The student explains in terms of inter-molecular bonds
- (4)
- The student gives general examples
- (5)
- No response
- Question 8: What difference do you think there is between these two types of forces?
- (1)
- The student explains in terms of the different nature of the molecules
- (2)
- The student explains in terms of the different nature of the substances
- (3)
- The student explains introducing the vectorial nature of the forces
- (4)
- The student explains among whom the forces act
- (5)
- No response
- Question 9: Which quantities influence the rise of a liquid inside a capillary tube? Explain.
- (1)
- The student describes in terms of forces (tension, adhesive, cohesive forces etc.)
- (2)
- The student explains in terms of forces (tension, adhesive, cohesive forces etc.)
- (3)
- The student describes in terms on general geometric properties (diameter, density, friction, pressure, length of the tube, gravity, viscosity etc.)
- (4)
- No response
- Question 10: Do you think the soap modifies water properties? If yes, which ones?
- (1)
- The student describes in terms of physical-chemical properties
- (2)
- The student explains in terms of inter-molecular interaction
- (3)
- The student describes in terms of surface tension
- (4)
- The student explains in terms of surface tension
- (5)
- The student explains in terms of adhesive/cohesive forces (surfactants)
- (6)
- The student describes in terms of general physical quantities and/or forces (density, surface tension etc.)
- (7)
- The student cites everyday/common life situations
- (8)
- No response
- Question 11: If you put some soap into water and deposit a drop of this mixture on a horizontal plane, you will notice that the water is evenly distributed on the surface not forming a real drop. Explain this phenomenon.
- (1)
- The student describes in terms of physical-chemical properties
- (2)
- The student explains in terms of inter-molecular interaction
- (3)
- The student describes in terms of surface tension
- (4)
- The student explains in terms of surface tension
- (5)
- The student explains in terms of adhesive/cohesive forces (surfactants)
- (6)
- The student describes in terms of general physical quantities and/or forces (density, surface tension etc.)
- (7)
- The student describes on the basis of observed phenomena
- (8)
- No response
References
- Böttcher, F.; Meisert, A. Argumentation in Science Education: A Model-based Framework. Sci. Educ. 2011, 20, 103–140. [Google Scholar] [CrossRef]
- Gilbert, J.K.; Boulter, C.; Rutherford, M. Models in explanations: Part 1, Horses for courses? Int. J. Sci. Educ. 1998, 20, 83–97. [Google Scholar] [CrossRef]
- Zacharia, Z.C. Beliefs, attitudes, and intentions of science teachers regarding the educational use of computer simulations and inquiry based experiments in physics. J. Res. Sci. Teach. 2003, 40, 792–823. [Google Scholar] [CrossRef]
- Schiefer, J.; Edelsbrunner, P.A.; Bernholt, A.; Kampa, N.; Nehring, A. Epistemic Beliefs in Science—A Systematic Integration of Evidence From Multiple Studies. Educ. Psychol. Rev. 2022, 34, 1541–1575. [Google Scholar] [CrossRef] [PubMed]
- Soulios, I.; Psillos, D. Enhancing student teachers’ epistemological beliefs about models and conceptual understanding through a model-based inquiry process. Int. J. Sci. Educ. 2016, 38, 1212–1233. [Google Scholar] [CrossRef]
- Battaglia, O.R.; Di Paola, B.; Fazio, C. K-means Clustering to Study How Student Reasoning Lines Can Be Modified by a Learning Activity Based on Feynman’s Unifying Approach. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 2005–2038. [Google Scholar] [CrossRef]
- Fazio, C.; Battaglia, O.R.; Di Paola, B. Investigating the quality of mental models deployed by undergraduate engineering students in creating explanations: The case of thermally activated phenomena. Phys. Rev. ST Phys. Educ. Res. 2013, 9. [Google Scholar] [CrossRef]
- Rutten, N.; Van Joolingen, W.R.; Van der Veen, J.T. The learning effects of computer simulations in science education. Comput. Educ. 2012, 58, 136–153. [Google Scholar] [CrossRef]
- Rutten, N.; Van der Veen, J.T.; Van Joolingen, W.R. Inquiry-based whole-class teaching with computer simulations in physics. Int. J. Sci. Educ. 2015, 37, 1225–1245. [Google Scholar] [CrossRef]
- Crawford, B.A. From inquiry to scientific practices in the science classroom. In Handbook of Research on Science Education; Lederman, N.G., Abell, S.K., Eds.; Routledge: New York, NY, USA, 2014; Volume II, pp. 515–541. [Google Scholar]
- Psillos, D.; Kariotoglou, P. (Eds.) Iterative Design of Teaching-Learning Sequences; Springer Science+Business Media: Dordrech, The Netherlands, 2016. [Google Scholar]
- Meheut, M.; Psillos, D. (Eds.) Teaching-learning sequences: Aims and tools for science education research. Int. J. Sci. Educ. 2004, 26, 515–535. [Google Scholar] [CrossRef]
- Battaglia, O.R.; Di Paola, B.; Fazio, C. Unsupervised quantitative methods to analyze student reasoning lines: Theoretical aspects and examples. Phys. Rev. Phys. Educ. Res. 2019, 15. [Google Scholar] [CrossRef]
- Berry, M.V. The molecular mechanism of surface tension. Phys. Educ. 1971, 6, 79–84. [Google Scholar] [CrossRef]
- Marchand, A.; Weijs, H.; Snoeijer, H.J.; Andreotti, B. Why is surface tension a force parallel to the interface? Am. J. Phys. 2011, 79, 999–1008. [Google Scholar] [CrossRef]
- Roura, P. Thermodynamic derivations of the mechanical equilibrium conditions for fluid surfaces: Young’s and Laplace’s equations. Am. J. Phys. 2005, 73, 1139–1147. [Google Scholar] [CrossRef]
- Durand, M. Mechanical approach to surface tension and capillary phenomena. Am. J. Phys. 2021, 89, 261. [Google Scholar] [CrossRef]
- Besson, U.; Viennot, L. Using models at the mesoscopic scale in teaching physics: Two experimental interventions in solid friction and fluid statics. Int. J. Sci. Educ. 2004, 26, 1083–1110. [Google Scholar] [CrossRef]
- Battaglia, O.R.; Agliolo Gallitto, A.; Termini, G.; Fazio, C. A study of capillarity phenomena by using a computer-based simulation approach. Eur. J. Phys. 2021, 42, 055704. [Google Scholar] [CrossRef]
- Battaglia, O.R.; Agliolo Gallitto, A.; Fazio, C. Computer simulations to approach surface tension by means of a simple mesoscopic mechanical model. Comput. Appl. Eng. Educ. 2019, 27, 1333–1342. [Google Scholar] [CrossRef]
- Nair, P.; Pöschel, T. Dynamic capillary phenomena using Incompressible SPH. Chem. Eng. Sci. 2018, 176, 192–204. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Panchenko, A. Pairwise Force Smoothed Particle Hydrodynamics model for multiphase flow: Surface tension and contact line dynamics. J. Comput. Phys. 2016, 305, 1119–1146. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703–1759. [Google Scholar] [CrossRef]
- Tartakovsky, A.; Meakin, P. Modeling of surface tension and contact angles with smoothed-particle hydrodynamics. Phys. Rev. E 2005, 72, 026301. [Google Scholar] [CrossRef] [PubMed]
- Akinci, N.; Akinci, G.; Teschner, M. Versatile surface tension and adhesion for SPH fluids. ACM Trans. Graph. 2013, 32, 182. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Meakin, P. Pore scale modeling of immiscible and miscible fluid flows using smoothed particle hydrodynamics. Adv. Water Resour. 2006, 29, 1464–1478. [Google Scholar] [CrossRef]
- Hoover, W.G. Isomorphism linking smooth particles and embedded atoms. Phys. A 1998, 260, 244–254. [Google Scholar] [CrossRef]
- Lion, T.W.; Allen, R.J. Computing the local pressure in molecular dynamics simulations. J. Phys. Condens. Matter 2012, 24, 284133. [Google Scholar] [CrossRef]
- Duit, R.; Gropengießer, H.; Kattmann, U.; Komorek, M.; Parchmann, I. The Model of Educational Reconstruction—A Framework for Improving Teaching and Learning Science1. In Science Education Research and Practice in Europe. Cultural Perspectives in Science Education; Jorde, D., Dillon, J., Eds.; Sense Publishers: Rotterdam, The Netherlands, 2012; Volume 5, pp. 13–37. [Google Scholar] [CrossRef]
- Bonwell, C.; Eison, J. Active Learning: Creating Excitement in the Classroom AEHE-ERIC Higher Education Report No. 1; Jossey-Bass: Washington, DC, USA, 1991; ISBN 978-1-878380-08-1. [Google Scholar]
- Ericsson, K.A. Deliberate practice and the modifiability of body and mind: Toward a science of the structure and acquisition of expert and elite performance. Int. J. Sport Psychol. 2007, 38, 4–34. [Google Scholar]
- Fleming, N.D. Teaching and Learning Styles: VARK Strategies, 1st ed.; Neil Fleming: Christchurch, New Zealand, 2001. [Google Scholar]
- Felder, R.M.; Silverman, L.K. Learning and teaching styles in engineering education. Eng. Educ. 1988, 78, 674–681. [Google Scholar]
- Saddler-Smith, E. The relationship between learning style and cognitive style. Pers. Indiv. Diff. 2001, 30, 609–616. [Google Scholar] [CrossRef]
- Jensen, M. Questionnaire validation: A brief guide for readers of the research literature. Clin. J. Pain 2003, 19, 345–352. [Google Scholar] [CrossRef]
- Bandura, A. Self-efficacy: Toward a unifying theory of behavioral change. Psychol. Rev. 1977, 84, 191–215. [Google Scholar] [CrossRef] [PubMed]
- Bandura, A. Self-Efficacy: The Exercise of Control; W. H. Freeman: New York, NY, USA, 1997. [Google Scholar]
- Boekaerts, M. Being concerned with well-being and with learning. Educ. Phychol. 1993, 28, 149–167. [Google Scholar] [CrossRef]
- Wenning, C.J. Levels of inquiry: Hierarchies of pedagogical practices and inquiry processes. J. Phys. Teach. Educ. Online 2005, 2, 3–12. [Google Scholar]
- Wenning, C.J. Assessing inquiry skills as a component of scientific literacy. J. Phys. Teach. Educ. Online 2007, 4, 21–24. [Google Scholar]
- McDermott, L.C.; Shaffer, P.S.; Constantinou, C.P. Preparing teachers to teach physics and physical science by inquiry. Phys. Educ. 2000, 35, 411–416. [Google Scholar] [CrossRef]
- Specht, M.; Frömbgen, T.; Wessely, H.; Sokolowski, M. A simple mechanical apparatus for measuring the surface tension of soap bubbles. Am. J. Phys. 2019, 87, 1014–1019. [Google Scholar] [CrossRef]
- Marton, F. Phenomenography—A research approach to investigating different understandings of reality. J. Thought 1986, 21, 28–49. [Google Scholar]
- Krippendorff, K. Content Analysis: An Introduction to Its Methodology, 4th ed.; SAGE: Los Angeles, CA, USA, 2018. [Google Scholar]


| Practical/Everyday | Descriptive | Explicative |
|---|---|---|
| Reflects the creation of situational meanings derived from everyday contexts. The student uses other situations, perceived as analogous to the one proposed in the question, to try to describe/explain it. | The student describes and characterizes the proposed situation/analyzed process by searching in memory the variables perceived as relevant and/or recalling their relations. The variables and the relationships among them are expressed by means of different languages (verbal, iconic, mathematic). Causal relations among the variables on the basis of a functioning model (microscopic/macroscopic) are not given. | The student gives an explanation of the proposed situation referring to a model (qualitative and/or quantitative) based on cause/effect relations. He may also provide explanatory hypotheses by introducing models which can be seen at a theoretical level. |
| Practical/Everyday | Descriptive | Explicative |
|---|---|---|
| (according to my) experience … Like I see in real life … usually … real object … like an insect on water … | I remember that … I studied that … I know that … The formula says … There are adhesive and cohesive forces … There is surface tension … Chemistry/Physics says … | molecular movement …. is similar to … microscopic … inter-molecular forces … interaction … equilibrium … molecules … |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Battaglia, O.R.; Agliolo Gallitto, A.; Termini, G.; Fazio, C. Outcomes of a Teaching Learning Sequence on Modelling Surface Phenomena in Liquids. Educ. Sci. 2023, 13, 425. https://doi.org/10.3390/educsci13040425
Battaglia OR, Agliolo Gallitto A, Termini G, Fazio C. Outcomes of a Teaching Learning Sequence on Modelling Surface Phenomena in Liquids. Education Sciences. 2023; 13(4):425. https://doi.org/10.3390/educsci13040425
Chicago/Turabian StyleBattaglia, Onofrio Rosario, Aurelio Agliolo Gallitto, Giulia Termini, and Claudio Fazio. 2023. "Outcomes of a Teaching Learning Sequence on Modelling Surface Phenomena in Liquids" Education Sciences 13, no. 4: 425. https://doi.org/10.3390/educsci13040425
APA StyleBattaglia, O. R., Agliolo Gallitto, A., Termini, G., & Fazio, C. (2023). Outcomes of a Teaching Learning Sequence on Modelling Surface Phenomena in Liquids. Education Sciences, 13(4), 425. https://doi.org/10.3390/educsci13040425









