Where Is It Best to Sit in Class? Description of an Experience Based on STEM Problem Solving in a School Context
Abstract
1. Introduction
2. Theoretical Framework
2.1. STEM Problem Solving Activities
- It should promote the improvement of critical thinking and problem solving skills. One way to achieve this is to provide an activity that starts from a real-world problem and allows students to integrate mathematical procedures with non-mathematical concepts.
- Creativity should be encouraged, so it is necessary to design complex STEM problem-solving activities that challenge students to develop creative solutions.
- Teamwork and collaboration should be encouraged. This is a key aspect of teaching students to learn to work effectively with and through others.
- The activity should provide learning opportunities, including those as a practical nature. Indeed, finding applications of academic content to real-world problems can contribute to increased student motivation and a greater sense of achievement.
2.2. The Role of Teachers, Students and Technology in STEM Problem-Solving
- use of manipulatives and hands-on learning;
- cooperative learning;
- discussion and enquiry;
- questioning and conjecture;
- use of justification of thinking;
- writing for reflection and problem solving;
- use of a problem-solving approach;
- integration of technology;
- teacher as facilitator;
- use of assessment as part of instruction.
- Enhancing the learning experience: Technology can make STEM subjects more engaging and interactive for students. It can provide visual aids, simulations, and interactive tools that allow students to experiment and test their hypotheses. This helps to bring abstract concepts to life and makes learning more enjoyable and memorable.
- Developing problem-solving skills: Technology can help students develop problem-solving skills by providing them with opportunities to work on real-world problems using technology-based tools. This allows students to apply their knowledge and skills to solve problems and challenges they may face in the future.
- Fostering collaboration: Technology can facilitate collaboration among students, teachers, and experts from various fields. Students can work together on projects, share ideas and resources, and collaborate with experts to find solutions to complex problems.
2.3. Mathematics Learning Opportunities
3. Goals of the Study
- What learning opportunities are provided by the development of a STEM problem-solving activity based on sound intensity and involving the mathematical concept of a two-variable function?
- What is the catalyst for each of these learning opportunities?
4. Methods
4.1. Participants and Data Collected
4.2. The STEM Problem-Solving Activity
4.2.1. The Sound Measure Experiment
4.2.2. Data Representation
4.3. Data Analysis
T: How do you think sound propagates?
A2: There needs to be some always air for sound to propagate
A3: And if there is a wall near the source of the sound, it can bounce, that produces the echo.
A1: So, there are vibrations in the air!
T: Indeed, the emitting source vibrates and, in doing so, the molecules in the air receive this vibration and transmit it to neighboring particles. This promotes a pressure fluctuation, which is called a wave.
[Students try to take measurements with the iPad at their desks. The intensity of the emitting source is constant, but they observe that the measurement result is variable]
B1: The measurements are not always the same, but no we haven’t moved!
T: Wow, did you expect the measurements to be always the same?
A2: Of course!
B1: I’m thinking that perhaps the noise is irregular… or maybe the iPad’s sensor is not accurate.
T: How can we get a reliable measurement at a specific point?
B1: We can measure several times and…!
B2: Take the average of the values!
B3: I’m thinking that maybe the differences appeared because we changed the orientation of the iPad…see that the microphone is here [points to the exact spot on the device].
[Students are discussing how to use the cubes to represent the data]
B1: We must use these little coloured cubes…
B2: Yeah, no idea what we can do with this.
B3: This kind of reminds me of the histograms we did in statistics.
B2: Wait…if we look at the data in one row…
B3: We can try to make several columns of cubes, one that represents each of the measurements in that row!
B1: However are we going to use the colours for anything? We don’t have the same number of cubes of each colour…
B2: Well, let’s forget about the colours for the moment… Let’s focus on seeing how to raise a column in each cell.
[After this discussion the students have already understood the first step in the representation of the data. They then begin to collect the pieces to make the first columns. This is an important moment in the solving process, as the notion of function appears. Indeed, the discussion among the students allows them to see that they must associate a value with each point on the plane a value corresponding to the measure of intensity at that point and that, in addition, this relationship can be represented by raising a column at each of the points].
[Once the students have the data and are ready to represent them using the multilink cubes].
T: How could you represent this data?
C1: We could make a bar diagram…for each…
T: For each row?
C1: Exactly, we represent with bars the measurements obtained in each row of points.
T: Okay, what would you get then?
C2: I see…then we will have…five bar charts?
C1: No, not five, no. We would have about seven rows, so a bar chart for each row.
C2: And we can order them from closest to farthest.
[Students have already decided that they will raise a column of cubes in each cell according to the value of the intensity at that point].
D1: We must raise a column in each cell, it will be higher if the value of the measurement is higher.
T: That’s a good idea!
D2: Yes, but…how do we do it? If there are numbers like that…[gesticulates referring to big]
D1: 10 by 10!
T: Come on, give it a try.
[After a while of trying, the students realise that if they give this value to the cubes, there is hardly any difference]
T: How are you doing?
D2: It’s going badly, because we don’t know how to represent this data…
T: Yeah, they’re big and they’re not that different either… how about looking at the difference between the biggest and the smallest of the data?
D1: I have an idea! We can represent the lowest value with a cube and, from there, we increase…
5. Results: Mathematical Learning Opportunities
5.1. Sound Measure Experiment Phase
5.1.1. Session 1:
5.1.2. Session 2:
5.1.3. Session 3:
5.2. Data Representation Phase
5.2.1. Session 4:
5.2.2. Session 5:
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Maass, K.; Geiger, V.; Ariza, M.R.; Goos, M. The role of mathematics in interdisciplinary STEM education. ZDM 2019, 51, 869–884. [Google Scholar] [CrossRef]
- Chalmers, C.; Carter, M.; Cooper, T.; Nason, R. Implementing “big ideas” to advance the teaching and learning of science, technology, engineering, and mathematics (STEM). Int. J. Sci. Math. Educ. 2017, 15, 25–43. [Google Scholar] [CrossRef]
- Cai, J.; Morris, A.; Hohensee, C.; Hwang, S.; Robison, V.; Cirillo, M.; Kramer, S.L.; Hiebert, J.; Bakker, A. Maximizing the quality of learning opportunities for every student. J. Res. Math. Educ. 2020, 51, 12–25. [Google Scholar] [CrossRef]
- Albarracín, L.; Gorgorió, N. Mathematical modeling projects oriented towards social impact as generators of learning opportunities: A case study. Mathematics. 2020, 11, 2034. [Google Scholar] [CrossRef]
- Honey, M.; Pearson, G.; Schweingruber, H. (Eds.) STEM Integration in K-12 Education: Status, Prospects, and an Agenda for Research; National Academies Press: Washington, DC, USA, 2014. [Google Scholar]
- Doerr, H.; Ärlebäck, J.B. Fostering students’ independence in modelling activities. In Proceedings of the CERME 9-Ninth Congress of the European Society for Research in Mathematics Education, Prague, Czech Republic, 4–8 February 2015; pp. 855–861. [Google Scholar]
- Stender, P.; Kaiser, G. Scaffolding in complex modelling situations. Zdm 2015, 47, 1255–1267. [Google Scholar] [CrossRef]
- Blum, W.; Niss, M. Applied mathematical problem solving, modelling, applications, and links to other subjects—State, trends and issues in mathematics instruction. Educ. Stud. Math. 1991, 22, 37–68. [Google Scholar] [CrossRef]
- Lawrenz, F.; Gravemeijer, K.; Stephan, M. Introduction to this Special Issue. Int. J. Sci. Math. Educ. 2017, 51, S1–S4. [Google Scholar] [CrossRef]
- Li, Y.; Schoenfeld, A.H. Problematizing teaching and learning mathematics as “given” in STEM education. Int. J. Stem Educ. 2019, 6, 44. [Google Scholar] [CrossRef]
- Duijzer, C.; den Heuvel-Panhuizen, V.; Veldhuis, M.; Doorman, M. Supporting primary school students’ reasoning about motion graphs through physical experiences. ZDM 2019, 51, 899–913. [Google Scholar] [CrossRef]
- Hallström, J.; Schönborn, K.J. Models and modelling for authentic STEM education: Reinforcing the argument. Int. J. Stem Educ. 2019, 6, 22. [Google Scholar] [CrossRef]
- Lesh, R.; Harel, G. Problem solving, modeling, and local conceptual development. Math. Think. Learn. 2003, 5, 157–189. [Google Scholar] [CrossRef]
- Academy of Learned Academies (ACOLA). STEM: Country Comparisons: International Comparisons of Science, Technology, Engineering and Mathematics (STEM) Education; Final Report; ACOLA: Canberra, Australia, 2013. [Google Scholar]
- Venville, G.J.; Wallace, J.; Rennie, L.J.; Malone, J.A. Curriculum integration: Eroding the high ground of science as a school subject? Stud. Sci. Educ. 2002, 37, 43–84. [Google Scholar] [CrossRef]
- Pang, J.; Good, R. A review of the integration of science and mathematics: Implications for further research. Sch. Sci. Math. 2000, 100, 73–82. [Google Scholar] [CrossRef]
- Zemelman, S.; Daniels, H.; Hyde, A. Best Practice: New Standards for Teaching and Learning in America’s School; Heinemann: London, UK, 2005. [Google Scholar]
- Burkhardt, H. Modelling in Mathematics Classrooms: Reflections on past developments and the future. ZDM 2006, 38, 178–195. [Google Scholar] [CrossRef]
- Blomhøj, M.; Jensen, T.H. What’s all the fuss about competencies? In Modelling and Applications in Mathematics Education; Springer: Berlin/Heidelberg, Germany, 2007; pp. 45–56. [Google Scholar]
- Blomhøj, M.; Kjeldsen, T.H. Teaching mathematical modelling through project work. ZDM 2006, 38, 163–177. [Google Scholar] [CrossRef]
- Torras Galán, A.; Pastor, S.L.; Llach, M.C. El aprendizaje basado en proyectos en el ámbito STEM: Conceptualización por parte del profesorado. Rev. Electron. Ensen. Las Cienc. 2021, 20, 359–380. [Google Scholar]
- DeRuntz, B.; Henson, H.; Withee, T. Leadership Development and STEM Student Success Using the Social Interdependence Model. In Proceedings of the 2022 ASEE Annual Conference and Exposition, Minneapolis, MN, USA, 26–29 June 2022. [Google Scholar]
- Doerr, H.M. Experiment, simulation and analysis: An integrated instructional approach to the concept of force. Int. J. Sci. Educ. 1997, 19, 265–282. [Google Scholar] [CrossRef]
- Geiger, V. Factors affecting teachers’ adoption of innovative practices with technology and mathematical modelling. In Trends in Teaching and Learning of Mathematical Modelling; Springer: Berlin/Heidelberg, Germany, 2011; pp. 305–314. [Google Scholar]
- Brown, J.P. Visualisation tactics for solving real world tasks. In Mathematical Modelling in Education Research and Practice; Stillman, G.A., Blum, W., Biembengut, M.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 431–442. [Google Scholar]
- Frejd, P.; Ärlebäck, J.B. Initial results of an intervention using a mobile game app to simulate a pandemic outbreak. In Mathematical Modelling and Applications: Crossing and Researching Boundaries in Mathematics Education; Stillman, G.A., Blum, W., Kaiser, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 517–527. [Google Scholar]
- Perrenet, J.; Zwaneveld, B. The many faces of the mathematical modeling cycle. J. Math. Model. Appl. 2012, 1, 3–21. [Google Scholar]
- Törnroos, J. Mathematics textbooks, opportunity to learn and student achievement. Stud. Educ. Eval. 2005, 31, 315–327. [Google Scholar] [CrossRef]
- Floden, R.E. The measurement of opportunity to learn. In Methodological Advances in Cross-National Surveys of Educational Achievement; Porter, A.C., Adam, G., Eds.; National Academy Press: Washington, DC, USA, 2002; pp. 231–266. [Google Scholar]
- Cobb, P.; Whitenack, J.W. A method for conducting longitudinal analyses of classroom videorecordings and transcripts. Educ. Stud. Math. 1996, 30, 213–228. [Google Scholar] [CrossRef]
- Wijaya, A.; van den Heuvel-Panhuizen, M.; Doorman, M. Opportunity-to-learn context-based tasks provided by mathematics textbooks. Educ. Stud. Math. 2015, 89, 41–65. [Google Scholar] [CrossRef]
- Vermont Department of Education. Vermont’s Framework of Standards and Learning Opportunities; Vermont Department of Education: Montpelier, VT, USA, 2000.
- Gallart, C.; Ferrando, I.; García-Raffi, L.M.; Albarracín, L.; Gorgorió, N. Design and Implementation of a Tool for Analysing Student Products When They Solve Fermi Problems. In Mathematical Modelling and Applications: Crossing and Researching Boundaries in Mathematics Education; Springer: Berlin/Heidelberg, Germany, 2017; pp. 265–276. [Google Scholar]
- Diana, N. Analysis of teachers’ difficulties in implementing STEM approach in learning: A study literature. J. Phys. Conf. Ser. 2021, 1806, 012219. [Google Scholar] [CrossRef]
- Shekhar, P.; Borrego, M.; DeMonbrun, M.; Finelli, C.; Crockett, C.; Nguyen, K. Negative Student Response to Active Learning in STEM Classrooms. J. Coll. Sci. Teach. 2020, 49, 45–54. [Google Scholar]
- Ortega, M.; Puig, L. Using modelling and tablets in the classroom to learn quadratic functions. In Mathematical Modelling and Applications; Springer: Berlin/Heidelberg, Germany, 2017; pp. 565–575. [Google Scholar]
- Ortega, M.; Puig, L.; Albarracín, L. The Influence of Technology on the Mathematical Modelling of Physical Phenomena. In Lines of Inquiry in Mathematical Modelling Research in Education; Springer: Berlin/Heidelberg, Germany, 2019; pp. 161–178. [Google Scholar]
- Greefrath, G. Using technologies: New possibilities of teaching and learning modelling–Overview. In Trends in Teaching and Learning of Mathematical Modelling; Springer: Berlin/Heidelberg, Germany, 2011; pp. 301–304. [Google Scholar]
- Daher, W.M.; Shahbari, J.A. Pre-service teachers’modelling processes through engagement with model eliciting activities with a technological tool. Int. J. Sci. Math. Educ. 2015, 13, 25–46. [Google Scholar] [CrossRef]



| Description | Catalysts |
|---|---|
| Sound wave: it is explained in class that a sound wave is a disturbance of molecules, caused by vibrations that propagate in a material medium, usually air, or even in a vacuum. | Nature of the physical phenomenon; Teacher |
| Sound intensity: it is explained to students that sound intensity is the amount of energy proportional to the vibrations and pressure changes created in the passage of a sound wave. | Nature of the physical phenomenon; Teacher |
| Logarithmic scale: A measurement scale that uses the logarithm of a quantity, rather than the quantity itself. It is commonly used when the data are large numbers. | Teacher |
| Ways of representing information on a surface: the teacher asks the students about various ways known to the students for representation on a plane. Students propose different types of graphics or maps. | Mathematical model of the physical phenomenon; Teacher |
| Decibel Ultra Pro software: students are instructed to use the software to make accurate measurements. | Technologies for data acquisition |
| Using real data: At the beginning of the session, the teacher makes it clear to the students that in the real world, the empirical work of collecting data is not always an easy task and that it is necessary to obtain valid and authentic information to enable them to make judgements. | Technologies for data acquisition |
| Description | Catalysts |
|---|---|
| Decrease in intensity with distance: students experiment with the phenomenon of decreasing intensity with distance from the sound source and provide their explanations for the change in the values obtained. | Nature of the physical phenomenon; Technologies for data acquisition |
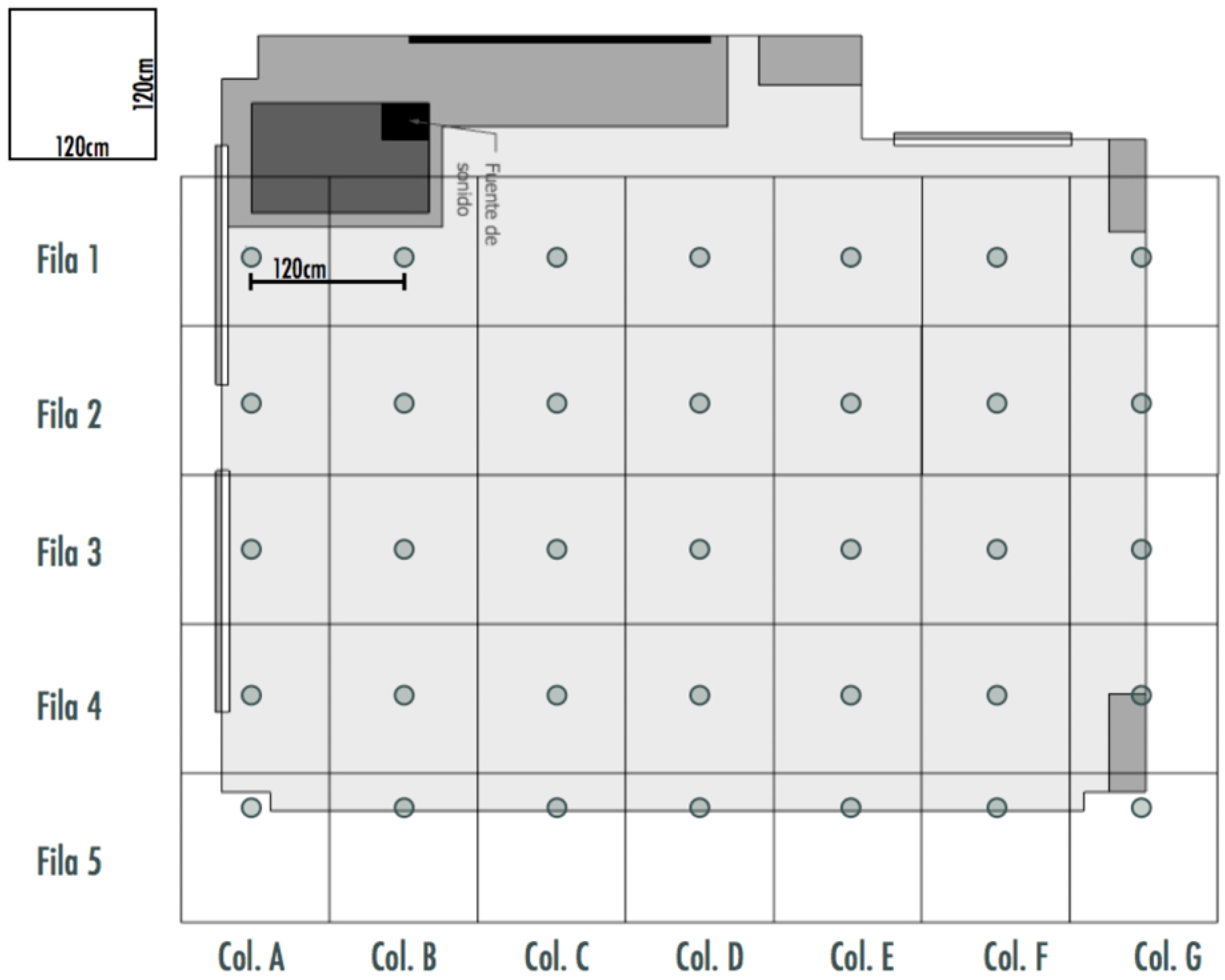
| Verbal descriptions of physical constraints considered in the real situation: students discuss the variations in sound intensity in each area of the classroom due to the constraints introduced by the furniture, the distance to the sound source and the geometry of the classroom boundary. | Nature of the physical phenomenon |
| Ways of dividing a plane surface: since it is not possible to get data for each point on the class plane, students discuss ways of dividing the plane and note that there are multiple ways and that some ways fit the needs of the study better than others. | Teacher |
| Grid: students discretise the plane from a structure of rows and columns to obtain representative measurements of the entire surface of the classroom. | Technologies for data acquisition |
| Adequate distance between measurement points: students note that it is necessary to maintain a balance between the effort required to carry out all the measurements and the desired accuracy. | Technologies for data acquisition; Group work interaction |
| Need of discrete measurement: Students identify the need to make divisions in the classroom to make measurements. | Group work interaction |
| The grid as a two-dimensional form of representation: students observe that the plane can be represented using two dimensions and that this fact conditions the way in which they must refer to each measuring point, so that a notation referring to two variables must be generated to denote each point on the plane. | Mathematical model of the physical phenomenon; Teacher |
| Description | Catalysts |
|---|---|
| Arithmetic mean as a form of error minimisation: Measurement errors can be systematic or random. Systematic errors are due to the use of poorly calibrated instruments and therefore, not taking these effects into account influences the measurements taken. Others can be random and unavoidable, which are those due to the observer, or those that reflect the dispersion of the magnitude measured when repeating the experiment. The errors detected in the experiment were of both types. | Technologies for data acquisition; Group work interaction; Teacher |
| Use of an application to measure sound intensity: The Decibel Ultra Pro® application provides sound intensity values, but like any device it can have accuracy errors. The students tested the robustness of the app in capturing data. In the same area, without moving and in silence, two different intensity values are obtained, which makes us think of ways to help us avoid this technological obstacle. | Technologies for data acquisition |
| Description | Catalysts |
|---|---|
| Three-dimensional representation: they are made to see that an object or entity is three-dimensional if each point can be located by specifying three numbers within a certain range. For example, in our classroom case, height, length and depth. This concept is closely linked to the concept of a function of two variables. | Mathematical model of the physical phenomenon; Teacher |
| Function of two variables: in experimental sciences, it is very common that we are interested in expressing one variable (variable we are often interested in expressing a variable (response variable or independent variable) as a function of two or more variables. | Mathematical model of the physical phenomenon; Teacher |
| Range: when designing the strategy, students find the obstacle of the lack of cubes to execute it, and therefore, they will have to reflect on the concept of range, which is the interval between the maximum and minimum value of the values they have available to them. From it, they will be able to estimate the value that they have to to assign to a cube to make a representation without missing any cube. | Group work interaction; Teacher |
| Using visual strategies to represent data: Students have to make a three-dimensional representation of the data found in the table representing the mean sound intensity values for the marked points in the classroom. Students introduce the use of different colours of the cubes in their representation. This promotes a learning situation in which the need to use visual representations to provide information is appreciated. | Mathematical model of the physical phenomenon; Group work interaction |
| Learning to ask questions to validate results: The teacher uses interventions such as strategy redirection to manage the strategies that groups devise. manage the strategies devised by the groups. In both groups, the same error arises the same mistake, which consists of omitting the decimal values and using only the integer part. For this reason, the teacher emphasises the need to provide meaningful information that is coherent with the data provided in the table. If two columns have the same height, this would mean that that the same loudness has been reached at the two measurement points. Asking questions such as “What does the height of these columns mean? helps students to check the status of their solutions. | Teacher |
| Description | Catalysts |
|---|---|
| Heat maps: This is a graphic in which specific areas are highlighted using colour coding based on criteria, such as highlighting areas of higher or lower sound intensity. | Mathematical model of the physical phenomenon; Group work interaction; Teacher |
| Contour lines or contour maps: Very often the functions of two variables are represented by their contour lines. Indeed, the representation of functions of two variables by means of contour lines is particularly interesting, because they are simple to interpret and much easier to represent. They are those lines on a map that join those the points that have equal sound intensity, thus clustering the regions of the plane with sound intensities in the same sound intensity range. | Mathematical model of the physical phenomenon; Group work interaction; Teacher |
| Search for alternatives to show the same result: The teacher stresses the need to work in a productive and efficient way. To this end, he uses resources such as the invitation to reflection and the conduction of the strategy, so that the idea of improving the strategy carried out during session 4, which was based on a three-dimensional representation of the data, is reflected. The teacher uses resources such as inviting reflection and conducting the strategy to reflect the idea of improving the strategy carried out during session 4, which was based on a three-dimensional representation of the data, and to obtain the same information but using a two-dimensional representation that is much more manageable. | Mathematical model of the physical phenomenon; Group work interaction; Teacher |
| Relate the result obtained to everyday information: The teacher talks about and shows a picture of contour lines, which appears continuously on isobar maps when we hear about the weather. This fact allows them to have a real reference of the functionality of the heat maps. | Teacher |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferrando, I.; Albarracín, L.; Diago, P.D. Where Is It Best to Sit in Class? Description of an Experience Based on STEM Problem Solving in a School Context. Educ. Sci. 2023, 13, 417. https://doi.org/10.3390/educsci13040417
Ferrando I, Albarracín L, Diago PD. Where Is It Best to Sit in Class? Description of an Experience Based on STEM Problem Solving in a School Context. Education Sciences. 2023; 13(4):417. https://doi.org/10.3390/educsci13040417
Chicago/Turabian StyleFerrando, Irene, Lluís Albarracín, and Pascual D. Diago. 2023. "Where Is It Best to Sit in Class? Description of an Experience Based on STEM Problem Solving in a School Context" Education Sciences 13, no. 4: 417. https://doi.org/10.3390/educsci13040417
APA StyleFerrando, I., Albarracín, L., & Diago, P. D. (2023). Where Is It Best to Sit in Class? Description of an Experience Based on STEM Problem Solving in a School Context. Education Sciences, 13(4), 417. https://doi.org/10.3390/educsci13040417








