Abstract
Mathematical reasoning is an essential ability that students must have in every mathematics lesson. However, student behavior during the process of mathematical reasoning has yet to be widely studied. This research explores the mathematical reasoning behavior of selected eighth-grade students to solve problems requiring a mathematical reasoning process. A qualitative methodology based on grounded theory was implemented, which included an in-depth analysis of student answers and student interviews. The data show that students are engaged in imitative, algorithmic, semi-creative, and creative reasoning behavior. Next, an in-depth explanation was carried out for four students from each level of mathematical reasoning behavior. Students from the imitative, algorithmic, semi-creative, and creative reasoning behavior groups showed consistency in answers and behavior for the given problems. The findings of this study can encourage teachers to focus on fostering the highest level of mathematical reasoning, namely creative mathematical reasoning, in students.
1. Introduction
Mathematics is an essential subject taught in school. In learning mathematics, students are trained to improve their logical thinking and reasoning [1]. Logical thinking can hone students’ abilities to reason correctly. Logical reasoning is important for everyone and is a crucial aspect of developing critical thinking [2]. Reasoning is a thought process that connects known facts to a conclusion. Reasoning activity is closely related to mathematics lessons, often referred to as mathematical reasoning. Mathematical reasoning is defined as tracing lines of inquiry to generate statements and develop arguments to reach and justify conclusions [3,4].
Mathematical reasoning is an essential ability for students to have and must appear in every mathematics lesson [5,6,7,8,9,10,11,12]. Reasoning is needed to build a mathematical idea and show proof of the truth of the idea [13]. Reasoning is essential for mathematics users because it contains active, dynamic, and generative processes. Reasoning allows students to actively structure their mathematical ideas and understand mathematics [14]. Reasoning abilities can also support students’ understanding of mathematics and develop creative thinking skills [15].
Students must have mathematical reasoning abilities in their learning environment for effective learning [16,17,18,19]. Students need this mathematical reasoning ability to build a complete understanding of mathematics. All students must have equal opportunities to develop their ability to reason mathematically [20]. The characterization of students’ scientific reasoning should be realized for every student reasoning activity [21]. Students’ mathematical reasoning abilities can be explored by observing the behavior that arises when working on questions that require students’ mathematical reasoning processes and students’ verbal explanations of their answers.
2. Theoretical Framework
2.1. Mathematical Reasoning
The National Council of Teacher Mathematics (NCTM) emphasizes mathematical reasoning as an ability that must be present in students [22]. NCTM outlines the objectives of learning mathematics concerning reasoning and proof in four indicator items:
- Recognizing reasoning and proof as essential aspects of mathematics.
- Constructing and finding mathematical conjectures.
- Developing and assessing arguments.
- Choosing and using various types of reasoning and methods of proof.
In this study, the three leading indicators of reasoning that we chose to observe more deeply are drawing logical conclusions, testing conjectures, and compiling valid arguments.
Although mathematical reasoning is included in mathematics curricula worldwide, research has found that teachers need help understanding, teaching, and assessing mathematical reasoning [23] and developing students’ reasoning capacities [24]. Reasoning abilities can be developed through classroom learning by providing mathematical reasoning questions [25,26,27,28] and discussions between teachers and students to identify and develop arguments for solving a problem [28]. Cognitively, students’ mathematical reasoning abilities can be seen when they solve a problem. In developing students’ mathematical reasoning abilities, besides the cognitive aspect, which is a central aspect, the metacognitive part also plays an important role [29,30]. Metacognition should be a significant concern in the problem-solving process [31,32,33,34,35,36]. In the context of this study, the metacognitive aspect seen in students’ mathematical reasoning process is students’ meta-reasoning.
2.2. Meta-Reasoning
Meta-reasoning is an extension of metacognitive concepts into the domain of mathematical reasoning [35,36,37]. Meta-reasoning is a person’s knowledge of his or her reasoning process. Meta-reasoning refers to processes that monitor the progress of our reasoning and problem-solving activities and manage the time and effort devoted to these processes [35]. The two main aspects of meta-reasoning concerning reasoning are metacognitive monitoring and metacognitive control [35]. Metacognitive monitoring includes an assessment of knowledge and reasoning strategies, a core assessment of reasoning, and students feeling that the answers chosen are correct, with sufficient confidence (on average). Meanwhile, metacognitive control is related to stimulating memory search, being involved in problem-solving, not giving up easily, providing initial responses, reconsidering the solutions provided, providing the latest responses, trying other strategies, and providing selective responses such as not understanding or trying to seek help. The final conviction and final assessment of solvency will emerge from these two metacognitive aspects.
2.3. Affective Aspect in Mathematical Reasoning
In addition to the cognitive and meta-reasoning aspects, the affective aspect also has a vital role for students in learning mathematics, including the process of mathematical reasoning. One part of the affective aspect observed in this study is student self-confidence. Foster [38] defines mathematical confidence as a student’s perception of their ability to achieve good results and assurance that they can handle difficulties in mathematics. Self-confidence is a crucial concept in research on metacognitive and its relation to mathematical reasoning [37].
2.4. Mathematical Reasoning Behavior
Research by [39,40,41] has suggested that the critical factor influencing learning outcomes is student involvement in imitative or creative reasoning. Lithner [41] broadly divides the types of reasoning often used by students in solving mathematical tasks into imitative reasoning and creative mathematical reasoning. Imitative reasoning consists of memory reasoning and algorithmic reasoning. In memory reasoning, students recall previously learned processes or answers. Meanwhile, in algorithmic reasoning, students recall the procedure of solving. Creative reasoning fulfills the elements of novelty, flexibility, plausibility, and mathematical foundation. Students are expected to be trained in solving problems through creative reasoning processes. Another researcher, Brookhart [42], developed an analytical rubric that describes performance along a continuum with highly creative, creative, regular/routine, and imitative levels. This study was inspired by research conducted by Muir et al. [43] and Harisman et al. [44], who observed students’ problem-solving behavior in non-routine problems.
In this study, all the aspects described above, namely cognitive, meta-reasoning, and affective, were present to varying degrees in the reasoning behavior of the students with the different levels of reasoning. The description of students’ reasoning behavior is expected to produce a fundamental theory in problem-solving activities in mathematics learning that requires mathematical reasoning. Furthermore, we adapted the opinion of Bergner [45] regarding the definition of behavior and associated it with students’ behavior in mathematical reasoning. Behavior is all activities or actions, both physical and mental, that lead to maintaining a condition or changing a particular state to another, accompanied by the drive to succeed.
Furthermore, we concluded that students’ mathematical reasoning behavior is all activities carried out by students when solving problems related to mathematical reasoning, both in writing or orally, and physically or mentally, which leads to the successful solving of these mathematical problems. Rohati et al. [46] designed an analytical rubric to assess students’ behavior in mathematical reasoning with three primary levels, namely imitative, algorithmic, and creative. The analytical rubric is used as a reference here to describe students’ behavior in solving problems requiring mathematical reasoning.
Therefore, this study aimed to explore the mathematical reasoning behavior of eighth-grade junior high school mathematics students based on the type of mathematical reasoning with unique behavioral characteristics at each level. Knowing the behavior of each level of students’ mathematical reasoning will make it easier for teachers to increase the level of students’ reasoning from the lowest level to the highest level so that in the end, students can have sufficient and creative mathematical reasoning abilities. The study described in this paper was designed to answer the main research question: What behaviors are exhibited by grade 8 junior high school students when solving mathematical reasoning problems?
3. Materials and Methods
The grounded theory design was suitable for this study because of the lack of research on high school students’ mathematical reasoning and because the aim was to conduct systematic research to develop general explanations of their behavior in mathematical reasoning. In line with Creswell [47], grounded theory is an inquiry design from sociology where researchers approach from the general, abstract theory of a process, action, or interaction based on participants’ views. Specifically, this research is a constructive theoretical design, referring to Charmaz [48], which has the characteristics of abductive reasoning, memos, and constant comparisons. According to Store [13], constructive foundation theory is different from the traditional grounding theory of Glaser and Strauss [49]. The constructive foundational theory recognizes that theories lie within the context in which they were generated; consequently, they are only partially conclusive. The collection and analysis of data in this study reflect this theory in practice.
Data were collected through students’ written answers from the tasks given. Data were also collected through video and audio recordings from interviews with selected students from each category of mathematical reasoning behavior. All notes on changes in student answers during the interview were also collected for further analysis. Discussions with colleagues are also recorded to analyze and interpret student answers from the tasks given. Memos of the researcher’s reflections during data collection and analysis also became part of the data.
3.1. Selection of Subjects
The subjects examined in this study were eighth-grade junior high school students from three schools in Jambi Province, Indonesia. Each mathematics teacher at each school was asked to select six students to participate in this study: two with low levels of mathematical ability, two with moderate abilities, and two with high abilities. The selection criteria were based on the students’ mathematical abilities, which the teacher has observed since the students were in seventh grade. According to the mathematics teachers, students in grade eight have experienced online learning for about a year since they were in seventh grade. The teacher revealed that students’ mathematical understanding and reasoning abilities since the COVID-19 pandemic have tended to decline. The total number of students used as research subjects is 18. Each student was labeled to facilitate the process of grouping students based on their reasoning behavior at the end of the presentation.
3.2. Tasks
Three math questions (Appendix A) were chosen to measure each indicator of mathematical reasoning ability. The three assignments were also given based on the teacher’s experience teaching in a class by paying attention to the level of challenge offered to grade 8 students following the mathematics material that they must master. For example, Question 1 is classified as easy and directed to explore the first indicator of mathematical reasoning, i.e., draw logical conclusions. The second question is more complex to measure the second indicator of mathematical reasoning, namely construct and test conjectures. The third question is designed to see students’ ability to compose valid arguments. In addition, the three questions were arranged to explore meta-reasoning and affective aspects of students during in-depth interviews based on the answers given by students.
3.3. Data Analysis
Data analysis was carried out following open, axial, and selective coding procedures, which led to constructing the “students’ mathematical reasoning behavior” category, meta-reasoning, and affective aspects. After students were given test questions to gauge their cognitive behavior, students were interviewed using a semi-structured approach. A copy of each problem was presented, and the researcher asked students to answer the questions. After completing each problem, each student was asked to explain their work. The researcher recorded their responses, made observation notes, and asked questions to clarify the written answers given.
4. Results
The four main categories that emerge from the data on students’ mathematical reasoning behavior are imitative, algorithmic, semi-creative, and creative behavior. Each student was labeled to group them based on the behavior categories. The previously developed mathematical reasoning behavior rubric [46] was used as an initial reference for classifying students’ mathematical reasoning behavior. The findings show six students in the imitative group, nine algorithmic students, and three creative students. The research findings show different results on algorithmic students. Algorithmic students have two different characteristics that are not the same in behavior category as one another. The student data presented in the results section are typical representatives of each category of students’ mathematical reasoning behavior. In addition, IS, AS, SS, and CS students have the most prominent or dominant orientational tendencies of each behavior category.
4.1. Student with Imitative Reasoning Behavior (IS)
4.1.1. Drawing Logical Conclusions
The inability to draw logical conclusions was demonstrated by the imitative student (IS). IS’s reasoning in solving the first problem is shown in Figure 1.

Figure 1.
IS’s answer to Question 1.a.
Based on Figure 1, IS can utilize the information provided in the problem and translate it to find a solution. IS wrote the word “explanation” on the answer sheet to confirm that he observed the picture given in the question. Then, IS writes that the number of matchsticks in the first picture is 4. The number of matchsticks in the second picture is 8. The number of matchsticks in the third picture is 12. The number of matchsticks in the fourth picture is 16. The number of matchsticks in the tenth picture is 40. However, IS was unable to show and explain how he knew this. At the end of the answer, IS answered that the number of matchsticks needed from pictures 1 to 10 is 220. Meanwhile, the expected target of this question is that students can find the rules for finding the number of matchsticks used in each picture, namely 4n. At the time of the interview, to re-check the answers given by IS, IS could only write down the number of each match from the first picture to the fourth picture. Furthermore, IS could determine the number of matchsticks in the fifth to the tenth image with guidance from the researcher (Figure 2). IS could only determine the number of matchsticks until the tenth image. IS needed clarification when finding the rule for the number of matchsticks for the nth drawing.

Figure 2.
IS’s answer to the first question when interviewed.
Furthermore, for Question 1.b, IS gave the wrong answer (Figure 3). IS wrote answers that were entirely unrelated to the pattern of the picture given. After being confirmed through interviews, IS stated that he did not understand and only looked at examples from the mathematics books he used at school. IS verbally explained: “for Question 1.b, I am confused about determining the rules for the nth term; I just searched and looked in the book of questions like that”.
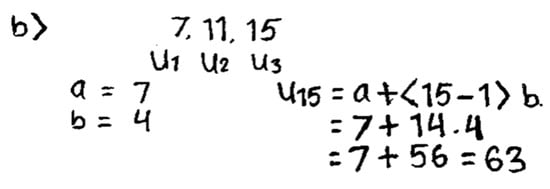
Figure 3.
IS’s answer to Question 1.b.
Based on the results of the interviews, IS still shows a tendency to reason in an imitative way, that is, only by observing what is in the picture, and is not yet able to draw logical conclusions from this one problem. IS can only utilize the information provided in the problem but has yet to find the rule for the number of matchsticks for the nth image of this first problem.
4.1.2. Constructing and Testing Conjectures
The second indicator of the cognitive aspects of students’ mathematical reasoning behavior is compiling and testing conjectures by arranging numbers. Four numbers repeatedly appear in the pattern (Figure 4). However, IS can only explain the unit digit of the pattern. IS can only take advantage of available information but is not yet able to choose a set of rules that can construct and test conjectures. During the interview, IS explained orally the strategy for solving this problem: “…. To find the unit digit for the result of 399, I write down all 3 to the power from 1 to 99. That is the only strategy I can do”. Based on the interview results above, one can observe the pattern of the unit digits given in the questions, but IS has not been able to compile and test conjectures. IS is still confused and seems unable to connect the four numbers, each of which is the unit digit of the power of 3, with the question, what is the ones place digit in 399?

Figure 4.
IS’s answer to Question 2.
4.1.3. Composing Valid Arguments
The third indicator of the cognitive aspects of students’ mathematical reasoning behavior is that students construct valid arguments, which are explanations about the choice of strategy, implementation of the strategy, and explanations about why a strategy or solution will work or not in the matter of number patterns and object configurations. Students are asked to precisely arrange the numbers 1, 2, 3, 4, 5, 6, 7, 8, and 9 in small circles, with the total number in each line being 23. Based on Figure 5, IS gave an incorrect answer. IS can place the correct numbers for the lines on the left side, 3, 5, 7, and 8. The total of the four numbers is 23. However, on the right side of the line, IS fills the small circles with the numbers 7, 3, 5, and 8 again, repeating the numbers. Numbers 1, 2, and 6 are not arranged in the figure.
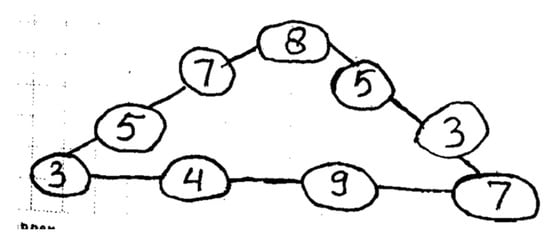
Figure 5.
IS’s answer to Question 3.
During the interview, IS explained how he placed the numbers in a way “Just try to put four numbers on each side”. IS only refers to putting the numbers on each side so that the total is 23. However, IS does not notice that he must put nine numbers precisely in the little circles, and that there is no repetition of numbers. IS stated, “... the condition is that the sum of the four numbers must be equal to 23 for all sides”. IS has not been able to place all the numbers 1 through 9 exactly in the small circles. IS repeats the placement of the numbers 3, 5, and 7 twice. IS can only utilize the information provided but is not able to choose a set of rules that lead to the preparation of valid arguments.
4.1.4. Monitoring and Control Metacognitive
Furthermore, while analyzing student behavior when completing questions and interviews, the researcher also examined students’ meta-reasoning behavior both in writing and orally. Metacognitive monitoring can be seen in how IS chooses the right strategies or rules to solve given mathematical reasoning problems. The findings show that IS only has one rule (strategy) for solving non-routine problems and persists with that strategy even though he knows that the strategy is wrong. For example, the researcher observed the students’ written answers to Question 3 (Figure 5) and confirmed them during the interview. IS only sticks to one strategy in arranging numbers 1 to 9 so that each side is 23. Even though the rules or strategies used need to be corrected, IS still sticks with these rules. IS ignores the requirement that the numbers 1 through 9 in the small circles must not be repeated. In the final part of the interview, the researcher ascertained whether IS had another strategy or a different possible answer in correctly arranging the numbers 1 to 9 on the sides of the circle. IS said there was no other possibility.
Metacognitive control in writing is observed from the answers given by IS. For example, in his answer to Question 2 (Figure 4), IS only writes 31 = 3, 32 = 9, 33 = 27, and 34 = 81. Then, IS writes “and so on”, indicating that there will be a pattern repetition. IS also writes that the unit digit that always repeats is four numbers (Figure 4). However, after that, IS still needs to complete the answer. These answers show that IS was not writing when compiling or assembling intermediate targets (rules used) from the information given in the questions.
Furthermore, metacognitive control (verbally) is seen when students can control their cognitive processes verbally, namely starting, stopping, or changing the allocation of effort in the reasoning process, and this is conveyed verbally when solving mathematical reasoning questions. IS’s metacognitive control can be observed during interviews, following up written answers to given reasoning questions. For example, in the first question, IS can still show the number of matchsticks up to the fourth picture in Question 1.a. Next, IS calculates the number of square sides one by one for each image. For the fifth image and so on, IS was guided by the researcher to find the number of matchsticks. From the results of observations during the interview, IS can only convey thoughts orally on the part of the available information.
4.1.5. Self-Confidence
The researcher also explored the affective aspects of students by looking at their self-confidence when giving written answers and during interview sessions. Students who behave imitatively equate confidence with giving answers quickly even though they do not understand whether the rules chosen are right or wrong. During interviews, IS often gives answers without thinking first. The self-confidence of imitative students goes hand in hand with the quick answers they give.
For example, during an interview on Question 3, IS said “it seems right”, but with a doubtful expression. Furthermore, IS also stated, “it is possible”. This shows IS’s need for more confidence in his answer. IS also stated that he did not know the rules for placing the numbers on each side of the triangle so that he could derive the sum of 23. At the end of the interview session, IS stated, “I do not understand”. IS equates confidence with giving answers quickly, even if he does not understand whether the rules chosen are right or wrong.
4.2. Student with Algorithmic Reasoning Behavior (AS)
4.2.1. Drawing Logical Conclusions
Based on the results of the answers to Question 1, AS can already utilize the information provided and can choose several sets of rules. However, AS still needs to come to a logical conclusion. In the first question, AS determines the number of matchsticks in the tenth picture, directly leading to the formula un = a + (n − 1) × b. AS’s behavior follows the characteristics of algorithmic students, who are accustomed to using direct formulas in finding solutions. AS prefers to use the formula without paying attention to the pattern given first. AS has not been able to creatively show a settlement solution without using the nth-term formula. On the answer sheet, AS deleted the answer. AS’s answer to solving the first question is shown in Figure 6 below.
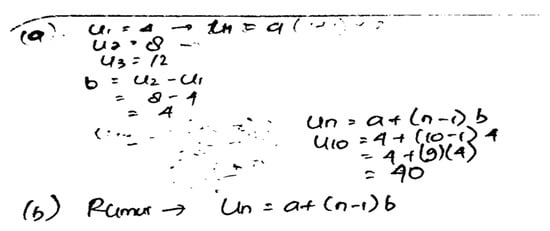
Figure 6.
AS’s answer to Question 1.
Furthermore, for Question 1.b, AS was unable to explain the rules for finding the required number of matchsticks in each picture. AS again writes down the formula un = a + (n − 1) × b. The answer given by AS in this first problem is included in the orientation of algorithmic behavior for indicators to draw logical conclusions. AS is accustomed to using formulas in solving every math problem and problem.
Based on the interview results, AS can provide the correct answer to find the number of matchsticks in the tenth picture. AS first writes down the first term, second term, and third term, then calculates the difference between the second and first term. Furthermore, by using the formula un = a + (n − 1) × b, AS can find the number of matchsticks in the tenth picture, which is 40. However, when answering Question 1.b, AS can only write down the un formula. When confirmed through interviews, AS stated, “just use the formula”. AS did not derive the formula to obtain a rule for determining the number of matchsticks in the nth term. When the researcher directed AS to find the 4n formula, AS replied, “No, that is enough. Just use that rule”. Based on the analysis of written answers and interviews, AS tends to reason algorithmically; that is, he can utilize the information provided but has yet to reach a logical conclusion.
4.2.2. Constructing and Testing Conjectures
Furthermore, compiling and testing conjectures is the second indicator of the cognitive aspects of students’ mathematical reasoning behavior. When working on Question 2, AS observes the final digit of the power of three, forming a pattern of 3, 9, 7, and 1 sequentially. The pattern changes are four numbers that constantly change repeatedly. AS divides 99 by 4 and sees four repeated digit changes. In the end, AS found that the ones place digit of 399 is 7 (Figure 7).

Figure 7.
AS’s answer to Question 2.
Next, AS writes 399 to the answer’s right by dividing 99 by 4. AS shows the result is 24 with a remainder of 3 from the division. So, the ones place digit in 399 is 7. From these answers, AS can utilize known information but has yet to explain how to choose a set of rules that can be used to compile and test conjectures. During the interview, AS explained how he developed the rules for solving this problem. AS said, “I observed that the final digits of the power of three formed a pattern of 3, 9, 7, 1, respectively. In total, the pattern changes are four numbers that always change repeatedly. The next step is to divide 99 by 4 (change the pattern four times) and get the result 24 with a remainder of three”. Based on the results of the interviews, AS can utilize the information provided, observing the pattern of the unit digits given in the questions. AS can compile several sets of rules but has yet to come to the preparation and testing of conjectures; however, AS can connect between four numbers with the unit digit of 399.
4.2.3. Composing Valid Arguments
The third indicator of the cognitive aspect of students’ mathematical reasoning behavior is that students construct valid arguments. Based on the answers given by AS (Figure 8), AS argues that one should try to arrange these numbers by first placing large numbers in the corner points of the triangle. The reason is to make it easier to derive the expected value of 23. AS explained that the numbers 7, 8, and 9 were placed first. The next step was to add the numbers on the left side of the triangle, i.e., numbers 4 and 3, to obtain 9 + 3 + 4 + 7 = 23. The next step is for AS to place the numbers 6 and 2 so that the lower side contains the numbers 7, 6, 2, and 8, totaling 23. The final step is to place the numbers 1 and 5 so that the total of the four numbers on the right side of the triangle is 23. AS also writes the number of numbers on each side of the triangle and the right side: 8 + 1 + 5 + 9 = 23.
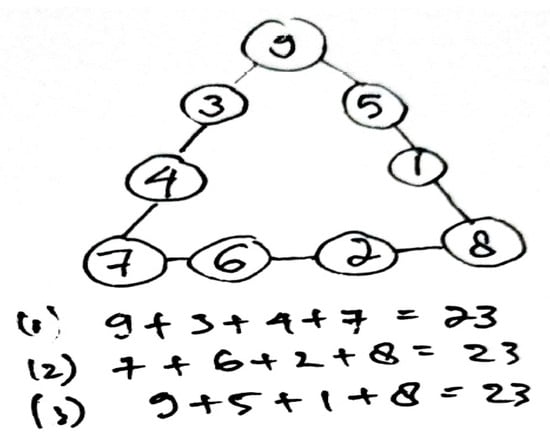
Figure 8.
AS’s answer to Question 3.
During the interview, the researcher explored other possible alternatives that we could provide in solving Question 2. However, AS said, “I only have one alternative solution to solve this problem”. The researcher then asks AS to try first to find a combination of numbers that are different from the first solution written. The AS still says, “Nothing, only one possibility it seems”. AS stated that no alternative solution could be written.
4.2.4. Monitoring and Control Metacognitive
Metacognitive monitoring can be seen in how AS chooses the right strategy or rule to solve a mathematical reasoning problem. Particularly, students’ metacognitive monitoring was observed in Question 3. Based on the student’s written answers (Figure 8) and the answers during the AS interview, a strategy was established to solve this problem by trying to place large numbers in the corner points of the triangle. AS reasoned that this would make it easier to obtain the expected value of 23. This method fills each circle on the sides of the triangle. AS could answer correctly even though he only provided one alternative solution. AS’s metacognitive monitoring process is quite good. AS has one rule (strategy) in solving non-routine problems. In addition, AS has no desire to try other rules (strategies) to derive the correct result.
Written metacognitive control was observed from the answers given by AS. In the first question, AS directly determines the number of matchsticks in the tenth picture using the formula un = a+ (n − 1) × b. AS’s behavior follows the characteristics of algorithmic students, who are accustomed to using direct formulas to find solutions without paying attention to the patterns that appear in each problem. Based on the written answers (Figure 6), it appears that AS deleted the answers. Scribble with Tipp-Ex indicates AS’s metacognitive control process. AS wrote the wrong formula, so he needed to fix it by writing the correct un formula.
AS’s verbal metacognitive control can be observed during interviews, following up on written answers to the reasoning questions. For example, in Question 1, AS controls his metacognitive behavior verbally by giving an initial response to solve the problem by first determining u1, u2, u3, and the difference (b). Overall, AS showed good metacognitive control behavior based on the results of interviews answering the three mathematical reasoning questions. AS has been able to convey his thoughts verbally regarding several sets of rules, but has not been able to make the correct conclusions on the final target. However, when asked to re-examine or change the settlement strategy, he has yet to make the correct conclusions on the final target. AS prefers to stick with the previous strategy and rely on the formula.
4.2.5. Self-Confidence
Furthermore, based on the interview transcripts with AS, it appears that AS is often self-confident because he finds his answers on the internet, and AS can solve questions using formulas. However, occasionally, AS also needs more confidence when explaining the reasons for his written answers. For example, AS said, “I only understand one way; I do not understand the reason”. This sentence indicates that AS’s self-doubt appears when he cannot correctly explain the answer to Question 3. From the answers given by AS during the interview, the characteristics of the behavioral orientation possessed by AS were algorithmic; that is, AS often showed confidence in solving mathematical reasoning questions but was not able to draw the correct conclusions.
4.3. Student with Semi-Creative Reasoning Behavior (SS)
This study found that students with a behavioral orientation of algorithmic reasoning were different from AS. The behavioral orientation tendency that emerged from these students was not found in its category in the analytical rubric of mathematical reasoning behavior [46], which had been developed by previous researchers based on a literature review. Henceforth, these students are referred to as semi-creative students and are symbolized by SS. Semi-creative students show better behavioral tendencies than algorithmic students but have yet to reach the category of creative students (CS). Next, the description of the orientation of SS’s mathematical reasoning behavior is presented one by one based on the aspects that influence students’ mathematical reasoning behavior.
4.3.1. Drawing Logical Conclusions
Based on the answers to Question 1, SS can already utilize the information provided, choose several sets of rules, and arrive at logical conclusions. This condition is shown by SS’s answer to the first problem, as shown in Figure 9. SS creates an image representation of the configuration of square objects and square combinations, then immediately writes down the number of matchsticks needed for each image. SS also immediately writes u10 = 4n by relying on information from the number patterns 4, 8, 12, 16, and so on. Next, SS writes u10 = 40. SS can write down the rules for finding the nth pattern, un = 4n.
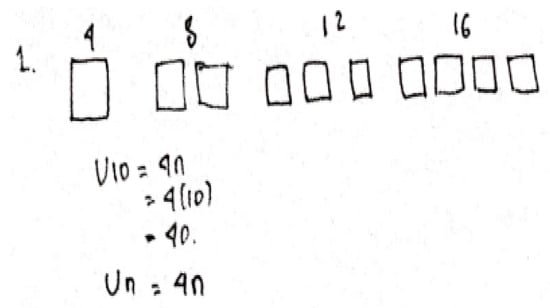
Figure 9.
SS’s answer to Question 1.
4.3.2. Constructing and Testing Conjectures
When working on Question 2, SS wrote down the resulting pattern of the number raised to the power of 3 and circled every last digit. From the circled unit numbers, the sequences 3, 9, 7, and 1 were obtained repeatedly. SS provides a dividing line between the numbers 34 and 35. SS does this to show the repeating pattern of the number’s last digit obtained from the power of three (Figure 10). However, during the interview, SS could not explain the relationship between the remainder 3 and the conclusion that the unit digit of 399 is 7. SS stated, “I am still confused after finding the remainder 3 with the last digit of the 399”. SS can already utilize known information but is not yet able to choose a set of rules that can be used to construct and test conjectures.
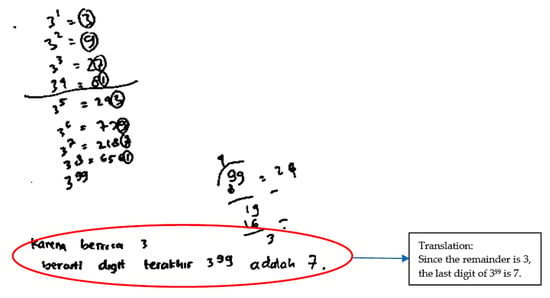
Figure 10.
SS’s answer to Question 2.
4.3.3. Composing Valid Arguments
Based on SS’s answer (Figure 11), it can be seen that SS initially entered the numbers in the small circles on each side of the triangle. SS places the numbers 2, 9, 8, and 4 in the small circles on the line on the left side of the triangle. The sum of the four numbers is 23. However, on the right side of the triangle, SS fills the small circles with the numbers 5 and 1. SS adds up the numbers (4, 5, and 1) on that side, and the sum is 10. Next, SS needs the number 13 in the empty circle on the right side of the triangle to make the sum of all four numbers equal to 23. However, the number 13 is not a number that can be used to fill the small circles on the side of the triangle. In the end, SS did not fill the circle at the triangle’s base with numbers.
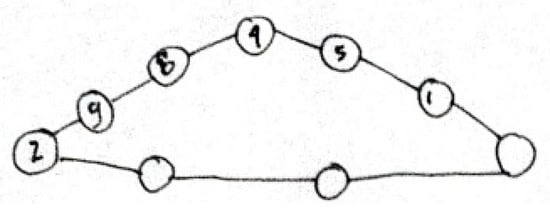
Figure 11.
SS’s preliminary answer to Question 3.
SS tries to fill in the small circles on the sides of the triangle again. SS initially added 7 + 3 + 5 and obtained 15, which he then wrote on the left side of the triangle (Figure 12a). SS can place all numbers correctly on each side of the triangle. The next step was for the researchers to encourage SS to find other possibilities. At first, SS wondered whether he could come up with another possibility. However, because he was continuously motivated, SS then tried a second method. SS tried a different method by first inputting the numbers 7, 8, and 9 in each corner of the triangle. SS could place nine numbers correctly in the small circles of the triangle with the direction of the researcher (Figure 12b). SS can take advantage of the information provided and choose a series of rules that lead to the preparation of valid arguments with guidance from the researchers.
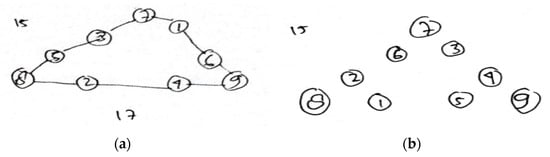
Figure 12.
SS’s answer to Question 3: (a) first possibility and (b) second possibility.
4.3.4. Monitoring and Control Metacognitive
Metacognitive monitoring can be seen from how SS chooses the right strategy or rule to solve the given mathematical reasoning problems. As an example, for Question 3, it can be seen that SS can place all the numbers 1 to 9 in the small circles of the triangle. Even though SS tried, at first, it did not work. SS tried again by establishing rules based on the researcher’s directions to make it easier to place the numbers from 1 to 9, and SS had to put the three most significant numbers in the corners of the triangle. The next step was to fill in the empty circles with the remaining numbers. SS was finally able to answer correctly, with the direction and guidance of the researcher. SS’s metacognitive monitoring process is quite good. SS has one rule (strategy) for solving non-routine problems but has the desire to try other rules (strategy) to find the right results.
Written metacognitive control was observed from the answers given by SS. This condition can be seen from the way students arrange numbers into a certain number based on the rules given to problems related to number patterns. When working on Question 2, SS provides a dividing line between the numbers 34 and 35. SS does this to show the repeating pattern of the number’s last digit obtained from the power of three (Figure 10). Circling the last digit and giving a dividing line between the numbers 34 and 35 is a strategy SS uses to control his cognitive processes in this problem.
SS metacognitive control can be observed during interviews, following up on written answers to the reasoning questions. As an example of the first problem, SS explained that he answered this problem by making an image representation of the configuration of square objects and square combinations, then immediately writing down the number of matchsticks needed for each image (Figure 9). Based on the results of the interviews, SS was able to convey his thoughts (results of reasoning) verbally regarding the several sets of rules he chose and could make correct conclusions on the final target with the guidance of the teacher. Overall, based on the results of interviews with SS and based on the answers given to the eight mathematical reasoning questions, SS showed fairly good metacognitive control behavior. SS can convey his thoughts (results of reasoning) verbally regarding the several sets of rules he chooses and can make the correct conclusions on the final target, but with the teacher’s guidance.
4.3.5. Self-Confidence
At the time of the interview, SS showed confidence when responding to questions from researchers. SS was confident when explaining how to answer the first to the third question. Even though SS sometimes looked confused, SS could regain confidence when he received directions from researchers. The conclusion from the observation of SS’s self-confidence is that SS will look excited and have higher self-confidence if he is directed and receives guidance from researchers. The behavioral orientation of SS is different from the algorithmic student characteristics listed in the mathematical reasoning rubric [46]; SS often shows confidence in solving mathematical reasoning questions and can draw the correct conclusions with directions and guidance from researchers or teachers.
4.4. Student with Creative Reasoning Behavior (CS)
4.4.1. Drawing Logical Conclusions
The first indicator of the cognitive aspect of students’ mathematical reasoning behavior is that students can draw logical conclusions from patterns of number sequences. In Question 1, CS could show the number of matchsticks for each square of the first pattern and the second pattern to the tenth pattern. Furthermore, CS can also generalize for the nth pattern, which is in the form of 4n. The answer to Question 1 from CS is shown in Figure 13.

Figure 13.
CS’s answer to Question 1.
Based on the answers and results of the interview, CS can quickly determine the number of matchsticks in the tenth picture. CS can also immediately draw logical conclusions by only writing down the order up to the third pattern and immediately showing the tenth pattern. CS can also show that the rule for the nth pattern of the drawing is 4×n. CS said that there is “no need to use a formula; just look at the pattern that appears in the picture”. CS can utilize the information provided and establish his own rules to arrive at a logical conclusion.
4.4.2. Constructing and Testing Conjectures
The second indicator of the cognitive aspects of students’ mathematical reasoning behavior is compiling and testing conjectures. When working on Question 2, CS could show the ones place digit of the exponential number, 399. Only creative students could answer this question. CS’s strategy is to divide 99 by 4, to obtain the result of 24 with a remainder of 3. Furthermore, CS states that the ones place digit pattern of the number 3 to the power of n is 3, 1, 9, and 7. The pattern will repeat for the sequence’s next rank in succession. CS can show that the ones place digit of 399 is 7 (Figure 14).

Figure 14.
CS’s answer to Question 2.
Based on the results of the interviews, CS can utilize the information provided and establish his own set of rules for constructing and testing correct conjectures. CS carefully observes the pattern of the unit digits given in the question. CS could connect the four numbers, the ones place digits, to answer the question of what the ones place digit in is 399. CS said, “…Yes, and I just have to look at the patterns of the numbers in the ones digit, so we can determine whatever the exponential number appears in the question”. CS can also answer correctly when researchers develop questions during interviews. CS can correctly determine the unit digit of 3104 as 1.
4.4.3. Composing Valid Arguments
The third indicator of the cognitive aspects of students’ mathematical reasoning behavior is that students construct valid arguments. The students must place the numbers 1, 2, 3, 4, 5, 6, 7, 8, and 9 in a small circle, with a total of 23 in each row. CS can provide different strategies and take advantage of the rules in mathematics, a hallmark of creative reasoning abilities. CS states that there are two ways to solve Question 3. The first possibility is to add three even numbers and one odd number to obtain an odd number, 23. Then, the second possibility is to add three odd numbers and one even number to obtain the result of 23 (Figure 15).
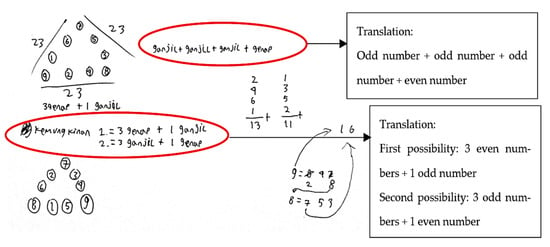
Figure 15.
CS’s answer to Question 3.
Based on the results of interviews, CS can easily place all the numbers from 1 to 9 in the small circles in the triangle. CS said, “These are the largest numbers we put in the corners of the triangle to make it easier to get to the number 23. From 8 + 7, the result is 16. Then, we subtract, namely 23 − 16 = 7. Then add 1 and 6 because 1 + 6, the result is 7. So, the total is 23”. CS can demonstrate a valid argument that there are two possibilities for constructing the four numbers that have a sum of 23. Compared to students who showed an orientation of imitative and algorithmic reasoning behavior, CS could utilize the information provided and choose a set of rules that led to the preparation of valid arguments.
4.4.4. Monitoring and Control Metacognitive
Students’ metacognitive monitoring was observed in Question 3. Based on the written answers (Figure 15) and the results of the interviews, CS showed that the cognitive monitoring process ensured that there were two possible formations of four numbers which, when added together, resulted in 23. CS can develop new rules (strategies) to solve non-routine problems and obtain the right results. CS understands that there are two possibilities for constructing the four numbers that have a sum of 23.
Metacognitive control (in writing) was observed from the answers given by CS. For example, in his answer to Question 2, CS writes 31 = 3, 32 = 9, 33 = 27, 34 = 81, 35 = 243, 36 = 729, 37 = 2187, 38 = 2561. Next, CS writes the small numbers at the end of the power of 31, 32, 33, and 34, with the numbers 1, 2, 3, and 4. CS then writes the number 4, which shows the last digit of the third power consisting of four numbers repeated (Figure 14). CS then writes 99 divided by 4 and obtains the result of 24 with a remainder of 3. The remainder of 3 is also circled by CS to control the answer. Furthermore, CS concluded that the last digit of 399 is 7. From the written answers given by CS, CS monitors his cognitive processes well. CS’s metacognitive control was seen in writing when compiling or arranging intermediate targets (rules used) and up to the final target.
CS’s verbal metacognitive control was observed during interviews, following up written answers to reasoning questions. As an example, for Question 1, CS quickly explained the written answer during the interview. CS can show the number of matchsticks up to the third picture. Furthermore, CS can immediately write down the tenth pattern, 4 × 10 = 40. CS no longer wrote down the fourth to ninth patterns when writing down the answers because CS could already understand the patterns formed from observing the first to the third picture. CS can conclude the patterns formed by observing each image in the problem (Figure 13).
Based on the answers and interview results, CS can quickly determine the number of matchsticks in the tenth picture. CS can draw logical conclusions by only writing down the sequence up to the third pattern and can immediately show the tenth pattern. CS can also explain that the rule for the nth pattern of the image is 4×n. At the end of the interview session, the researcher ascertained why CS did not use the formula (un = a + (n − 1) × b) explained by the teacher to determine the nth term. CS stated that there was no need to use the formula because CS was able to observe the pattern shown in the picture. Based on the interview, CS could convey his thoughts orally in a coherent, complete, and systematic manner and arrive at the correct conclusion on the final target.
4.4.5. Self-Confidence
CS’s confidence was seen when explaining how to solve mathematical reasoning questions related to the number pattern. CS showed high self-confidence and arrived at the correct conclusion when explaining all the written answers he gave to solve the three mathematical reasoning problems. In this case, all the problems given were answered correctly by CS and accompanied by confidence when explaining his answers to researchers.
Based on the exposure to research data, four categories of students’ mathematical reasoning behavior were found. Table 1 shows an additional category of students’ mathematical reasoning behavior: semi-creative. This category complements the findings of our previous study, which found only three categories of behavior [46] based on a literature review.

Table 1.
Rubric of students’ mathematical reasoning behavior.
5. Discussion
5.1. Drawing Logical Conclusions
This section describes each indicator of the aspects that influence students’ mathematical reasoning behavior. For example, the first indicator is drawing logical conclusions on the cognitive aspect. Students with an imitative orientation category can only take advantage of the information provided and are not able to choose a set of rules to arrive at a logical conclusion. This condition is in line with the research conducted by Octriana et al. [50], which revealed that the indicator of students’ mathematical reasoning abilities that rarely appears is the indicator of drawing logical conclusions.
Furthermore, algorithmic students can utilize the information provided and choose several rules but are not able to reach a logical conclusion. This condition is in line with research conducted by Flegas and Charalampos [51] on sixth-grade elementary school students in Greece who had difficulty drawing logical conclusions, justifying arguments, and proving mathematical conjectures. Rosita et al. [52] revealed students’ difficulties in drawing logical conclusions when analyzing students’ mathematical reasoning abilities when solving problems.
Students with a semi-creative orientation can utilize the information provided, choose several sets of rules, and arrive at logical conclusions with the help of directions from the teacher. The teacher’s direction and guidance are essential in improving students’ mathematical reasoning. Mathematical reasoning involves drawing logical conclusions based on assumptions and definitions [53]. Therefore, the teacher should understand, monitor, and guide the development of reasoning and assist students in mathematical reasoning.
Furthermore, creative students demonstrate behavior capable of utilizing the information provided and can establish their own set of rules so that they arrive at logical conclusions. In line with the research of Bronkhorst et al. [2], reasoning to draw logical conclusions is important for students, seen as an essential aspect of developing critical thinking. In addition, Dawkins and Cook [1] show how logical reasoning must appear in students’ mathematical activities.
5.2. Constructs and Tests Conjectures
The second indicator of the cognitive aspect of students’ mathematical reasoning is constructs and tests conjectures. According to Lannin et al. [54], conjecture involves mathematical reasoning to develop statements that are temporarily considered accurate but whose truth is unknown. The findings of this study group students into four categories based on the indicators of constructing and testing conjectures.
Imitative students can utilize known information but cannot choose a set of rules that can construct and test conjectures. In line with the opinion of Lithner [41], students with imitative reasoning choose strategies based on remembering answers. This type of reasoning is helpful as a complete method of solving only a relatively small proportion of tasks, such as remembering each step of evidence or facts [41]. Imitative students’ reason by utilizing the memory of the subject matter obtained before, causing difficulties in choosing a set of rules that can construct and test conjectures.
Algorithmic students can take advantage of the information provided and choose several sets of rules but cannot exercise the preparation and testing of conjectures. Students with algorithmic reasoning usually work on assignments using algorithms and procedures [39], where the choice of strategy is to remember an algorithm and apply it to the data in the problem. The findings show that algorithmic students can choose rules and develop strategies but have not reached conjectural proof.
Semi-creative students can take advantage of the information provided, choose several sets of rules, and carry out the preparation and testing of conjectures with directions from the teacher. The teacher’s direction is essential when encouraging students to make and test conjectures. This condition is in line with research by Aaron and Herbst [55], which looked at mathematics teachers’ perceptions of students constructing and testing conjectures on reasoning tasks and qualitatively observing them. The findings show that in constructing conjectures, the teacher perceives students especially in terms of the resources that students have. Students will know and be able to construct and test mathematical conjectures inseparable from the teacher’s perception of the students’ opportunities in class and how they give directions to students. In addition, according to Lesseig [56], advancing students’ abilities to engage in mathematical reasoning practices, including constructing and testing conjectures, places significant new demands on teachers.
Creative students can take advantage of the information provided and establish their own set of rules for constructing and testing correct conjectures. In their efforts to solve problems, students with creative mathematical reasoning (CMR) characteristics were found to be different from students with Lithner’s imitative and algorithmic reasoning characteristics [39]. Creative students show practical reasoning and fulfill the logical value of reasoning. In line with the research conducted by Hapizah et al. [57], creative students can construct and test conjectures well. However, simply understanding the problem is not enough to guarantee that students can propose conjectures. Although conjectures can be true and false, the underlying theory and concepts must support a reasonable conjecture. Students who do not understand basic concepts often cannot make conjectures and prove these conjectures. Prior knowledge influences students’ ability to make conjectures.
The stages of making a conjecture consist of understanding the problem, exploring the problem, formulating the conjecture, justifying the conjecture, and proving the conjecture [57]. The research findings show that students with creative reasoning can fulfill all stages of making and proving conjectures. Coles and Ahn [58] stated that developing algebraic activities through conjecture encourages students to ask themselves how they construct and prove their conjectures. This step begins with the ability of students to be creative in understanding and exploring problems and then being able to construct and prove conjectures.
5.3. Constructing Valid Arguments
The third indicator of the cognitive aspects of students’ mathematical reasoning is constructing valid arguments. Imitative students can only take advantage of the information provided but are not able to choose a set of rules that lead to the preparation of valid arguments. According to Sidenvall et al. [59], who analyzed students’ textbook task-solving in Swedish high schools, 80% of all tasks are completed correctly using imitative strategies, rote memorization, and low-level reasoning. In many cases, students copy solutions from other students without accepting or asking for mathematical justification. The research results also show that examples of textbook work and theoretical sections are not used as tools to aid students in solving assignments.
Algorithmic students can take advantage of the information provided and choose several suitable sets of rules but have yet to formulate valid arguments. According to Liu and Manouchehri [60], students tend to give incomplete arguments mathematically. In addition, students may need help learning proof and providing valid arguments.
Semi-creative students can take advantage of the information provided, choose several suitable sets of rules, and prepare valid arguments with directions from the teacher. This finding is in line with what was explained by Stacey and Vincent [61], that mathematics is based on reasoning and not just a set of rules that must be applied. Teachers need to think that compiling valid arguments is an important message that must be conveyed to students. Teachers need to encourage students to be able to reason correctly, including by compiling valid arguments. The teacher must be able to check and encourage student reasoning so that it is different from most textbooks which only present “rules without reason”. According to Stacey and Vincent [61], rules without reason are interpreted as rules without reasons that appear in most textbooks. The primary purpose is only to explain the derivation of rules or justifications in the preparation of practice questions, without explaining that these rules are supposed to be a tool for thinking.
Creative students can take advantage of the information provided and can choose their own set of rules so that they arrive at the preparation of valid arguments. According to Glassner [62], argument evaluation involves not only critical thinking but also creative thinking. Students who can construct valid arguments along with the accompanying rules show creativity. In addition, students who have arguments show clarity in their reasoning. While gathering information and creating knowledge, students must learn how to generate alternative ideas and meanings, use creative thinking, and choose the best alternative arguments [15].
5.4. Monitoring and Control Metacognitive
5.4.1. Metacognitive Monitoring
The first indicator of the meta-reasoning aspect is metacognitive monitoring. The research findings show that imitative students only have one rule (strategy) in solving non-routine problems and persist with the strategy even though they know it is wrong. Imitative students tend to stick with their choice of strategy even though it is explained that the chosen strategy cannot solve the problem. According to Morsanyi et al. [37], metacognitive monitoring involves processes such as judgments regarding task solvency and confidence in reaching solutions. Solvability can be interpreted as the ability of students to solve mathematical reasoning problems given in class. In line with Morsanyi’s opinion, imitative students’ metacognitive monitoring processes tend to have low solvency.
Algorithmic students only have one rule (strategy) in solving non-routine problems but want to try other rules (strategies) to find the correct solution. In line with Clark’s opinion [63], when students solve problems, we commonly expect students to re-check their work. This condition is a form of metacognition and self-regulation. Concerning the findings of this study, what Clark [63] conveyed is part of metacognitive monitoring. The desire of algorithmic students to try other strategies is an effort to monitor their cognitive processes in solving mathematical reasoning problems. Furthermore, Daher and Hashash [64] stated that metacognitive monitoring involves students’ awareness of the actions they follow to regulate the cognitive processes that are planned to be carried out. In addition, metacognitive monitoring aims to detect errors or delays in the implementation process. Further metacognitive monitoring also verifies the correct use of strategies and tools.
Semi-creative students have more than one rule (strategy) in solving non-routine problems and want to try other rules (strategies) and obtain the right results but with guidance from the teacher. In this case, students try to monitor their cognitive processes by looking at the previously selected rules or strategies (in the beginning) and predicting that the choice of rules is inappropriate. Students then try to see different strategies that are expected to solve the given reasoning problem. This is in line with the opinion of Nelson [65] that various metacognitive monitoring processes are differentiated in terms of whether these processes are related to one’s future performance (prospective monitoring) or one’s past performance (retrospective monitoring). In contrast to imitative students who only stick with one strategy (performance at the beginning), students with a semi-creative orientation focus on performance at the end. This condition shows that semi-creative students try to solve problems by considering different strategies and have the desire to try these other strategies with directions from the teacher.
Creative students can develop new rules (strategies) to solve non-routine problems and find the right solutions. According to Hargrove [66], monitoring and managing skills include several activities. Cognitive monitoring activities include keeping goals focused, maintaining the sequence of steps in the thinking process, determining how to achieve goals, knowing the right time to move to the following action, choosing the appropriate thinking process, finding errors and obstacles, and overcoming them. Activities that include this monitoring process can be seen when students are creative in solving problems involving mathematical reasoning and trying to find the correct solution.
5.4.2. Metacognitive Control
The second indicator of the meta-reasoning aspect is metacognitive control (in writing). The observed ability is that students can control their cognitive processes in writing by starting, stopping, or changing the allocation of effort in their reasoning processes related to number patterns and object configurations. The findings of this study indicate that imitative students do not show metacognitive control in writing when compiling or assembling intermediate targets (rules used) from the information given in the questions. Furthermore, metacognitive control has been seen in writing when compiling or assembling intermediate targets (rules used) for algorithmic students but has yet to reach the final target. This finding is in line with the opinion of Foster [38] that student responses in class (both written and oral) can range from random guesses to answers that are guaranteed to be correct.
Furthermore, semi-creative students’ metacognitive control can be seen in writing when compiling or assembling intermediate targets (rules used), as well as arriving at the final target with directions from the teacher. In contrast to semi-creative students, creative students’ metacognitive control can be seen in writing when compiling or arranging intermediate targets (rules used) and arriving at the final target. According to Gannaio [67], written metacognitive strategies are defined as physical articulations in a permanent format through written symbols that reflect cognitive behavior about the material and support the new knowledge organization during the learning process. In line with Gannaio’s opinion, semi-creative and creative students reflect the orientation of cognitive behavior seen in writing and reach the final target (the right solution to the given mathematical reasoning problem).
Furthermore, research investigating whether students write about their mathematical problem-solving process shows evidence of a metacognitive framework established by Pugalee [68]. According to Pugalee, the students’ written descriptions show the involvement of various metacognitive behaviors during the orientation, organization, execution, and verification of mathematical problem-solving. Furthermore, Pugalee describes the more dominant metacognitive behaviors identified through data analysis.
The last indicator of the meta-reasoning aspect is metacognitive control (verbally). Imitative students can only convey thoughts (the results of their reasoning) orally on the part of the available information. Algorithmic students can verbally convey their thoughts regarding the several sets of rules they choose but are not able to make correct conclusions on the final target. Morsanyi et al. [37] stated that metacognitive control consists of starting, changing, or stopping the allocation of effort to a cognitive task (e.g., starting a search for a new solution strategy, giving up on completing the task). This approach investigates reasoning and problem solving as they unfold over time. It also involves recognizing that evaluations regarding task solvency and people’s beliefs fluctuate during the solution process. This condition can be seen in how imitative and algorithmic students convey the results of their thoughts orally in finding rules and strategies to solve problems. Some students can write down their ideas in writing but need help to convey them orally. Conversely, other students can convey their thoughts orally but need help conveying them in written language.
Furthermore, semi-creative students can verbally convey their thoughts (results of reasoning) regarding a series of rules they have chosen but are not able to make the correct conclusions on the final target with directions from the teacher. Creative students can convey thoughts (results of their reasoning) orally in a coherent, complete, and systematic manner and arrive at the correct conclusions on the final target. According to Gannaio [67], verbal metacognitive strategies are defined as plans and responses that are spoken or stated that support the organization of new knowledge during the learning process. This verbal dialogue during the learning process can be produced independently or with other students. In the context of this study, students with semi-creative tendencies could verbally convey several sets of rules they had chosen and arrive at the correct conclusions on the final target with directions from the teacher. Meanwhile, creative students are seen to be independent and able to convey their reasoning coherently, completely, and systematically and arrive at the correct conclusions on the final target.
Overall, the description of this meta-reasoning aspect is seen for each student’s orientation tendency. Students with a creative reasoning orientation show that their cognitive monitoring and control processes are improving. According to Jia et al. [69], metacognition refers to knowledge and regulation of one’s cognitive processes, which have been considered essential components of creative thinking. In the context of mathematical reasoning, meta-reasoning students influence their behavior orientation to the best category, creative mathematical reasoning.
5.5. Self-Confidence
The indicator of the affective aspect explored in this study is self-confidence. The findings show that imitative students equate self-confidence with giving answers quickly, even though they do not understand whether the rules chosen are right or wrong. In line with Boaler’s research [70], which explained that when students realized that they could not solve math problems well, they began to feel their self-confidence disappear.
Furthermore, algorithmic students often show confidence in solving mathematical reasoning questions but need help to make correct conclusions. Boaler [71] described a student completing a math task and obtaining the correct answer but needing help understanding what he was doing. As Boaler found, his students said, “I can get the answer; I just do not understand why”. Based on this, Foster [38] stated that such a student might show high procedural competence and self-confidence and be considered a successful student. However, supporting students’ procedural beliefs is an essential first step in directing them to be more creative in completing their mathematical tasks.
Semi-creative students often show confidence in solving mathematical reasoning problems and can make the correct conclusions with directions from the teacher. According to Foster [38], a student may be confident that their answer will be assessed correctly (high procedural confidence) without having self-confidence based on prior mathematical understanding. Therefore, there is a need to further increase student self-confidence by bringing up expressions of correct concept beliefs so that teachers can help support the growth of student self-confidence.
Creative students show high self-confidence and arrive at the correct conclusions. Creative students move beyond the rules of expression when solving problems that involve mathematical reasoning processes with high self-confidence. In line with Schoenfeld’s opinion [72], students should focus on finding solutions, not just memorizing procedures. In addition, students must also be able to explore patterns, not only memorize formulas. Furthermore, students must be able to formulate conjectures in addition to completing exercises. This condition can occur when students have high self-confidence and can show their processes and arrive at the correct conclusions in solving problems related to mathematical reasoning. The level of self-confidence has a potential role in mathematical reasoning. Students with high and moderate mathematical abilities demonstrate the ability to think creatively and have confidence in solving problems [73,74,75,76]. Conversely, low-level students need to achieve indicators of creative thinking skills and have better self-confidence.
6. Conclusions
The data from this study yielded a wealth of information about the mathematical reasoning behavior of eighth graders. An explanation of the behavior that arises when students complete mathematical reasoning questions has been presented in this paper, considering cognitive, meta-reasoning, and affective aspects. This work contributes positively to student behavior research, which is associated with mathematical reasoning and has not yet been studied intensively by previous researchers. By examining the behavior exhibited by students, this research contributes to understanding the characteristics of student behavior and builds on research related to imitative and creative mathematical reasoning.
The category of reasoning behavior of each student is presented to help teachers map student potential and work to nurture creative student reasoning behavior. For example, one of the characteristics associated with imitative mathematical reasoning behavior is that students can only use the information provided but are not able to choose a set of rules that arrive at a logical conclusion. Meanwhile, students with algorithmic behavior tendencies have been able to utilize the information provided and can choose several sets of rules but have yet to reach a logical conclusion. Based on the findings about the characteristics of imitative, algorithmic, and semi-creative students, it is hoped that teachers will take the initiative to encourage students’ creative mathematical reasoning behavior. It is expected that students will be able to utilize the information provided and establish their own set of rules to arrive at a logical conclusion.
The interview technique used to collect data for this research yielded rich insights into students’ thinking. Teachers should, where possible, incorporate a similar approach into their assessment of students’ mathematical reasoning abilities. This finding is in line with Muir’s opinion [43], who found that flexible interviews can provide insight into the strengths and weaknesses of students’ mathematical thinking processes in individual problem solving, which can inform future teaching decisions.
7. Limitations and Future Research
This study is limited to students’ mathematical reasoning behavior in a group of grade 8 students. This research also only explores student behavior at three schools in one province in Indonesia. The COVID-19 situation when the research was conducted was an obstacle in collecting research data. In-depth research on the factor that supports students’ reasoning behavior (i.e., meta-reasoning) has yet to be developed. Further research is needed to explore students’ mathematical reasoning behavior in various topics of mathematics, not limited to junior high schools. Affective aspects of students also need to be explored more thoroughly to achieve a balance of cognitive and affective behavior simultaneously. Research can also be conducted on elementary school, high school, and university students. In addition, teachers’ encouragement of mathematical reasoning behavior deserves further research. Finally, because of the small sample size of students in this study, the study’s findings must be interpreted considering other extensive sample studies.
Author Contributions
Conceptualization, R.R. and K.K.; methodology, R.R.; validation, Y.S.K. and K.K.; formal analysis, R.R.; investigation, K.K.; resources, R.R.; data curation, K.K. and Y.S.K.; writing— original draft preparation, R.R.; writing—review and editing, Y.S.K.; visualization, R.R.; supervision, K.K. and Y.S.K.; project administration, R.R.; funding acquisition, R.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This study involving several junior high school students was carried out with permission (recommendation) and under the academic ethics adopted by the Provincial Government of Jambi. Ap-proval number: 1616201/388/DPM-PTSP-6.2/RP/VII/2021.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data are available from the authors upon reasonable request.
Acknowledgments
The authors would like to thank The Ministry of Education, Culture, Research, and Technology of the Republic of Indonesia through the Domestic Postgraduate Education Scholarship (Beasiswa Program Pasca Sarjana Dalam Negeri/BPPDN) for the study scholarship grant.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Mathematical reasoning problems.
Table A1.
Mathematical reasoning problems.
| No | Problems |
|---|---|
| 1. | Matchsticks are arranged in the following way.
|
| 2. | Arrange the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9 in the following circles so the sum of the numbers along each line of four is 23!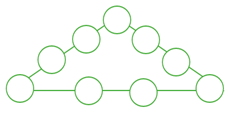 |
| 3. | Consider 31 = 3, 32 = 9, 33 = 27, 34 = 81, 35 = 243, 36 = 729, 37 = 2187, 38 = 6561. Perhaps the ones digits of these numbers form a pattern that can be used to predict the ones digit of 399. Find the ones digit in 399! |
References
- Dawkins, P.C.; Cook, J.P. Guiding reinvention of conventional tools of mathematical logic: Students’ reasoning about mathematical disjunctions. Educ. Stud. Math. 2017, 94, 241–256. [Google Scholar] [CrossRef]
- Bronkhorst, H.; Roorda, G.; Suhre, C.; Goedhart, M. Logical Reasoning in Formal and Everyday Reasoning Tasks. Int. J. Sci. Math. Educ. 2020, 18, 1673–1694. [Google Scholar] [CrossRef]
- Barnes, A. Perseverance in mathematical reasoning: The role of children’s conative focus in the productive interplay between cognition and affect. Res. Math. Educ. 2019, 21, 271–294. [Google Scholar] [CrossRef]
- Barnes, A. Enjoyment in learning mathematics: Its role as a potential barrier to children’s perseverance in mathematical reasoning. Educ. Stud. Math. 2020, 106, 45–63. [Google Scholar] [CrossRef]
- Schmidt FT, C.; Lindner, C.; Etzel, J.M.; Retelsdorf, J. Self-Control Outdoes Fluid Reasoning in Explaining Vocational and Academic Performance—But Does It? Front. Psychol. 2020, 11, 757. [Google Scholar] [CrossRef]
- Zaini, A.H.; Retnawati, H. What Difficulties that Students Working in Mathematical Reasoning Questions? J. Phys. Conf. Ser. 2019, 1397, 1–9. [Google Scholar] [CrossRef]
- Andrews-Larson, C.; Johnson, E.; Peterson, V.; Keller, R. Doing math with mathematicians to support pedagogical reasoning about inquiry-oriented instruction. J. Math. Teach. Educ. 2021, 24, 127–154. [Google Scholar] [CrossRef]
- Sumpter, L. Grade 9 Students’ Reasoning about Division of Fractions: What Are their Arguments Anchored in? In Students’ and Teachers’ Values, Attitudes, Feelings and Beliefs in Mathematics Classrooms; Palmér, H.J., Skott, J., Eds.; Springer: Cham, Switzerland, 2018; pp. 135–143. [Google Scholar] [CrossRef]
- Buckley, J.; Seery, N.; Canty, D. Investigating the use of spatial reasoning strategies in geometric problem solving. Int. J. Technol. Des. Educ. 2019, 29, 341–362. [Google Scholar] [CrossRef]
- Stein, M.K.; Grover, B.W.; Henningsen, M. Building student capacity for mathematical thinking and reasoning: An analysis of mathematical tasks used in reform classrooms. Am. Educ. Res. J. 1996, 33, 455–488. [Google Scholar] [CrossRef]
- Medová, J.; Bulková, K.; Čeretková, S. Relations between Generalization, Reasoning and Combinatorial Thinking in Solving Mathematical Open-Ended Problems within Mathematical Contest. Mathematics 2020, 8, 2257. [Google Scholar] [CrossRef]
- Lim, K.H.; Buendía, G.; Kim, O.-K.; Cordero, F.; Kasmer, L. The role of prediction in the teaching and learning of mathematics. Int. J. Math. Educ. Sci. Technol. 2010, 41, 595–608. [Google Scholar] [CrossRef]
- Store, J.C. Grounded theory of productive practices for algebraic thinking. Investig. Math. Learn. 2018, 10, 9–32. [Google Scholar] [CrossRef]
- Kilpatrick, J.; Swafford, J.; Findell, B. Adding It Up: Helping Children Learn Mathematics; National Academy Press: Washington, DC, USA, 2001. [Google Scholar]
- Glassner, A.; Schwarz, B.B. What stands and develops between creative and critical thinking? Argumentation? Think. Ski. Creat. 2007, 2, 10–18. [Google Scholar] [CrossRef]
- Tshabalala, F.L. Exploring How a Grade 7 Teacher Promotes Mathematical Reasoning in a Multilingual Mathematics Class of English Second Language Learners. In Language and Communication in Mathematics; Moschkovich, J., Wagner, D., Bose, A., Mendes, J., Schütte, M., Eds.; Springer International Publishing AG: Cham, Switzerland, 2018; pp. 249–261. [Google Scholar] [CrossRef]
- Zhang, D.; Qi, C. Reasoning and proof in eighth-grade mathematics textbooks in China. Int. J. Educ. Res. 2019, 98, 77–90. [Google Scholar] [CrossRef]
- Lai, M.Y.; Murray, S. Hong Kong Grade 6 Students’ Performance and Mathematical Reasoning in Decimals Tasks: Procedurally Based or Conceptually Based? Int. J. Sci. Math. Educ. 2014, 13, 123–149. [Google Scholar] [CrossRef]
- Hilton, A.; Hilton, G.; Dole, S.; Goos, M. Promoting middle school students’ proportional reasoning skills through an ongoing professional development programme for teachers. Educ. Stud. Math. 2016, 92, 193–219. [Google Scholar] [CrossRef]
- Fuentes, S.Q.; Crawford, L.; Angelo, H. Reasoning for all: An instructional model. Aust. Prim. Math. Classr. 2016, 22, 20–25. [Google Scholar]
- Cabello, V.M.; Moreira, P.M.; Morales, P.G. Elementary Students’ Reasoning in Drawn Explanations Based on a Scientific Theory. Educ. Sci. 2021, 11, 581. [Google Scholar] [CrossRef]
- NCTM. Principles and Standards for School Matematics; The National Council of Matematics, Inc.: Reston, VA, USA, 2000. [Google Scholar]
- Loong, E.; Vale, C.; Herbert, S.; Davidson, A. Developing a rubric for assessing mathematical reasoning: A design-based research study in primary classrooms. In Proceedings of the 41st Annual Conference of the Mathematics Education Research Group of Australasia, Auckland, New Zealand, 1–5 July 2018; pp. 503–510. [Google Scholar]
- Vale, C.; Widjaja, W.; Doig, B.; Groves, S. Anticipating students’ reasoning and planning prompts in structured problem-solving lessons. Math. Educ. Res. J. 2018, 31, 1–25. [Google Scholar] [CrossRef]
- Bozkuş, F.; Ayvaz, Ü. Middle School Mathematics Teachers’ Knowledge of Mathematical Reasoning. Eur. J. Educ. Stud. 2018, 4, 16–33. [Google Scholar] [CrossRef]
- Mastuti, A.G.; Abdillah, A.; Rijal, M. Teachers Promoting Mathematical Reasoning in Tasks. JTAM J. Teor. Dan Apl. Mat. 2022, 6, 371–385. [Google Scholar]
- Elena, L.; Moguel, S.; Landa, E.A.; Cabañas-Sánchez, G. Characterization of Inductive Reasoning in Middle School Mathematics Teachers in a Generalization Task. Int. Electron. J. Math. Educ. 2019, 14, 563–581. [Google Scholar]
- Rumsey, C.; Langrall, C.W. Promoting Mathematical Argumentation. Teach. Child. Math. 2016, 22, 412–419. [Google Scholar] [CrossRef]
- Temur, D.; Özsoy, G.; Turgut, S. Metacognitive instructional behaviours of preschool teachers in mathematical activities. ZDM 2019, 51, 655–666. [Google Scholar] [CrossRef]
- García, T.; Rodríguez, C.; González-Castro, P.; González-Pienda, J.A.; Torrance, M. Elementary students’ metacognitive processes and post-performance calibration on mathematical problem-solving tasks. Metacogn. Learn. 2015, 11, 139–170. [Google Scholar] [CrossRef]
- Yang, K.-L. Structures of cognitive and metacognitive reading strategy use for reading comprehension of geometry proof. Educ. Stud. Math. 2011, 80, 307–326. [Google Scholar] [CrossRef]
- Mevarech, Z.; Fridkin, S. The effects of IMPROVE on mathematical knowledge, mathematical reasoning and meta-cognition. Metacogn. Learn. 2006, 1, 85–97. [Google Scholar] [CrossRef]
- Kapa, E. A Metacognitive Support during the Process of Problem Solving in a Computerized Environment. Educ. Stud. Math. 2001, 47, 317–336. [Google Scholar] [CrossRef]
- Tsai, P.-Y.; Yang, T.-T.; She, H.-C.; Chen, S.-C. Leveraging College Students’ Scientific Evidence-Based Reasoning Performance with Eye-Tracking-Supported Metacognition. J. Sci. Educ. Technol. 2019, 28, 613–627. [Google Scholar] [CrossRef]
- Ackerman, R.; Thompson, V.A. Meta-Reasoning: Monitoring and Control of Thinking and Reasoning. Trends Cogn. Sci. 2017, 21, 607–617. [Google Scholar] [CrossRef]
- Ackerman, R.; Thompson, V. Meta-Reasoning: Shedding Meta-Cognitive Light on Reasoning Research. In The Routledge International Handbook of Thinking and Reasoning; Ball, L.J., Thompson, V.A., Eds.; Routledge/Taylor & Francis Group: Abingdon, UK, 2020. [Google Scholar]
- Morsanyi, K.; Cheallaigh, N.N.; Ackerman, R. Mathematics anxiety and metacognitive processes: Proposal for a new line of inquiry. Psihol. Teme 2019, 28, 147–169. [Google Scholar] [CrossRef]
- Foster, C. Confidence and competence with mathematical procedures. Educ. Stud. Math. 2015, 91, 271–288. [Google Scholar] [CrossRef]
- Lithner, J. A research framework for creative and imitative reasoning. Educ. Stud. Math. 2007, 67, 255–276. [Google Scholar] [CrossRef]
- Lithner, J. Principles for designing mathematical tasks that enhance imitative and creative reasoning. ZDM 2017, 49, 937–949. [Google Scholar] [CrossRef]
- Lithner, J. Learning Mathematics by Creative or Imitative Reasoning. In Proceedings of the 12th International Congress on Mathematical Education, Seoul, Republic of Korea, 8–15 July 2012; pp. 1–18. [Google Scholar]
- Brookhart, S.M. How to Create and Use Rubrics for Formative Assessment and Grading; ASCD: Alexandria, VA, USA, 2013; Volume 148. [Google Scholar]
- Muir, T.; Beswick, K.; Williamson, J. ‘I’m not very good at solving problems’: An exploration of students’ problem solving behaviours. J. Math. Behav. 2008, 27, 228–241. [Google Scholar] [CrossRef]
- Harisman, Y.; Noto, M.S.; Hidayat, W. Investigation of Students’ Behavior in Mathematical Problem Solving. Infin. J. 2021, 10, 235. [Google Scholar] [CrossRef]
- Bergner, R.M. What is behavior? And so what? New Ideas Psychol. 2011, 29, 147–155. [Google Scholar] [CrossRef]
- Rohati, R.; Kusumah, Y.S.; Kusnandi, K. The development of analytical rubrics: An avenue to assess students’ mathematical reasoning behavior. Cypriot J. Educ. Sci. 2022, 17, 2553–2566. [Google Scholar] [CrossRef]
- Creswell, J.W. Research Design: Qualitative, Quantitative, and Mixed Methods Approaches; SAGE Publications Ltd.: Thousand Oaks, CA, USA, 2014. [Google Scholar]
- Charmaz, K. Constructivist theory analysis of losing and regaining a valued self. In Five Ways of Doing Qualitative Analysis: Phenomenological Psychology, Grounded Theory, Discourse Analysis, Narrative Research, and Intuitive Inquiry; Wertz, F.J., Charmaz, K., McMullen, L.M., Josselson, R., Anderson, R., McSpadden, E., Eds.; Guilford Press: New York, NY, USA, 2011; pp. 165–204. [Google Scholar]
- Glaser, B.G.; Strauss, A.L. The Discovery Ofgrounded Theory: Strategies for Qualitative Research; Aldine; Sociology Press: Chicago, IL, USA, 1967. [Google Scholar]
- Octriana, I.; Putri, R.I.I.; Nurjannah, N. Penalaran Matematis Siswa Dalam Pembelajaran Pola Bilangan Menggunakan PMRI Dan LSLC. J. Pendidik. Mat. 2019, 13, 131–142. [Google Scholar] [CrossRef]
- Flegas, K.; Charalampos, L. Exploring Logical Reasoning and Mathematical Proof in Grade 6 Elementary School Students. Can. J. Sci. Math. Technol. Educ. 2013, 13, 70–89. [Google Scholar] [CrossRef]
- Rosita, N.T.; Sukestiyarno, Y.L.; Kartono; Mulyono. The Analysis of Students Mathematical Reasoning in Completing the Word Problem in SMPN 7 Sumedang. In Proceedings of the International Conference on Science and Education and Technology (ISET 2019), Semarang, Indonesia, 29 June 2019; Volume 443, pp. 115–119. [Google Scholar]
- NCTM. A Teacher’s Guide to Reasoning and Sense Making. Math. Teach. 2017, 111, 65. [Google Scholar] [CrossRef]
- Lannin, J.K.; Ellis, A.B.; Elliott, R. Developing Essential Understanding of Mathematical Reasoning for Teaching Mathematics in Prekindergarten-Grade 8; National Council of Teachers of Mathematics: Reston, VA, USA, 2011. [Google Scholar]
- Aaron, W.R.; Herbst, P.G. Teachers’ perceptions of students’ mathematical work while making conjectures: An examination of teacher discussions of an animated geometry classroom scenario. Int. J. STEM Educ. 2015, 2, 10. [Google Scholar] [CrossRef]
- Lesseig, K. Fostering Teacher Learning of Conjecturing, Generalising and Justifying through Mathematics Studio. Math. Teach. Educ. Dev. 2016, 18, 100–119. [Google Scholar]
- Riana, S.T.A.; Susanti, E.; Simarmata, R.H.; Nurhasanah, F. Conjecture in Completing Creative Problem-Solving Question as a Part of Development. In Proceedings of the 4th Sriwijaya University Learning and Education International Conference (SULE-IC 2020), Palembang, Indonesia, 24–26 October 2020; Volume 513, pp. 673–680. [Google Scholar]
- Coles, A.; Ahn, A. Developing algebraic activity through conjecturing about relationships. ZDM 2022, 54, 1229–1241. [Google Scholar] [CrossRef]
- Sidenvall, J.; Lithner, J.; Jäder, J. Students’ reasoning in mathematics textbook task-solving. Int. J. Math. Educ. Sci. Technol. 2014, 46, 533–552. [Google Scholar] [CrossRef]
- Liu, Y.; Manouchehri, A. Middle School Children’s Mathematical Reasoning and Proving Schemes. Investig. Math. Learn. 2013, 6, 18–40. [Google Scholar] [CrossRef]
- Stacey, K.; Vincent, J. Modes of reasoning in explanations in Australian eighth-grade mathematics textbooks. Educ. Stud. Math. 2009, 72, 271–288. [Google Scholar] [CrossRef]
- Glassner, A. Evaluating arguments in instruction: Theoretical and practical directions. Think. Ski. Creativity 2017, 24, 95–103. [Google Scholar] [CrossRef]
- Clark, C. The Impact of Confidence-Based Marking on Unit Exam Achievement in a High School Physical Science Course. 2020. Available online: https://scholarworks.uni.edu/grp/1449 (accessed on 15 December 2022).
- Daher, W.; Hashash, I. Mathematics Teachers’ Encouragement of Their Students’ Metacognitive Processes. Eur. J. Investig. Health Psychol. Educ. 2022, 12, 1272–1284. [Google Scholar] [CrossRef] [PubMed]
- Nelson, T.O. Psychology of Metamemory. In International Encyclopedia of the Social & Behavioral Sciences, 2nd ed.; Wright, J.D., Ed.; Elsevier Ltd.: Grand Rapids, MI, USA, 2001; Volume 1, pp. 9733–9738. [Google Scholar]
- Hargrove, R.A. Assessing the long-term impact of a metacognitive approach to creative skill development. Int. J. Technol. Des. Educ. 2012, 23, 489–517. [Google Scholar] [CrossRef]
- Gannaio, J.E. A Comparison of Verbal and Written Metacognitive Strategies Used by High School Students in a Language Arts Classroom. Doctoral Dissertation, Southeastern University, Lakeland, FL, USA, 2017. [Google Scholar]
- Pugalee, D.K. Writing, Mathematics, and Metacognition: Looking for Connections Through Students’ Work in Mathematical Problem Solving. Sch. Sci. Math. 2010, 101, 236–245. [Google Scholar] [CrossRef]
- Jia, X.; Li, W.; Cao, L. The Role of Metacognitive Components in Creative Thinking. Front. Psychol. 2019, 10, 2404. [Google Scholar] [CrossRef]
- Boaler, J. Mathematical Mindsets: Unleashing Students’ Potential through Creative Math, Inspiring Messages and Innovative Teaching; Jossey-Bass, A Wiley Brand: San Francisco, CA, USA, 2016. [Google Scholar]
- Boaler, J. The Elephant in the Classroom: Helping Children Learn and Love Maths; Souvenir Press: London, UK, 2009. [Google Scholar]
- Schoenfeld, A.H. Learning to Think Mathematically: Problem Solving, Metacognition, and Sense Making in Mathematics (Reprint). J. Educ. 2016, 196, 1–38. [Google Scholar] [CrossRef]
- Nufus, H.; Duskri, M.; Bahrun, B. Mathematical Creative Thinking and Student Self-Confidence in the Challenge-Based Learning Approach. J. Res. Adv. Math. Educ. 2018, 3, 57. [Google Scholar] [CrossRef]
- Inkeeree, H.K.; Fauzee, M.S.O.; Othman, M.K.H. The Effect of Students Confidence Level toward Mathematics Performance among Southern Thailand Primary School Children. Int. J. Acad. Res. Progress. Educ. Dev. 2017, 6, 20–34. [Google Scholar] [CrossRef]
- Aulia, R.; Rohati, R.; Marlina, M. View of the students’ self-confidence and their mathematical communication skills in solving problems. Edumatika J. Ris. Pendidik. Mat. 2021, 4, 90–102. [Google Scholar] [CrossRef]
- Hendriana, H.; Johanto, T.; Sumarmo, U. The role of problem-based learning to improve students’ mathematical problem-solving ability and self-confidence. J. Math. Educ. 2018, 9, 291–300. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
