Abstract
The interleaving effect indicates that students learn better from multiple areas that are interleaved rather than blocked. Two experiments tested the hypothesis that the effect is because interleaving facilitates comparisons between areas and is a variation of the variability effect that increases intrinsic cognitive load. Experiment 1 used an interleaved design with two obviously different topics and found no interleaving effect. Experiment 2 used a similar design but used topics that were more difficult to discriminate between, resulting in a clear advantage for the interleaved group associated with an increase in cognitive load. These results support the hypothesis that the interleaving and variability effects are closely related.
1. Introduction
Students prefer to practice a single concept or procedure repeatedly before switching to a new concept or procedure (i.e., AAABBBCCC) compared to interleaving concepts or procedures (i.e., ABCABCABC) as they rate interleaving to be less enjoyable and more difficult, as well as being less common [1]. Counterintuitively, under some circumstances, interleaving two or more concepts during practice leads to better learning than practicing a single concept repeatedly, indicating the interleaving effect [2,3,4].
We designed two experiments to investigate the hypothesis that the interleaving effect is due to learning to categorise problems. Previously, using cognitive load theory [5], the variability effect was also hypothesised to be due to learning to categorise problems. If the two effects have similar causes, we further suggest that they are closely related and both may be combined under a cognitive load theory umbrella.
2. Cognitive Load Theory
Cognitive load theory [6,7] aims to generate novel instructions to facilitate learning. The following points summarise the theory.
- Information can be categorised as either biologically primary if we have specifically evolved to acquire it or biologically secondary if we have not specifically evolved to acquire it [8,9,10].
- Novel, secondary information can be acquired either by randomly generating it during problem solving and testing it for effectiveness or, more efficiently, by obtaining it from other people.
- Irrespective of how the secondary information is obtained, it must be processed by a limited-capacity [11,12] and limited-duration [13] working memory.
- If that information is to be used subsequently, it can be stored in long-term memory for subsequent use. Long-term memory has no known capacity or duration limits [14].
- When environmental signals indicate that it is needed, information can be transferred from long-term memory back to working memory to generate appropriate action. Unlike when processing novel information, working memory has no known limits when processing familiar information retrieved from long-term memory [15].
- Intrinsic cognitive load is imposed by the nature of learning materials, which is determined by the levels of element interactivity. Element interactivity is a concept determining the complexity of learning materials [16,17] in which an element is a concept or procedure.
- Extraneous cognitive load is imposed by suboptimal instructional designs that artificially and unnecessarily increase element interactivity. Altering the design of instruction can reduce or eliminate extraneous cognitive load.
- Germane cognitive load refers to the working-memory resources that are devoted to dealing with the element interactivity associated with intrinsic cognitive load [17,18].
Hence, intrinsic cognitive load and germane cognitive load represent beneficial cognitive loads that enhance learning. Conversely, extraneous cognitive load stems from suboptimal instructional designs that interfere with learning. In the realm of teaching, our objective is to optimise the presence of intrinsic and germane cognitive loads while minimising the presence of extraneous cognitive load [19,20,21].
3. Explanations of the Interleaving Effect
Any explanation of the interleaving effect must also explain why the effect cannot be demonstrated under some conditions. In other words, it must explain the limits of the effect. Cognitive load theory can be used as a construct to explain both the interleaving and variability effects based on their common characteristics.
3.1. Interleaving and the Discrimination Hypothesis
Discrimination Learning. When students learn multiple concepts that are similar to each other, a greater degree of similarity increases learning difficulty [22]. Failing to distinguish similar concepts is known as discrimination failure, and learning to discriminate similar concepts is called discrimination learning [2]. Discrimination learning has been found in a very wide range of domains, ranging from discriminating concepts outside the classroom, such as face recognition, to concepts in the classroom, such as learning language, mathematics, or science. Discrimination learning has been suggested to provide a theoretical foundation for explaining the interleaving effect, particularly in the domains of mathematics and physics, which is beneficial for learning in a very wide range of domains [2]. From a cognitive load theory perspective, an increase in similarity that needs to be distinguished will cause an increase in intrinsic cognitive load. Accordingly, as indicated below, the theory can potentially be used to predict when the interleaving effect is likely to occur.
Discrimination Hypothesis. An interleaved design was shown to be superior to a blocked design by several experimenters who used the discrimination hypothesis as an explanation for their results [23,24,25,26,27]. The authors in [25] investigated learning concepts or categories by observing exemplars, with participants randomly allocated to either the interleaved or blocked group. Six paintings were selected from each of 12 artists. During the intervention, the six paintings from each of the artists were either blocked or interleaved. Learners were informed of the correct response on each occasion and were tested on their ability to identify the artist of an unfamiliar painting from one of the 12 artists. The results favoured the interleaved design, with the effect explained by better learning to discriminate different artists’ painting styles.
The study [24] replicated this finding and included a third group in which multiple paintings from multiple artists were shown simultaneously, with participants tested to identify the artist of a new painting that was from one of the artists. The results replicated the interleaving effect found before [25] and also found that the interleaved design performed equally as well as the simultaneously presented group, which further supported the discrimination hypothesis as an explanation of the interleaving effect.
The authors in [26] tested the interleaving effect on teaching mathematics in real classrooms. Four mathematics problems—the face, corner, edge, and angle of a prism—were taught in interleaved or blocked groups. Although the interleaved design impaired mathematics performance during the learning phase, performance on the post-test indicated that it significantly improved learning. The experiment suggested again that the interleaving effect depended on task similarity requiring learners to discriminate between different problems with similar solutions.
In the study, ref. [26] controlled the spacing factor for their interleaved design, suggesting that the spacing and the interleaving effects might be distinct. The interleaving effect might depend on learning to discriminate [25], whereas the spacing effect might depend on other factors such as the depletion of working memory after cognitive effort and recovery during rest [28,29]. Both explanations depend on different facets of cognitive load theory. Importantly, the explanation of the interleaving effect is identical to cognitive load theory’s explanation of the variability effect. Both effects depend on people learning which concepts are similar and which are different.
3.2. Relations between the Interleaving Effect and the Variability Effect
The variability effect suggests that engaging in tasks with high surface variability enhances learning compared to tasks with low surface variability [30]. Tasks with higher variability impose a higher intrinsic cognitive load during learning due to more interactive elements being processed simultaneously in working memory [5]. With an increase in variability, the number of interactive elements is increased as learners need to distinguish more varied tasks requiring similar solutions. Learning to categorise problems is central to both the variability and interleaving effects.
The experimental procedures used to demonstrate the variability effect and the interleaving effect differ [5,26,31], but they have the same goal; teaching students to distinguish problem categories. The interleaved sequence in effect increases variability. Learners see a greater variety of problems or tasks in rapid succession with multiple changes between episodes compared to a single change from one block to another when the information is presented in a blocked sequence.
While the interleaving and variability effects have a common goal of teaching students to appropriately categorise problems, one difference between the two effects is that there is a common experimental design for all demonstrations of the variability effect but there are two designs for the interleaving effect. The variability effect always requires comparing highly variable examples of the same concept or procedure with less-variable examples. The interleaving effect can similarly compare interleaved examples of different surface structure versions of the same concept or procedure, but alternatively, one can use interleaved examples of different concepts or procedures that have similar surface structures [2,32]. In other words, interleaving can teach students to treat in the same way problems that look different but are in fact the same or to distinguish between different problems that look the same. The variability effect only teaches students to treat in the same way problems that look different but are the same. The current work tested the former version of the interleaving effect by using problems that appeared different but were structurally the same.
4. Present Study
There were two main goals for this study. Firstly, two experiments aimed to test that the interleaving effect is due to discrimination, with its increased intrinsic cognitive load leading to an increase in the depletion of working memory resources. Based on previous results [28], measuring working memory resource depletion is positively correlated with measuring the intrinsic cognitive load, namely, the more working memory resources that are depleted, the higher is the level of intrinsic cognitive load imposed. Therefore, using working memory tests to measure working memory resource depletion can be used as a proxy for the level of intrinsic cognitive load, assuming all other factors such as levels of extraneous cognitive load are equal across groups.
Secondly, the study aimed to provide evidence for and extend the current literature by indicating that the interleaving effect is a variation of the variability effect that can be explained from a cognitive load theory perspective. If the interleaving effect is not obtained by using obviously different problems that really are different but is instead obtained using obviously different materials that actually require identical solutions, that result suggests that the increase in variability caused by interleaving provides the explanation of the effect.
Experiment 1 compared an interleaved design with a blocked design, using two dissimilar materials: mathematics and language materials. Learners do not need to learn to discriminate between mathematics and language materials because the differences are obvious. Accordingly, there should be no advantages to interleaving with no evidence for an interleaving effect. The following hypotheses were tested. There would be no significant differences between the interleaved design and the blocked design upon conducting a post-test (H1), and no significant differences between the two groups on working memory resource depletion (H2) as students do not have to learn to discriminate between mathematics and language materials because the differences are obvious.
Experiment 2 compared the interleaved design with the blocked design but used two different sets of mathematics problems solved by similar solutions. Unlike Experiment 1, students must learn that these problems that appear very different on the surface are in fact, similar. It was hypothesised that the interleaved group would perform better than the blocked group on the post-test (H3) when learning that two visually distinct problem categories require identical solutions, and that the interleaved group would deplete more working memory resources compared to the blocked group (H4) due to an increased intrinsic cognitive load due to having to discriminate between learning materials.
In summary, the two experiments were designed to test the general hypothesis that when dissimilar-looking information really is dissimilar because it requires unrelated problem solutions, it is less likely to lead to the interleaving effect (Section 5), while dissimilar-looking information that really is similar is more likely to lead to the interleaving effect (Section 6). This issue is important to counter the view that interleaving is always beneficial irrespective of the relations between interleaved tasks. To improve ecological validity, the two experiments were designed and conducted in real classrooms and based on a real national curriculum for school children.
Power Analysis and Ethics Approval
To obtain the interleaving effect, a sample of 120 participants was recommended considering an a priori effect size f(V) = 0.27 [large size effect, based on data from 26], α error probability = 0.05, power (1 − β error probability) = 0.80.
All the experiments were conducted following the University ethics policy, with ethics approval numbers for Experiment 1 (IRB-2018-11-044) and 2 (160/UN.34.13/M/TU/2022).
5. Experiment 1
This experiment compared an interleaved with a blocked design using Mathematics (M) and Language (L) learning materials. Because students do not have to be taught to distinguish between the two topic areas, it was predicted that an interleaving effect would not be obtained.
5.1. Method
5.1.1. Participants
One hundred and forty-three Year-7 students (mean age: 13 years old; 75 females) were recruited. They were randomly assigned to four groups, namely, the Mathematics–Language blocked group (MMLL), the Language–Mathematics blocked group (LLMM), the Mathematics–Language interleaved group (MLML), and the Language–Mathematics interleaved group (LMLM). Each group had four learning episodes. All participants were novices concerning the mathematics and language topics taught. The experiment was conducted during regular class periods with the supervision of teachers.
5.1.2. Materials
Two mathematics booklets about measuring the angle made by parallel lines and transversal lines that cross them were designed for the two mathematics learning episodes for each of the four groups. Three worked example–problem solving pairs were designed for teaching the topic in each booklet (see Appendix A).
Two language booklets about coconuts were designed for the two language learning episodes for each of the four groups. Each booklet included a passage of three paragraphs followed by summaries of each of the three paragraphs that were designed to demonstrate how to write summaries of the ideas in each paragraph. The booklet also included information on how to answer a comprehension question based on the given passage (see Appendix B). This information was followed by another similar-length passage on the same topic with three paragraphs that the students had to summarise themselves before answering a comprehension question. In this way, a worked example was followed by a similar problem to solve.
Two versions of the working memory test were designed to measure working memory resources after every two learning episodes. The language working memory test included a storage task (memorising the final word of each sentence) and an information-processing task (assessing the logical coherence of each sentence) designed to measure the information storage and information processing functions of working memory [33]. The test began with a practice trial containing two sentences (Level 2), followed by Level 2, Level 3, and Level 4 trials, with each level containing 3 trials with 2, 3, or 4 sentences per trial, respectively. During each trial, the sentences were serially presented to participants, each appearing for 3 s. After every sentence, the participants selected either the ‘Made sense’ or ‘Did not make sense’ responses (processing function) before being shown the next sentence. At the end of each trial, the participants had to type the final word of each of the presented sentences (storage function).
The mathematics working memory test applied the same design principles but with equations instead of sentences, such as 3 + 2 − 1 = 6. Participants needed to judge the validity of each equation, indicating ‘right’ or ‘wrong’, and memorise the first digit of the equation, for example, “3”. The internal consistency of the working memory test (including mathematics and language), estimated using Cronbach’s alpha, was 0.69.
Two delayed post-tests measuring the understanding of mathematics and language were designed. For the mathematics test, four questions that were similar to those taught were included. For the language test, two similar-length passages discussing coconuts were designed. Each passage had three paragraphs to be summarised and a comprehension question about this passage to answer. The internal consistency of the post-test, estimated using Cronbach’s alpha, was 0.85 for the language test and 0.61 for the mathematics test. For analyses, one of the questions was deleted from the mathematics test because it failed to discriminate between students.
5.1.3. Procedure
Before the experiment, the schoolteachers introduced the researcher to the students. Consent forms were distributed and collected. For mathematics learning, the relevant pre-requisite theorems were re-visited, whereas for language learning, the structure of a passage and a paragraph for summarising it were explained. This preparation phase was 5 min.
The experiment was conducted over two days (see Table 1). During Day 1, participants were randomly assigned to one of the four experimental groups. For the first block of 60 min, they either studied two mathematics problems, two language activities, or one mathematics problem with one language activity. Teachers instructed students who finished the task early to review their answers, thus equating learning periods. This procedure was followed by the mathematics working memory test (15 min). For the second block of 60 min, the procedure was similar to the first block. Next, the language working memory test replaced the mathematics working memory test. On the second day, the mathematics and language post-tests were conducted for two 30 min periods.

Table 1.
Experiment 1: procedure.
5.1.4. Scoring
For the language working memory test, one point was assigned for each correct judgement of grammatical coherence (i.e., the score for information processing), and another point was assigned for each correctly recalled last word (i.e., the score for information storage). The maximum score was 27 for both information processing and storage. The mathematics working memory test was scored in the same manner as the language working memory test. For the mathematics working memory test, one point was assigned for correctly memorising the first digit and one point was assigned for a correct judgment of equation equivalence.
For the mathematics post-test, each question could be solved via 4 steps. Each correct step was allocated 1 point. The total score for the mathematics test was 16 (4 questions).
For the language post-test, 1 point was allocated for correctly summarising a paragraph (maximum 3), and 1 point was allocated for the comprehension question, providing a maximum of 4 points for each passage. The total score for the language test was 8 (two passages).
5.2. Results
The means and standard deviations of the mathematics and language working memory test scores can be found in Table 2. The means and standard deviations of the mathematics and language post-test scores can be found in Table 3.

Table 2.
Experiment 1: means (and standard deviations) of mathematics and language working memory scores.

Table 3.
Experiment 1: means (and standard deviations) of mathematics and language post-test scores.
5.2.1. Mathematics Working Memory Test
Two ANOVAs were conducted to analyse the processing and storage scores separately. For both the processing scores, F(3, 139) = 0.27, MSE = 10.50, p = 0.85, ηp2 = 0.006, and the storage scores, F(3, 139) = 0.17, MSE = 39.42, p = 0.92, ηp2 = 0.004, the effect of group was not significant. Following these non-significant ANOVAs, Bayes analyses were calculated to provide grounds for accepting the null hypothesis. For the storage scores, BF01 = 22.2, suggesting the data were about 22 times more likely under the null hypothesis compared to the alternative hypothesis. Similarly, for the processing scores, BF01 = 19.6, suggesting the data were 20 times more likely under the null hypothesis compared to the alternative hypothesis. These results indicate that there was no evidence of working memory resource depletion differences between the groups.
5.2.2. Language Working Memory Test
Identical analyses were carried out on the language working memory test data. For the processing scores, the effect of group was not significant, F(3, 139) = 0.69, MSE = 6.27, p = 0.56, ηp2 = 0.015, and BF01 = 12.2, suggesting the data were about 12 times more likely under the null hypothesis compared to the alternative hypothesis. For the storage scores, the effect of group was again not significant, F(3, 139) = 1.18, MSE = 19.37, p = 0.32, ηp2 = 0.025, and BF01 = 6.90, suggesting the data were about seven times more likely under the null hypothesis compared to the alternative hypothesis. Again, there were no significant working memory resource depletion differences found between the groups.
5.2.3. Post-Tests
A mixed 4 (Groups: MMLL, LLMM, MLML, LMLM) 2 (Mathematics vs. Language) ANOVA with repeated measures on the last factor was used to analyse the data for the post-tests. For the mathematics post-test, the effect of group was not significant, F(3, 139) = 0.31, MSE = 18.03.02, p = 0.82, ηp2 = 0.010, and BF01 = 10, suggesting the data were about 10 times more likely under the null hypothesis than the alternative hypothesis. For the language post-test, the effect of group also was not significant, F(3, 139) = 1.04, MSE = 4.81, p = 0.38, ηp2 = 0.022, and BF01 = 10, suggesting the data were about 10 times more likely under the null hypothesis than the alternative hypothesis.
5.3. Discussion
In Experiment 1, there was no evidence of either an interleaving effect (H1) or of working memory resource depletion due to an increased intrinsic cognitive load for the interleaved group (H2), which supported our hypotheses for Experiment 1. The failure to find an interleaving effect or working memory resource depletion is likely to have been caused by the absence of a need to learn to discriminate between the materials. Because they were so dissimilar, the difference between the language and mathematics information was obvious. We hypothesised that an interleaving effect would not be found when interleaving two dissimilar topics that students can easily discriminate between.
Interestingly, these results do not support the suggestion that the interleaving effect is due to spacing. For half of the groups, the topics were interleaved and therefore spaced (i.e., the MLML and LMLM groups). If spacing had been relevant in this context, these groups should have obtained higher learning outcomes on the post-test and less working memory resources depleted on the working memory test than the two blocked groups (i.e., the MMLL and LLMM groups), based on the framework of Chen and colleagues [29,34]. However, neither of these tests revealed evidence indicating the superiority of the interleaved design. The failure to find an effect can be attributed to students not needing to learn to discriminate between the mathematics- and language-based content.
6. Experiment 2
This experiment further investigated the discrimination hypothesis of the interleaving effect. There are two ways in which this hypothesis can be tested. Students may need to learn that seemingly similar-looking materials are in fact distinct and must be treated as being distinct, or they may need to learn that specific types of materials that look different are in fact the same and should be treated as being the same. In Experiment 2, different = appearing mathematics materials that in fact required the same solution were used. It was hypothesised that interleaving such materials would assist students to learn to recognise them and learn to treat them as being functionally identical.
6.1. Method
6.1.1. Participants
A 2 (Design: Interleaved vs. Blocked) 2 (Testing Time: Immediate vs. Delayed) between-subject design was used. One hundred and fifteen Year-7 students were recruited for this experiment. They were randomly assigned to one of the four groups: interleaved with immediate testing, interleaved with delayed testing, blocked with immediate testing, and blocked with delayed testing. The mathematics topic of creating auxiliary lines to solve an unknown angle was chosen. No participants had been taught this topic and so it was new to them. The experiment was conducted during regular class periods.
6.1.2. Materials
Sixteen slides were created to introduce basic concepts associated with the learning objective of how to create auxiliary lines in a geometrical figure in such a way that angle theorems can be used to measure the unknown angles. Four booklets were designed with two types of problems. For type A problems, the unknown angle was formed between two parallel lines (see Appendix C), whereas for type B problems, the unknown angle was formed by two squares within two parallel lines (see Appendix D).
The two types of problems could both be solved by creating auxiliary lines. For each of type A and B problems, three worked example–problem solving pairs were designed, totalling six worked example–problem solving pairs. They were presented in either interleaved or blocked form to teach the two types of problems for each group. For the interleaved group, one worked example–problem solving pair teaching the type A category of problems was followed by a worked example–problem solving pair teaching the type B category of problems, and so the six pairs were arranged using an ABABAB format. For the blocked group, all the type A problems were taught before any type B problems were seen, followed by all the type B problems, resulting in the six pairs following an AAABBB format.
The same mathematics working memory test in Experiment 1 was used in Experiment 2. The internal reliability of the working memory test was 0.86. For the post-test, we designed six questions that were similar to those taught during the instruction period. The internal reliability of the post-test was 0.84.
6.1.3. Procedure
The procedure is summarised in Table 4. Initially, all students were presented and taught the introductory materials for 20 min. Next, during the first learning phase, students in each group studied three worked example pairs for 3 min/pair. For groups with delayed testing, students then had a 20 min break after 9 min of studying the three worked example pairs. During the second learning phase, another 9 min were used to study the remaining three worked example–problem solving pairs. For groups with delayed testing, they had another 20 min break. Teachers instructed students who finished tasks earlier to review their answers, thus ensuring that the learning and resting periods were controlled and equal irrespective of group. The working memory test (15 min) was conducted after these two learning phases. Finally, the post-test lasted 20 min.

Table 4.
Experiment 2: procedure.
6.1.4. Scoring
The scoring system used in this experiment was the same as for Experiment 1. The maximum scores for the processing and storage parts of the working memory test were both 27. The maximum score for the post-test was 6.
6.2. Results
The means and standard deviations of the working memory test scores can be found in the Table 5. The means and standard deviations of the post-test scores are displayed in Table 6.

Table 5.
Experiment 2: means (and standard deviations) of working memory scores.

Table 6.
Experiment 2: means (and standard deviations) of post-test scores.
6.2.1. Working Memory Test: Processing
A 2 (Design: Interleaved vs. Massed) 2 (Testing Time: Immediate vs. Delayed) ANOVA was conducted on the processing scores. The effect of design was not significant, F(1, 111) = 2.70, MSE = 56.15, p = 0.10, partial η2 = 0.024, and BF01 = 1.43, suggesting the data were slightly above one time more likely under the null hypothesis compared to the alternative hypothesis. The effect of testing time was not significant, F(1, 111) = 0.44, MSE = 56.15, p = 0.51, partial η2 = 0.004, and BF01 = 5, suggesting the data were about five times more likely under the null hypothesis compared to the alternative hypothesis. The Design Testing Time interaction was also not significant, F(1, 111) = 0.86, MSE = 56.15, p = 0.36, partial η2 = 0.008, and BF01 = 20, suggesting the data were about 20 times more likely under the null hypothesis compared to the alternative hypothesis.
6.2.2. Working Memory Test: Storage
A 2 (Design: Interleaved vs. Massed) 2 (Testing Time: Immediate vs. Delayed) ANOVA on the storage scores was conducted. The effect of design was significant, F(1, 111) = 6.66, MSE = 33.61, p = 0.011, partial η2 = 0.057, and BF01 = 5.2. The effect of testing time was significant, F(1, 111) = 8.28, MSE = 33.61, p = 0.005, partial η2 = 0.069, and BF01 = 1.4. The interaction Design Testing Time was also significant, F(1, 111) = 13.39, MSE = 33.61, p < 0.001, partial η2 = 0.108, and BF01 = 4.8. The Bayes factors were more than 1, which was due to the large sample size and relatively small effect size.
The significant interaction was followed by simple effects tests. For the immediate testing groups, interleaving depleted working memory resources to a greater extent than blocking, t(54) = −4.77, SEDiff = 1.41, p < 0.001, d = 1.08, and BF01 = 0.01 (suggesting the data were about 100 times more likely under the alternative hypothesis). For the delayed testing groups, there was no significant difference between the interleaved and blocked designs, t(57) = 0.72, SEDiff = 1.63, p = 0.48, d = 0.56, and BF01 = 142.9 (suggesting the data were about 143 times more likely under the null hypothesis than the alternative hypothesis).
6.2.3. Post-Test
A 2 (Design: Interleaved vs. Blocked) 2 (Testing Time: Immediate vs. Delayed) ANOVA was used to analyse the post-test scores. The effect of design was significant, F(1, 111) = 4.77, MSE = 3.19, p = 0.03, partial η2 = 0.041, and BF01 = 1.3, indicating that the interleaved design outperformed the blocked design, showing an interleaving effect. The effect of testing time was significant, F(1, 111) = 4.09, MSE = 13.07, p = 0.046, partial η2 = 0.036, and BF01 = 1.7, indicating that groups with immediate testing outperformed those with delayed testing. Again, the Bayes factor values above 1 are due to the large sample size and relatively small effect size. The interaction between design and testing time was not significant, F(1, 111) = 0.09, MSE = 0.31, p = 0.76, ηp2 = 0.001, and BF01 = 3.3 (suggesting the data were about three times more likely under the null hypothesis than the alternative hypothesis).
6.3. Discussion
Using different learning materials requiring a similar solution generated a conventional interleaving effect (H3). In addition, the storage part of the working memory test indicated that the interleaved groups depleted more working memory resources than the blocked groups (H4), which was shown with immediate testing but not with delayed testing. According to the working memory resources depletion hypothesis [28], that difference in working memory scores disappeared for the delayed memory scores since the rest period should have permitted the recovery of working memory resources, eliminating any differences. The increased depletion of working memory resources by the interleaved group when measured immediately without rest suggests an increased cognitive load in this group compared to the equivalent blocked group. An increase in cognitive load should generate an increase in working memory resource depletion [28]. Therefore, the results supported the hypotheses of Experiment 2.
As working memory resources depletion is positively correlated with the levels of intrinsic cognitive load [28], therefore, a higher depletion of working memory resources indicates a higher level of intrinsic cognitive load. We suggest that interleaving increases intrinsic cognitive load (as evidenced by the increased depletion of working memory resources) for the same reason that variability increases cognitive load. Learners needed to learn to recognise the differences and similarities between the two types of problems and learn which differences did not matter when solving the problems and which similarities did matter because both problem types required the same solution. Attempting to learn to detect the critical similarities and irrelevant differences as well as learning how to generate a similar solution for problems that do not look similar are activities that are likely to be engaged in when faced with interleaving but less likely to be engaged in when faced with blocking, resulting in an increase in intrinsic cognitive load when interleaving. If the same factors result in the variability effect, interleaving may result in the same increase in intrinsic cognitive load for the same reason as increasing variability. If so, the interleaving effect is related to the variability effect, and both occur for the same cognitive load theory reasons.
7. General Discussion
The primary aim of this research was to investigate the discrimination hypothesis used to explain the interleaving effect. In addition, using a cognitive load theory perspective, we wished to link the interleaving and variability effects.
Experiment 1 interleaved two tasks that were clearly distinct, with one task involving mathematics and the other task involving language content. Students did not have to learn the important characteristics that distinguished the two tasks because they were very familiar with the relevant distinguishing characteristics. As hypothesised, the interleaving effect was not found. Because of the tendency to assume that all interleaving is beneficial, we believe the failure to find an effect in Experiment 1 is important, especially in conjunction with the results of Experiment 2.
By using two similar mathematics tasks in Experiment 2, the interleaving effect was obtained: we observed higher post-test scores (learning) and more depletion of working memory resources associated with interleaving than with blocking. Learners in Experiment 2 had to learn to identify the characteristics of the mathematics problems that were relevant to the solution and learn to detect those critical characteristics despite the different surface structures of the two problem types. Testing problems appearing different but in fact the same in Experiment 2 also echoed the mechanism of the variability effect that could aid in generalisation within a concept due to more elaborate and differentiated encoding during learning.
Interleaving allowed students to compare two different structures and learn to identify the specific structures that must be present to allow for the solution while also learning which structures to ignore. For the blocked groups, comparing and contrasting the structures was less important, thus reducing the intrinsic cognitive load and learning. The study by [28] introduced working memory depletion and recovery as concepts relevant to cognitive load theory and suggested that at least under some circumstances, the spacing effect could be treated as a cognitive load theory effect. In contrast, in [29] it was suggested that the interleaving effect is due to learning to discriminate and is not a cognitive load theory effect. That conclusion may be erroneous, with the two effects caused by different cognitive load theory concepts. The variability effect is a cognitive load theory effect [5,30], and a comparison between the variability and interleaving effects reveals very close similarities. We suggest that learning to discriminate increases intrinsic cognitive load, as is the case for the variability effect [5]. Provided that the increase does not exceed working memory limits, more may be learned by interleaving than by blocking.
Limitations and Future Directions
There are two main limitations of this study: Firstly, although working memory resources are positively correlated with levels of intrinsic cognitive load [28], future research might use cognitive load scales, such as recent multidimensional instruments [20,35,36], to directly measure the level of intrinsic cognitive load. Secondly, for Experiment 2, we only used visually distinct problems that required identical solutions but did not use visually identical problems that required distinct solutions, providing a possible follow-up for the current study.
8. Conclusions
Based on the current experiments, the results support the suggestion that the interleaving effect is due to discrimination and relies on interleaving leading to a higher intrinsic cognitive load, thus providing learners with more to learn. The same cognitive mechanism suggests that the interleaving effect is related to the variability effect. The failure to find a spacing effect embedded in the interleaved design in Experiment 1 provides some evidence supporting the framework in [29] that the spacing effect may be due to working memory resource depletion, while the interleaving effect is due to the discrimination of learning items.
Author Contributions
Conceptualization, O.C.; methodology, O.C., J.S. and F.P.; formal analysis, O.C. and E.R.; investigation, O.C. and E.R.; data curation, E.R.; writing—original draft preparation, O.C.; writing—review and editing, J.C.C.-A., J.S. and F.P.; funding acquisition, J.C.C.-A. All authors have read and agreed to the published version of the manuscript.
Funding
Funding from ANID/PIA/Basal Funds for Centers of Excellence FB0003 is gratefully acknowledged.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board (or Ethics Committee) of Yogyakarta State University (IRB-2018-11-044 and 160/UN.34.13/M/TU/2022 and August 2020).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data could be shared by contacting with the first and the second authors.
Conflicts of Interest
The authors declare no conflict of interest.
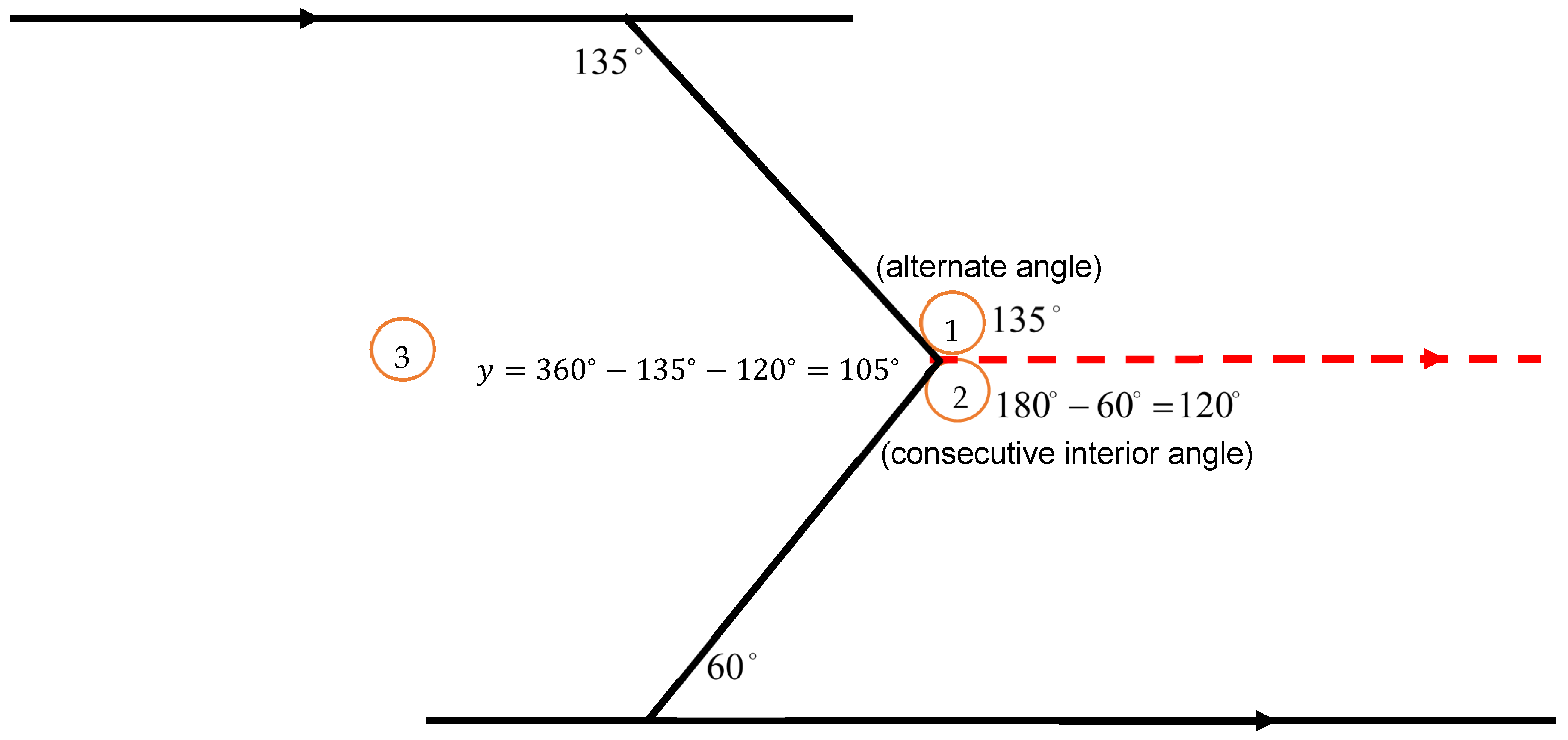
Appendix A. Sample of Mathematics Material Used in Experiment 1
Please calculate the value of angle y
Appendix B. Sample of Language Material Used in Experiment 1 (Translated from the Original Bahasa Indonesia)
Reading 1. (15 min)
Read the following three paragraphs about the benefits of consuming coconut water and learn how to write a summary for each paragraph and how to answer a comprehension question about this reading.
| Paragraph | Summary |
| One of the benefits of coconut is to prevent premature aging and relieve diarrhoea. The relevant part is coconut water. The water in coconut fruit contains cytokinin hormones that prevent premature aging, while the minerals, amino acids, and enzymes it contains are useful for relieving diarrhoea. | This paragraph describes the benefits of coconut water to prevent premature aging and relieve diarrhoea. |
| The content of cytokinin in coconut water serves to regulate the growth, development, and aging of cells. The cytokinin content in coconut water has anti-aging, anti-carcinogenic, and anti-thrombotic effects. | This paragraph describes the content of cytokinin as anti-aging, anti-carcinogenic, and anti-thrombotic effects. |
| Coconut water is useful when you have diarrhoea because it can replace the fluid lost from the gastrointestinal tract. This is because coconut water contains amino acids, enzymes, minerals, and fatty acids that result in coconut water having high osmolarity. In addition, coconut water also contains low amounts of sodium chloride as well as high amounts of sugars and amino acids. It has a balanced composition of fluids to prevent dehydration during diarrhoea. | This paragraph describes the content of coconut water in the form of minerals with the right composition that can restore body fluids lost during diarrhoea. |
What are the benefits of coconut water for the body?
| Answer | Explanation |
| Coconut fruit has benefits for the body. One part is that coconut water can prevent premature aging and relieve diarrhoea. Coconut water contains cytokinins that have anti-aging, anti-carcinogenic, and anti-thrombotic benefits. The content of coconut water in the form of minerals with the right composition can restore body fluids lost during diarrhoea. | The answer consists of four sentences, namely: The main idea of all three paragraphs; Summary of the first paragraph; Summary of the second paragraph; Summary of the third paragraph |
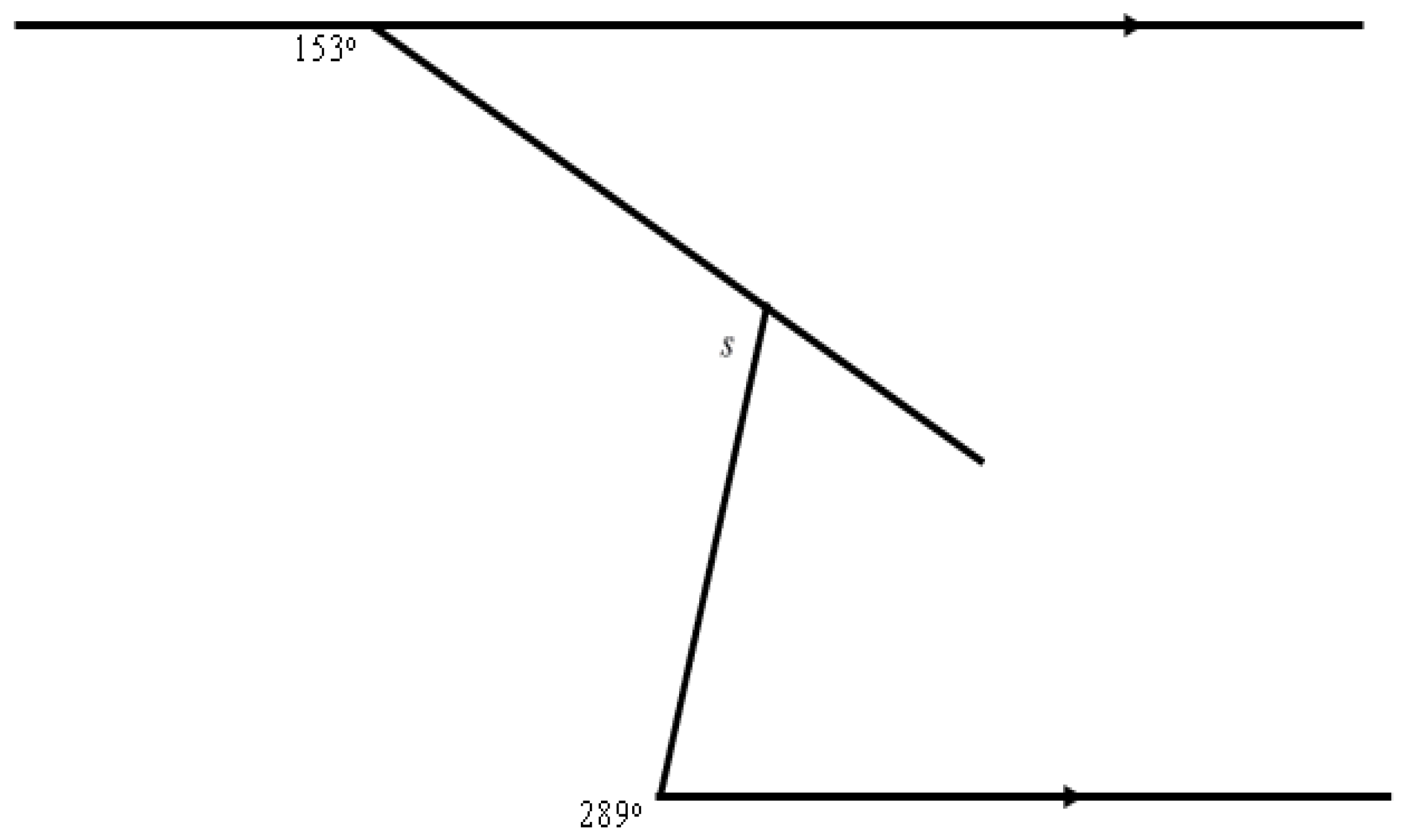
Appendix C. Sample of Type A Problem Used in Experiment 2
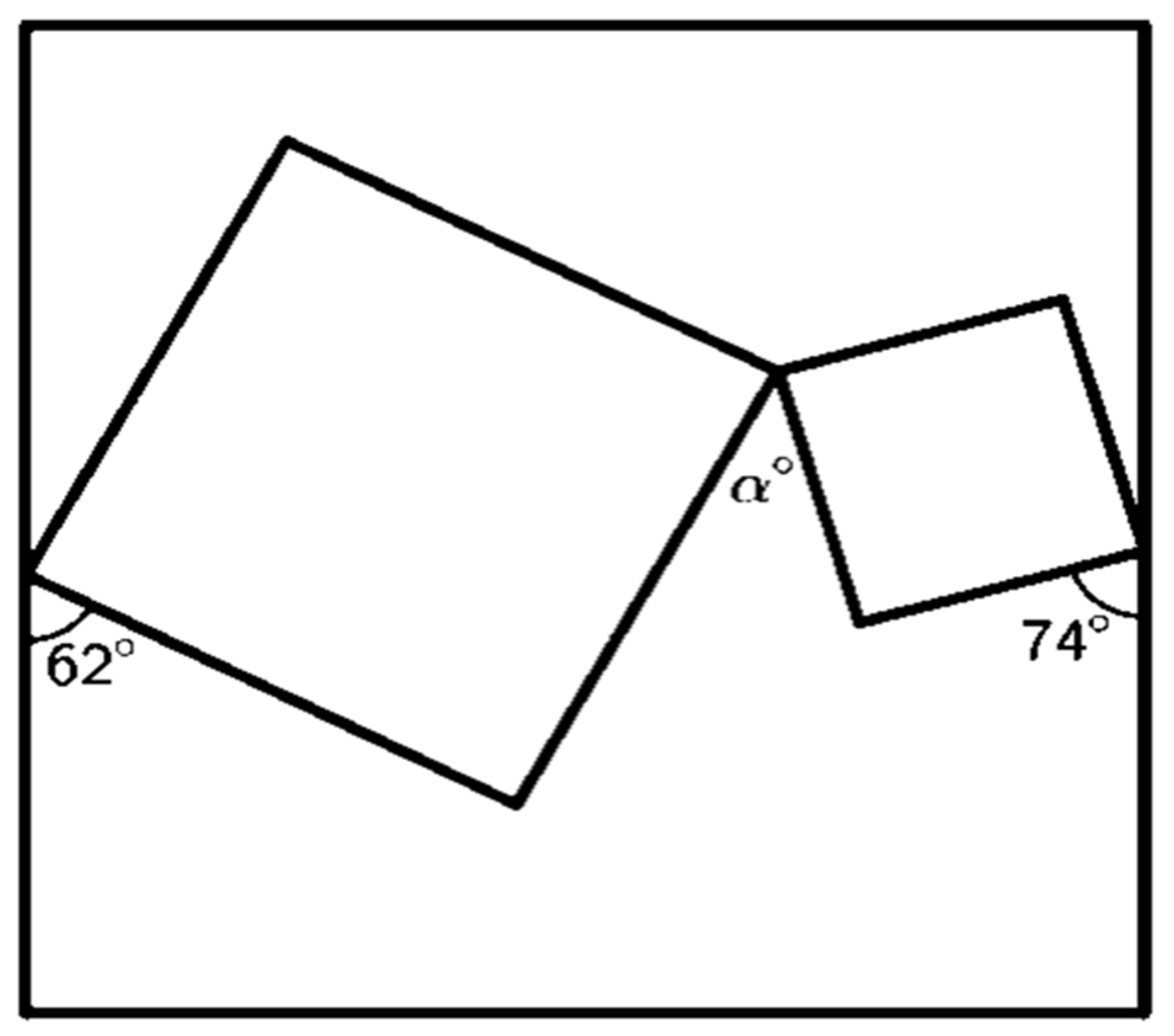
Appendix D. Sample of Type B Problem Used in Experiment 2
References
- Hartwig, M.K.; Rohrer, D.; Dedrick, R.F. Scheduling math practice: Students’ underappreciation of spacing and interleaving. J. Exp. Psychol. Appl. 2022, 28, 100–113. [Google Scholar] [CrossRef] [PubMed]
- Rohrer, D. Interleaving helps students distinguish among similar concepts. Educ. Psychol. Rev. 2012, 24, 355–367. [Google Scholar] [CrossRef]
- Sana, F.; Yan, V.X. Interleaving retrieval practice promotes science learning. Psychol. Sci. 2022, 33, 782–788. [Google Scholar] [CrossRef]
- Brunmair, M.; Richter, T. Similarity matters: A meta-analysis of interleaved learning and its moderators. Psychol. Bull. 2019, 145, 1029–1052. [Google Scholar] [CrossRef]
- Likourezos, V.; Kalyuga, S.; Sweller, J. The variability effect: When instructional variability is advantageous. Educ. Psychol. Rev. 2019, 31, 479–497. [Google Scholar] [CrossRef]
- Sweller, J.; Sweller, S. Natural information processing systems. Evol. Psychol. 2006, 4, 434–458. [Google Scholar] [CrossRef]
- Sweller, J.; van Merriënboer, J.; Paas, F. Cognitive architecture and instructional design: 20 years later. Educ. Psychol. Rev. 2019, 31, 261–292. [Google Scholar] [CrossRef]
- Geary, D.C. An evolutionarily informed education science. Educ. Psychol. 2008, 43, 179–195. [Google Scholar] [CrossRef]
- Geary, D.C. Evolutionary educational psychology. In APA Educational Psychology Handbook, Vol 1: Theories, Constructs, and Critical Issues; Harris, K.R., Graham, S., Urdan, T., McCormick, C.B., Sinatra, G.M., Sweller, J., Eds.; American Psychological Association: Worcester, MA, USA, 2012; pp. 597–621. [Google Scholar] [CrossRef]
- Geary, D.C.; Berch, D.B. Evolution and children’s cognitive and academic development. In Evolutionary Perspectives on Child Development and Education; Geary, D.C., Berch, D.B., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 217–249. [Google Scholar] [CrossRef]
- Cowan, N. The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behav. Brain Sci. 2001, 24, 87–185. [Google Scholar] [CrossRef]
- Miller, G.A. The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychol. Rev. 1956, 63, 81–97. [Google Scholar] [CrossRef]
- Peterson, L.R.; Peterson, M.J. Short-term retention of individual verbal items. J. Exp. Psychol. 1959, 58, 193–198. [Google Scholar] [CrossRef] [PubMed]
- Simon, H.A.; Gilmartin, K. A simulation of memory for chess positions. Cogn. Psychol. 1973, 5, 29–46. [Google Scholar] [CrossRef]
- Ericsson, K.A.; Kintsch, W. Long-term working memory. Psychol. Rev. 1995, 102, 211–245. [Google Scholar] [CrossRef] [PubMed]
- Chen, O.; Paas, F.; Sweller, J. A cognitive load theory approach to defining and measuring task complexity through element interactivity. Educ. Psychol. Rev. 2023, 35, 63. [Google Scholar] [CrossRef]
- Sweller, J. Element interactivity and intrinsic, extraneous, and germane cognitive load. Educ. Psychol. Rev. 2010, 22, 123–138. [Google Scholar] [CrossRef]
- Kalyuga, S. Cognitive load theory: How many types of load does it really need? Educ. Psychol. Rev. 2011, 23, 1–19. [Google Scholar] [CrossRef]
- Klepsch, M.; Seufert, T. Making an effort versus experiencing load. Front. Educ. 2021, 6, 645284. [Google Scholar] [CrossRef]
- Krieglstein, F.; Beege, M.; Rey, G.D.; Sanchez-Stockhammer, C.; Schneider, S. Development and validation of a theory-based questionnaire to measure different types of cognitive load. Educ. Psychol. Rev. 2023, 35, 9. [Google Scholar] [CrossRef]
- Paas, F.; van Merriënboer JJ, G. Cognitive-load theory: Methods to manage working memory load in the learning of complex tasks. Curr. Dir. Psychol. Sci. 2020, 29, 394–398. [Google Scholar] [CrossRef]
- Skinner, B.F. The rate of establishment of a discrimination. J. Gen. Psychol. 1933, 9, 302–350. [Google Scholar] [CrossRef]
- Carvalho, P.F.; Goldstone, R.L. The benefits of interleaved and blocked study: Different tasks benefit from different schedules of study. Psychon. Bull. Rev. 2015, 22, 281–288. [Google Scholar] [CrossRef] [PubMed]
- Kang SH, K.; Pashler, H. Learning painting styles: Spacing is advantageous when it promotes discriminative contrast. Appl. Cogn. Psychol. 2012, 26, 97–103. [Google Scholar] [CrossRef]
- Kornell, N.; Bjork, R.A. Learning concepts and categories: Is spacing the “enemy of induction”? Psychol. Sci. 2008, 19, 585–592. [Google Scholar] [CrossRef]
- Taylor, K.; Rohrer, D. The effects of interleaved practice. Appl. Cogn. Psychol. 2010, 24, 837–848. [Google Scholar] [CrossRef]
- Wahlheim, C.N.; Dunlosky, J.; Jacoby, L.L. Spacing enhances the learning of natural concepts: An investigation of mechanisms, metacognition, and aging. Mem. Cogn. 2011, 39, 750–763. [Google Scholar] [CrossRef] [PubMed]
- Chen, O.; Castro-Alonso, J.C.; Paas, F.; Sweller, J. Extending cognitive load theory to incorporate working memory resource depletion: Evidence from the spacing effect. Educ. Psychol. Rev. 2018, 30, 483–501. [Google Scholar] [CrossRef]
- Chen, O.; Paas, F.; Sweller, J. Spacing and interleaving effects require distinct theoretical bases: A systematic review testing the cognitive load and discriminative-contrast hypotheses. Educ. Psychol. Rev. 2021, 33, 1499–1522. [Google Scholar] [CrossRef]
- Paas, F.; van Merriënboer JJ, G. Variability of worked examples and transfer of geometrical problem-solving skills: A cognitive-load approach. J. Educ. Psychol. 1994, 86, 122–133. [Google Scholar] [CrossRef]
- Pan, S.C.; Tajran, J.; Lovelett, J.; Osuna, J.; Rickard, T.C. Does interleaved practice enhance foreign language learning? The effects of training schedule on Spanish verb conjugation skills. J. Educ. Psychol. 2019, 111, 1172–1188. [Google Scholar] [CrossRef]
- Birnbaum, M.S.; Kornell, N.; Bjork, E.L.; Bjork, R.A. Why interleaving enhances inductive learning: The roles of discrimination and retrieval. Mem. Cogn. 2013, 41, 392–402. [Google Scholar] [CrossRef]
- Daneman, M.; Carpenter, P.A. Individual differences in working memory and reading. J. Verbal Learn. Verbal Behav. 1980, 19, 450–466. [Google Scholar] [CrossRef]
- Chen, O.; Paas, F.; Sweller, J. Reply to Sana et al.’s (2022) Commentary on rest-from-deliberate-learning as a mechanism for the spacing effect. Educ. Psychol. Rev. 2022, 34, 1851–1858. [Google Scholar] [CrossRef]
- Leppink, J.; Paas, F.; van der Vleuten CP, M.; van Gog, T.; van Merriënboer JJ, G. Development of an instrument for measuring different types of cognitive load. Behav. Res. Methods 2013, 45, 1058–1072. [Google Scholar] [CrossRef] [PubMed]
- Klepsch, M.; Schmitz, F.; Seufert, T. Development and validation of two instruments measuring intrinsic, extraneous, and germane cognitive load. Front. Psychol. 2017, 8, 1997. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).