Learning and Motivation When Using Multiple-Try in a Digital Game for Primary Students in Chile

Abstract

The number of attempts to provide students is a key instructional characteristic in computer-based learning (CBL). However, it has not been covered extensively, and there is a need to delve deeper into the factors affecting multiple-try performance and allowing its successful use, including the learner’s involved emotional processes. This study examines the effects of multiple-try on a drill-and-practice mathematical game devoted to primary school students. A total of 73 students from four courses from two schools participated in the experiment. They were randomly assigned to a 3-attempt multiple-try (MTF) and a single-try knowledge of correct response (KCR) conditions. The study covered impacts on learning performance, together with motivation, effort, pressure, and the value of students regarding the learning activity based on the self-determination theory (SDT) perspective and its cognitive evaluation sub-theory (CET). The study’s main findings were that (a) the MTF condition outperformed KCR in terms of students’ learning gains; (b) MTF presented higher levels of perceived competence and autonomy, which, according to SDT, fosters motivation and learning; (c) a cost was yielded in students’ perceived pressure under MTF; and (d) perceived effort and value was similarly high for both conditions despite learning differences. This study complements the existing literature on multiple-try, providing insights into what conditions are beneficial for multiple-try use.

1. Introduction

Computer-based learning (CBL) has been raised over the years as an exciting complement to traditional education [1,2,3].

The success of digital educational training depends on various factors associated with the activity, such as instructional strategies and task complexity. Still, other factors are associated with the student, such as prior knowledge, metacognitive knowledge, and motivation [4]. Within the instructional characteristics, we find the number of attempts offered to the student to answer each question. Many studies have assumed a single try per item, although others have considered the possibility of providing multiple try to answer the same question [4].

Multiple-try has its roots in the pioneering work of Pressey [5,6] involving a technological device for automated testing. It provided immediate feedback on the result (KR), allowing the learner to try again until the right response was reached, thus coining the expression of answer-until-correct (AUC).

Nowadays, there is a greater possibility of using multiple-try mechanics in learning management systems like Moodle and H5P, and online educational games like Educaplay.

Despite its early beginnings and possibilities of actual use, diverse authors agree that the existing literature considering multiple-try is scarce [7,8], especially under a digital formative context. Currently, using multiple attempts by practitioners and researchers is not easy because the conditions for its effective use are not clear.

This problem may be partially explained because this field traditionally considers multiple-try as a feedback-type feature [9]. Hence, many past meta-analyses considered multiple attempts as part of elaborated feedback or knowledge of results [10,11,12,13]. More recently, [4] and [14] have classified multiple-try as a separate feedback type. But still, few reviews exist tackling multiple-try and its effects, besides being outdated [15,16,17]. Therefore, it becomes difficult to measure the impacts of multiple attempts across conditions and provide straightforward conclusions about multiple-try effects.

Another issue is that past research regarding multiple attempts has mainly focused on students’ learning effects rather than searching for the conditions under which the use of multiple attempts is effective, together with the circumstances that allow such positive effects to be long-lasting and efficient [18].

While some studies report substantial learning gains when using multiple-try [8,16,19], others describe no significant differences when contrasting it to single-try solutions [20,21,22].

In particular, the review by Van der Kleij et al. [17] considered 18 studies, where six involved try-again solutions. None of them obtained significant positive effects for multiple-try when considering diverse timing, feedback level, and task complexity conditions except for Murphy’s work [23]. His delayed elaborated feedback with hints + try again performed significantly higher with students working in pairs but not when working individually.

The existing literature on instructional feedback points out that diverse situational variables influence student learning and performance in educational contexts [4,18]. Research exists analyzing the moderating role of task complexity [13,14] and previous knowledge [24] in student learning outcomes. However, in what contexts multiple-try can be administered effectively and successfully is still open.

We argue that an adequate control on these two variables, task complexity, and prior knowledge, should promote positive effects on multiple-try use. There are some insights on MTF being preferable for high-order learning outcomes, especially in text-comprehension scenarios [13,16] and vocabulary lessons [25]. However, there is no consensus on whether those findings extend to the K-12 math domain or what levels of prior knowledge are appropriate for MTF use.

Another aspect is the role that motivation and other emotional variables have in the learning process, either under traditional education [26,27] or in computer-based learning (CBL) settings [28]. More focus is needed “on the processes induced by feedback interventions and not on the general question of whether FIs improve performance” [18]. Hence, further attention is needed on what happens to students internally and emotionally when using multiple tries.

Therefore, the present study objective is to explore the impacts of using multiple-try feedback (MTF) and knowledge of correct response (KCR) feedback under a drill-and-practice mathematical digital game devoted to primary students. It focuses on three high-order math learning objectives: 3-digit number identification, ordering, and money counting.

Our study also uses self-determination theory (SDT) and its cognitive evaluation sub-theory (CET) [29,30] to investigate the emotional factors that are affected by feedback and, in particular, by multiple-try use. SDT is a model of human motivation that has been revealed as appropriate, as it has been used to explain students’ emotional processes in other contexts of computer-based learning [31,32]. SDT postulates that the psychological needs for competence, autonomy, and relatedness must be fulfilled to foster motivation.

Competence refers to the need “for being effective in one’s interactions with the environment” [29], and autonomy involves experiencing “freedom in initiating one’s behavior” [33]. Autonomy and competence are necessary for a good learning environment with greater motivation and creativity [29].

The CET theory complements the above, holding that high levels of pressure negatively affect motivation, while adequate levels of effort are indicators of a suitable level of challenge and the absence of controlling situations that may negatively affect motivation [30]. Finally, there is the level of the learner’s perceived value, indicating the degree to which the behavior is internalized and integrated into his or her personal values and the degree of self-determination [33].

No previous works have been found that use SDT or CET as a theoretical model to explain the effects of multiple-try. Therefore, the main contributions to the literature in this field are as follows:

• To develop a successful experience using multiple tries under school mathematics and its effects on students’ learning, motivation, and related emotional processes.
• To explain why multiple attempts generate certain learning effects from the SDT + CET perspective, mainly by developing a greater sense of competence and autonomy in students while fostering suitable levels of effort and pressure.
• Progress in devealing under what conditions, primarily related to prior knowledge and in a K-12 math setting, the use of multiple-try generates positive results regarding learning, motivation, and self-determination.

1.1. Feedback and Attempts

Feedback can be understood as providing the student with some information about correcting an answer [34] and “Can help students identify and correct errors and misconceptions, develop more effective and efficient problem-solving strategies, and improve their self-regulation.” [13]. From a more general perspective, feedback corresponds to any piece of information given by an agent regarding a person’s performance or understanding, being such an agent as a teacher, peer, book, parent, and experience [35,36].

The scope of feedback in the present study focuses on the task level and its learning (formative) instead of summary feedback [14] or feedback focusing on task motivation or the self [18].

Most research has focused on the type of information provided in the feedback. Starting from merely informing students if the answer was correct or not [37], named knowledge of result (KR), and followed by specifying the right answer without further explanations, called knowledge of correct response (KCR) [38,39]. Finishing with more elaborate feedback (EF) presented as explanations, strategies, hints, informative tutoring [13], or interactive feedback [35] to arrive at the correct answer.

Besides these types based on message content, we can also consider the number of attempts the student will have upon an incorrect response before moving to the next exercise or question. It can also be seen as the number of learner expositions to the same item before moving on.

Regarding implementations of multiple attempts, in between single-try and the early answer-until-correct, multiple-try feedback (MTF) exists. In its simplest form, MTF gives students a limited number of attempts and KR between tries [4]. The literature presents different ways of implementing multiple-try by varying the number of trials given (2, 3, 5, and until-correct) and the feedback information provided between tries (KR, KCR, or EF). These diverse implementations make it hard to provide any generalizable conclusions about which multiple-try implementations are preferable under what situations.

A close relationship exists between the number of attempts and the feedback type delivered to the student. Both are part of the instructional characteristics to be delivered within the learning process, among other aspects such as the item type. In this sense, multiple-try was often considered a type of elaborated feedback because it performs a directive function in informing about the answer’s correctness and giving another opportunity upon error. However, aside from such a directive function, MTF provides an interactive mechanism [4] with multiple immediate exposures [40] to the same question. These features are not present in any other type of elaborated feedback, so it is better to consider the number of attempts in a separate dimension.

MTF has both immediate and delayed feedback features. It is similar to single-try (STF) regarding immediacy concerning feedback timing. However, it is also similar to delayed feedback (DF) regarding the number of direct exposures to the problem or question. In this sense, Clariana, Wagner, and Murphy [40] observed that MTF provided learning effects midway between single-try and delayed feedback.

Different theories have been used to explain the effects of multiple-try. Many authors agree that for feedback to affect learning, it has to be processed mindfully [13,15]. According to Kulhavy and Stock [41], when feedback is available to learners before they begin their memory search and construction of their answers, presearch availability exists. This causes mindless behavior by stopping the learner’s response–evaluation–adjustment process. On the contrary, confirming or disconfirming feedback (KR) should stimulate mindfulness.

Hence, learning settings that promote a student’s active generation of answers from his or her understanding and internal mental schemas, as it happens with MTF, should have a stronger influence than activities only showing information to the learner [40], as in KR or KCR.

However, the literature reports mixed results on multiple-try effects, so certain conditions are required for these principles to work. In addition, these theories do not consider the learner’s internal and emotional processes that could explain the obtained effects.

1.2. Motivation and Self-Determination

Emotions are vital for motivation, performance, and self-regulation [42,43]. Feedback influences both motivation and performance [18] as well as students’ regulation processes [36]. However, most research has focused on student performance, but few have covered feedback effects on motivation [4] and self-regulation [17].

The self-determination theory (SDT) [29,30] corresponds to a psychological model that can help describe the motivation construct and the emotional processes during learning. It has been effectively used in other learning situations, such as the use of gamification techniques [44,45], educational games [31,32], collaborative computer activities [46], and students’ conditions to achieve good grades [47].

SDT has its roots in the notion that curiosity and the desire to explore, discover, and comprehend the world are innate in human nature [29]. It understands the concept of intrinsic motivation as the natural inclination toward curiosity and interest in an activity. Three primary conditions or psychological needs facilitate its development: the individual feels competent, has autonomy, and feels related.

Competence refers to the result of exploration, learning, adaptation, and related processes in the interaction with the environment. In wider terms, competence can be understood as “the capacity for effective interactions with the environment that ensure the organism’s maintenance” [29]. For this reason, in 1959, White named it an effectance motivation [48]. He also states that the sensation resulting from competent actions is the reward per se. Hence, an innate satisfaction exists in training and broadening one’s abilities. This need for being effective in the environment’s interactions (competence) supplies the power for learning [48], and higher levels of self-efficacy have positive effects on student performance [49]. Diverse motivation theories propose that self-perceptions of competence and task processing are critical aspects of students’ motivation [4,50]. For that reason, situations generating feelings of higher competence will increase intrinsic motivation [29].

Autonomy involves experiencing free choice [33], where the locus of causality is perceived as internal rather than external. Although feelings of competence are essential for intrinsic motivation, they are not enough, and a sense of autonomy is required [29]. The third condition is relatedness, “the need to feel belongingness and connectedness with others” [33]. This dimension will not be considered in the present work, as the digital learning activity for the current research is individual, and the relatedness construct has proven to be important for internalization processes not covered in this study.

Cognitive evaluation theory (CET), the first of the six SDT sub-theories, focuses on the factors or conditions that stimulate or discourage intrinsic motivation. In this sense, when leveraging greater competence during an activity, diverse instructional elements such as feedback, rewards, or communications can increase intrinsic motivation toward that activity [51]. On the contrary, when the learner cannot be effective and attain a minimum level of competence, amotivation arises. CET states that learners need to perceive that their actions are self-determined and not imposed by external conditions [51]. For example, various studies have revealed that real rewards, pressured deadlines and evaluations, threatening communication and directives, and forced goals reduce intrinsic motivation because they all make the learner perceive the locus of causality as external [51]. From the SDT-CET perspective, learners’ intrinsic motivation is negatively affected whenever rewards are experienced as controlling, such as grades and other classroom rewards [29]. According to the authors, different characteristics of the learning environment (teacher’s attitude, existence of limits, grading system, etc.) can be perceived as controlling, negatively impacting the learner’s autonomy. However, they argue that it is possible to minimize these effects to the extent that they are presented in a more propositive and informative manner instead of being presented in a coercive, imposed, and controlling way.

Therefore, controlling conditions make learners feel pressure, which inhibits intrinsic motivation. For example, Ryan, Mims, and Koestner [52] found that controlling conditions positively correlated to expressed tension. Gottfried [53] reported that intrinsic motivation was negatively correlated to anxiety. The relationship between learners’ perceived competence and achievement is mediated by anxiety [27,54], and a negative correlation exists between anxiety and mathematics performance [55].

According to CET [30], an educational environment that fosters intrinsic motivation should provide a wide range of stimulating instructional elements, with adequate challenges, and an environment that promotes learner initiative and autonomy without controlling conditions and pressure. In this way, learning and achievement are more expected to arise.

Activities that generate optimal challenge and effort promote intrinsic motivation and self-determination [29]. When the student is in an activity that presents adequate levels of challenge, he or she will make a certain level of effort that will lead to feelings of competence. Therefore, optimal challenges will tend to generate higher levels of effort and competence. The level of effort can also be affected by controlling conditions [29]. A study by Ryan in 1982 [56] revealed that when subjects were controlled with evaluative feedback, they spent less effort, and their performance tended to be worse than those who received informational feedback. It seems that they accomplished what was requested but with less effort and in a poorer manner to react against the control.

When a learner has a high value for an activity, it shows that the regulation of that specific behavior (of performing such activity) has a high degree of internalization [30], meaning that it has been entirely accepted as one’s own, so one behaves, feels, and thinks that way and not because of rewards, punishments, or beliefs about society’s expected values [29].

Finally, there is scarce empirical research examining the SDT-CET dimensions considering feedback types and attempts (including MTF) under CBL settings. There is a need to advance the literature on how multiple-try inclusion affects students’ engagement, motivation, and related environmental conditions that foster motivation.

1.3. The Present Study

The present study aimed to explore the impacts of using MTF and KCR feedback under a CBL environment for primary students—three high-order math learning objectives were selected for exercising. The effects to explore were performance (learning improvements), motivation (in terms of interest, competence, and autonomy), and supportive learning conditions measured as effort, pressure (absence of), and value regarding the activity following the SDT-CET theory.

Research Hypothesis

Based on the literature review, positive effects should result from the use of multiple-try. In addition, these effects are expected to be greater than KCR for the selected learning objectives. Hence, we state the following:

Hypothesis 1.

Students learning in the educational game is higher in the Multiple-Try condition than in the KCR condition.

Better performance of MTF should be expected concerning promoting a greater perception of competence in students. Being a more active mechanism makes students relate their mental models with the wrong answer and adjust based on their knowledge. However, it is also possible that MTF generates frustration, trial-and-error behavior (mindlessness), and a lower feeling of competence if the learner’s errors increase and cannot be corrected. It will largely depend on the existence of an adequate level of challenge. By providing external information and being more passive, KCR could lower students’ sense of efficiency.

Regarding autonomy, higher levels could be expected in MTF than in KCR due to its interactive feature on the same question, which allows the solution or error-finding to be investigated more autonomously than if the correct answer was given immediately after the first response, as is the case of KCR. In this way, we anticipate the following:

Hypothesis 2.

Multiple-try generates in students higher motivation levels in terms of interest (H2a), competence (H2b), and autonomy (H2c) than KCR.

The concept of pressure is associated with conditions perceived as controlling by students that affect the degree of perceived autonomy. In this sense, KCR could be perceived as more controlling when indicating the correct answer after one attempt. And MTF could exert more pressure by not giving clear guidelines on continuing or correcting the question after an error. In this case, it would be pressure, not due to external control but rather feelings of loss of control or orientation. Thinking about the controller-informative dimension, MTF, to some degree, forces the person to try again after an error. That could be considered a controlling factor by some students.

Regarding the perceived effort, we believe that it will depend mainly on factors more related to an optimal level of challenge. In this sense, an adequate level of prior knowledge (medium-high) together with a high level of task complexity should generate an appropriate level of effort (medium-high) that causes a higher perception of competence. Then, in the particular case of MTF, its process of re-attempting the question without further information (KR) may require more effort when contrasted against KCR.

Regarding the perceived value, given that MTF generates a more active and profound reflection on errors and provides the opportunity to correct them, it is expected that this mechanism generates a greater sense of value than in the case of KCR. Such is especially true considering that the latter provides the correct answer externally to the individual, and as the activities are complex, concepts need to be understood rather than merely memorized. Based on the above, we consider the following:

Hypothesis 3.

Using multiple tries yields higher levels of students’ perception of effort (H3a), pressure (H3b), and value (H3c) than KCR.

Finally, there is no literature covering the effects of MTF and KCR from an emotional perspective, so it is not feasible to anticipate possible magnitudes for such differences if they occur.

2. Materials and Methods

2.1. Matematicast Learning Game

“MatematicaST” is a web platform with three mini-games to exercise diverse topics in mathematics. After logging in, students can select the game to be played each time. The question is displayed in the upper area and can be listened to when pressing the play button nearby (see Figure 1). The player has three lives per game, displayed as red hearts at the left. Each correct answer awards ten points, and the total points are on the upper-right. Also, on the right side is the list with the highest scores.

The “Numbers Identification” mini-game determines a number’s symbolic representation according to its place value (Learning Objective 1). The information is provided in units, tens, and hundreds, while four alternatives are presented as boxes. Options are built up by combining the digits shown in the question.

The “Numbers Ordering” mini-game asks to order four numbers from smallest to largest within 10 to 1000 (Learning Objective 2). Numbers appear in disorder at the top inside a box (See Figure 2a). Boxes can be dragged to an empty place and confirm the answer by pressing the “ESTE ES EL ORDEN” button (this is the order). This button will only evaluate the order of the boxes once all the empty places have a number.

The “Money Counting” mini-game (Figure 2b) requires counting coins of a different amount (Learning Objective 3). Coins are limited to one instance maximum for 5, 50, and 500 coins, while up to four instances for 1, 10, and 100. Figure 2b shows an exercise displaying one 50-coin, three 10-coins, and four 1-coins (coins are in Chilean peso—CLP).

MTF and KCR Game Versions

The KCR version for all three mini-games provides immediate feedback to the student after each answer. When answering correctly, the game presented to the user a motivating message chosen randomly between samples as “Buena respuesta!” (Good answer!) or “Sigue así!” (keep it up!), which remained on the screen for 1.1 s before going to the next exercise (See Figure 3a). If the selected answer was incorrect, the game presented a message indicating so, including the correct answer and the text “keep trying” (Figure 3b). The game displays a continue button to the next exercise after 2.2 s of showing the message. In addition, the game provided sounds to complement the correct/incorrect feedback.

The MTF version gives the student three attempts per exercise, with KR among attempts. They are displayed graphically below the life section by using three yellow dices. The student obtains total points and has no life discounted when answering correctly within those three attempts. The game reduces one life when losing and goes to the next exercise without providing the correct answer. It also displays the selected incorrect alternatives in red boxes as a memory aid for previously chosen options. Figure 4 shows the Money counting mini-game with one attempt left after answering incorrectly 384 and 438 while having one 500-, three 100-, four 10-, and three 1-coins. No additional hints, clues, or strategies were provided.

2.2. Participants and Design

Students from four courses (3° and 4° grade) from two schools in the region of Valparaíso, Chile, participated in the intervention. Initially, we anticipated the participation of 84 students. However, some students were absent on the activity days, did not have their parents’ signed consent, or did not complete all the instruments (post-test or post-IMI), so the final number of participants was 73.

The study considered a randomized pre-test–post-test design, with feedback type as a factor with two conditions: a multiple-try with KR and a single-try with KCR. Students were randomly assigned to a condition with 36 (13 male and 23 female) for Multiple-try and 37 (14 male and 23 female) for the KCR condition.

2.3. Instruments

2.3.1. Math Tests

Pre- and post-tests were built up following the three learning objectives considered from the Chilean mathematics program and its guide textbook. Teachers from the two schools were involved in test construction and validated their instructions, exercises, and conditions. Pre-test and post-test considered six exercises for each learning objective (number identification, number order, and money counting), with a total of 9 points.

2.3.2. IMI Questionnaire

The Intrinsic Motivation Inventory (IMI) [57] is a measurement instrument for evaluating the SDT-CET constructs in subjects participating in a given activity. The tool has been applied in various studies concerning intrinsic motivation [29,30]. The present research considered six constructs: interest, perceived competence, pressure, effort, perceived choice (autonomy), and perceived value. Perception tests had 16 sentences with a 5-point Likert scale (from 1 “strongly disagree” to 5 “strongly agree”). All dimensions had three sentences each except for pressure and effort, with only two items each. We translated from English to Spanish and validated it with the schoolteachers, adjusting some vocabulary. For example, sentences using the words tense or pressure were changed to the word nervous, as students did not understand those first words.

2.4. Procedure

In the beginning, students received a motivational talk with the general purpose of the experiment. Some instructions were also explained regarding the procedure and instruments (tests) to be applied (10 min). Then, students completed the pre-IMI test and the learning pre-test, both in a paper-and-pencil format for 15 min. After that, they logged into the web platform and played the games in the school computer laboratory for 55 min. After playing, they answered the post-IMI test to measure their self-report of motivation, pressure, effort, and utility. Students completed the learning post-test not only after finishing the game activity but also after a 15-minute recess period to allow them to rest.

The learning objectives involved in the study were already taught and evaluated several weeks before the experiment. Therefore, the games’ playing corresponded to an exercise of previous knowledge, voluntary and without any external motivators regarding school points or grades.

3. Results

Data was processed with SPSS software version 29 for the statistical analyses and graphs generation. Partial eta squared (η²) was used as a measure of effect size.

3.1. MTF and KCR Learnings

First,

Table 1. Pre- and post-test descriptive statistics per condition.

	Condition	Mean	Std. Deviation	N
Pre-test	MTF	7.17	2.21	36
	KCR	7.41	1.83	37
	Total	7.29	2.01	73
Post-test	MTF	8.53	0.93	36
	KCR	7.80	1.76	37
	Total	8.16	1.45	73

shows the descriptive statistics for pre- and post-test scores per condition. A 2-way repeated measures ANOVA was conducted to evaluate the effects of test type (pre-test/post-test) and condition (MTF/KCR). The simple main effect of test type was significant with F(1, 71) = 27.064, p < 0.001, η² = 0.276, meaning that overall, post-tests scored higher than pre-tests. The two-way interaction between test type and condition was also significant with F(1, 71) = 8.096, p = 0.006, η² = 0.102. Now, when analyzing the effect of condition on each test type, significant differences were obtained for the post-test F(1, 71) = 4.800, p = 0.032, η² = 0.06 but not for the pre-test F(1, 71) = 0.254, p = 0.62, η² = 0.004, meaning that pre-test scores were not significantly different among MTF and KCR conditions, but their post-test scores were significantly different, as Figure 5a shows.

Then, the effect of each test type was analyzed at each condition, showing that significant differences existed for MTF (F(1, 71) = 31.944, p < 0.001, η² = 0.31) but not for KCR (F(1, 71) = 2.816, p = 0.098, η² = 0.038), meaning that significant learning occurred in the MTF condition but not in the KCR one.

In addition, a 1-way ANCOVA was carried out to determine the effect of condition (MTF vs. KCR) on learning gains (post-test–pre-test scores) after controlling for the pre-test score of students, showing a significant difference between the conditions with F(1, 70) = 12.481, p < 0.001, η² = 0.15. This means that MTF outperforms KCR in learning gains after adjustment for pre-test, as Figure 5b depicts.

3.2. MTF and Motivation

Table 2. IMI perception constructs’ descriptive statistics per condition.

Construct	Condition	Pre-Test		Post-Test		Delta		N
		Mean	SD	Mean	SD	Mean	SD
Interest	MTF	4.57	0.58	4.86	0.35	0.29	0.66	36
	KCR	4.58	0.60	4.78	0.44	0.20	0.65	37
	Total	4.58	0.59	4.82	0.40	0.24	0.66	73
Competence	MTF	4.00	0.80	4.62	0.56	0.60	0.67	36
	KCR	4.20	0.76	4.46	0.76	0.27	0.69	37
	Total	4.10	0.78	4.54	0.67	0.43	0.70	73
Effort	MTF	4.57	0.80	4.24	0.87	−0.33	1.10	36
	KCR	4.43	0.86	4.07	0.91	−0.36	1.15	37
	Total	4.50	0.83	4.15	0.88	−0.35	1.12	73
No-Pressure	MTF	3.88	0.94	3.89	1.06	0.01	1.19	36
	KCR	3.88	0.90	4.43	0.78	0.55	0.70	37
	Total	3.88	0.91	4.16	0.96	0.29	1.00	73
Choice	MTF	3.40	1.11	4.21	0.74	0.80	1.08	36
	KCR	3.58	1.07	3.88	0.80	0.29	1.02	37
	Total	3.49	1.09	4.04	0.79	0.54	1.07	73
Value	MTF	4.55	0.58	4.76	0.42	0.22	0.56	36
	KCR	4.39	0.85	4.62	0.75	0.23	0.74	37
	Total	4.47	0.73	4.69	0.61	0.22	0.65	73

shows the descriptive statistics of IMI dimensions per condition. Pre- and post-IMI test values are considered measures for the dimensions of interest, perceived competence, perceived choice, effort, no pressure (reverse of pressure), and value. A Cronbach alpha of 0.74 for pre-IMI and 0.68 for post-IMI perception tests were obtained.

First, the post-IMI values were analyzed. A 2-way repeated measures ANOVA was carried out to evaluate the effects of conditions (MTF/KCR) and IMI dimensions on test values, resulting in a significant interaction (F(5, 67) = 2.422, p = 0.044, η² = 0.153). Pairwise comparisons under Bonferroni adjustment for multiple comparisons contrasted both experimental conditions for each IMI construct. Significant differences for No-Pressure (F(1, 71) = 6.210, p = 0.015, η² = 0.080) and Choice (F(1, 71) = 3.442, p = 0.068, η² = 0.046) were obtained. This means that MTF presented higher levels of pressure and perceived choice than KCR on post-test values (see Figure 6).

Secondly, were analyzed the differences between post-IMI and pre-IMI values. A 2-way repeated measures ANOVA was carried out to evaluate the effects of conditions (MTF/KCR) and the six IMI dimensions on the pre-post IMI delta values. Results show a significant interaction with F(5, 67) = 3.394, p = 0.009, η² = 0.202). Pairwise comparisons under Bonferroni correction contrasted both experimental conditions for each IMI-CET construct. Now, significant differences were found for the dimensions of Competence (F(1, 71) = 4.445, p = 0.039, η² = 0.059), No-Pressure (F(1, 71) = 5.673, p = 0.020, η² = 0.074), and Choice (F(1, 71) = 4.363, p = 0.040, η² = 0.058). Therefore, MTF presented significantly higher increases in perceived competence and perceived autonomy (choice) than KCR but also presented a significantly lower gain on the No-Pressure dimension (see Figure 7).

4. Discussion

4.1. H1: Students Learning in the Educational Game Is Higher in the Multiple-Try Condition Than in the KCR Condition

First, results show that both conditions provided learning gains; however, only in the MTF group were they significant. It is especially relevant considering that the intervention involved a lapse of 55 min of playing with the games only. According to what was expected in H1, and despite the limited intervention time, MTF rose with higher learning improvements. In addition, such differences were mostly due to post-test differences as pre-test scores per condition did not differ significantly.

Our MTF implementation reported similar effects as Van der Kleij et al. [13] meta-analysis for elaborated feedback, higher than Clariana and Koul [16] reporting an ES 0.11 for MTF under high-order LOs, but lower improvements than Attali’s [8] MTC and MTH implementations.

Initially, one might think that KCR feedback should have given better results in learning gains than MTF. The first provides more direct and immediate information about the correct answer than the other alternative. On the contrary, results suggest that the MTF exploratory process allowed a more hands-on role for the student to think of the correct answer, as MTF did not directly provide it but only knew that the chosen alternative was incorrect (KR), thus allowing for a more active approach that led to deeper learning. This result is consistent with the idea that multiple-try “provides an opportunity for elaboration and reorganization of information that may be beneficial for learning” [8].

However, for this information reorganization to occur, you need learners to have a minimum level of prior knowledge (PK) to work internally. In this sense, the students in our experiment presented average pre-test levels of around 80%. These prior knowledge ranges are consistent with the literature reviewed that had good results using MTF [8,58]. In any case, additional studies are needed to more precisely establish the PK levels required for efficient use of the different types of feedback and, in particular, of multiple-try.

A relevant issue is the MTF implementation. To the best of our knowledge, this study is the first considering under a CBL context an MTF with three attempts + KR and no KCR nor EF at the end. No hints nor correct responses were provided even after the third try. This fact, together with the appropriate prior knowledge level, could have discouraged students from following a trial-and-error strategy [58] or an automatic and mindless behavior [17] as presearch availability [41] was avoided.

Furthermore, the idea of not presenting the correct answer after a first attempt is not new. In the context of intelligent tutoring systems (ITS), the informative tutoring feedback model (ITF) [4,59] involves providing different components without explicitly indicating the correct answer. It seeks to guide students to identify and correct errors by applying more effective learning strategies.

Therefore, more studies on the effects of using multiple tries with a diverse number of attempts, prior knowledge levels, and interaction mechanics are required. Also, to consider how the effects of multiple-try are affected when using item types different from multiple choice.

4.2. H2: Multiple-Try Generates in Students Higher Motivation Levels in Terms of Interest (H2a), Competence (H2b), and Autonomy (H2c) Than KCR

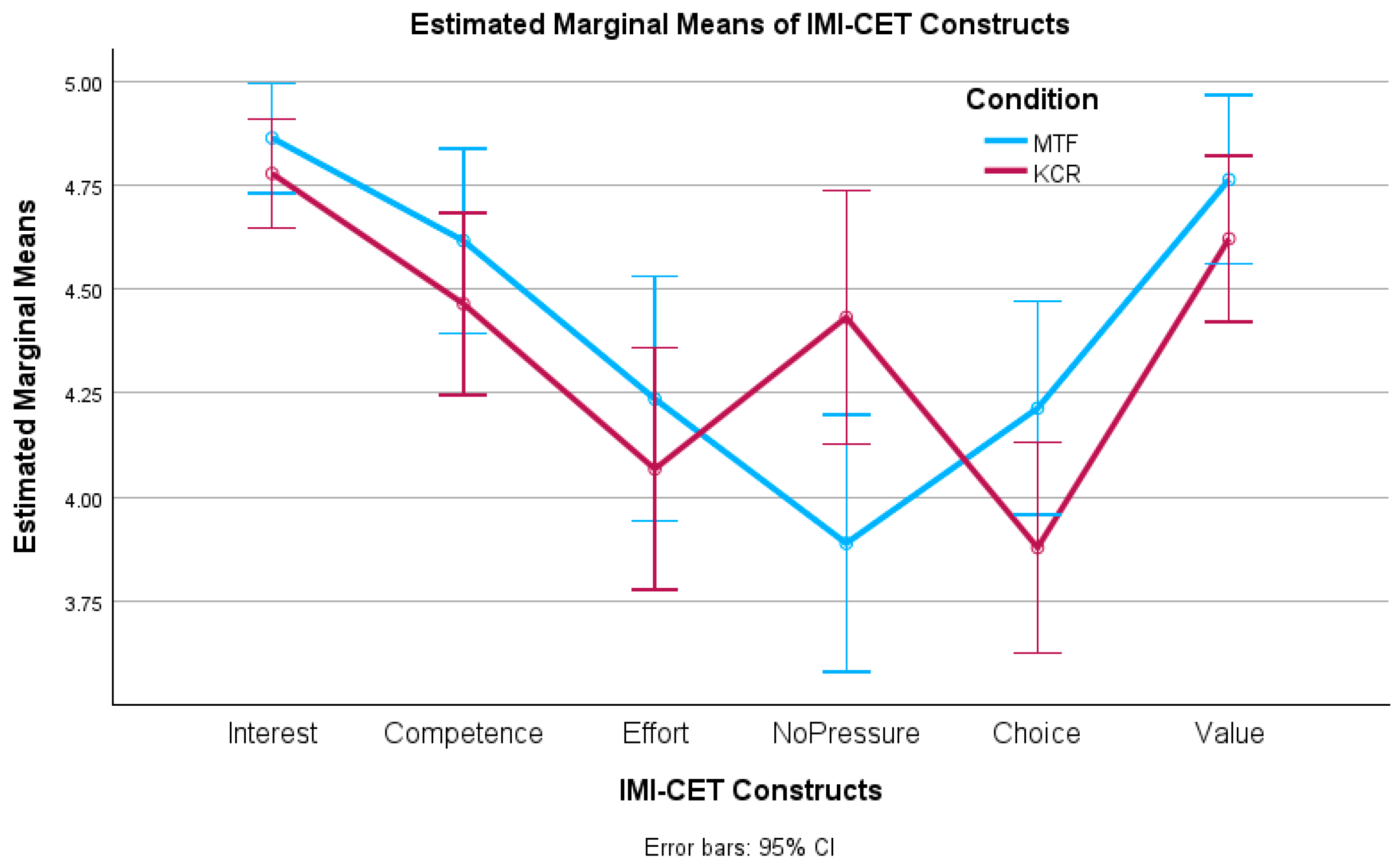
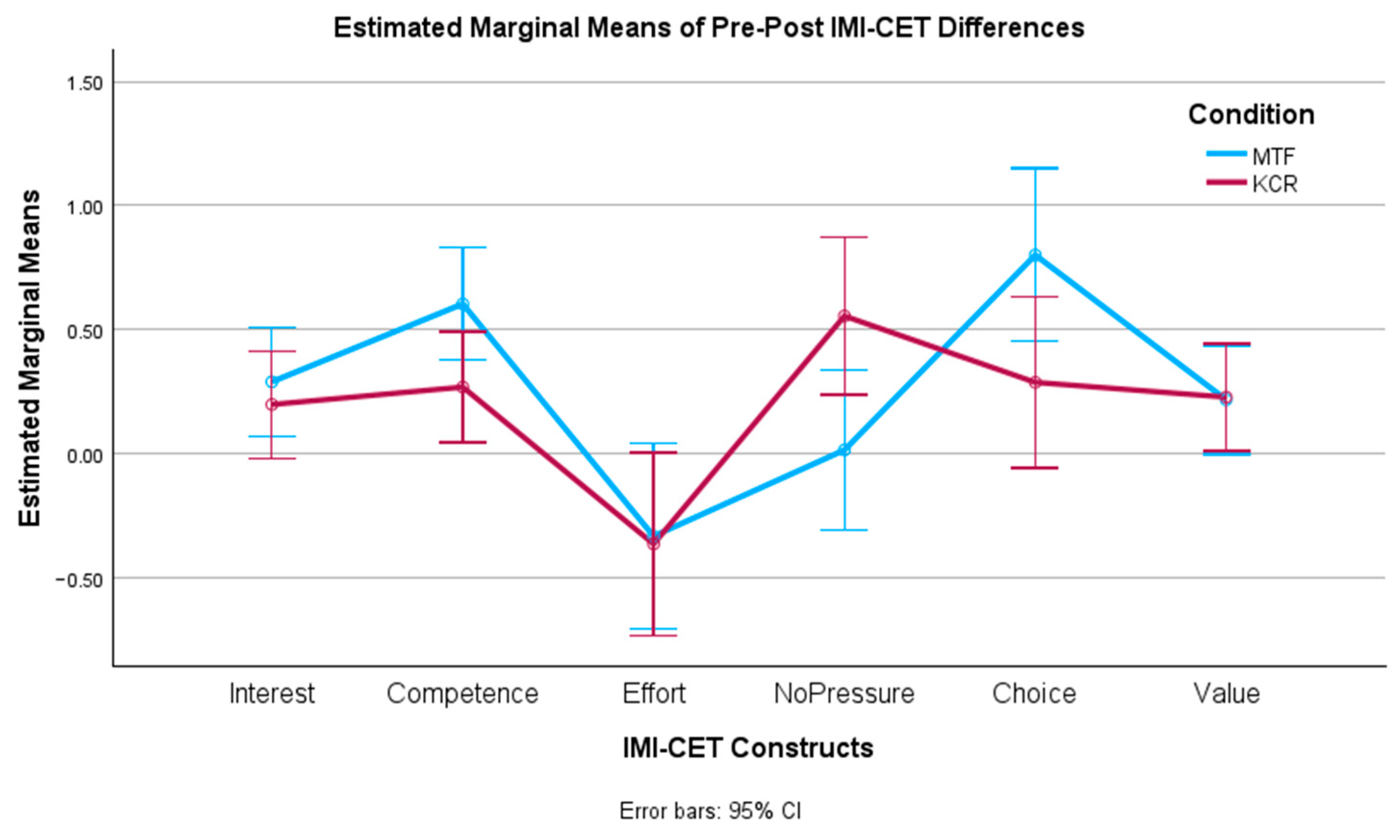
When analyzing H2 and students’ perception of motivation, our study revealed very high levels of interest and competence during the activity. Also, positive delta values on pre- and post-test IMI measures for both conditions were obtained on interest, perceived competence, and choice (autonomy), meaning that the activity enhanced those feelings. In addition, the differences (increases) in competence and choice were significantly higher for MTF when contrasted against KCR. Therefore, MTF outperformed KCR on two out of three of the most relevant dimensions supporting motivation, which are competence (H2b) and autonomy (H2c), but not in the dimension of interest (H2a).

Results are consistent with previous research demonstrating that motivational variables were stronger predictors of achievement in mathematics [60]. The implemented gamification mechanisms (points, lives, and leaderboard) providing progression and competition dynamics seemed to have helped maintain high engagement and motivation levels, minimizing emotional differences across conditions.

The implemented MTF only provided KR (and not KCR at the end as in other studies); it seemed to have a cost in interest when contrasted to providing explicit content feedback, such as in KCR, in terms of not presenting a significant difference. Despite the above, MTF presented higher competence perception effects than KCR. Firstly, the activity seems to have generated an optimal sense of challenge [29] that helped the development of larger feelings of competence for both conditions (MTF and KCR).

Multiple-try also presented higher effects than KCR on perceptions of autonomy. It seems to confirm that the MTF characteristic of iterating over the same question when answering wrongly without giving the correct answer activates internal processes that are beneficial for learning as it does not interrupt the response–evaluation–adjustment process with external information [41].

From a certain point of view, MTF could act as relatively negative feedback, thus affecting competence since it is activated upon error and, in our case, provides only the response correctness (KR). However, the degree of involvement in the task, sense of challenge, and commitment were high enough to overcome the negative feelings and transform the wrong answer into a motivating situation since the additional attempts of the MTF allowed the student to discover on their own (sense of autonomy) the mistakes and correct them immediately and for a next time (sense of competence).

External rewards negatively affect the sense of autonomy. Within our experiment, no real incentives were given, such as marks or points that could be used academically. Therefore, a fictional environment was created in which to explore and learn without direct consequences in the real world, which promoted freedom and autonomy during the game.

An interesting result was that despite presenting higher levels of competence and autonomy, MTF did not generate higher levels of interest than KCR. A possible explanation could be that the intervention duration may have affected or, more likely, the fact that the interactive mechanism provided by MTF + KR did not make the game more interesting than a single attempt + KCR. The instructional material and the rest of the game were the same: history, context, exercises, and gamification elements such as points and ranking. So, the control condition selection was very relevant because presumably, if MTF were compared against traditional classes or an online pdf with exercises, the results would have been different and in favor of the game without being possible to distinguish the effects of the MTF from those of the game itself.

4.3. H3: Using Multiple Tries Yields Higher Levels of Students’ Perception of Effort (H3a), Pressure (H3b), and Value (H3c) Than KCR

As mentioned above, there must be a suitable environment and students’ attitudes toward learning. It was evaluated using the dimensions of effort, pressure, and value. H3 anticipated higher levels of students’ perception of effort (H3a), pressure (H3b), and value (H3c) for the MTF condition. In general, results revealed high levels for the value dimension while medium levels for effort and no pressure across conditions. MTF presented a significantly higher post-test score than KCR in the no-pressure dimension. Regarding pre- and post-tests, IMI differences only effort presented a decrease (negative delta) for both conditions, meaning that students expected to make more effort than they needed. KCR presented a significantly higher difference in the no-pressure construct but no significant differences in effort and value when contrasted against MTF. Therefore, H3 was partially accepted, confirming H3b but rejecting H3a and H3c. We expected higher levels of effort and pressure for students under MTF because they had a long and indirect way of arriving at the correct answers (via the attempts in case of a previous failure) when contrasted to KCR. Also, our implemented MTF did not provide much guidance or information, supposing more difficulty and pressure to find the correct answer. In this sense, it would be interesting to study what would happen to the levels of effort and pressure when combining MTF with KCR or hints such as those implemented in Atali [8]. The hints consist of partial pieces of information that helped solve the math problem but without providing the result explicitly, as happens in KCR.

External regulations generate less interest, value, and effort toward the activity, delegating the success responsibility to others [51]. During the present experience, the levels of effort, no-pressure, and value constructs were adequately high for both conditions, giving general indications of learners’ high commitment, self-determination, and mindfulness.

Pressure is also a measure of external coercion or controlling conditions (and lack of autonomy), generating less intrinsic motivation. Therefore, the high levels of no-pressure (H3b) throughout the experiment support the idea of little existence of coercive or controlling elements, thus promoting intrinsic motivation.

The effort levels (H3a) were relatively medium-high throughout the entire experience, reinforcing the impression that there was an adequate level of challenge: the exercises’ difficulty level versus students’ ability level, especially in terms of prior knowledge. Likewise, the high level of effort reported indicates the small existence of factors perceived as controlling. There was no evidence of less effort as a reaction to external control by students in contrast to what was reported by Ryan in his study [56].

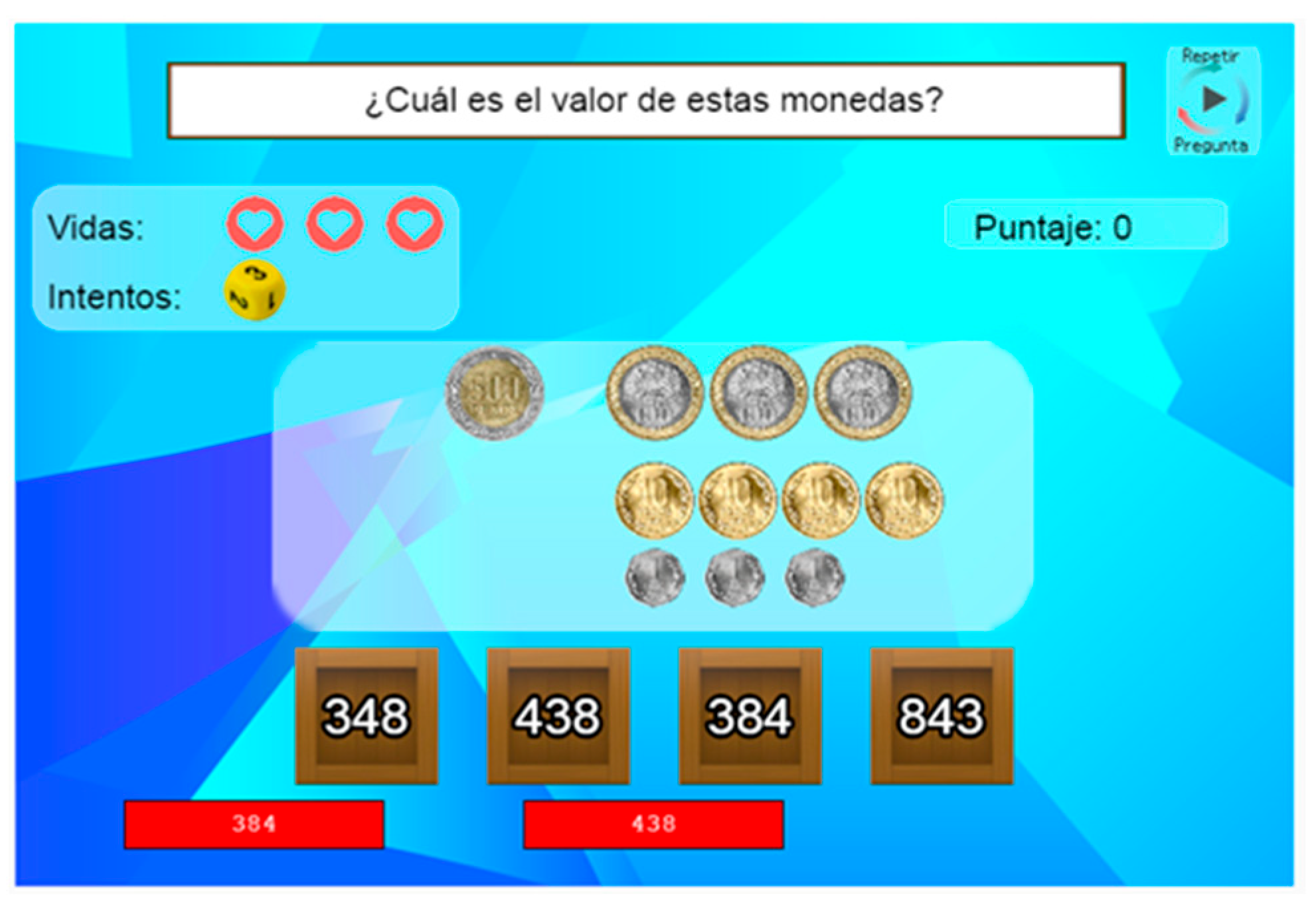
Another factor that could affect the level of effort is the mechanism for generating item alternatives. The existence of easily discarded or obvious options was avoided. For this, part of the digits of the correct answer or permutations of said digits were used to construct the remaining alternatives to deliver options close to the correct one but which were not. For example, when faced with the number representing seven units and three hundred, the alternatives were 307, 37, 370, and 703. In this way, students’ sense of challenge and effort was reinforced, but without taking them out of their comfort zone, which would have generated frustration and pressure. Therefore, these challenging alternatives promoted more active attention and a greater sense of competence after solving them correctly.

In our MTF, responses to earlier attempts for the same exercise were provided to students as a visual aid to help them remember previous answers. It could have reduced the effort required to arrive at the correct answer via the attempts while diminishing the frustration or pressure when going trial after trial. We think that the exercises’ complexity level and item type could have moderated such differences, as choosing from four alternatives is different from a constructed response (or fill-in-the-blank question) in a similar way as reported by Attali and Van der Kleij [61].

Regarding the value dimension (H3c), the intervention presented high levels before and after the experience, indicating that the students found it helpful and implying high levels of self-determination and self-regulation for the whole group. On value per condition, no significant differences were observed. Thus, H3c was rejected. Students perceived the multiple-try as valuable as KCR despite significant differences in learning. To a certain extent, MTF students did not acknowledge their progress and improvement the same way as KCR students did. Maybe more time was needed to internalize the improvements and lessons learned. Then, it would be interesting to see the effects of incorporating delayed summary feedback to improve self-reflection processes.

5. Conclusions

The present study explored the impacts of using multiple-try feedback (MTF) and Knowledge of Correct Response Feedback (KCR) in a computer-based learning (CBL) environment for third and fourth-primary students, focusing on 3-digit number identification, ordering, and money counting as part of the math national curriculum. The research aimed to assess performance, motivation, and supportive learning conditions based on self-determination theory (SDT) and its cognitive evaluation sub-theory (CET).

Results indicate that MTF led to significant learning gains, outperforming KCR in the high-order math learning objectives involved. The iterative process of MTF allowed an active approach that positively influenced students’ confidence in their abilities, leading to deeper learning. MTF encouraged student engagement, allowing them to explore, learn from mistakes, and adjust their understanding independently, fostering a sense of autonomy. Also, MTF presented higher levels of pressure due to the iterative process and the absence of immediate correct answers. However, the pressure was not excessive and seemed to not negatively impact intrinsic motivation.

The experimental setup effectively managed task complexity and students’ prior knowledge. This control facilitated positive outcomes related to the use of multiple-try feedback. The study supports previous research indicating that multiple-try feedback is beneficial for high-order learning outcomes in text-comprehension contexts. Moreover, this study extends these findings to the K-12 math domain.

The MatematicaST educational platform proved to be an effective medium for math learning. The games maintained high levels of student interest and competence during the activity, together with relatively high effort levels, indicating a suitable level of challenge during the learning activities. Overall, the training activity was perceived as valuable by students, indicating that they found the learning activities meaningful and helpful. All of the above resulted in high learning gains in both conditions.

The study utilized various instruments, including pre- and post-tests for learning objectives and the Intrinsic Motivation Inventory (IMI) questionnaire. The inclusion of both pre- and post-IMI questionnaires allowed for a comprehensive analysis of students’ self-perceptions regarding the activity. This approach provided valuable insights into students’ perspectives, which would not have been achievable with the post-IMI questionnaire alone.

The study involved primary students from third and fourth grade from two schools in the region of Valparaíso. They showed high motivation during the activity, which resulted in active and meaningful participation. However, the short nature of the training could have limited the time for students to internalize their progress and learning. Therefore, future research should consider longer interventions and assess diverse outcomes, especially regarding students’ perceived usefulness.

Other future research directions should include exploring the combination of MTF with other feedback types, such as KCR, hints, or delayed summary feedback, as they could enhance students’ self-reflection processes and further improve learning outcomes. Also, to research deeper on the levels of prior knowledge and learning objective complexity suitable for effective utilization of multiple-try feedback. There is a lack of gender-specific studies examining differences in the use of multiple-try feedback and its outcomes. Further research in this area is necessary.