1. Introduction
1.1. Guidance for Inquiry-Based Learning
Several meta-analyses from controlled research studies have confirmed the benefits of inquiry-based learning (IBL) versus other instructional practices [
1,
2]. In this study, we define IBL as an activity or educational strategy where learners
“…study complex phenomena by identifying variables that are potentially instrumental to their mechanisms, changing the levels of those variables, observing the resulting changes in outcomes, and drawing conclusions” [
3] (pp. 898–899). The contemporary view of IBL emphasizes that support or guidance for IBL is necessary [
4], i.e., “
assistance offered before and/or during the inquiry learning process that aims to simplify, provide a view on, elicit, supplant, or prescribe the scientific reasoning skills involved” [
5] (p. 687). Indeed, research has shown that IBL is beneficial to learning only when proper guidance is offered [
1,
6,
7,
8]. Because IBL promotes the active role of the learners and their responsibility for their learning [
9], guidance should be provided only in situations where it is necessary, i.e., guidance should be adapted to the needs of the learners [
10,
11]. Indeed, providing guidance when it is not necessary challenges the self-directed nature of IBL [
11] and could result in the expertise reversal effect [
12,
13], where learners’ performance suffers from the unnecessary guidance.
1.2. Scientific Reasoning, Learner Age, and Engagement
The “need of the learner” to which the guidance for IBL should be adapted is central when designing proper guidance. One option to conceptualize “the need of the learner” is to concentrate on the learners’ previous knowledge, the role of which in learners’ performance is well documented [
14]. Factors other than previous knowledge need to also be taken into account when designing proper guidance for IBL. School systems are usually not based around grouping together learners with similar levels of knowledge but are instead based around grouping learners of the same age together. Planning decisions regarding guidance for IBL are often made at a class level, i.e., learners’ age plays a large role when teachers make decisions about guidance for IBL. Research regarding learner age and its effect on their need for guidance is still lacking; cross-sectional research with different-aged learners working a similarly guided task has been called for [
5]. It is evident that scientific reasoning skills develop during childhood [
15,
16]. Learners start to develop the metacognitive skills needed to direct their learning at the age of 8 to 10 years old [
17]. The ability to generate hypotheses seems to develop between the ages of 6 to 8 years old [
18,
19]. The ability to carry out properly designed investigations into the relationship between two variables can develop by the age of 10 years old [
20], but with appropriate support, 7-year-olds can design proper experiments [
21] and 5- to 6-year-olds can apply control-of-variables strategy [
22].
An often-used framework for describing the scientific reasoning process and the possible individual differences in it is the Scientific Discovery as Dual Search (SDDS) model [
23]. The SDDS model outlines three iterative processes that IBL consists of: hypothesizing, experimenting, and evaluating evidence, and two problem spaces: the hypothesis space and the experiment space. The hypothesis space contains all the hypotheses learners can generate during the IBL process and the experiment space contains all the possible experiments they can conduct with the equipment at hand. Some learners do have the prior knowledge and skills that allow them to start the learning process from the hypothesis space, i.e., to start by generating hypotheses that are then tested in the experiment space and finally evaluated against collected evidence. The result of the evaluation can be that the hypothesis is accepted, rejected, or possibly considered further. Other learners miss the necessary prior knowledge and skills to come up with a suitable hypothesis, i.e., they must start their work from the experiment space via a series of exploratory experiments that enable them to come up with a testable hypothesis. This hypothesis can then be tested in the experimentation space and finally evaluated against the collected evidence.
As learners develop their scientific reasoning skills during childhood and adolescence, at the same time the level of school-related engagement decreases as learners grow older [
24]. Engagement has been proposed as a construct consisting of five different components: (1) behavioral engagement (i.e., effort, persistence, and concentration), (2) emotional engagement (i.e., interest and happiness), (3) cognitive engagement (i.e., preference for hard work and effort toward learning), (4) agentic engagement (i.e., offering input or suggestions and expressing a preference), and (5) disaffection (i.e., passivity, lack of initiation, and lack of effort) [
25,
26,
27]. Engagement in general has a positive influence on achievement [
25]. Engagement has also been shown to be responsive to variations within different learning contexts and situations [
25,
28,
29]. This responsiveness enables one to study how different forms of guidance affect individual learners’ specific situations, which has been called for [
13].
1.3. Model Progressions
In this study, we focus on guidance provided through process constraints that restrict the comprehensiveness of the learning task by reducing the number of options students need to consider [
5,
11]. In particular, the focus is on a subset of process constraints [
30,
31] called model progressions [
32]. The basic idea of model progressions is to structure the task content according to a simple-to-complex sequence, and they are often used to promote successive refinements to the students’ mental models [
32]. Models can vary on three dimensions: their perspective (i.e., different phenomena are represented through different models), their degree of elaboration (i.e., the number of variables and relations), and their order (i.e., whether qualitative or quantitative reasoning is needed) [
32]. Examples of research into the use of model progressions includes a study [
33] where adults worked with a simulation about oscillation. Learners that used the simulation with model progression achieved better results than those who used a simulation without it. Another study [
34] compared inquiry-based learning environments containing two different types of model progression with a learning environment without it with high school students learning about electrical circuits. The results showed the superiority of the learning environment with model order progression over the one with model elaboration progression. Both types of model progressions were superior to the learning environment without it. Another study [
35] found that both allowing students to move between problem-solving phases and restricting moving from one phase to another without the necessary knowledge promoted learning compared to model progression without these features. There is also a call for more research on how model progressions can be used in different ways to guide inquiry-based learning [
35].
1.4. Introducing Implicit and Explicit Model Progressions
This exploratory study introduces a novel classification of model progressions by dividing them into explicit model progressions (EMP) and implicit model progressions (IMP). Both of these follow the basic principle [
32] that states that model progressions should promote refinements to the learners’ mental models. The division of explicit and implicit model progressions stems from SDDS [
23]. EMP entails that the model progression is aimed at all three processes central to SDDS: hypothesizing, experimenting, and evaluating evidence. This means that there are certain limitations for these processes, which are then removed as the task progresses, e.g., starting out with a more limited number of variables to choose from. EMP can be seen as the most common type of model progression configuration where all the scientific discovery processes are supported. On the other hand, IMP entails that the processes of hypothesizing and experimenting are mostly unguided, and the model progression is aimed only at the process of evaluating evidence. The hypothesis and experimentation spaces are mostly open, i.e., learners’ actions there are not limited. Only after the learners start to evaluate the results of their experiment does the guidance through model progression take place via, e.g., tasks that require the learners to apply the results of their experimentation and start to require more in-depth results as learning progresses. Even though the guidance is aimed directly only at the evidence evaluation, it still indirectly affects the other two processes as well. If the result of the evaluation is that the hypothesis is rejected or considered further, the learners then return to the processes of hypothesis generation and experimentation, but with the information gained from the process of evidence evaluation.
Our proposed classification of IMP and EMP adds to the discussion on how model progression could be further developed [
34,
35] and different possibilities to move or not move between problem-solving phases in a learning environment guided by model progressions [
35]. As a novel configuration, IMP could offer a new approach to model progression by focusing guidance on just the process of evaluating information.
1.5. Research Questions
This current exploratory study adds to the literature in studying the effects of two different configurations of simulation-based learning environment on learning outcomes and situation-specific engagement. The data comes from 8-, 10- and 12-year-old Finland students (n = 96). The setting of the study is collaborative, with students working in groups to solve tasks presented to them via the learning environment. Previous research has shown that the type of model progression affects the learning outcomes [
34], but because the two types of model progression are introduced in this article and the situation-specific engagement has not been studied in the context of simulation-based learning environments, exact hypotheses cannot be made.
Our research questions are:
How do the implicit or explicit model progression learning environments compare in improving primary school-aged learners’ knowledge of balance?
What is the effect of learner age and the type of model progression in the learning environment on the normalized change of the learners’ knowledge of balance?
What is the effect of learner age and the type of model progression in the learning environment on the learners’ situation-specific engagement?
2. Materials and Methods
2.1. Participants
The data were collected from second, fourth, and sixth graders in six primary classes (2 classes per grade) from the same primary school in a medium-sized city in Finland. These grades were chosen to ensure a wide range of age groups in Finnish primary schools. The study had a 3 × 2 quasi-experimental design. One class from each grade was randomly chosen to use the EMP environment and the other class used the IMP environment. All the classes came from the same school, which ensured similar socioeconomic status. The number of learners and their genders per class and the means and standard deviations of their ages are presented in
Table 1.
Even though the learning environments contained all the tasks and information needed to navigate the environments, assistance was provided due to the young age of the learners and the possibility that the transparency (i.e., ease of perceiving the content of the learning environment [
33,
36]) would be too low. Thus, one pre-service primary teacher (PST) was assigned to work with each group of learners. The PSTs took part in the study as a part of a course about the pedagogy of science and mathematics. The PSTs were instructed to provide help for the learners only when needed and to provide this help only based on the learners’ ideas.
2.2. The Learning Environments
The data for this study come from a large research project aimed at studying guidance for IBL in both mathematics and science learning. As part of this study, two differently guided configurations of a simulation-based learning environment—one with EMP and another with IMP—for learning about balance were developed. The context chosen for the simulations was experimenting with a seesaw where two birds (one per side) with different weights sit at different distances from the fulcrum. GeoGebra [
37] was used to design and program the balance simulations embedded in the learning environments. The Graasp authoring platform [
38] was used to construct the learning environments that the simulations were a part of. The large age scale of the learners was considered by using small values (from 1 to 12) for all possible variables.
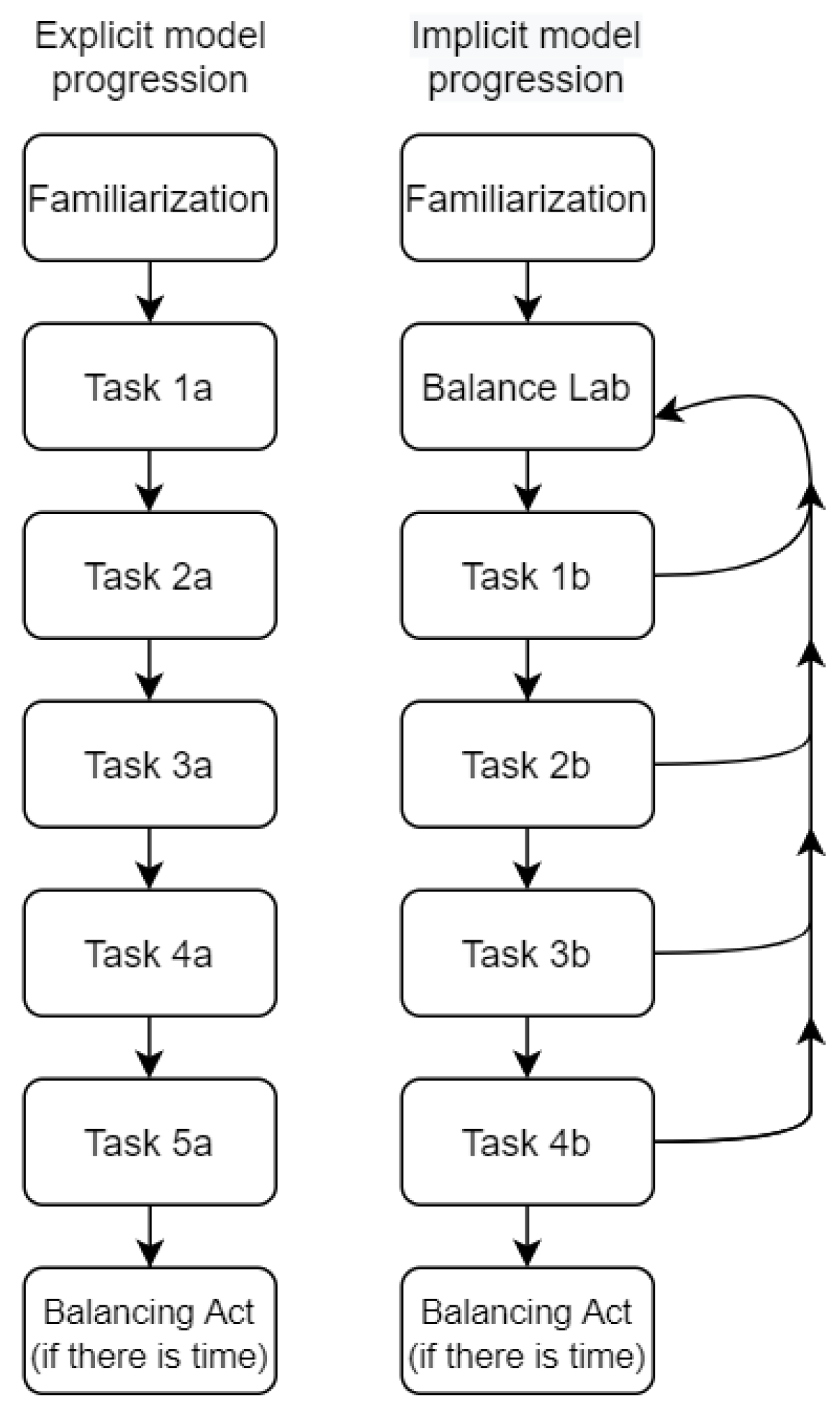
Figure 1 showcases the progression in both the EMP and IMP learning environment.
The EMP learning environment consisted of seven different tabs (presented in detail in
Appendix A). The first was a familiarization tab where the learners learned how to manipulate the simulation (e.g., how to move the birds). The middle five tabs contained different tasks where the processes of hypothesis generation, experimentation, and evaluation took place. Each task was designed to be more complex than the previous one. By “complex,” we mean first a progression from a qualitative model to a quantitative one and then a necessary progression towards the general moment rule. This was done by limiting the number of possible correct answers in the later tasks and by making the ratios between weights of the birds more complex, i.e., model progression through the dimension of model order [
32]. After this, the progression happened through an increase in the number of variables the learners were able to change or by an increase in the number of choices learners had for each variable, i.e., model progression through the degree of elaboration [
32]. At the end of each task, the learners were prompted to formulate a rule about how to balance the seesaw. This rule was then shown to the learners at the start of the next task. The aim of this prompt was to make it explicit for the students that they were expected to start each task by evaluating their previous rule.
As an example, Task 1a asked the learners to find all the configurations that balance the seesaw using two birds. The birds were either large-sized or small-sized and could sit “near the fulcrum” or “far from the fulcrum,” i.e., task 1a called for a qualitative model. Task 2a then prompted the learners to find all the configurations that balance the seesaw again using two birds. Now the bird on the right was fixed 1 m away from the fulcrum, and its weight could be chosen from two options: 6 kilos or 8 kilos. For the bird on the left, the learners were able to choose its position between 1 and 8 m from the fulcrum and its weight from the options of 1, 2, 3, or 4 kilos. Task 2a thus required the learners to produce a quantitative model by changing three variables with limited options per variable. The seventh and final tab contained the Game section of the “Balancing Act” PhET simulation [
39]. The purpose of the last tab was to provide the learners with extra activities if they completed all the other tasks in the time allotted.
The IMP learning environment consisted also of seven tabs, with the first being the same familiarization tab in the model progression environment. The second tab was the “Balance Lab” (
Figure 2), and the simulation embedded in this tab allowed the learners to change the weight of the two birds between 1 and 6 kilos and move them between 1 and 8 m from the fulcrum. The Balance Lab was open for hypothesis generation and experimentation, with all four variables being available with only very few limitations to weight and distance. The learners were asked to use the Balance Lab simulation to formulate a rule or multiple rules for balancing the seesaw by experimenting with multiple different combinations of weights and distances from the fulcrum. The next four tabs contained tasks aimed at evaluating the rule(s) the learners had formulated in the Balance Lab. In each task, the learners were presented with the rule(s) they had formulated in the Balance Lab tab and had one chance to balance the beam by moving the birds or changing their weight. Each of the four tasks differed in the weight of the birds, their distances from the fulcrum, and which variables the learners had to change. As the tasks progressed, they became more complex, i.e., there was a progression towards the general moment rule via changing the degree of elaboration [
32]. This was done by limiting the number of possible correct answers in the later tasks and by making the ratios between weights of the birds more complex. The tasks are presented in
Appendix A. If the learners were able to complete the task and balance the balance beam, they were instructed via text to move on to the next task. If they did not succeed on their first try, they were instructed via text to return to the Balance Lab tab and develop their rule for balancing the beam further. The learners were unable to use the same values for weight and distance in the Balance Lab as they had to use in the tasks. This return to the Balance Lab meant that the leaners had to re-engage with the hypothesis generation and experimentation processes. The seventh and final tab contained the same embedded Balancing Act PhET simulation as the EMP learning environment.
2.3. Data
The often-used Balance Scale Task (BST) [
40] was used to study the content knowledge of balance. The BST’s internal consistency has been reported as good with a large sample of different-aged learners (Cronbach’s α = 0.80), and it is usable even with learners as young as five years old [
40] and has also been used with similar age groups as in this study [
41]. The BST consists of five blocks of five items each. The items in each block are each of a different problem type. The purpose of the different problem types is to tap into the different levels of learners’ knowledge of balance. Each item showed a balance beam with four pegs on each side of the fulcrum. In each item a maximum of six weights was placed on one of the pegs on each side. The learners answered by choosing whether the beam would tip to the right, to the left, or stay balanced. Each item was simply scored as correct or incorrect. The number of correct responses (from 0 to 25) to the BST was used to quantify the learners’ content knowledge of balance.
To measure learner situation-specific engagement, the InSitu instrument [
42] was used. This instrument is aimed at measuring learners’ self-rated, situation-specific engagement in learning. The InSitu instrument has previously been used to measure the situation-specific engagement in a similar context in Finland [
28,
29] with good reliability scores. Previous studies indicate a five-factor structure (Behavioral Engagement, Emotional Engagement, Competence Experiences, Disaffection, and Help Seeking). In this study, only the Emotional Engagement, Competence Experiences, and Disaffection factors were analyzed, as the other two focus more on the role of the teacher. The Emotional Engagement factor deals with the learners’ intrinsic motivation and positive emotions [
26], the Competence Experiences factor deals with the learners’ expectations for success in their tasks [
43], and the Disaffection factor deals with the learners’ negative emotions, boredom, and lack of concentration [
26]. The InSitu instrument originally contains 18 5-point Likert scale items. For this study, the item “To what extent were you prepared for the lesson?” was removed, as it was incompatible with the study setting where the learners were unable to prepare for the data collection. Thus, the administered instrument contained 17 items. All the items and factors are listed in
Appendix B.
2.4. Procedure
The BST was administrated for the learners by a researcher as a pre-test some days before the lesson where they used the learning environments. During this lesson, the learners were randomly divided into groups of 3 to 5 (usually 3) learners per computer where the learning environments were run. They worked in these groups for the full duration of the lesson (approx. 40 min). The InSitu instrument was administered to the learners right after they finished the lesson. The BST was administrated to the learners by a researcher as a post-test approximately three days after the lesson.
2.5. Data Analysis
Only data from learners who completed both the BST (pre- and post-test) and InSitu instrument were used for the analysis. The normalized change [
44] score was calculated for each participant as a learning outcome metric that considers the differences in pre-test performance. The normalized change score is mathematically equivalent to the commonly used normalized gain score [
45] when the post-test performance is better than the pre-test performance. Its advantage over the normalized gain score is that it is better suited for situations where the post-test performance is worse than the pre-test performance, as the normalized gain score is asymmetric between −∞ and 1 and the normalized change score is symmetric between −1 and 1.
A paired-samples
t-test was used to analyze the possible statistical significance of the difference between the mean scores in the pre- and post-tests for the BST for each class (i.e., combination of grade and learning environment). Hedges’ g with 95% confidence intervals was used to measure the effect size of the statistically significant differences between the pre- and post-tests. Hedges’ g is interpreted similarly as Cohen’s d, and it is more suitable than Cohen’s d to be used with small sample sizes and when the sample sizes differ from each other [
46]. The effect of grade (i.e., learner age) and the learning environment used on the normalized change was analyzed using one-way ANOVA. Tukey’s post hoc test was used for possible pairwise comparisons, and Hedges’ g with 95% confidence intervals was used to measure the size of the possible effect. For the emotional engagement, competence experiences, and disaffection, the data violated the assumption of equal variances. In these cases, Welch’s ANOVA has more statistical power than ANOVA [
47]. Thus, Welch’s ANOVA was used to study the effect of learner age and type of learning environment on the learners’ situation-specific engagement. The Games–Howell post hoc test was used for the possible pairwise comparisons and Hedges’ g with 95% confidence intervals was used to measure the size of the possible effect.
3. Results
Table 2 presents the results from the BST pre- and post-tests per student age group and learning environment used. A paired-sample
t-test showed that the differences between the pre- and post-test scores were statistically significant for the fourth and sixth graders, but not for the second graders. In addition, using both the EMP and IMP configuration of the learning environment had a statistically significant effect on the BST scores.
Table 3 showcases the results from the BST pre- and post-tests per class. A paired-sample
t-test showed that the differences between the pre- and post-test scores were statistically significant for the fourth graders using both learning environments and for the sixth graders that used the learning environment containing IMP. The effect sizes ranged from medium to large [
48], but for the fourth graders the 95% confidence intervals signaled also the possibility of no or small effect. For the other classes, the differences between pre- and post-tests were not statistically significant.
Table 4 presents the normalized change scores for each group. There was a statistically significant difference in the normalized change between learners from different grades as determined by one-way ANOVA (F(2, 93) = 3.096,
p = 0.05). A Tukey post hoc test revealed that the normalized change was statistically significantly higher for the sixth graders (
p = 0.039) than for the second graders (0.12 ± 0.26). The effect size g was 0.649, 95% CI [0.129–1.168]. There was no statistically significant difference between the fourth graders’ normalized change and the second graders’ (
p = 0.348) or the sixth graders’ normalized change (
p = 0.454). There was also no statistically significant difference in the normalized change between learners using the EMP or IMP configurations of the learning environment (F(1, 94) = 1.754,
p = 0.189).
Table 5 showcases the results regarding the learners’ situation-specific engagement (scale 1–5) for each group. The scores for emotional engagement were over 3 for learners from all grades, implying that they enjoyed the lesson. The competence experience scores were all over 3.5 for all grades, indicating that the learners all felt that they had succeeded in the lesson. Finally, the disaffection scores were all under 2.6 for all grades, which indicates that the learners felt that they were focused on the tasks at hand and were not bored.
There were statistically significant differences in the emotional engagement and disaffection between learners from different grades determined by one-way Welch’s ANOVA (emotional engagement: F(2, 91) = 5.950, p = 0.004, disaffection: F(2, 91) = 3.374, p = 0.041). A Games–Howell post-hoc test revealed that the emotional engagement was statistically significantly higher for the second graders than for the fourth graders (p = 0.010) or the sixth graders (p = 0.011). For the difference in emotional engagement between the second and fourth graders, the effect size g was 0.735, 95% CI [0.227–1.243], and for the difference between the second and sixth graders, g was 0.794, 95% CI [0.263–1.324]. Games–Howell post-hoc tests revealed that none of the differences in disaffection between any two grades were statistically significant. There were no statistically significant differences in the competence experiences between the second graders, fourth graders, and sixth graders as determined by one-way Welch’s ANOVA (F(2, 91) = 0.41, p = 0.67).
There were no statistically significant differences in engagement between learners using the learning environment containing EMP and learners using the learning environment containing IMP as determined by one-way Welch’s ANOVA (emotional engagement: F(1, 92) = 0.033, p = 0.856, competence experiences: F(1,92) = 0.932, p = 0.337, disaffection: F(1, 92) = 0.005, p = 0.944).
4. Discussion
The results show that that both the IMP and EMP configurations of the learning environment are generally beneficial for learning about balance for primary-aged students. The effect size for the IMP configuration was large but the confidence intervals point to a possibility of a small or medium effect as well. For the EMP configuration, the effect size was medium but the 95% confidence intervals point to a possibility of a negligible effect as well. There was no statistically significant difference in the normalized change scores between the learners who used the IMP environment and those learners who used the EMP environment. Previous research suggests that evidence evaluation skill might be a necessary precursor for mastery of hypothesis generation and experimentation [
19]. Our results complement this by suggesting that supporting just the process of evidence evaluation (i.e., IMP) seems to be as effective as supporting all the processes of hypothesis generation, experimentation, and evidence evaluation [
23] for primary-aged learners.
When comparing the results for different-aged students, the results show that the second graders did not benefit from using either the IMP or EMP learning environment. With the fourth graders, both the IMP and EMP environments had a statistically significant effect on the learning outcomes. For the sixth graders, only the IMP environment had the same effect. The effect sizes ranged from medium to large, but as the confidence intervals point to a possibility of no effect for the fourth graders using the IMP environment, that result should be approached cautiously. When pooling results from both environment configurations together, the results show that the sixth graders’ normalized change scores were statistically significantly higher than those of the second graders. The effect size was medium, but the confidence intervals point also to the possibility of just a small effect.
It seems that for at least in learning balance, guidance provided by model progression in general is not specific enough for second graders. A possible explanation for this is the fact that learners’ scientific reasoning and metacognitive skills develop during childhood years [
15,
16,
17]. Second graders lack many of the reasoning skills that sixth graders already possess, and thus, more specific forms of guidance such as heuristics [
5] could be more beneficial for younger learners. This result answers the call about the need for cross-sectional research in which the same task is used with different-aged learners [
5]. Using IMP could offer a chance to provide even less specific guidance than EMP with similar learning effects. It is also possible that because using IMP keeps the hypothesis generation and experimentation processes open and unguided, it could influence how these processes are enacted. This would need to be studied using process-oriented variables, e.g., quality of hypotheses. One explanation for the advantage of the IMP over the EMP environment for the sixth graders could be that their ability to generate hypotheses and experiment was too constrained by the tasks embedded into the EMP environment, and thus, they invoked the expertise reversal effect [
12,
13]. This would also require more research.
The second graders were more emotionally engaged while using the learning environments than either the fourth graders or sixth graders. There were no statistically significant differences in situation-specific engagement between learners using learning environments containing IMP or EMP. This suggests that the type of model progression contained in a simulation-based learning environment does not have a notable effect on the learners’ situation-specific engagement. The highest emotional engagement in the youngest age group is in line with results on the decline of engagement throughout the school years [
24].
5. Conclusions
Based on the findings, IMP may offer a way to offer less specific guidance to primary-aged students than EMP and still reach similar learning outcomes and engagement. Age-related differences do exist. For the second graders, more specific forms of guidance than model progressions are needed. For the sixth graders, it is possible that the EMP learning environment constrained their learning process too much, as using it did not have an effect on students’ knowledge of balance. Overall, the sixth graders’ learning outcomes were higher than the second graders’, even when taking into account their previous knowledge. These results suggest that older learners are better able to utilize less specific forms of guidance. This would require more research with specifically designed study settings.
One limitation of this study is that the number of learners per class (age x configuration of the learning environment) was small. With more data, regression analysis could be used to study the possible interaction effect between student age and type of model progression used. Another limitation is that even though the PSTs were instructed to provide help for the learners only when needed and to provide this help only based on the learners’ ideas, their individual guiding actions might have affected the results in some groups. The instructions given to the PSTs were the same whether the group of students was working with the IMP or EMP environment, so in this way the comparison between conditions should remain valid. Future research should take a closer look at the role of PSTs in a similar context.
The learners also worked in randomly divided groups, but the data were collected from individuals. Thus, different group level effects, e.g., poor interaction between group members or different amounts of pre-knowledge on balance, are possible. Additionally, the role of some factors external to the study (e.g., the tiredness or previous learning experiences of the learners) might have had an impact on the learners’ situation-specific engagement. The learners came from different classes where they could have had different academic experiences even though they were from the same school and following the same curriculum. In addition, the learners using the IMP environment were a few months older than the learners using the EMP environment.
Future research could further investigate how the different types of model progressions influence the rules that the learners use to balance the beam. The role of guidance and learner age could be studied by having multiple learning environments that would contain more and less specific forms of guidance and in contexts other than balance. The interaction effect of the form and type of guidance and learner age could be studied with a more extensive data set to study the role that learner age has on the effectiveness of the different forms of guidance. The role of individual differences in metacognitive abilities and scientific reasoning could also be considered. The span of learner age could be extended to include younger and older learners, and engagement could be studied as well via, for example, learner interviews.
Author Contributions
Conceptualization, A.L., P.N. and M.H.; Data curation, A.L. and S.P.; Formal analysis, A.L.; Funding acquisition, M.H., A.L. and P.N.; Investigation, A.L., P.N., S.P. and M.H.; Methodology, A.L., P.N. and M.H.; Project administration, M.H.; Visualization, A.L.; Writing—original draft, A.L.; Writing—review & editing, A.L., P.N., S.P. and M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Academy of Finland, grant number 318010.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are available on request from the authors.
Acknowledgments
We wish to thank the participants of the study and the research assistants who aided in data collection.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A
Table A1.
The tasks in the different tabs of the explicit and implicit model progression learning environments.
Table A1.
The tasks in the different tabs of the explicit and implicit model progression learning environments.
| Tab | Explicit Model Progression | Implicit Model Progression |
|---|
| 1 | Familiarization:
how to move the birds and remove the supports. | Familiarization:
how to move the birds and remove the supports. |
| 2 | Left and right side of the fulcrum: a small-sized or a large-sized bird sitting either near or far from the fulcrum.
Task: Find all the configurations that result in balance. Formulate a rule for balancing the beam. | Balance lab:
Left side of the fulcrum: 1 to 6 kg bird that can sit between 1 and 6 m from the fulcrum.
Right side of the fulcrum: 1 to 6 kg bird that can sit between 1 and 6 m from the fulcrum.
Task: Formulate a rule for balancing the seesaw by experimenting with different combinations of bird weight and distance from the fulcrum. |
| 3 | Left side of the fulcrum: 1, 2, 3 or 4 kg bird that can sit between 1 and 8 m from the fulcrum.
Right side of the fulcrum: 6 or 8 kg bird that sits 1 m from the fulcrum (cannot be moved).
Task: Balance the beam using each of the smaller birds. Formulate a rule for balancing the beam. | Left side of the fulcrum: 7 kg (cannot be changed) bird that sits 2 m from the fulcrum (cannot be moved).
Right side of the fulcrum: Bird weighing between 1 and 20 kg that sits between 1 and 8 m from the fulcrum.
Task: Balance the beam using the rule you formulated. |
| 4 | Left side of the fulcrum: 1, 2, 3 or 4 kg bird that can sit between 1 and 8 m from the fulcrum.
Right side of the fulcrum: 6 or 8 kg bird that sits 2 m from the fulcrum.
Tasks: (1) Guess where the 3 kg bird should sit for the beam to be in balance using your rule. (2) Balance the beam using each of the smaller birds. How can your previous rule for balancing the beam be improved? | Left side of the fulcrum: 12 kg (cannot be changed) bird that sits 1 m (cannot be moved) from the fulcrum.
Right side of the fulcrum: Bird weighing between 1 and 7 kg that sits between 1 and 8 m from the fulcrum.
Task: Balance the beam using the rule you formulated. |
| 5 | Left side of the fulcrum: 1, 2, 3 or 4 kg bird that can sit between 1 and 8 m from the fulcrum.
Right side of the fulcrum: 6 or 8 kg bird that can sit between 1 and 8 m from the fulcrum.
Task: Test your previous rule in this situation. Does it have to be changed? | Left side of the fulcrum: 3 kg (cannot be changed) bird that sits between 2 and 8 m from the fulcrum.
Right side of the fulcrum: 9 kg (cannot be changed) bird that sits between 2 and 8 m from the fulcrum.
Task: Balance the beam using the rule you formulated. |
| 6 | Left side of the fulcrum: 1, 2, 3 or 4 kg bird that can sit between 1 and 8 m from the fulcrum.
Right side of the fulcrum: Bird with unknown weight sitting 3 m from the fulcrum.
Task: How much does the bird weigh? (Correct answer: 8 kg) | Left side of the fulcrum: 6 kg (cannot be changed) bird that sits between 1 and 8 m from the fulcrum.
Right side of the fulcrum: 9 kg (cannot be changed) bird that sits 4 m (cannot be moved) from the fulcrum.
Task: Balance the beam using the rule you formulated. |
| 7 | The “Balancing Act” PhET-simulation | The “Balancing Act” PhET simulation |
Appendix B
Table A2.
The InSitu instrument as used in the study. Factors and items in bold were used in this paper.
Table A2.
The InSitu instrument as used in the study. Factors and items in bold were used in this paper.
| Factor and Item | Item |
|---|
| Beh 3 | How important did you find the studied contents? |
| Beh 4 | How much did you try to act according to the teacher’s wishes? |
| Beh 5 | How much did you invest effort into making the teacher pleased with you? |
| Beh 8 | How well did you concentrate during the lesson? |
| Beh 10 | How persistent were you in studying during the lesson? |
| Beh 11 | How much did you plan your tasks ahead instead just doing them right away? |
| Emo 1 | How much did you like this lesson? |
| Emo 2 | How pleasing did you find the studied tasks? |
| Emo 14 | How enjoyable was the lesson? |
| Comp 6 | How easy the lesson was for you? |
| Comp 7 | How well did you understand what was taught? |
| Daff 9 | How much did you do other things than the tasks at hand? |
| Daff 12 | How tired did you feel during the lesson? |
| Daff 13 | How boring was the lesson? |
| Help 15 | How much did you ask for help from the teacher/another adult during the lesson? |
| Help 16 | How much did you ask for help from your classmates during the lesson? |
| Help 17 | How much personal attention did you get from the teacher during the lesson? |
References
- Alfieri, L.; Brooks, P.J.; Aldrich, N.J.; Tenenbaum, H.R. Does discovery-based instruction enhance learning? J. Educ. Psychol. 2011, 103, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Minner, D.D.; Levy, A.J.; Century, J. Inquiry-based science instruction—What is it and does it matter? Results from a research synthesis years 1984 to 2002. J. Res. Sci. Teach. 2010, 47, 474–496. [Google Scholar] [CrossRef]
- Keselman, A. Supporting inquiry learning by promoting normative understanding of multivariable causality. J. Res. Sci. Teach. 2003, 40, 898–921. [Google Scholar] [CrossRef]
- Hmelo-Silver, C.E.; Duncan, R.G.; Chinn, C.A. Scaffolding and achievement in problem-based and inquiry learning: A response to Kirschner, Sweller, and Clark. Educ. Psychol. 2007, 42, 99–107. [Google Scholar] [CrossRef]
- Lazonder, A.W.; Harmsen, R. Meta-analysis of inquiry-based learning: Effects of guidance. Rev. Educ. Res. 2016, 86, 681–718. [Google Scholar] [CrossRef]
- Furtak, E.M.; Seidel, T.; Iverson, H.; Briggs, D.C. Experimental and quasi-experimental studies of inquiry-based science teaching: A meta-analysis. Rev. Educ. Res. 2012, 82, 300–329. [Google Scholar] [CrossRef] [Green Version]
- Kirschner, P.A.; Sweller, J.; Clark, R.E. Why minimal guidance during instruction does not work: An analysis of the failure of constructivist, discovery, problem-based, experiential, and inquiry-based teaching. Educ. Psychol. 2006, 41, 75–86. [Google Scholar] [CrossRef]
- Mayer, R.E. Should there be a three-strikes rule against pure discovery learning? Am. Psychol. 2004, 59, 14–19. [Google Scholar] [CrossRef] [Green Version]
- de Jong, T.; van Joolingen, W.R. Scientific discovery learning with computer simulations of conceptual domains. Rev. Educ. Res. 1998, 68, 179–201. [Google Scholar] [CrossRef]
- van de Pol, J.; Volman, M.; Beishuizen, J. Scaffolding in teacher–student interaction: A decade of research. Educ. Psychol. Rev. 2010, 22, 271–296. [Google Scholar] [CrossRef] [Green Version]
- de Jong, T.; Lazonder, A.W. The guided discovery learning principles in multimedia learning. In The Cambridge Handbook of Multimedia Learning, 2nd ed.; Mayer, R.E., Ed.; Cambridge University Press: Cambridge, UK, 2014; pp. 371–390. [Google Scholar]
- Kalyuga, S.; Ayres, P.; Chandler, P.; Sweller, J. The expertise reversal effect. Educ. Psychol. 2003, 38, 23–31. [Google Scholar] [CrossRef] [Green Version]
- Kalyuga, S. Expertise reversal effect and its implications for learner-tailored instruction. Educ. Psych. Rev. 2007, 19, 509–539. [Google Scholar] [CrossRef]
- Dochy, F.; Segers, M.; Buehl, M.M. The relation between assessment practices and outcomes of studies: The case of research on prior knowledge. Rev. Educ. Res. 1999, 69, 145–186. [Google Scholar] [CrossRef]
- Koerber, S.; Sodian, B.; Thoermer, C.; Nett, U. Scientific reasoning in young children: Preschoolers’ ability to evaluate covariation evidence. Swiss J. Psychol. 2005, 64, 141–152. [Google Scholar] [CrossRef]
- Zimmerman, C. The development of scientific thinking skills in elementary and middle school. Dev. Rev. 2007, 27, 172–223. [Google Scholar] [CrossRef]
- Veenman, M.V.; Spaans, M.A. Relation between intellectual and metacognitive skills: Age and task differences. Learn Ind. Diff. 2005, 15, 159–176. [Google Scholar] [CrossRef]
- Lawson, A.E. Deductive reasoning, brain maturation, and science concept acquisition: Are they linked? J. Res. Sci. Teach. 1993, 30, 1029–1051. [Google Scholar] [CrossRef]
- Piekny, J.; Maehler, C. Scientific reasoning in early and middle childhood: The development of domain-general evidence evaluation, experimentation, and hypothesis generation skills. Br. J. Dev. Psychol. 2013, 31, 153–179. [Google Scholar] [CrossRef]
- Kanari, Z.; Millar, R. Reasoning from data: How students collect and interpret data in science investigations. J. Res. Sci. Teach. 2004, 41, 748–769. [Google Scholar] [CrossRef]
- Chen, Z.; Klahr, D. All other things being equal: Acquisition and transfer of the control of variables strategy. Child Dev. 1999, 70, 1098–1120. [Google Scholar] [CrossRef] [Green Version]
- van der Graaf, J.; Segers, E.; Verhoeven, L. Scientific reasoning abilities in kindergarten: Dynamic assessment of the control of variables strategy. Instr. Sci. 2015, 43, 381–400. [Google Scholar] [CrossRef] [Green Version]
- Klahr, D.; Dunbar, K. Dual space search during scientific reasoning. Cogn. Sci. 1988, 12, 1–48. [Google Scholar] [CrossRef]
- Eccles, J.S.; Roeser, R.W. Schools as developmental contexts during adolescence. In Handbook of Psychology, 2nd ed.; Lerner, R.M., Easterbrooks, M.A., Mistry, J., Weine, I.B., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013; pp. 321–337. [Google Scholar]
- Fredricks, J.A.; Blumenfeld, P.C.; Paris, A.H. School engagement: Potential of the concept, state of the evidence. Rev. Educ. Res. 2004, 74, 59–109. [Google Scholar] [CrossRef] [Green Version]
- Skinner, E.A.; Kindermann, T.A.; Furrer, C.J. A motivational perspective on engagement and disaffection: Conceptualization and assessment of children’s behavioral and emotional participation in academic activities in the classroom. Educ. Psychol. Meas. 2009, 69, 493–525. [Google Scholar] [CrossRef] [Green Version]
- Reeve, J. How students create motivationally supportive learning environments for themselves: The concept of agentic engagement. J. Educ. Psychol. 2013, 105, 579–595. [Google Scholar] [CrossRef] [Green Version]
- Vasalampi, K.; Muotka, J.; Pöysä, S.; Lerkkanen, M.K.; Poikkeus, A.M.; Nurmi, J.E. Assessment of students’ situation-specific classroom engagement by an InSitu instrument. Learn. Ind. Diff. 2016, 52, 46–52. [Google Scholar] [CrossRef]
- Pöysä, S.; Vasalampi, K.; Muotka, J.; Lerkkanen, M.K.; Poikkeus, A.M.; Nurmi, J.E. Variation in situation-specific engagement among lower secondary school students. Learn. Instr. 2018, 53, 64–73. [Google Scholar] [CrossRef]
- de Jong, T. Technological advances in inquiry learning. Science 2006, 312, 532–533. [Google Scholar] [CrossRef] [Green Version]
- Zacharia, Z.C.; Manoli, C.; Xenofontos, N.; de Jong, T.; Pedaste, M.; van Riesen, S.A.; Tsourlidaki, E. Identifying potential types of guidance for supporting student inquiry when using virtual and remote labs in science: A literature review. ETRD Educ. Technol. Res. 2015, 63, 257–302. [Google Scholar] [CrossRef]
- White, B.Y.; Frederiksen, J.R. Causal model progressions as a foundation for intelligent learning environments. Artif. Intell. 1990, 42, 99–157. [Google Scholar] [CrossRef]
- Swaak, J.; van Joolingen, W.R.; de Jong, T. Supporting simulation-based learning: The effects of model progression and assignments on definitional and intuitive knowledge. Learn. Instr. 1998, 8, 235–252. [Google Scholar] [CrossRef]
- Mulder, Y.G.; Lazonder, A.W.; de Jong, T. Comparing two types of model progression in an inquiry learning environment with modelling facilities. Learn. Instr. 2011, 21, 614–624. [Google Scholar] [CrossRef]
- Mulder, Y.G.; Lazonder, A.W.; de Jong, T.; Anjewierden, A.; Bollen, L. Validating and optimizing the effects of model progression in simulation-based inquiry learning. J. Sci. Educ. Technol. 2012, 21, 722–729. [Google Scholar] [CrossRef] [Green Version]
- Zacharia, Z.C.; Olympiou, G. Physical versus virtual manipulative experimentation in physics learning. Learn. Instr. 2011, 21, 317–331. [Google Scholar] [CrossRef]
- GeoGebra Math Apps. Available online: http://geogebra.org (accessed on 13 May 2022).
- Graasp—A Space for Everything. Available online: http://graasp.eu (accessed on 13 May 2022).
- PhET Interactive Simulations for Science and Math. Available online: https://phet.colorado.edu/ (accessed on 13 May 2022).
- Jansen, B.R.; Van der Maas, H.L. The development of children’s rule use on the balance scale task. J. Exp. Child Psychol. 2002, 81, 383–416. [Google Scholar] [CrossRef] [Green Version]
- van der Graaf, J. Inquiry-based learning and conceptual change in balance beam understanding. Front. Psych. 2020, 11, 1621. [Google Scholar] [CrossRef]
- Lerkkanen, M.K.; Vasalampi, K.; Nurmi, J.E. InSituations (InSitu) Instrument; University of Jyvaskyla: Jyväskyla, Finland, 2012. [Google Scholar]
- Eccles, J.S.; Midgley, C.; Wigfield, A.; Buchanan, C.M.; Reuman, D.; Flanagan, C.; MacIver, D. Development during adolescence: The impact of stage-environment fit on young adolescents’ experiences in school and in families. Am. Psychol. 1993, 48, 90–101. [Google Scholar] [CrossRef]
- Marx, J.D.; Cummings, K. Normalized change. Am. J. Phys. 2007, 75, 87–91. [Google Scholar] [CrossRef]
- Hake, R.R. Interactive-engagement versus traditional methods: A six-thousand-student survey of mechanics test data for introductory physics courses. Am. J. Phys. 1998, 66, 64–74. [Google Scholar] [CrossRef] [Green Version]
- Lakens, D. Calculating and reporting effect sizes to facilitate cumulative science: A practical primer for t-tests and ANOVAs. Front. Psychol. 2013, 4, 863. [Google Scholar] [CrossRef] [Green Version]
- Delacre, M.; Leys, C.; Mora, Y.L.; Lakens, D. Taking parametric assumptions seriously: Arguments for the use of Welch’s F-test instead of the classical F-test in one-way ANOVA. Int. Rev. Soc. Psychol. 2019, 32, 13. [Google Scholar] [CrossRef] [Green Version]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates: New York, NY, USA, 1988. [Google Scholar]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).