Assessing Learners’ Conceptual Understanding of Introductory Group Theory Using the CI2GT: Development and Analysis of a Concept Inventory
Abstract
:1. Introduction
- To adequately define what conceptual understanding of group theory means;
- To operationalize this construct via test items leading to a concept inventory that allows for the valid investigation of students’ conceptual understanding of introductory group theory.
2. Literature Review
2.1. Conceputal Understanding of Group Theory
“[…] conceptual understanding reflects knowledge of concepts and linking relationships that are directly connected to (or logically necessitated by) the definition of a concept or meaning of a statement.”[15] (p. 2)
“Conceptual mathematics understanding is a knowledge that involves thorough understanding of underlying and foundation concepts behind the algorithms performed in mathematics.”[16] (p. 1)
2.2. APOS Theory
“APOS Theory is principally a model for describing how mathematical concepts can be learned; it is a framework used to explain how individuals mentally construct their understandings of mathematical concepts. [⋯] Individuals make sense of mathematical concepts by building and using certain mental structures (or constructions) which are considered in APOS Theory to be stages in the learning of mathematical concepts.”[25] (p. 17)
3. Objectives of This Study
- 1.
- We aim at providing a new concept inventory to assess conceptual understanding of introductory group theory (for a proper definition of the target group cf. Section 4.1).
- 2.
- We present an in-depth psychometric characterization of the concept inventory both from the viewpoint of classical test theory as well as item response theory.
- 3.
- Lastly, an evidence-based argument for valid test score interpretation is to be established throughout the article.
4. Development of the CI2GT
4.1. Determining the Target Group and Test Objective
4.2. Description of Knowledge Domain
- 1.
- Definitional fundamentals: Binary operations on arbitrary sets and properties of those operations such as associativity or closure.
- 2.
- The neutral element and inverses: Elements that emphasize certain properties of a binary operation, i.e., “reversing something”.
- 3.
- Cyclical and Dihedral groups: Groups that are generated by one or two elements and have a strong geometric connotation, i.e., rotating a regular n-gon.
- 4.
- Cayley Tables: Tables that contain every possible result of the binary operation and thus the entire information about the group.
- 5.
- Subgroups: Subsets of the underlying set that are groups themselves if equipped with the same operation.
- 6.
- Homomorphisms: Structure-preserving maps between groups that eventually allow to differentiate groups from a mathematical point of view.
4.3. Decision of Task Format
4.4. Creating Appropriate Distractors
- An extensive literature review on mathematics education research regarding teaching and learning of abstract algebra. (cf. [1])
- An interview study which we conducted to collect students conceptions prior to test development (cf. [12]). For example, we found that the meaning of the symbol 0 usually becomes inflated in the context of neutral elements (cf. item 5) or that closure is a property often left unchecked (cf. item 3).
5. Methods and Samples
- 1.
- An expert survey with experts from mathematics education research.
- 2.
- A quantitative evaluation with pre-service primary school teachers
5.1. Expert Survey: Study Design and Data Analysis
5.1.1. Study Design
5.1.2. Data Analysis
5.2. Quantitative Evaluation: Study Design and Data Analysis
5.2.1. Study Design
5.2.2. Data Analysis: Classical Test Theory
5.2.3. Data Analysis: Rasch Scaling
“it is not just another statistical technique to apply to data, but it is a perspective as to what is measurement, why measurement matters and how to achieve better quality measurement in an educational setting.”[44] (p. 1)
- Skewness and kurtosis of the items do not exceed the range of to ;
- The items are locally independent;
- Uni-dimensionality of the concept inventory can be assumed.
6. Results
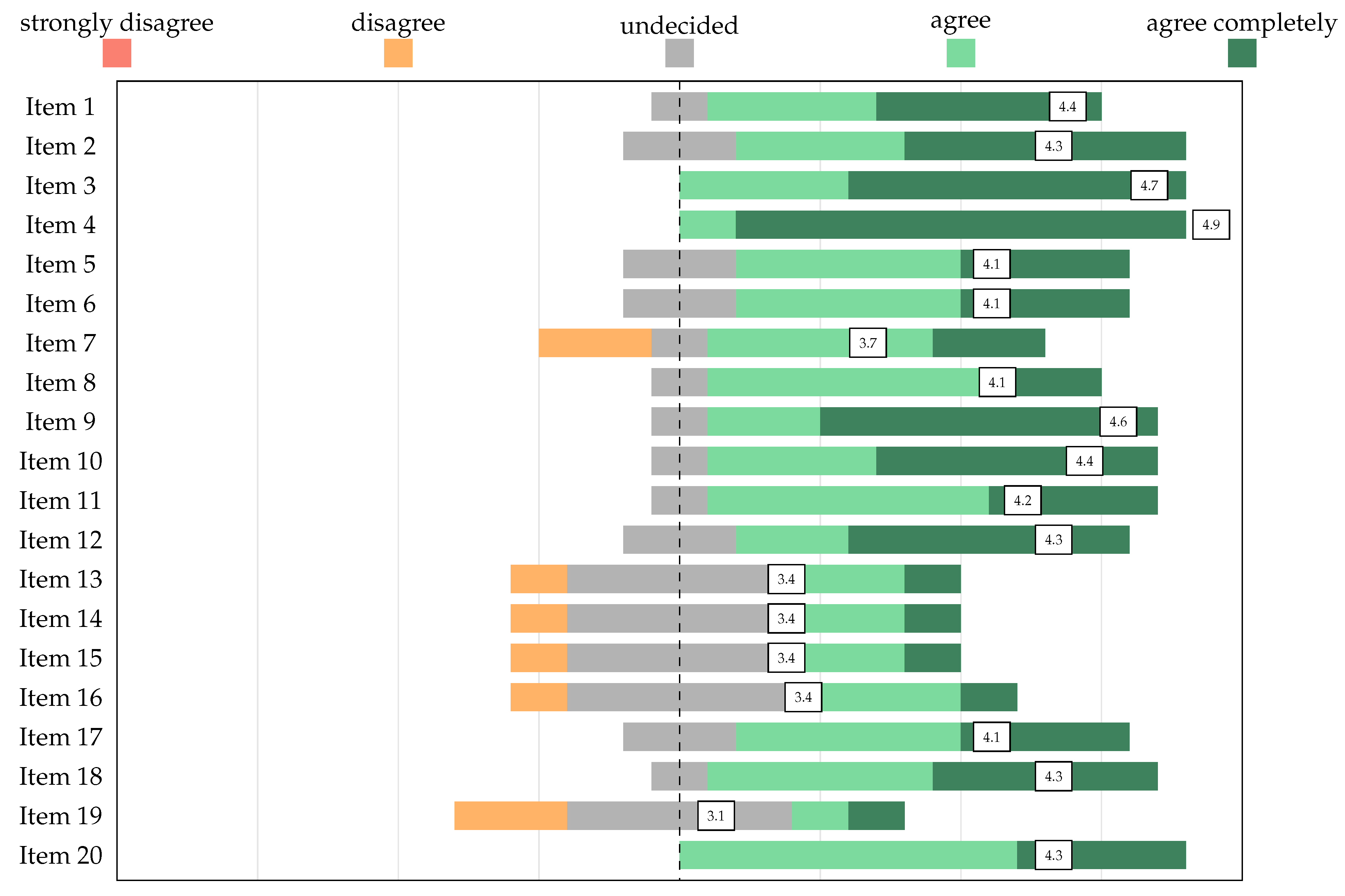
6.1. Results of the Expert Survey
Interim Conclusion on Expert Survey results
6.2. Results of the Quantitative Evaluation of the CI2GT
6.2.1. Psychometric Characterization Using Classical Test Theory
6.2.2. Interim Conclusion on the Psychometric Characterization
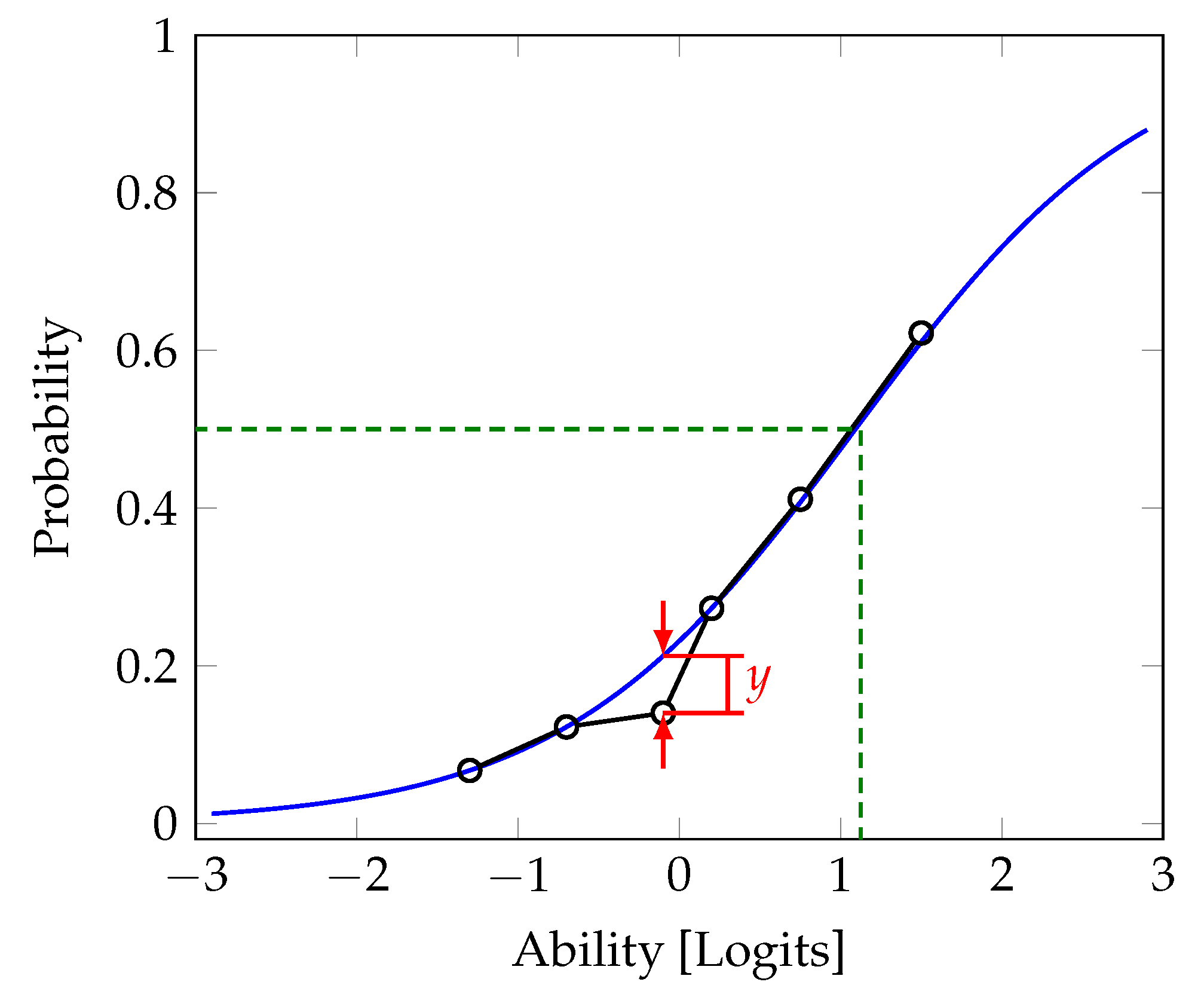
6.2.3. Results of the Rasch Scaling
6.2.4. Interim Conclusion on the Rasch Scaling
7. Discussion
“it is not sufficient for developers to create tools to measure conceptual understanding; educators must also evaluate the extend to which these tools are valid and reliable indicators of student understanding.”[34] (p. 455)
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

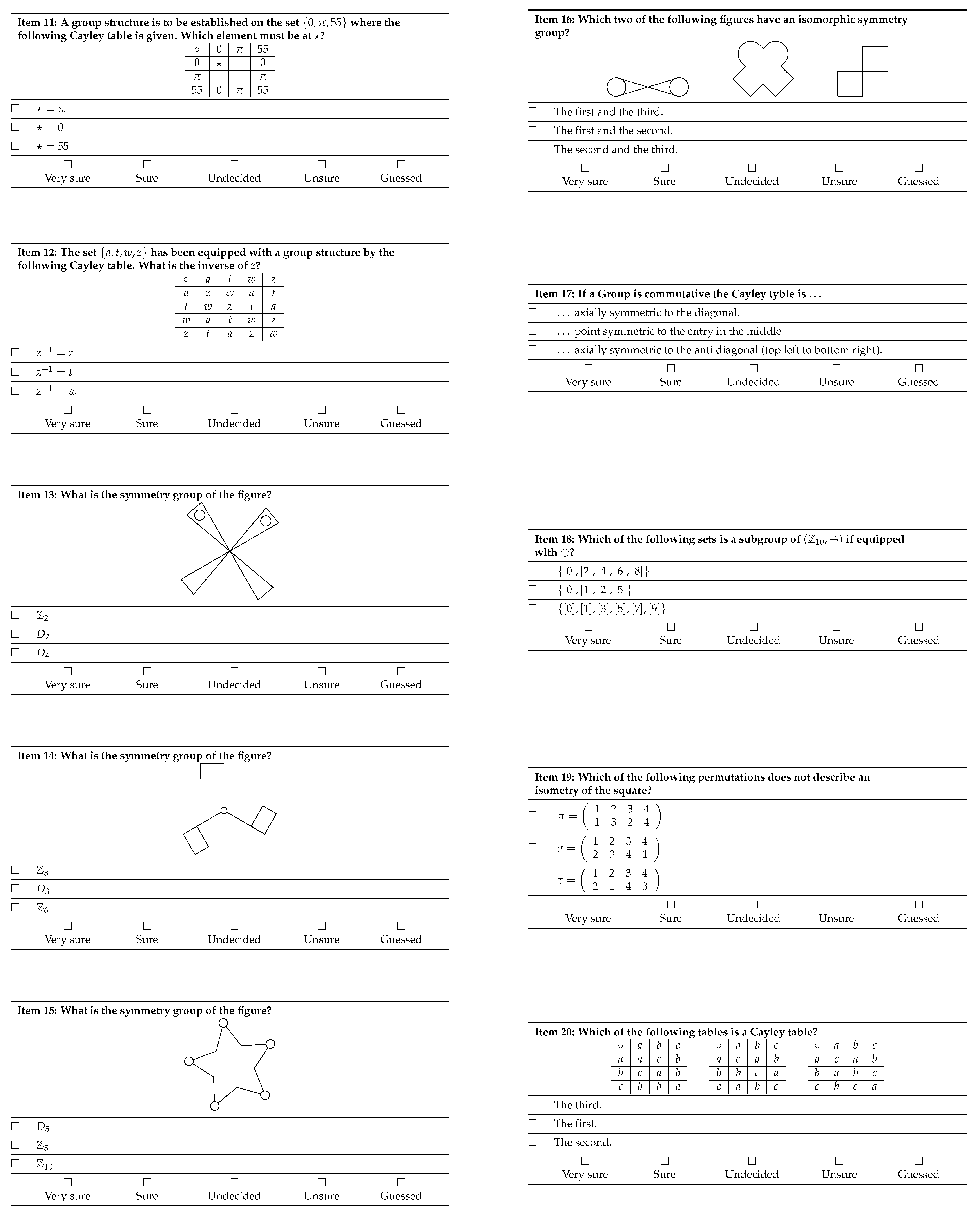
References
- Veith, J.M.; Bitzenbauer, P. What Group Theory Can Do for You: From Magmas to Abstract Thinking in School Mathematics. Mathematics 2022, 10, 703. [Google Scholar] [CrossRef]
- Wasserman, N.H. Introducing Algebraic Structures through Solving Equations: Vertical Content Knowledge for K-12 Mathematics Teachers. PRIMUS 2014, 24, 191–214. [Google Scholar] [CrossRef]
- Even, R. The relevance of advanced mathematics studies to expertise in secondary school mathematics teaching: Practitioners’ views. ZDM Math. Educ. 2011, 43, 941–950. [Google Scholar] [CrossRef]
- Shamash, J.; Barabash, M.; Even, R. From Equations to Structures: Modes of Relevance of Abstract Algebra to School Mathematics as Viewed by Teacher Educators and Teachers. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Switzerland, Basel, 2018; pp. 241–262. [Google Scholar] [CrossRef]
- Burn, R. What Are the Fundamental Concepts of Group Theory? Educ. Stud. Math. 1996, 31, 371–377. [Google Scholar] [CrossRef]
- Baldinger, E.E. Learning Mathematical Practices to Connect Abstract Algebra to High School Algebra. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Switzerland, Basel, 2018; pp. 211–239. [Google Scholar] [CrossRef]
- Shimizu, J.K. The Nature of Secondary Mathematics Teachers’ Efforts to Make Ideas of School Algebra Accessible. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 2013. [Google Scholar]
- Zbiek, R.M.; Heid, M.K. Making Connections from the Secondary Classroom to the Abstract Algebra Course: A Mathematical Activity Approach. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Switzerland, Basel, 2018; pp. 189–209. [Google Scholar] [CrossRef]
- Leron, U.; Dubinsky, E. An abstract algebra story. Am. Math. Mon. 1995, 102, 227–242. [Google Scholar] [CrossRef]
- Melhuish, K.; Fagan, J. Connecting the Group Theory Concept Assessment to Core Concepts at the Secondary Level. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Switzerland, Basel, 2018; pp. 19–45. [Google Scholar] [CrossRef]
- Veith, J.M.; Bitzenbauer, P. Two Challenging Concepts in Mathematics Education: Subject-Specific Thoughts on the Complex Unit and Angles. Eur. J. Sci. Math. Educ. 2021, 9, 244–251. [Google Scholar] [CrossRef]
- Veith, J.M.; Bitzenbauer, P.; Girnat, B. Towards Describing Student Learning of Abstract Algebra: Insights into Learners’ Cognitive Processes from an Acceptance Survey. Mathematics 2022, 10, 1138. [Google Scholar] [CrossRef]
- Baroody, A.J.; Feil, Y.; Johnson, A.R. An alternative reconceptualization of procedural and conceptual knowledge. J. Res. Math. Educ. 2007, 38, 115–131. [Google Scholar] [CrossRef]
- Melhuish, K. The Design and Validation of a Group Theory Concept Inventory. Ph.D. Thesis, Portland State University, Portland, OR, USA, 2015. [Google Scholar]
- Melhuish, K. The Group Theory Concept Assessment: A Tool for Measuring Conceptual Understanding in Introductory Group Theory. Int. J. Res. Undergrad. Math. Educ. 2019, 5, 359–393. [Google Scholar] [CrossRef]
- Andamon, J.C.; Tan, D.A. Conceptual Understanding, Attitude And Performance In Mathematics Of Grade 7 Students. Int. J. Sci. Technol. Res. 2018, 7, 96–105. [Google Scholar]
- Weber, K.; Larsen, S. Teaching and Learning Group Theory. In Making The Connection; Carlson, M.P., Rasmussen, C., Eds.; Mathematical Association of America: Washington, DC, USA, 2008; pp. 139–151. [Google Scholar]
- Edwards, B.W.; Ward, M.B. Surprises from mathematics education research: Student (mis) use of mathematical definitions. Am. Math. Mon. 2004, 111, 411–424. [Google Scholar] [CrossRef] [Green Version]
- Lajoie, C.; Mura, R. What’s in a Name? A Learning Difficulty in Connection with Cyclic Groups. Learn. Math. 2000, 20, 29–33. [Google Scholar]
- Novotná, J.; Hoch, M. How structure sense for algebraic expressions or equations is related to structure sense for abstract algebra. Math. Educ. Res. J. 2008, 20, 93–104. [Google Scholar] [CrossRef]
- Dubinskiy, E.; Dautermann, J.; Leron, U.; Zazkis, R. On learning fundamental concepts of group theory. Educ. Stud. Math. 1994, 27, 267–305. [Google Scholar] [CrossRef]
- Carlson, M.; Oehrtman, M.; Engelke, N. The pre-calculus concept assessment: A tool for assessing students’ reasoning abilities and understandings. Cogn. Instr. 2010, 28, 113–145. [Google Scholar] [CrossRef]
- Epstein, J. The calculus concept inventory—Measurement of the effect of teaching methodology in mathematics. Not. Am. Math. Soc. 2013, 160, 1018–1027. [Google Scholar] [CrossRef]
- Dubinsky, E.; Mcdonald, M.A. APOS: A Constructivist Theory of Learning in Undergraduate Mathematics Education Research. In The Teaching and Learning of Mathematics at University Level; Springer: Switzerland, Basel, 2001; pp. 275–282. [Google Scholar] [CrossRef]
- Arnon, I.; Cottrill, J.; Dubinsky, E.; Oktac, A.; Fuentes, S.R.; Trigueros, M.; Weller, K. Mental Structures and Mechanisms: APOS Theory and the Construction of Mathematical Knowledge. In APOS Theory; Springer: Ney York, NY, USA, 2014; pp. 17–26. [Google Scholar] [CrossRef]
- Messick, S. Validity of Psychological Assessment. Validation of Inferences from Persons’ Responses and Performances as Scientific Inquiry into Score Meaning. Am. Psychol. 1995, 5D, 741–749. [Google Scholar] [CrossRef]
- Kane, M.T. Current concerns in validity theory. J. Educ. Meas. 2001, 38, 319–342. [Google Scholar] [CrossRef]
- Kane, M.T. Validating the Interpretations and Uses of Test Scores. J. Educ. Meas. 2013, 50, 1–73. [Google Scholar] [CrossRef]
- Meinhardt, C. Entwicklung und Validierung eines Testinstruments zu Selbstwirksamkeitserwartungen von (Angehenden) Physiklehrkräften in Physikdidaktischen Handlungsfeldern, 1st ed.; Logos: Berlin, Germany, 2018. [Google Scholar] [CrossRef] [Green Version]
- Bitzenbauer, P. Development of a Test Instrument to Investigate Secondary School Students’ Declarative Knowledge of Quantum Optics. Eur. J. Sci. Math. Educ. 2021, 9, 57–79. [Google Scholar] [CrossRef]
- Lindell, R.S.; Peak, E.; Foster, T.M. Are they all created equal? A comparison of different concept inventory development methodologies. AIP Conf. Proc. 2007, 883, 14. [Google Scholar]
- Zenger, T.; Bitzenbauer, P. Exploring German Secondary School Students’ Conceptual Knowledge of Density. Sci. Educ. Int. 2022, 33, 86–92. [Google Scholar] [CrossRef]
- Flateby, T.L. A Guide for Writing and Improving Achievement Tests; University of South Florida: Tampa, FL, USA, 1996; Available online: https://evaeducation.weebly.com/uploads/1/9/6/9/19692577/guide.pdf (accessed on 15 April 2022).
- Jorion, H.; James, B.D.; Schroeder, K.; DiBello, L.; Pellegrino, J.W. An Analytic framework for Evaluating the Validity of Concept Inventory Claims. J. Eng. Educ. 2015, 104, 454–496. [Google Scholar] [CrossRef]
- Hasan, S.; Bagayoko, D.; Kelley, E.L. Misconceptions and the certainty of response index. Phys. Educ. 1999, 34, 294–299. [Google Scholar] [CrossRef]
- Moosbrugger, H.; Kelava, A. Testtheorie und Fragebogenkonstruktion, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Robbins, N.; Heiberger, R. Plotting Likert and other rating scales. In Proceedings of the 2011 Joint Statistical Meeting, Miami Beach, FL, USA, 30 July 2011–4 August 2011; pp. 1058–1066. [Google Scholar]
- Landis, J.R.; Koch, G.G. The Measurement of Observer Agreement for Categorial Data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [Green Version]
- Engelhardt, P.V. An Introduction to Classical Test Theory as Applied to Conceptual Multiple-Choice Tests; Tennessee Technological University: Cookeville, TN, USA, 2009; Available online: https://www.compadre.org/Repository/document/ServeFile.cfm?ID=8807&DocID=1148 (accessed on 15 April 2022).
- Kline, T.J.B. Psychological Testing: A Practical Approach to Design and Evaluation, 1st ed.; SAGE Publications, Inc.: Newbury Park, CA, USA, 2005. [Google Scholar] [CrossRef] [Green Version]
- Taber, K.S. The Use of Cronbach’s Alpha When Developing and Reporting Research Instruments in Science Education. Res. Sci. Educ. 2018, 48, 1273–1296. [Google Scholar] [CrossRef]
- Embretson, S.E. The new rules of measurement. Psychol. Assess. 1996, 8, 341–349. [Google Scholar] [CrossRef]
- Hambleton, R.K.; Jones, R.W. Comparison of classical test theory and item response theory and their applications to test development. Educ. Meas. Issues Pract. 1993, 12, 38–47. [Google Scholar] [CrossRef]
- Planinic, M.; Boone, W.J.; Susac, A.; Ivanjek, L. Rasch analysis in physics education research: Why measurement matters. Phys. Rev. Phys. Educ. Res. 2019, 15, 020111. [Google Scholar] [CrossRef] [Green Version]
- Cantó-Cerdán, M.; Cacho-Martínez, P.; Lara-Lacárcel, F.; García-Munoz, A. Rasch analysis for development and reduction of Symptom Questionnaire for Visual Dysfunctions (SQVD). Sci. Rep. 2021, 11, 14855. [Google Scholar] [CrossRef]
- Wu, M.L.; Adams, R.J.; Wilson, M.R.; Haldane, S.A. ACER ConQuest: Version 2.0. Generalised Item Response Modelling Software, 1st ed.; ACER Press: Camberwell, Australia, 2007. [Google Scholar]
- Wright, B.D.; Geofferey, N.M. Rating Scale Analysis, 1st ed.; MESA Press: Chicaco, IL, USA, 1982. [Google Scholar]
- Hölzl-Winter, A.; Wäschle, K.; Wittwer, J.; Watermann, R.; Nückles, M. Entwicklung und Validierung eines Tests zur Erfassung des Genrewissens Studierender und Promovierender der Bildungswissenschaften. Zeitschrift für Pädagogik 2015, 61, 185–202. [Google Scholar] [CrossRef]
- Chen, W.-H.; Thissen, D. Local Dependence Indexes for Item Pairs Using Item Response Theory. J. Educ. Behav. Stat. 1997, 22, 265–289. [Google Scholar] [CrossRef]
- Christensen, K.B.; Makransky, G.; Horton, M. Critical Values for Yen’s Q3: Identification of Local Dependence in the Rasch Model Using Residual Correlations. Appl. Psychol. Meas. 2017, 41, 178–194. [Google Scholar] [CrossRef]
- Jang, E.E.; Roussos, L. An Investigation into the Dimensionality of TOEFL Using Conditional Covariance-Based Nonparametric Approach. J. Educ. Meas. 2007, 44, 1–21. [Google Scholar] [CrossRef]
- George, D.; Mallery, P. SPSS for Windows Step by Step: A Simple Guide and Reference, 1st ed.; Allyn & Bacon: Boston, CA, USA, 2010. [Google Scholar]
- Nguyen, T.H.; Han, H.; Kim, M.T.; Chan, K.S. An Introduction to Item Response Theory for Patient-Reported Outcome Measurement. Patient 2014, 7, 23–35. [Google Scholar] [CrossRef] [Green Version]
- Kerlinger, F.N.; Lee, H.B. Foundations of Behavioral Research, 4th ed.; Hartcourt College Publishers: San Diego, CA, USA, 2000. [Google Scholar]
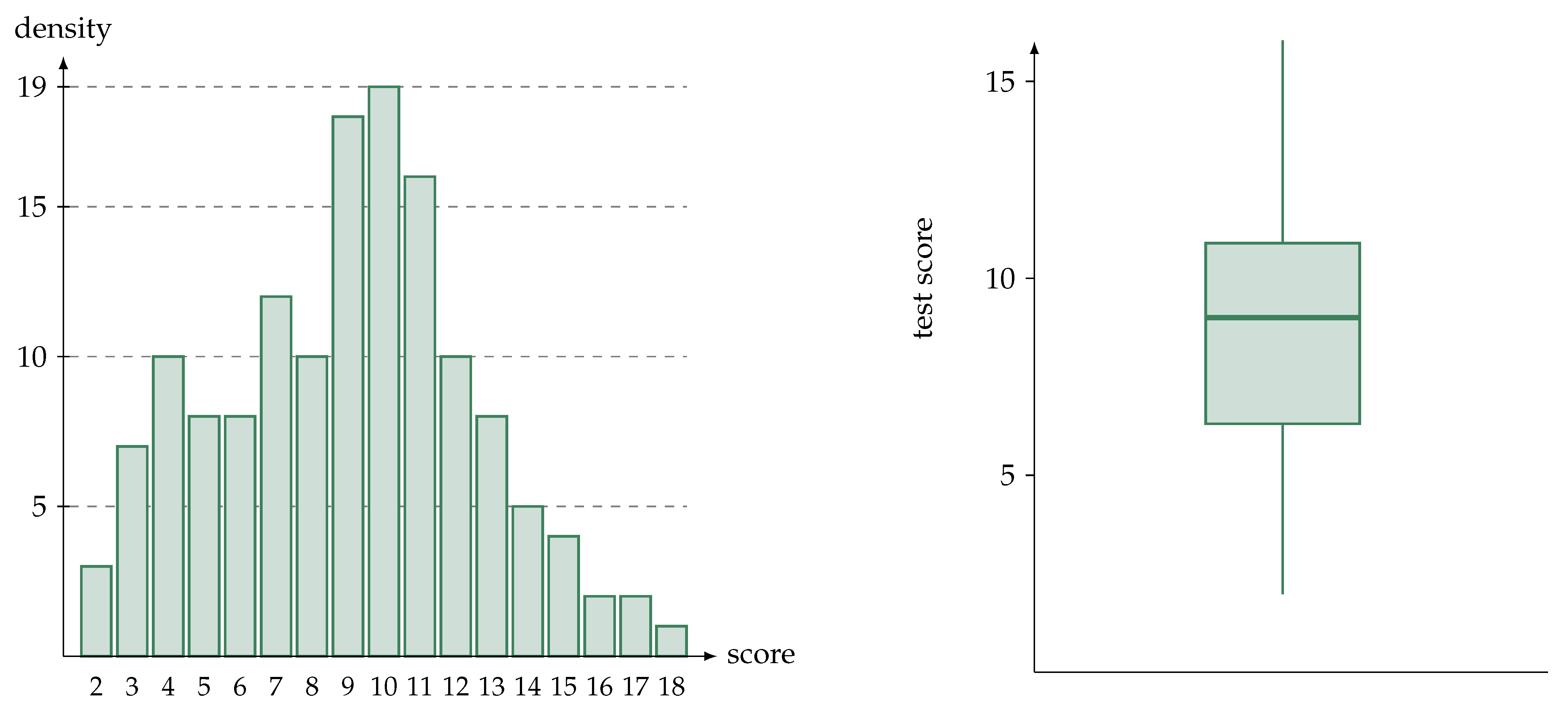
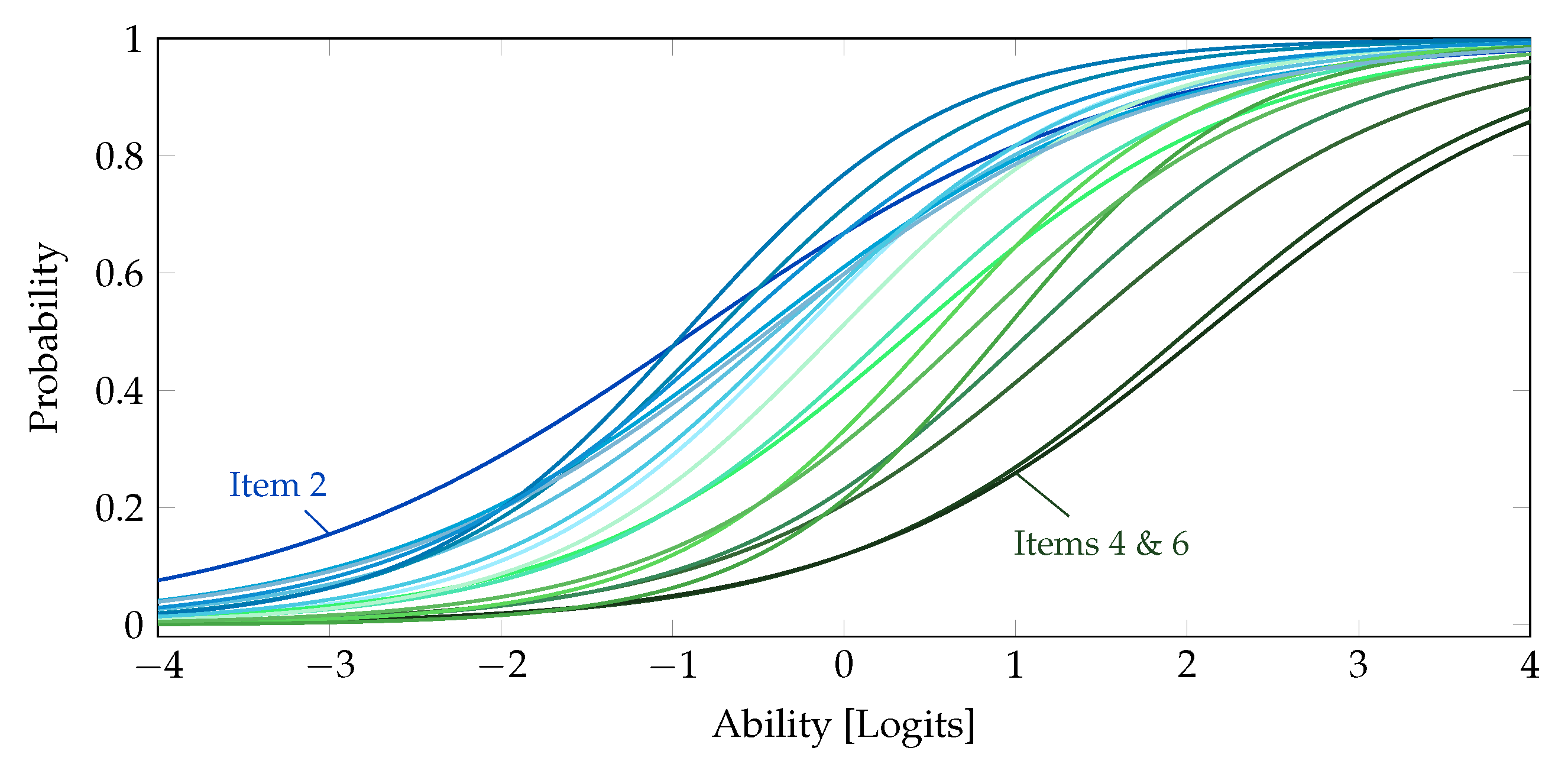
| Item No. | Description | Schemas | Number of Schemas |
|---|---|---|---|
| 2 | Assessing whether a binary operation on M is a map , a map or a map . | binary operations | 1 |
| 5 | Finding the neutral element of 🟉 where such that . | binary operations, identity element | 2 |
| 6 | Finding the inverse of with respect to • where such that . | binary operations, identity element, inverse element | 3 |
| Assumptions | Analysis Method |
|---|---|
| A1: The items adequately represent the one-dimensional construct conceptual understanding of introductory group theory | Rasch analysis (cf. Section 5.2.3 and Section 6.2.3), Expert Survey (cf. Section 5.1 and Section 6.1). |
| A2: The items are unambiguous and the instructions are clear from a mathematical and didactical point of view | Expert survey |
| A3: The items and distractors are authentic | Response distribution (cf. Section 6.2), Expert Survey |
| A4: The construct is distinguishable from different or similar constructs | Correlation analysis (cf. Section 6.2) |
| X.1 | The content of this item is relevant for learning about group theory. | □1 | □2 | □3 | □4 | □5 |
| X.2 | This item assesses a crucial aspect of the knowledge domain. | □1 | □2 | □3 | □4 | □5 |
| X.3 | The item’s distractors are authentic. | □1 | □2 | □3 | □4 | □5 |
| X.4 | The formulation of task assignment is clear and unambiguous. | □1 | □2 | □3 | □4 | □5 |
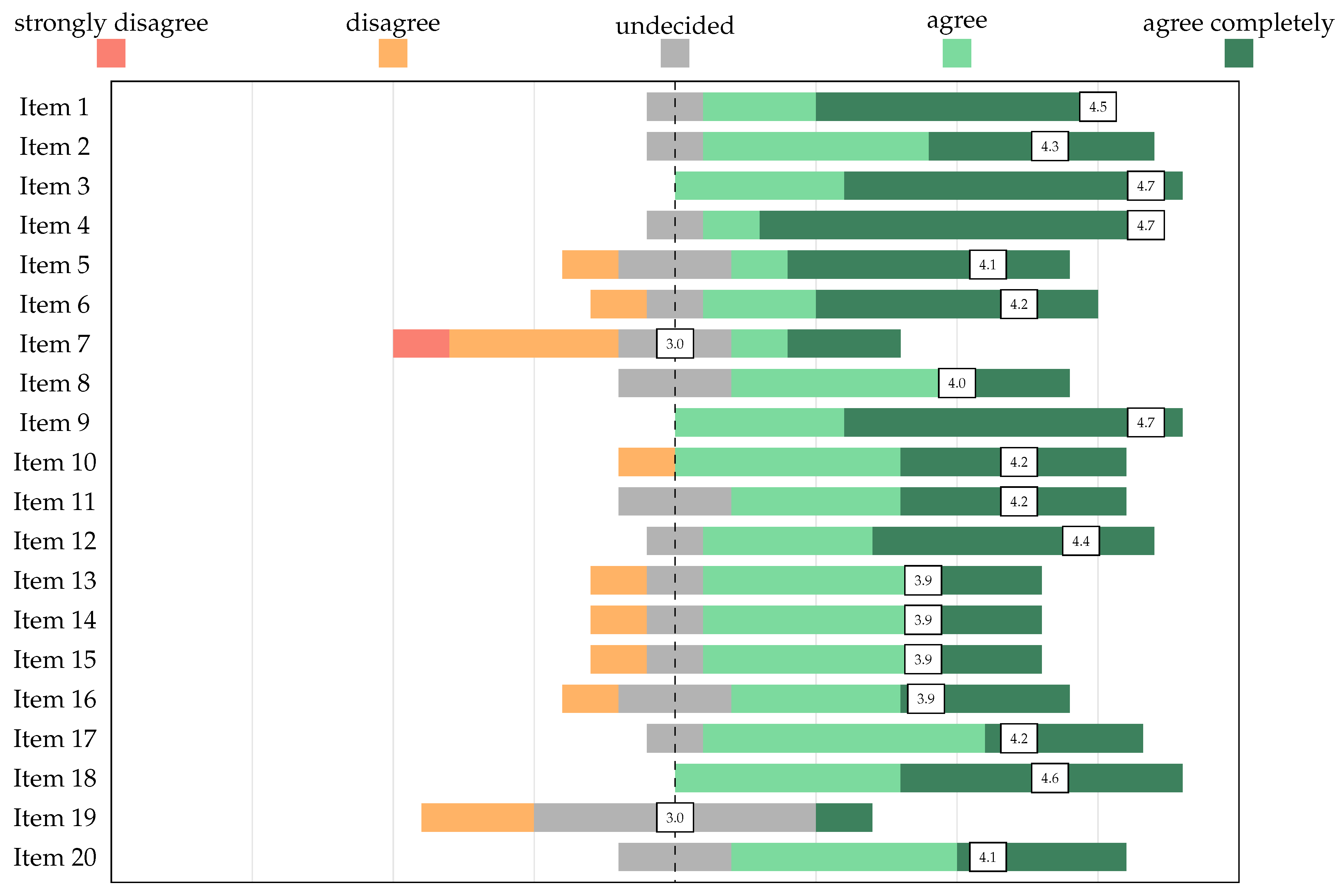
| “The content of this item is relevant for learning about group theory” | |||||
|---|---|---|---|---|---|
| Item 1 | 4.4 | 0.7 | Item 11 | 4.2 | 0.7 |
| Item 2 | 4.3 | 0.9 | Item 12 | 4.3 | 0.9 |
| Item 3 | 4.7 | 0.5 | Item 13 | 3.4 | 0.9 |
| Item 4 | 4.9 | 0.3 | Item 14 | 3.4 | 0.9 |
| Item 5 | 4.1 | 0.8 | Item 15 | 3.4 | 0.9 |
| Item 6 | 4.1 | 0.8 | Item 16 | 3.4 | 0.9 |
| Item 7 | 3.7 | 1.1 | Item 17 | 4.1 | 0.8 |
| Item 8 | 4.1 | 0.6 | Item 18 | 4.3 | 0.7 |
| Item 9 | 4.6 | 0.7 | Item 19 | 3.1 | 1.0 |
| Item 10 | 4.4 | 0.7 | Item 20 | 4.3 | 0.5 |
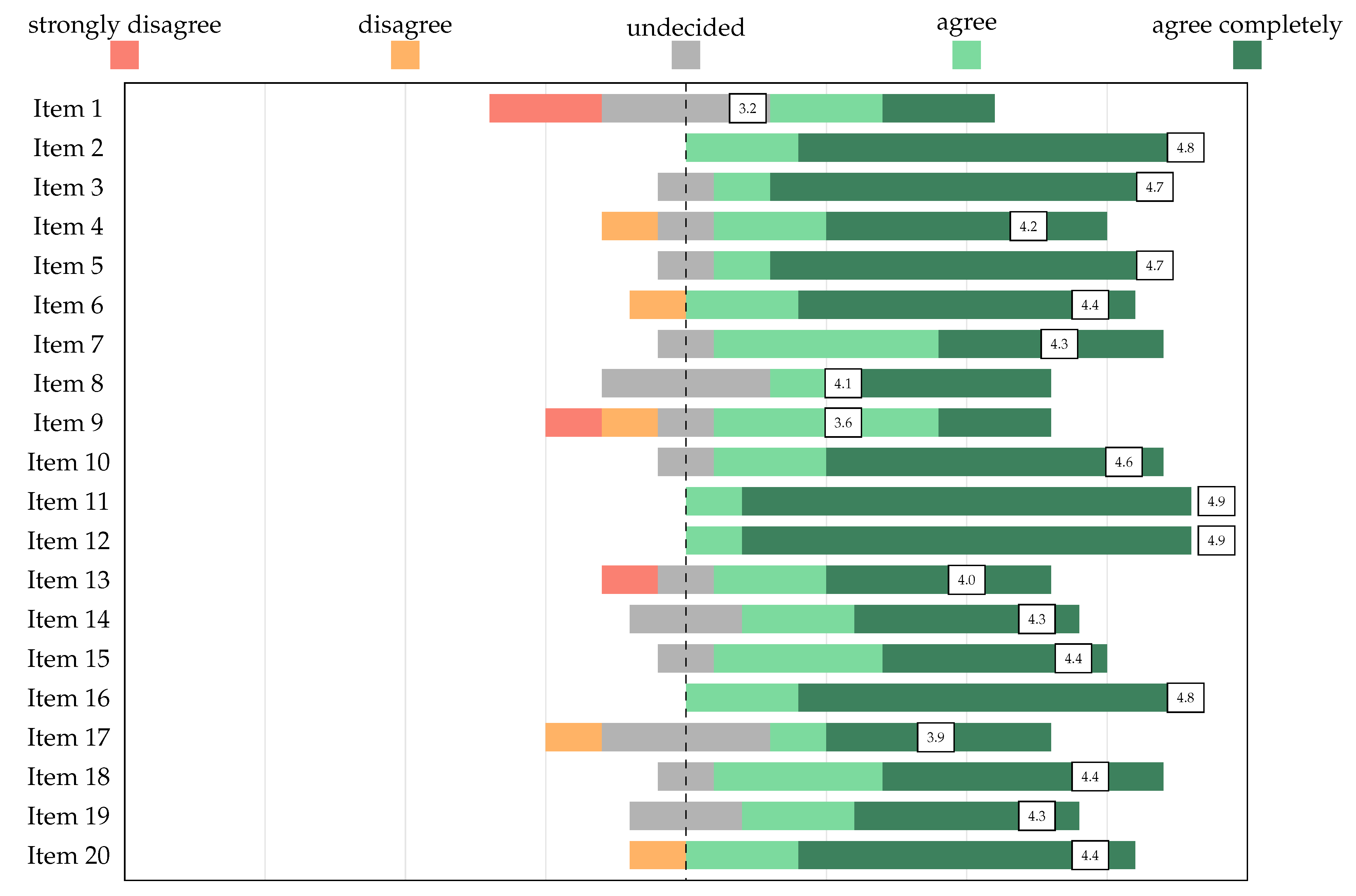
| “This item assesses a crucial aspect of the knowledge domain” | |||||
|---|---|---|---|---|---|
| Item 1 | 4.5 | 0.8 | Item 11 | 4.2 | 0.8 |
| Item 2 | 4.3 | 0.7 | Item 12 | 4.4 | 0.7 |
| Item 3 | 4.7 | 0.5 | Item 13 | 3.9 | 1.0 |
| Item 4 | 4.7 | 0.7 | Item 14 | 3.9 | 1.0 |
| Item 5 | 4.1 | 1.2 | Item 15 | 3.9 | 1.0 |
| Item 6 | 4.2 | 1.1 | Item 16 | 3.9 | 1.1 |
| Item 7 | 3.0 | 1.4 | Item 17 | 4.2 | 0.7 |
| Item 8 | 4.0 | 0.8 | Item 18 | 4.6 | 0.5 |
| Item 9 | 4.7 | 0.5 | Item 19 | 3.0 | 0.9 |
| Item 10 | 4.2 | 1.0 | Item 20 | 4.1 | 0.8 |
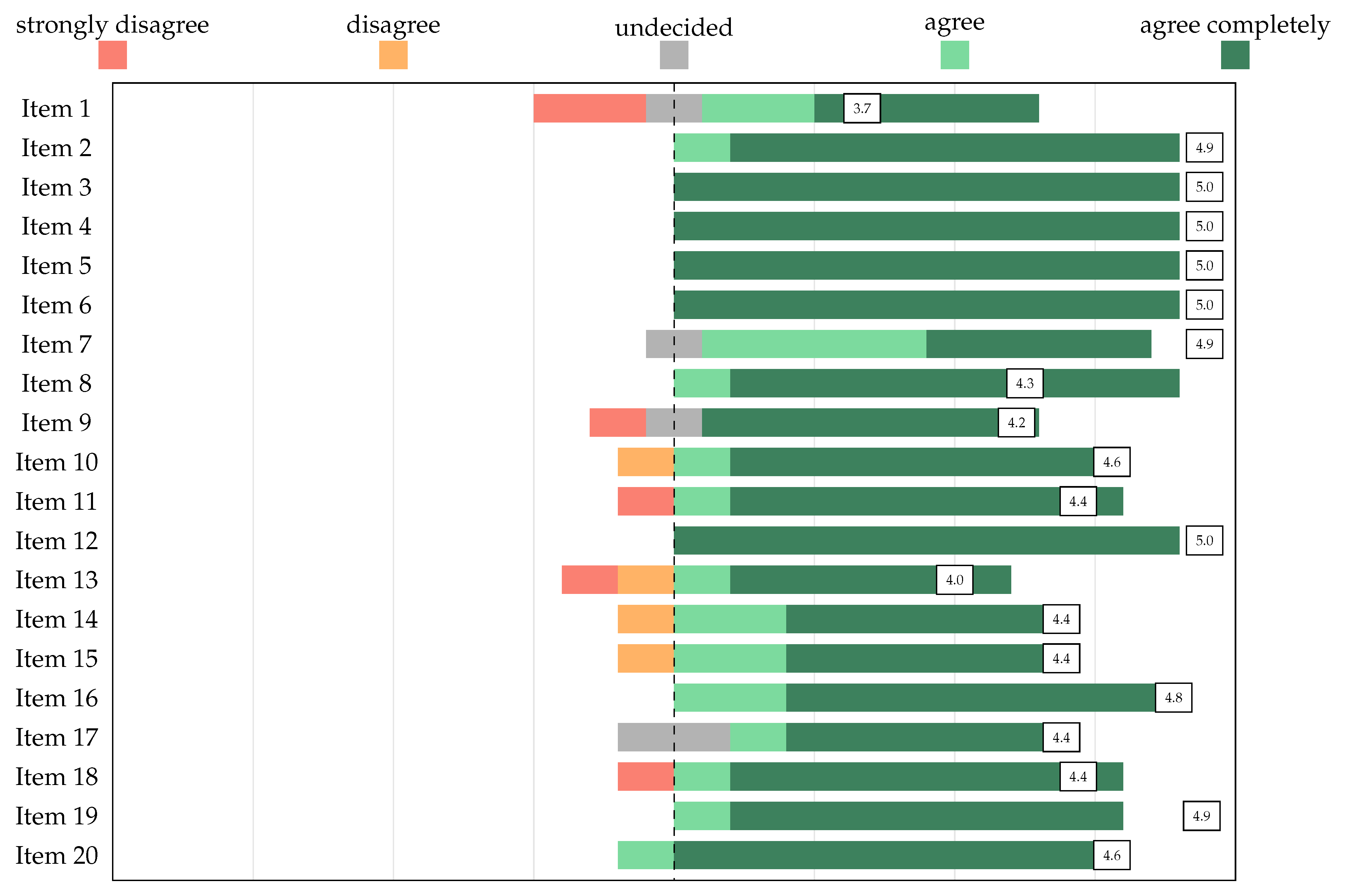
| “The item’s distractors are authentic” | |||||
|---|---|---|---|---|---|
| Item 1 | 3.2 | 1.5 | Item 11 | 4.9 | 0.3 |
| Item 2 | 4.8 | 0.4 | Item 12 | 4.9 | 0.3 |
| Item 3 | 4.7 | 0.7 | Item 13 | 4.0 | 1.4 |
| Item 4 | 4.2 | 1.1 | Item 14 | 4.3 | 0.9 |
| Item 5 | 4.7 | 0.7 | Item 15 | 4.4 | 0.7 |
| Item 6 | 4.4 | 1.0 | Item 16 | 4.8 | 0.4 |
| Item 7 | 4.3 | 0.7 | Item 17 | 3.9 | 1.2 |
| Item 8 | 4.1 | 1.0 | Item 18 | 4.4 | 0.7 |
| Item 9 | 3.6 | 1.3 | Item 19 | 4.3 | 0.9 |
| Item 10 | 4.6 | 0.7 | Item 20 | 4.4 | 1.0 |
| “The formulation of task assignment is clear and unambiguous” | |||||
|---|---|---|---|---|---|
| Item 1 | 3.7 | 1.7 | Item 11 | 4.4 | 1.3 |
| Item 2 | 4.9 | 0.3 | Item 12 | 5.0 | 0.0 |
| Item 3 | 5.0 | 0.0 | Item 13 | 4.0 | 1.1 |
| Item 4 | 5.0 | 0.0 | Item 14 | 4.4 | 1.1 |
| Item 5 | 5.0 | 0.0 | Item 15 | 4.4 | 1.1 |
| Item 6 | 5.0 | 0.0 | Item 16 | 4.8 | 0.4 |
| Item 7 | 4.9 | 0.3 | Item 17 | 4.4 | 0.9 |
| Item 8 | 4.3 | 1.5 | Item 18 | 4.4 | 1.3 |
| Item 9 | 4.2 | 1.1 | Item 19 | 4.9 | 0.4 |
| Item 10 | 4.6 | 1.0 | Item 20 | 4.6 | 1.3 |
| Answer Option 1 | Answer Option 2 | Answer Option 3 | |
|---|---|---|---|
| Item 1 | 0.27 | 0.66 | 0.07 |
| Item 2 | 0.81 | 0.15 | 0.04 |
| Item 3 | 0.63 | 0.18 | 0.19 |
| Item 4 | 0.17 | 0.10 | 0.73 |
| Item 5 | 0.53 | 0.33 | 0.14 |
| Item 6 | 0.34 | 0.15 | 0.52 |
| Item 7 | 0.33 | 0.36 | 0.31 |
| Item 8 | 0.71 | 0.23 | 0.06 |
| Item 9 | 0.45 | 0.22 | 0.34 |
| Item 10 | 0.72 | 0.22 | 0.06 |
| Item 11 | 0.62 | 0.19 | 0.19 |
| Item 12 | 0.38 | 0.13 | 0.50 |
| Item 13 | 0.18 | 0.62 | 0.20 |
| Item 14 | 0.49 | 0.46 | 0.05 |
| Item 15 | 0.69 | 0.20 | 0.10 |
| Item 16 | 0.80 | 0.10 | 0.10 |
| Item 17 | 0.73 | 0.09 | 0.18 |
| Item 18 | 0.52 | 0.22 | 0.27 |
| Item 19 | 0.65 | 0.18 | 0.17 |
| Item 20 | 0.66 | 0.10 | 0.24 |
| Item Difficulty P | Discriminatory Power D | Adjusted Cronbach’s Alpha | |
|---|---|---|---|
| Item 1 | 0.27 | 0.13 | 0.70 |
| Item 2 | 0.73 | 0.13 | 0.70 |
| Item 3 | 0.58 | 0.21 | 0.70 |
| Item 4 | 0.14 | 0.18 | 0.70 |
| Item 5 | 0.41 | 0.45 | 0.67 |
| Item 6 | 0.13 | 0.12 | 0.70 |
| Item 7 | 0.27 | 0.30 | 0.69 |
| Item 8 | 0.59 | 0.34 | 0.68 |
| Item 9 | 0.45 | 0.35 | 0.68 |
| Item 10 | 0.66 | 0.26 | 0.69 |
| Item 11 | 0.60 | 0.30 | 0.69 |
| Item 12 | 0.34 | 0.28 | 0.69 |
| Item 13 | 0.10 | 0.01 | 0.71 |
| Item 14 | 0.28 | 0.20 | 0.70 |
| Item 15 | 0.55 | 0.34 | 0.68 |
| Item 16 | 0.69 | 0.26 | 0.69 |
| Item 17 | 0.62 | 0.43 | 0.67 |
| Item 18 | 0.38 | 0.33 | 0.68 |
| Item 19 | 0.58 | 0.28 | 0.69 |
| Item 20 | 0.62 | 0.36 | 0.68 |
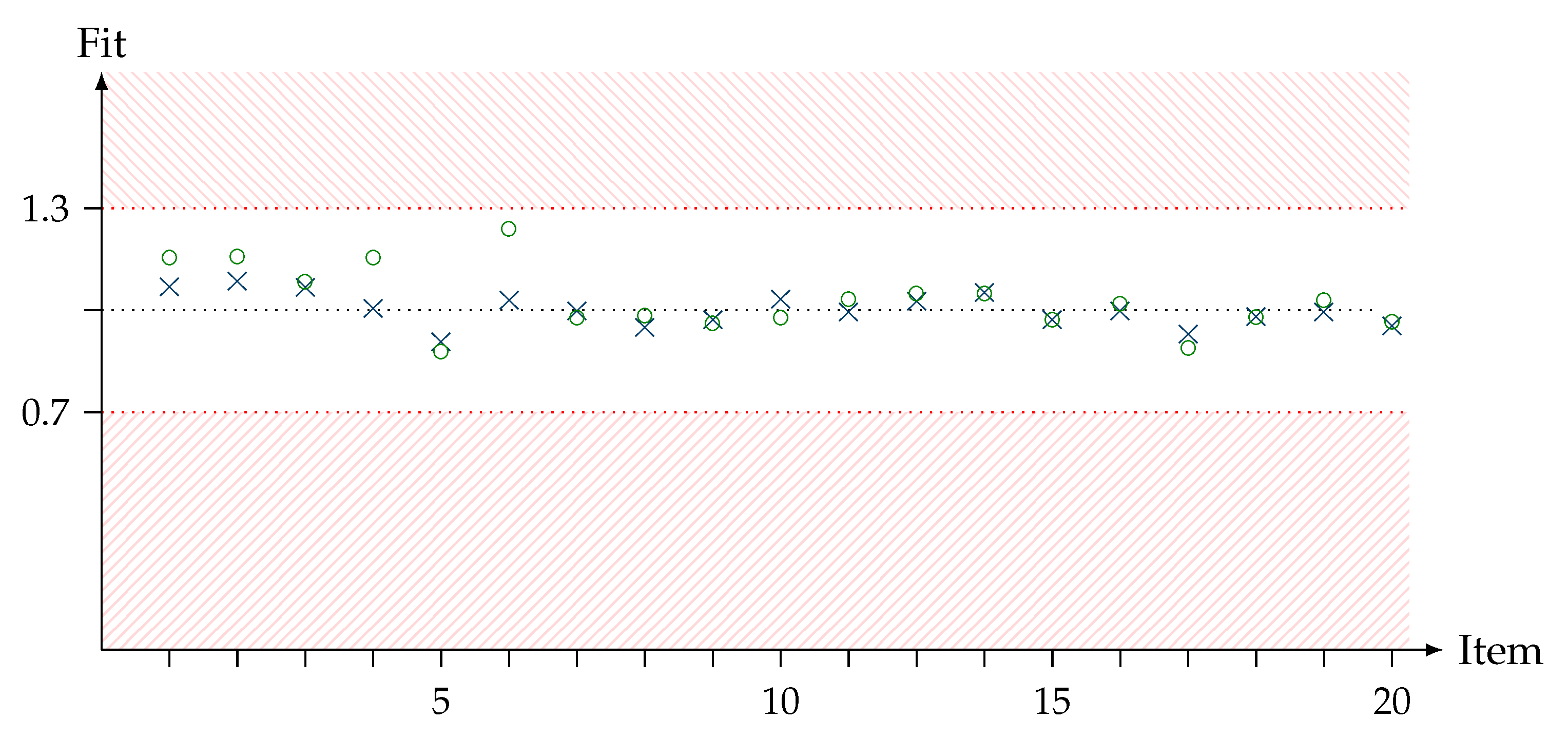
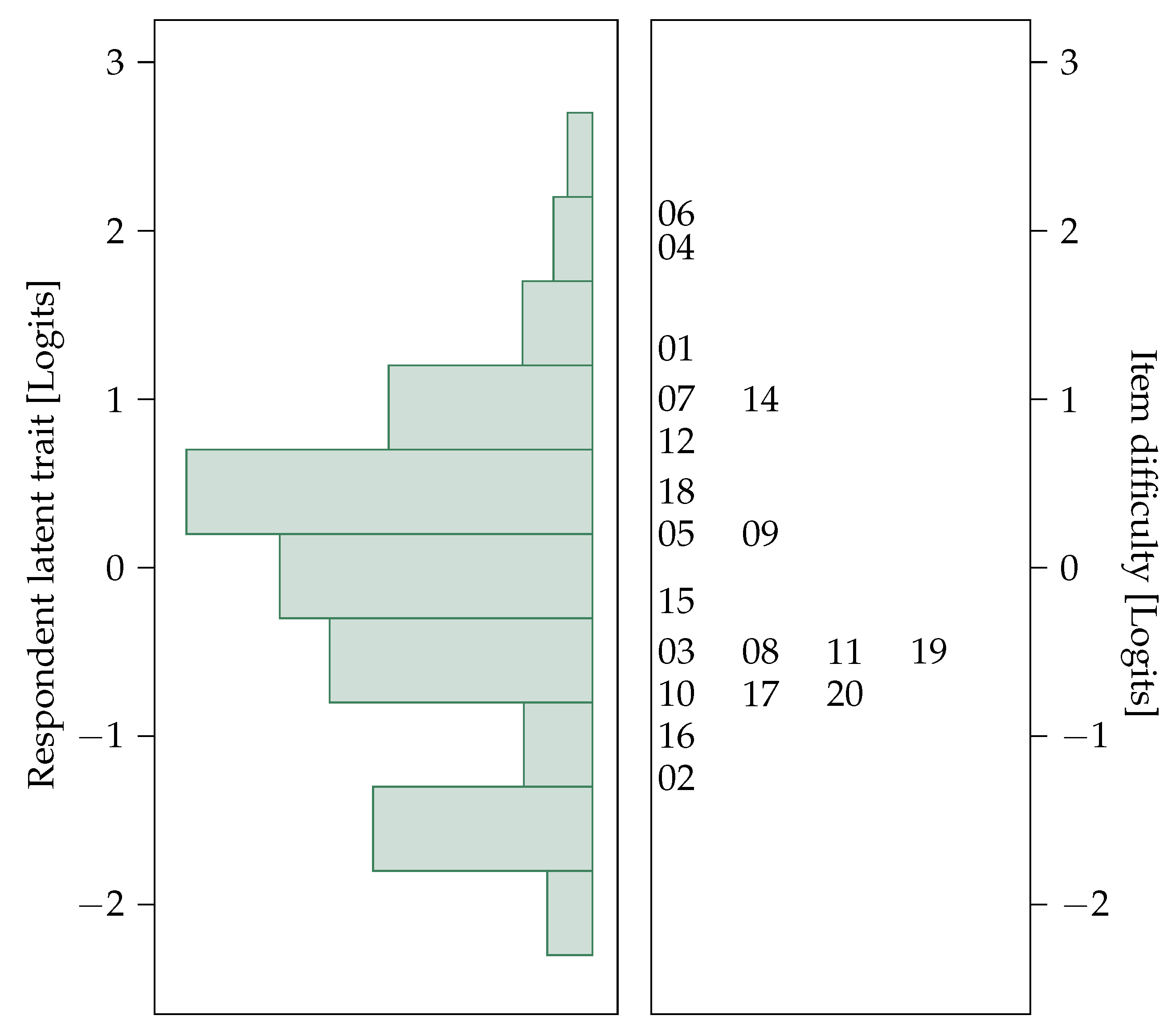
| Item | Skewness | Kurtosis | Item Difficulty | SE | Infit MNSQ | Outfit MNSQ |
|---|---|---|---|---|---|---|
| Item 1 | 1.25 | −0.44 | 1.34 | 0.21 | 1.07 | 1.16 |
| Item 2 | −1.08 | −0.85 | −1.16 | 0.20 | 1.07 | 1.16 |
| Item 3 | −0.33 | −1.91 | −0.37 | 0.18 | 1.06 | 1.08 |
| Item 4 | 2.11 | 2.48 | 2.04 | 0.25 | 1.01 | 1.15 |
| Item 5 | 0.36 | −1.89 | 0.41 | 0.18 | 0.92 | 0.88 |
| Item 6 | 2.29 | 3.28 | 2.17 | 0.26 | 1.03 | 1.24 |
| Item 7 | 1.04 | −0.94 | 1.12 | 0.20 | 0.98 | 0.97 |
| Item 8 | −0.39 | −1.87 | −0.44 | 0.18 | 0.96 | 0.98 |
| Item 9 | 0.21 | −1.97 | 0.24 | 0.18 | 0.97 | 0.96 |
| Item 10 | −0.71 | −1.52 | −0.78 | 0.19 | 1.02 | 0.98 |
| Item 11 | −0.42 | −1.84 | −0.47 | 0.18 | 1.00 | 1.03 |
| Item 12 | −0.67 | −1.56 | 0.75 | 0.19 | 1.01 | 1.05 |
| Item 14 | 1.00 | −1.02 | 1.08 | 0.20 | 1.06 | 1.05 |
| Item 15 | −0.19 | −1.99 | −0.21 | 0.18 | 0.97 | 0.97 |
| Item 16 | −0.85 | −1.30 | −0.93 | 0.19 | 1.00 | 1.02 |
| Item 17 | −0.51 | −1.76 | −0.57 | 0.18 | 0.91 | 0.89 |
| Item 18 | 0.48 | −1.79 | 0.54 | 0.18 | 0.98 | 0.98 |
| Item 19 | −0.33 | −1.91 | −0.37 | 0.18 | 1.01 | 1.03 |
| Item 20 | −0.51 | −1.71 | −0.57 | 0.18 | 0.96 | 0.96 |
| Item 2: A binary operation on a set M is ⋯ | |||||
|---|---|---|---|---|---|
| □ | ⋯ a map . | ||||
| □ | ⋯ a map . | ||||
| □ | ⋯ a map . | ||||
| □ | □ | □ | □ | □ | |
| Very sure | Sure | Undecided | Unsure | Guessed | |
| Item 5: One can show that defines an operation on such that is a group. The neutral element of this operation is ⋯ | |||||
|---|---|---|---|---|---|
| □ | ⋯ 5 | ||||
| □ | ⋯ 0 | ||||
| □ | ⋯ | ||||
| □ | □ | □ | □ | □ | |
| Very sure | Sure | Undecided | Unsure | Guessed | |
| Item 6: One can show that defines an operation on such that is a group. The inverse of is given by ⋯ | |||||
|---|---|---|---|---|---|
| □ | ⋯ | ||||
| □ | ⋯ | ||||
| □ | ⋯ | ||||
| □ | □ | □ | □ | □ | |
| Very sure | Sure | Undecided | Unsure | Guessed | |
| Analysis | Excellent | Good | Average | Poor | CI2GT | ||
|---|---|---|---|---|---|---|---|
| Classical Test theory | |||||||
| Item Statistics | |||||||
| Difficulty | – | – (3) | – | – (3) | good | ||
| Discrimination | > | > | >0 | > | good | ||
| Total score reliability | |||||||
| of total score | > | > | > | > | average | ||
| -with-item-deleted | All items less than overall | (3) | (6) | (9) | excellent | ||
| Item Response Theory | |||||||
| Individual item measures | |||||||
| Infit MNSQ | – | – | – | – | excellent | ||
| Outfit MNSQ | – | – | – | – | excellent | ||
| All items fit the model | (2) | (4) | (6) | (8) | excellent | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veith, J.M.; Bitzenbauer, P.; Girnat, B. Assessing Learners’ Conceptual Understanding of Introductory Group Theory Using the CI2GT: Development and Analysis of a Concept Inventory. Educ. Sci. 2022, 12, 376. https://doi.org/10.3390/educsci12060376
Veith JM, Bitzenbauer P, Girnat B. Assessing Learners’ Conceptual Understanding of Introductory Group Theory Using the CI2GT: Development and Analysis of a Concept Inventory. Education Sciences. 2022; 12(6):376. https://doi.org/10.3390/educsci12060376
Chicago/Turabian StyleVeith, Joaquin Marc, Philipp Bitzenbauer, and Boris Girnat. 2022. "Assessing Learners’ Conceptual Understanding of Introductory Group Theory Using the CI2GT: Development and Analysis of a Concept Inventory" Education Sciences 12, no. 6: 376. https://doi.org/10.3390/educsci12060376
APA StyleVeith, J. M., Bitzenbauer, P., & Girnat, B. (2022). Assessing Learners’ Conceptual Understanding of Introductory Group Theory Using the CI2GT: Development and Analysis of a Concept Inventory. Education Sciences, 12(6), 376. https://doi.org/10.3390/educsci12060376






