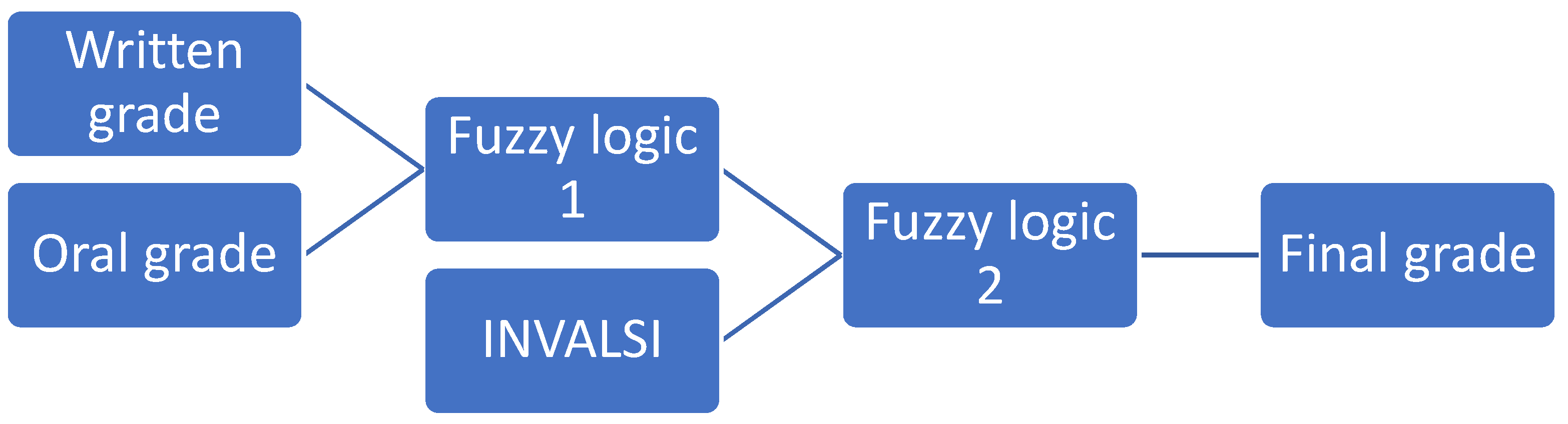
5. Discussion and Conclusions
The present research aimed to analyze how the two proposed fuzzy-logic-based assessment methods differ from the traditional teacher assessment. Before doing so, we screened the raw sample data to gain a clearer view of student achievements. Our preliminary analysis reveals that written grades, oral grades, and achievements on the INVALSI test are not normally distributed. Oral and written grades are strongly and positively correlated, indicating that students with higher written grades have higher oral grades and vice versa. A deeper investigation demonstrates that oral grades are generally higher than written grades. The underlying reason for this difference might be explained by considering what comprises oral grades. For instance, oral grades include information about oral examinations, written tests that are not compiti in classe, homework, project work, and attendance. Thus, several elements are included in this information [
3,
4,
5]. In contrast, written grades consist solely of in-class written tests compiti in classe, which do not include other information about the students.
Although the correlation between written and oral grades is strong, the correlation between written grades and achievements on the INVALSI assessment and between oral grades and INVALSI is moderate. The results indicate that students with higher school grades have higher achievements on the Italian national assessment and vice versa. The correlation agrees with previous research in the Italian context [
11]; however, it is much lower than the correlations found in the international literature [
3,
10]. This fact indicates that several factors influence teacher-given grades, not solely student academic knowledge. The INVALSI assessment, although an objective measure of student mathematical outcomes [
23], cannot measure some metacognitive and cognitive factors involved in learning and understanding mathematics [
18]. Thus, the fact that the correlations are not strong might be explained by considering what comprises each grade and the peculiarity of the INVALSI assessment.
Moreover, from the initial analysis, the average score on the INVALSI was
M = 178, which is lower than the national average of
M = 200, and the standard deviation
SD = 35.4 is lower than the national
SD = 40 [
18,
19]. Thus, additional care should be taken when data are interpreted and generalized to the whole population of Grade 13 Italian students.
Furthermore, we analyzed student grades between different typologies of high schools, finding statistically significant differences concerning written and oral grades and the INVALSI assessment. Students from SLs have the highest achievements on the INVALSI assessment, followed by TSs, OLs, and, finally, VSs. Such differences have also been found by the INVALSI Institute [
18,
19] and other research [
11] and might be understood considering the different focuses of the schools [
12]. Students from SLs have the most hours of mathematics per week [
13]; thus, they are more likely to study some topics in detail that are assessed by the INVALSI tests. However, VSs aim to provide students practical knowledge, and mathematics represents a marginal subject. Students from all schools have similar grades, except for VSs, which have the lowest achievements concerning student written and oral grades. This fact might be explained by considering that individual teachers use different assessment methods and criteria, leading to different grades between the four high school typologies.
After a general analysis of the sample, we applied the procedure of fuzzification, inference, and defuzzification using both the COG and MOM methods. First, we checked the final student (hypothetical) grades found using the COG method. The minimal grade was 3, and the maximal grade was 9. No student obtained an excellent (10) grade.
Our first research question regarded student COG hypothetical grades and whether they are different from traditional school grades. First, we aimed to determine whether a correlation exists between hypothetical grades and student grades and INVALSI scores. The correlational analysis found that hypothetical grades are positively and strongly correlated with written and oral grades and achievements on the national test, suggesting that students with higher grades or achievements on the INVALSI test obtained a higher hypothetical grade. This result is unsurprising because hypothetical grades are created using student school grades and scores on the INVALSI test.
Second, a deeper analysis of the differences between traditional teacher-given grades and hypothetical grades reveals a statistically significant difference between these variables. Hypothetical grades are lower than written and oral grades. Considering the Cohen’s
d measure of the effect size (
d = 0.835 for written grades and
d = 0.931 for oral grades), substantial differences might exist between hypothetical grades and student grades. Thus, the fuzzy logic assessment method is stricter than the traditional grading system. Considering a student with oral and written grades of 10 and INVALSI of 280 (i.e., very good), the student would obtain a 9.36 as a Fuzzy logic 1 output and an 8.45 (i.e., a score of 9) as the final output, which does not correspond to what one would expect for excellent performance. Moreover, a student with oral and written grades of 10 and an INVALSI score of 311 (the maximum for the INVALSI in this sample) would obtain a total grade of 8.65 (i.e., a score of 9 once again). A student with a 100 on the INVALSI test (i.e., very low) and a 1 for the oral and written grades would obtain a 2.06 for the Fuzzy logic 1 output and a 2.53 (i.e., a score of 3) as the final grade. Thus, from the presented limitations, the proposed method penalizes excellent students and is a more lenient grading method for extremely low-achieving students. The proposed COG method is unfair considering the three models of grading [
42]. Considering a fair grade as the achievement students receive as a reward or punishment for learning or failing to learn course content or institutional values, we understand that excellent students are penalized because they master the course topics (their school grades are excellent) and other institutional material (the grade on the INVALSI test is excellent). Hence, excellent grades are unjustly lowered by at least one grade level in this specific case.
Finally, an analysis of the grade distribution between the four high school typologies was considered. The results indicate a statistically significant difference between the four school typologies. Students from the SLs had the highest average, followed by students from TSs, OLs, and VSs. Although no statistically significant difference was found in oral and written grades for the school typology, with the only exception of VS with the lowest mean, hypothetical grades no longer reflect such a distribution. Nevertheless, hypothetical grades reflect the situation depicted concerning the INVALSI test, where students from the SLs outperformed students from all other school typologies. Thus, the hypothetical grades, reflecting student performances on the INVALSI test, maintain such differences between the four school typologies, with the only exception in comparing OLs and TSs, which have a statistically nonsignificant difference in hypothetical grades.
Our second research question regarded student MOM hypothetical grades and whether they are different from traditional school grades. First, we aimed to understand the correlation between the MOM hypothetical grades and student grades and INVALSI scores. A correlational analysis found that hypothetical grades are positively and statistically significantly moderately correlated with school grades and are strongly correlated with achievements on the INVALSI test. Once again, the result is unsurprising because the MOM hypothetical grades also include information from both student grades and achievements on the national assessment of mathematical knowledge.
Second, we verified whether a difference exists between traditional grades and MOM hypothetical grades. The results demonstrated that hypothetical grades are statistically significantly lower than written and oral grades. The interpretation of the Cohen’s
d measures of the effect size (
d = 0.738 for written grades and
d = 0.806 for oral grades) revealed that the differences between the traditional and novel methods of assessing student knowledge are substantial; hence, the MOM hypothetical grades are generally stricter than traditional ones. A student with oral and written grades of 10 and an INVALSI of 280 (i.e., very good) would obtain a 10 as a Fuzzy logic 1 output and a 10 as a final output, which corresponds to what one would expect from excellent performance. Moreover, a student with oral and written grades of 10 and an INVALSI score of 311 (the maximum possible INVALSI score in this sample) would obtain a total grade of 9.78 (i.e., a 10). In contrast, a student with a 100 on the INVALSI test (i.e., very low) and a 1 for oral and written grades would obtain a 1.50 (i.e., a score of 2) as a Fuzzy logic 1 output and a 1.59 (i.e., a score of 2) as a final grade. Hence, the MOM hypothetical grade does not penalize excellent students as much as the COG method. Thus, the MOM hypothetical grade might be considered a fairer method than the COG, despite some anomalies (e.g., those presented in
Table 6 (**)). These anomalies are related to the way data are fuzzified and defuzzified. A graphical example is presented in
Figure 5, where the surface of the COG Fuzzy logic 2 (denoted by fuzzy2) is depicted. The anomalies are present due to the waves and irregularities of the surface.
Finally, the results indicate a statistically significant difference in student MOM hypothetical grades between the four high school typologies. A deeper analysis confirmed that students from SLs have the highest grades, followed by TSs, OLs, and VSs. All differences in grades are statistically significant, except the OL and TS difference in grades. Hence, the results reveal that the MOM hypothetical grades, similarly to the COG method, discriminate between the school typology similarly to the INVALSI score.
This fact partially answers the last research question (i.e., whether differences exist between the COG and MOM hypothetical grades). Both methods privilege SL students, who had the highest scores on the INVALSI assessment [
11,
18]. Nevertheless, students from VSs have the lowest hypothetical grades. Thus, both fuzzy methods create a gap in achievements between students from the four high school typologies. Students from SLs have a stronger theoretical basis and a higher-level academic preparation [
12]; thus, it is unsurprising that their scores on the INVALSI test are the highest; however, SL students in the sample had written and oral grades similar to those of students from other school typologies. Thus, although their levels of mathematical knowledge measured through the INVALSI test are higher than those of students from other schools, their final grade, which universities can later use to select future students [
43,
44] or employers to select employees [
45], might provide incomplete information about their real knowledge and competencies in mathematics. Thus, including information about student performance on the national assessment (or, in general, other standardized assessments) might contribute to a clearer view of student knowledge and competencies [
1,
9].
The results demonstrated that the COG and MOM methods produced lower grades than the grades the students obtained on their report cards, both written and oral. Further analysis identified the MOM method as statistically stricter than the COG method, although the latter did not produce any grade below 3 or higher than 9. The correlation between the two kinds of hypothetical grades is strong and positive, indicating that higher grades of one kind would produce higher grades of the other. An analysis of student grades between the four school typologies reveals that SL students received higher grades when graded using MOM methods, whereas students from any other school typology received statistically significantly higher grades using the COG method.
Overall, this research highlights that lower achievements are expected when student scores on the INVALSI test are added to student school grades. Higher-achieving students were penalized using the COG defuzzification method, whereas lower-achieving student grades increased, similar to the findings by [
31,
35]. Thus, the COG method is unfair in this case. The MOM defuzzification method represents a fairer grading method, despite some anomalies detected due to the definition of the membership functions and inference rules [
29]. Nevertheless, the proposed grading system also considers student achievements on standardized assessments, promoting the objectivity of the final student grade [
36].