Abstract
According to the Programme for International Student Assessment (PISA) 2015 measurements, Slovak primary school pupils commonly can reach some below average scores in terms of scientific literacy and have less and less positive attitudes towards the natural sciences. Natural sciences and statistics are intertwined disciplines. This implies that there is a room for teachers to try using interdisciplinarity and including basic statistics in the laboratory lessons of natural sciences. The aim of this research paper is to identify the difficulties that can occur when primary pupils collect and process data during a practical research task, combining, here, the knowledge stemming from the natural sciences and statistical reasoning. The research sample consisted of nine primary pupils from grade 1 to grade 4; the average age was 9.44 ± 1.33 years. Pupils were divided into the three age heterogeneous groups who were assigned a laboratory exam. The data were collected via an unstructured participatory observation. The results of our analysis of verbal expressions and practical activities suggest that pupils in our research sample are in the range of levels of nonformal and inconsistent understanding of statistics. In addition, we observed here some characteristics of consistent noncritical understanding. These findings suggest that, with the proper stimulation and frequent research activities requiring the direct activity and involvement of pupils, they could achieve higher levels of statistical literacy as well.
1. Introduction
In the Programme for International Student Assessment (PISA) 2015 measurement organized by the Organisation for Economic Co-operation and Development [1], Slovak lower secondary school pupils used to lag behind the international average score in the field of scientific literacy. In reality, they usually reach only 461 points compared to 493. Since the first measurement in 2003, unluckily and moreover, there has been a steady decline in their performance as well. Further analysis revealed that this could be largely influenced by teachers’ pedagogies. On the other hand, pupils, who were regularly exposed to any type of laboratory work as a part of classwork in the field of natural sciences, scored higher than the pupils who reported not having such experience [2] at all. Thus, cognitive performance is related to other noncognitive factors, such as attitudes or motivation, which is also demonstrated by the PISA 2015 results. The observed pupils largely agreed with the statement that the study of natural sciences can increase their chances of success in the labour market, but their index of internal motivation in relation to the sciences was even lower than in 2006. This clearly indicates that there are less and less positive attitudes towards the natural sciences, as such, in the population of Slovak lower secondary school pupils. Moreover, their performance in the test performed was also strongly correlated with their current self-confidence [2], which could be another important factor. In addition, it is likely that just self-confidence is in a positive feedback loop with performance. A pupil with a lower level of self-confidence is likely developing and contributing a lesser effort to problem-solving situations and topics, thus, this can further diminish their performance and decrease their level of self-confidence in the end. On the other hand, a good performance definitely leads to a higher level of self-confidence, and so, consequently, further increases the likelihood of good performance in the future. Whereas the frequent inclusion of practical exams in the teaching process is positively related to performance, as such, it could positively increase their self-confidence as well. Similarly to inquiry based learning in mathematics [3], including inquiry in science education helps students to develop accurate scientific knowledge and skills, increases the understanding of science and facilitates the development of the understanding of the nature of science [4] and even gives students an opportunity to practice metacognitive skills [5].
Laboratory and research exercises also require pupils to work with some factual data; where it needs to be collected, recorded, analysed, and interpreted as well. During laboratory exercises aiming at the verification of well-established laws and principles, students often gather data without a deeper understanding of the meaning of their actions [6], yet involving students in the inquiry in science leads to more robust comprehension of collected data and their analysis, and even the transference of the obtained abilities to new contexts [7]. Obviously, statistical literacy includes such motions, abilities and capacities as numeracy, orientation in tables and charts, as well as some knowledge of basic statistical concepts (such as percentage or arithmetic mean), among other things [8,9,10]. On the other hand, statistical reasoning is largely based on advanced concepts such as understanding terms such as probability and sampling, or knowing the difference between causation and correlation, but the Slovak curriculum states that primary pupils, on whom our study is focused, should be at a level where they are able to read simple tables or bar charts [11,12]. When statistics education at the primary level is reduced solely to frequency counts and bar graphs, then pupils have only a limited basis for developing statistical literacy skills in later years and, therefore, they possess only an inadequate capacity to make sense of data in context or assess claims derived from data [13].
As is well known, the natural sciences can build on their body of knowledge through the processes of the accumulation and examination of really huge amounts of data, which comprise the main domain of statistics in the first place. Certainly, just statistics can be used for answering various questions in the science, technology, engineering and mathematics (STEM) disciplines [14]. The overlap between the two disciplines is quite apparent, which implies that there is room to integrate some basic statistics and the laboratory education of natural sciences, creating what can be, according to [15], considered an interdisciplinary education, as “learning goals transcend the individual disciplines, since they involve various disciplines” (p. 3). Several studies have demonstrated the positive influence of interdisciplinary activities in developing statistical literacy, especially at primary level [16,17,18].
Even though there is a broad consensus that interdisciplinary teaching brings certain additional values to mathematics education, as it enhances the overall understanding of the word [19], interdisciplinary teaching definitely involves the greater demands on the expanded effort and the organization of the educational process [20]. According to [21], pupils report an increased mathematical anxiety and decreased self-confidence while solving problems in the field of statistics. As some authors [22,23,24,25,26] report an increase in intrinsic motivation in statistical reasoning while processing data obtained by their own activity, we assume that integrating any reasonable laboratory work and statistical reasoning can also enhance disciplinary knowledge in mathematics and science, as an exemplification of the investigative cycle producing data to be investigated.
When integrating statistics into the education of natural sciences (or to teach any subject in an interdisciplinary way), it is useful to know possible difficulties that pupils might encounter, bringing us to the purpose of our study. The aim of this research paper is to suggest the basic key design principles and identify any difficulties that could arise when primary pupils collect and process data during a practical research task, combining here some pieces of the knowledge stemming from the natural sciences and statistical reasoning together. The following research questions are addressed there:
What are the key design features of interdisciplinary activities, combining the knowledge from the natural sciences and statistical reasoning, that can support the learning of statistics?
What are the difficulties that primary pupils can encounter while providing statistical reasoning based on their laboratory work?
2. Methodology
The presented study is a part of the longitudinal design based study about summer camps for primary pupils about STEM that builds on experience from the even longer study focused on summer camps for lower secondary students described in [27]. During the camp activities, the pupils are divided into 6 groups, heterogeneous in terms of age, gender and previous experience with leisure time activities in STEM. The work of three groups was analysed and presented in the paper. In each year, the camp has a different overarching topic, namely, liquids, water, natural elements, physical quantities, or motion. Six to eight activities on the overarching topic for the heterogeneous groups of 3–4 students were designed. Some of the activities were focused on science (mostly physics) and mathematics, some of them used interdisciplinary teaching.
In this study, we explicitly formulate the design principles for designing the interdisciplinary activities developed within the long-term study and exemplify them in the chosen activity. The analysed activity was designed by the primary preservice teacher. The schedule of the camp allows six rounds of conducting the activity. The first three rounds were used for the cycles of the implementation–reflection–adjustment of the designed activity. The last three parts were implemented in the form of mini case studies. Each group consisted of three pupils and, therefore, a total of nine pupils participated in this study. The data was collected through unstructured participatory observation [28]. The researcher was a partially active participator who mostly let the pupils perform the work on their own, but occasionally interfered or engaged in Socratic dialogue with them.
The nature of the study is narrative, as, according to Polkinghorne [29], “narrative inquiries produce a storied description of a practice process carried out in a concrete life space. … they do not produce a list of techniques or procedures that are promised to work in every setting. They offer their readers a vicarious experience of how a practice was conducted in a concrete situation. From this the readers’ experiential background is enlarged, their repertoire of possible actions is increased, and the judgments about what might be done in their own practice in similar situations is sharpened” (p. 396).
Data were recorded in the two forms—researcher’s verbal notes describing the pupils’ behaviour and an audio record to enable a more thorough analysis. Pupils were informed about audio-recording beforehand and the device was placed where it would not disturb or distract them. Informed written consent signed by their parents was collected before the camp started. The analysis was carried out in the two ways.
First, the deductive analysis was performed according to the levels of statistical thinking. There are several theoretical models of the stages of statistical reasoning [30,31], but in this study, we present the 6-level framework proposed by Watson (Figure 1).
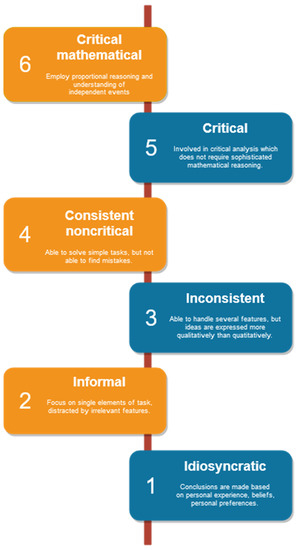
Figure 1.
Levels of statistical literacy (visualized based on [31] (own source).
At the most basic level of statistical literacy is just idiosyncratic understanding, which means that pupils are not thinking in the context of the task and they draw their conclusions based on their own experience and attitudes. However, on the other hand, they can read basic tables and charts. At an informal level of understanding, they are able to think in the context of the task, but their predictions are based on some irrelevant factors and they do not grasp the necessity for a representative sample. They prefer the median to mean as a central value. The next level is inconsistent understanding, where the pupils’ answers are more strongly connected to the context of the task, but they do not fully understand dependency and the arithmetic mean. They can commonly form conclusions, but their argumentation is factually incorrect. At the level of consistent noncritical understanding, the context of a task is looked at uncritically. Pupils would prefer representative over a random sampling and the mean is understood solely algorithmically. The next step is the critical level of understanding, which includes the ability to examine claims critically, combine random and representative sampling, draw a chart appropriate to the given requirements, differentiate between the mean and median, etc. The final level—the critical mathematical understanding—is then characterized by the ability to consider confounding variables in the research, understand uncertainty and variation or work with multiple forms of data presentation. For instance, some grade 6 pupils are capable of refining a research question to a specific data set they are given (this also proved to be true for grade 4 pupils) and they can make some predictions based on multiple variables [22,32,33]. Statistical literacy is necessary not only for academics and researchers, but also for any person in contemporary society, to evaluate the countless information received from the media and other sources [31]. Therefore, it is important to cultivate our statistical reasoning from the time of childhood and actual, proper research of the education process can give us some basic useful hints on how to improve the teachers’ work in the end. Besides that, inductive analysis was carried out to determine the difficulties that the pupils would encounter while solving the interdisciplinary problems that integrate laboratory work in physics and providing plausible statistical reasoning.
The design principles implemented in the study were based on principles identified as especially important by Barron et al. [34]. As the designed activity was intended for informal settings, the principles had to be adjusted and tailored to the needs of interdisciplinary teaching:
- (a)
- During the laboratory inquiry, cover the whole cycle of the data investigation to allow pupils to formulate research questions; state the hypothesis; design investigations; collect data using observations, surveys, and experiments; describe and compare data sets; and propose and justify conclusions and predictions based on some data in the extent appropriate for 45-min timeslot;
- (b)
- Provide appropriate scaffolding in both science and statistics;
- (c)
- Provide the pupils with opportunities to learn from their own mistakes;
- (d)
- Allow the peer instruction by asking appropriate questions;
- (e)
- Respect the expected low levels of statistical literacy related to the age of the participants.
We looked at the curricula for the primary school and took some inspiration from the approved natural sciences textbooks as well. The overarching topic of the camp was “Water” and the activities were aimed at the properties of liquids. The activity was designed with an intention to cover the whole cycle of the data investigation. Another requirement of the designed activity was that the collected data should be related to the viscosity of liquids and statistical reasoning should be used for comparing central values. Several ideas were produced by the student teacher and each of them were assessed by the organizers of the camp. In the end, the activity called “Fish Eggs” was designed. The goal of this laboratory work is to determine in which of the two liquids an object sinks faster. Firstly, rice grains were used, but the grains did not sink evenly due to their shape. The student teacher realized that a more regular shape must be used. Then, identical glass balls were used and, later, they were all marked by an insoluble felt pen so they could be seen well in liquids. Water and rapeseed oil, which were chosen as the liquids for this exam, were poured in the self-made plastic tanks that had the starting and finishing line drawn on them so that there could be uniform measuring by stopwatch. The distance of the glass ball’s sinking was 16 cm. The settings of the laboratory work can be seen in Figure 2.

Figure 2.
Settings of the “Fish Egg” activity.
The pupils were also given a tablet as a stopwatch and a worksheet, where they were supposed to write down their time predictions, three measurements for both liquids, and conclusions in the form of finishing preprinted sentences. In the initial stages of the activity, pupils were engaged by the lecturer who talked to them about the fish eggs whose appearance was demonstrated by the glass balls. Before the pupils began their own measurements, they were asked which of the three measurement tools—ruler, weighing machine, or stopwatch—is appropriate to determine in which liquid the glass ball sinks faster. They were also supposed to come up with their own time predictions of sinking in both liquids—water and rapeseed oil. During the measurement, each of the three pupils had an assigned role. One was dropping the glass ball into the liquid, the other was signalling when to start and finish the time measurement, and the last one was operating the stopwatch. For each of the three measurements, pupils exchanged their roles.
3. Results
In this section, we present the three mini case studies. The pupils in the three groups were from grade 1 to grade 4; the average age was 9.44 ± 1.33 years. The procedure of each group is described and wrapped up with a concluding comment in the final paragraph.
3.1. First Group
The first group consisted of two fourth grade pupils, A and B, and a second grade pupil, C (8–11 years old). The initial stage was swift-the older pupils were familiar with fish eggs, so they explained the term to the younger one. When making time predictions, pupils in this group vastly differed and they based their predictions on the density, not the viscosity of liquids. Pupil A made a prediction as follows: “In oil, the ball will fall to the bottom more slowly than in water”. He justified his claim by saying that oil is thicker than water, so the bottom ball in the oil will fall “harder”. Pupil C agreed with this statement and, thus, formulated a prediction in the same wording. Pupil B opposed his classmates and made the opposite prediction in this way: “In oil, the ball will fall to the bottom faster than in water”. He argued that oil has a lower density than water. The resulting situation, in which two different predictions appeared concurrently in one group, offered an ideal space for the implementation of the research activity. The difference in their views was a problem for the pupils, which motivated them to perform some scientific research. After formulating the estimate, we handed out worksheets to the pupils, where they had to enter their own estimate of the result. Subsequently, we gave them some space to think and formulate how they could meet the goal of the activity and what tools they would need for it. After a short conversation, the group agreed that they would need some glass balls, oil, water and containers for liquids. Then, we provided them with these aids. The pupils began to throw the balls into the liquids and observed the speed of their movement, which resulted in the expression of the opinion that the balls fall in both liquids at the same speed. We intervened in the formulation of such a prediction and challenged the pupils to prove their new statement with something. The pupils argued that they formulated their claim based on observation. In this case, we guided their activities and required them to measure the time required for the ball to hit the bottom. As part of this, we demonstrated the three measuring tools to the participants. The participating pupils unanimously chose a digital stopwatch on a tablet as the most appropriate tool for time measuring.
The height of the tanks or the proportions of glass balls were not checked, which was supposed to be carried out to prevent possible error in measurements. Afterwards, pupil A did not manage to start the stopwatch on time, so the glass ball had to be thrown into the tank again. After a successful first round of measurements, pupils had to be guided when writing entries into the table, as was the case when they were drawing their results on the time axis. They did not yet have their own terms for table orientation in their active vocabulary (they used left, right, up and down instead of row and column). Moreover, they automatically wrote down the first entry into the first empty cell, suggesting they did not pay proper attention to the table, as such. As for the entries on the time axis, one of the pupils had already the right understanding of time units (one second is one hundred centiseconds), so he corrected and explained it to his co-operators.
Factually, during each trial, the starting and stopping of the stopwatch was inaccurate. Nevertheless, the measured time was shorter for water in the all trials. Pupil C formulated the correct conclusion, and pupils A and B agreed. Since all the values shown on the axis corresponding to the measured values in the water medium were significantly below all the values shown on the numerical axis belonging to the oil medium, we did not consider it necessary to determine the mean value at this stage of the work. Based on the measured and displayed values, pupils could clearly determine in which liquid the ball fell to the bottom of the vessel faster and in which slower, which resulted in the possibility to formulate a conclusion of the research activity. Before writing the conclusion in the worksheet, we guided the pupils’ activities and suggested that they choose from the three measured values within one fluid to select one value that would best characterize the time interval during which the ball fell to the bottom in that fluid. The older pupils suggested calculating the arithmetic mean. We asked them to explain how they would calculate this value. The participants characterized the arithmetic mean as a “number in the middle” and their verbal description of the procedure by which this number was calculated was correct, so we allowed them to calculate the arithmetic mean from the measured values. However, the addition of decimal numbers was problematic for the pupils and they could not further agree on the procedure. Since working with decimal numbers and calculating the arithmetic mean were not the subject of research or our qualitative research, we intervened in the activities of pupils and recommended that they choose from the measured values that would be closest to the arithmetic average. In the pupil’s definition of the term arithmetic mean, they had already described where, in the series of numbers, there is a number expressing the central-tendencyvalue. Displaying the measured values on the numeric axis ensured that the elements of the file were sorted by size, thus creating a space for determining the median of the file. Pupils thus correctly determined the mean value from the measured numbers, and they also correctly entered it in the pre-printed sentences in the worksheet. In the end, the pupils decided on the correctness of their statement from the beginning of the activity.
Based on the fact that the pupils formulated a conclusion based on the data they collected, we can rule out they are now on the level of idiosyncratic understanding. Instead, they showed some signs of the informal (not accounting for possible variations caused by error in measurement) and inconsistent understanding (incorrect argumentation for a claim—density instead of viscosity). They were able to compare the measured values and they chose just the arithmetic mean as the most appropriate central tendency. The pupils’ performance was most negatively affected mainly by their lack of skills with the operating stopwatch and an imprecise conception of time units.
After displaying the measured data on the numerical axis, all pupils clearly agreed at the end of their research. Pupils were successful in comparing the gained data, which in this case consisted of comparing numerical values; which is, again, one of the hallmarks of the level of informal understanding. However, the fact that the pupils chose to calculate the arithmetic mean when requesting the most appropriate value to compare the results does not coincide with the definition of the mentioned level of statistical literacy. Through the visualization of measured phenomena by graphical displaying, the pupils demonstrated their ability to more compactly perceive the collected data, which again coincides with the level of inconsistent understanding that we assigned to the pupils when formulating their predictions. During the phases of data collection and the formulation of conclusions, the pupils relied on the data that they found in their own research, and, therefore, they did not proceed only from a personal point of view; thus, these two aspects support that we can exclude any inclusion of these pupils in the level of idiosyncratic understanding.
Based on the above analysis of the activities of the participants in the first research group, we can say quite daringly that these primary school pupils are in the range of levels of informal understanding and inconsistent understanding (Figure 3). Their statistical work was rather adversely affected by the lack of skills in time-measuring using the electrical equipment with digital stopwatches, as well as the lack of sufficient concepts about time units, as such, and their transformation.
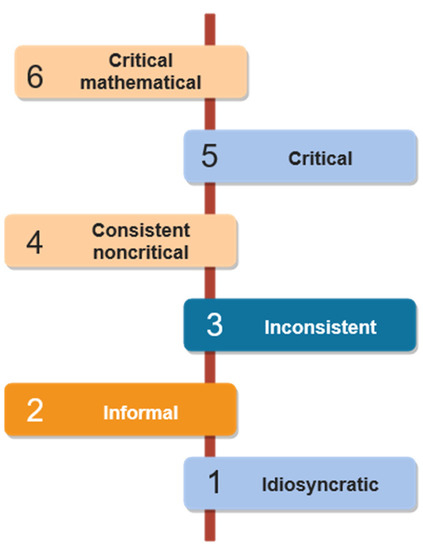
Figure 3.
Visualization of the observed level of statistical literacy among the observed pupils in all groups.
3.2. Second Group
The second group consisted of a second grade pupil, D, third grade pupil, E, and fourth grade pupil, F (9–11 years old). Pupils in this group correctly chose a stopwatch as their working instrument. The pupils measured the height of the tanks and performed one trial to test the operation of the stopwatch. Similarly to the pupils from the first group, they did not have a working vocabulary for their orientation in the table, but they understood they should check whether the height of the two tanks was identical. After the researcher asked them what would happen if one of the tanks was higher, they correctly answered it would take longer for the glass ball to sink in the higher tank. Impreciseness in the time measurement was yet again present, but the entries in the table and time axis were correct.
The participants did not initially express their opinion. We tried to activate their thought activity by asking whether the balls would fall to the bottom in both liquids. Pupil E expressed this opinion: “The ball will float in oil”. However, he did not immediately substantiate his claim, and pupil D interrupted his statement by formulating his own estimate: “I think it will fall in both”. However, when he was again asked about his opinion, he agreed with his classmate and did not think more about his statement. Pupil E independently transformed his statement into a prediction and justified it: “It will fall more slowly in oil because it is thicker than water”. The other pupils in the group shared the same opinion. As their predictions coincided, a different situation arose than in the first group, and it was not possible to motivate the pupils by the variability in their predictions until the implementation of the research activity. Therefore, we wanted to motivate them into some practical activities by playing researchers.
The following activities within the activity—writing a prediction in the worksheet, deciding on the necessary tools—took place almost in the same way as in the first group, but these participants also included a tool for time-measuring in the tools. The participating pupils identified digital stopwatches on the tablet as the most appropriate tool for time-measuring.
We again focused the pupils’ attention on a clean table drawn on the blackboard. As in the previous group, their orientation in it was characterized by the terms left, right, etc. When entering the word WATER in the table, the pupils guided us to the right to write the word OIL. So we moved to the right within the same column, to create a situation when the pupils would be forced to use the word column, or another term, to direct us to the right place. Pupil E described this place as “the next frame on the right”. We wrote the table on the basis of similar instructions.
The next step in the pupils’ research activity was the measurement itself. Again, we allocated the positions of initiator, observer and meter among individual participants. They proceeded with the measurement in the same way as the pupils in the first group, so they started by measuring in water. Based on our own experience with the first measurement in the previous group, we recommended the pupils in this group perform at least one test measurement. We observed that pupil D, in the role of the meter, after starting the stopwatch observed the movement of the ball in the liquid and, after signalling the end of the measurement, it was difficult for him to orient himself on the tablet screen and press the correct button to stop the stopwatch. After the test measurement, the pupils performed the first measurement. The observer was more consistent in this measurement and signalled individual time breaks in time. However, pupil D joined his role with the observer’s role after the stopwatch was started, which resulted in an inaccurate stopwatch stopping after the signal. The first data measured was a time of 1 s and 15 hundredths. The observer asked us how to write the measured time, and, in order to eliminate formalism, we did not give him a clear form of how to write the data.
The pupils came to a disagreement when forming a conclusion from their measurements. Pupil D said that the glass ball sank faster in seed oil, which is at odds with how real time works as a physical quantity. Pupil E argued against his claim with the fact that the two measurements for water were below one second. Pupil F also argued that this was also the case for seed oil in one measurement. The observing researcher encouraged the pupils to choose the most precise measurement for both liquids.
After collecting the measured data, we drew the numerical axes on the board, which was the first to display the measured values of pupil E. In this phase of the activity, we asked to find out whether the pupils had already met with the terms line and the column in the course of working with the table, as they did not use these terms in their orientation. Pupil E showed a specific line that he filled in during the measurement. To support orientation in the table and the active use of these terms, we asked pupil E to state his order. Pupil E correctly identified the row as the third in the table. The first measured time value—1 s 15 hundredths—was drawn by this pupil in the range of points 1 s and 2 s. However, the point at which he displayed the value would be more equivalent to the value of 1 s 50 hundred, but we did not interfere in the pupil’s activity. When displaying the first measured data in the work with oil, the pupil again displayed a time of 1 s 66 hundredths in the correct range of points on the numerical axis and the exact location of the value conditioned the position of the blue line on the numerical axis expressing the values measured in water. Thus, the drawn blue line was again more at the level of 1 s 90 hundred, but to visualize the arrangement of numbers by size, a specific display was sufficient. Pupil F helped himself with the display, similarly to pupil B in the previous group, and he drew all the values correctly. The third pupil also displayed the numbers on the axis correctly, making their placements conditional on the values already displayed.
We allowed the pupils to formulate a conclusion of their research activities based on the measured values. Pupil D stated this statement: “The ball fell faster in the oil”, which he justified by the fact that the highest displayed value belongs to the oil. He formulated the statement regardless of the physical quantity that was shown on the numerical axes, and thus characterized the longer fall time as a higher fall velocity. This statement was opposed by pupil E, who made an argument with the two measured values when working with water for less than 1 s: “It fell faster in water”. Pupil F opposed the last statement. The pupils’ conclusions differed significantly, so we guided their activities and asked them to determine the most accurate value from the measured time data. However, the participants did not agree on a single number. Therefore, we advised them to determine for each a series of numbers that was in the middle. The pupils correctly identified the median from the set of data measured when working with water and from the set that corresponded to the values measured when working with oil. These values were considered authoritative in formulating a conclusion on which everyone agreed in the final phase of the research activity. Since no pupil made continuous notes during the implementation of the activity, it was only at this stage that they wrote down the necessary data in their worksheets. Similarly to the first group, the pupils based their predictions before the trials on the density and not viscosity of liquids. There were some inaccuracies in their operation of stopwatch, but fewer than in the first group. One of the pupils demonstrated a misconception in his understanding of time, but the researcher did not return to this moment and did not question the pupil to check whether the pupil would correct himself, which we see as a mistake, in retrospect.
In the second group, the very formulation of the prediction, which the pupils did not express after our challenge, seemed problematic. We initially attributed the origin of this situation to misconceptions that the participants expressed in the initial phase of the research activity, or a lack of experience with similar phenomena. However, after our guidance, they began to express their assumptions based on predictions that we did not anticipate when planning the activity. Unfortunately, we did not find out from what experience the pupils formulated these predictions. At the end of this thought activity, all pupils agreed on the same statement, which they argued using the term density, as did the previous participants. For the same reason, we therefore concluded that the pupils are at the level of inconsistent understanding in terms of formulating predictions.
The participants in the second group also mentioned the need for a measurement tool, which signalled a higher level of statistical literacy, but again did not take into account any measurement deviations that could occur due to the possible variability in ball sizes or fluid levels. In the verbal modelling of a situation in which fluids with a higher level would be used, the pupils correctly estimated the phenomenon that would occur. However, they did not incorporate the variability in conditions into their research activities and did not initially consider it important to balance them. Even in this group, pupils did not pay any attention to the representativeness of the conditions under which they carried out their research, which signals the level of informal understanding.
When working with the table, the orientation of the pupils on the area and in the table was sufficient, but, in their active vocabulary, we did not observe any use of terms to accurately indicate the location of the data. As this phenomenon appeared in our research for the second time, we formulated additional questions supporting the orientation of pupils in the table and the use of the terms row, column and data. Based on the successful identification of the order of the rows, we found that the pupils know this concept and work with it, but in the work with the table it is an absence in their active vocabulary. During the entry of the first measured data into the table, we observed, as in the first group, its incorrect placement, which was again related to a thorough analysis of particular parts of the table, despite the orientation in it when rewriting the terms on the table.
The time data collection phase was similar to the previous research group. The last measurements in this group were taken by the grade four pupil, and his measurements were more accurate due to greater concentration on the activity, which showed a greater skill in working with digital stopwatches than the other participants. However, even with a higher concentration, the pupil was unsuccessful in stopping the stopwatch accurately. We concluded that the problems with the accurate measurement of the time of the ball fall for all pupils could be related not only to their skills and abilities, but also to the too fast course of the measured phenomenon and the cognitive and thought processes that had to take place at the moment when the ball crossed the line. The pupils in the role of observer had to visually perceive the fall of the ball and, at a specific moment, to process information about the need to signal the end of the measurement, activate speech and issue an order to stop the stopwatch. Even these cognitive processes actually take place later than when the ball crosses the line. At the same time, for the purpose of accurate measurement, the pupils in the role of meter should also activate auditory analysers and process acoustic sensation, which should result in a movement being performed at the touch of a button on the tablet. Based on the implementation of our research, it seems that the speed of the execution of these cognitive processes in individual participants significantly affects their performance in measuring time data while they are working in a group.
The initial formulation of the conclusion was incorrect, and, after the pupil’s argument, we found that this arose due to limited knowledge about the units of physical quantities, speed and time, and their interdependence. The other participants immediately made their statements, which meant that we did not return to the exclusion of the youngest pupil’s misconception about the dependence of time and speed, which we considered to be wrong during the analysis. Any neglect of this activity can, in the future, be the result of the equally erroneous conclusions of the pupil in similar research activities or laboratory work.
The pupils did not show significant problems when they were comparing numbers by size or when displaying values on the number axis. The display of a specific value was often inaccurate within the axis, but, in the arrangement of the measured data, the pupils were successful as well as in comparing the medians of both sets. In this area, therefore, the participants are at the level of informal understanding (Figure 3). When formulating the conclusions, the participants did not take into account their personal view, but argued them by comparing the data they measured in the practical activity, which is characteristic of statistical literacy levels higher than idiosyncratic understanding.
The analysis of the work of the pupils in the second research group led us to formulate the statement that participating primary pupils in the field of statistical literacy demonstrate certain abilities and skills characteristic for the level of informal understanding and inconsistent understanding. This statement is identical to the statement based on the analysis of the activities of the participants in the first group. The collection of time data and the incorrect use of physical terms proved to be particularly problematic. The results of the research activity were also negatively affected by the insufficient knowledge about the units of physical quantities and the relations between them. Moreover, inconsistent reading of the text and incorrect addition of data can also have negative impacts on the future research activity or laboratory work.
3.3. Third Group
The third group consisted of a first grader, G, second grader, H, and third grader, I (7–10 years old). Pupil I explained the term “fish egg” and her co-operators agreed with the explanation. Pupil G asked, during the manipulation of the glass balls, whether they were all the same size. He was stimulated by the researcher to find out for himself and he measured them with the ruler afterwards. The pupils came to the conclusion that they were indeed identical. Pupil H predicted that the glass ball would not sink in the rapeseed oil, however, his co-operators disagreed about this. The researcher advised the pupils to try his assumption out, so they could see the glass ball does indeed sink in the seed oil. Afterwards, pupils G and H predicted that the glass ball would sink equally fast in the two liquids, while pupil I thought it would sink slower in seed oil. As in the previous two groups, she based her prediction on density.
Pupil H expressed this opinion: “In my opinion, it will fall down in the water but it will not fall in the oil”. We asked pupil H to argue his statement and he replied that: “It will not fall in the oil because it is denser than water”. He placed one ball into each fluid and observed the phenomenon that was to occur. The described activity refuted the statement of pupil H and his idea of the position of the glass ball in oil and water was clarified. As a result of this observation, the pupils already had an experience with the speed at which the ball moved in the fluid containers. However, the formulated predictions differed because pupils G and H claimed that the ball would fall equally fast in both liquids, but pupil I predicted: “It will fall more slowly in oil than in water because the water is not so dense”. This was a problem for the pupils that motivated them to perform scientific research and an ideal space was offered there for carrying out research activities, similarly as in the first group of participants.
After formulating the predictions, pupils wrote down their own estimates in the provided worksheets. After a short conversation, the group agreed that they would need some glass balls, oil and water. We asked the pupils on what basis they could confirm their estimates, i.e., what would be appropriate to measure. Then pupil H stated the need to measure the “size of the cup”, which we allowed him to do, and we also recommended measuring the level of liquids and deciding whether the height of both liquids is the same. All pupils agreed that the fluid levels were the same. Since the pupils only mentioned the need to measure the level so far, we asked them to throw the ball into one of the containers and determine how fast it sunk. We observed that the pupils did not determine the speed at which the ball fell after falling, so we transformed our guideline into the question: “How long do you think the ball fell to the bottom?”. The pupil G answered: “I think one second”. The other pupils also made their estimates, using the same unit of time. From this we concluded that all the present participants had already encountered these concepts, whether in a school or home environment. As part of this, we demonstrated three measurement tools to the pupils and asked, “Which of these tools would we use to verify that your estimates were correct?”. The participants agreed to use digital stopwatches on a tablet.
We had a predrawn table on the board, the same as in the worksheet. When entering the words into the table, we proceeded in the same way as in the second group, while the pupils were using the terms next to, below, to the right for orientation. Again, we observed the absence of the terms row and column. After unifying the appearance of the tables, we invited pupil H to add some data on the height of the liquid levels to the table on the board. He entered the data in the correct places, but did not convert the length values to the required unit. After completing the measured lengths, we started the phase of collecting time data.
We assigned the pupils the roles of initiator, observer and meter. The first measurement was to measure the time when the ball fell in the water. Each participant fulfilled his role. Pupil H, in the position of observer, focused on the movement of the ball and almost exactly signalled the beginning and end of the measurement. We observed that pupil I, in the position of the meter, concentrated her gaze on the stopwatch and started and stopped it almost exactly at the time of signalling. The pupil asked for guidance on how to write the measured value of 45 hundredths of a second. We did not recommend a clear way of entering the value and the pupil recorded the measured time in the table in the manner of 0 s 45. After entering this value, we asked the pupil how he knew that he should write it in that particular place. The pupil replied: “Because we measured in water, and up there is water, and we measured for the first time, and here is measurement 1”. He pointed to the individual frames with his finger during the explanation. Based on this activity, we could observe that the pupil in the table was oriented on the basis of written terms and not only on the basis of blank spaces that needed to be filled. The first measurement of the fall time of the ball in the oil was the same, which again resulted in an almost accurate measurement. We observed that pupil I made continuous entries after the first measurements and wrote down the values in her table. After observing her activity, other pupils also made continuous records. When working with the table, we observed that the way of writing the time data was repeated throughout the table.
After collecting the measured data, we drew the number axes on the board. Pupil H, who was the first to display the measured data on the numerical axes, proceeded with marking similarly to pupil B in the first research group, and thus helped himself by dividing the interval 0 s–1 s in half. We considered the display of values to be correct in terms of visualizing the order of the numbers by size. We observed that the other pupils in the group were also on the number line, and, therefore, our intervention in their activities was not necessary.
The graphic display again highlighted the variability in measurements, on the basis of which it was difficult for the pupils to draw a clear conclusion, and they did not agree on the formulation of a conclusion of the research. We thus guided the pupils’ thinking activities and recommended that they can determine the most accurate value from the measured data. At first, the pupils did not respond to our recommendation and did not determine the required values. We showed a numerical axis showing the fall times of the ball in the water and asked: “Which of these colour values do you think is the most accurate?”. Pupil G did not recommend using the value he measured because he did not press the stopwatch in time. From this, we concluded that the pupil was aware of his mistake in collecting data. The participants did not agree on a single number that would be the most suitable for formulating the conclusion of the research activity. Therefore, we advised them to determine in each a series of numbers that was in the middle. Pupils correctly identified the medians of both sets of measured values and considered them to be authoritative in formulating a conclusion on which all agreed. This group of pupils showed interest in both the height of the tanks and size of the glass balls, which indicates their ability to think critically in the domain of statistics. On the other hand, they encountered difficulties with the identification of the appropriate value for comparison between the speed of sinking in water and rapeseed oil. They also based their initial predictions on density. However, they were the most capable in their work with the table and time axis.
In the initial phase of the research activity of the pupils in group 3, one pupil posed the question of the similarity of the size of the used balls. The fact that this question was asked by the youngest pupil increased the importance of determining the level of statistical literacy of primary school pupils. Based on this, we expected that the pupils would pay attention to the feature as representativeness of the data collection conditions, which would be a manifestation of the level of consistent noncritical understanding, while we had not assigned this level to the pupils in previous analyses, despite the presence of senior participants. One of the pupils in this group suggested measuring cup size before the data collection phase, which also signalled a higher level of statistical literacy. However, his proposal was probably conditioned by our question, which preceded his, as a result of which it was not possible to clearly determine the nature of the pupil’s thought activity or the impact of this activity on his level of statistical literacy. We therefore attributed the initial question about the conformity of the balls to curiosity, or to more experience and more precise concepts about this concept, than to the need to ensure a level playing field in the data collection. We also identified the absence of the need for representativeness of the research sample due to the failure to provide any measuring tool for conducting the pupil’s research. However, at the end of the activity, we observed the pupil’s critical opinion of his own measurement, on the basis of which he decided on the values measured by him as unsuitable for determining the conclusion. As a result, we considered the possibility of the presence of the fourth level of statistical literacy among primary school pupils. However, the other verbal expressions and skills of the pupils did not confirm this statement.
Similarly as in the previous groups, these pupils showed their ability to formulate predictions based on their own experiences, and their arguments were also based on their own concepts and misconceptions about the concept of density. Since the use of solely this term to argue predictions about the rate of fall of a ball in a liquid is not correct and unambiguous, the ability of the third group pupils to make judgments and arguments is one feature belonging to the level of inconsistent understanding.
During the pupils’ activity consisting of the data collection, we again observed the negative effect of inconsistent concentration on the results of individual measurements. While there was the proper concentration of the pupil—the observer—on the movement of the ball and its position in the vessel, the signalling of its position was almost accurate. The pupil in the position of the meter was successful as well who, thanks to maintaining attention on the digital stopwatch, became better oriented on the tablet screen and stopped the measurement in time, which made the measured value one of the most accurate in all research activities. However, there was still a short time interval between the moment when the ball passed over the bottom line on the vessel and the moment when the stopwatch stopped, which distorted the resulting measurement. We assume that this phenomenon is related to some cognitive processes and thought operations on the basis of which we have also some justified inaccurate measurements in the second research group. We did not observe specific problems when writing values to the tables and displaying them on the number axis.
The choice of the standard value for the formulation of a conclusion of the research activity was problematic for the pupils as a result of which we could not unambiguously determine whether the pupils would prefer the choice of the median or average for the characteristics of the group. In comparing the measured time values within the one timeline as well as in comparing the later medians from the created two sets of values, they were successful, which led to a problem-free formulation of the conclusion of the research activity. The described ability is one of the characteristic levels of informal understanding within the levels of statistical literacy.
Through analysing the verbal expressions and practical activities of the participants in the third research group, we came to the conclusion that the primary pupils in this group were in the field of statistical literacy at the level of levels of informal understanding and inconsistent understanding (Figure 3). Some features characteristic of a level of consistent noncritical understanding also emerged in this group, suggesting that certain higher levels of statistical literacy could be achieved with the proper stimulation and frequent research activities requiring direct activity and pupil involvement.
While we analysed worksheets, we observed the pupil’s inattention when reading sentences to which time data had to be added. As in the previous group, there was no thorough reading comprehension and words were added to the sentences instead of time data. Definitely, problems with consistent reading can bring and have serious negative consequences for any side of life, not just the research, future work, job and life applications of the current pupil. Interestingly, we identified the same problems as in the previous two groups. However, the most negative impacts were on the implementation of research activities and additional formulation of a conclusion of the work featuring the actual inaccuracy of time measuring in the data collection phase.
4. Discussion
This study builds on the work of Watson, English and their colleagues [14,32,33,35,36,37,38] who advocate including the whole investigation cycle in statistics education and aiming at out of school activities as well. Here, we describe our emergent findings with respect to the design of the activity:
4.1. What Are the Key Design Features of Interdisciplinary Activities Combining Knowledge from the Natural Sciences and Statistical Reasoning That Can Support the Learning of Statistics?
The principles implemented in this study listed in the methodology stemmed from the recommendations from [34], namely: “(1) Learning-appropriate goals; (2) scaffolds that supports both student and teacher learning; (3) frequent opportunities for formative self-assessment and revision; and (4) social organisations that promote participation and result in a sense of agency” (p. 273). The learning goals aimed at the awareness of data investigation, so we tried to include the data investigation circle in the broadest extent feasible for the 45 min long timeslot. The pupils were led to the formulation of research questions, they got the pre-formulated hypothesis, chose the proper measuring tools, collected data into pre-prepared tables, described and compared collected data sets, and proposed and justified the conclusions, again in the form of pre-formulated statements. Based on available literature (e.g., [39,40,41,42]), only limited knowledge in statistics was predicted. Therefore, the hypothesis and conclusions were given in the form of pre-formulated sequences. The reasoning about the central value was facilitated by the camp-leader. Thus, the pupils were capable of deriving conclusions from their experimenting, despite the limited knowledge in statistics foreseeable for primary pupils. The activity was designed by applying the predict–test–explain strategy [34], so it was natural for the pupils that some of them were right and some were wrong, so the pupils were guided to explain why their predictions were not correct. The camp-leader led the pupils to work on their own as much as possible and the scaffolding was given in form of Socratic dialogue.
We observed the primary pupils while performing a task at the summer camp focused to cultivate scientific literacy. We expected these pupils to be motivated due to their voluntary participation at the camp and to compensate for intellectual differences caused by age heterogeneity via co-operation, which seemed to be the case. Based on these observations, we conclude that the measuring tasks offer suitable data to be collected, analysed and reported. The composition of groups comprising at least one pupil of the grade 1 or 2 and one pupil of the grade 3 or 4 allows ideal peer instruction within the activity.
The activity was designed with the objective of raising a question aimed at a certain scientific fact. Pupils were asked the questions about a given fact that can be answered based on the results of the laboratory work. As the primary pupils are not familiar with the concept of a hypothesis as such, we found to be particularly useful the three step approach used, e.g., in [33]: predict–test–explain. Their predictions about the results could be stated in the form of preformulated statements. The reformulated hypothesis was subsequently tested by the data collection, analysis and interpretations. Regardless of the correctness of the prediction, the obtained answer was explained.
The prediction could be confirmed or rejected based on the data collected in the laboratory work. The environment of the laboratory investigations offered several ample opportunities to provide statistical reasoning. The pupils can provide reasoning about central tendencies [43], variation (e.g., [14]) or, as in the presented activity, about the comparison of measured characteristics. The statistical analysis performed at the level of statistical thinking of primary pupils is used in the scientific investigation in a way similar to the way in which statistical analysis is used within a common scientific task. The experience with analysing data could be a foundation for further development of statistical thinking. The procedure leading the activity mimics the work of actual scientists and therefore affords the authentic integration of mathematics and science as well as proper room for disciplinary learning at the same time.
4.2. What Are the Actual Difficulties That Primary Pupils Can Encounter While Providing Statistical Reasoning Based on Their Laboratory Work?
The participating pupils were mostly able to solve the task with some assistance from the researcher. In all the three analysed cases, there were some pupils with an informal to inconsistent understanding of statistics, but in the last group there was a pupil who had repeatedly attended the camp for several years who, luckily, manifested more advanced statistical skills. Nevertheless, they were some difficulties (rooted in their level of statistical literacy) prevalent among the all three groups, such as impreciseness in operating a stopwatch, which influenced their results to the point where the glass ball was moving slower in water in some trials. When the measured values are so low overall, the error of measurement caused not only by the lack of skills, but also by the lack of concentration at some points, had a greater impact on results in the end. Despite these facts, all three groups came up with the correct conclusion; however, this suggests that a lack of practical skills can be an obstacle in laboratory work [25].
The pupils were able to orient themselves within the table, but they totally lacked any active vocabulary for it—probably due to the lack of experience with such a task. However, making entries on the time axis was problematic in some cases, which is most likely related to the fact that such young pupils had not previously mentally operated with centiseconds. This implies that a lack of knowledge about units of physical quantities can be another barrier on the side of pupils involved in a task such as this. However, the pupils were mostly able to at least draw the values in the correct order, which enabled them to come to the right conclusion. Moreover, the pupils did not account for possible differences in experimental conditions (i.e., the size of the glass ball and length of the trajectory inside the tank), even though the task directly asked them to check the height of the liquid level at least. Another issue was the pupils’ misconception about density being the factor influencing the glass ball’s movement. Definitely, certainly and clearly said, a proper understanding of physical quantities needs to be established before conducting any experiment where it features as one of the variables.
On the one hand, some of the pupils’ shortcomings were caused by the design of the task as such. The time measurement would probably be more accurate if the pupils were given a standard stopwatch and the roles of the measurer and observer were merged into one. Possible errors of measurement would have less impact on data when the liquid level was higher. On the other hand, the reasoning would be very different than in the described activity. The pre-printed sentences on the work sheet strongly suggested that there will be a difference between the speed of the ball’s sinking in water and seed oil, which we retrospectively see as a mistake. However, the creators of the task were unaware of these issues when designing the activity.
The findings of the presented study support the data oriented approach to teaching statistics suggested by several authors [44,45]. This confirms that even primary pupils are able to collect data using observations, surveys, and experiments; describe and compare data sets; and propose and justify conclusions and predictions based on the data on an informal level or the level of inconsistent understanding. Problems grounded in the cycle of investigating data—identification of the problem, planning the investigation, data collection, creating representations and interpreting the data in the context—provide quite a natural environment for developing both verbal and written communication skills in each phase of the data investigative cycle [46]. The advantages of this approach, particularly holistic experiential learning, have been identified at the all educational levels [47]. We agree with Gattuso and Ottaviani [48], that when pupils collect their own data these aspects shall matter: “concepts–such as centre and variability–and measures of concepts–such as arithmetic mean, median, mode and standard deviation, interquartile range, range–and not just numbers and formulae” (p. 125). However, we suggest complementing the activity with more conceptual understanding and experiencing different contexts with the same concepts [49,50].
The participating pupils manifested the misconception that the measured time depends on the density instead of viscous behaviour of the liquids, which can be observed even in the reasoning of higher secondary students [51,52]. Besides statistical reasoning, the pupils experienced the processes mirroring the usual practice of science [53] and the nature of scientific investigations [54]. Due to the limited number of repeating measurements, pupils were able to relate the incorrect measuring with the outlying values and, therefore, experience the uncertainty inherent to a particular measurement [55] and gain knowledge about appropriate practices in measuring, i.e., strengthening their laboratory-related abilities [56]. The results are in accordance with the findings of Leave and Hourigan [57,58], concluding that the appropriate problems related to pupils’ everyday lives give them an agency and ownership that results in the ability to grasp statistical concepts usually beyond their capacities. Furthermore, solving problems related to pupils’ reality positively influence the pupils’ perceptions of STEM subjects [59,60,61].
We are aware of the limited potential for generalization. Firstly, the participants in the study are not representative of the general population, but were pupils with a good attitude towards and beliefs in science, as they took part in the science summer camp voluntarily. On the other hand, the aim of the study was not to screen the level of statistical thinking, but rather to point out the difficulties that can pupils encounter while solving interdisciplinary problems to outline and boost the design of interdisciplinary activities. Moreover, the study extended the findings of English [62] and Mulligan [63], that even primary pupils are capable of providing reasoning based on the data and conducting statistical analysis far beyond the level expected in the curriculum. However, the design of any activity needs to be tailored according to the needs and capabilities of the age group [64].
5. Conclusions
We carried out research on small groups of primary school pupils within a day camp. The research took place in the form of the implementation of research activities aimed at time measuring. The principles underlying the design of the interdisciplinary activities were formulated. We exemplify that the full investigation cycle—starting by formulating research question, including data collection and analysis and finishing by the formulation of conclusions based on collected data—can be enacted with sufficiently motivated primary pupils when the appropriate scaffolding was provided.
Here, we observed the verbal expressions and practical skills of the pupils associated with the formulation of predictions, conclusions and data collection. We analysed these manifestations and skills at a later stage of the research and compared the results of the three analyses. Based on this, we were able to identify situations that are problematic for primary school pupils in their research activities. The pupils’ performances and attitudes also differed from each other, in terms of their previous experience with the concepts used or activities carried out. The pupils demonstrated their ability to provide statistical reasoning far beyond what is expected in the national curricula. The most problematic for the pupils was the measurement of time, especially its accuracy. In some groups, the measurements were so inaccurate that the pupils themselves refused to incorporate them into the conclusion formulation which afforded profound discourse. The pupils participating in our research did not show any specific problems with the orientation in the table and graphical representation of the measured data.
The measurement, as such, did cause problems to the pupils, however it was a necessary part of the proposed activity. Only through it could the pupils work with meaningful and concrete data. In order for the pupils to be more successful in future practical activities, it is important that this activity is also directed, to some extent, by their teachers. However, moreover, this has to be preceded by thorough preparation as well. By carrying out our research, we have revealed not only some difficulties that can arise in the research activities of pupils, but also some details that the teacher should take into account before organizing similar activities.
The results of our work emphasize the importance of research activities in the development of statistical and science literacy and also the importance of thorough teacher training for each lesson. Taking into account the findings of the study and specificities of the cognitive development of primary pupils, the pre-concepts should be the main content of activities; in our study the pre-concepts of table and measuring were addressed. The pupils participating in this research had the biggest problems during the data collection phase due to their lack of measuring knowledge and this suggests to us that there is a need to change something in this area to ensure their success and motivate them to continue. After all, the problems are there to be solved, and it is no different from the problems occurring with the implementation of research activities. Likely and factually, not all pupils are equally successful in every school activity. However, by analysing their verbal expressions, skills or behaviour, we can identify in advance some basic problems they will be struggling with, and by reflecting on our own pedagogical activities, we can eliminate such problems with the future similar activities. Indeed, the question of how the designed activities can be adjusted for the everyday school practice remain open.
Author Contributions
Conceptualization, Z.S., B.U. and J.M.; methodology, J.M.; formal analysis, Z.S. and B.U.; investigation, Z.S. and Ľ.V.; resources, Ľ.V.; data curation, J.M.; writing—original draft preparation, B.U.; writing—review and editing, J.M.; supervision, J.M.; project administration, Ľ.V.; funding acquisition, Ľ.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Slovak Research and Development Agency under the contract No. APVV-20-0599 andby the Scientific Grant Agency of the Ministry of Education, Science, Research and Sport of the Slovak Republic and the Slovak Academy of Sciences under contracts No. VEGA 1/0815/18 and KEGA 015UKF-4/2021.
Institutional Review Board Statement
As the pupils were observed in the natural conditions of the summer camp and for the short time, there is no harm to them and therefore it is not necessary to have the confirmation of ethical committee. Their parents were informed about the research based on participation of their children in the camp and signed the informed consent.
Informed Consent Statement
Informed consent was obtained from all parents of the participants involved in the study.
Data Availability Statement
The transcripts of the pupils’ work are available upon the request by the first author.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Ward, M. PISA for development: Results in focus. PISA Focus 2018, 91, 1–20. [Google Scholar]
- Miklovičová, J.; Galádová, A.; Valovič, J.; Gondžúrová, K. PISA 2015: Národná Správa Slovensko. PISA 2015: National Report Slovakia; NÚCEUM: Bratislava, Slovakia, 2017; p. 87. [Google Scholar]
- Bruder, R.; Prescott, A. Research evidence on the benefits of ibl. ZDM 2013, 45, 811–822. [Google Scholar] [CrossRef]
- Ireland, J.; Watters, J.J.; Lunn Brownlee, J.; Lupton, M. Approaches to inquiry teaching: Elementary teacher’s perspectives. Int. J. Sci. Educ. 2014, 36, 1733–1750. [Google Scholar] [CrossRef]
- Kipnis, M.; Hofstein, A. The inquiry laboratory as a source for development of metacognitive skills. Int. J. Sci. Math. Educ. 2008, 6, 601–627. [Google Scholar] [CrossRef]
- Roychoudhury, A.; Roth, W.M. Interactions in an open-inquiry physics laboratory. Int. J. Sci. Educ. 1996, 18, 423–445. [Google Scholar] [CrossRef]
- Etkina, E.; Murthy, S.; Zou, X. Using introductory labs to engage students in experimental design. Am. J. Phys. 2006, 74, 979–986. [Google Scholar] [CrossRef]
- Gal, I. Adults’ statistical literacy: Meanings, components, responsibilities. Int. Stat. Rev. 2002, 70, 1–25. [Google Scholar] [CrossRef]
- Tractenberg, R.E. How the Mastery Rubric for Statistical Literacy Can Generate Actionable Evidence about Statistical and Quantitative Learning Outcomes. Educ. Sci. 2017, 7, 3. [Google Scholar] [CrossRef] [Green Version]
- Koga, S. Characteristics of statistical literacy skills from the perspective of critical thinking. Teach. Stat. 2022. [Google Scholar] [CrossRef]
- National Institute for Education in Slovak Republic. Inovovaný štátny vzdelávací program pre 1. Stupeň zš: Prvouka. In Innovated State Educational Programme for Primary Education: Science; National Institute for Education in Slovak Republic: Bratislava, Slovakia, 2014. [Google Scholar]
- Muñiz-Rodríguez, L.; Rodríguez-Muñiz, L.J.; Alsina, Á. Deficits in the Statistical and Probabilistic Literacy of Citizens: Effects in a World in Crisis. Mathematics 2020, 8, 1872. [Google Scholar] [CrossRef]
- Chick, H.L.; Pierce, R.U. Teaching statistics at the primary school level: Beliefs, affordances, and pedagogical content knowledge. In Joint ICMI/IASE Study: The 18th ICMI Study: Teaching Statistics in School Mathematics-Challenges for Teaching and Teacher Education. Proceedings of the ICMI Study 18 and 2008 IASE Round Table Conference; Batanero, C., Burrill, G., Reading, C., Rossman, A., Eds.; ITESM: Monterrey, Mexico, 2008; pp. 1–6. [Google Scholar]
- Watson, J.; Fitzallen, N.; English, L.; Wright, S. Introducing statistical variation in year 3 in a STEM context: Manufacturing licorice. Int. J. Math. Educ. Sci. Technol. 2020, 51, 1–34. [Google Scholar] [CrossRef]
- Aguilera, D.; Lupiáñez, J.L.; Vílchez-González, J.M.; Perales-Palacios, F.J. In search of a long-awaited consensus on disciplinary integration in STEM education. Mathematics 2021, 9, 597. [Google Scholar] [CrossRef]
- Ardiansyah, A.S.; Novita, N.A.; Zhintya, H.; Kurnianto, D. Realistic-science, technology, engineering, and mathematics assisted by google classroom as a learning innovation in the new normal era to improve statistical thinking skill. J. Phys. Conf. Ser. 2021, 1918, 042084. [Google Scholar] [CrossRef]
- Margot, K.C.; Kettler, T. Teachers’ perception of STEM integration and education: A systematic literature review. Int. J. STEM Educ. 2019, 6, 2. [Google Scholar] [CrossRef] [Green Version]
- Hourigan, M.; Leavy, A.M. Using integrated STEM as a stimulus to develop elementary students’ statistical literacy. Teach. Stat. 2020, 42, 77–86. [Google Scholar] [CrossRef]
- Maass, K.; Geiger, V.; Ariza, M.R.; Goos, M. The role of mathematics in interdisciplinary STEM education. ZDM 2019, 51, 869–884. [Google Scholar] [CrossRef]
- Boix Mansilla, V.; Miller, W.C.; Gardner, H. On disciplinary lenses and interdisciplinary work. In Interdisciplinary Curriculum: Challenges to Implementation; Wineburg, S., Grossman, P., Eds.; Teacher College Press: New York, NY, USA, 2000; pp. 17–38. [Google Scholar]
- Peiró-Signes, Á.; Trull, Ó.; Segarra-Oña, M.; García-Díaz, J.C. Attitudes towards statistics in secondary education: Findings from FSQCA. Mathematics 2020, 8, 804. [Google Scholar] [CrossRef]
- English, L.D.; Watson, J.M.; Fitzallen, N. Fourth-Graders’ Meta-Questioning in Statistical Investigations. In Proceedings of the 40th annual conference of the Mathematics Education Research Group of Australasia (MERGA), Melbourne, Australia, 2–6 July 2017; pp. 229–236. [Google Scholar]
- Melušová, J.; Vidermanová, K. Matematická štatistika v interdisciplinárnych projektoch žiakov základných a stredných škôl =: Mathematical statistics in interdisciplinary projects of secondary-school students. Forum Stat. Slovacum 2012, 8, 97–102. [Google Scholar]
- Plothová, L.; Páleníková, K.; Naštická, Z.; Florková, M.; Šubová, L. An analysis of students’ use of mathematical models in solving tasks with real-life context. APLIMAT 2017. In Proceedings of the 16th Conference on Applied Mathematics, Bratislava, Slovakia, 31 January–2 February 2017; pp. 1207–1223. [Google Scholar]
- Nisbet, S. Getting organised: The role of data organisation in students’ representation of numerical data. In Proceedings of the 27th International Group for the Psychology of Mathematics Education Conference Held Jointly with the 25th PME-NA Conference, Honolulu, Hawaii, 13–18 July 2003; Volume 3, pp. 389–396. [Google Scholar]
- Kadijevich, D.M.; Stephens, M. Modern statistical literacy, data science, dashboards, and automated analytics and its applications. Teach. Math. 2020, 23, 71–80. [Google Scholar]
- Valovičová, L’.; Ondruška, J.; Zelenický, L’.; Chytrý, V.; Medová, J. Enhancing computational thinking through interdisciplinary STEAM activities using tablets. Mathematics 2020, 8, 2128. [Google Scholar] [CrossRef]
- Cohen, L.; Manion, L.; Morrison, K. Research Methods in Education; Routledge: London, UK, 2013. [Google Scholar]
- Polkinghorne, D.E. The practice of narrative. Narrat. Inq. 2010, 20, 392–396. [Google Scholar] [CrossRef]
- Jones, G.A.; Thornton, C.A.; Langrall, C.W.; Mooney, E.S.; Perry, B.; Putt, I.J. A framework for characterizing children’s statistical thinking. Math. Think. Learn. 2000, 2, 269–307. [Google Scholar] [CrossRef]
- Watson, J.M. Statistical Literacy at School: Growth and Goals; Routledge: London, UK, 2013; p. 320. [Google Scholar]
- Watson, J.M.; English, L.D. Statistical problem posing, problem refining, and further reflection in grade 6. Can. J. Sci. Math. Technol. Educ. 2017, 17, 347–365. [Google Scholar] [CrossRef]
- English, L.D.; Watson, J. Modelling with authentic data in sixth grade. ZDM 2017, 50, 103–115. [Google Scholar] [CrossRef] [Green Version]
- Barron, B.J.S.; Schwartz, D.L.; Vye, N.J.; Moore, A.; Petrosino, A.; Zech, L.; Bransford, J.D. Doing with understanding: Lessons from research on problem- and project-based learning. J. Learn. Sci. 1998, 7, 271–311. [Google Scholar]
- Watson, J.; English, L. Eye color and the practice of statistics in grade 6: Comparing two groups. J. Math. Behav. 2017, 49, 35–60. [Google Scholar] [CrossRef]
- English, L.D.; Watson, J.M. Statistical literacy in the elementary school: Opportunities for problem posing. In Mathematical Problem Posing: From Research to Effective Practice; Singer, F.M., F. Ellerton, N., Cai, J., Eds.; Springer: New York, NY, USA, 2015; pp. 241–256. [Google Scholar]
- English, L.D.; Watson, J.M. Exploring variation in measurement as a foundation for statistical thinking in the elementary school. Int. J. STEM Educ. 2015, 2, 3. [Google Scholar] [CrossRef] [Green Version]
- English, L.D. Interdisciplinary modelling in the primary mathematics curriculum. In Mathematics: Essential Research, Essential Practice; Watson, J., Beswick, K., Eds.; Mathematics Education Research Group of Australia (MERGA): Hobart, Australia, 2007; pp. 275–284. [Google Scholar]
- Jones, G.A.; Langrall, C.W.; Thornton, C.A.; Mooney, E.S.; Wares, A.; Jones, M.R.; Perry, B.; Putt, I.J.; Nisbet, S. Using students’ statistical thinking to inform instruction. J. Math. Behav. 2001, 20, 109–144. [Google Scholar] [CrossRef]
- Pallauta, J.D.; Arteaga, P.; Garzón-Guerrero, J.A. Secondary School Students’ Construction and Interpretation of Statistical Tables. Mathematics. 2021, 9, 3197. [Google Scholar] [CrossRef]
- Tak, B.; Kim, D. An analysis on error types of graphs for statistical literacy education: Ethical problems at data analysis in the statistical problem solving. J. Elem. Math. Educ. Korea 2020, 24, 1–30. [Google Scholar]
- Maass, K.; García, F.J.; Doorman, M.; Wake, G.; Čeretková, S.; Mousoulides, N.; Mikelskis-Seifert, S.; van der Kooij, H.; Howes, A.; Hardy, G.; et al. Enhancing Mathematics and Science Learning through Interdisciplinary Enquiry; The University of Manchester: Manchester, UK, 2011. [Google Scholar]
- Valovičová, L’.; Medová, J. Physical measurements as an environment supporting primary pupils’ reasoning about central tendency. In Proceedings of the 14th International Congress on Mathematical Education, Shanghai, China, 11–18 July 2021; East China Normal University and ICMI: Shanghai, China, 2021. [Google Scholar]
- Moore, D.S. New pedagogy and new content: The case of statistics. Int. Stat. Rev. 1997, 65, 123–137. [Google Scholar] [CrossRef]
- Burrill, G.; Camden, M. Curricular Development in Statistics Education: International Association for Statistical Education 2004 Roundtable; International Statistical Institute: Voorburg, The Netherlands, 2005. [Google Scholar]
- MacGillivray, H.; Pereira-Mendoza, L. Teaching statistical thinking through investigative projects. In Teaching Statistics in School Mathematics-Challenges for Teaching and Teacher Education: A Joint ICMI/IASE Study: The 18th ICMI Study; Batanero, C., Burrill, G., Reading, C., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 109–120. [Google Scholar]
- Holmes, P. Assessing project work by external examiners. In The Assessment Challenge in Statistics Education; Gal, I., Garfield, J., Eds.; IOP Publishers: Amsterdam, The Netherlands, 1997; pp. 153–164. [Google Scholar]
- Gattuso, L.; Ottaviani, M.G. Complementing mathematical thinking and statistical thinking in school mathematics. In Teaching Statistics in School Mathematics-Challenges for Teaching and Teacher Education: A Joint ICMI/IASE Study: The 18th ICMI Study; Batanero, C., Burrill, G., Reading, C., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 121–132. [Google Scholar]
- Gamze, K. In Young children’s informal statistical inference experiences through constructing a pictograph. In Proceedings of the Eleventh Congress of the European Society for Research in Mathematics Education (CERME11), Utrecht, The Netherlands, 6 February 2019; Freudenthal Group: Utrecht, The Netherlands, 2019. Available online: https://hal.archives-ouvertes.fr/hal-02412787/document (accessed on 24 March 2022).
- Ben-Zvi, D.; Aridor-Berger, K. Children’s wonder how to wander between data and context. In The Teaching and Learning of Statistics: International Perspectives; Ben-Zvi, D., Makar, K., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 25–36. [Google Scholar]
- Faltin, L.; Feser, M.S. Secondary school students’ conceptions about the viscous behaviour of liquids. Phys. Educ. 2021, 56, 035018. [Google Scholar] [CrossRef]
- Sabaz, L. Can bubbles explain viscosity? Phys. Educ. 2006, 41, 112–114. [Google Scholar] [CrossRef]
- Emden, M. Reintroducing “the” scientific method to introduce scientific inquiry in schools? Sci. Educ. 2021, 30, 1037–1073. [Google Scholar] [CrossRef]
- Pedaste, M.; Mäeots, M.; Siiman, L.A.; de Jong, T.; van Riesen, S.A.N.; Kamp, E.T.; Manoli, C.C.; Zacharia, Z.C.; Tsourlidaki, E. Phases of inquiry-based learning: Definitions and the inquiry cycle. Educ. Res. Rev. 2015, 14, 47–61. [Google Scholar] [CrossRef] [Green Version]
- Wadhwa, A. An innovative method to study stokes’ law in the laboratory. Phys. Educ. 2008, 43, 301–304. [Google Scholar] [CrossRef]
- Etkina, E.; Karelina, A.; Ruibal-Villasenor, M.; Rosengrant, D.; Jordan, R.; Hmelo-Silver, C.E. Design and reflection help students develop scientific abilities: Learning in introductory physics laboratories. J. Learn. Sci. 2010, 19, 54–98. [Google Scholar] [CrossRef]
- Hourigan, M.; Leavy, A.M. Interrogating a measurement conjecture to introduce the concept of statistical association in upper elementary education. Teach. Stat. 2021, 43, 62–71. [Google Scholar] [CrossRef]
- Leavy, A.M.; Hourigan, M. Expanding the Focus of Early Years Mathematics Education: Statistics and Probability. In Handbook of Research on the Education of Young Children; Routledge: London, UK, 2019; pp. 99–112. [Google Scholar]
- Gravemeijer, K. A socio-constructivist elaboration of realistic mathematics education. In National Reflections on the Netherlands Didactics of Mathematics; Springer: Cham, Switzerland, 2020; pp. 217–233. [Google Scholar]
- Páleníková, K.; Naštická, Z.; Vitézová, Z.; Vallo, D.; Rumanová, L.; Vargová, L.; Smieskova, E.; Záhorská, J. Examples of Good Practices of Experiential Learning and Students’ Opinions on Experiential Learning. APLIMAT 2017. In Proceedings of the 16th Conference on Applied Mathematics, Bratislava, Slovakia, 31 January–2 February 2017; pp. 1153–1163, ISBN 978-80-227-4650-2. [Google Scholar]
- Ulandari, L.; Amry, Z.; Saragih, S. Development of Learning Materials Based on Realistic Mathematics Education Approach to Improve Students’ Mathematical Problem Solving Ability and Self-Efficacy. Int. Electron. J. Math. Educ. 2019, 14, 375–383. [Google Scholar] [CrossRef] [Green Version]
- English, L.D. Data modelling with first-grade students. Educ. Stud. Math. 2012, 81, 15–30. [Google Scholar] [CrossRef] [Green Version]
- Mulligan, J. Moving beyond basic numeracy: Data modeling in the early years of schooling. ZDM 2015, 47, 653–663. [Google Scholar] [CrossRef]
- Valovičová, L’.; Medová, J. Tailoring empirical inquiry in physics to pupils’ needs according to their knowledge about density and statistical literacy. TEM J. Technol. Educ. Manag. Inform. 2019, 8, 1433–1439. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).