Early Elementary Students’ Use of Shape and Location Schemas When Embedding and Disembedding

Abstract

Elementary students’ early development of embedding and disembedding is complex and paves the way for later STEM learning. The purpose of this study was to clarify the factors that support students’ embedding (i.e., overlapping shapes to form a new shape) and disembedding (i.e., identifying discrete shapes within another shape) through the use of filled shapes as opposed to shape frames. We recruited 26 Grade 1 students (~6–7 years old) and 23 Grade 3 students (~8–9 years old), asked them to work on two layered puzzle designs from the Color Code puzzle game, and interviewed them about their thinking processes. The first graders had higher success rates at fixing and embedding the tiles correctly, and students at both grade levels improved on the three-tile design when encountering it a second time about two months later. The four-tile design was more difficult, but students improved if they could identify a correct sub-structure of the design. Successful students used a combination of pictorial shape strategies and schematic location strategies, systematically testing tiles and checking how they could be embedded. The results suggest that helping students focus on sub-structures can promote their effective embedding.

1. Introduction

Current standards in the United States explicitly call for kindergarteners and first graders to have opportunities to compose shapes, to make compositions using those composite shapes, and to decompose shapes into equal parts [1]. However, embedding and disembedding have received relatively limited attention (see [2] for one exception), particularly in mathematics education (e.g., [3]), which is unfortunate because being able to embed and disembed shapes is important in STEM fields (e.g., geology, medicine, and chemistry [4]; see also [5,6,7]). Shape composition and embedding both involve “piecing together objects into more complex configurations” [8] (p. 7), although we restrict the definition of embedding to situations where the objects overlap partially or fully, and shape disembedding involves “perceiving objects, paths, or spatial configurations amidst distracting background information” [8] (p. 7); see also [9]. Although there is no separate embedding learning trajectory, the current learning trajectories for shape composition and for disembedding [10] involve a progression from students using pictorial schemas (i.e., visual images of shapes, including their color, size, and orientation) toward using schematic schemas (i.e., understanding of the relations between shapes) [10,11,12]. For example, between the ages of four and seven, the learning trajectory for disembedding geometric figures progresses from students being able to identify non-overlapping frames (i.e., outlines) of shapes—only pictorial schemas needed, then shape frames embedded inside of other shape frames (e.g., a triangle inside a rectangle on a geoboard [13]), then secondary frames created from embeddings [10]—focused on schematic schema use. Missing from this trajectory is the consideration of filled shapes (i.e., the result of disembedding a filled shape from a layered design).

A focus on filled shapes is central to the composing learning trajectory [10,14], which focuses on giving students opportunities to complete pattern block or tangram puzzles, where pieces connect [10,15,16] but do not overlap. Students progress from completing shape puzzles, where each shape is separate and outlined—only pictorial schemas needed—to completing shape puzzles, where multiple shapes make up parts of a picture (i.e., two trapezoids make a person’s arm) and there are no internal lines to provide hints on where the pieces go [10]—schematic schemas can help. However, because overlapping shapes are not considered in this trajectory, we need more information on the factors that play a role in embedding tasks.

Across a range of spatial tasks, the use of pictorial schemas is considered less advanced than schematic schemas. Some studies investigating students’ spatial skill acquisition have focused on students’ attempts to coordinate verbal descriptions with meaningful spatial information; they found that while many eight-year-olds attended to pictorial imagery (i.e., sequence and specific spatial details) contained in the verbal descriptions, they were less accurate at making spatial inferences using schematic imagery [17,18]. However, their tasks may have been more difficult than other spatial tasks because of the verbal components involved. Hegarty and Kozhevnikov [11] found that sixth graders’ use of schematic schemas was positively associated with their spatial visualization abilities when solving complex Block Design tasks. The Block Design test [19] involves students composing a set of red and white cube faces with solid or right triangle designs to make a target three-by-three block (or larger) figure.

A few years later, Rozencwajg and Corroyer [12] gave a modified Block Design test to 12-year-olds, 17-year-olds, and adults. They found evidence that participants used global strategies (i.e., pictorial schemas), analytic strategies (i.e., schematic schemas), and a new synthetic strategy. Those using the global pictorial strategy focused on the overall design and relied mostly on guess-and-check. Those using the analytic strategy focused on the elements of the design, moving sequentially by rows or columns to place the blocks while checking the overall design frequently. The synthetic strategy involved participants breaking up the design into recognizable sub-designs (i.e., diamond shapes, larger triangles) so that they did not need to refer to the larger design as often. Similar to Hegarty and Kozhevnikov’s [11] results, they found that the 12-year-olds were most likely to use the global pictorial strategy; however, a close second (and the most common strategy in the other age groups) was using the synthetic strategy [12]. These results suggest that the coordination between pictorial and schematic schema use might be important.

Similar to the Block Design and other composing tasks, in shape embedding and disembedding tasks, students must attend to the larger structure (schematic schemas) and the elements that make up the larger structure (pictorial schemas) in addition to applying other spatial skills, such as rotating and flipping [8,9]. When these tasks involve filled, layered shapes, students may also benefit from coordinating schematic and pictorial schemas as with the synthetic strategy [12]. Therefore, further exploration of early elementary students’ embedding and disembedding could provide additional insight into their attempts to integrate pictorial and schematic spatial information. We present the results of a study that investigated first and third graders’ strategies for embedding and disembedding filled shapes while also investigating the role of repeated exposure and the role of targeting students’ interpretations of sub-structures to support their efforts to embed shapes.

2. Neo-Piagetian Learning Theory and Spatial Thinking

Neo-Piagetian theories of learning build on the constructivist learning theory and emphasize that children build on prior knowledge, but they place a stronger emphasis on the role of working memory, instruction, and culture [20]. As part of Case’s [20] theory of central conceptual structures, he used children’s drawings to detail central conceptual structures underlying children’s spatial thought. He posited that by age four, children have developed two different schemas—an object shape schema and an object location schema. The object shape schema relates to capturing the shapes of objects and their parts [20]. At this age, children could draw objects (e.g., a face) with internal parts located correctly (e.g., eyes). The object location schema relates to being able to represent the position of objects [20]. By age four, children can place an object in the correct position in a picture [20]. However, at this age, the two schemas are not coordinated (e.g., children may be able to draw two people in a scene but will not represent the relations between the people and other parts of the scene). By the time children are six, they can coordinate these two schemas and consider both the object and its relation to other objects simultaneously. Further, by the time they are eight, they can mentally break up a scene into subscenes and use multiple axes as reference points [20]. Instructional activities that help lessen the cognitive demand of tasks can help students progress along these stages even earlier than is typical [20]. Although the schemas described by Case [20] were not described with shape embedding and disembedding in mind, a variety of studies and frameworks support the object shape–object location distinction with a connection to embedding and disembedding. Spatial tasks are generally considered to focus on intrinsic or extrinsic dimensions [21], which align with the shape schema and location schema, respectively [20].

2.1. Intrinsic, Pictorial Shape Spatial Reasoning

Intrinsic tasks target objects [9,21] and align with pictorial schemas, focusing on shapes and their appearance [11]; therefore, they are aligned with Case’s [20] description of the object shape schema. In relation to solving puzzles, intrinsic spatial reasoning strategies include rotating or flipping two- and three-dimensional objects [9]. This strategy is important because children have difficulty purposefully turning or flipping shapes in ways that counter prototypical images of shapes, and typically, their ability to strategically turn or flip shapes progresses between the ages of six and eight [10,14]. Another important strategy, particularly for disembedding, is abstraction, which is being able to ignore unnecessary details in visual representations [22]. Clements and colleagues [3] explored 3- to 6-year-old students’ static spatial knowledge of two-dimensional shapes (e.g., circles, squares, triangles, rectangles) and embedded shapes (e.g., a circle in a square). Students were asked to identify specific shapes, along with distractors. Circles and squares were easier than triangles and rectangles to identify because the students were more likely to identify shapes through matching with visual prototypes (e.g., looks like) instead of properties (e.g., number of sides). However, circle–square embedded shapes were the most difficult to identify. Only one-third of the students identified the square inside the circle, although over two-thirds of the students identified the circle itself [3]. Prior to this, Ayers et al. [23] found that second graders were able to identify embedded squares and rectangles to a greater extent than kindergarteners, but after they had brief instruction, the kindergarteners’ performance increased and was similar. Identifying squares was harder than rectangles [23]; there is limited evidence that identifying embedded triangles might be even more difficult [24]. Further, the first graders were significantly better at creating embedded shapes than the kindergarteners [23].

2.2. Extrinsic, Schematic Location Spatial Reasoning

Extrinsic tasks align with schematic schemas and target relations between objects [9,11,21]; therefore, they are aligned with Case’s [20] description of the object location schema. Although shape disembedding and composition tasks are generally considered intrinsic tasks because the focus is on identifying or creating an object [9], we argue that shape embedding tasks, in particular, could be considered extrinsic tasks because the focus is on creating a relation among objects, such that the final composite object has a new appearance. Students must use logic-based reasoning about spatial relationships (e.g., “this one must be a corner piece”) [25] (p. 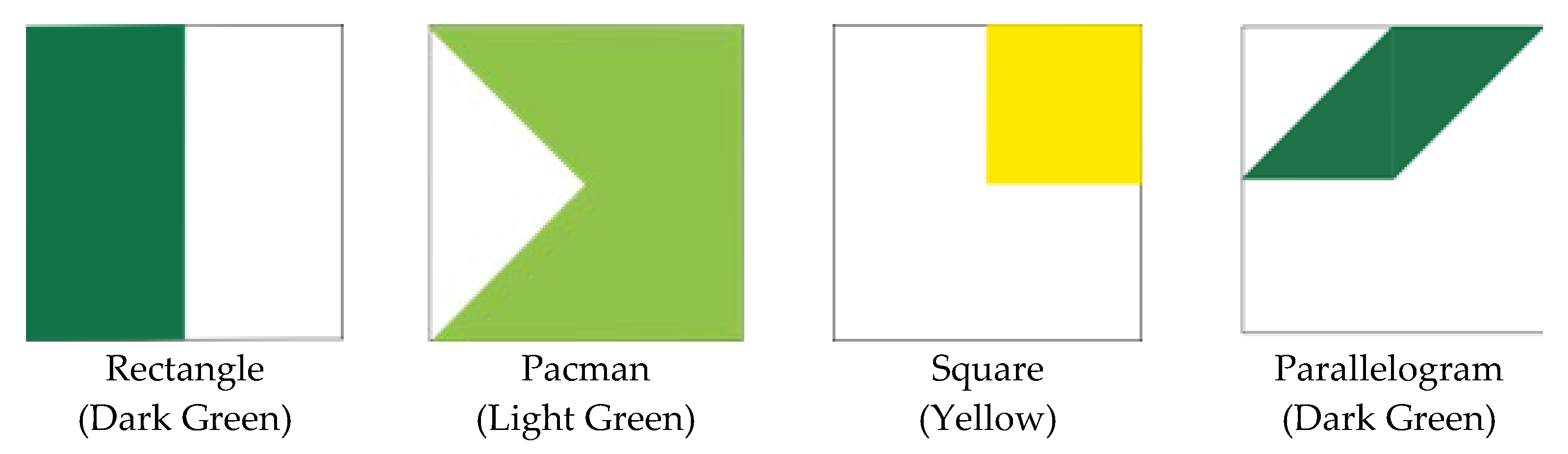38); see also [10]. For example, in the Color Code game, which is the focus of this paper, students manipulate a set of clear tiles with colored shapes imprinted on them. They must stack a set of the tiles, such that the stacked design matches the target (e.g., see Figure 1 and Figure 2); therefore, students must attend to how one tile is oriented in relation to the other tiles and in what order.

Through the examples of drawing, Case [20] suggested that students can integrate their object shape and object location schemas around the age of six. Supporting this suggestion, Pennings [2] tested out five- to eight-year-olds’ “modes of processing” (p. 69) for solving embedded figures tasks by encouraging students to use four strategies successively until they successfully disembedded a hidden figure from an image. At the two highest modes of processing, students were shown a target figure, with or without being told to look at the lines of the figure, and then had to find the target figure embedded in a complex design. The other two strategies involved physical support [2]. For the externalized successive strategy, students placed bars on each line of the target figure and then mirrored this action on the figure embedded in a complex design. Finally, for the most supportive, global manipulatory strategy, students placed a transparent cut-out of the target figure over parts of the complex figure until the hidden figure was found [2]. This implies that students may improve on embedding and disembedding tasks when given opportunities to do tasks that increase in complexity [10].

In line with Case’s [20] theory, five-year-olds tended to use the global manipulatory strategy [2], suggesting the students were not yet able to use the features of the shapes to find them, likely because younger students may have difficulty considering multiple aspects of shape (e.g., paying attention to both orientation as well as how well the shapes fit in boundaries [26]). Creating embedded figures may be more difficult than finding embedded figures [27]. In an exploratory study with three- to five-year-olds, none of the three-year-olds and few four- and five-year-olds correctly created a figure for which they needed to partially overlap three shapes; yet, they were more successful at finding hidden figures [27]. Experience may play a role; for example, one kindergartener who had played with pattern blocks on a computer was able to reason about the result of overlapping the blocks [28]. There is some evidence that intrinsic skills improve more between the ages of six and eight (such as students using more internalized strategies to disembed as they got older [2]), while extrinsic skills improve more between the ages of eight and ten [8,10]). These results are not necessarily contradictory. It may be that although students can integrate and use both intrinsic and extrinsic skills simultaneously, they initially tend to prioritize object shape information before later attending more to object location information.

2.3. Current Study

The aim of the current study was to clarify factors that support students’ embedding and disembedding through the use of filled shapes as opposed to shape frames. We present the results from two age groups—first graders, who fall in the age range when they should be coordinating shape and location schemas, and third graders, who fall toward the upper range of the trajectory, when they should be able to detect complex figures. Our research questions were as follows:

• How does students’ performance on layered, shape embedding tasks differ with age?
• How do students use intrinsic, pictorial shape schemas and extrinsic, schematic location schemas to solve a layered spatial puzzle involving embedding and disembedding?

The results of this study have the potential to clarify strategies students use to embed and disembed shapes and clarify how the pictorial shape and schematic location schemas play a role. Further, the results have potential practical implications for supporting and promoting effective embedding and disembedding strategies and students’ schema development.

3. Methods

3.1. Participants

After we obtained university IRB approval, we recruited students to participate in a study that spanned several months and investigated how students explained and fixed errors in programming tasks and their relation to explaining and correcting mathematics problems. The main experimental design involved repeated measures and a sufficient sample size to test the effectiveness of a programming intervention [29]. The data we present here focus on a spatial mathematics task from individual testing sessions that took place at the beginning, middle, and end of the study. We excluded six students from this analysis for whom we were missing accuracy data; our remaining 49 participants included 26 Grade 1 students (~6–7 years old) and 23 Grade 3 students (~8–9 years old) from an elementary school in the midwestern United States. To create pseudonyms for students, we gave each classroom an animal name (e.g., Duck) and each student a number within the classroom (e.g., 7). The subscript at the end of each pseudonym details whether the student is a first grader or third grader (e.g., Duck7_first is the seventh first grader in a classroom code-named Duck). For the spatial mathematics tasks, we worked with students individually at a table in a hallway outside of their classrooms and video recorded each session.

3.2. Materials and Design

The materials for this study consisted of a set of see-through square tiles with colored shapes printed on them from the Color Code puzzle game from Smart Game. We focused on two layered puzzle designs, each of which the students worked with twice at different time points—at the beginning and end of the study (design 1) and at the middle and end of the study (design 2).

Design 1 consisted of three tiles—a light green triangle, an orange square, and a blue partial star (see Figure 1), and we presented it the same way at both time points. First, we showed the students a video of the three tiles being stacked (by an invisible, hypothetical student) to make the target design (see Figure 2B); instead of making the target design, the hypothetical student had the point of the blue partial star oriented down instead of up (see Figure 2A). We then showed the students a static picture of this incorrect design (see Figure 2A) and the target design (see Figure 2B) for the students to refer to, handed them the tiles stacked as in the video, and asked the students if the hypothetical student made the correct design. If the students thought the two designs were the same, we double-checked by asking if they matched or looked exactly the same. If students thought they were different, we asked them to identify what was different and then change the hypothetical student’s design (using the tiles) to match the target (see Figure 2B). To successfully change the design, the students would need to turn the blue partial star tile (intrinsic, pictorial shape reasoning) and realize that the point of the blue star would be hidden by the green triangle (extrinsic, schematic location reasoning).

Design 2 consisted of four tiles—a dark green rectangle, a light green pacman, a yellow square, and a dark green parallelogram (see Figure 3), but we presented the task in two different ways between the two time points. The first time the students worked with the design, halfway through the overall study, they saw a picture of the target design that a hypothetical student made using four tiles (see Figure 4A) and the target design that the student was supposed to make (see Figure 4B). We asked the students if the designs matched and, if they indicated that the designs did not match, we asked them to fix it using the tiles. In this case, the students needed to turn the light green pacman so that the uncolored portion faced the left instead of the top (intrinsic shape reasoning) and realize that the uncolored part of the tile would reveal the dark green triangle from the dark green rectangle below it (extrinsic location reasoning). The second time students worked with the design, at the end of the larger study, they first determined, from six sub-structure choices, which embedding of the pacman and rectangle tiles could help them make the target design; the correct embedding was number four in Figure 5A. We chose to focus on these two tiles because they presented the students with the most difficulty during their previous experience with design 2. Finally, we asked them to create the target design (see Figure 5B).

3.3. Analysis

Our analysis focused on the students’ use of intrinsic, pictorial (shape-based) strategies and extrinsic, schematic (location-based) strategies [9,11,20]. We used the lens of pictorial and schematic schemas to analyze the students’ focus on color, order, shape, and orientation when they solved the puzzles (see

Table 1. Students’ focus and strategies for solving the puzzles.

Focus	Intrinsic: Pictorial Shape	Extrinsic: Schematic Location
Order	Students placed or justified tiles based on the order of the tiles shown in the video or given to them.	Reorder: Students switched the order of a tile or tiles in the stack.
Color	Students placed or justified tiles based on their color.	Students placed or justified tiles based on what color they needed to cover or reveal.
Shape	Students placed or justified tiles based on the shape of the tiles shown in the video or given to them.	Embedded Parts: Students attempted to create part of the design (e.g., the trapezoid shape in design 2).
Orientation	Flip: Students flipped the tiles, which resulted in the colored portions not being visible. Isolated Turn: Students rotated tiles on their own to the left or the right.	Slide: Students moved tiles by sliding them up or partially overlapping them. Embedded Turn: Students rotated a tile or tiles to the left or the right. If students rotated them other than 90°, 180°, 270°, 360°, this would leave the tiles partially overlapping.
Strategy	Intrinsic: Pictorial Shape	Extrinsic: Schematic Location
Testing	Individual: Students studied each tile separately or transformed one tile separately multiple times.	Systematic Embedding: Students systematically moved around tiles (in order or orientation) in relation to each other.
Disembed	Students removed a tile from the stack.	Isolate: Students broke down the design into sub-structures and worked with a sub-embedded part of the design.
Embed	Understand: Students placed the tile on top of the provided picture to check orientation.	Recreate: Students started over and attempted to recreate the design from the bottom to the top or the top to the bottom.

). For example, the students could reorganize tiles based on the colors they saw in the target design, which demonstrated their intrinsic, pictorial schema, or the students could place tiles based on what color they needed to cover or reveal, which showed their extrinsic, schematic schema. In addition, the strategies students used to organize the tiles revealed the evidence of their schema use (see Table 1). For example, when testing out the tile placement, some students worked with individual tiles (emphasizing an intrinsic pictorial schema), and some considered the relations among tiles and tried out different ways of embedding the tiles (emphasizing an extrinsic, schematic schema). In addition to our coding students’ focus and strategies for fixing and embedding the tiles for designs 1 and 2, we analyzed the students’ ability to reinterpret the partial star and pacman shapes by recording how students first oriented the shapes, which directions they rotated them, as well as their final orientation of the shapes. Likewise, we recorded which tiles students had in the correct orientation and order when they said they were finished. We also took notes on the combinations of shapes the students struggled with (or found easy) and other observations on how they tried to integrate or manipulate the tiles. Finally, for design 2, we recorded which of the six sub-structure combinations they chose and computed the Pearson correlation coefficient to assess the relationship between choosing the correct combination and correctly creating the composite design.

4. Results

4.1. Design 1

On their first encounter with the design, when they determined if the hypothetical student correctly made the three-tile design, 70% of the third graders and 58% of the first graders identified the difference in the design. However, 46% of the first graders then fixed the design, while only 39% of the third graders fixed it. When working with this task a second time roughly two months later, 83% of the third graders and 88% of the first graders identified the difference in the design (an increase of 13% for the third graders and 30% for the first graders). The first graders continued to outperform the third graders on fixing the design, with 77% of the first graders correctly fixing it and 61% of the third graders fixing it.

On their first encounter with the three-tile design, the 18 students who said that the hypothetical student’s design matched the target (and, therefore, did not make any changes) reasoned at the pictorial shape level. They primarily justified their reasoning by referring to the video or order of the tiles, either in terms of the order of the shapes or the order of the colors (11/18, 61%), not how the tiles were embedded or oriented relative to each other. The others made generic comments, or we were unable to determine their reasoning, compared to the students who reasoned at the schematic location level and correctly identified that the point on the blue partial star needed to be hidden. During their second encounter with the design, fewer students thought that the hypothetical student made the correct design (seven students as opposed to the prior 18). However, these seven students were even less inclined to justify their answers, and the two that did justify made general comments about the designs being the same.

The students who correctly identified that the hypothetical students’ design did not match the target design had different strategies for trying to fix the tiles. Especially during their first encounter, students who said the design did not match but did not correct the design tried to slide a tile or tiles so that they partially overlapped in an attempt to cover up the extra blue point, a schematic location strategy (see Figure 6A). On the other hand, those who were successful were more likely to use an embedded turn, a different type of schematic location strategy. Seven first graders and seven third graders correctly turned the blue tile while it was embedded in the stack; four of these first graders and five of the third graders made this turn as their only move, suggesting some intentionality. The others used a combination of the pictorial shape and schematic location strategies by first isolating the blue tile or turning it as they then recreated the stack (see Figure 6B). On their second encounter with the design, students continued to successfully use an embedded turn to fix the design (schematic location strategy); 10 first graders and 6 third graders did so immediately, while the others made the turn as they were recreating the design. Interestingly, during this second encounter, students were more likely to start over multiple times.

4.2. Design 2

When the students first worked with the four-tile design and had to determine if the hypothetical student correctly made the design, 20% of the students (27% of the first graders, 13% of the third graders) indicated that the light green triangle at the top of the design was missing or in the wrong spot, 24% of the students (23% of the first graders, 26% of the third graders) said that part of the dark green portion was missing, and 41% (35% of the first graders, 48% of the third graders) referred to both the light and dark green portions as problematic. Rabbit5, a third grader, noticed that the light green trapezoid shape, formed by the added dark green portion in the target design, was missing. However, only 15% of the first graders and 13% of the third graders fixed the design.

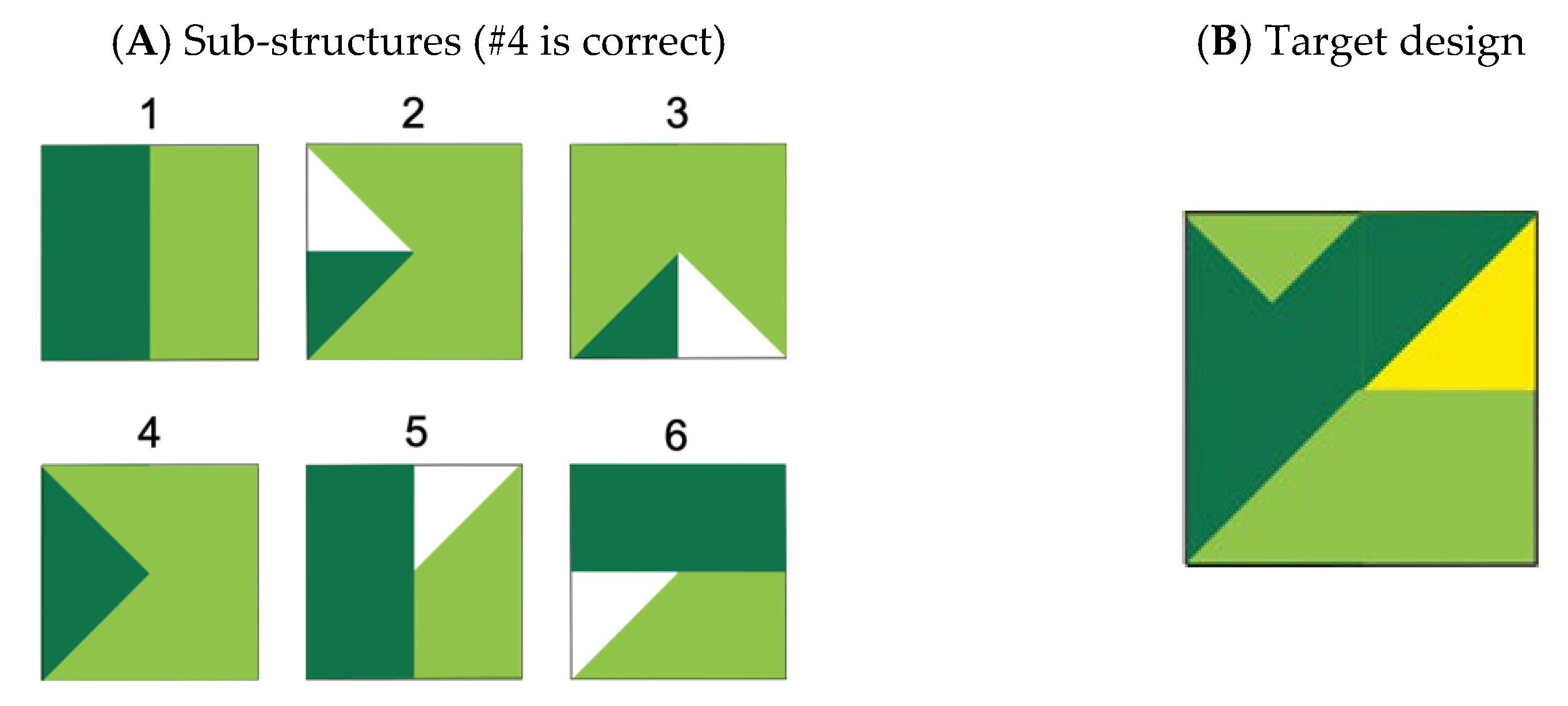
When working with the four-tile design during the second encounter roughly a month later, 33% of the students (38% of the first graders and 26% of the third graders) correctly identified sub-structure #4 (see Figure 5A) as an embedded sub-structure of the design. Another common option picked was #5 (25% of the students—27% of the first graders; 26% of the third graders), and third graders were also as likely to pick #6 (26%). Options #5 and #6 preserved the light green trapezoid shape in the target design but involved placing the rectangle in the wrong order and orientation relative to the pacman tile. Overall, 27% of the students (31% of the first graders and 22% of the third graders) correctly made the target design. Based on the Pearson correlation coefficient, identifying the correct sub-structure was significantly correlated with making the target design: r(47) = 0.469, p < 0.001. Interestingly, of the 16 students who chose sub-structure #4, only half of them had even tried turning the pacman piece to the left during their previous, first encounter with the design.

During their first encounter with the four-tile design, two-thirds of the students did not correctly fix the tiles because they also rotated tiles other than the pacman tile, sometimes turning two tiles at the same time in opposite directions, or they reordered the tiles. For example, although Goose3_first correctly rotated the pacman tile, he did not fix the tiles correctly because he also rotated the rectangle tile. Likewise, all the tile rotations were correct on Sheep5_third’s final design, but she did not fix it correctly because she changed the order by putting the rectangle on the top instead of the bottom of the stack. Another unhelpful schematic location strategy that students tried was to turn and slide the dark green rectangle tile, partially overlapping it on the stack to try and make it look like the parallelogram to fill the diagonal dark green space (see Figure 7).

Students were more successful at orienting the square and parallelogram than the rectangle and pacman tiles during both encounters (see

Table 2. Percentages of students correctly orienting (turning) and ordering the tiles for design 2.

Feature	Rectangle	Pacman	Square	Parallelogram
Orientation
1st Encounter	31%	31%	63%	61%
2nd Encounter	49%	39%	65%	55%
Order
1st Encounter	39%	37%	43%	47%
2nd Encounter	39%	51%	45%	51%

). On their first encounter with the four-tile task, 18% of the students had the correct rotation of all four tiles, which increased to 29% on their second encounter. Further, 29% of the students had all tiles in the correct order on their first encounter, and 35% did so on their second encounter. The rest of the students reordered the tiles but did not fix the order even if they had the correct orientation of the four tiles (see Table 2). The students were fairly adept at embedding the square and the parallelogram correctly; however, many students flipped the order of the pacman and rectangle tiles or placed the rectangle on top of the stack (aligned with sub-structure #5 or #6) with the pacman tile on the bottom.

Students who kept doing well or improved in fixing or embedding the tiles often disembedded the problematic tiles from the incorrect design and isolated specific tiles. Using a schematic location strategy, the students set aside the square and parallelogram tiles that they had correctly combined and focused their attention on the rectangle and pacman tiles, reducing the number of tiles they had to monitor. For example, Goose7_first embedded the pacman tile on top of the rectangle and set them aside (see Figure 8A). Then, she embedded the parallelogram on top of the square and placed them aside, picking up the other two tiles again (see Figure 8B). She turned the rectangle on the bottom (see Figure 8C), embedding them correctly (see Figure 8D). Then, she embedded the parallelogram on top correctly (see Figure 8E), lifted it up (see Figure 8F), and slid the square in underneath it (see Figure 8G). Placing all tiles back together, she had the target design (see Figure 8H).

In general, the students were persistent in trying to make the target design. The students used the pictorial shape, individual, and understanding intrinsic strategies to gain insight into how each tile looked from different orientations in relation to the target design. For example, some students overlaid tiles onto the printed design in order to compare the shapes (see Figure 9), and others used their hands to limit what they were looking at; such strategies could help them disembed sub-structures or embed tiles to make portions of the design. In fact, many students used the schematic location strategy of systematic embedding at some point in their attempt by trying to combine two tiles in multiple ways—a form of testing. Horse8_third systematically turned and reordered the rectangle, the pacman, and the parallelogram tiles until she got the correct combination.

5. Discussion

5.1. Grade Differences and Practice

Overall, the results of this study provide an interesting addition to current learning trajectories [10] and research on pictorial and schematic schemas. The result that the first graders performed slightly better than the third graders is surprising given that Case’s [20] theory and results from spatial thinking studies (e.g., [2,10,23]) suggest that students improve in their ability to coordinate their pictorial shape schema and schematic location schema across the ages of the students participating in this study. Students at each grade level spent roughly the same average amount of time on each task and used similar strategies; however, when third graders gave up, they often indicated that their attempt was “the best I can do” or that “I can’t do it,” especially for the four-tile task. Therefore, a possible explanation for the third graders’ performance was that they had lower motivation or had already decided that they could not do these types of tasks (and knew we would move on to another task if they told us they were done). We did not evaluate their motivation or beliefs about solving these types of tasks, but this information would be helpful in future studies to contextualize the results.

Students improved on their second encounter with design 1, suggesting that repeated exposure [29] to the embedding task is helpful [28]. Part of the benefit of repeating the task may have been that some students better understood the directions (similar to the benefits gained from brief instruction in finding embedded figures, e.g., [23,24]). The first time students completed design 1, more students referred to pictorial information on the tiles to justify that the design was okay; they may not have understood that they needed to make a judgment beyond the features of the individual tiles. Students’ responses across the time points sometimes got more complicated (i.e., they took more steps to make the target design), suggesting they were not just remembering what they did before. Because they worked with the more complicated design 2 for the first time in-between the first and second encounters for design 1, they might have been more willing to move the tiles around the second time they encountered design 1.

5.2. Embedding and Disembedding Learning Trajectories

Just as embedding two shape frames can create secondary structures [10], embedding two filled shapes, as in design 2, can create both secondary structures due to the shapes themselves, their colors, and the order in which they were embedded. Similar to Rozencwajga and Corroyer’s [12] findings that students struggle with stripe block designs over triangle and square ones, the irregular shape (i.e., pacman) and parallelogram were decidedly more difficult for students to fix and recreate in design 2 than shapes in design 1. Another contributor to design 2′s difficulty, beyond involving an extra tile, was that two of the tiles had shapes with the same color. Therefore, the students not only had to coordinate the embedding of the shapes but also the colors, adding to our understanding of factors that could contribute to stages of difficulty apart from the extent to which shape frames (i.e., outlines) overlap [2]. The students’ difficulty with correctly embedding the dark green rectangle suggests that the similar color made it hard for students to distinguish how to embed it.

Therefore, if we revise the disembedding learning trajectory [10] to include filled shapes, finding secondary structures of the same color might be more advanced than finding secondary structures involving different colors. According to Wolfe and Horowitz [30], color, motion (i.e., order), and orientation could be guiding attributes of attention; when orientation is obscured among similar colors, order becomes the dominating guiding attribute. Likewise, an embedding learning trajectory might involve students first embedding differently colored shapes by focusing on the order of tiles (e.g., in terms of their colors or shapes) without considering their orientations or relations to the other tiles. At the next level, students can make partial embeddings, such as with students who correctly embedded the parallelogram and square tiles. Next, students might be able to make more complex embeddings with multiple colors, followed by complex embeddings involving some tiles with the same color.

5.3. Pictorial Shape and Schematic Location Schemas

Helping students draw on schematic location schemas by choosing a sub-structure, similar to [12], helped some students identify the correct embedding of the pacman on top of the rectangle; however, for others, the light green trapezoid shape on the target design demanded their attention and drew them to use the rectangle on or near the top of the stack to break up the space of the light green pacman. There was a fine line between students using intrinsic, pictorial shape strategies to make sense of embeddings versus using them to compose parts. Students who tried to compose the trapezoid prioritized using the rectangle to block off the rest of the pacman design, disregarding the extra dark green area this created. Others were focused on composing the dark green slanted part of design 2 and turned the rectangle on a diagonal, ignoring that the tile no longer aligned with the stack. Incorporating class discussions or encouraging students to focus on and test making multiple sub-structures, similar to physical strategies used by Pennings [16], might help students break away from focusing on parts that are not helping them or consider the resulting embedded design as a whole.

In fact, successful students used a combination of pictorial shape strategies and schematic location strategies and systematically turned or reordered tiles when figuring out the correct design. The systematic testing helped students focus on portions of the embedded design, which is important to support making the target design. In particular, using a combination of systematic disembedding (e.g., isolating, similar to the synthetic strategy [12]) and systematic embedding (e.g., testing) was particularly effective. Students who isolated tiles could focus on the important features of those tiles without the distraction of the other tiles. Exposing students to strategies for testing different orientations may help them consider new spatial elements.

This study provides evidence of how developmentally appropriate layered puzzle tasks can support students’ embedding and disembedding. Students used systematic embedding and disembedding to fix the stacks, which were particularly effective when they isolated tiles and focused on important details. This study also addressed a practical concern of scaffolding young children’s embedding and disembedding; by providing potential sub-structure options for the complex four-tile task, we supported students to be systematic and analytical in their interpretation of spatial information. Incorporating more embedding and disembedding tasks in early elementary classrooms, especially leading toward tasks in which multiple shapes have the same color, could especially prepare students for more complex embedding and disembedding tasks involved in STEM subjects.