Next Article in Journal
Pocket Restorative Practice Approaches to Foster Peer-Based Relationships and Positive Development in Schools
Previous Article in Journal
A Systems Approach to Improving Foundational Reading Skills at a Preschool in India
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Education Sciences
Volume 12
Issue 12
10.3390/educsci12120879
education-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Role of Interactive Features within a Mathematics Storybook in Interpreting a Conflict and Conflict Resolution: The Case of Three Fifth Graders

by
Mahtob Aqazade
Rice University School Mathematics Project (RUSMP), Rice University, Houston, TX 77005, USA
Educ. Sci. 2022, 12(12), 879; https://doi.org/10.3390/educsci12120879
Submission received: 7 October 2022 / Revised: 26 November 2022 / Accepted: 28 November 2022 / Published: 30 November 2022
(This article belongs to the Section STEM Education)
Browse Figures
Versions Notes

Abstract

:
Students often experience cognitive conflicts when trying to interpret negative numbers’ order and values because they do not correspond to their prior whole number knowledge. One way to trigger students’ cognitive conflicts and support their conflict resolution meaningfully is through stories. Thus, I used a temperature-related mathematics storybook—Temperature Turmoil—to highlight the cognitive conflict students often experience because of relying on the integers’ absolute value and introduce conflict resolution (i.e., integers have both absolute value and directed value). By incorporating interactive features, I used a multiple-case approach to describe three fifth graders’ cognitive conflict and conflict resolution experiences. Harry, Lola, and Claire were engaged in control, interactive language, and interactive visual version of the storybook, respectively. I analyzed their responses to integer order and value questions on the pretest, session tests, and posttest as well as retellings to characterize the extent of their conflict and conflict resolution. All three benefited from the storybook with Lola making the most growth and using the mathematical language in her retellings more often. Harry, more accurately than others, described the mathematical ideas of the storybook in his retellings. Claire did not make large progress because of misinterpreting the language used in the integer values questions. This paper provides implications for how to make use of students’ common conflicts to facilitate their learning, which adds to the current understanding of using cognitive conflict as a teaching strategy. Further, the findings contribute to underdeveloped research on the benefits and limitations of interactive mathematics storybooks.

1. Introduction

Isabel correctly ordered a mixed set of positive and negative numbers, yet chose −6 as the hottest temperature among −6, −2, and −3. She reasoned, “Six is higher negative… since six is higher than three… two is closest to zero” (Fifth-grade interview, February 2016). How can Isabel work toward resolving her cognitive conflict about negative number values? And in what ways can we support her as she does so? Negative numbers are difficult to learn because of their abstract nature and the difficulty of relating them to concrete or quantitative interpretations [1,2]. Additionally, the discrepancy between students’ previous whole number knowledge and newly introduced knowledge around negative numbers may generate cognitive conflicts. For example, many students interpret negative numbers that are further from zero to be more than negative numbers closer to zero—the same as how they interpret whole numbers. Even students who, like Isabel, know negative numbers are below zero still rely on numbers’ absolute values (e.g., −6 > −2 because |−6| > |−2|; [3,4,5]).
Although prior research had classified students’ (across ages 5–14) ways of reasoning about integers’ order and values (e.g., [3,4,5,6,7,8,9,10,11,12,13]), there is limited work describing these ways of reasoning through the lens of cognitive conflict and conflict resolution (see [14,15]). Using this lens can help to identify students’ common cognitive conflict with integer order and values, detail their processes of resolving them (i.e., reconciling the conflict between numbers having both absolute and directed value), and explore the supports they require to do so.
One way to elicit students’ cognitive conflict and support them to resolve it is through stories. A mathematics storybook with a meaningful and relevant context, mathematical language in the story’s content, and instructional models in the story’s illustrations can help students to notice the discrepancy between their existing and new knowledge—cognitive conflict—and work towards conflict resolution. Moreover, in an electronic mathematics storybook, an assortment of interactive features (e.g., hotspot) can be embedded in the story’s content and illustration to further support students’ conflict resolution. The interactive features can, for instance, reinforce mathematical language and instructional models and highlight their relations with the new knowledge.
In this paper, I used a temperature-related electronic mathematics storybook—Temperature Turmoil [16] (the electronic version of this storybook used in this study is based on an earlier draft of the book. A revised version is now published with the same title)—to highlight the cognitive conflict students often experience because of relying on only the integers’ absolute value and to introduce the conflict’s resolution (i.e., integers have both absolute value and directed value). Further, I created two interactive versions by incorporating interactive features in the book: interactive language (highlighting mathematical language) and interactive visual (highlighting instructional model). I chose the context of temperature because it is a commonly used context for integers [2,17,18,19,20], it uses relative numbers [21], it provides an opportunity to interpret the negative numbers as relative numbers below zero, it uses a thermometer representing a number line model [22,23,24], and it allows for formal notation of negative numbers as opposed to other contexts such as negative as debt or negative as below sea level. In addition, students who participated in this study have lived in an environment where they experience negative temperatures and can relate to this context. In this study, using a multiple-case approach [25], my goal was to describe three fifth graders’ cognitive conflict and conflict resolution interpretations after listening to either a control version or only one of two interactive versions of the book. To do so, I explored whether they responded to integer order and value questions on the pretest, session tests, and posttest by relying on the absolute value perspective, whether they referred to mathematical ideas of the story in their story’s retellings, and whether they drew their thermometers with both positive and negative numbers and in the correct order.

2. Cognitive Conflict and Conflict Resolution

Based on Piaget’s cognitive development theory, invoking cognitive conflict is at the core of the learning process [14,15]. A cognitive conflict occurs when learners notice the discrepancy between newly acquired knowledge and their existing knowledge [26,27,28]. Many scholars have operationalized Piaget’s notion of cognitive conflict and explored its use as a teaching strategy (e.g., [27,28,29,30,31,32]). For example, Watson [30] presented students with conflicting ideas when comparing two data sets to investigate how their statistical inferences change. She found that up to 57% of students could improve their inferential reasoning after encountering conflicting ideas.
To ensure that presenting conflicting ideas leads to appropriate learning, they need to be meaningful for students [26,33] and followed by opportunities for conflict resolution [27,28,34]. In Piaget’s work, conflict resolution involves the processes of assimilation—fitting the new knowledge into existing knowledge—and accommodation—restructuring existing knowledge to provide consistency with newly acquired knowledge [14,15,35]. However, prior research has not provided sufficient detail on how those processes look (e.g., [27,28,34]). Understanding how students interpret conflicting ideas and work towards resolving them can inform ways to present them meaningfully and provide instructional methods that facilitate their conflict resolution. For instance, Shahbari and Peled [27] found that a realistic modeling situation around changing references in fraction calculations results in generating students’ cognitive conflict and motivating them to resolve it.

The Case of Integers’ Order and Values

Prior research has illuminated students’ common difficulties when learning about negative numbers’ order and values using different contexts and comparison language (e.g., [1,4,5,6,7,11,12,13,19,22,36,37,38]. For example, Whitacre et al. [13] investigated second-, fourth-, seventh-, and eleventh-grade students’ reasoning about integer comparisons by having them find the larger number between two integers. They found comparing two positive numbers was the easiest and comparing two negative numbers was the most difficult across grade levels. Bofferding and Farmer [7] used the temperature context to explore how second- and fourth-grade students responded to integer comparisons involving different question phrasing (e.g., most hot, most cold, least hot, and least cold). Students’ responses differed based on their integer values and question phrasing interpretation. The findings indicated that students had more difficulties finding the coldest, as opposed to the hottest, temperature on positive number comparisons and mixed positive-negative integer comparisons. Students had less difficulty with most cold than least hot comparisons. They also did better with most hot for positive-number-only comparisons and least cold for negative-number-only comparisons.
When introducing negative numbers as new knowledge, Bofferding [4,5] classified students’ reasoning about integers’ order and values (i.e., integer order and values mental models), which reflected their common cognitive conflicts. Some students may not notice the discrepancy between their whole number and negative number order and value knowledge. Thus, these students do not experience a cognitive conflict, reflecting what Bofferding [4,5] described as the initial mental model level. These students ignore negative signs and treat all numbers as positive; alternatively, they order negative numbers separate from positive numbers but treat all as equaling their absolute value. Using a real-world context can trigger these students’ cognitive conflict, provide tangible opportunities to differentiate the negative and positive numbers, and support their conceptualizations of integers as relative numbers and translation (e.g., [5,20,22,39,40,41,42]). For example, by using a thermometer—representing a number line instructional model—to measure positive and negative temperatures, students can see numbers presented on two sides of zero as opposite quantities [1,4,5,42].
Some students experience a cognitive conflict regarding how to order negative numbers or relate them to their values [4,12,43,44]. However, their conflict resolution processes may differ. Some students notice the minus sign next to negative numbers, but their conflict resolution approach is to interpret the negative sign as taking away a number from itself (e.g., −9 = 9 − 9; [45,46]) corresponding to Bofferding’s [4,5] transition I mental model level. In other words, students with this conflict resolution approach treat the negative numbers as equivalent to zero. Thus, when asked to find the colder, smaller, or lower integer between a negative and a positive number, they correctly choose the negative number. However, they struggle to do so among only negative numbers because to them, all negative numbers equal zero [4,5,6,7]. To support these students’ conflict resolution process, they need to see that a minus sign does not only mean subtraction but also can be attached to a number designating a negative number (i.e., unary meaning; [45,46]). One way to provide this support is through contrasting worked examples; comparing negative numbers’ values accompanied by an instructional model. For example, modeling changes in negative temperatures on a thermometer can help students to see that negative numbers have smaller values than zero and their distances from zero differ [47,48].
Although some students conceive of the negative sign as attached to a number and interpret negative numbers as being below zero, their conflict resolution is still in process. They consider, for instance, negative numbers with a larger absolute value as greater than negative numbers with a smaller absolute value (e.g., −9 > −2), reflecting the magnitude mental model level [4,5]. Bofferding [4,5] describes students at the integer order and values transition II mental model level as similar to those in the magnitude mental model level. However, their conflict resolution changes depending on the question phrasing or problem type: sometimes they interpret negative numbers as they do at the magnitude level, but sometimes they interpret them correctly. Their conflict resolution can be supported by using integers as relative numbers or directed numbers and conceptualizing them as having directed values [4,5,21,41,46]. The relative or directed number “relates to the idea of opposite quantities in the discrete domain or the idea of symmetry in the continuous domain” ([46], p. 557). This means integers have two components: magnitude and direction. Magnitude refers to an integer’s absolute value or its distance from zero, and the direction designates it as negative or positive. For positive numbers, absolute and directed values are the same as their distance from zero increases, but for negative numbers, distance from zero results in an increase in absolute values and a decrease in directed values (see [4,7,13,49]). Using directed magnitude language is one way to facilitate using directed values [4,7]. For example, −5 is more in the negative direction—more negative—than −3. In terms of temperature context, although it is an intensive quantity measurement ([24,50]), the directed magnitude language can be also nicely used to describe the relativity of numbers (e.g., −25° is more hot than −45°). Finally, some students’ cognitive conflict is resolved; and they demonstrate complete integer values and order understanding, i.e., formal mental model level [4,5].
In the case of integers, to explicitly evoke students’ cognitive conflicts and support their conflict resolution processes, a meaningful context, relevant instructional model, and appropriate mathematical language are fundamental.

3. Mathematics Storybooks

Mathematics storybooks can expose students to a cognitive conflict they often experience with a new mathematical idea and propose its resolution through a real-world context, supported by instructional models in the illustrations and mathematical language in the text. Research on mathematics storybook reading interventions indicates a significant improvement in mathematics achievement, interest, and using mathematical language [51,52,53,54]. Electronic mathematics storybooks can even be more effective than traditional printed books for learning mathematics (e.g., [55]). An electronic mathematics storybook has also the advantage of providing features for greater interactions [56]. With traditional printed books, such interactions often involve the student-student and student-teacher interactions but with interactive mathematics storybooks, student-content interactions can be enhanced by embedding interactive features (e.g., hotspot) in the story to support learning.

Interactive Mathematics Storybooks

Most interactive features in electronic storybooks are puzzles, memory tasks, amusing visual or sound effects, a dictionary function, or word or picture labels appearing when activating a hotspot [57,58,59,60,61,62,63]. Research on using interactive electronic storybooks has shown both effective and ineffective outcomes on children’s literacy development and story comprehension [57,64,65]. A body of experimental research documents the negative impact of interactive features because they distract children’s attention from central aspects of the learning materials (e.g., [57,58,65]). Although using interactive features does not automatically create learning, they can engage children in substantial cognitive activities that, if carefully designed, can promote deep cognitive processing. Thus, some researchers celebrate interactive features as a possible way to motivate and engage children in reading [64,65]. These contrasting findings could be explained by the difficulty and inconsistency in defining the interactive features [64,65,66].
Despite existing research on exploring the effects of interactive electronic storybooks in language development and story comprehension, research on investigating the role of interactive features within an electronic mathematics storybook is limited [56]. Ginsburg et al. [56] created an interactive electronic mathematics storybook, Monster Music Factory, to promote three- to five-year-old children’s mathematical thinking. Besides the animation and sound effects, the child can interact with the story’s characters or objects by touching the screen and activating a hotspot. For example, in a scene of the story, one character miscounted a set of tambourines. A father engaged in shared reading with his child (Eddy), asked: “Are those three tambourines?” Eddy touched the tambourines on the screen and correctly counted, “One, two, three, four” ([67], p. 117). Each time Eddy touched a tambourine, it became animated by shaking and lighting up and making a tambourine sound. Eddy’s active participation was a result of his father’s question, the animation and sound effect features, and the touch-screen hotspot embedded in the story [67].

4. Present Study

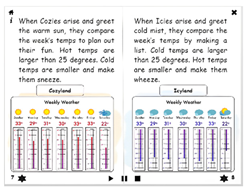
4.1. Temperature Turmoil

In this study, I used the Temperature Turmoil mathematics storybook [16], a book purposefully designed to highlight the common cognitive conflict that students experience when learning about integers’ order and values—interpreting integers only using their absolute values (see [3,4,5,13])—and to introduce the conflict resolution by unfolding the difference between positive versus negative numbers and absolute value versus directed value. To do so, the story uses a temperature context, thermometers in the illustrations, and directed magnitude language in the text. The author of Temperature Turmoil intentionally designed this mathematics storybook because there are limited mathematics storybooks to focus on integers, particularly around students’ common cognitive conflicts and conflict resolution with positive and negative numbers’ order and values within the temperature context. Throughout this mathematics storybook, the author incorporated different mathematical language (e.g., smaller, more hot, opposite) and thermometer representations to illustrate the common cognitive conflicts arising from relying on only absolute value perspective and distinguishing the integers’ absolute value and directed value.
In this mathematics storybook, the two characters, Curt from Cozyland representing a land with only positive temperatures, and Ilana from Icyland representing a land with only negative temperatures, describe their lands’ temperatures by only relying on their absolute values. Thus, when Cozy and Ilana feel less comfortable with changes in their lands’ temperatures and look for another land, they choose each other’s lands. They made this decision because of describing their land’s temperature change using absolute values, which made them think each other’s land’s temperature is more favorable. The story continues as Curt and Ilana meet up again confused. For instance, Curt says, “Your 20 [−20] is more cold than back in my land [Cozyland, land of positive temperatures only]”. Ilana says, “Your 20 [+20] is more hot than back in my land [Icyland, land of negative temperatures only]”. They realize each other’s land’s temperature is opposite when one character says, “Each 20 is far from zero but in an opposite spot” ([44], p. 319). Thus, they decide to use a notation for temperatures below zero to distinguish their lands’ temperatures and extend their thermometers to include both positive and negative temperatures. Finally, they decide to go back to their lands where they adapt to their changing temperatures and use new notation and extended thermometers to compare the temperatures on a continuum.
In the Temperature Turmoil mathematics storybook, the focus is on the context of temperature because, in a recent survey of how teachers introduce negative numbers to students, temperature was a popular context [17]. Although there are other contexts to introduce negative numbers to students (e.g., money, elevation [18,19,20,21,22]), a temperature context allows for (a) using a thermometer as a number line instructional model to present integers as relative or directed numbers with reference to zero [1,5,41] and (b) using formal notation to differentiate positive and negative temperatures (as opposed to, for instance, the context of debt where $−5 is not often used). Although “temperatures are intensive measurements” ([24], p. 46), this storybook uses the temperature as a relative scale where the designation of hot and cold is arbitrary. By using directed magnitude language, the Temperature Turmoil mathematics storybook aims to emphasize integers’ directed values and use them as a relative number (e.g., −5 is more hot than −10; [5]). Additionally, the participants of this study have experienced negative temperatures in winter yet struggled to compare and make sense of the integers’ values. Thus, it was important to introduce the negative and positive numbers using the temperature context.

4.2. The Study Goals

With the author’s permission, I created three different electronic versions of Temperature Turmoil: control, interactive language, and interactive visual. The interactive versions include focusing on language (e.g., emphasizing integer comparisons with directed magnitude language, such as −3 is more hot than −10) and visual (e.g., highlighting integer comparisons using thermometers that embody a number line).
In this paper, I took a multiple-case approach [25] with three fifth graders who each engaged with only one version of the storybook throughout the study. I explored their interpretations of the conflict and conflict resolution presented in the story and the role of interactive features in their interpretations. To do so, I analyzed their test responses, retellings, and drawn thermometers across the study. For their test responses, I explained the extent to which they relied on the integers’ absolute value for each integer comparison question phrasing (e.g., most hot, least cold). For their retellings, I classified whether they referred to the story’s mathematical ideas (e.g., referring to the story’s characters relying on temperatures’ absolute values). For their drawn thermometers, I determined whether they included both positive and negative numbers in the correct order. I argue that interactive features can (1) draw students’ attention to the conflict presented in the story, (2) facilitate their conflict resolution, and (3) promote using directed magnitude language and thermometer representation more accurately than the control version.
I examine the subsequent research questions: By focusing on three fifth-grade students who are still in the process of resolving some of their cognitive conflicts around integer order and values, in what ways do interactive features support their conflict resolution as (a) reflected in their responses to integer order and value questions and (b) expressed during their retellings?

5. Methods

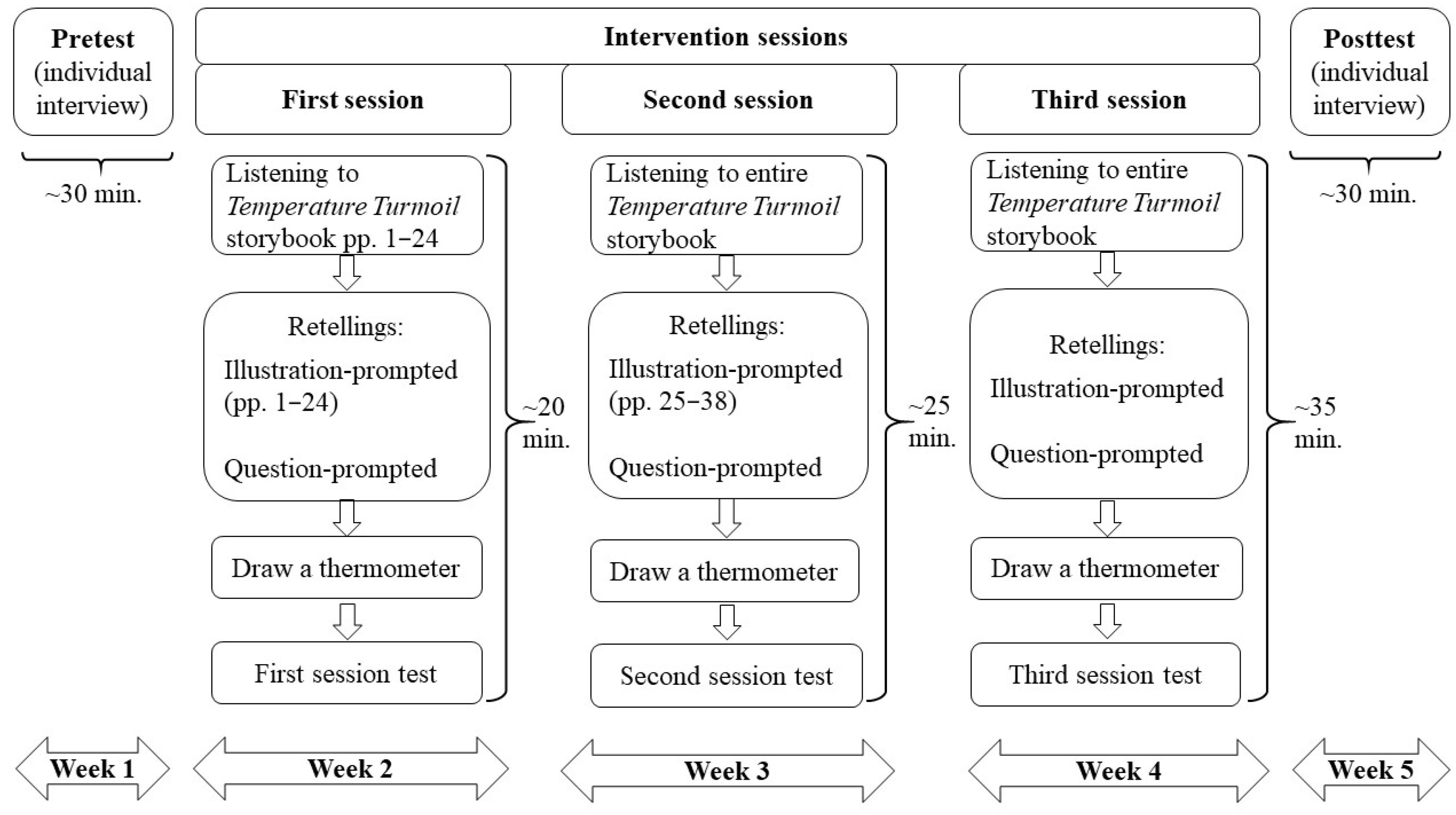
5.1. Participants, Setting, and Study Design

This paper’s data are from a study with third- to fifth-grade students from a public suburban elementary school in the Midwest, United States. The school’s population comprised 66% White, 17% Hispanic, 12% Black/African American, and 5% other ethnicities/races as well as 45% economically disadvantaged, and 11% English Learners. After receiving Institutional Review Board and the school district approval, I sent home consent forms with all third (one class), fourth (two classes), and fifth graders (two classes). Overall, I recruited three third-, five fourth-, and six fifth-grade students who returned signed forms. The study included a pretest, three intervention sessions, and a posttest spanned over five weeks (see Figure 1).
After the pretest, I purposefully assigned the students to one of four conditions: control (three students, one from each grade level), interactive language (four students: one third grader, one fourth grader, and two fifth graders), and interactive visual (three students: one from each grade level), and a mix of both interactive language and interactive visual (four students: two fourth graders and two fifth graders). To do this purposeful assignment, I had two main criteria: (1) at least one student from each grade level in each condition and (2) having students with similar pretest performance across conditions. Regardless of their condition, students listened to the same story on an iPad. In the Control condition, students listened to the story with audio to play/pause/stop and buttons to go to the next/previous page.
In addition to what the control version had, I embedded interactive features in the form of hotspots in the interactive language and visual versions (12 out of 38 pages contained hotspots with a total of 35 hotspots; see Table 1). I placed the hotspots on either a thermometer in the illustration or a directed magnitude word in the text. Additionally, I marked pages with a hotspot by a star.
In the Interactive Language condition, when students activated a hotspot, a mathematical question aligned with the story’s mathematical ideas appeared, and students received feedback after responding. This version’s goal was to highlight differences in numbers’ values using different mathematical language (e.g., smaller, more cold), particularly directed magnitude language.
In the Interactive Visual condition, activating a hotspot resulted in an animation, a slider, or a combination thereof that centered on a thermometer representation. The animations involved a magnified thermometer illuminating a temperature change or opposite temperatures. When students dragged the slider on the thermometer, the temperature and background image changed. This version’s goal was to show differences in numbers’ values and oppositeness of positive and negative numbers using a thermometer.
Finally, students who were in a mix of both interactive language and interactive visual condition engaged with both types of interactive features during the intervention sessions (half of the hotspots were as interactive language and the other half were as interactive visual).

5.1.1. Pretest and Posttest

On the pretest and posttest, for each question, students individually read, solved, and explained their reasoning without receiving feedback (see Table 2 for examples). After the intervention sessions, all students took the posttest. The pretest and posttest, given as individual interviews, each took approximately 30 min and were recorded. I compiled the pretest and posttest questions from assessments and questions developed by prior research on integer learning and teaching (see Table 2 for references). Beyond the order and value questions, the pretest and posttests contained directed magnitude language questions (e.g., The thermometer shows yesterday’s temperature. Today, the temperature will be 5 degrees less hot. Circle today’s temperature on the thermometer [a thermometer with yesterday’s temperature will be shown to students].) as well as integer addition and subtraction questions including number-sentence (e.g., 8–12) and story-based problems (e.g., Today, Cozyland’s temperature was 5 degrees hot. Tomorrow’s forecast predicts that the temperature will be 7 degrees less hot than today’s temperature. What will Cozyland’s temperature be tomorrow?). In this paper, I focused on the integer order and value questions because the intervention with the Temperature Turmoil mathematics storybook targeted the concepts of integer order and values. More specifically, at different points of the story, the characters of two lands compare and describe the changes in their temperatures using different directed magnitude language (e.g., comparing temperatures with least hot or most hot). For example, Cozy says, “Today is less hot—from 33° to 22°, it’s getting more cold. What will we do?” Also, the story’s illustrations represent thermometers with ordered temperatures (both negative and positive numbers). Thus, I chose these specific questions to better document students’ learning from the Temperature Turmoil mathematics storybook.

5.1.2. Intervention Sessions

In the First Session, students only listened to the initial part of the story highlighting the conflict of characters relying on only temperatures’ absolute value and retold the same part of the story (pp. 1–24). This way, I could see if there were any guesses about the story’s conflict resolution. In the Second Session, students listened to the entire book but only retold the second part (pp. 25–38). This way, I could see if students referred to the conflict while describing the conflict resolution. In the Third Session, students listened to and retold the entire book. For retellings, I asked students to retell the story as if telling it to a friend who had not read it by going through a wordless version of the book (or a part of the book) (see [69]). Although I did not explicitly prompt students to describe the story’s conflict and conflict resolution, the illustrations may have prompted or assisted them. Thus, I refer to these retellings as illustration-prompted retellings (see Figure 1).
After each illustration-prompted retelling, students described the story’s conflict and conflict resolution based on the following questions: “The people in these two lands seem to have some problems—what problems are they having? How do you think they will solve their problems?” I refer to these descriptions as question-prompted retellings (see Figure 1). Next, students drew a thermometer that could resolve the two lands’ conflict. Students’ drawn thermometers could illustrate the extent to which they paid attention to thermometer representations in the story’s illustrations and illuminate whether they resolved the cognitive conflict or in-process resolution around integers’ order. Finally, students answered some integer order and value questions (see Table 2). I refer to these questions as session tests (see Figure 1). I recorded the intervention sessions, and each took no more than 40 min.

5.2. Data Sources and Analysis

In this paper, I focused on fifth graders (~ages 10–11) because they have been most likely introduced to negative numbers [18] and consequently, experienced cognitive conflicts and worked towards resolving them as opposed to third- and fourth graders. Additionally, research on the effects of mathematics storybooks (interactive or non-interactive) has primarily targeted early childhood and early elementary students (K-3 students, ~ages 3–9).
I used a multiple-case approach [25] to explore three fifth graders for in-depth case analysis: Harry from control, Lola from interactive language, and Claire from interactive visual. I eliminated students who were in the mix of both interactive language and interactive visual from the analysis for this paper because my goal was to draw a distinct comparison between interactive visual and interactive language and control conditions. Harry and Claire were the only fifth graders in the control and interactive visual conditions, respectively. Harry scored 85% and Claire scored 56% on the pretest integer order and value questions. Among the two fifth graders who were in the interactive language condition, Lola’s pretest responses were similar to both Harry’s and Claire’s responses and represented an average of their scores (Harry: 85%, Lola: 71%, Claire: 56% and the other fifth grader’s score was 54%). Additionally, choosing Lola could potentially help to illuminate students’ different interpretations of cognitive conflict and conflict resolution that were presented around mathematical ideas in the story. Overall, they all could differentiate between positive and negative numbers (i.e., negative numbers are below zero and smaller than positive numbers). However, depending on the task or question phrasing, sometimes they over-relied on numbers’ absolute value and sometimes correctly interpreted the integers’ values. Thus, they were still in the process of resolving some of their cognitive conflicts around integer order and values, reflecting the transition II mental model level (see [4,5]).
The units of analysis within each case were their test responses, retellings, and drawn thermometers. First, I analyzed each case’s responses to the integer order and values questions throughout the study (pretest, session tests, posttest). This way, I could characterize if their responses exhibited a resolved cognitive conflict or in-process resolution. Thus, I considered students experiencing a cognitive conflict when answering the questions by relying on only numbers’ absolute value. I determined their cognitive conflict was entirely resolved if answering all the questions correctly or an in-process resolution depending on the question phrasing, sometimes treated integers with their absolute values and sometimes correctly.
Second, I classified whether students’ reference to the conflict and conflict resolution (if any) in their retellings (illustration-prompted and question-prompted) reflected the story’s mathematical ideas (see Table 3). Then, I determined what aspects of the mathematical idea were more salient to them (e.g., thermometers’ directions). The two types of retellings prompted students about conflict and conflict resolution either explicitly or implicitly so, I report them separately to highlight their differences (if any).
Third, I determined if students’ drawn thermometers had only positive numbers, positive numbers with reversed negative numbers, or positive and negative numbers in the correct order. Finally, I created a cross-case synthesis to compare Harry’s, Lola’s, and Claire’s progress based on their test responses; the accuracy of their retellings (reflecting conflict and conflict resolution around the mathematical ideas) and their drawn thermometers (reflecting the conflict resolution in the story’s illustrations); and their use of directed magnitude language in their retellings.

6. Findings

To an extent, all three students experienced a cognitive conflict when answering integer order and value questions.

6.1. Pretest

Table 4 shows the breakdown of students’ responses on pretest integer comparison questions based on question phrasing and number types.
Harry chose “none” for the most hot temperature among only negative numbers and said, “They are negatives and that isn’t really warm”. Expect for correctly choosing among −24, −30, and 34, he continued to choose “none” even for the most hot temperatures with both positive and negative numbers. Although Harry answered the other questions correctly (see Table 4), in this particular integer comparison question phrasing, Harry’s choice suggests experiencing a cognitive conflict and an in-process conflict resolution.
Lola’s responses to the most cold temperature question phrasing reflected a cognitive conflict of interpreting integers by their absolute values. She described, “Negative is like small number… lower… and colder” but when choosing among more than one negative temperature, she chose the negative temperature with the smallest absolute value (e.g., choosing −18 among −33, −18, and −22). In two instances for the most cold temperature, she ignored the negative sign and chose the temperature with the smallest absolute value (e.g., choosing 14 among −19, 14, and 26). On all the other question phrasing, Lola had only five incorrect responses, reflecting an in-process conflict resolution (see Table 4). Two of her incorrect responses were on the most hot and two other incorrect responses were on the least cold questions phrasing where she chose the middle-value temperature (e.g., choosing −25 as the most hot among −25, −31, and −17; see Table 4). On the least hot question phrasing, her only incorrect response was choosing the middle-value, (i.e., 15) among 0, 21, and 15 (see Table 4).
Claire’s incorrect responses to the least cold temperatures showed a reliance on the absolute value perspective and misinterpretation of the question phrasing. Claire described the least cold as “least” and looked for the “lowest number”. When choosing among all negative numbers, she chose the temperature with the smallest absolute value (e.g., choosing −14 among −21, −14, and −24; see Table 4), which reflected experiencing a cognitive conflict with integers’ values. However, because Claire differentiated positive and negative numbers, for example, among −31, 19, and 23, she chose −31 as the least cold temperature “because it’s negative”. Claire explained the least hot as “not super-duper hot but still pretty hot” and answered as if the questions were asking for the most hot temperature. For example, among −31, −28, and 23, Claire chose 23 because “it doesn’t have a negative”. Claire answered the most hot temperature questions correctly and only had one incorrect response for the most cold temperature question phrasing (see Table 4). On this incorrect response, she chose the smallest absolute value number (i.e., −22) among −22, −26, and 33. Overall, Claire’s incorrect responses suggest experiencing a cognitive conflict and an in-process conflict resolution.

6.2. Harry

6.2.1. Retellings

Because Harry was in the control condition, his retellings only reflected his interpretation of the story’s content and illustrations. In the first session, Harry’s retellings referred to the story’s mathematical conflict and conflict resolution. In his question-prompted retelling, Harry explained the two lands showing “different sides of zero… one was negative and, one was positive”. Similarly, in his illustration-prompted retelling, he described the thermometers’ different directions:
Their temperatures are different because this [Cozyland] is going up from zero and this [Icyland] is going down from zero. This [Icyland], it’s negatives and this [Cozyland] is positives. So, they think that’s the same temperature cause thirty-three positive and thirty-three negative
(pp. 7–8).
For Harry, the direction of positive and negative numbers in reference to zero was the most noticeable story’s mathematical idea.
In both types of retellings during the next two sessions, Harry continued to refer to the story’s mathematical conflict and conflict resolution. Additionally, Harry noticed the notation that distinguishes positive and negative numbers. During the illustration-prompted retelling, Harry said, “They made a line next to the negatives because there’s a line [for numbers] below zero and it was colder. Then you could tell it was different going down below [zero]” (pp. 31–32). Similarly, for the question-prompted retelling, he said, “They made the negative side with a minus sign”. Furthermore, during his third illustration-prompted retelling, Harry mentioned making “a different thermometer… [for] showing [both] positives and negatives” (pp. 31–32).

6.2.2. Session Tests

Compared to the pretest, Harry’s responses did not demonstrate a cognitive conflict around misinterpreting value and over-relying on absolute value reasoning. Instead, he sometimes misinterpreted the question phrasing. For the most hot temperatures in the first session, he chose the temperatures as if the question was asking for the most cold temperature (see Table 5). For example, he chose 20 as the most hot temperature among 26, 33, and 20. Harry answered all the other questions in the first session correctly. In the second session, Harry answered all the questions correctly (see Table 5). In the third session, he interpreted least cold as “cold” and chose the temperature as if answering for most cold temperatures (see Table 5).

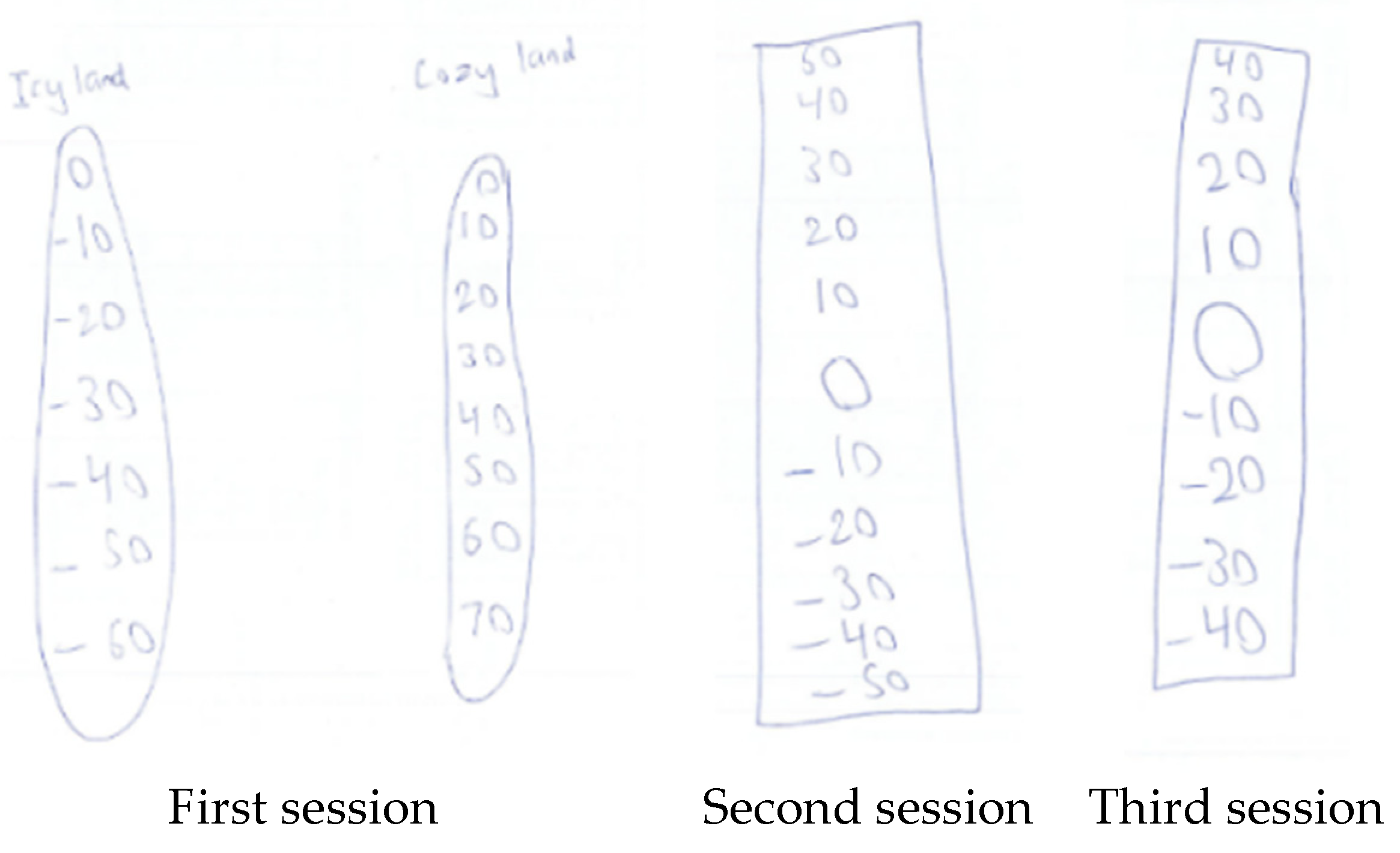
6.2.3. Drawn Thermometers

In the first session, Harry’s drawing included two thermometers, one with positive and one with negative numbers in the correct order. In the next two sessions, his thermometers reflected the conflict resolution of the story’s illustrations: one continuous thermometer from negative to positive temperatures (see Figure 2). He referred to the story’s mathematical ideas when explaining how his thermometer would resolve the two lands’ conflict:
This side is the positive side with kind of like the Cozyland [be]cause it added up here, and that’s the more warm side. This side is more cold side [be]cause of the negatives and below zero. Now, that sign can show you that’s [a] minus ten from zero.

6.3. Lola

6.3.1. Retellings

In the first session, Lola activated six hotspots across pages 7, 17, and 18. For example, one hotspot asked: “In Cozyland, which day’s temperature is smaller than Tuesday [showing 33°]?” She chose Saturday (showing 22°) and said, “Yes” confirming her answer by only reading the beginning of the feedback. Later, another hotspot asked: “Which town’s temperature is the opposite of Sandiana [showing 19°]?” Lola wondered, “Opposite?” and incorrectly chose 5°. Although activating a few hotspots may have reinforced some of the story’s mathematical ideas, both types of Lola’s retellings focused on the story’s non-mathematical conflict and conflict resolution. For example, in the illustration-prompted retelling, she said, “This one [Cozyland] was getting too cold, this one [Icyland] was getting too hot, they try to do a lot of fire… and a lot of ice” (pp. 9–14).
In the second and third sessions, Lola activated four (pages 28, 29, 33, and 34) and six hotspots (pages 7, 8, 17, 28, 33, and 34) respectively. One hotspot asked: “The opposite of 30° from Icyland”. She chose the correct temperature. However, for “the opposite of 30° from Cozyland”, she chose 10° and then 0° incorrectly. By the third session, Lola paid attention to the feedback and began answering the questions more accurately. For example, she first incorrectly answered “which of the temperatures are correctly ordered from least to greatest?” by relying on integers’ absolute value (i.e., choosing 0°, 10°, −15°, −25°, 25°, 30°, −35°). However, after reading the feedback completely, she attempted again and chose the correct answer.
In the last two sessions, by activating several hotspots and listening to the story more, Lola’s reference to the story’s conflict and conflict resolution for both types of retellings corresponded to some mathematical ideas of the story. She described the difference between the two lands’ temperatures by highlighting zero as a reference point. For instance, for her second question-prompted retelling, Lola explained an agreement between the two lands “that zero above or below means hot and cold”. Unlike Harry, Lola did not describe how the above and below zero references connected to the positive and negative numbers.
In her third question-prompted retelling, Lola thought, “Draw[ing] a little chart [referring to thermometer]” could be sufficient to distinguish the two lands’ temperatures. Further, in her third illustration-prompted retelling, Lola explained the contrasts between the two lands’ thermometers, “Theirs is like upside down so you are going to go up and that’s why it’s getting hot and that one is getting cold” (pp. 31–32). Altogether, Lola’s references to the mathematical ideas centered around recognizing two sides of zero as two categories of numbers, which can suggest she thought of these categories as being opposite. This illuminates how questions asking her to choose opposite temperatures or feedback distinguishing positive and negative numbers by referencing zero were powerful interactive features for Lola to conceptualize some of the story’s mathematical ideas.

6.3.2. Session Tests

Lola still exhibited some cognitive conflicts when interpreting integers’ values, but sometimes differed from her pretest. In the first session, among all negative temperatures for the most hot temperatures, she chose the middle-value temperature (i.e., choosing −21 among −21, −24, −14; see Table 6). For the most cold temperature among negative numbers, Lola relied on integers’ absolute values and chose the temperature with the smallest absolute value (see Table 6). Lola described the least cold as “it means down” and chose the temperatures as if the question was asking for the most cold temperature. To Lola, least hot meant “negatives” with the smallest absolute value. In the second session, Lola often answered the questions correctly but, in a few instances, treated the numbers with their absolute values. By the third session, Lola answered all the questions correctly (see Table 6).

6.3.3. Drawn Thermometers

Lola, in the first session, drew one thermometer showing 33° and explained, “So they both had thirty-three degrees at the beginning, if they go back to thirty-three, like in Icyland, I think it will get cold for them and hot for the other one”. In the next two sessions, her thermometers included only positive numbers on both sides of zero (see Figure 3). For example, she described her second thermometer, “It’s just like in the story drawing. They drew like that, and it was hot and cold down here”. Interestingly, Lola labeled “hot” on the bottom and “cold” on the top for her third thermometer, which was the opposite of the story’s illustrations. Lola’s thermometers showed the two lands opposite temperatures as two sides of zero, which were present in parts of the story’s illustrations. However, without formally notating the negative numbers to distinguish two opposite sides of zero, her thermometers did not reflect the conflict resolution of the story’s illustrations.

6.4. Claire

6.4.1. Retellings

In the first session, Claire activated 21 hotspots on all pages containing a hotspot. Although Claire activated more hotspots than Lola and thought dragging a thermometer to change the temperature was “cool”, these hotspots did not help Claire to refer to the story’s mathematical ideas in her retellings. Claire’s illustration-prompted retelling was like Lola’s. In her question-prompted retelling, she said, “Each other’s temperatures are different from what they have it [be]cause there is hotter people and colder people”. She vaguely referred to different thermometers, but without more details, it is difficult to ensure Claire’s first question-prompted retelling was related to the story’s mathematical ideas.
In the second session, Claire activated 13 hotspots across pages 10, 12, 17, 18, 26, 28, 32, 33, and 34. Either because of listening to the book one more time or continuing to engage with hotspots, Claire’s illustration-prompted retelling referred to some mathematical ideas of the story’s conflict and conflict resolution. She said, “They drew the thermometer and saw that theirs was opposite from each other” (pp. 27–28). Claire’s statement was more accurate than Lola’s reference to “upside down” thermometers. However, only referring to “opposite thermometers” cannot be interpreted as Claire making a connection that opposite thermometers are represented by positive numbers and negative numbers. Claire did not refer to the story’s mathematical ideas in her second question-prompted retelling: “The Cozyland like went to water… and the Icyland, wear like black clothing to attract the heat”.
In the third session, Claire activated 17 hotspots, which were all in the initial part of the book (pages 7, 8, 10, and 12) where the story’s conflict resolution was not introduced. Like the second session, in the third session, Claire only mentioned the “opposite” thermometers in the illustration-prompted retelling referring to some mathematical ideas. She only focused on the temperature change as getting colder and hotter in the question-prompted retelling. The only and most salient story’s mathematical idea in Claire’s retellings was the opposite thermometers.

6.4.2. Session Tests

Unlike the pretest, Claire experienced some cognitive conflicts around integers’ values. In the first session, her responses for the least cold temperature were like Lola’s (see Table 7). Occasionally, for the most cold temperature, Claire chose the middle-value temperature. For the least hot temperature with positive temperatures, Claire chose the middle temperature, but for other least hot temperature questions, she chose the negative temperature with the smallest absolute value (see Table 7). In the second session, for all the integer value questions except for the most cold temperature, Claire chose the middle-value temperature (see Table 7). In the third session, she answered most of the questions correctly. On a few incorrect instances, she responded the same as in the second session (see Table 7).

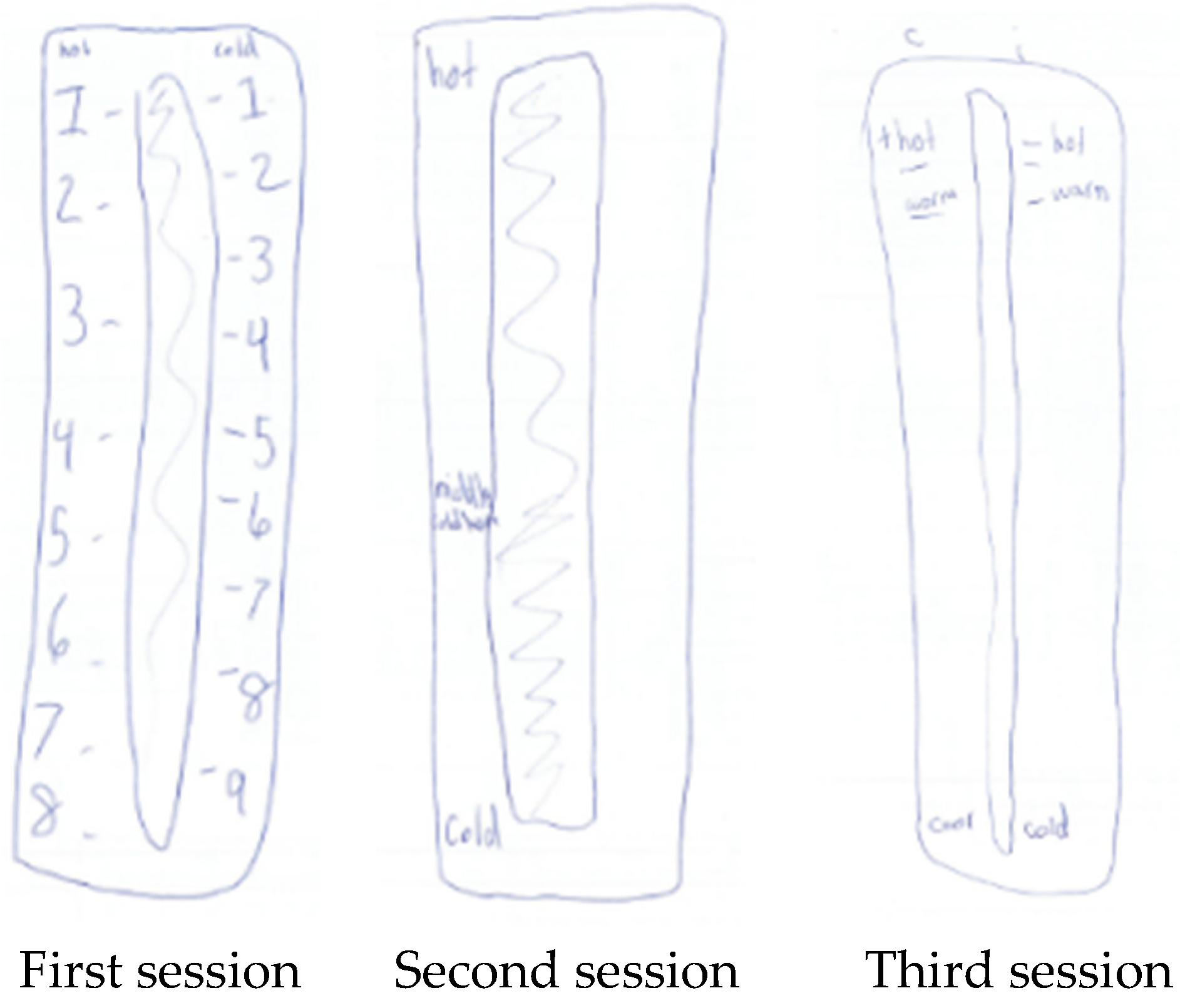
6.4.3. Drawn Thermometers

In the first session, Claire drew one thermometer containing numbers on both sides, with one side labeled hot and one side labeled cold. To clarify whether the numbers on the right side were negative, I asked:
Researcher:
What are these numbers that are here? [pointing to the left of Claire’s thermometer]
Claire:
These are hot.
Researcher:
What about these? [pointing to the right of Claire’s thermometer].
Claire:
They are negatives.
Because in the first session, students did not listen to the story’s conflict resolution, noticing negative numbers in Claire’s thermometer was interesting. In the next two sessions, Claire drew one thermometer without any numbers on it. She labeled them hot, cold, and cold/warm (see Figure 4). In both thermometers, when I asked for an explanation, she only focused on the idea of cold and hot without referencing negative or positive numbers. Thus, Claire’s last two thermometers did not indicate a reference to the conflict resolution of the story’s illustrations.

6.5. Posttest

On the posttest, all three students improved compared to the pretest. Table 8 shows the breakdown of students’ responses on posttest integer comparison questions based on question phrasing and number types.
Harry answered all the integer comparison questions correctly, illustrating a resolved cognitive conflict and a complete integer order and values understanding. Although Lola did not correctly answer all the questions, her incorrect responses were not due to relying on integers’ absolute values. On only three incorrect responses (one from the most hot temperature, one from least cold temperature, and one from least hot temperature; see Table 8), she chose the middle-value temperature. For example, she chose −12 among −12, 19, and −20 for the least hot temperature, which is between −20 and 19. Lola still exhibited an in-process conflict resolution, yet she improved from the pretest to the posttest.
Most of Claire’s responses to the least cold and least hot temperatures showed her challenges in interpreting the question phrasing (see Table 8). She chose the middle-value temperature by describing the least cold as “not as cold as most cold but still cold” and least hot as “in the middle”. Claire’s misinterpretation of least cold and least hot led her to incorrect answers and not her misinterpretation of integers’ values. For example, for the least cold temperature among −24, 34, and −30, she chose −24 because thought least cold meant “the middle of two numbers”. Claire was correct on the most hot and most cold temperature questions. Yet, she exhibited an in-process conflict resolution due to misinterpreting the question phrasing and not using absolute value reasoning.

7. Cross-Case Synthesis and Conclusion

7.1. Test Responses

Because Harry already started higher than Lola and Claire on the pretest, his room for growth was limited compared to them. Harry who was in the control condition gained 15% from the pretest to the posttest, which reflects his progress in the conflict resolution process. By the posttest, Harry’s responses demonstrated that he no longer associated negative numbers with only cold and positive numbers with only hot. Rather, he used the integers as relative numbers (a negative number can be more hot than another negative number) and conceptualized them as having directed values.
Between Lola and Claire, Lola made the most growth from the pretest to the posttest (17% versus 2%). Although Lola did not perform the same as Harry, her growth demonstrated that she no longer over-relied on integers’ absolute values. Lola’s progress in her conflict resolution process occurred by conceptualizing the difference between directed and absolute values within negative numbers. Claire did not progress significantly because she continued to misinterpret the meaning of the directed magnitude language in the integer comparison questions (or question phrasing; e.g., least cold is least). By the posttest, her incorrect responses did not reflect cognitive conflicts about integers’ values. Claire was not the only case misinterpreting the meaning of the directed magnitude language, Lola and Harry also sometimes misinterpreted them. For Lola, like Claire, the least hot and least cold temperatures were challenging to interpret, and for Harry, the most hot temperature was.

7.2. Retellings and Drawn Thermometers

Lola and Claire both referenced mathematically relevant conflict and conflict resolution in their retellings. Despite Claire activating more hotspots than Lola and Harry being in the control condition, Harry’s retellings were the most accurate. Harry connected the thermometers’ direction to positive and negative numbers and distinguished them by the minus sign. Claire’s use of “opposite” was more accurate than Lola’s use of “upside down”. However, Lola also connected the “upside down” to numbers being below or above zero.
Over time, Harry and Lola used more directed magnitude language in their illustration-prompted retellings. Claire also used directed magnitude language during her illustration-prompted retellings in some instances but this did not increase over time. For the third question-prompted retelling, only Lola, who was in the interactive language condition, used the directed magnitude language. Unlike the expectation for Claire to draw more accurate thermometers over time because she was in the interactive visual condition, her thermometers did not reflect the conflict resolution of the story’s illustrations. Although Claire’s first thermometer included negative temperatures, she wrote them next to positive numbers instead of on a continuum. Lola’s thermometers did not include negative temperatures but Harry’s thermometers in the last two sessions reflected the conflict resolution of the story’s illustrations.

8. Discussion and Implications

In this paper, I described three fifth graders’ experiences of cognitive conflict and conflict resolution around the integers’ order and values as a result of engaging in only one version of the Temperature Turmoil storybook: control, interactive language, or interactive visual. Therefore, this paper has implications for how to use students’ common cognitive conflicts to support learning, which in turn adds to the current understanding of using cognitive conflict as a teaching strategy (e.g., [27,28,29,30,31,32]). Prior research has explored students’ difficulties with integers by classifying their ways of reasoning (e.g., [3,4,5,6,7,8,9,10,11,12,13,36,37,38]). The results of this study provide new insights into ways in which students make sense of integers’ order and values by explaining their responses through the lens of cognitive conflict and conflict resolution. Using this lens helped to depict not only why students experience a cognitive conflict with integers but also detail how the processes of resolving them might look. Taking the cognitive conflict and conflict resolution lens to study students’ mathematical learning could establish a more holistic and humanistic view of what so-called their “misconceptions”.
The interactive features within the Temperature Turmoil book set the ground to create opportunities for students to interact with and learn from the story independently without adults’ (or teachers’) guidance. Overall, listening to any version of Temperature Turmoil supported students’ conflict resolution as reflected in their responses to integer order and value questions. Similar to Bofferding and Farmer [7], Harry’s, Lola’s, and Claire’s difficulties with integer comparison questions reflected their interpretation of integer values and question phrasing, particularly for least hot and least cold. Harry and Lola overcame these difficulties by the posttest, but Claire continued to misinterpret the question phrasing (or directed magnitude language of the comparison question). One can describe such misinterpretation as Claire’s by experiencing a cognitive conflict of directed magnitude language. Thus, Claire could have benefited more by engaging in the interactive language condition because by activating some hotspots, an integer comparison question with a directed magnitude language followed by feedback would appear. In fact, a meaningful understanding of addition and subtraction with negative numbers requires using double language [68], which requires determining them with directional movements [4,5]. Research on using directed magnitude language with integers has indicated positive results in students’ learning of integer addition and subtraction (e.g., [4,5,44,68]). For example, adding a negative integer no longer relates to getting more or larger; rather, it represents more in the negative direction or downwards on a vertical number line [4,5,68]. For example, solving 5 + −3 results in a smaller number by getting more negative. Future studies should continue exploring the significance of using different directed magnitude languages in students’ learning of integers’ order and values.
Beyond students’ test responses, their retellings can illuminate the effectiveness of the Temperature Turmoil versions. Retelling can be a means to not only determine students’ conceptualization of the story’s events but also benefit students’ language development (e.g., [69]). In this paper, retellings were used to assess students’ understanding of the story’s conflict and conflict resolution but may have also become their learning tool. Using retellings can open a new pathway to not only consider nontraditional approaches in investigating students’ understanding of a mathematical idea but also address ways in which students interpret and make use of mathematical language in their explanations. In the retellings, students described different or opposite directions in thermometers or above or below zero temperatures, which implicitly referenced the story’s conflict resolution (i.e., differentiating numbers below and above zero as negative and positive numbers and comparing their values). Perhaps, using such language was influenced by the context of temperature in the Temperature Turmoil mathematics storybook. Thus, it is essential to investigate students’ learning of integers’ order and values in other real-world contexts, particularly those with extensive quantities such as money or elevation ([18,19]; see [37,38] for examples). This is particularly important when teaching and learning about integer operations because the temperature context does not always realistically work, meaning temperature cannot be summed [24,50].
Among the three fifth graders in this study, Harry’s retellings were the most accurate in containing the story’s mathematical ideas. One reason could be related to Harry’s higher pretest score compared to Lola and Claire. In instances, Lola activated a hotspot and answered the question, but did not pay attention to the feedback, and on the third session, Claire activated only the hotspots in the first half of the book. Thus, another reason for Harry’s more accurate retellings could be that exploring interactive features distracted Lola and Claire from the story’s central mathematical ideas. This reason aligns with prior research documenting the negative impact of interactive storybooks (e.g., [56,57,65]). On the other hand, Lola used directed magnitude language during her retellings even more consistently than Harry. The interactive language version was possibly helpful for Lola to recall, and use directed magnitude language more than the control and interactive visual versions were for Harry and Claire. Despite the extensive research on interactive storybooks within the world of literacy education [57,58,59,60,61,62,63,64,65], there is limited research on the development of an interactive mathematics storybook [56]. This paper’s findings contribute to this underdeveloped line of inquiry. However, one way to undertake this line of inquiry further is to investigate hypotheses with a larger number of students. These hypotheses can develop an understanding of whether an interactive language can generate more use of directed magnitude language like it did for Lola and whether students like Claire could have responded more correctly to integer value questions if they were engaged in an interactive language condition.
Although it is nearly impossible to find students with identical experiences, still one limitation of this paper is the different pretest performances of the cases. Their differences may have led them to experience cognitive conflict and conflict resolution differently and impacted how they benefited from the story. Perhaps, Harry was at a level that could better absorb the complexity of the story content and illustrations and thus, was more successful. Thus, it is important to continue exploring the role of interactive mathematics storybooks in the learning of students with diverse experiences. In such exploration, the interactive mathematics storybooks can become a space that exposes students to new mathematical ideas that may be conflicting with their prior knowledge and prepare them for future learning. To bring these learning opportunities into the daily practice of future and current elementary teachers, researchers and educators need to incorporate them into their teaching of elementary methods courses and designing of professional development opportunities. Through this transformation, teachers not only can use such interactive mathematics storybooks in their classrooms but also can design new ones and make them more accessible based on their students’ needs.

Funding

This research was funded by Purdue University Bilsland Dissertation Fellowship, West Lafayette, IN, USA.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and approved by Purdue University’s Institutional Review Board (protocol code 1907022405 and date of approval: 18 July 2019).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

Data are available upon request.

Acknowledgments

I am grateful for Adem Ekmekci’s and Laura Bofferding’s insightful feedback on this paper.

Conflicts of Interest

The author declares no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Wessman-Enzinger, N.M.; Tobias, J.; Olanoff, D. Prospective teachers’ attention to realism and consistency with negative integers, addition, and temperature. Investig. Math. Learn. 2020, 12, 226–241. [Google Scholar] [CrossRef]
  2. Whitacre, I.; Bihop, J.P.; Lamb, L.L.; Philipp, R.A.; Schappelle, B.P.; Lewis, M. Integers: History, textbook approaches, and children’s productive mathematical intuitions. In Proceedings of the 33rd Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Reno, NV, USA, 20–23 October 2011. [Google Scholar]
  3. Bishop, J.P.; Lamb, L.L.; Philipp, R.A.; Whitacre, I.; Schappelle, B.P. Using order to reason about negative numbers: The case of Violet. Educ. Stud. Math. 2014, 86, 39–59. [Google Scholar] [CrossRef]
  4. Bofferding, L. Negative integer understanding: Characterizing first graders’ mental models. J. Res. Math. Educ. 2014, 45, 194–245. [Google Scholar] [CrossRef] [Green Version]
  5. Bofferding, L. Understanding negative numbers. In Constructing Number: Merging Perspectives from Psychology and Mathematics Education; Norton, A., Alibali, M., Eds.; Springer Nature: Cham, Switzerland, 2019; pp. 251–277. [Google Scholar] [CrossRef]
  6. Bofferding, L.; Aqazade, M.; Farmer, S. Playing with integers: A quest for structure. In Exploring the Integer Addition and Subtraction Landscape; Bofferding, L., Wessman-Enzinger, N.M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 3–25. [Google Scholar] [CrossRef]
  7. Bofferding, L.; Farmer, S. Most and least: Differences in integer comparisons based on temperature comparison language. Int. J. Sci. Math. 2019, 17, 545–563. [Google Scholar] [CrossRef]
  8. Nurnberger-Haag, J. Take it away or walk the other way? Finding positive solutions for integer subtraction. In Exploring the Integer Addition and Subtraction Landscape: Perspectives on Integer Thinking; Bofferding, L., Wessman-Enzinger, N.M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 109–142. [Google Scholar] [CrossRef]
  9. Schindler, M.; Huβmann, S. About students’ individual concepts of negative integers—In terms of the order relation. In Proceedings of the Eighth Congress of the European Society for Research in Mathematics Education (CERME 8), Ankara, Turkey, 6–10 February 2013; pp. 373–382. [Google Scholar]
  10. Schindler, M.; Huβmann, S.; Nilsson, P.; Bakker, A. Sixth-grade students’ reasoning on the order relation of integers as influenced by prior experience: An inferentialist analysis. Math. Educ. Res. J. 2017, 29, 471–492. [Google Scholar] [CrossRef] [Green Version]
  11. Stephan, M.; Akyuz, D. A proposed instructional theory for integer addition and subtraction. J. Res. Math. Educ. 2012, 43, 428–464. [Google Scholar] [CrossRef] [Green Version]
  12. Stephan, M.; Akyuz, D. Teaching integers to students with disabilities: Three case studies. In Exploring the Integer Addition and Subtraction Landscape; Bofferding, L., Wessman-Enzinger, N.M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 75–108. [Google Scholar] [CrossRef]
  13. Whitacre, I.; Azuz, B.; Lamb, L.; Bishop, J.S.; Philipp, R.A. Integer comparison across the grades: Students’ justifications and ways of reasoning. J. Math. Behav. 2017, 45, 47–62. [Google Scholar] [CrossRef] [Green Version]
  14. Piaget, J. The Origins of Intelligence in Children; International Universities Press: London, UK, 1952. [Google Scholar]
  15. Piaget, J. Piaget’s Theory. The Equilibration of Cognitive Structures: The Central Problem of Intellectual Development; University of Chicago Press: Chicago, IL, USA, 1985. [Google Scholar]
  16. Bofferding, L. Temperature Turmoil, 1st ed.; Purdue University: West Lafayette, IN, USA, 2021. [Google Scholar]
  17. Bofferding, L.; (Department of Curriculum and Instruction, College of Education, Purdue University, West Lafayette, IN, USA); Wessman-Enzinger, N.M.; (School of Education, George Fox University, Newberg, OR, USA). Recent survey of how teachers introduce negative numbers to students. Personal communication, 2021. [Google Scholar]
  18. National Council of Teachers of Mathematics. Principles and Standards for School Mathematics; National Council of Teachers of Mathematics: Reston, VA, USA, 2000. [Google Scholar]
  19. National Governors Association Center for Best Practices; Council of Chief State School Officers. Common Core State Standards for Mathematics. Washington, DC, USA, 2000. Available online: http://www.corestandards.org/assets/CCSSI_Math%20Standards.pdf (accessed on 5 April 2019).
  20. Wessman-Enzinger, N.M.; Mooney, E.S. Conceptual models for integer addition and subtraction. Int. J. Math. Educ. Sci. Technol. 2019, 52, 349–376. [Google Scholar] [CrossRef]
  21. Gallardo, A. The extension of the natural-number domain to the integers in the transitions from arithmetic to algebra. Educ. Stud. Math. 2002, 49, 171–192. [Google Scholar] [CrossRef]
  22. Altiparmak, K.; Özdoğan, E. A study on the teaching of the concept of negative numbers. Int. J. Math. Educ. Sci. Technol. 2010, 41, 31–47. [Google Scholar] [CrossRef]
  23. Wessman-Enzinger, N.M.; Tobias, J.M. The dimensions of prospective elementary and middle school teachers’ problem posing for integer addition and subtraction. J. Math. Teach. Educ. 2020, 1–33. [Google Scholar] [CrossRef]
  24. Schwarz, B.B.; Kohn, A.S.; Resnick, L.B. Positives about negatives: A case study of an intermediate model for signed numbers. J. Learn. Sci. 1993, 3, 37–92. [Google Scholar] [CrossRef]
  25. Yin, R.K. Case Study Research and Applications: Design and Methods, 6th ed.; Sage: Los Angeles, CA, USA, 2018. [Google Scholar]
  26. Limón, M. On the cognitive conflict as an instructional strategy for conceptual change: A critical appraisal. Learn. Instr. 2001, 11, 357–380. [Google Scholar] [CrossRef]
  27. Shahbari, J.A.; Peled, I. Resolving cognitive conflict in a realistic situation with modeling characteristics: Coping with a changing reference in fractions. Int. J. Sci. Math. 2015, 13, 891–907. [Google Scholar] [CrossRef]
  28. Zazkis, R.; Chernoff, E.J. What makes a counterexample exemplary? Educ. Stud. Math. 2008, 68, 195–208. [Google Scholar] [CrossRef]
  29. Gal, H. When the use of cognitive conflict is ineffective—Problematic learning situations in geometry. Educ. Stud. Math. 2019, 102, 239–256. [Google Scholar] [CrossRef]
  30. Watson, J.M. Inferential reasoning and the influence of cognitive conflict. Educ. Stud. Math. 2002, 51, 225–256. [Google Scholar] [CrossRef]
  31. Watson, J.M. The role of cognitive conflict in developing students’ understanding of average. Educ. Stud. Math. 2007, 65, 21–47. [Google Scholar] [CrossRef]
  32. Zaslavsky, O. Seizing the opportunity to create uncertainty in learning mathematics. Educ. Stud. Math. 2005, 60, 297–321. [Google Scholar] [CrossRef]
  33. Chan, C.; Burtis, J.; Bereiter, C. Knowledge building as a mediator of conflict in conceptual change. Cogn. Instr. 1997, 151, 1–40. [Google Scholar] [CrossRef] [Green Version]
  34. D’Ambrosio, B.S.; Mendonça Campos, T.M. Pre-service teachers’ representations of children’s understanding of mathematical concepts: Conflicts and conflict resolution. Educ. Stud. Math. 1992, 23, 213–230. [Google Scholar] [CrossRef]
  35. Schunk, D. Learning Theories: An Educational Perspective, 6th ed.; Pearson Education: Boston, MA, USA, 2012. [Google Scholar]
  36. Chen, L.; Bofferding, L.; Aqazade, M. Comparison with closest and most: Second and fifth graders’ conceptions of integer value. In Proceedings of the 40th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Greenville, SC, USA, 15–18 November 2018; pp. 187–191. [Google Scholar]
  37. Swanson, P.E. The intersection of language and mathematics. Math. Teach. Middle Sch. 2010, 15, 516–523. [Google Scholar] [CrossRef]
  38. Whitacre, I.; Bishop, J.P.; Philipp, R.A.; Lamb, L.L.; Schappelle, B.P. Dollars and sense: Students’ integer perspectives. Math. Teach. Middle Sch. 2014, 20, 84–89. [Google Scholar] [CrossRef]
  39. Thompson, P.W.; Dreyfus, T. Integers as transformations. J. Res. Math. Educ. 1988, 19, 115–133. [Google Scholar] [CrossRef]
  40. Wessman-Enzinger, N.M. Integer Numbers and Temperature Problems. Math. Teach. Middle Sch. 2019, 24, 266–272. [Google Scholar] [CrossRef]
  41. Wessman-Enzinger, N.M. Integers as directed quantities. In Constructing Number: Merging Perspectives from Psychology and Mathematics Education; Norton, A., Alibali, M., Eds.; Springer Nature: Cham, Switzerland, 2019; pp. 279–305. [Google Scholar] [CrossRef]
  42. Wessman-Enzinger, N.M.; Mooney, E.S. Making sense of integers through storytelling. Math. Teach. Middle Sch. 2014, 20, 202–205. [Google Scholar] [CrossRef]
  43. Aqazade, M. The Roles of Interactive Features, Language, Context, and Stories in Students’ Conceptions of Integers. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, August 2021. [Google Scholar]
  44. Aqazade, M. Exhibiting integers’ conflict and resolution using a mathematics storybook: The case of four fifth graders. In Proceedings of the 43rd Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Philadelphia, PA, USA, 14–17 October 2021; pp. 318–322. [Google Scholar]
  45. Vlassis, J. Making sense of the minus sign or becoming flexible in ‘negativity’. Learn. Instr. 2004, 14, 469–484. [Google Scholar] [CrossRef]
  46. Vlassis, J. The role of mathematical symbols in the development of number conceptualization: The case of the minus sign. Philos. Psychol. 2008, 21, 555–570. [Google Scholar] [CrossRef]
  47. Aqazade, M.; Bofferding, L.; Farmer, S. Benefits of analyzing contrasting integer problems: The case of four second graders. In Proceedings of the 38th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Tucson, AZ, USA, 3–6 November 2016; pp. 132–139. [Google Scholar]
  48. Bofferding, L.; Aqazade, M.; Farmer, S. Second graders’ integer addition understanding: Leveraging contrasting cases. In Proceedings of the 39th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Indianapolis, IN, USA, 5–8 October 2017; pp. 243–250. [Google Scholar]
  49. Ball, D.L. With an eye on the mathematical horizon: Dilemmas of teaching elementary school mathematics. Elem. Sch. J. 1993, 93, 373–397. [Google Scholar] [CrossRef] [Green Version]
  50. Piaget, J. The Child’s Conception of Number; Routledge & Kegan Paul, Ltd.: London, UK, 1952. [Google Scholar]
  51. Capraro, R.M.; Capraro, M.M. Are you really going to read us a story? Learning geometry through children’s mathematics literature. Read. Psychol. 2006, 27, 21–36. [Google Scholar] [CrossRef]
  52. Hassinger-Das, B.; Jordan, N.C.; Dyson, N. Reading stories to learn math: Mathematics vocabulary instruction for children with early numeracy difficulties. Elem. Sch. J. 2015, 116, 242–264. [Google Scholar] [CrossRef] [Green Version]
  53. Jennings, C.M.; James, J.; Richey, J.; Dixon-Krauss, L. Increasing interest and achievement in mathematics through children’s literature. Early Child. Res. Q. 1992, 7, 263–276. [Google Scholar] [CrossRef]
  54. van den Heuvel-Panhuizen, M.; Elia, I.; Robitzsch, A. Effects of reading picture books on kindergartners’ mathematics performance. J. Educ. Psychol. 2016, 36, 323–346. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  55. Segal-Drori, O.; Kalmanovich, L.B.H.; Shamir, A. Electronic book for promoting emergent math: A comparison between kindergarteners at risk for learning disabilities and with typical development. J. Educ. Comput. 2019, 57, 954–977. [Google Scholar] [CrossRef]
  56. Ginsburg, H.P.; Uscianowski, C.; Almeda, V.M. Interactive mathematics storybooks and their friends. In Contemporary Research and Perspectives on Early Childhood Mathematics Education, ICME-13 Monographs; Mulligan, E.J., Anderson, A., Baccaglini-Frank, A., Benz, C., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 245–263. [Google Scholar]
  57. Bus, A.G.; Takacs, Z.K.; Kegel, C.A.T. Affordances and limitations of electronic storybooks for young children’s emergent literacy. Dev. Rev. 2015, 35, 79–97. [Google Scholar] [CrossRef]
  58. De Jong, M.T.; Bus, A.G. Quality of book-reading matters for emergent readers: An experiment with the same book in a regular or electronic format. J. Educ. Psychol. 2002, 94, 145–155. [Google Scholar] [CrossRef]
  59. De Jong, M.T.; Bus, A.G. How well situated are electronic books to supporting literacy? J. Early Child. Lit. 2003, 3, 147–164. [Google Scholar] [CrossRef]
  60. De Jong, M.T.; Bus, A.G. The efficacy of electronic books in fostering kindergarten children’s emergent story understanding. Read. Res. Q. 2004, 39, 378–393. [Google Scholar] [CrossRef]
  61. Guernsey, L.; Levine, M.; Chiong, C.; Severns, M. Pioneering Literacy in the Digital Wild West: Empowering Parents and Educators; Joan Ganz Cooney Center: New York, NY, USA, 2012; Available online: http://joanganzcooneycenter.org/publication/pioneering-literacy/ (accessed on 3 March 2019).
  62. Korat, O.; Shamir, A. Do Hebrew electronic books differ from Dutch electronic books? A replication of Dutch content analysis. J. Comput. Assist. 2004, 20, 257–268. [Google Scholar] [CrossRef]
  63. Smeets, D.J.; Bus, A.G. The interactive animated e-book as a word learning device for kindergarteners. Appl. Psycholinguist. 2015, 36, 899–920. [Google Scholar] [CrossRef] [Green Version]
  64. Kucirkova, N. An integrative framework for studying, designing and conceptualising interactivity in children’s digital books. Br. Educ. Res. J. 2017, 43, 1168–1185. [Google Scholar] [CrossRef]
  65. Takacs, Z.K.; Swart, E.K.; Bus, A.G. Benefits and pitfalls of multimedia and interactive features in technology-enhanced storybooks: A meta-analysis. Rev. Educ. Res. 2015, 85, 698–739. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  66. Zipke, M. Preschoolers explore interactive storybook apps: The effect on word recognition and story comprehension. Educ. Inf. Technol. 2017, 22, 1695–1712. [Google Scholar] [CrossRef]
  67. Uscianowski, C.; Almeda, V.; Ginsburg, H. Interactive digital storybooks and the role of parents in supporting young children’s mathematics development. In Promising Practices for Engaging Families in STEM Learning; Caspe, M., Woods, T., Lorenzo Kennedy, J., Eds.; Information Age: Charlotte, NC, USA, 2018; pp. 113–131. [Google Scholar]
  68. Bruno, A.; Martinon, A. The teaching of numerical extensions: The case of negative numbers. Int. J. Math. Educ. Sci. Technol. 1999, 30, 789–809. [Google Scholar] [CrossRef]
  69. Lysaker, J.; Nie, A.Y. Social and relational aspects of comprehending in one fourth grader’s unaided and illustration-aided picturebook retellings: Retelling as co-authoring. J. Lit. Res. 2017, 49, 38–67. [Google Scholar] [CrossRef]
Education 12 00879 g001 550
Figure 1. Study Design.
Figure 1. Study Design.
Education 12 00879 g001
Education 12 00879 g002 550
Figure 2. Harry’s Thermometers.
Figure 2. Harry’s Thermometers.
Education 12 00879 g002
Education 12 00879 g003 550
Figure 3. Lola’s Thermometers.
Figure 3. Lola’s Thermometers.
Education 12 00879 g003
Education 12 00879 g004 550
Figure 4. Claire’s Thermometers.
Figure 4. Claire’s Thermometers.
Education 12 00879 g004
Table
Table 1. Interactive Features on Interactive Language and Visual Versions of Temperature Turmoil.
Table 1. Interactive Features on Interactive Language and Visual Versions of Temperature Turmoil.
HotspotsDescriptionsExamples of Interactive Language Examples of Interactive Visual
Mathematical QuestionFeedback
Education 12 00879 i001Each thermometer is a hotspot. Thus, a total of 14 hotspots is on these two pages.In Cozyland, which day’s temperature is smaller than Monday’s?
(Choosing among six weekdays’ temperatures)		Correct answer: Yes. In Cozyland, Friday’s temperature is smaller than Monday’s temperature.Showing a magnified thermometer.
Incorrect answer: No. In Cozyland, Wednesday’s temperature is larger than Monday’s temperature.
Education 12 00879 i002Each sentence on page 10 is a hotspot. Additionally, less hot and more cold are bolded to re-emphasize the hotspots. Thus, there are two hotspots on this page.In Cozyland, which temp is less hot? 33° or 22°?
(Choosing between 33° and 22°)		Correct answer: Yes. In Cozyland, 22° is less hot than 33°.Less hot hotspot: Showing an animation of the temperature change from 33 to 22.
Incorrect answer: No. In Cozyland, 33° is more hot than 22°.More cold hotspot: Showing a thermometer slider to drag and see numbers on the thermometer and background view change.
Education 12 00879 i003Each sentence on page 12 is a hotspot. Additionally, less cold and more hot are bolded to re-emphasize the hotspots. Thus, there are two hotspots on this page.In Icyland, which temp is less cold? 33° or 22°?
(Choosing between 33° and 22°)		Correct answer: Yes. In Icyland, 22° is less cold than 33°.See above.
Incorrect answer: No. In Icyland, 33° is more cold than 22°.
Education 12 00879 i004Each town is a hotspot. Thus, a total of eight hotspots are on these two pages. Which town’s temperature is the opposite of Chilito?
(Choosing among seven towns’ temperatures)		Correct answer: Yes. Tepidona’s temperature is the opposite of Chilito’s temperature.Showing a complete thermometer of the clicked town with a thermometer of the town that shows the opposite temperature.
Incorrect answer: No. Sunlandia’s temperature is the opposite of Cloudlandia’s temperature.
Education 12 00879 i005The two bubble speeches are hotspots on page 26. Additionally, more cold and more hot are bolded to re-emphasize the hotspots.For Cozies, which 30° is more cold?
(choosing between two opposite thermometers, one showing 0 down to 30 and one showing 0 up to 30)		Incorrect answer: No. If you are in Cozyland, moving away from 0° makes temperatures more hot and if you are in Icyland, moving towards 0° makes temperatures more hot.Showing two towns’ thermometers side-by-side.
Incorrect answer: No. If you are in Cozyland, moving away from 0° makes temperatures more hot and if you are in Icyland, moving towards 0° makes temperatures more hot.
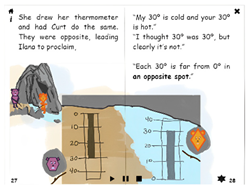Education 12 00879 i006The sentence, “Each 30 is far from 0 in an opposite spot”, on page 28 is the hotspot. Additionally, an opposite spot is bolded to re-emphasize the hotspot.What is the opposite of 30° from Icyland?
(Choosing among four thermometers: showing 0 to 25 upward, 0 to 20 downward, 0 to 25 downward, 0 to 30 upward, 0 to 20 upward)		Correct answer: Yes. The opposite of 30° from Icyland is 30° from Cozyland.Showing two towns opposite thermometers side-by-side.
Incorrect answer: No. 25° from Cozyland is the opposite of 25° from Icyland.
Education 12 00879 i007The sentence, “Degrees exist on a larger continuum”, in page 29 is the hotspot. Additionally, a larger continuum is bolded to re-emphasize the hotspot.On a larger continuum, choose the opposite of 30° from Cozyland.
(Choosing among 20 and 10 above 0 and 10, 20, and 30 below 0)		Correct answer: 30° from Icyland is the opposite of 30° from Cozyland.Showing an animation of temperature changing of two opposite thermometers side-by-side.
Incorrect answer: No. 20° from Cozyland is the opposite of 20° from Icyland.
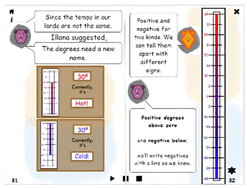Education 12 00879 i008Two sentences, “positive degrees above zero” and “negative below” on page 32 are two hotspots. Additionally, positive degrees above zero and negative below are bolded to re-emphasize the hotspots.Which temperatures are positive numbers?
(Choosing among −20°, −30°, 15°, 25°, −25°, 20°)		Correct answer: Yes. 15, 20, and 25 are positive numbers.Showing an animation of temperature changing on a single thermometer from positive to negative.
Incorrect answer: No. Positive numbers are above zero and do not have a line.
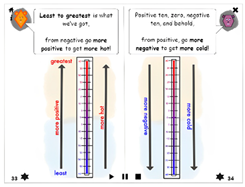Education 12 00879 i009Three sentences, “Least to greatest is what we’ve got”, “from negative go more positive to ger more hot!”, and “positive ten, zero, negative ten, and behold, from positive go more negative to get more cold” across both pages are three hotspots. Additionally, least to greatest, more positive, more hot, more negative, and more cold are bolded to re-emphasize the hotspots.Which of the temperatures are correctly ordered from least to greatest?
(Choosing (a) −15°, −25°, −35°, 0°, 10°, 25°, 30°, (b) −35°, −25°, −15°, 0°, 10°, 25°, 30°, and (c) 0°, 10°, −15°, −25°, 25°, 30°, −35°)		Correct answer: Yes. −35°, −25°, −15°, 0°, 10°, 25°, 30° shows least to greatest temperatures.Showing a thermometer slider to drag and see temperature comparison to 30° (e.g., 5° is more negative than 30°)
Incorrect answers: No. Negative numbers are below zero and positive numbers are above zero (if choose (c))
No. Negative and positive numbers are on opposite sides such symmetry (if choose (a)).
Table
Table 2. Examples of Pretest and Posttest Order and Value Questions.
Table 2. Examples of Pretest and Posttest Order and Value Questions.
Order and Value QuestionsReference(s)
Filling the numbers (2 items)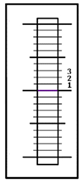Education 12 00879 i010[4,6]
Ordering integers (2 items)Put these temperatures in order from least to greatest:
−12, 20, 29, −35, −20, 0, 16		[4,24]
Integer comparison a (48 items)12 itemsWhat does most hot mean to you?
Circle the temperature that is most hot:
−16, 24, −28, none		[7,13]
12 itemsWhat does most cold mean to you?
Circle the temperature that is most cold:
−22, 33, −26, none
12 itemsWhat does least cold mean to you?
Circle the temperature that is least cold:
−22, 18, 27, none
12 itemsWhat does least hot mean to you?
Circle the temperature that is least hot:
−31, −28, 23, none
Note: The number of items is for the pretest and posttest. The session tests included a different subset of these items (the first and second sessions each had 12 items and the third session had 8 items). a The numbers in the most hot and least cold temperatures and the numbers in the most cold and least hot temperatures in the integer comparison questions were the same but presented in a different order. I chose to do so because most hot is synonymous with least cold and most cold is synonymous with least hot. Thus, I could see how students compare the same numbers using different but synonymous question phrasing.
Table
Table 3. Conflict and Conflict Resolution Categories during Retellings.
Table 3. Conflict and Conflict Resolution Categories during Retellings.
CategoriesDescriptionExample(s)
ConflictMathematicalReferring to how the story’s characters relied on only temperatures’ absolute values or discarded their directed values.One land’s temperature was above 0 and one land’s temperature was below 0.
The people of the two lands used different numbers.
Non-mathematicalReferring to how the story’s characters felt about their lands’ temperatures or describing how the change in their land’s temperature made them feel.There are two lands: hot and cold lands, and they do not like them.
Conflict resolutionMathematicalReferring to how the story’s characters realized the differences in their temperatures or attempted to distinguish them in some way.They will use positive and negative numbers to see the difference.
They will use a new thermometer.
Non-mathematicalReferring to how the story’s characters went back to their lands or adjusted to the temperature change.They will switch lands.
They will get used to being cold and hot.
Table
Table 4. Harry’s, Lola’s, and Claire’s Responses on Pretest Integer Comparison Questions.
Table 4. Harry’s, Lola’s, and Claire’s Responses on Pretest Integer Comparison Questions.
Most Hot Temperature
All positive or zero aAll negative or zero bMixed numbers c
Items222621−25−210−16−31−22−24−29−11
31330−31−24−29242318−30−3215
162025−17−14−232819273426−18
nonenonenonenonenonenonenonenonenonenonenonenone
Harry313325nonenonenonenonenonenone34nonenone
Lola313325−25−14−23282327342615
Claire313325−17−140282327342615
Least Cold Temperature
All positive or zero aAll negative or zero bMixed numbers c
Items 222621−25−210−16−31−22−24−29−11
31330−31−24−29242318−30−3215
162025−17−14−232819273426−18
nonenonenonenonenonenonenonenonenonenonenonenone
Harry313325−17−140282327342615
Lola223325−17−14028232734−3215
Claire16200−17−14−29−16−31−22−30−32−18
Most Cold Temperature
All positive or zero aAll negative or zero bMixed numbers c
Items 20220−11−33−17−1315−19−22−31−12
173315−24−18021−2714−262319
281921−16−22−3018102633−28−20
nonenonenonenonenonenonenonenonenonenonenonenone
Harry17190−24−33−30−13−27−19−26−31−20
Lola17190−11−18−1718−2714−22−28−12
Claire17190−24−33−30−13−27−19−22−31−20
Least Hot Temperature
All positive or zero aAll negative or zero bMixed numbers c
Items20220−11−33−17−1315−19−22−31−12
173315−24−18021−2714−262319
281921−16−22−3018102633−28−20
nonenonenonenonenonenonenonenonenonenonenonenone
Harry17190−24−33−30−13−27−19−26−31−20
Lola171915−24−33−30−13−27−19−26−31−20
Claire283321−16−18018−2726332319
Note: The bolded numbers represent a correct response. a All numbers were positive numbers or two positive numbers with one zero. b All numbers were negative numbers or two negative numbers with one zero. c Numbers were a mix of both positive and negative numbers.
Table
Table 5. Harry’s Responses to Session Tests Integer Comparison Questions.
Table 5. Harry’s Responses to Session Tests Integer Comparison Questions.
First Session
Most hotItem26, 33, 20, none−21, −24, −14, none−29, −32, 26, none
Response 20−24−32
Least coldItem 26, 33, 20, none−21, −24, −14, none−29, −32, 26, none
Response 33−1426
Most coldItem 19, 22, 33, none−33, −22, −18, none−31, −28, 23, none
Response 19−33−31
Least hotItem 19, 22, 33, none−33, −22, −18, none−31, −28, 23, none
Response 19−33−31
Second Session
Most hotItem 22, 31, 16, none−25, −31, −17, none−24, −30, 34, none
Response 31−1734
Least coldItem 22, 31, 16, none−25, −31, −17, none−24, −30, 34, none
Response 31−1734
Most coldItem 20, 28, 17, none−16, −11, −24, none33, −22, −26, none
Response 17−24−26
Least hotItem 20, 28, 17, none−16, −11, −24, none33, −22, −26, none
Response 17−24−26
Third Session
Most hotItem −25, −12, −28, none−32, 20, 26, none
Response −1226
Least coldItem −25, −12, −28, none−32, 20, 26, none
Response −28−32
Most coldItem −20, −32, −15, none18, −28, −25, none
Response −32−28
Least hotItem −20, −32, −15, none18, −28, −25, none
Response −32−28
Note: The bolded numbers represent a correct response.
Table
Table 6. Lola’s Responses to Session Tests Integer Comparison Questions.
Table 6. Lola’s Responses to Session Tests Integer Comparison Questions.
First Session
Most hotItem 26, 33, 20, none−21, −24, −14, none−29, −32, 26, none
Response 33−2126
Least coldItem 26, 33, 20, none−21, −24, −14, none−29, −32, 26, none
Response 20−24−32
Most coldItem 19, 22, 33, none−33, −22, −18, none−31, −28, 23, none
Response 19−18−31
Least hotItem 19, 22, 33, none−33, −22, −18, none−31, −28, 23, none
Response 19−18−28
Second Session
Most hotItem 22, 31, 16, none−25, −31, −17, none−24, −30, 34, none
Response 22−1734
Least coldItem 22, 31, 16, none−25, −31, −17, none−24, −30, 34, none
Response 31−17−24
Most coldItem 20, 28, 17, none−16, −11, −24, none33, −22, −26, none
Response 17−24−22
Least hotItem 20, 28, 17, none−16, −11, −24, none33, −22, −26, none
Response 17−24−26
Third Session
Most hotItem −25, −12, −28, none−32, 20, 26, none
Response −1226
Least coldItem −25, −12, −28, none−32, 20, 26, none
Response −1226
Most coldItem −20, −32, −15, none18, −28, −25, none
Response −32−28
Least hotItem −20, −32, −15, none18, −28, −25, none
Response −32−28
Note: The bolded numbers represent a correct response.
Table
Table 7. Claire’s Responses to Session Tests Integer Comparison Questions.
Table 7. Claire’s Responses to Session Tests Integer Comparison Questions.
First Session
Most hotItem 26, 33, 20, none−21, −24, −14, none−29, −32, 26, none
Response 33−1426
Least coldItem 26, 33, 20, none−21, −24, −14, none−29, −32, 26, none
Response 20−24−32
Most coldItem 19, 22, 33, none−33, −22, −18, none−31, −28, 23, none
Response 19−22−28
Least hotItem 19, 22, 33, none−33, −22, −18, none−31, −28, 23, none
Response 22−18−28
Second Session
Most hotItem 22, 31, 16, none−25, −31, −17, none−24, −30, 34, none
Response 22−25−24
Least coldItem 22, 31, 16, none−25, −31, −17, none−24, −30, 34, none
Response 22−17−24
Most coldItem 20, 28, 17, none−16, −11, −24, none33, −22, −26, none
Response 17−24−26
Least hotItem 20, 28, 17, none−16, −11, −24, none33, −22, −26, none
Response 20−16−22
Third Session
Most hotItem −25, −12, −28, none−32, 20, 26, none
Response −1226
Least coldItem −25, −12, −28, none−32, 20, 26, none
Response −2520
Most coldItem −20, −32, −15, none18, −28, −25, none
Response −32−28
Least hotItem −20, −32, −15, none18, −28, −25, none
Response −20−28
Note: The bolded numbers represent a correct response.
Table
Table 8. Harry’s, Lola’s, and Claire’s Responses on Posttest Integer Comparison Questions.
Table 8. Harry’s, Lola’s, and Claire’s Responses on Posttest Integer Comparison Questions.
Most Hot Temperature
All positive or zero aAll negative or zero bMixed numbers c
Items 222621−25−210−16−31−22−24−29−11
31330−31−24−29242318−30−3215
162025−17−14−232819273426−18
nonenonenonenonenonenonenonenonenonenonenonenone
Harry313325−17−140282327342615
Lola312625−17−140282327342615
Claire313325−17−140282327342615
Least Cold Temperature
All positive or zero aAll negative or zero bMixed numbers c
Items 222621−25−210−16−31−22−24−29−11
31330−31−24−29242318−30−3215
162025−17−14−232819273426−18
nonenonenonenonenonenonenonenonenonenonenonenone
Harry313325−17−140282327342615
Lola223325−17−140282327342615
Claire222621−25−21−23281927−24−2915
Most Cold Temperature
All positive or zero aAll negative or zero bMixed numbers c
Items 20220−11−33−17−1315−19−22−31−12
173315−24−18021−2714−262319
281921−16−22−3018102633−28−20
nonenonenonenonenonenonenonenonenonenonenonenone
Harry17190−24−33−30−13−27−19−26−31−20
Lola17190−24−33−30−13−27−19−26−31−20
Claire171915−24−33−30−13−27−19−22−31−20
Least Hot Temperature
All positive or zero aAll negative or zero bMixed numbers c
Items 20220−11−33−17−1315−19−22−31−12
173315−24−18021−2714−262319
281921−16−22−3018102633−28−20
nonenonenonenonenonenonenonenonenonenonenonenone
Harry17190−24−33−30−13−27−19−26−31−20
Lola171915−24−33−30−13−27−19−26−31−12
Claire202215−16−22−17181526−22−28−12
Note: The bolded numbers represent a correct response. a All numbers were positive numbers or two positive numbers with one zero. b All numbers were negative numbers or two negative numbers with one zero. c Numbers were a mix of both positive and negative numbers.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Aqazade, M. The Role of Interactive Features within a Mathematics Storybook in Interpreting a Conflict and Conflict Resolution: The Case of Three Fifth Graders. Educ. Sci. 2022, 12, 879. https://doi.org/10.3390/educsci12120879

AMA Style

Aqazade M. The Role of Interactive Features within a Mathematics Storybook in Interpreting a Conflict and Conflict Resolution: The Case of Three Fifth Graders. Education Sciences. 2022; 12(12):879. https://doi.org/10.3390/educsci12120879

Chicago/Turabian Style

Aqazade, Mahtob. 2022. "The Role of Interactive Features within a Mathematics Storybook in Interpreting a Conflict and Conflict Resolution: The Case of Three Fifth Graders" Education Sciences 12, no. 12: 879. https://doi.org/10.3390/educsci12120879

APA Style

Aqazade, M. (2022). The Role of Interactive Features within a Mathematics Storybook in Interpreting a Conflict and Conflict Resolution: The Case of Three Fifth Graders. Education Sciences, 12(12), 879. https://doi.org/10.3390/educsci12120879

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop