Abstract
This study measures and analyzes the performances of the participating nations at the International Mathematical Olympiad (IMO). A country’s success at the IMO is evaluated by the number of gold, silver, and bronze medals won. To measure and compare the performances of the countries, the data envelopment analysis approach is employed and all countries that have won at least one medal have been included in our dataset. As measures for the inputs, two macro-level determinants that can support the effort made by a country are considered: population size and gross domestic product (GDP) per capita. Our findings indicate a mean level of technical efficiency for the nations analyzed. The results suggest that, on average, the inefficient countries in the sample could achieve improved results by increasing the number of outputs produced while maintaining the same level of effort spent.
1. Introduction
This study analyzes the performances of countries at the International Mathematical Olympiad that was held in remote format and administered from Saint Petersburg (the Russian Federation) in 2021. The International Mathematical Olympiad (IMO) is the oldest international annual science Olympiad, and 619 students from 107 countries participated in this competition. The IMO is the world championship mathematics competition for high school students and is held annually in different countries. In this study, the macro-level determinants of the Olympians’ performances at the IMO are investigated in order to measure the performances of the participating countries. A nation’s success at the IMO can be judged by various measures, including by the number of gold, silver, and bronze medals [1].
In order to measure the performances of the nations in terms of their mathletes’ achievements, the data for the year 2021, published by IMO.org, were utilized and appropriately modified as required. The current research concentrated on the country-specific characteristics that can support the performances of the mathletes. The results from this study provide information concerning the technical efficiency of the nations analyzed. The study indicates that by solving our model, one can obtain the efficiency scores for the participating nations investigated. Our approach draws on studies of the performances of nations at international sporting events, where researchers employ various social economic measures as inputs to measure and compare various outputs, but mainly the medals won [2,3,4].
The results of our analysis show an average level of technical efficiency for the nations analyzed and indicate that further training for the targeting of realistic objectives for future events can become a plan to pursue. The method can help nations to compare themselves with their peers and to discover the gap in their outputs and can thus be utilized as a tool that shows that some countries may not be performing as they should. In our investigated sample, there are nations with sufficient inputs which are efficient in their outputs, whereas the less efficient ones could be considered undersized in terms of the outputs achieved.
The purpose of the present study, however, is not only to assess the performances in mathematics of the students and young people from the various countries from some analytics point of view, but also to discuss the common features existing in mega-events and to confirm the degree of effect that the size and wealth of the participating nations has on the outcomes of these events. Although one can easily agree that no direct relevance exists between the International Mathematical Olympiads and the athletic mega-events in terms of the number of participants and the intensity of the investments involved, one can easily recognize, however, that performance in such major international competitions is still related to the economic and social prosperity of the individual participating nations and that there is also a strong relationship with the traditions and history of the participating nations. Some researchers also relate the IMO’s results to the efficiency of the individual national educational systems [5]. Moreover, as prior research has proved [6], for athletic mega-events one can provide both the organizers and the participants with valuable advice on how to manage and organize these events more effectively. This can be achieved by creating the optimal processes and environment; by implementing systems and structures; by developing an engaging and inclusive culture; and by providing appropriate support. All these factors are especially important for young people. Finally, assessing the mathematical capabilities of a nation, with respect to the performances of the other nations in a major international event, provides a very useful tool for education policy makers for adjusting national educational policies and/or adopting, perhaps, the successful practices of other nations. To the best of the authors’ knowledge, the present work is the first to assess the performances of countries in mathematical Olympiads using data envelopment analysis (DEA).
The remaining sections of this article are organized as follows. In the next section, the literature related to measuring performance in Olympic events using DEA is presented. In Section 3, the methodology employed to implement the assessment of the participating countries in the 2021 Mathematical Olympiad is discussed, and an analysis of the results is then presented. In the following section, the data utilized in this study are thoroughly presented and discussed. Finally, in the last section, the conclusions are drawn and recommendations for future work are provided for those who manage and participate in these non-athletic events.
2. Literature Review
All organizations use resources (materials, labor, etc.) to produce goods and services. This transformation adds value to the outputs produced, and managers are always interested in how efficiently this transformation is achieved. Measuring performance efficiency is of major importance to organization leaders. Numerous quantitative approaches, both parametric and non-parametric, have been applied to evaluate performance. Parametric methods such as stochastic frontier analysis (SFA) measure efficiency using random error terms [4], while non-parametric methods such as data envelopment analysis are based on mathematical programming techniques.
DEA is a powerful method to evaluate the relative performance of distinct decision making units (DMU) using various input and output measures [7]. Over the last three decades, DEA has consistently progressed and improved its modelling approaches to cater for complex real-world problems [8,9,10,11,12,13,14,15].
Several studies to measure the efficiency of Olympic athletic events or other athletic mega-events have been presented recently. However, although considerable research has been devoted to Olympic athletic events, only limited attention has been paid to Olympic non-athletic events, particularly the mathematical Olympiads.
In the DEA-based studies of Olympic events, the participating countries are mainly evaluated according to the number of gold, silver, and bronze medals won. Furthermore, the evaluation takes into account the specific conditions for each participating country, such as population and GNP, as input measures.
DEA has been applied to assess the performances in the Olympic Games in several studies [16,17,18,19,20,21,22], where the relative efficiency of the participating countries that won at least one medal in relation to their available resources was analyzed. In [16], the authors used an input-oriented model, where the number of athletes was considered as an input, and the number of gold, silver, and bronze medals won was considered as the output parameter. Moreover, DEA has been applied for the evaluation of soccer leagues (in, e.g., [23,24,25]). Moreover, the performance of Major League Baseball was also evaluated through DEA models [26], while ref. [27] focused on the analysis of the efficiency of NBA teams with the use of DEA. To tackle more realistic problems, researchers (in, e.g., [17,28]) applied weight restrictions on the outputs by introducing the assurance region approach for all participating nations. As mentioned before, most of the prior research looked at a variety of measuring parameters. However, there are two measures that are common in almost all studies: population and GDP. The reasons for the inclusion of these two measures are almost obvious: more populous countries have a greater pool of talent to draw on and thus have enhanced chances of success at the Olympics. Moreover, wealthier nations can afford increased investments in sports projects and thus would be more likely to win medals at the Olympics.
There are also few studies that evaluate the utilization of non-DEA methods for analyzing the performances of nations. For instance, in [29] the authors used a weighted directed graph to build a dominance network, which in turn can be used to characterize the performance differences between the countries participating in the Olympic Games. In [30], the researchers examined two different performance-ranking approaches based on weighted mean values and volume-based sensitivity analysis. Most recently, the researchers also experimented with optimization methods such as particle swarm optimization (PSO) [31] or machine learning (ML) and data mining (DM) techniques in order to evaluate the performances of athletes and teams [32,33]. These methods have been applied mainly to sports events (such as basketball), for which a variety of data concerning athlete and team performances can be collected via automated tracking devices due to technological advances.
3. Methodology
Data envelopment analysis (DEA) is a method for measuring the relative performance of distinct units where the presence of multiple consumed resources and end results achieved makes it difficult to compare these units in a direct way. In data envelopment analysis, those units whose efficiency is estimated are generally referred to as decision making units (DMUs). DMUs consume resources to generate a set of outputs of varying levels. The resources used and the end results of a decision making unit can be numerous and measurable in different units. In the context of a system of such units, all the decision making units are considered to consume the same resources and produce the same end results (i.e., the metric units are alike) and only their input and output levels differ.
The typical performance measure for efficiency, i.e.,
is not sufficient to evaluate the DMUs because of the presence of multiple inputs and outputs associated with different sources, activities, and environmental factors. Thus, a common measure of relative performance is defined as the ratio of the weighted sum of the outputs to the weighted sum of the inputs. The sum of the weights of all the input/output criteria must be equal to the unit. The above relative performance measure requires the definition of the weight factors.
efficiency = output/input
Charnes, Cooper, and Rhodes [6] proposed one of the most basic DEA models, appropriately termed the CCR model. Given that there are n DMUs and associated numerical data for each of the m inputs and s outputs for all the DMUs, the fractional mathematical programming problem that is solved in order to obtain values for the input weight (vi) (i = 1, ..., m) and the output weight (ur) (r = 1, …, s) variables is the following [34]:
subject to
ur ≥ 0, (r = 1, …, s),
vi ≥ 0, (i = 1, …, m),
In the above model, index j refers to the DMU being evaluated. Objective function (1) maximizes the ratio of the output to the input of the DMU under evaluation by calculating the appropriate weights vi and ur. Constraints (2) ensure that this ratio does not exceed 1 for every DMU. This implies that the objective function value lies between 0.0 and 1.0; the latter value denotes that the DMU under examination is efficient. The above non-linear program is linearized, and the solution of its linear equivalent produces the efficiency score of the DMU being evaluated.
However, a common problem in several real-world DEA applications is that all the inputs and outputs may not be equally important to the decision maker. This study reports an application where weight restrictions are imposed in a DEA model to overcome the above problem. A weight-restricted DEA model is employed by introducing a discrimination criterion between several efficient units. This criterion is based on the fact that the input and/or output weights can be restricted since the decision maker knows the policies, i.e., the importance of the inputs and/or outputs. Introducing weight restrictions in DEA may decrease the efficiency scores and decrease the number of efficient DMUs. The following constraints are thus added to the CCR model:
where ur is the weight attached to the rth output and corresponds to the variables of the CCR model. The Greek letters αr and βr are user-specified constants to reflect the value judgements related to the relative importance of the output factors [35].
For the validation of the results, two basic parameters, which describe the method, must be defined:
- Input/output orientation of the model: the model is configured so as to determine how much the input/output consumed/produced could decrease/increase if resources are used efficiently;
- Constant/variable returns to scale (CRS/VRS) assumption: CRS reflects the fact that output will change by the same proportion by which the inputs are changed (e.g., a doubling of all inputs will result in double the outputs); VRS reflects the fact that production technology may exhibit increasing, constant, or decreasing returns to scale.
In the present study, an output-oriented DEA model that assesses the efficiency of the countries is utilized in order to maximize the outputs/medals obtained given the inputs of each of the countries. The most general assumption that can be made is that the returns to scale parameter is variable; thus, a variable returns to scale (VRS) and weight restriction DEA model is formulated and solved as our data also have some special features. As mentioned above, weight restrictions are incorporated in our model to allow for the integration of preferences in terms of the relative importance levels of the various inputs and outputs. In our case, the weight restrictions are incorporated to account for the relative importance of gold, bronze, and silver medals.
4. Data
Perhaps the most important step in conducting a DEA study is to determine the input and output indicators to be used in order to evaluate the efficiency of the decision making units (DMUs) in the sample. Several studies have attempted to ascertain the factors affecting the number of Olympic medals won by countries. Most studies have found that population and GDP were positively related to the number of Olympic medals awarded. Although some of the previous literature on the participants at the International Mathematical Olympiad focuses on the theories related to individual talent formation, this study focusses on country characteristics. National teams from countries with a higher level of material wealth and larger populations win on average more medals at the Olympic Games than the teams from smaller and poorer countries.
Models (1)–(5), as presented above, are applied to the competition of the International Mathematical Olympiad that was held in a remote format and administered from Saint Petersburg, the Russian Federation, in 2021. The DMUs consisted of the 80 participating countries in the 2021 IMO competition that won at least one medal. The participants are ranked based on their individual scores. Medals are awarded to the highest ranked participants. The input and output indicators for the studied 2021 IMO studied as follows.
Inputs:
- Participating country’s population;
- GDP per capita.
Outputs:
- Total score accumulated resulting in the award of gold medals;
- Total score accumulated resulting in the award of silver medals;
- Total score accumulated resulting in the award of bronze medals.
A total of 52 gold medals were awarded to the participants who had accumulated a score ≥ 24 points. One hundred and three silver medals were awarded to the participants who had accumulated a score ≥ 19 points. Moreover, 148 bronze medals were awarded to the participants who had accumulated a score ≥ 12 points. In relation to the weight restriction constraints, the coefficients αr and βr were set equal to 1 and 2.5 for the gold to silver medal output ratio (r = 1). For r = 2 in the constraints (5) above, αr and βr were set equal to 1 and 1.5 for the silver to bronze medal output ratio This latter judgment is based on the guidance given by the fact that the numbers of gold, silver, and bronze medals awarded are approximately in the ratio of 1:2:3 and on the results announced by the IMO organization concerning the actual number of medals in each category awarded in the IMO 2021 event.
The datasets of the population and of the GDP per capita of the participating countries are both collected from the official website of the World Bank. Olympic medal counts and the corresponding recorded scores were obtained from the official website of the IMO organization [Appendix A].
The descriptive statistics characterizing the inputs and outputs of the 80 participating countries that won at least one medal appear in Table 1, which contains the average level, the standard variance, the minimum level, and the maximum level. The large standard deviation of the inputs in Table 1 demonstrates that the input data vary significantly. The latter evidence indicates that the appropriate model to use in the current case study is the VRS DEA model.

Table 1.
Descriptive statistics of inputs and outputs for 80 participating countries.
5. Results and Discussion
The data envelopment analysis provides a collection of useful information on the efficiency scores. Table 2 summarizes the findings from the VRS analysis and the efficiency score that each participating country achieved, while Figure 1 illustrates a histogram of the efficiency scores.

Table 2.
The efficiencies of 80 countries based upon CCR VRS weight restricted model.
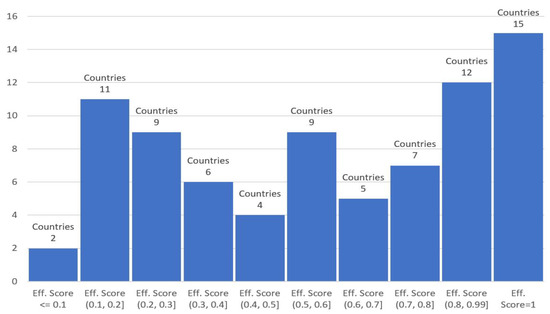
Figure 1.
Histogram of efficiency scores of the 80 countries.
As mentioned before, the CCR VRS model is used with the weight restriction coefficients αr and βr, which are equal to 1 and 2.5 and 1.5, respectively, for all outputs, r (r = 1, …, s), with the aim of discriminating between the values of the three categories of models.
In Table 2 above, out of 80 countries participating, only 15 countries are shown to be efficient. Moreover, the average efficiency score is equal to 0.5823. It is interesting to note, however, that when the DEA model is solved without the weight restrictions imposed on the three outputs, then the number of efficient countries is increased from 15 to 30 while the average efficiency score is calculated to be equal to 0.7308. The reason for this is that the feasible region of the output multiplier constraints in the model gets smaller. It is assumed in this study that one gold medal is worth at least 2.5 silver medals, and a silver medal is worth at least 1.5 bronze medals. Even though it seems quite reasonable to assume that coefficient βr is equal to 2.5 or 1.5, depending on parameter r, a sensitivity analysis is usually performed in similar applications for different values of βr. However, for the purposes of this study a sensitivity analysis seems to be unnecessary as the ratios between the numbers of different medal categories are defined by the IMO organization for all IMO events.
These results show that our proposed model provides a comprehensive ranking system tool for assessing the performances of the participating countries. The results provided by our approach can be compared to the country results published by the official site of the 62nd IMO 2021, where the countries were ranked based on the total score achieved by the individual contestants in all the problems for each country. In Table 3, the 80 participating countries are listed. In the second column, the ranking order associated with each country, as published by the IMO organization, is presented. In the third column of Table 3, the ranking of the 80 participating countries based solely on the number of gold, silver, and bronze medals won, without taking into account the relative importance of the medals according to their weight restrictions, is presented for comparison purposes. The ranking order associated with each country, as derived from the CCR VRS weight-restricted model discussed in Section 3 above, is also presented in column 4 of Table 3 and graphically in Figure 2 and Figure 3.

Table 3.
IMO2021org., CCR-VRS model, and CCR-VRS weight restricted model rankings.
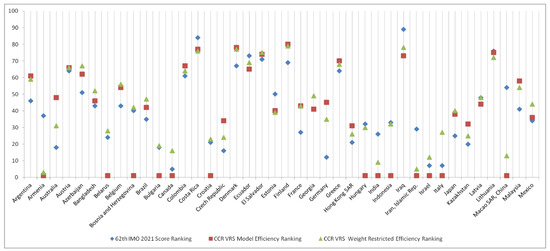
Figure 2.
The 62nd IMO 2021 score ranking versus CCR VRS ranking and CCR VRS weight restricted ranking (Argentina–Mexico).
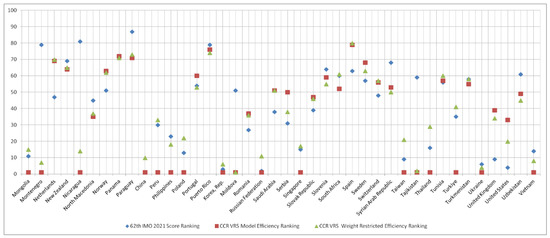
Figure 3.
The 62nd IMO 2021 score ranking versus CCR VRS ranking and CCR VRS weight restricted ranking (Mongolia–Vietnam).
In Table 3, the 62nd IMO 2021 ranking has been appropriately adjusted to include the 303 gold, silver, and bronze medals awarded by the IMO organization only. The 98 honorable mentions that were awarded to the participants of the 62nd IMO 2021 have not been taken into account in this ranking. Any participant who receives a score of 7 on any one question but who does not receive a medal is awarded an honorable mention. In our study, honorable mentions were not taken into account for the assessment of the participating countries, nor were any of the scores achieved by the participants that were not awarded a medal or an honorable mention.
As can be ascertained from the results in Table 3, some countries have been completely differently ranked by the IMO organization and the DEA approach. It is interesting to note for example that Moldova was ranked 51st out of 80 countries according to the 62nd IMO 2021 ranking while it was ranked first according to the DEA model rankings. The reason for this is that both the input measures for Moldova are well below the corresponding averages presented in Table 1, and thus, it can be proved that this DMU is efficient. The results show that our proposed approach is more general and reasonable. This is mainly due to the fact that in our model we also consider the value judgment for the weight relationships among the three outputs. In addition, our approach also provides a guide for performance improvement.
6. Conclusions and Recommendations
This study contributes to the measurement of the performances of the participating countries in an International Mathematical Olympiad competition by using a comprehensive model that evaluates the efforts of the participating teams more accurately. Although IMOs do not gain great international visibility when compared to some athletic events, the concern about the results of the countries in such events has been increasing.
With the aim of analyzing the results and improving the performance of the participating countries, the efficiency of the countries participating in the 62nd IMO 2021 was analyzed by implementing the DEA method. The input and output indicators for the 62nd 2021 IMO that were considered were the population and GDP per capita of the participating countries, as related to the three outputs utilized. The three outputs were the total scores accumulated that resulted in the award of gold medals, silver medals, and bronze medals, respectively. In our model, a variable returns to scale model was used with the output orientation.
A common issue occurring in real-world DEA applications is that often all the input and output measures may not be equally important to the decision makers. This study reports an application whereby, in a DEA model, weight restrictions are imposed on the three outputs of the model to overcome the above problem. A weight-restricted DEA model is thus constructed by introducing a discrimination criterion between the several efficient units.
Regarding the results obtained from this study, out of the 80 countries participating in this event, only 15 countries are shown to be efficient, with some countries being completely differently ranked by the IMO organization and our DEA model. The efficient DMUs that define a target are peers or references that can help to improve the whole efficiency of the competition. These measures describe the countries’ potential to generate a number of participants (mathletes) in the IMOs and are often considered as the most important factors explaining both sport and cognitive performance.
Future work for this research can focus more on the measures utilized and aim to investigate potential resources and outputs that would cover a wider range of measures that are more representative of the efforts put in and the results obtained. Moreover, the aim is to provide future researchers with some testimony on how these non-athletic mega-events can provide useful insights into the management of the mega-events by comparing and contrasting similarities and differences. Finally, regarding the comparison of the rankings produced by the present study and other international surveys, we strongly believe that the results of this study can add to the information about international performances in order to drive up education standards to a higher level.
Author Contributions
Conceptualization, S.S.; methodology, V.C. and S.S.; formal analysis, V.C. and S.S.; investigation, V.C. and S.S; data curation, V.C.; writing—original draft preparation, V.C. and S.S.; writing—review and editing, V.C. and S.S.; visualization, V.C.; supervision, S.S.; funding acquisition, S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been partly supported by the University of Piraeus Research Center [VAT Registration Number: EL 090037284 91].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Population and GDP per Capita Are Both Collected from the Official Website of World Bank
| Countries | GDP_per_Capita | Population | Countries | GDP_per_Capita | Population |
| Argentina | 10,729.23258 | 45,808,747 | Mongolia | 4534.918589 | 3,329,282 |
| Armenia | 4670.008798 | 2,968,128 | Montenegro | 9367.016884 | 620,173 |
| Australia | 59,934.12941 | 25,739,256 | Netherlands | 58,061.00167 | 17,533,405 |
| Austria | 53,267.93275 | 8,956,279 | New Zealand | 48,801.68513 | 5,122,600 |
| Azerbaijan | 5384.034998 | 10,145,212 | Nicaragua | 2090.753461 | 6,702,379 |
| Bangladesh | 2503.04388 | 166,303,494 | North Macedonia | 6720.896285 | 2,065,092 |
| Belarus | 7303.696266 | 9,340,314 | Norway | 89,202.75054 | 5,408,320 |
| Belgium | 51,767.78857 | 11,587,882 | Panama | 14,516.45805 | 4,381,583 |
| Bosnia and Herzegovina | 6916.438315 | 3,263,459 | Paraguay | 5400.103826 | 7,219,641 |
| Brazil | 7,518.834284 | 213,993,441 | China | 12,556.33312 | 1,412,360,000 |
| Bulgaria | 11,634.97102 | 6,899,125 | Peru | 6692.248375 | 33,359,416 |
| Canada | 52,051.35146 | 38,246,108 | Philippines | 3548.828323 | 111,046,910 |
| Colombia | 6131.225922 | 51,265,841 | Poland | 17,840.92105 | 37,781,024 |
| Costa Rica | 12,508.61563 | 5,139,053 | Portugal | 24,262.18094 | 10,299,423 |
| Croatia | 17,398.76598 | 3,899,000 | Puerto Rico | 31,429.86612 | 3,263,584 |
| Czech Republic | 26,378.49996 | 10,703,446 | Korea. Rep. | 34,757.72007 | 51,744,876 |
| Denmark | 67,803.0471 | 5,856,733 | Moldova | 5314.531461 | 2,573,928 |
| Ecuador | 5934.875496 | 17,888,474 | Romania | 14,861.90917 | 19,115,146 |
| El Salvador | 4408.520365 | 6,518,500 | Russian Federation | 12,172.78516 | 143,446,060 |
| Estonia | 27,280.65844 | 1,329,254 | Saudi Arabia | 23,585.88563 | 35,340,680 |
| Finland | 53,982.61427 | 5,541,696 | Serbia | 9214.993546 | 6,844,078 |
| France | 43,518.53851 | 67,499,343 | Singapore | 72,794.00302 | 5,453,566 |
| Georgia | 5042.385528 | 3,708,610 | Slovak Republic | 21,087.8461 | 5,447,247 |
| Germany | 50,801.78671 | 83,129,285 | Slovenia | 29,200.81988 | 2,107,007 |
| Greece | 20,276.54467 | 10,664,568 | South Africa | 6994.211654 | 60,041,996 |
| Hong Kong SAR | 49,660.63424 | 7,413,100 | Spain | 30,115.70589 | 47,326,687 |
| Hungary | 18,772.67329 | 9,709,886 | Sweden | 60,238.98656 | 10,415,811 |
| India | 2277.434347 | 1,393,409,033 | Switzerland | 93,457.4404 | 8,697,723 |
| Indonesia | 4291.812554 | 276,361,788 | Syrian Arab Republic | 1265.60619 | 18,275,704 |
| Iraq | 5048.387813 | 41,179,351 | Taiwan | 32,123 | 23,859,912 |
| Iran, Islamic Rep. | 2756.749977 | 85,028,760 | Tajikistan | 897.087902 | 9,749,625 |
| Israel | 51,430.07968 | 9,364,000 | Thailand | 7233.388858 | 69,950,844 |
| Italy | 35,551.28499 | 59,066,225 | Tunisia | 3924.343925 | 11,935,764 |
| Japan | 39,285.16311 | 125,681,593 | Turkiye | 9586.61245 | 85,042,736 |
| Kazakhstan | 10,041.48984 | 19,002,586 | Turkmenistan | 7612.03518 | 6,117,933 |
| Latvia | 20,642.16792 | 1,883,162 | Ukraine | 4835.571777 | 43,814,581 |
| Lithuania | 23,433.39091 | 2,795,321 | United Kingdom | 47,334.35531 | 67,326,569 |
| Macao SAR, China | 45,421.62663 | 658,391 | United States | 69,287.53659 | 331,893,745 |
| Malaysia | 11,371.09902 | 32,776,195 | Uzbekistan | 1983.064723 | 34,915,100 |
| Mexico | 9926.422768 | 130,262,220 | Vietnam | 3694.019046 | 98,168,829 |
References
- Henseke, G. Country performance at the International Mathematical Olympiad. In Thuenen-Series of Applied Economic Theory; No. 108; University of Rostock, Institute of Economics: Rostock, Germany, 2009. [Google Scholar]
- Li, Y.; Lei, X.; Dai, Q.; Liang, L. Performance Evaluation of Participating Nations at the 2012 London Summer Olympics by a Two-Stage Data Envelopment Analysis. Eur. J. Oper. Res. 2015, 243, 964–973. [Google Scholar] [CrossRef]
- Sekitani, K.; Zhao, Y. Performance Benchmarking of Achievements in the Olympics: An Application of Data Envelopment Analysis with Restricted Multipliers. Eur. J. Oper. Res. 2021, 294, 1202–1212. [Google Scholar] [CrossRef]
- Gómez-Déniz, E.; Dávila-Cárdenes, N.; Leiva-Arcas, A.; Martínez-Patiño, M.J. Measuring Efficiency in the Summer Olympic Games Disciplines: The Case of the Spanish Athletes. Mathematics 2021, 9, 2688. [Google Scholar] [CrossRef]
- Dincă, M.S.; Dincă, G.; Andronic, M.L.; Pasztori, A.M. Assessment of the European Union’s Educational Efficiency. Sustainability 2021, 13, 3116. [Google Scholar] [CrossRef]
- Arnold, R.; Fletcher, D.; Molyneux, L. Performance Leadership and Management in Elite Sport: Recommendations, Advice and Suggestions from National Performance Directors. Eur. Sport Manag. Q. 2012, 12, 317–336. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Parker, B.; Tavares, G. Evaluation of Research in Efficiency and Productivity: A Survey and Analysis of the First 30 Years of Scholarly Literature in DEA. Socio-Econ. Plan. Sci. 2008, 42, 151–157. [Google Scholar] [CrossRef]
- Cook, W.D.; Seiford, L. Data Envelopment Analysis (DEA)—Thirty Years On. Eur. J. Oper. Res. 2009, 192, 1–17. [Google Scholar] [CrossRef]
- Liu, J.S.; Lu, L.Y.Y.; Lu, W.-M.; Lin, B.J.Y. A Survey of DEA Applications. Omega 2013, 41, 893–902. [Google Scholar] [CrossRef]
- Kao, C. Network Data Envelopment Analysis: A Review. Eur. J. Oper. Res. 2014, 239, 1–16. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Yang, G. A Survey and Analysis of the First 40 Years of Scholarly Literature in DEA: 1978–2016. Socio-Econ. Plan. Sci. 2018, 61, 4–8. [Google Scholar] [CrossRef]
- Dedoussis, V.; Konstas, C.; Kassimis, A.; Sofianopoulou, S. Efficiency evaluation of hydroelectric power plants using data envelopment analysis. J. Appl. Oper. Res. 2010, 2, 94–99. [Google Scholar]
- Sofianopoulou, S. Manufacturing Cells Efficiency Evaluation Using Data Envelopment Analysis. J. Manuf. Technol. Manag. 2006, 17, 224–238. [Google Scholar] [CrossRef]
- Sofianopoulou, S. Efficiency evaluation of Greek commercial banks using DEA. J. Appl. Oper. Res. 2012, 4, 183–193. [Google Scholar]
- Lozano, S.; Villa, G.; Guerrero, F.; Cortés, P. Measuring the Performance of Nations at the Summer Olympics Using Data Envelopment Analysis. In Operational Research Applied to Sports; Wright, M., Ed.; Palgrave Macmillan UK: London, UK, 2015; pp. 144–164. ISBN 978-1-137-53467-5. [Google Scholar]
- Lins, M.P.E.; Gomes, E.G.; Soares de Mello, J.C.C.B.; Soares de Mello, A.J.R. Olympic ranking based on a zero sum gains DEA model. Eur. J. Oper. Res. 2003, 148, 312–322. [Google Scholar] [CrossRef]
- Li, Y.; Liang, L.; Chen, Y.; Morita, H. Models for measuring and benchmarking olympics achievements. Omega 2008, 36, 933–940. [Google Scholar] [CrossRef]
- de Mello, J.C.C.B.S.; Angulo-Meza, L.; Lacerda, F.G. A Dea Model with a Non Discritionary Variablefor Olympic Evaluation. Pesqui. Oper. 2012, 32, 21–30. [Google Scholar] [CrossRef][Green Version]
- de Mello, J.C.C.B.S.; Angulo-Meza, L.; Lacerda, F.G.; Neto, L.B. Performance Team Evaluation in 2008 Beijing Olympic Games. In Proceedings of the ICIEOM 2009—XV International Conference on Industrial Engineering and Operations Management, Salvador, Brazil, 6–9 October 2009. [Google Scholar] [CrossRef]
- Zhang, D.; Li, X.; Meng, W.; Liu, W. Measuring the Performance of Nations at the Olympic Games Using DEA Models with Different Preferences. J. Oper. Res. Soc. 2009, 60, 983–990. [Google Scholar] [CrossRef]
- Wu, H.; Chen, B.; Xia, Q.; Zhou, H. Ranking and benchmarking of the asian games achievements based on dea: The case of Guangzhou 2010. Asia Pac. J. Oper. Res. 2013, 30, 1350028. [Google Scholar] [CrossRef]
- Anderson, T.R.; Sharp, G.P. A New Measure of Baseball Batters Using DEA. Ann. Oper. Res. 1997, 73, 141–155. [Google Scholar] [CrossRef]
- Espitia-Escuer, M.; García-Cebrián, L.I. Performance in Sports Teams: Results and Potential in the Professional Soccer League in Spain. Manag. Decis. 2006, 44, 1020–1030. [Google Scholar] [CrossRef]
- Bosca, J.; Liern, V.; Martinez, A.; Sala, R. Increasing Offensive or Defensive Efficiency? An Analysis of Italian and Spanish Football. Omega 2009, 37, 63–78. [Google Scholar] [CrossRef]
- Chen, W.-C.; Johnson, A.L. The Dynamics of Performance Space of Major League Baseball Pitchers 1871–2006. Ann. Oper. Res. 2010, 181, 287–302. [Google Scholar] [CrossRef]
- Moreno, P.; Lozano, S. A Network DEA Assessment of Team Efficiency in the NBA. Ann. Oper. Res. 2014, 214, 99–124. [Google Scholar] [CrossRef]
- Lozano, S.; Villa, G.; Guerrero, F.; Cortés, P. Measuring the Performance of Nations at the Summer Olympics Using Data Envelopment Analysis. J. Oper. Res. Soc. 2002, 53, 501–511. [Google Scholar] [CrossRef]
- Calzada-Infante, L.; Lozano, S. Analysing Olympic Games through Dominance Networks. Phys. A Stat. Mech. Its Appl. 2016, 462, 1215–1230. [Google Scholar] [CrossRef]
- Sitarz, S. Mean Value and Volume-Based Sensitivity Analysis for Olympic Rankings. Eur. J. Oper. Res. 2012, 216, 232–238. [Google Scholar] [CrossRef]
- Ouyang, B.; Wu, R. Evaluation Model of Youth Basketball Training Performance Based on PSO Algorithm. Wirel. Commun. Mob. Comput. 2022, 2022, 1830318. [Google Scholar] [CrossRef]
- Metulini, R.; Gnecco, G. Measuring Players’ Importance in Basketball Using the Generalized Shapley Value. Ann. Oper. Res. 2022. [Google Scholar] [CrossRef]
- Sarlis, V.; Tjortjis, C. Sports Analytics—Evaluation of Basketball Players and Team Performance. Inf. Syst. 2020, 93, 101562. [Google Scholar] [CrossRef]
- Cooper, W.W.; Tone, K. Measures of Inefficiency in Data Envelopment Analysis and Stochastic Frontier Estimation. Eur. J. Oper. Res. 1997, 99, 72–88. [Google Scholar] [CrossRef]
- Allen, R.; Athanassopoulos, A.; Dyson, R.G.; Thanassoulis, E. Weights Restrictions and Value Judgements in Data Envelopment Analysis: Evolution, Development and Future Directions. Ann. Oper. Res. 1997, 73, 13–34. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).