Abstract
In this article, we propose an educational path to learn mathematics in the framework of the European Community Action Scheme for the Mobility of University Students (ERASMUS) project developed in an Italian high school class on the topic of the contribution of women in science. The choice of the educational path fell on Maria Gaetana Agnesi and the particular curve, the “versiera” (witch), studied by her. During the experimentation, the students have been divided into four groups, each one taking care of particular aspects of the human and cultural experience of Maria Gaetana Agnesi, and the construction of her famous curve under different mathematical registers: the geometric, algebraic, analytical, mechanical and computer science, as well as non-mathematical ones such as the gestural and voice registers. The effectiveness of the proposed educational path was evaluated through interviews with the students during the course and at the end of the activities. All the students, even those less skilled in mathematics, have shown enthusiasm and satisfaction by recognizing the mathematical object, the “witch”, presented by using different languages.
1. Introduction
The purpose of this work is to present a path for learning mathematics carried out in Italy at the Einaudi-Casaregis-Galilei Technical Institute in Genoa within the European Community Action Scheme for the Mobility of University Students (ERASMUS) project, a student mobility project ran by the European Union. The starting point was the proposal of the ERASMUS scientific commission, made up of teachers from different European countries, to work on female scientists or mathematicians from their own country.
The choice of teachers at the Institute, shared by the students, fell on Maria Gaetana Agnesi [1,2,3]. The choice was motivated from the fact that she was a scholar capable of conversing in many languages, very well versed in mathematics and particularly attentive to its teaching [4,5], lived in an interesting historical period for the evolution of the social problems she herself dealt with, with wide literary and philosophical interests [6,7].
In particular, the teachers at the Technical Institute started by considering a particular curve studied by Gaetana Agnesi whose characteristics are reminiscent of those of the Diocles cissoid [8]. This curve, known as the versiera (the name currently used in anglophone countries is witch, due to a mistranslation of the Italian word “versiera” and it will be used hereinafter to indicate such a curve), was the subject of study by Pierre De Fermat [9,10,11] and Guido Grandi [12] and is still used for significant modeling in Physics.
A study on the witch responded to the aims indicated in the ERASMUS project entitled “New Paths in Maths”, becoming the common thread to build a shared path between the Italian students directly involved and the European students interested in knowing it. In it, the still recently focused goal in Radford (2020a) [13] of making “the activity of learning an activity that, in addition to enabling the students to become familiar with cultural knowledge in a deep, critical, and reflective manner, provides opportunities for emancipation, allowing the students to assert themselves as social, historical, and cultural subjects” (p. 15).
The students worked to produce specific contributions, complementary to each other, for the realization of the project, suitable for enhancing diversified skills, in order to induce positive relationships between young people with expressive potential and different cultural backgrounds, sometimes confused in discriminating mode, with different levels of intellectual merit [14]. The development of the activities therefore had as a driving element the counterpoint between a particular attention to the collegial aspects [15] of the interventions developed by the students, essential for both human and cultural growth, and the construction of awareness for how shared activity [16] drew lymph from the individual and diversified knowledge and characteristics for each of them. All of this was in order to strengthen the personal identity of each student and self-esteem in the relationship with mathematics and its learning. The environment used for this objective was an excursus appropriately constructed through different semiotic fields [17,18,19], starting from the gestural and vocal one [20] up to those geometric and algebraic [21,22,23] and finally mechanical and computer science [24,25], which in various ways described the witch object.
The point of view and the tools that supported the initial phases of the work are reflected in the studies on the role of gestures in learning with the consequent relationships between gesture and sign expressed in [26,27] and also in the role of prodromes for the introduction to mathematical modeling [28,29,30].
Within specific semiotic and epistemological considerations [31], observations were raised on the development of knowledge generated by the use of different alphabets made available to mathematics [32,33], on the comparison between ways of operating, and on the results achieved in the different linguistic expressions within which the witch was treated.
Some suggestions deriving from considerations related to the history of mathematics [34,35,36] gave an overall depth of field to the work, introducing the children to the perception that the conceptual and operational mathematical tools learned and used can sometimes show a chronology of historical and conceptual development in analogy with the phases and naturalness of their personal learning, as highlighted in [37] and as specified in [38]: “This pedagogical use of history is that it interweaves our knowledge of past conceptual developments with the design of class-room activities, the goal of which is to enhance the students’ development of mathematical thinking”.
We also tried to work on the dissonances between the skills of the students, which, at first sight, may be viewed as obstacles but, if properly exploited [39], they can be effective tools to implement their creativity and create the possibility of expanding communication channels through a choral action. At the conclusion of the work, the students found that the object “witch” in every semiotic field had received a specific and diversified re-cognition [40], which consequently produced diversified knowledge of the mathematical object considered and the possibilities of its use. Paying attention to the role of learning artifacts was productive, especially as a vector for increasing knowledge potential [41,42] in the experience of creating the graphic of the witch using a machine designed and handcrafted by the students. This artifact, through its manipulations, was then a source of inspiration to build a new artifact suitable for easily drawing curves of degree at will.
2. Materials and Methods
Before describing the work made in the classroom, we synthetize here the basic information concerning the life of Maria Gaetana Agnesi and the cultural context in which she lived and operated.
Maria Gaetana Agnesi was born on 16 May 1718 from Pietro Agnesi Mariani and Anna Brivio. Her father, a rich merchant from Milan, was the mentor of his daughter and strongly influenced her choices. He exploited his goods to ensure his family a position in the aristocratic society and he chose the best available tutors (N. Gemelli, G. Tagliazucchi, G. Reina, F. Manara, M. Casati, C. Belloni, R. Rampinelli) for his sons and daughters. He had the habit to host meetings in his house, where he invited both Italian and foreign intellectuals. In 1727, Maria Gaetana Agnesi played in her father’s house living room a latin translation made by her of a speech in Italian of the Abbot Gemelli: Oratio, qua ostenditur: artium liberalium studia a femineo sexu neutiquam aborrere.
She was considered by her father as the right person to ensure a good reputation for the family, being a child prodigy, gifted with an exceptional mind, able to speak seven different languages.
The living room of Agnesi’s house became a meeting place for thinkers who tried to harmonize ratio and faith, also in relation with the new scientific theories that were starting to spread.
In 1737, Maria Gaetana Agnesi began to study philosophy and mathematics, being busy with logic, physics, biology and meteorology and discussing her opinions in the society of the time, even though her interests for topics of mechanical and geometrical nature dated back to years before.
In 1738, she published 191 theses with the title Propositiones Philosophicae, a collection of essays of natural philosophy and history inspired by her discussions with the guests of her family.
During the same period, she began to show a deep interest for topics of religious nature and she devoted most time to her spiritual life. In 1739, she expressed the desire to quit the mundane life and take the religious vows. Her father did not allow her to become a nun, but he permitted her to conduct a retired life, far from events and public meetings and be devoted to charity activities, under the condition that she continued her scientific studies and taught her brothers and sisters.
Maria Gaetana Agnesi went on to study mathematics, which she considered as a tool through which human beings could reach and contemplate the truth.
In 1740, she met Ramiro Rampinelli, with whom she studied differential and integral calculus, also with the intention of writing a text to be used in teaching mathematics. The result of this research was the publication of the Istituzioni Analitiche ad Uso della Gioventù Italiana (Analytical Institutions for the Use of the Italian Youth) in 1748.
Among the curves studied by Maria Gaetana Agnesi is the famous versiera (witch of Agnesi), a cubic curve still studied today. Agnesi dedicated her work to the Austrian empress Maria Theresa who, feeling particularly honored, rewarded her with a diamond-encrusted ring.
In 1750, Pope Benedict XIV appointed Maria Gaetana Agnesi as Honorary Lecturer of the University of Bologna but she did not accept any teaching positions, by now shunning any worldliness.
After the death of her father in 1752, she devoted herself completely to works of religion.
She died on 9 January 1799 and was buried in a mass grave, as she wished.
The cultural environment in which Agnesi was operating was that of the Catholic Enlightenment of the Muratorian mold, present in the church of Milan in the early eighteenth century. Ecclesiastical institutions favorably accepted the increase in the presence of women in charitable interventions and related to the education of young people. The volume of Agnesi, the first written by a woman on the subject, explained the new techniques of the infinitesimal calculus starting from elementary algebra, with an excellent systematic structure in order to make the theories covered accessible to all who had even a basic knowledge of mathematics. For Maria Gaetana Agnesi, the fundamental value of mathematics and therefore also of the infinitesimal calculus was constituted by the refinement of the intellect in order to make the spiritual life of those involved in these studies better and more participatory. These and other interesting references to the cultural context of Milan at the beginning of the eighteenth century where Maria Gaetana Agnesi lived can be found in [43].
Let us now describe the activities made in the classroom.
The work began with a lesson from the physics teacher who introduced the witch by talking about the current use of the curve in physics. The teacher communicated, on a qualitative level and without going into specialized technical details, that the curve studied by Agnesi performs the task of indicating the shape of the probability distribution function of the energy emitted during the passage of an electron from an energy level to another within an atom, thus providing a probabilistic description of an aspect of nature.
The same teacher then said that the witch had also been treated by other mathematicians, such as Fermat (P. De Fermat is among the first mathematicians to deal with this family of curves (witches): Ouvres, Vol. I, p. 279–280 and Vol. III, p. 233–234. The first work is in Latin, the second in French. The author shows how the squaring of curves is obtained by considering circles, hyperbolas and parabolas [44] and calculates the area under the witch in relation to that of the circumference that generates it) and Grandi (Guido Grandi, in his works Quadratura Circuli et Hyperbolae (1st edition 1703, 2nd edition 1710) and Notes to Galileo’s Treatise on naturally accelerated motion (1718), studies the witch in depth. In the second treatise the term in Latin “versoria” appears for the first time.), and that Agnesi had calculated the area under the curve with the use of integral calculus in her treatise Istituzioni Analitiche (Analytical Institutions) of 1748. Taking an interest in the witch within the ERASMUS project could therefore be a way to get in touch with the study of a very interesting female personality in the history of Mathematics [45] through an object that is still significant for science. Hence, the teacher devoted part of the lecture to some aspects of the life and personality of Agnesi, inviting the students who wanted to get more involved in them.
After this initial phase, in which the physics teacher presented the witch curve explaining its use in Physics, the students were divided into four groups (A, B, C, D), each of which developed different themes:
Group A: A historical research on the life, the philosophical and scientific works, the human and intellectual characteristics of Maria Gaetana Agnesi, and on the social and cultural environment of the Italian and European eighteenth century in which she lived (George, Giada, Giorgia, Lin);
Group B: A performance, a game that involved the positioning of a certain number of red discs on the floor of the school terrace according to a predefined scheme and the use of common objects; a drawing, to be made on the blackboard with chalk, of the elements and positioning of the objects involved in the performance; the search for the possibility of talking about the elements drawn on the blackboard first in the register of Euclidean geometry and then in the register of algebra (Alessio, Daniel, Davide P., Gabriele, Mattia);
Group C: The search for the generalized algebraic expression of the witch in the analytical register (Davide F., Leonardo, Mario C.);
The exposure of the activity of the previous groups to all the other students at the same Institute subsequently led to the formation of a fourth group (D) which developed a further theme:
Group D: The construction of a mechanical artifact to draw the witch and the possibility of “generalizing” this artifact to draw higher degree curves (Mario G., Nicholas).
After the common lesson, each group began its specific activity.
The purpose of the experimentation was to show that the vision and description of the same mathematical problem with different registers (historical-cultural, for Group A; gestural-vocal-geometric, in the performance of Group B; algebraic, developed by Group C; mechanical-computer science, developed by Group D) through the sharing of experiences and results between the various groups, and at an educational and cultural level it brings benefits for all students, even those who have attitudes and skills less oriented to the scientific aspects of the problems.
Given the cultural inhomogeneity of the various students involved, we preferred not to propose a questionnaire to assess the students’ initial and final skills, limiting ourselves to collect their impressions and what they expressed during the various proposed activities and in a final interview. In the latter, the interest of students in the figure of Maria Gaetana Agnesi emerged in her historical and cultural context, in the dynamic aspects of geometry, created using elementary tools, in the effectiveness of algebraic language, also for the purpose of a generalization of the considered problem. Finally, the enthusiasm of the students and their proactive skills emerged in the form of the production of hardware and software artifacts to give a graphical representation of Agnesi’s curve.
3. Results
The students involved in the project, as explained above, were divided into four distinct groups based on their attitudes and expressions of interest.
Group A was made up of students with a particular inclination for research in literature and history. Guided by teachers, they have collected a significant bibliography on Maria Gaetana Agnesi. The students, left free to turn their attention to the issues that they considered most meaningful for them, tried above all to understand how Agnesi could deal with scientific and moral issues at the same time with the same energy and effectiveness. Their conclusive explanation was that, apart from her father’s desire to show a daughter particularly versed in mathematics and philosophy in society, she had a particular affection that guided her towards youth problems and towards the possibility of facilitating the access of young people to knowledge and its research frontiers, not least the studies on the infinitesimal calculus, favoring the understanding of the real world. The students took as their starting point a particularly fascinating communication Al Lettore (To the Reader) found in the introduction to Analytical Institutions:
Non avvi alcuno, il quale informato essendo delle Matematiche cose, non sappia altresì quanto, in oggi spezialmente, sia necessario lo studio dell’analisi e quali progressi si sieno con questa fatti, si facciano tuttora, e possano sperarsi nell’avvenire; che però non voglio, né debbo trattenermi qui in lodando questa scienza, che punto non ne abbisogna, e molto meno da me. Ma quanto è chiara la necessità di lei, onde la Gioventù ardentemente s’invoglj di farne acquisto, grandi altrettanto sono le difficoltà, che vi s’incontrano, essendo noto, e fuor di dubbio, che non ogni Città, almeno nella nostra Italia,ȃpersone, che sappiano, o vogliano insegnarla, e non tuttiȃnno il modo di andar fuori della Patria a cercarne i Maestri (An attempt to translate the sentence (which, by the way, is not in modern Italian) is: Do not initiate anyone, who being informed of Mathematical things, does not also know how much, in particular today, the study of analysis is necessary and what progresses have been made with this, are still being made, and can be hoped for in the future; which, however, I do not want, nor must I hold back here in praising this science, which just does not need it, and much less from me. However, how clear is the need for her it, so that Youth ardently desires to buy it, as well as great are the difficulties, which are encountered there, being known, and beyond doubt, that not every City, at least in our Italy, has people, who know, or want to teach it, and not all of them have the way to go out of the Homeland to look for its Masters).
After reading the quoted passage, the girls in Group A above all felt the need to better understand the female condition of the Italian eighteenth century, in which “school” could be talked about in that period to go into the details of the education received by Maria Gaetana Agnesi and of her relationship with her family.
To the students of Group B, the mathematics teacher proposed a performance, specifically a “dynamic” activity to be carried out with a hula hoop, three nylon ropes, two rigid rods and red discs. With this equipment, the students would have had to perform a series of gestures to place the discs on the floor of a school terrace. The teacher had anticipated that the positions of the discs would later be reflected in the witch of Agnesi that the physics professor had spoken of in his lesson.
The performance created by the students is visible in the video: https://www.youtube.com/watch?v=jq7-C50X8H0 (accessed on 6 October 2018).
Figure 1 shows two frames extracted from the video.

Figure 1.
Two moments of the performance made by the students.
As one can see, two of the cords available are knotted in two opposite points of the plastic circle of the hula hoop. The two ropes are fixed in such a way as to maintain reciprocally the distance that the knots on the hula hoop have between them. The third rope is knotted on the knot of one of the first two (first rope) and, kept taut, can be rotated at will in order to intercept a point on the hula hoop and a point on the other rope (second rope). Two rigid rods are positioned one for each of the two points just identified, the first rod parallel to the two fixed strings and passing through the point intercepted on the circle by the third string, and the second perpendicular to the first and passing through the point intercepted by the third string on the second rope. At the meeting point of the two auctions, the boys placed a colored token.
At this point, the math teacher asked the students to discuss their experience. The students gave a lively verbal account in terms of hula hoop, tight ropes, crossings of metal rods, their movements on the floor, red discs, etc., retracing in their story the succession of movements that had been constitutive of the performance. The teacher pointed out that in their presentation they had used natural language, their mother tongue.
For the next step, the teacher proposed to draw the most significant elements involved in the performance on the blackboard with chalk. The students then traced signs on the blackboard, reflections of their actions, passing from the movements executed in the performance to the graphic translation of the product of these movements, creating correspondences between the traits of the nylon ropes, the rigid rods, their intersections and the lines left on the blackboard by the chalk, gradually becoming aware that they were building a graphic model of the effects of their actions. As expressed in words by one of them, they had worked “like the tailor who reproduces on paper the model of a dress he saw in the window”.
Some of the drawings made by the students are visible in Figure 2.

Figure 2.
Some drawings made by the students on the blackboard during the performance.
The teacher, pointing out to the students that the register of natural language, with which they had described the operations performed, had approached a graphic register, stressed that there were now two expressive registers to which they could refer to communicate their experience. Any spectator, in addition to listening to the story, could also look at a figure which kept the memory of the development of the story, in that it was clear to the eyes and allowed the students to coexist the traces of the experiences of different moments fixed in the positions of the points on the blackboard, signs representative of the disk positions on the floor.
At this point, the teacher suggested that the students try to “immerse” the communication of their activity in the register of Euclidean geometry.
The teacher began by inviting the students to identify the geometric figures to be associated with the drawings they had drawn on the blackboard, evoking the configurations produced during the tension of the strings in the various moments of placing the discs on the floor.
The students, following the style of Euclid, named the meeting points of the lines they had drawn on the blackboard with capital letters and then recognized, in these graphic traces, objects of geometry such as segments, the circle, its diameter, parallel lines between them, the straight lines tangent to the circle, the right triangles, a rectangle, all geometric elements that were repeated in each of the configurations produced to find the position of the disk to be deposited on the floor. Again, urged by the teacher, they recalled some properties that characterize the identified figures. An example of such activities is shown in Figure 3.

Figure 3.
An excerpt from the video (left) and a chalkboard drawing (right) in which the students reported the different configurations produced during the performance.
The students then came to share the account of their experience in terms of a third register, that of Euclid’s geometry, expressing themselves as follows:
We took a circle, two of its diametrically opposite points A and C, we considered the tangent to the circumference at point C. Then, we considered a point D on the circumference different from A and C and we traced the line AD. We called Q the meeting point of the line AD with the tangent in C to the circumference. We have considered the line parallel to the tangent in C, passing through D, and we have seen that it meets the line parallel to the diameter AC, passing through Q, at a point M. The point M is the place where we placed our red disk. To find other points analogous to M we changed the choice of point D on the circumference and we repeated the procedure, reproducing the same pattern each time.
At this point the teacher moved on to the next objective of the path which consisted in ferrying the group of students from the Euclidean register to the algebraic one, leading them, through a series of steps, to express themselves in algebraic terms to write a formula that identified the points of the witch in a Cartesian plane. Moreover, the teacher enriched the lecture with comments taken from references to studies of history of mathematics with the aim to make the students understand the role played by Descartes when, especially in the Géométrie, he presented the passage between geometry and algebra, relaying on the theory of proportions as a bridge between the two [46].
The path followed by the teacher was structured in such a way that the perception and contact with the object they were talking about remained unaltered while the signs with which it was described were transformed. The algebraic language not only had to disconnect them from their initial experience and from the techniques adopted until then to express it, but they also had to promote a recognition of the object of study and its characteristics that would induce new knowledge in the students and awareness of the acquisition of new expressive potentials provided by the new register.
The teacher started with an input like this:
I would like to offer you another step in our walk into mathematics. We have just described our experience to identify the points M using Euclid’s geometry which with its terms and figures “records” the effect of our movements on the floor, movements that are repeated according to a well-defined pattern, as you have noticed and which you have just expounded in Euclid’s language of geometry. Let’s move forward together and try to find another way to describe and characterize the product of our movements. Mathematics will still offer us a new way to tell it using a mathematical language that you already know, as on the other hand you have already heard about Euclidean geometry. I intend, in this fourth phase of our journey, to use algebra. Let’s make this attempt together starting from this question: can we identify something that characterizes the nature of our points, something that is common to all configurations, that remains when we pass from one configuration to another?
Here are some typical phrases enunciated by the students, recorded during class discussions and representative of their reactions to the expression “something that is common to all configurations”:
Alessio: … but prof… the triangles are all different from each other…
Davide P.: … yes… you see, the angles always change…
Gabriele: … every time we move the rope tilts more and more…
Alessio: … it seems that nothing stays the same as we move…
Daniel: … the sides of the triangles change… with each movement certain sides stretch more than others … the more the string is inclined, the more this angle shrinks… while the triangle seems to become more extended…
The students, as can be seen from the previous sentences, made observations in which they made comparisons between a figure and its correspondent in the next configuration, fixed the attention on an object and then commented on how the elements of that object had transformed while the point D moved on the circumference.
Everything is transformed! Each configuration is different from the other … concludes Alessio.
Teacher: Ok, if we look at an object in one configuration and then the analog in the next configuration we see that its dimensions have changed … and it seems that all the observations we make do not suggest anything useful to answer our question. However, it should be noted that so far we have looked at the figures and their magnitudes in a geometric context and we have fixed our attention on how these quantities occupy space, we have observed with our eyes the presence of particular traces in our design of objects defined by Euclid’s geometry. I would then propose to make the attempt to “enter another environment” and pass from the observations of the qualities of these quantities in space to their possible relationships in the space of numbers. Let’s try to achieve this “transfer to another environment” by getting help from the very environment we are in now, that of geometry, which will act as a springboard for us. Let’s think about the “way of operating” between the dimensions of the objects we are studying that is suggested to us by some propositions of Euclidean geometry and let’s try to see if some relationship concerning the measurement of the segments of the figures we are considering can be useful for talking about our experience. Going into our specifics, do you perhaps remember some operation that Euclidean geometry enunciates about the figures involved in our configurations?
Mattia: So … let’s go back to the figures we drew…
Davide P.: … The circumference with diameter AC,… the rectangle BCQM,… some triangles ACQ, ABD, DQM.
Teacher: Ok, let’s focus our attention on the triangles… of the four arithmetic operations you know, are there any that are performed by involving the sides of the triangles? I’ll help you… something that for example speaks of relationships between the sides of triangles, something that suggests how the side of a triangle can fit into another…
Gabriele: You’re helping us a lot… prof!… Maybe we can think of the relationships between the sides in similar triangles?
Teacher: That’s right. What does the geometry suggest about the corresponding sides of similar triangles?
Alessio: … here… we can think that… in similar triangles between the corresponding sides… the ratios are the same…
Mattia: Ah… do you mean that we are thinking about the division operation?
Teacher: That’s right!… then let’s see if we have “produced” similar triangles in our performance on the floor and, if so, what can we write regarding the relationships between their sides in each of our configurations… I would suggest looking at the triangles in the order and in the way we produced them following the pattern of our initial performance. Which triangle did we produce first?
Davide P.: It’s all recorded on the video tape and on the blackboard…
The students then looked at the video of their performance and the drawings made on the blackboard.
Daniel: The first triangle we produced in our movements was CAQ, and then BAD and then immediately after that DQM, the one that has the red disk in the vertex M.
Guided by the teacher, the students found the similarity between the triangles ACQ and ABD and agreed on the proportion: AB : BD = AC : CQ (see Figure 4).
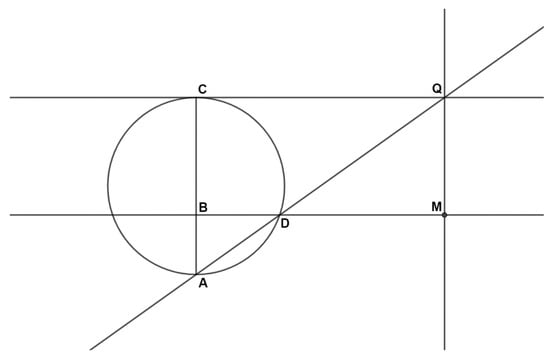
Figure 4.
Geometric construction of a point () of the witch.
Observing subsequently that in the rectangle the side is equal to the side, it is agreed that the proportion also exists:
Daniel: The one in which there is the segment that has point as its extreme.
At this point the teacher asked the students to follow him while he expressed the segment in another way, still using Euclidean knowledge.
The teacher reminded the students that a triangle inscribed in a semicircle is a right triangle and that in a right triangle the square built on the height relative to the hypotenuse is equivalent to the rectangle having the projections of the catheti on the hypotenuse as sides. For these reasons, it is possible to write the proportion from which to derive .
So he expressed the proportion (1) like this:
or also, if we remember the meaning of the fractions, as follows: .
The teacher continued to speak to the students in these terms:
To decrease the number of segments with which to operate we note that BC we can also see it as the difference between AC and AB… Now let’s imagine that we superimpose on our figure, originating in point A, a system of coordinate axes, which you all already know, by fixing as the x axis the tangent line to the circumference at A and the diameter AC as the y axis, as inFigure 5.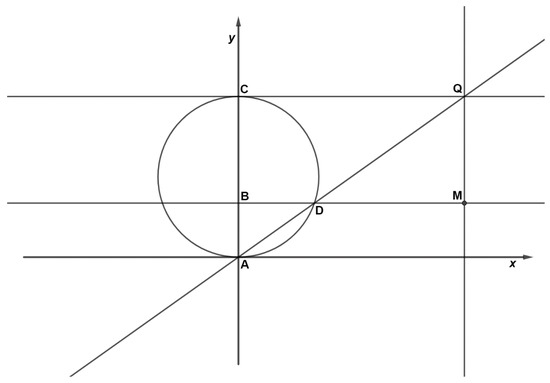 Figure 5. Geometric construction of a point () of the witch in a system of coordinate axes.
Figure 5. Geometric construction of a point () of the witch in a system of coordinate axes.
Teacher: Let us undertake to build a grid that contains on the left the story of our figures expressed in the language of Euclid and on the right the same story expressed in the language that Descartes proposed to us, that is, naming with a lowercase letter the segments that Euclid names by writing below the two capital letters with which he called their extremes…
In Table 1, we report a synthetic form of the grid developed in the class:

Table 1.
Correspondence between procedure in the geometric register (left) and procedure in the Cartesian register (right).
The students of Group B thus concluded their journey, noting how the relationships “told” quantitative relationships among the lengths of the segments focused on by the terms of geometry.
This experience constituted a specific objectification for some geometric, arithmetic and algebraic knowledge already known to the students who were visibly happy with it.
exclaimed a student who in some circumstances, lowering his eyes and looking at his knees, had said:Now I have understood something too… that in mathematics it is a matter of realizing that one goes on learning to speak the same thing in another way…
Prof… I don’t get along with Maths…
At that point, the students from Group B were ready for the meeting with the students from Group C, the ones who, according to their mates, “really knew how to do it with mathematics…”
Here is the path of the students of Group C, those able to easily use analytical knowledge. The results obtained by them naturally agree with the results exhibited by the students of Group B, constituting the generalized mathematical model.
The students of Group C also placed the origin of the Cartesian axis system at point . The straight line , which rotates around point , can be identified by the equation: .
So, the students from Group C explained:
Then arises the need to describe the circumference. It, again from Euclidean geometry, is the set of points on the plane equidistant from a given point. This condition, when the origin of the axes coincides with the center of the circumference, is given to us by the Pythagorean theorem, being abscissa and ordinate between them always perpendicular: . To this we must add because the center is not in the origin of the coordinates but higher than a quantity , so .
At this point, to determine the coordinates of point , we make a system with the beam of straight lines and the equation of the circumference, paying attention to the fact that not the whole beam is involved, only some values of are needed.
After some algebraic passages, the students obtained the following solutions:
Here are the coordinates of point D:
We now find the coordinates of point Q:
The coordinates of Q are: .
The coordinates of the point M will be the abscissa of Q and the ordinate of D, therefore:
For the Cartesian equation of the witch, the conditions must apply at the same time:
To obtain the Cartesian equation (see Figure 6), we obtain the parameterfrom the first and replace it in the second, obtaining .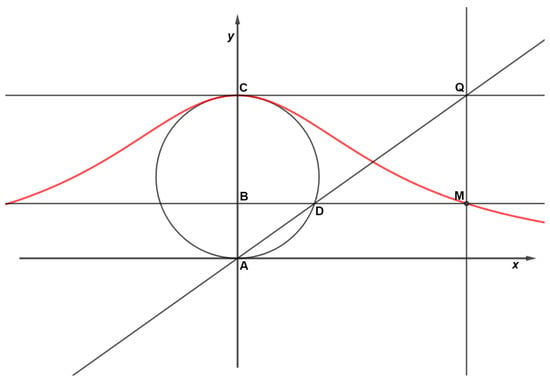 Figure 6. Cartesian representation of the witch of Agnesi.
Figure 6. Cartesian representation of the witch of Agnesi.
A further register to visit this “corner of mathematics” (as the participants named it) was born during the report provided as the dissemination of the results obtained and made at the end of the ERASMUS for the students at the whole Institute. On that occasion, the physics professor made a historical reference to the existence of mathematical machines capable of drawing curves, used from antiquity to the nineteenth century [47]. The question particularly struck a group of two students (Group D) of the “mechanics” course, Mario and Nicholas, experts in 3D design and printing, who tried to imagine a machine that would design the witch.
M. and N.: Prof, what if we try to design a machine that draws the witch?
Teacher: It is not impossible, but there are some practical issues that are not easy…
M.: We could use arms, we make the prototype with Inventor and we make them with the 3D printer.
Teacher: Yes, but how do we move them?
N.: By moving them with your hands? Indeed no, a crank and a series of gears.
Teacher: It seems to me already more effective, how many cogwheels are needed?
The machine, in the minds of the students, had to reproduce the effect of the movements of their mates in the video and of those who had drawn the witch on the blackboard. Those movements could be obtained with a gear with three cogwheels and slotted arms: one free to move parallel to itself and the other constrained to simulate a beam of straight lines. The main difficulty was the sizing of the parts that had to overcome the frictions. After countless attempts, approximations, and improvements, they have produced a prototype, as can be seen in Figure 7, capable of drawing a part of the curve.
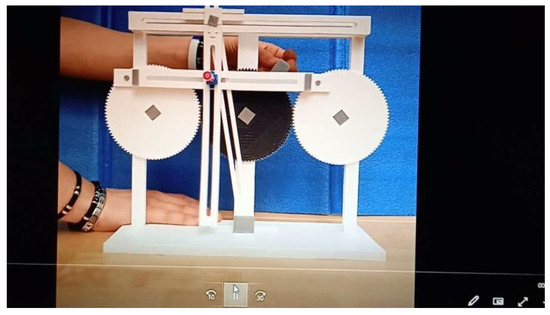
Figure 7.
Machine made by students to mechanically draw the witch.
The students went even further: while Mario was concentrating on the production of the witch machine, Nicholas, through a system of four gears and four perforated wheels, built a machine to draw the composition, on two axes, of the sine and cosine functions (see Figure 8). He thus obtained a wide range of “Lissajous figures”, used for the measurement of frequency and phase of sinusoidal signals.

Figure 8.
Machine made by students to mechanically draw Lissajous figures.
The presentation and explanation of the machines by the two students to their mates, who already knew the curve, and to the teachers at the Institute aroused enthusiasm and curiosity.
The didactic importance of these machines is remarkable, precisely in the vision of the transition from a dynamic of rotation over time to a linear expansion of the same.
To complement the construction of the machines, the students also produced a visualization of the curves using tools made available by computer science [48], in particular using the GeoGebra dynamic geometry software [49]. The result of the construction with GeoGebra is represented in Figure 9, where five witches are constructed interactively, using suitable sliders, for five different values of the radius of the circumference.
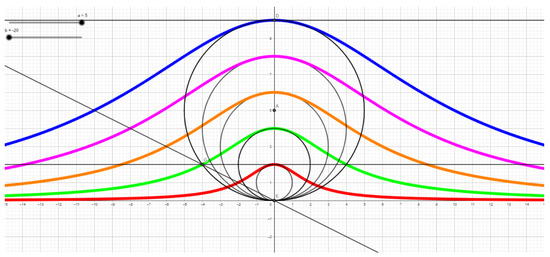
Figure 9.
Graphic representation using the GeoGebra dynamic geometry software of five witches.
4. Discussion/Conclusions
In this article we have presented an educational path that, through the use of various semiotic registers, has fostered knowledge of the figure of Italian mathematician Maria Gaetana Agnesi and the algebraic curve that bears her name (witch). This curve is not only an example of the mathematical production of one of the very few women mathematicians of the century XVIII, but it has various applications in physics and science in general and, therefore, represents an example of great historical-cultural and interdisciplinary value.
The study was introduced by the physics teacher, who briefly recalled the importance of the witch of Agnesi in physics, then the experimentation continued dividing the students into four groups, each with a different task to perform, taking into account the interest shown by them.
Some elements of the history of mathematics have been in the background and have fostered a fruitful dialogue between the students of the different groups after some observations by the teacher. The latter highlighted how their activities were in tune with the chronology of the development of the mathematical objects used, how a long historical path had produced Euclidean geometry, which constitutes a model of the space in which we move, and how an even longer path had immersed from the Euclidean space in the properties of numbers and in the register of symbols, leading us to operationally manage the measurement of space and its objects with the development of algebra.
The experimental path that the students experienced helped to transform their relationship with mathematics and its meaning. This path was developed along a series of successive moments:
- the performance, the game, “silent gestures” whose execution had as its purpose the positioning of red discs in the space of our perceived reality;
- the narration of the experience in the register of natural language;
- the graphic production, created by drawing on the blackboard, with chalk, lines and points representing the same objects treated in the performance according to a specific scheme;
- the translation of the graphic production in the register of Euclidean geometry;
- the translation of the terms identified by the Euclidean narrative in the register of algebra;
- the graph of the witch produced with a mechanical artifact, a new register to produce the trend of the curve, and the consequent possibility of “generalizing” this artifact to higher degree curves;
- the reproduction of the curves made in the computer science register with Geogebra.
A synthetic scheme is represented in Figure 10:

Figure 10.
Synthetic diagram of the various expressive registers used in the didactic path.
The effectiveness of the educational path proposed to students was confirmed by the interviews held with the students during and at the end of the proposed activities. The sharing of lived experiences in different fields has led to a cultural enrichment of all the students involved in the experimentation. The presentation of the same curve in different expressive registers has helped to strengthen the knowledge of the object, making it recognizable even in new and different contexts, and at the same time, it has helped to trace a first approach to the meaning of mathematical model processing. Even students with less interest and aptitude for mathematics expressed satisfaction at understanding how the diversification of knowledge had helped them in understanding the developed speech and in the acquisition of skills they thought they could not access. All the students were fascinated by Maria Gaetana Agnesi’s personality and also felt stimulated by her multi-disciplinary interests.
Author Contributions
Conceptualization, G.C., G.F. and E.F.; methodology, G.C., G.F. and E.F.; validation, G.C., G.F. and E.F.; investigation, G.C., G.F. and E.F.; resources, G.C., G.F. and E.F.; data curation, G.C.; writing—original draft preparation, G.C., G.F. and E.F.; writing—review and editing, G.C., G.F. and E.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Truesdell, C.A. Maria Gaetana Agnesi. Arch. Hist. Exact Sci. 1989, 40, 113–142. [Google Scholar] [CrossRef]
- Truesdell, C.A. Corrections and additions for “Maria Gaetana Agnesi”. Arch. Hist. Exact Sci. 1991, 43, 385–386. [Google Scholar] [CrossRef][Green Version]
- Minonzio, F. Chiarezza e Metodo: L’indagine Scientifica di Maria Gaetana Agnesi; Lampi di stampa: Milano, Italy, 2001. [Google Scholar]
- Agnesi, M.G. Instituzioni analitiche ad uso della gioventù italiana. In Milano, Nella Regia-Ducal Corte; Regia Ducal Corte: Milano, Italy, 1748. [Google Scholar]
- Roero, C.S.M.G.; Agnesi, R. Rampinelli and the Riccati family: A cultural fellowship formed for an important scientific purpose, the Instituzioni analitiche. Hist. Math. 2015, 42, 296–314. [Google Scholar] [CrossRef]
- Agnesi, M.G. Propositiones Philosophicae; Giuseppe Richino Malatesta: Milano, Italy, 1738. [Google Scholar]
- Zen, S. Maria Gaetana Agnesi between newtonianism, mathematics and catholicism in enlightenment Italy. In Frammenti di Filosofia Contemporanea; Pozzoni, I., Ed.; Casa Editrice Limina Mentis: Villasanta, Italy, 2018; Volume XXIII, pp. 1–13. [Google Scholar]
- Florio, E. John Wallis and the “Rectification” of the Parabola. Mathematics 2022, 10, 1170. [Google Scholar] [CrossRef]
- Fermat, P. Varia Opera Mathematica; Johannem Pech: Tolosa, France, 1679. [Google Scholar]
- Fermat, P. Oeuvres; Gauthier-Villars et fils: Paris, France, 1891; Volume I. [Google Scholar]
- Fermat, P. Oeuvres; Gauthier-Villars et fils: Paris, France, 1896; Volume III. [Google Scholar]
- Grandi, G. De Infinitis Infinitorum, et Infinite Parvorum Ordinibus Disquisitio Geometrica, ex Typographia Francisci Bindi impress; archiepisch.: Pisa, Italy, 1710. [Google Scholar]
- Radford, L. ¿Cómo sería una actividad de enseñanza-aprendizaje que busca ser emancipadora? La labor conjunta en la teoría de la objetivación. RECME—Rev. Colomb. Matemática Educ. 2020, 5, 15–31. [Google Scholar]
- Zan, R. Mio Figlio ha Paura Della Matematica; Giunti EDU: Firenze, Italy, 2021. [Google Scholar]
- Boero, P.; Pedemonte, B.; Robotti, E. Approaching theoretical knowledge through voices and echoes: A Vygotskian perspective. In Proceedings of the XXI International Conference for the Psychology of Mathematics Education, Lahti, Finland, 14–19 July 1997; Volume 2, pp. 81–88. [Google Scholar]
- Radford, L. Le concept de travail conjoint dans la théorie de l’objectivation. In Cahiers du Laboratoire de Didactique André Revuz n 21; González, M.F., Kuzniak, A., Nechache, A., Vivier, L., Eds.; IREM de Paris: Paris, France, 2020; pp. 19–41. [Google Scholar]
- D’Amore, B. Oggetti matematici e senso. Le trasformazioni semiotiche cambiano il senso degli oggetti matematici. La Mat. E La Sua Didatt. 2006, 4, 557–583. [Google Scholar]
- D’Amore, B.; Radford, L. Enseñanza y Aprendizaje de Las Matemáticas: Problemas Semióticos, Epistemológicos y Prácticos; Universidad Distrital Francisco José de Caldas: Bogotá, Columbia, 2017. [Google Scholar]
- Duval, R. Understanding the Mathematical Way of Thinking: The Registers of Semiotic Representations; Springer International: Cham, Switzerland, 2018. [Google Scholar]
- Radford, L. Corps, matière et signes dans la constitution du sens en mathématiques [Body, matter and signs in the constitution of meaning in mathematics]. In Sémiotique et Apprentissages Scientifiques; Houdement, C., Hache, C., de Hosson, C., Eds.; ISTE Editions: Paris, France, 2022; pp. 245–280. [Google Scholar]
- Florio, E.; Maierù, L.; Fenaroli, G. The construction of regular polygons between geometry and algebra: A didactic-historical example. Learn. Math. 2020, 40, 23–24. [Google Scholar]
- Florio, E. A Synergy between History of Mathematics and Mathematics Education: A Possible Path from Geometry to Symbolic Algebra. Educ. Sci. 2020, 10, 243. [Google Scholar] [CrossRef]
- Florio, E. The parabola: Section on of a cone or locus of points in of a plane? Tips for teaching of geometry from some writings by Mydorge and Wallis. Mathematics 2022, 10, 974. [Google Scholar] [CrossRef]
- Bussi, M.B.; Mariotti, M.A. Semiotic mediation in the mathematics classroom: Artefacts and signs after a Vygotskian perspective. In Handbook of International Research in Mathematics Education, 2nd ed.; English, L.D., Kirshner, D., Eds.; Routledge, Taylor and Francis: New York, NY, USA, 2008; pp. 746–783. [Google Scholar]
- Arzarello, F.; Ferrara, F.; Robutti, O. Mathematical modelling with technology: The role of dynamic representations. Teach. Math. Appl. 2012, 31, 20–30. [Google Scholar] [CrossRef]
- Arzarello, F.; Robutti, O.; Thomas, M. Growth point and gestures: Looking inside mathematical meaning. Educ. Stud. Math. 2015, 90, 19–37. [Google Scholar] [CrossRef]
- Arzarello, F.; Sabena, C. Analytic-Structural Functions of Gestures in Mathematical Argumentation Processes. In Emerging Perspectives on Gesture and Embodiment; Edwards, L.D., Ferrara, F., Moore-Russo, D., Eds.; Information Age Publishing: Charlotte, NC, USA, 2014; pp. 75–103. [Google Scholar]
- Blum, W.; Leiss, D. How Do Students and Teachers Deal with Mathematical Modelling Problems? The Example Sugaloaf und the DISUM Project. In Mathematical Modelling (ICTMA12)-Education, Engineering and Economics; Haines, C., Galbraith, P.L., Blum, W., Khan, S., Eds.; Horwood: Chichester, UK, 2007. [Google Scholar]
- Stillman, G.A.; Kaiser, G.; Blum, W.; Brown, J.P. Mathematical Modelling: Connecting to Teaching and Research Practices–The Impact of Globalization; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Schukajlow, S.; Kaiser, G.; Stillman, G. Empirical research on teaching and learning of mathematical modelling: A survey on the current state-of-the-art. ZDM 2018, 50, 5–18. [Google Scholar] [CrossRef]
- Radford, L.; Schubring, G.; Seeger, F. Semiotics in Mathematics Education: Epistemology, History, Classroom, and Culture; Sense Publishers: Rotterdam, The Netherlands, 2008. [Google Scholar]
- Sáenz-Ludlow, A.; Kadunz, G. Semiotics as a Tool for Learning Mathematics: How to Describe the Construction, Visualisation, and Communication of Mathematical Concepts; Sense Publishers: Rotterdam, The Netherlands, 2016. [Google Scholar]
- Presmeg, N.; Radford, L.; Roth, M.; Kadunz, G. Signs of Signification. Semiotics in Mathematics Education Research; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Guillemette, D. History of mathematics in secondary school teachers’ training: Towards a nonviolent mathematics education. Educ. Stud. Math. 2017, 96, 349–365. [Google Scholar] [CrossRef]
- Jankvist, U.T.; Clark, K.M.; Mosvold, R. Developing mathematical knowledge for teaching teachers: Potentials of history of mathematics in teacher educator training. J. Math. Teach. Educ. 2020, 23, 311–332. [Google Scholar] [CrossRef]
- Clark, K.M.; Kjeldsen, T.H.; Schorcht, S.; Tzanakis, C. History of Mathematics in Mathematics Education—An Overview. Math. Didact. 2019, 42, 3–28. [Google Scholar]
- Maierù, L. A proposito di Didattica Della Matematica, Un punto di vista; Aracne: Aprilia, Italy, 2020. [Google Scholar]
- Furinghetti, F.; Radford, L. Contrasts and oblique connections between historical conceptual developments and classroom learning in mathematics. In Handbook of International Research in Mathematics Education, 2nd ed.; English, L., Ed.; Routledge, Taylor and Francis: New York, NY, USA, 2009; pp. 626–655. [Google Scholar]
- Frank, A.B.; Zan, R. Avere Successo in Matematica. Strategie per L’inclusione e il Recupero; UTET Università: Torino, Italy, 2017. [Google Scholar]
- Radford, L. Un recorrido a través de la teoría de la objetivación. In Teoria da Objetivação: Fundamentos e Aplicações Para o Ensino e Aprendizagem de Ciências e Matemática; Gobara, S.T., Radford, L., Eds.; Livraria da Física: São Paulo, Brazil, 2020; pp. 15–42. [Google Scholar]
- Bussi, M.G.B.; Maschietto, M.; Turrini, M. Mathematical laboratory in the Italian curriculum: The case of mathematical machines. In Proceedings of the ICMI Study 24 School Mathematica Curriculum Reforms: Challenges, Changes and Opportunities, Tsukuba, Japan, 26–30 November 2018. [Google Scholar]
- Bussi, M.G.B.; Inprasitha, M.; Arzarello, F.; Bass, H.; Kortenkamp, U.; Ladel, S.; Lajoie, C.; Ni, Y.; Rottmann, T.; Sarungi, V.; et al. Aspects that affect whole number learning: Cultural artifacts and mathematical tasks. In Building the Foundation: Whole Numbers in the Primary Grades: The 23rd ICMI Study; Bussi, M.G.B., Sun, X.H., Eds.; Springer: Cham, Switzerland, 2018; pp. 181–226. [Google Scholar]
- Mazzotti, M. The World of Maria Gaetana Agnesi, Mathematician of God; The Johns Hopkins University Press: Baltimore, MD, USA, 2007. [Google Scholar]
- Florio, E. Claude Mydorge Reader and Interpreter of Apollonius’ Conics. Mathematics 2021, 9, 261. [Google Scholar] [CrossRef]
- Roero, C.S.; Luciano, E. L’altra metà del cielo nella scienza italiana dal Settecento al Novecento. Ricerche e studi recenti. Quad. Stor. Fis. 2013, 18, 107–124. [Google Scholar]
- Panza, M. Rethinking geometrical exactness. Hist. Math. 2011, 38, 42–95. [Google Scholar] [CrossRef][Green Version]
- Raggi, A. Macchine Matematiche Dalla Storia Alla Scuola. Percorso in una Secondaria di Secondo Grado. Master’s Thesis, Alma Mater Studiorum Università di Bologna, Bologna, Italy, 2019. [Google Scholar]
- Gallegos, R.R.; Rivera, S.Q. Developing Modelling Competencies Through the Use of Technology. In Mathematical Modelling in Education Research and Practice; Stillman, G.A., Blum, W., Biembengut, M.S., Eds.; Springer: Cham, Switzerland, 2015; pp. 443–452. [Google Scholar]
- Robutti, O. La Formazione Docenti con GeoGebra; Ledizioni: Milano, Italy, 2016. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).