Abstract
Many secondary school students have encountered difficulties when dealing with absolute value equations and inequalities. This condition might be brought to higher education, including by pre-service mathematics teachers in teacher training colleges. The difficulties in dealing with absolute value equations and inequalities, which can be observed from solution strategies, indicate the lack of symbol sense. This study aims to investigate strategies that pre-service teachers used while solving absolute value equations and inequalities from the perspective of symbol sense. To investigate this, we conducted a qualitative case study through two written tests followed by interviews involving 36 pre-service mathematics teachers in one of the state universities in Bandung, Indonesia. The results revealed three different solution strategies for solving either absolute value equations or inequalities. Also, difficulties that occurred during the solution processes of equations and inequalities were addressed. We conclude that the symbol sense characteristics are fruitful for interpreting the selection of solution strategies used by pre-service teachers in solving absolute value equations and inequalities.
1. Introduction
Equations and inequalities are two related fundamental mathematics topics for understanding further study, among others, in algebra, geometry, statistics, and calculus. However, over the globe, most secondary school students have encountered difficulties in dealing with these topics [1,2,3,4], including in Indonesia [5,6]. Among many types, absolute value equations and inequalities are often difficult for school students [1,2]. The condition of encountering difficulties dealing with absolute value equations and inequalities might be brought to higher education, including the case of pre-service secondary mathematics teachers in teacher training colleges [7,8].
Previous research on pre-service teachers’ ability to deal with equations or inequalities as a prerequisite for understanding absolute value equations and inequalities shows similar results. Bicer, Capraro, and Capraro [9] revealed that some pre-service teachers have misconceptions and difficulties in dealing with linear and quadratic inequalities. Serhan and Almeqdadi [10] reported that some pre-service teachers made errors when solving linear inequalities, particularly in representing the solution as an interval and multiplying or dividing by negative numbers. Ozkaya, Ocal, and Konyalioglu [11] found that pre-service teachers encountered difficulties using visual solutions, such as graphs or number lines, when solving inequalities. Research about pre-service teachers’ ability in dealing with absolute value equations and inequalities also shows similar results. For instance, Ali and Wilmot [12] revealed that pre-service teachers faced difficulties in understanding the definition of absolute value and in solving absolute value and quadratic inequalities. In Indonesia, Aziz, Supiat, and Soenarto [13] found that pre-service mathematics teachers struggled with absolute value tasks, including tasks on absolute value equations and inequalities. The difficulties in absolute value tasks include, inter alia, doing algebraic manipulations, removing absolute value bars, drawing absolute value function graphs, and using the definition of absolute value in solving equations and inequalities [13,14].
The difficulties in dealing with algebra problems, which often deal with symbols, indicate the lack of basic skills, which is fundamental for having symbol sense behavior [2,5,13,15,16]. Symbol sense refers to an ability to give meaning to and see important structures in symbols, expressions, equations, and inequalities [17,18]. Characteristics of symbol sense that are relevant to solving absolute value equations or inequalities include the ability to see important structures in symbols, to display generalization, and to do proving; the ability to read through and manipulate equations or inequalities; and the ability to check for the symbol meanings before or after the implementation of a procedure, the solution of a problem, or during the inspection of a result [17,18,19,20].
The lens of symbol sense has been used in previous research, among others, for analyzing student difficulties with the concept of parameter [21], for revealing student algebraic expertise in a digital algebra environment [15], for evaluating algebraic proficiency [20], and for investigating the relationship between graphing formulas by hand and students’ symbol sense [22]. For the current study, the lens of symbol sense was used for analyzing pre-service teachers’ solution strategies in dealing with absolute value equations and inequalities. Taking the above into account, we conducted a qualitative case study that aims to investigate strategies that pre-service teachers used while solving absolute value equations and inequalities from the perspective of symbol sense.
2. Materials and Methods
2.1. Participants
The participants of this qualitative case study included 36 pre-service secondary mathematics teachers (20–21-year-olds), 29 females and 7 males, from one of the state universities in Bandung, Indonesia. They were at the end of the second year of a degree in mathematics education. The participants had studied core mathematics courses for a mathematics education program, such as number theory, calculus, analytical geometry, elementary linear algebra, statistics, and selected topics in school mathematics. The first author taught some of the participants in the selected topics in a school mathematics course, in which absolute value equations and inequalities are addressed within it through conventional or procedural solution strategies. The topics of absolute value equations and inequalities were also taught at secondary school levels in the Indonesian school curriculum. Therefore, the review of these topics in the teacher education program is to refine and deepen pre-service teachers’ conceptual understanding. With this background, we assume that they have sufficient mathematics knowledge to participate in this study.
2.2. Data Collection
To collect data on pre-service mathematics teachers’ strategies in solving absolute value equations and inequalities, we designed two test instruments and a semi-structured interview guideline. The first test instrument concerns the test for assessing the ability to solve absolute value equations, which consists of four types of tasks (shown in Table 1). The second test instrument consists of four types of tasks on absolute value inequalities (Table 2). For each test instrument, based on the tasks’ complexities, the tasks are ordered from easy to a more difficult one. So, for absolute value equations, we predicted that task one is easier than task two, task two is easier than task three, and task three is easier than task four. The direction (exact question) for each task is the same, i.e., “Solve each equation below and show your work! If it is possible, please use one or more other strategies to solve each equation!” Also, for absolute value inequalities, we predicted that task five is easier than task six, task six is easier than task seven, and task seven is easier than task eight. Similarly, the direction (exact question) for each task is the same, i.e., “Solve each inequality below and show your work! If it is possible, please use one or more other strategies to solve each inequality!” The interview guideline provides general non-intervening questions to clarify pre-service teachers’ written work on the results of the two tests, including for detecting symbol sense behavior. The main questions in the interview include, for instance, asking participants to explain their written work, asking participants to provide reasons for their solution strategies, and asking participants whether they read through the equations or inequalities before doing solution processes.

Table 1.
Absolute value equations tasks.

Table 2.
Absolute value inequalities tasks.
The process of data collection was as follows. First, we administered an individual written test on absolute value equations, involving 36 pre-service mathematics teachers, which lasted for 40 min. Next, we administered an individual written test on absolute value inequalities, also involving 36 pre-service mathematics teachers, which lasted for 40 min. The participants were involved voluntarily because the first author has taught some of them in several courses, including geometry and selected topics in school mathematics courses. In each test, even if it was not obligatory, the participants were encouraged to use more than one solution strategy (if possible). We collected the pre-service teachers’ written work from each test via a Google Classroom platform. After the two tests, we interviewed five pre-service teachers to clarify some of their unclear written work from the two tests and provide reasons for their use of specific solution strategies to solve absolute value equations or inequalities. The five participants involved in the interview were selected based on their written work containing various solution strategies for equations and inequalities which represents other participants’ written work.
2.3. Data Analysis
In the data analysis, we analyzed the written work and interview data of pre-service mathematics teachers using the framework of symbol sense. In line with the aims of the study, during data analysis, from various written solution strategies we distinguished three solution strategies for solving absolute value equations, i.e., definition, properties, and graph strategy. By the definition strategy, we mean the strategy of solving absolute value equations using the definition of absolute value. By the properties strategy, we mean the strategy of solving absolute value equations using properties of absolute value expressions. By the graph strategy, we mean the strategy of solving absolute value equations using graphs produced by the pre-service teachers. Interview data, which are transcribed and analyzed using a symbol sense perspective, were used to strengthen or clarify the written work data. The perspective of symbol sense was used to interpret the selection of a particular strategy for solving equations or inequalities, and to interpret the action of verifying whether a particular solution is correct or not.
Similarly, from the analysis of written work, we also distinguished three solution strategies for solving absolute value inequalities, i.e., definition, properties, and graph strategy. By the definition strategy, we mean the strategy of solving absolute value inequalities using the definition of absolute value. By the properties strategy, we mean the strategy of solving absolute value inequalities using properties of absolute value expressions. By the graph strategy, we mean the strategy of solving absolute value inequalities using graphs. For the definition and properties strategies, the use of the number line is apparent during the solution processes. Interview data regarding the inequalities, that were transcribed and analyzed, were also used to strengthen and clarify the written work data.
3. Results
This section presents the results of pre-service teachers’ written work from the two tests and their corresponding interviews. First, we present the findings of the written test on absolute value equations and its corresponding interview results. Next, we present the findings of the written test on absolute value inequalities also with its corresponding interview results.
3.1. Pre-Service Teachers’ Solution Strategies in Solving Absolute Value Equations
Table 3 presents findings from the pre-service teachers’ written work on solving absolute value equations. In general, the number of correct solutions is more than 90%, except for Task 3 (75%). This finding suggests that the pre-service teachers who participated in this study have sufficient skills and conceptual understanding in solving equations. An important finding concerns the three different solution strategies in dealing with absolute value equations, i.e., the definition strategy, properties strategy, and graph strategy.

Table 3.
Results from data analysis of the written test on absolute value equations (n = 36).
We found that the definition strategy was the most frequent solution strategy used by the pre-service teachers for solving absolute value equations, except for Task 2. In Task 2, the properties strategy was used more frequently than the definition strategy because it is more efficient than the latter strategy, as acknowledged by the participants of the interview. The decision to choose the best strategy (the most efficient strategy to solve a particular equation), from a symbol sense perspective, shows the ability to read through the equation before the problem-solving process. As encouraged to use more than one strategy (if possible) during the test, more than one-third of the number of participants used the properties strategy as an addition to the use of the definition strategy. We found that the most frequent strategy emerged showing the first strategy used by the participants, followed subsequently by the less frequent, and the least frequent one. For the graph strategy, even if it is not frequent, it was used by several participants for checking whether the solutions produced by other strategies are correct or not. As revealed in the interview, four interviewees acknowledged that the graph strategy is easier to use to check the correctness of the solutions produced by other strategies. One of the interviewees mentioned that:
“…as encouraged in the direction, I used the graph strategy as an additional strategy for solving absolute value equations. This strategy is visually easier to use and see. Also, it is used for checking whether solutions produced by the definition strategy or properties strategy are correct or not.”
From the response of the interviewee above, we interpret that the use of the graph strategy for solving equations shows the pre-service teachers’ symbol sense ability in which a symbolic algebra expression can be understood meaningfully in a visual manner [22]. The use of the graph strategy shows a meaningful relationship between symbolic algebra and geometry.
To illustrate the above findings, we address the pre-service teachers’ solution strategies for solving absolute value equations from their written work and corresponding interview results for Task 3. A typical definition strategy for solving Task 3 is as follows. Using the definition of the absolute value for the term , a student considers this term in two cases. For the case of , then the equation can be rewritten into , and, as such, it can be concluded that is the solution to the equation. For the case of , then the equation can be rewritten into , which can be simplified into . However, because is beyond the interval , then it is not the solution of the absolute value equation. Regarding this, eight participants incorrectly concluded that is one of the solutions of the absolute value equation. This occurred because it seemed that they did not do the checking process by substituting it into the initial equation. Concerning this, one of the interviewees said that “… often the checking process of the solutions through substitution is not written explicitly, but it is done in the mind! So, sometimes it is forgotten!” The action of checking the correctness of the solution through substitution, to get the feeling of the meaningfulness of the solution process, concerns the characteristics of symbol sense. In this case, symbol sense plays an important role in verifying whether the solution is correct or not in a meaningful manner.
A typical properties strategy for solving Task 3 is as follows. Using the property of absolute value, i.e., for , a student rewrites the equation into . Next, squaring both sides of the equation and doing algebraic manipulation and simplification leads to . This quadratic equation has the solutions or . By substituting each of these solutions to the initial equation, it can be concluded that is the only solution for the absolute value equation in Task 3. The action of verifying the solution through substitution concerns the characteristics of symbol sense in the sense of checking for the symbol meanings after the implementation of a solution procedure. Figure 1 shows representative examples of the pre-service teachers’ written work for Task 3. Figure 1a shows the use of the definition strategy, and Figure 1b shows the use of the properties strategy.

Figure 1.
Representative examples from pre-service teachers’ written work for Task 3 on solving absolute value equation : Part (a) shows the use of the definition strategy; Part (b) shows the use of the properties strategy.
A typical graph strategy for solving Task 3 is as follows. A student draws the graphs for and on the same Cartesian coordinate. The solution of the absolute value equation can be interpreted geometrically as the abscissa of the intersection point(s) of the two graphs. As the intersection point of the two graphs is (5, 9), the solution of the equation is . We view that the ability to interpret the solution of the equation geometrically concerns symbol sense characteristics [22]. Figure 2 presents an example of the use of the graph strategy in solving the absolute value equation .
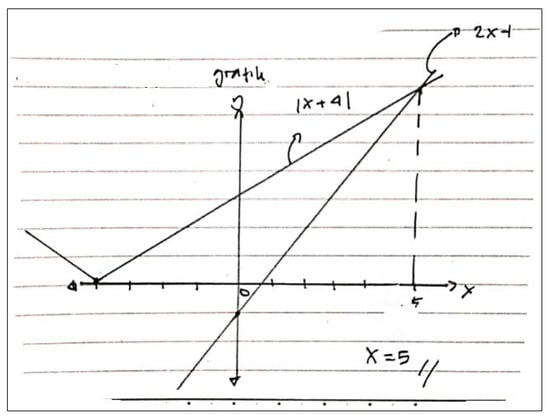
Figure 2.
A representative example from pre-service teachers’ written work for Task 3 on solving the absolute value equation using the graph strategy.
3.2. Pre-Service Teachers’ Solution Strategies in Solving Absolute Value Inequalities
Table 4 summarizes findings from the pre-service teachers’ written work on solving absolute value inequalities. In general, the number of correct solutions is more than 86% for all tasks. This finding indicates that the pre-service mathematics teachers who participated in this study have sufficient algebraic skills and conceptual understanding in solving absolute value inequalities. Similar to the finding on absolute value equations, we found three different solution strategies in dealing with absolute value inequalities, i.e., the definition strategy, properties strategy, and graph strategy.

Table 4.
Results from data analysis of the written test on absolute value inequalities (n = 36).
From the data analysis, we found that the properties strategy was the most frequent solution strategy used by the pre-service teachers for solving absolute value inequalities, except for Task 7. In Task 7, the use of the properties strategy was as frequent as the definition strategy. The use of the definition strategy for Tasks 6 and 8 was less frequent than the use of the graph strategy. Similar to the finding for the case of equations, we also found that the most frequent strategy emerged, that is, the properties strategy, showing the first strategy used by the participants and followed by the less frequent one of the definition strategy. For the graph strategy, even if it was used by one participant for Tasks 5 and 7, it was used by pre-service teachers for checking visually whether the solutions produced by other strategies are correct or not. Similar to the findings for the case of absolute value equations, we consider that the selection of the best solution strategy over other strategies shows the ability to read through and check for symbol meanings, which is the characteristic of symbol sense. In the interview, four interviewees acknowledged that the graph strategy is used to check the correctness of the solutions produced by other strategies.
Regarding the use of different solution strategies, when pre-service teachers were asked whether they consider specific solution strategies, all interviewees acknowledged that they consider possible efficient solution strategies for solving absolute value inequalities before carrying out the solution processes. One of the interviewees said:
“For me, I need to consider first the absolute value inequality to solve. As using the properties strategy seems easier, I use it. If we use the definiton strategy in solving an absolute value inequality, then it would take time, and the solution process would often be lengthy. In this case, often we need to find the intersections of the interval of solutions on the number line. In my opinion, it is not efficient for using the definiton strategy.”
From this interview response, as the definition strategy is not efficient, we consider that the use of this strategy is difficult to use for solving absolute value inequalities. Therefore, we interpret that the selection of a more efficient strategy in the solution process concerns the characteristics of symbol sense ability.
In what follows, we address the pre-service teachers’ solution strategies for solving absolute value inequalities to illustrate the above findings. In this case, we describe pre-service teachers’ written work and corresponding interview results for Task 6. A typical definition strategy used for solving Task 6 is as follows. Using the definition of the absolute value for the terms on both sides of the inequality , a student will end up with three cases of inequality intervals to consider, i.e., , , and . After a quite meticulous process of considering each interval in the solution process, the student will obtain as the solution of the absolute value inequality. Probably because the use of the definition strategy needs accuracy and patience in considering each case of solution intervals, we found three pre-service teachers who used this strategy. The ability to use the definition of absolute value for any absolute value expressions to obtain inequality intervals shows the ability to use basic procedural knowledge and, from the perspective of symbol sense, see important structures in symbols.
A typical properties strategy used by the pre-service teachers is as follows. Using the property of absolute value, i.e., for , a student rewrites the inequality into . Next, squaring both sides of the inequality, doing algebraic manipulation and simplification, leads to . The solution of this quadratic inequality is . Using and applying appropriate properties of absolute value for solving inequalities, in our view, shows not only the skill to use procedural knowledge but also the characteristics of symbol sense, i.e., the ability to see important structures in symbols and to check for the symbol meanings before the implementation of solution strategies. Figure 3 presents representative examples of the written work for Task 6. Figure 3a shows the use of the definition strategy, and Figure 3b shows the use of the properties strategy.

Figure 3.
Representative examples from pre-service teachers’ written work for Task 6 on solving absolute value inequality: Part (a) shows the use of the definition strategy; Part (b) shows the use of the properties strategy.
A typical graph strategy for solving Task 6 is as follows. A student draws the graphs for and on the same Cartesian coordinate. The solution of the absolute value inequality is geometrically interpreted as the interval(s) of values such that the graph is below the graph of . From this graph strategy, it can be obtained that the solution of the inequality is the interval . Figure 4 presents an example of the use of the graph strategy in solving the absolute value inequality . A small number of participants who used this strategy might be caused by the fact that drawing the absolute value function graphs is not easy without using, for instance, graphing software. One of the interviewees said that “Using the graph method is quite easy and practical to see the solution of an absolute value inequality. However, drawing graphs are often difficult without using any mathematical software!” We view that the ability to understand the relationship between the algebraic expressions in the form of inequalities and their corresponding graphs shows a symbol sense behavior [22].
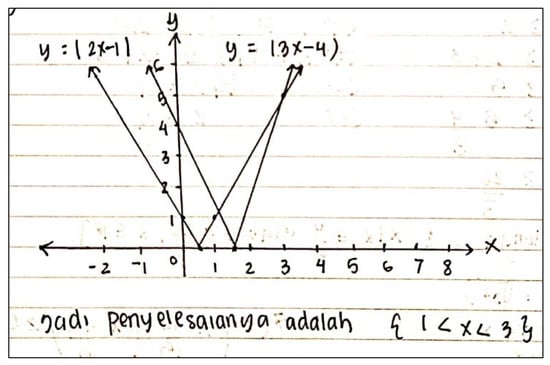
Figure 4.
A representative example from pre-service teachers’ written work for Task 6 on solving absolute value inequality using the graph strategy.
4. Discussion
4.1. Discussion on Absolute Value Equations
Based on the findings described in the previous section, we note several points to discuss concerning pre-service mathematics teachers’ strategies in solving absolute value equations. First, this study found that even if the definition strategy is more frequently used than the properties strategy, the occurrence of these two strategies has little difference. This finding indicates that the pre-service teachers had considered choosing a solution strategy for solving absolute value equations. From the perspective of symbol sense, this means that they are consciously reading through the equations before or during solving problems [17,18,19]. So, choosing a solution strategy to find an effective and efficient solution process is showing symbol sense ability, which shows a relational understanding of the symbols at hand [23]. For future research, it is worth investigating the use of a particular solution strategy over other strategies and the correlation between the correct solution and the use of solution strategies from the perspective of symbol sense.
Second, concerning the use of graph strategy, this study revealed that it is mainly used to check whether the solutions found with other strategies are correct or not. From the perspective of symbol sense, this means that the pre-service teachers realize the need to check the correctness of the symbol meanings during and after the process of solving problems [17,18]. In other research [24,25], this concerns the “looking back” process in problem-solving. Another technique for checking the correctness of the solution of an equation is a substitution technique. This study found that the checking process through substitution is often not written explicitly because this was done in mind after the solution process. The ability to check the meaningfulness of an equation through substitution, from the symbol sense perspective, indicates friendliness with symbols and numbers [17,18,20].
Third, even if more than 90% of pre-service teachers can solve the absolute value equation tasks correctly, we still found some difficulties regarding this topic. In line with other studies [13,26], the difficulties in solving absolute value equations found in this study include determining intervals of solutions based on the definition of absolute value and drawing absolute value function graphs. For future research, these difficulties can be investigated further to obtain a clearer picture of pre-service teachers’ difficulties in solving absolute value equations involving a larger number of participants.
4.2. Discussion on Absolute Value Inequalities
Regarding pre-service mathematics teachers’ strategies in solving absolute value inequalities, we note several points to discuss. First, we found that the properties strategy is the most frequently used by pre-service teachers for solving absolute value inequalities. The definition strategy is the second-most frequent, followed by the graph strategy. The less frequent the emergence of the definition strategy than the properties strategy might be caused by the fact that using the definition strategy has made the solution process often becomes more lengthy and difficult to follow, which, in turn, needs more accuracy and patience. Similar to the finding on absolute value equations, this finding suggests that the pre-service teachers had considered choosing more efficient solution strategies for solving absolute value inequalities. Considerations for choosing the best strategy, from the view of symbol sense, show the ability to read through the inequalities before or during the problem-solving process [17,18]. We consider that exploring the use of a particular solution strategy over other strategies might be an interesting topic for future research.
Second, this study found that even if the graph strategy is often used for checking the solutions which resulted from other strategies, in practice, this strategy is not easy to be implemented. In line with other studies [13,27,28], the difficulties include drawing absolute value function graphs without using graphing software and determining values intervals from the graphs that are satisfying the absolute value inequalities. The difficulties dealing with absolute value function graphs show a lack of symbol sense, i.e., a lack of ability in recognizing function families and graph features from the structure of functions [22,29]. In other studies [30,31], the ability to switch from symbolic algebra to geometrical ideas, showing versatile thinking of different representations, which also shows symbol sense behavior, concerns the ability to intertwine between mathematical topics. Taking this finding into account, we recommend further investigation into the relationship between pre-service teachers’ ability in drawing absolute value function graphs and their symbol sense ability. Also, the provision of graph paper in the answer sheet might invite the use of graph strategy, which is an interesting idea to investigate in the future.
Third, difficulties in using the definition strategy in solving absolute value inequalities, which is similar to the results of other studies [12,13,27], are also in line with the difficulties encountered by pre-service mathematics teachers in learning abstract algebra [32,33]. The difficulties in abstract algebra that show a lack of symbol sense behavior include, for instance, visualizing abstract notions in a group theory [32], and recognizing a binary operation in either familiar or non-familiar structures [33]. We consider that the difficulty encountered by pre-service teachers in abstract algebra may inform future research for the case of school algebra, including for the topic of inequalities.
5. Conclusions
From the results and discussion, we draw the following conclusions. This study revealed three solution strategies for solving absolute value equations and inequalities, i.e., the definition strategy, the properties strategy, and the graph strategy. The selection for using the definition or the properties strategies is based on the structure of the equations or inequalities at hand. The consideration of choosing the best solution strategy, from the perspective of symbol sense, shows the ability to read through symbolic expressions before the problem-solving process. For the practical purpose of mathematics teaching, we consider that the symbol sense ability can be fostered through not only the topics of equations and inequalities, but also other algebra topics, such as the system of equations, composite functions, and polynomials.
The graph strategy is practically often used for checking the solutions of absolute value equations or inequalities produced with other solution strategies. This strategy is visually easy and more meaningful. However, it is in practice difficult to be implemented if absolute value functions are relatively complex, so they are difficult to be drawn by hand without the help of graphing software. Probably, for future research, it is worth investigating the role of the use of graphing software in pre-service teachers’ ability in solving absolute value equations and inequalities. We view that the use of the graph strategy promotes visual and geometric thinking, which is often more meaningful in mind, in dealing with algebra problems.
The difficulties encountered by some of the pre-service mathematics teachers in solving absolute value equations and inequalities, observed from their written work in this study, include determining intervals of variables values when applying the definition strategy; using appropriate properties of absolute value expressions; and determining intersection points of graphs and intervals of variable values satisfying an inequality when applying the graph strategy. Regarding this, in the future, we recommend investigating pre-service teachers’ conceptual understanding of the definition and properties of absolute value expressions.
Overall, regarding solution strategies for solving absolute value equations and inequalities, the symbol sense perspective provides insight into what happened in pre-service teachers’ minds. In particular, this perspective is useful for interpreting pre-service mathematics teachers’ solution strategies, understanding the selection of solution strategies, comprehending the use of the graph strategy, and explaining difficulties encountered during the solution processes.
Author Contributions
Conceptualization, A.J.; methodology, A.J. and D.U.; validation, D.U., S.M.G.; formal analysis, A.J. and S.M.G.; investigation, A.J. and D.U.; resources, A.J. and D.U.; data curation, A.J. and D.U.; writing—original draft preparation, A.J.; writing—review and editing, A.J., D.U. and S.M.G.; project administration, D.U.; funding acquisition, A.J., D.U. and S.M.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Directorate of Research, Technology and Community Service, Directorate General of Higher Education, Research and Technology Ministry of Education, Culture, Research and Technology of the Republic of Indonesia, the year 2022, grant number 1289/UN40.LP/PT.01.03/2022. The APC was funded by the Directorate of Research, Technology and Community Service, Directorate General of Higher Education, Research and Technology Ministry of Education, Culture, Research and Technology of the Republic of Indonesia, the year 2022.
Institutional Review Board Statement
This study, which involved 36 pre-service mathematics teachers (mathematics education students), has been conducted according to the academic ethics that adhere to the rule of the Universitas Pendidikan Indonesia. Approval number: 618/UN40.4.4B/PL/2022.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Acknowledgments
We would like to thank the dean of the Faculty of Mathematics and Science Education, Universitas Pendidikan Indonesia, for permission of this current study. We also thank pre-service mathematics teachers who actively participated in this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tsamir, P.; Almog, N. Student’s strategies and difficulties: The case of algebraic inequalities. Math. Educ. Sci. Technol. 2001, 32, 513–524. [Google Scholar] [CrossRef]
- Almog, N.; Ilany, B.S. Absolute value inequalities: High school students’ solutions and misconceptions. Educ. Stud. Math. 2012, 81, 347–364. [Google Scholar] [CrossRef]
- Verikios, P.; Farmaki, V. From equation to inequality using a function-based approach. Int. J. Math. Educ. Sci. Technol. 2010, 41, 515–530. [Google Scholar] [CrossRef]
- Didis, M.G.; Erbas, A.K. Performance and difficulties of students in formulating and solving quadratic equations with one unknown. Educ. Sci. Theory Pract. 2015, 15, 1137–1150. [Google Scholar] [CrossRef][Green Version]
- Jupri, A.; Drijvers, P.; van den Heuvel-Panhuizen, M. Student difficulties in solving equations from an operational and a structural perspective. Math. Educ. 2014, 9, 39–55. [Google Scholar] [CrossRef]
- Jupri, A.; Sispiyati, R.; Chin, K.E. An investigation of students’ algebraic proficiency from a structure sense perspective. J. Math. Educ. 2021, 12, 147–158. [Google Scholar] [CrossRef]
- Tanisli, D.; Kose, N.Y. Pre-service mathematic teachers’ knowledge of students about the algebraic concepts. Aust. J. Teach. Educ. 2013, 38, 1–18. [Google Scholar] [CrossRef]
- Zapatera, A.; Quevedo, E. The initial algebraic knowledge of preservice teachers. Mathematics 2021, 9, 2117. [Google Scholar] [CrossRef]
- Bicer, A.; Capraro, R.; Capraro, M. Pre-service teachers’ linear and quadratic inequalities understandings. Int. J. Math. Teach. Learn. 2014, 5, 1–10. [Google Scholar]
- Serhan, D.; Almeqdadi, F. Pre-service teachers’ linear inequalities solving strategies and errors. Glob. J. Math. 2015, 6, 580–584. [Google Scholar]
- Ozkaya, M.; Ocal, M.F.; Konyalioglu, A.C. Visualization in solving inequality questions: Case of pre-Service mathematics teachers. J. Educ. Hum. Dev. 2016, 5, 119–137. [Google Scholar] [CrossRef][Green Version]
- Ali, C.A.; Wilmot, E.M. Pre-service teachers’ didactic conceptual structures in the absolute and quadratic inequalities. IOSR J. Math. IOSR JM 2016, 12, 62–69. [Google Scholar] [CrossRef]
- Aziz, T.A.; Supiat, S.; Soenarto, Y. Pre-service secondary mathematics teachers’ understanding of absolute value. J. Cakrawala Pendidik. 2019, 38, 203–214. [Google Scholar] [CrossRef]
- Jupri, A.; Gozali, S.M. Teaching and learning processes for prospective mathematics teachers: The case of absolute value equations. Math. Teach. Res. J. 2021, 13, 142–157. [Google Scholar]
- Bokhove, C.; Drijvers, P. Symbol sense behavior in digital activities. Learn. Math. 2010, 30, 43–49. [Google Scholar]
- Turşucu, S.; Spandaw, J.; de Vries, M.J. Search for symbol sense behavior: Students in upper secondary education solving algebraic physics problems. Res. Sci. Educ. 2020, 50, 2131–2157. [Google Scholar] [CrossRef]
- Arcavi, A. Symbol sense: Informal sense-making in formal mathematics. Learn. Math. 1994, 14, 24–35. [Google Scholar]
- Arcavi, A. Developing and using symbol sense in mathematics. Learn. Math. 2005, 14, 42–47. [Google Scholar]
- Jupri, A.; Sispiyati, R. Students’ algebraic proficiency from the perspective of symbol sense. Indones. J. Sci. Technol. 2020, 5, 86–94. [Google Scholar] [CrossRef]
- van Stiphout, I.; Drijvers, P.; Gravemeijer, K. The development of students’ algebraic proficiency. Int. Electron. J. Math. Educ. 2013, 8, 62–80. [Google Scholar] [CrossRef]
- Drijvers, P. Students encountering obstacles using a CAS. Int. J. Comput. Math. Learn. 2000, 5, 189–209. [Google Scholar] [CrossRef]
- Kop, P.M.; Janssen, F.J.; Drijvers, P.H.; van Driel, J.H. The relation between graphing formulas by hand and students’ symbol sense. Educ. Stud. Math. 2020, 105, 137–161. [Google Scholar] [CrossRef]
- Skemp, R.R. Relational understanding and instrumental understanding. Math. Teach. 1976, 77, 20–26. [Google Scholar]
- Dickman, B. Looking back to support problem solving. Math. Teach. 2016, 110, 54–58. [Google Scholar] [CrossRef]
- Cai, J.; Brook, M. Looking back in problem solving. Math. Teach. Inc. Micromath 2006, 196, 42–45. [Google Scholar]
- Kumari, A. Students’ difficulty with problems involving absolute value, how to tackle this using number line and box method. Math. Teach. Res. J. 2021, 13, 158–166. [Google Scholar]
- Sierpinska, A.; Bobos, G.; Pruncut, A. Teaching absolute value inequalities to mature students. Educ. Stud. Math. 2011, 78, 275–305. [Google Scholar] [CrossRef]
- Switzer, J.M. Graphing inequalities, connecting meaning. Math. Teach. 2014, 107, 580–584. [Google Scholar] [CrossRef]
- Kop, P.M.; Janssen, F.J.; Drijvers, P.H.; van Driel, J.H. Promoting insight into algebraic formulas through graphing by hand. Math. Think. Learn. 2021, 23, 125–144. [Google Scholar] [CrossRef]
- Florio, E. A Synergy between history of mathematics and mathematics education: A possible path from geometry to symbolic algebra. Educ. Sci. 2020, 10, 243. [Google Scholar] [CrossRef]
- Otten, M.; van den Heuvel-Panhuizen, M.; Veldhuis, M.; Boom, J.; Heinze, A. Are physical experiences with the balance model beneficial for students’ algebraic reasoning? An evaluation of two learning environments for linear equations. Educ. Sci. 2020, 10, 163. [Google Scholar] [CrossRef]
- Veith, J.M.; Bitzenbauer, P.; Girnat, B. Exploring learning difficulties in abstract algebra: The case of group theory. Educ. Sci. 2022, 12, 516. [Google Scholar] [CrossRef]
- Novotná, J.; Hoch, M. How structure sense for algebraic expressions or equations is related to structure sense for abstract algebra. Math. Educ. Res. J. 2008, 20, 93–104. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).