The Impact of Teacher Quality on Student Motivation, Achievement, and Persistence in Science and Mathematics
Abstract
1. Introduction
2. Theoretical Frameworks
2.1. Social Cognitive Career Theory (SCCT)
2.2. Teacher Quality Framework (TQF)
3. A Brief Review of Current Literature
3.1. Student Factors and Student STEM Outcomes
3.2. Teacher Factors and Student STEM Outcomes
3.3. Limitations of the Extant Literature
4. Research Questions
- To what extent do math and science teacher quality factors relate to high school students’ motivational beliefs (i.e., self-efficacy, utility, interest) for STEM?
- To what extent do math and science teacher quality factors relate to high school students’ STEM achievement and persistence (i.e., advanced course-taking, mathematics test performance)?
- To what extent do math and science teacher quality factors relate to high school students’ career plans in STEM while controlling for students’ motivational beliefs and achievement in STEM?
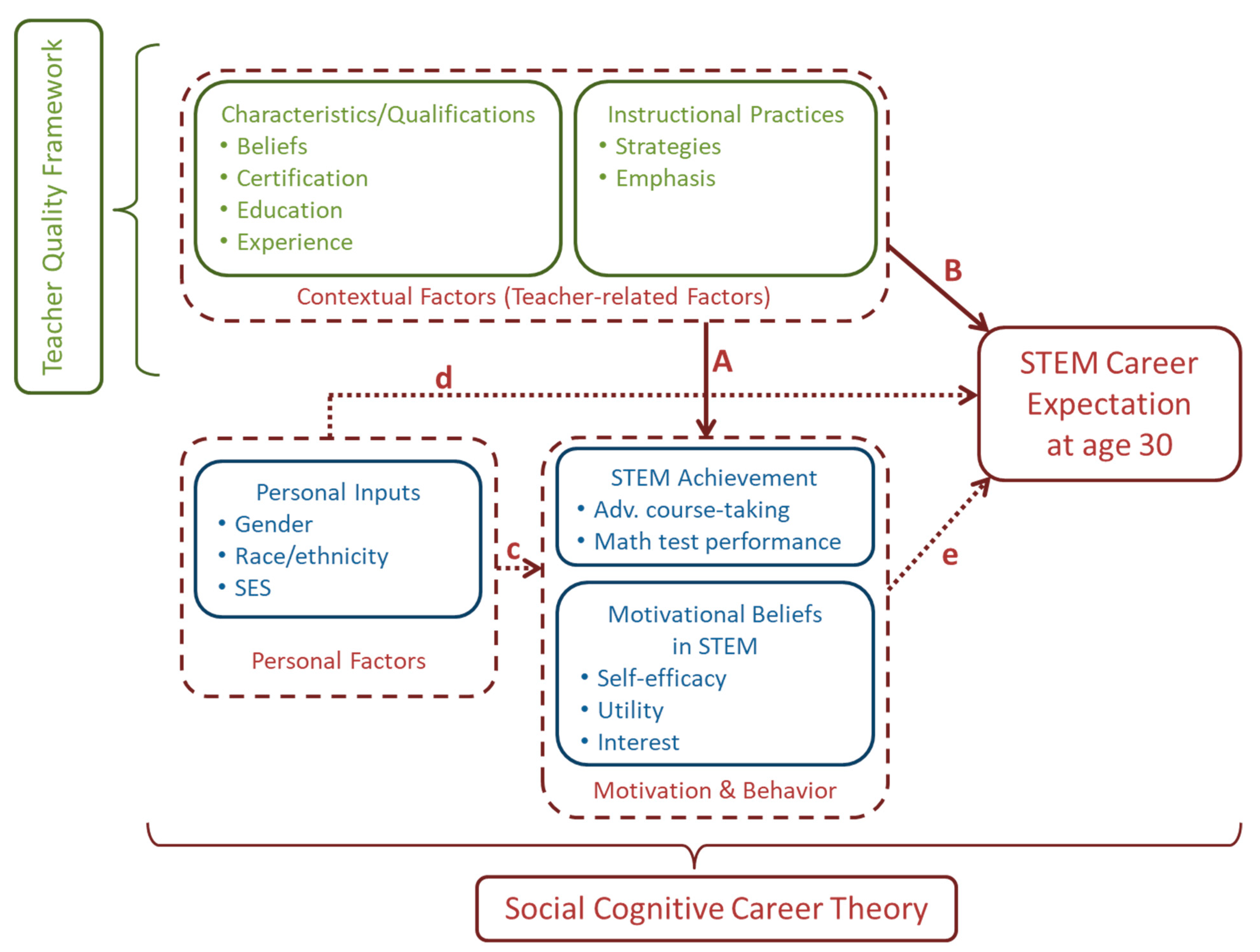
5. Conceptual Framework for the Study
6. Methodology
6.1. Data Set
6.2. Measures
6.2.1. Student Variables
6.2.2. Teacher Variables
6.2.3. Dimension Reduction for Teaching Practices
6.3. Analytic Techniques
7. Results
8. Discussion
8.1. Limitations
8.2. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- National Research Council. Monitoring Progress toward Successful K-12 STEM Education: A Nation Advancing? The National Academies Press: Washington, DC, USA, 2013. [Google Scholar] [CrossRef]
- National Science Board, National Science Foundation. Science and Engineering Indicators 2016 (NSB–2016–1). 2016. Available online: https://www.nsf.gov/statistics/indicators/ (accessed on 12 September 2022).
- National Science Board, National Science Foundation. Science and Engineering Indicators 2018 (NSB-2018-1). 2018. Available online: https://www.nsf.gov/statistics/indicators/ (accessed on 12 September 2022).
- National Science Board, National Science Foundation. Science and Engineering Indicators 2020: The State of U.S. Science and Engineering (NSB-2020-1). 2020. Available online: https://ncses.nsf.gov/pubs/nsb20201 (accessed on 12 September 2022).
- President’s Council of Advisors on Science and Technology. Engage to Excel: Producing One Million Additional College Graduates with Degrees in Science, Technology, Engineering, and Mathematics. 2012. Available online: https://obamawhitehouse.archives.gov/administration/eop/ostp/pcast/docsreports (accessed on 12 September 2022).
- President’s Council of Advisors on Science and Technology. Recommendations for Strengthening American Leadership in Industries of the Future. 2020. Available online: https://science.osti.gov/About/PCAST (accessed on 12 September 2022).
- Xue, Y.; Larson, R.C. STEM Crisis or STEM Surplus? Yes and Yes (U.S. Bureau of Labor Statistics). Monthly Labor Review, May 2015. Available online: https://www.bls.gov/opub/mlr/2015/article/stem-crisis-or-stem-surplus-yes-and-yes.htm (accessed on 12 September 2022).
- U.S. Bureau of Labor Statistics. Employment Projections Program. 1 September 2020. Available online: https://www.bls.gov/emp/tables/stem-employment.htm (accessed on 12 September 2022).
- Alfred, M.V.; Ray, S.M.; Johnson, M.A. Advancing women of color in STEM: An imperative for US global competitiveness. Adv. Dev. Hum. Resour. 2019, 21, 114–132. [Google Scholar] [CrossRef]
- Augustine, N.R. Rising above the Gathering Storm: Energizing and Employing America for a Brighter Economic Future; The National Academies Press: Washington, DC, USA, 2007. [Google Scholar]
- Noonan, R. STEM Jobs: 2017 Update (ESA Issue Brief # 02-17); Office of the Chief Economist, U.S. Department of Commerce: Washington, DC, USA, 2017. Available online: https://www.commerce.gov/sites/default/files/migrated/reports/stem-jobs-2017-update.pdf (accessed on 12 September 2022).
- National Academy of Sciences. Expanding Underrepresented Minority Participation: America’s Science and Technology Talent at the Crossroads; The National Academies Press: Washington, DC, USA, 2011; Available online: http://hdl.voced.edu.au/10707/173219 (accessed on 12 September 2022).
- Chen, X. STEM Attrition: College Students’ Paths into and out of STEM Fields: Statistical Analysis Report (NCES 2014-001); National Center for Education Statistics: Washington, DC, USA, 2013. Available online: https://files.eric.ed.gov/fulltext/ED544470.pdf (accessed on 12 September 2022).
- Paschal, J.; Taggart, A. An examination of the role of first-year college-level mathematics in STEM field major persistence at a Hispanic-Serving Institution. J. Hisp. High. Educ. 2021, 20, 297–312. [Google Scholar] [CrossRef]
- Sass, T.R. Understanding the STEM Pipeline (CALDER #125); American Institutes for Research: Washington, DC, USA, 2015; Available online: http://hdl.voced.edu.au/10707/364347 (accessed on 12 September 2022).
- Winterer, E.R.; Froyd, J.E.; Borrego, M.; Martin, J.P.; Foster, M. Factors influencing the academic success of Latinx students matriculating at 2-year and transferring to 4-year US institutions—Implications for STEM majors: A systematic review of the literature. Int. J. STEM Educ. 2020, 7, 34. [Google Scholar] [CrossRef]
- Dilek, H.; Tasdemir, A.; Konca, A.S.; Baltaci, S. Preschool children’s science motivation and process skills during inquiry-based STEM activities. J. Educ. Sci. Environ. Health 2020, 6, 92–104. [Google Scholar] [CrossRef]
- Eccles, J.S.; Midgley, C.; Wigfield, A.; Buchanan, C.M.; Reuman, D.; Flanagan, C.; Mac Iver, D. Development during adolescence: The impact of stage-environment fit on young adolescents’ experiences in schools and in families. Am. Psychol. 1993, 48, 90–101. [Google Scholar] [CrossRef] [PubMed]
- Graham, M.J.; Frederick, J.; Byars-Winston, A.; Hunter, A.; Handelsman, J. Increasing persistence of college students in STEM. Science 2013, 341, 1455–1456. [Google Scholar] [CrossRef]
- Wang, X. Why students choose STEM majors: Motivation, high school learning, and postsecondary context of support. Am. Educ. Res. J. 2013, 50, 1081–1121. [Google Scholar] [CrossRef]
- Darling-Hammond, L. Teacher quality and student achievement. Educ. Policy Anal. Arch. 2000, 8, 1–44. [Google Scholar] [CrossRef]
- Goe, L. The Link between Teacher Quality and Student Outcomes: A Research Synthesis; National Comprehensive Center for Teacher Quality: Washington, DC, USA, 2007. Available online: http://eric.ed.gov/?id=ED521219 (accessed on 12 September 2022).
- Goe, L.; Stickler, L.M. Teacher Quality and Student Achievement: Making the Most of Recent Research (TQ Research & Policy Brief); National Comprehensive Center for Teacher Quality: Washington, DC, USA, 2008. Available online: http://eric.ed.gov/?id=ED520769 (accessed on 12 September 2022).
- Hansen, M. Characteristics of schools successful in STEM: Evidence from two states’ longitudinal data. J. Educ. Res. 2014, 107, 374–391. [Google Scholar] [CrossRef]
- Muller, C.; Katz, S.R.; Dance, L.J. Investing in teaching and learning dynamics of the teacher-student relationship from each actor’s perspective. Urban Educ. 1999, 34, 292–337. [Google Scholar] [CrossRef]
- Schleicher, A. (Ed.) Preparing Teachers and Developing School Leaders for the 21st Century: Lessons from around the World; OECD Publishing: Mexico City, Mexico, 2012. [Google Scholar] [CrossRef]
- Ackerman, P.L.; Kanfer, R.; Calderwood, C. High school Advanced Placement and student performance in college: STEM majors, non-STEM majors, and gender differences. Teach. Coll. Rec. 2013, 115, 1–43. [Google Scholar] [CrossRef]
- Ingels, S.J.; Pratt, D.J.; Herget, D.R.; Dever, J.A.; Fritch, L.B.; Ottem, R.; Rogers, J.E.; Wilson, D. The High School Longitudinal Study of 2009 (HSLS: 09): 2013 Update and High School Transcript (NCES 2015-036); National Center for Education Statistics: Washington, DC, USA, 2015. Available online: https://nces.ed.gov/pubsearch/pubsinfo.asp?pubid=2015036 (accessed on 12 September 2022).
- Ingels, S.J.; Dalton, B.; Holder Jr, T.E.; Lauff, E.; Burns, L.J. The High School Longitudinal Study of 2009 (HSLS: 09): A First Look at Fall 2009 Ninth-Graders; NCES 2011–327; National Center for Education Statistics: Washington, DC, USA, 2011. Available online: https://nces.ed.gov/pubsearch/pubsinfo.asp?pubid=2011327 (accessed on 12 September 2022).
- Ingels, S.J.; Pratt, D.J.; Herget, D.R.; Dever, J.A.; Fritch, L.B.; Ottem, R.; Rogers, J.E.; Kitmitto, S.; Leinwand, S. The High School Longitudinal Study of 2009 (HSLS: 09): Base Year to First Follow-Up Data File Documentation (NCES 2014-361); National Center for Education Statistics: Washington, DC, USA, 2013. Available online: https://nces.ed.gov/pubsearch/pubsinfo.asp?pubid=2014361 (accessed on 12 September 2022).
- Lent, R.W.; Brown, S.D.; Hackett, G. Toward a unifying social cognitive theory of career and academic interest, choice, and performance. J. Vocat. Behav. 1994, 45, 79–122. [Google Scholar] [CrossRef]
- Hattie, J. Teachers Make a Difference, What Is the Research Evidence? Australian Council for Educational Research: Washington, DC, USA, 2003; Available online: http://research.acer.edu.au/research_conference_2003/4/ (accessed on 12 September 2022).
- Hattie, J.; Masters, D.; Birch, K. Visible Learning into Action: International Case Studies of Impact; Routledge: London, UK, 2016. [Google Scholar]
- Bandura, A. Social Foundations of Thought and Action: A Social Cognitive Theory; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1986. [Google Scholar]
- Ekmekci, A.; Sahin, A.; Waxman, H. Factors affecting students’ STEM choice and persistence: A synthesis of research and findings from the second year of a longitudinal high school STEM tracking study. In STEM Education 2.0: Myths and Truths: What Has Years of K-12 STEM Education Research Taught Us? Sahin, A., Mohr-Schroeder, M., Eds.; Brill: Leiden, The Netherlands, 2019; pp. 279–304. [Google Scholar]
- Yu, S.L.; Corkin, D.M.; Martin, J.P. STEM motivation and persistence among underrepresented minority students: A social cognitive perspective. In Race and Ethnicity in the Study of Motivation in Education; DeCuir-Gunby, J.T., Schutz, P.A., Eds.; Taylor & Francis: Abingdon, UK, 2016; pp. 67–81. [Google Scholar] [CrossRef]
- Eccles, J.S.; Wigfield, A. Motivational beliefs, values, and goals. Annu. Rev. Psychol. 2002, 53, 109–132. [Google Scholar] [CrossRef] [PubMed]
- Lent, R.W.; Brown, S.D. On conceptualizing and assessing social cognitive constructs in career research: A measurement guide. J. Career Assess. 2006, 14, 12–35. [Google Scholar] [CrossRef]
- Andersen, L.; Ward, T.J. Expectancy-value models for the STEM persistence plans of ninth-grade, high-ability Students: A comparison between Black, Hispanic, and White students. Sci. Educ. 2014, 98, 216–242. [Google Scholar] [CrossRef]
- Lee, S.W.; Min, S.; Mamerow, G.P. Pygmalion in the classroom and the home: Expectation’s role in the pipeline to STEMM. Teach. Coll. Rec. 2015, 117, 1–36. [Google Scholar] [CrossRef]
- Lent, R.W.; Brown, S.D. Social cognitive approach to career development: An overview. Career Dev. Q. 1996, 44, 310–321. [Google Scholar] [CrossRef]
- Navarro, R.L.; Flores, L.Y.; Worthington, R.L. Mexican American middle school students’ goal intentions in mathematics and science: A test of Social Cognitive Career Theory. J. Couns. Psychol. 2007, 54, 320–335. [Google Scholar] [CrossRef]
- Nye, B.; Konstantopoulos, S.; Hedges, L.V. How large are teacher effects? Educ. Eval. Policy Anal. 2004, 26, 237–257. [Google Scholar] [CrossRef]
- Hanushek, E.A. The economics of schooling: Production and efficiency in public schools. J. Econ. Lit. 1986, 24, 1141–1177. [Google Scholar]
- Rowan, B.R.; Correnti, R.; Miller, R.J. What large-scale survey research tells us about teacher effects on student achievement: Insights from the Prospects study of elementary schools. Teach. Coll. Rec. 2002, 104, 1525–1567. [Google Scholar] [CrossRef]
- Barnett, W.S. Better Teachers, Better Preschools: Student Achievement Linked to Teacher Qualifications; Rutgers National Institute for Early Education Research: Philadelphia, PA, USA, 2003. Available online: http://files.eric.ed.gov/fulltext/ED480818.pdf (accessed on 12 September 2022).
- Hill, J.G.; Dalton, B. Student math achievement and out-of-field teaching. Educ. Res. 2013, 42, 403–405. [Google Scholar] [CrossRef]
- National Council on Teacher Quality. Increasing the Odds: How Good Policies Can Yield Better Teachers. 2004. Available online: https://www.nctq.org/publications/home (accessed on 12 September 2022).
- Rice, J.K. Teacher Quality: Understanding the Effectiveness of Teacher Attributes; Economic Policy Institute: Washington, DC, USA, 2003. [Google Scholar]
- Goe, L.; Biggers, K.; Croft, A. Linking Teacher Evaluation to Professional Development: Focusing on Improving Teaching and Learning (Research Policy Brief); National Comprehensive Center for Teacher Quality: 2012. Available online: http://eric.ed.gov/?id=ED532775 (accessed on 12 September 2022).
- Ingersoll, R. A Comparative Study of Teacher Preparation and Qualifications in Six Nations; (CPRE RB-47); Consortium for Policy Research in Education: Philadelphia, PA, USA, 2007. [Google Scholar] [CrossRef]
- Rice, J.K. The Impact of Teacher Experience: Examining the Evidence and Policy Implications (Brief No. 11). National Center for Analysis of Longitudinal Data in Education Research. 2010. Available online: https://eric.ed.gov/?id=ED511988 (accessed on 12 September 2022).
- Zuzovsky, R. Teachers’ qualifications and their impact on student achievement: Findings from TIMSS 2003 data for Israel. IERI Monogr. Series. Issues Methodol. Large-Scale Assess. 2009, 2, 37–62. [Google Scholar]
- Blanton, L.P.; Sindelar, P.T.; Correa, V.I. Models and measures of beginning teacher quality. J. Spec. Educ. 2006, 40, 115–127. [Google Scholar] [CrossRef]
- Hanushek, E.A.; Kain, J.F.; O’Brien, D.M.; Rivkin, S.G. The Market for Teacher Quality; (No. w11154); National Bureau of Economic Research: Cambridge, MA, USA, 2006. [Google Scholar] [CrossRef]
- Sanders, W.L.; Horn, S.P. The Tennessee value-added assessment system (TVAAS): Mixed-model methodology in educational assessment. J. Pers. Eval. Educ. 1994, 8, 299–311. [Google Scholar] [CrossRef]
- American Educational Research Association. AERA statement on use of value-added models (VAM) for the evaluation of educators and educator preparation programs. Educ. Res. 2015, 44, 448–452. [Google Scholar] [CrossRef]
- Darling-Hammond, L. Research on teaching and teacher education and its influences on policy and practice. Educ. Res. 2016, 45, 83–91. [Google Scholar] [CrossRef]
- Hill, H.C.; Kapitula, L.; Umland, K. A validity argument approach to evaluating teacher value-added scores. Am. Educ. Res. J. 2011, 48, 794–831. [Google Scholar] [CrossRef]
- Klees, S.J. VAMs Are Never “Accurate, Reliable, and Valid”. Educ. Res. 2016, 45, 267. [Google Scholar] [CrossRef]
- Kupermintz, H. Teacher effects and teacher effectiveness: A validity investigation of the Tennessee Value Added Assessment System. Educ. Eval. Policy Anal. 2003, 25, 287–298. [Google Scholar] [CrossRef]
- Maltese, A.V.; Tai, R.H. Pipeline persistence: Examining the association of educational experiences with earned degrees in STEM among US students. Sci. Educ. 2011, 95, 877–907. [Google Scholar] [CrossRef]
- Howard, K.A.; Carlstrom, A.H.; Katz, A.D.; Chew, A.Y.; Ray, G.C.; Laine, L.; Caulum, D. Career aspirations of youth: Untangling race/ethnicity, SES, and gender. J. Vocat. Behav. 2011, 79, 98–109. [Google Scholar] [CrossRef]
- Riegle-Crumb, C.; Peng, M. Examining high school students’ gendered beliefs about math: Predictors and implications for choice of stem college majors. Sociol. Educ. 2021, 94, 227–248. [Google Scholar] [CrossRef]
- Jiang, S.; Simpkins, S.D.; Eccles, J.S. Individuals’ math and science motivation and their subsequent STEM choices and achievement in high school and college: A longitudinal study of gender and college generation status differences. Dev. Psychol. 2020, 56, 2137–2151. [Google Scholar] [CrossRef] [PubMed]
- Ehrenberg, R.G. Analyzing the factors that influence persistence rates in STEM field, majors: Introduction to the symposium. Econ. Educ. Rev. 2010, 29, 888–891. [Google Scholar] [CrossRef]
- Museus, S.D.; Palmer, R.T.; Davis, R.J.; Maramba, D.C. Racial and ethnic minority students’ success in STEM education. ASHE High. Educ. Rep. 2011, 36, 1–140. [Google Scholar] [CrossRef]
- Gottfried, M.A.; Williams, D. STEM club participation and STEM schooling outcomes. Educ. Policy Anal. Arch. 2013, 21, 1–27. [Google Scholar] [CrossRef]
- Riegle-Crumb, C.; Farkas, G.; Muller, C. The role of gender and friendship in advanced course taking. Sociol. Educ. 2006, 79, 206–228. [Google Scholar] [CrossRef]
- Gottlieb, J.J. STEM career aspirations in Black, Hispanic, and White ninth-grade students. J. Res. Sci. Teach. 2018, 55, 1365–1392. [Google Scholar] [CrossRef]
- Green, A.; Sanderson, D. The roots of STEM achievement: An analysis of persistence and attainment in STEM majors. Am. Econ. 2018, 63, 79–93. [Google Scholar] [CrossRef]
- Tai, R.H.; Liu, C.Q.; Maltese, A.V.; Fan, X. Planning early for careers in science. Science 2006, 312, 1143–1144. [Google Scholar] [CrossRef] [PubMed]
- Serrano Corkin, D.M.; Ekmekci, A.; Coleman, S. Navigating the challenges of student-centered mathematics teaching in an urban context. Urban Rev. 2019, 51, 370–403. [Google Scholar] [CrossRef]
- Wayne, A.J.; Youngs, P. Teacher characteristics and student achievement gains: A review. Rev. Educ. Res. 2019, 73, 89–122. [Google Scholar] [CrossRef]
- Lubienski, S.T.; Lubienski, C.; Crane, C.C. Achievement differences and school type: The role of school climate, teacher certification, and instruction. Am. J. Educ. 2008, 115, 97–138. [Google Scholar] [CrossRef]
- Hill, H.C.; Umland, K.; Litke, E.; Kapitula, L.R. Teacher quality and quality teaching: Examining the relationship of a teacher assessment to practice. Am. J. Educ. 2012, 118, 489–519. [Google Scholar] [CrossRef]
- Philipp, R.A. Mathematics teachers’ beliefs and affect. In Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics; Lester, F.K., Ed.; IAP: Reston, VA, USA, 2007. [Google Scholar]
- Aaronson, D.; Barrow, L.; Sander, W. Teachers and student achievement in the Chicago public high schools. J. Labor Econ. 2007, 25, 95–135. [Google Scholar] [CrossRef]
- Heck, R.H. Examining the relationship between teacher quality as an organizational property of schools and students’ achievement and growth rates. Educ. Adm. Q. 2007, 43, 399–432. [Google Scholar] [CrossRef]
- Stewart, J.; Rhoads, C.; Serdiouk, M.; Van Dine, D.; Cherasaro, T.; Klute, M. Associations between the Qualifications of Middle School Algebra-I Teachers and Student Math Achievement; (REL 2020-005); Regional Educational Laboratory Central: Washington, DC, USA, 2019. [Google Scholar]
- Yu, R.; Singh, K. Teacher support, instructional practices, student motivation, and mathematics achievement in high school. J. Educ. Res. 2018, 111, 81–94. [Google Scholar] [CrossRef]
- National Council of Teachers of Mathematics. Principles to Actions: Ensuring Mathematical Success for All; National Council of Teachers of Mathematics: Reston, VA, USA, 2014. [Google Scholar]
- Vekiri, I. Information science instruction and changes in girls’ and boy’s expectancy and value beliefs: In search of gender-equitable pedagogical practices. Comput. Educ. 2013, 64, 104–115. [Google Scholar] [CrossRef]
- Morrell, P.D.; Park Rogers, M.A.; Pyle, E.J.; Roehrig, G.; Veal, W.R. Preparing teachers of science for 2020 and beyond: Highlighting changes to the NSTA/ASTE Standards for Science Teacher Preparation. J. Sci. Teach. Educ. 2020, 31, 1–7. [Google Scholar] [CrossRef]
- NGSS Lead States. Next Generation Science Standards: For States, by States; The National Academies Press: Washington, DC, USA, 2013. [Google Scholar]
- Meyers, L.S.; Gamst, G.; Guarino, A.J. Applied Multivariate Research: Design and Interpretation, 3rd ed.; Sage: Newcastle upon Tyne, UK, 2017. [Google Scholar]
- Ekmekci, A.; Corkin, D. The influence of science teachers on high school students’ science motivation: An analysis using a nationally representative large-scale data set. In Proceedings of Society for Information Technology & Teacher Education International Conference (ISBN 978-1-939797-37-7); Graziano, K., Ed.; Association for the Advancement of Computing in Education: Las Vegas, NV, USA, 2019; pp. 2267–2272. [Google Scholar]
- Corkin, D.; Ekmekci, A. The impact of mathematics teachers on student learning and motivation. In Proceedings of the 46th Annual Meeting of the Research Council on Mathematics Learning; Redmond-Sanogo, A., Cribbs, J., Eds.; Research Council on Mathematics Learning: Charlotte, NC, USA, 2019; pp. 34–41. [Google Scholar]
- Riegle-Crumb, C.; King, B.; Irizarry, Y. Does STEM stand out? Examining racial/ethnic gaps in persistence across postsecondary fields. Educ. Res. 2019, 48, 133–144. [Google Scholar] [CrossRef]
- Stipek, D.J.; Givvin, K.B.; Salmon, J.M.; MacGyvers, V.L. Teachers’ beliefs and practices related to mathematics instruction. Teach. Teach. Educ. 2001, 17, 213–226. [Google Scholar] [CrossRef]
- Crisp, G.; Nora, A.; Taggart, A. Student characteristics, pre-college, college, and environmental factors as predictors of majoring in and earning a STEM degree: An analysis of students attending a Hispanic serving institution. Am. Educ. Res. J. 2009, 46, 924–942. [Google Scholar] [CrossRef]
- Sirin, S.R. Socioeconomic status and academic achievement: A meta-analytic review of research. Rev. Educ. Res. 2005, 75, 417–453. [Google Scholar] [CrossRef]
- Holland, P.W. Statistics and causal inference. J. Am. Stat. Assoc. 1986, 81, 945–960. [Google Scholar] [CrossRef]
- Schneider, B.; Carnoy, M.; Kilpatrick, J.; Schmidt, W.H.; Shavelson, R.J. Estimating Causal Effects Using Experimental and Observational Designs; American Educational Research Association: Washington, DC, USA, 2007. [Google Scholar]
- Stuart, E.A. Estimating causal effects using school-level data sets. Educ. Res. 2007, 36, 187–198. [Google Scholar] [CrossRef]
- Schmidt, W.H.; McKnight, C.C.; Houang, R.T.; Wang, H.; Wiley, D.E.; Cogan, L.S.; Wolfe, R.G. Why Schools Matter: A Cross-National Comparison of Curriculum and Learning; Jossey-Bass: San Francisco, CA, USA, 2001. [Google Scholar]
- Rosenbaum, P.R.; Rubin, D.B. The central role of the propensity score in observational studies for causal effects. Biometrika 1983, 70, 41–55. [Google Scholar] [CrossRef]
- Lesh, R.; Doerr, H. (Eds.) Beyond Constructivism: A Models Modeling Perspective on Mathematics Teaching, Learning, and Problems Solving; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 2003. [Google Scholar]
- O’Shea, J.; Leavy, A.M. Teaching mathematical problem-solving from an emergent constructivist perspective: The experiences of Irish primary teachers. J. Math. Teach. Educ. 2013, 16, 293–318. [Google Scholar] [CrossRef]
| Items | Factor Loading | |
|---|---|---|
| Math Understand | Math Connect | |
| M1concepts | 0.74 | −0.01 |
| M1problem | 0.56 | 0.13 |
| M1reason | 0.57 | 0.10 |
| M1ideas | 0.69 | 0.21 |
| M1prepare | 0.63 | 0.08 |
| M1logic | 0.58 | 0.04 |
| M1interest | −0.07 | 0.71 |
| M1history | 0.03 | 0.82 |
| M1explain | 0.25 | 0.67 |
| M1business | 0.09 | 0.69 |
| M1algorithm | 0.14 | -0.01 |
| M1compskills | −0.02 | 0.07 |
| M1compute | 0.03 | 0.13 |
| M1test | −0.07 | 0.12 |
| Items | Factor Loading | |
|---|---|---|
| Science Inquiry | Science Connect | |
| N1skills | 0.59 | 0.03 |
| N1prepare | 0.58 | −0.06 |
| N1evidence | 0.63 | 0.11 |
| N1ideas | 0.69 | 0.07 |
| N1interest | 0.12 | 0.71 |
| N1business | −0.08 | 0.83 |
| N1society | 0.09 | 0.58 |
| N1history | 0.03 | 0.64 |
| N1concepts | 0.13 | 0.09 |
| N1terms | 0.10 | −0.06 |
| N1test | 0.08 | 0.01 |
| Mathematics b | Science c | |||||
|---|---|---|---|---|---|---|
| Variable | Self-Efficacy | Utility | Interest | Self-Efficacy | Utility | Interest |
| β | β | β | β | β | β | |
| Male | 0.10 *** | 0.04 *** | 0.01 | 0.09 *** | -0.02 * | 0.02 |
| Black | 0.07 *** | 0.07 *** | 0.04 * | 0.03 * | 0.04 ** | 0.01 |
| Asian | 0.06 *** | 0.08 *** | 0.11 *** | −0.00 | 0.11 *** | 0.05 *** |
| Hispanic | 0.05 *** | 0.05 *** | 0.08 *** | −0.03 * | −0.01 | −0.03 |
| SES | 0.14 *** | 0.03 * | 0.10 *** | 0.10 *** | 0.07 *** | 0.05 *** |
| Teacher self-efficacy a | 0.03 ** | −0.01 | 0.02 | 0.01 | 0.00 | −0.00 |
| Teacher certification a | 0.01 | −0.01 | 0.01 | −0.01 | −0.02 * | −0.01 |
| Teacher degree a | 0.00 | −0.01 | −0.01 | 0.01 | 0.02 | 0.03 * |
| Teacher experience a | 0.01 | 0.01 | 0.02 | 0.00 | 0.01 | 0.01 |
| Understand (math) | 0.04 ** | 0.00 | 0.03 * | - | - | - |
| Connection (math) | 0.01 | 0.03 * | 0.02 | - | - | - |
| Inquiry (science) | - | - | - | 0.03 * | 0.02 | 0.01 |
| Connection (science) | - | - | - | −0.01 | 0.03 * | 0.01 |
| R-square | 0.04 *** | 0.01 *** | 0.03 *** | 0.02 | 0.02 *** | 0.01 |
| n | 8534 | 8604 | 7363 | 7809 | 7918 | 6244 |
| Variable | Achievement a |
|---|---|
| β | |
| Male | 0.00 |
| Black | −0.09 *** |
| Asian | 0.14 *** |
| Hispanic | −0.02 * |
| SES | 0.39 *** |
| Math teacher self-efficacy | 0.01 |
| Math teacher certification | 0.03 ** |
| Math teacher degree in math | 0.02 |
| Math teacher experience | 0.06 *** |
| Understand (math) | 0.14 *** |
| Connection (math) | −0.03 ** |
| R-square | 0.25 *** |
| Variable | Advanced Math Course-Taking b | Advanced Science Course-Taking |
|---|---|---|
| Exp(β) | Exp(β) | |
| Male | 1.28 *** | 1.14 * |
| Black | 1.17 | 1.18 |
| Asian | 1.58 *** | 2.22 *** |
| Hispanic | 0.96 | 0.95 |
| SES | 0.97 | 1.25 *** |
| Teacher self-efficacy a | 0.99 | 1.02 |
| Teacher certification a | 1.11 | 0.86 |
| Teacher degree a | 1.00 | 1.15 * |
| Teacher experience a | 1.02 *** | 1.01 * |
| Understand (math) | 1.51 ** | - |
| Connection (math) | 1.03 | - |
| Inquiry (science) | - | 1.08 |
| Connection (science) | - | 1.06 |
| Pseudo R-square | 0.02 *** | 0.03 *** |
| Variable | STEM Career Plans Math Predictors | STEM Career Plans Science Predictors |
|---|---|---|
| Exp (β) | Exp (β) | |
| Male | 0.67 *** | 0.60 *** |
| Black | 0.97 | 0.96 |
| Asian | 1.54 *** | 1.55 *** |
| Hispanic | 1.20 | 1.07 |
| SES | 1.09 | 1.16 ** |
| Math self-efficacy | 1.13 * | - |
| Math interest | 1.21 *** | - |
| Math achievement | 1.02 *** | - |
| Math advanced course-taking | 1.08 | - |
| Science self-efficacy | - | 1.16 ** |
| Science interest | - | 1.23 *** |
| Science advanced course-taking | - | 1.59 *** |
| Teacher self-efficacy a | 0.93 | 0.93 |
| Teacher certification a | 1.00 | 0.88 |
| Teacher degree a | 1.05 | 0.88 |
| Teacher experience a | 1.01 | 1.01 |
| Understand (math) | 0.78 | - |
| Connection (math) | 1.13 | - |
| Inquiry (science) | - | 1.10 |
| Connection (science) | - | 1.13 |
| Pseudo R-square | 0.05 *** | 0.05 *** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ekmekci, A.; Serrano, D.M. The Impact of Teacher Quality on Student Motivation, Achievement, and Persistence in Science and Mathematics. Educ. Sci. 2022, 12, 649. https://doi.org/10.3390/educsci12100649
Ekmekci A, Serrano DM. The Impact of Teacher Quality on Student Motivation, Achievement, and Persistence in Science and Mathematics. Education Sciences. 2022; 12(10):649. https://doi.org/10.3390/educsci12100649
Chicago/Turabian StyleEkmekci, Adem, and Danya Marie Serrano. 2022. "The Impact of Teacher Quality on Student Motivation, Achievement, and Persistence in Science and Mathematics" Education Sciences 12, no. 10: 649. https://doi.org/10.3390/educsci12100649
APA StyleEkmekci, A., & Serrano, D. M. (2022). The Impact of Teacher Quality on Student Motivation, Achievement, and Persistence in Science and Mathematics. Education Sciences, 12(10), 649. https://doi.org/10.3390/educsci12100649






