1. Introduction
In the last decade, a growing body of research has foregrounded teachers’ professional noticing as an important aspect of teacher professional learning. This notion, according to Philipp et al. [
1], differs from constructs such as beliefs and knowledge in the sense that it is “an interactive, practice-based process rather than a category of cognitive resource” (p. 465). What teachers notice before, during, and after instruction, how they make sense of their observations, and the ways they choose to respond to things observed are of high importance for decision-making and supporting learners in the moment [
2,
3,
4,
5]. The development of professional noticing is an important aspect of becoming and being a teacher. An issue for teacher education is that student teachers too readily default to seeing learning in the formal ways and places that they themselves were taught. For mathematics education in particular, this default to the formal obscures the importance of contexts beyond the classroom—the actual contexts where mathematics come to life.
This paper is built on the argument that pre-service skills for observing, identifying, and understanding pedagogy should not only be cultivated within the formal contexts of the university lecture theatre or the practice-placement classroom, but also beyond, in contexts that we later explain as ‘non-formal’. As discussed below, much research has focused on teachers’ noticing within the mathematics classroom; however, what teachers notice outside this setting is also important to their growing understanding of mathematics pedagogy. In the following sections, we turn our attention to how the current literature informs our thinking, followed by the specificities of the current study (research question, methodology, and findings). In closing, we discuss the contribution of our work to initial teacher education, with particular reference to implications for mathematics teacher education and suggestions on how research in the field could be moved forward.
2. On Teachers’ Professional Noticing
Teachers’ professional noticing is often seen as a specialised form of Goodwin’s [
6] notion of professional vision. For Goodwin, professional vision “consists of socially organized ways of seeing and understanding events that are answerable to the distinctive interests of a particular social group” (p. 606). Nevertheless, as far as mathematics teachers as professionals are concerned, varied conceptualisations of noticing appear. For example, van Es and Sherin [
7] describe noticing in relation to important classroom events, arguing that there are three key aspects in such a process: (a) identifying what is important and noteworthy about a classroom interaction; (b) making connections between the specifics of classroom interactions and the broader principles of teaching and learning; (c) using what one knows about the context to reason about classroom interactions. Others, such as Jacobs et al. [
8], follow more narrowed-down perspectives and associate the notion with noticing children’s mathematical thinking, which they describe as a set of three interrelated skills: (a) attending to children’s strategies; (b) interpreting children’s mathematical understanding; (c) deciding how to respond on the basis of children’s understandings. In this paper, our understanding of teachers’ professional noticing is closer to that of van Es and Sherin [
7], as we are interested in noticing from a broader perspective, with pupils’ mathematical thinking being one part of what a teacher may notice. Besides, where one turns their attention “depends on what one is looking for”, making it “difficult, if not impossible, to precisely delineate which aspect of classrooms are the ‘right’ things to notice and which are the ‘wrong’ things to notice” [
9] (p. 122).
To talk about teachers’ noticing, there are two main questions that need to be addressed. The first is concerned with what one may notice, related to what Sherin and van Es [
10] call selective attention. This may include issues such as the people involved (teacher and pupils) and more specific topics (e.g., issues of pedagogy, climate, content). From this perspective, Star and Strickland [
9] identify five aspects of a mathematics classroom: the environment (the physical setting of the classroom), issues of management (the ways a teacher deals with disruptive events and the teacher’s physical presence), tasks (the activities pupils do during the class period), mathematical content (representations, examples, problems), and communication (pupil–pupil and teacher–pupil talk). In a similar categorisation, Ding and Dominguez [
11] talk about teachers’ actions and/or decisions, pupils’ behaviour and/or learning, mathematical content, and pupils’ multiple mathematical knowledge bases (i.e., pupils’ mathematical thinking, and community, cultural, and linguistic knowledge funds). In other studies [
12,
13], the issues of power and participation, whether equal opportunities are provided to all learners regardless of their background, are addressed.
The second question that needs to be addressed regards how one notices or, in other words, the ways in which one reasons about what they chose to focus on. This is closer to what Sherin and van Es [
10] call knowledge-based reasoning. A common pattern in several published papers is concern with the extent to which teachers justify what they observe, usually ranging from mere description/documentation of events to taking highly analytical positions regarding interpretation and theorisation. For example, Mason [
3] looks at two approaches on how teachers account important events. The first, accounting of, aims at documenting phenomena without interpretation, judgement, or evaluation, while the second, accounting for, involves explanation and interpretation. In a similar vein, in their Learning to Notice Framework, van Es and Sherin [
7] describe pre-service teachers’ development of noticing skills as a trajectory of four levels: level 1 is predominantly descriptive; level 2 contains a mixture of descriptive, evaluative, and analytic chunks, or incomplete analytic chunks; level 3 includes pronominally analytic chucks with a few judgmental statements; level 4 is based on complete analytic chunks with teachers making explicit connections among callouts and evidence, and identifying pedagogical solutions. Similar approaches in identifying levels of criticality in teachers’ noticing paths in the form of trajectories or teacher profiles are employed in other studies as well [
14,
15,
16].
In the mathematics teacher education literature, studies involving both pre- and in-service teachers elaborate on a number of activities designed to help participants develop their noticing skills. Video analysis of one’s own teaching or the teaching of others appears to be the most prevalent approach, and can take place in different ways, such as analysis of lessons recorded for Lesson Study purposes [
17], participation in video clubs [
10,
18], and analysis of full-length classroom videos [
19] or of video vignettes [
2,
11,
20]. Other activities include analysis of animations [
21,
22,
23], technology-aided interventions [
24], reflection on teaching rehearsals [
25], examination of real pupils’ written responses to mathematical tasks [
26,
27], or combinations of different mediums mentioned above [
28]. Clearly, all these attempts are important in supporting participating pre- and in-service teachers in the development of their noticing skills, as they all report, to some extent, success in doing so. Nevertheless, we want to point out that these studies are concerned with mathematics teaching and learning in the classroom context. This may generate or maintain the misleading view among prospective teachers that mathematics learning is something that happens exclusively within schools. This does not necessarily help teachers, especially prospective teachers and novices, to appreciate mathematics learning as an activity that can take place in environments outside schools such as pupils’ homes and communities [
29,
30], through outdoor learning activities [
31], museums and historical sites [
32], or, in certain cases and specific contexts, children’s involvement in vending activities [
33].
3. Learning beyond Formal Environments
Before we proceed, we want to turn our attention to the literature on different learning environments, which has helped frame this paper. The origins of these discussions date back to the work of Coombs and Ahmed [
34], who, in advocating for more integrated rural development, introduced the terms formal, non-formal, and informal education. These terms have been widely discussed in the educational research literature for many years [
35,
36,
37]. Formal settings, such as school classrooms, are typically highly structured and employ various forms of assessment to measure outcomes. Non-formal settings concern learning outside formal settings, yet with some kind of organizational structure. Sports clubs, educational programs of museums, and reading groups constitute some examples. Finally, informal learning takes place outside formal or non-formal settings, as a result of learners’ involvement in activities not undertaken for meeting any specific learning intentions. Of course, drawing strict lines between these learning environments is not possible, as elements of each are included in the others. For example, in a classroom, both the “stated curriculum of the teacher and the school” and “the more subtle informal learning associated with how the classroom is organized, the rules by which it operates, and the knowledge transmitted among peers” [
35] (p. 162) are involved.
Learning in non-formal and informal settings has been widely examined in the field of science [
38] or, more recently, STEM education in its broader sense [
39]. Teacher education in relation to each of the STEM subjects can have many benefits from experiences in non-formal settings [
40,
41] such as supporting prospective and in-service teachers in understanding, valuing, and utilising pupils’ funds of knowledge and learning which takes place outside the formal classroom context. Acknowledging (a) the important role of teacher education in the development of teachers’ professional noticing, (b) how learning can take place in different formal, non-formal, and informal environments, and (c) the lack of research examining teachers’ noticing in non-formal settings, this paper poses the following research question: what do prospective primary teachers notice when pupils are provided with mathematics learning opportunities in non-formal environments?
While we consider how teachers notice to be equally important, in this paper, we focus on what they notice or, in Sherin’s and van Es’ [
10] terminology, the selective attention of prospective teachers when children interact with mathematics in settings other than the classroom.
4. This Study
This paper draws on our involvement as teacher educators organising a Mathematics Fair, during which undergraduate students in primary education and primary school pupils participated. We use the terms students and pupils in a British-English fashion: “students” refers to undergraduates (prospective teachers), and pupils refers to primary school children. The Fair took place as part of the activities of a compulsory mathematics teaching methods module. Throughout the semester, students were involved in several activities designed to help them develop their professional noticing skills in the formal learning of classrooms, such as video analysis, animation analysis, analysis of real learners’ written responses, and conversations. By organising a Mathematics Fair, we were, inter alia, interested in examining whether noticing skills developed through activities concerned with formal learning of the classroom would be transferred to non-formal learning environments.
4.1. The Mathematics Fair
Students worked in pairs and developed interactive mathematical games for upper-primary pupils (age 9–11). In one seminar, students presented their draft ideas in small groups and received feedback from their peers and seminar tutors on how to improve their ideas and maximise their games’ pedagogical benefits and mathematics learning opportunities. Subsequently, a Mathematics Fair was organised at the University towards the second half of the autumn semester 2019. Many papers in science education report research related to Science Fairs [
42,
43,
44,
45]. While fairs (also called carnivals) are often used in mathematics teacher education, they are, with a few exemptions [
46,
47], rarely reported in published academic research.
Invitations were sent to local primary schools, and three replied positively. Also, two mathematics/numeracy coordinators from one of the Regional Improvement Collaboratives (RICs) attended the Fair, discussed with students, and provided some valuable feedback/comments on the spot (for more about RICs, see the website of the Scottish Parliament,
https://spice-spotlight.scot/2020/01/06/rics/ Accessed on 18 December 2021). During the Fair, tutors from the University were present and made sure that different groups of children visited each game. As observed by the accompanying teachers, the university students, and this paper’s authors, the children interacted with all games enthusiastically. In
Figure 1,
Figure 2,
Figure 3 and
Figure 4, we present four examples of games designed by students. After each figure, we present a description of the game, as included in the respective student’s essay (Anna for
Figure 1; David for
Figure 2; Sandra for
Figure 3; Jenny for
Figure 4).
TMMW was designed to consolidate prior knowledge and can also be used as an assessment tool. The purpose of TMMW was to enable pupils to gain a deeper understanding of the links between equivalent forms of the mathematical areas; fractions, decimals and percentages. To play, the pair must spin the wheel and then work co-operatively to answer as many questions corresponding to the given emoji, in the set time of four minutes. Additionally, there is a bonus question which if answered correctly adds five points to their score. This question is a worded problem and aims to be more challenging. The winning pair will be those who get the most points by the end of the fair. (from Anna’s reflective essay)
The product we created (…) required students to work—individually or in small teams—to form patterns using given concrete materials from an envelope of their choice, which covered a variety of curricular areas. A mixture of fractions, decimals, geometrical shapes, geometrical concepts such as perimeter and complex number sequences including squared and prime numbers were mixed up in their sets to be subsequently ordered. Pupils were then given opportunities to explain their thinking processes and reasoning for their sequence to demonstrate understanding. (from David’s reflective essay)
Students have to work together as detectives to analyse clues and evidence given to solve the mystery. Pupils are instructed to roll a dice to move along the board game in order to receive new clues and evidence. With each piece of evidence, pupils can eliminate suspects until they are left with their prime suspect. During the process, students are encouraged to take notes like a detective would and use their knowledge and understanding of time ‘to solve the crime’. The purpose of our game was to promote the learning and development of time while also building pupils problem solving skills. We also aimed for pupils to work together to analyse the evidence and to all contribute to group success. The main intentions behind the theme and design of our game was to create a role-playing experience to motivate and engage learners and make children’s experiences more meaningful in a real-life context. (from Sandra’s reflective essay)
The game was designed to be played in pairs or a group of three where the children aimed to build a sequence bridge (cardboard with numbers ranging from 1 to 37) across the crocodile infested lagoon to reach the treasure chest. My partner and I captured pupil’s interest by exclaiming that we had a problem and needed them to help us. We then gave them a choice of tasks ranging in difficulty level which asked them to continue a pattern or fill in the ‘planks’ to complete the bridge. Although, the tasks had different levels of difficulty they were all based on triangle numbers, square numbers, Fibonacci or multiples to comply with the benchmarks. (from Jenny’s reflective essay)
4.2. Participants, Data Collection and Analysis
Sixty-four (64) third-year undergraduate students in primary education attended the mathematics teaching methods and pedagogy module and, therefore, took part in the Fair. While students were not explicitly introduced to the noticing literature per se, they were involved in noticing-related activities throughout the semester, including video analysis of lessons, teaching rehearsals, and analysis of pupils’ written responses and solutions to specific tasks. Fifty-four students identified as female and ten as male. The average age of the students was 22. The previous year, all participants attended another compulsory module coordinated by the first author, focusing on mathematical content knowledge for primary schools. Furthermore, in their second year of studies, all participants attended two semester-long modules (in autumn and in spring) on general pedagogy and learning/teaching theories and methods. In this paper, for confidentiality reasons, pseudonyms are used to maintain students’ anonymity.
Data were collected through the summative assignment for this module. Students were required to write an individual reflective essay of 1500 words, discussing issues from their participation in the Fair and, whenever appropriate, making links to relevant academic literature. Reflection is a tool often used for examining teacher noticing, especially in regard to teaching rehearsals [
25]. Here, we use this tool in a slightly different manner. The essay topic was given to students from the beginning of the semester so that, during the Fair, they would be particularly observant and keep notes of key incidents. They were submitted one week after students’ participation in the Fair, in order to draw on fresh memories, observations, and their notes from the Fair. We are fully aware that noticing in-the-moment, “the process of noticing while it is occurring” [
48] (p. 80), is extremely challenging, as teachers often tell us what and how “they think they noticed” (ibid.). To increase the opportunities for students to capture their own noticing in-the-moment, and to counter the issue of subjective memory, students developed their games in pairs. This meant that, at the Fair, each time pupils visited a pair’s game, one student would act as the teacher/guide/facilitator, while the other would observe and take notes. Subsequently, students would swap roles.
Taking into account that (a) the setting of this study was a non-formal learning environment (sharing similarities and differences to a typical mathematics classroom) and, (b) to the best of our knowledge, given that no previous studies have investigated what teachers notice when mathematics learning opportunities are provided outside the classroom, we decided not to employ pre-determined coding schemes such as those developed by other researchers and reported in their papers. Our analysis approach was data-driven [
49,
50] and can be labelled as exploratory, as it aims at mapping and understanding a phenomenon, as well as developing hypotheses for further studies [
51]. The process of moving from open to axial coding [
52,
53] yielded four general themes, which we present in the next pages. Namely, these are: the task, learning, teaching, and the non-formal learning environment.
In presenting our findings below, we are not particularly interested in quantitative measures (i.e., frequencies, percentages, number of respondents) for our themes. In fact, we adopt a phenomenographic approach. By taking a second-order perspective, mapping people’s experiences and attempting to see the world through the eyes of those experiencing it [
54], phenomenography explores variation in the ways a phenomenon is perceived by a group of people [
55,
56]. In this work, we focus on the variation in issues noticed by our participants related to the non-formal learning environment under scrutiny. Hence, we looked at a range of noticing experiences and related events, features, and dimensions to contribute to our understanding of noticing of prospective teachers in different learning environments.
4.3. Ethical Considerations
Following the British Educational Research Association’s [
57] guidelines, student consent to use their essays for research purposes was sought after their final grades had been released. Students were asked to fill in an online form and indicate whether they agreed to have quotes from their essays be presented. Thirty of them signed the form, while the remaining 34 students were informed that their essays would be used for analysis purposes but quotes from their essays would not be shown in this paper or elsewhere.
5. Findings
This section is structured around four themes concerning what students noticed before, during, and after the Fair: the task; learning; teaching; the non-formal learning environment. Readers are reminded that, in their essays, students were asked to make connections between their observations and the literature. Therefore, it should be noted that any references quoted in the students’ essays are not included in our reference list. Also, misuses of references in students’ quotes were not rectified. Below, we focus on mapping the variation in the themes noticed by students, keeping our discussion and links to the literature for the next section.
5.1. The Task
The task itself constituted a major part of what all students noticed and reflected upon. Attention was drawn to different aspects of the task, such as (a) aims and purposes, (b) content, and (c) the adaptive potential of the task and improvements that could be made.
5.1.1. Aims & Purposes
In their essays, students discussed issues related to the overall learning objective of the game. They made links between their game and curriculum documents, such as the learning Experiences & Outcomes (Es & Os) and/or Benchmarks of the Scottish Curriculum (Curriculum for Excellence—CfE), and described how the task was aligned with these (for more information:
https://education.gov.scot/nih/Documents/NumeracyandMathematicsBenchmarks.pdf Accessed on 18 December 2021). The excerpt from Rachel’s work, below, was similar to those found in almost all essays. Rachel linked the general objectives of the game to the CfE, and drew on the literature to talk about the challenges children face when learning fractions:
The mathematical game created for the fair was aimed at the Curriculum for Excellence’s second level numeracy benchmarks for fractions, decimal fractions and percentages emphasising the MNU-2-07A benchmark. “I have investigated the everyday contexts in which simple fractions, percentages or decimal fractions are used and can carry out the necessary calculations to solve related problems” (Benchmarks, 2017). As this benchmark is large the game created focusses on fractions but contains elements of decimals fractions and percentages in some of the questioning. This specific element of the curriculum was chosen as pupils often have difficulties with fractions due to a lack of conceptual understanding, as they are unable to understand that properties of whole numbers are not always like other numbers (Fazio and Sieglar 2011) therefore the activity is an exciting way to aid pupils understanding on the topic.
Many, such as Charles, talked about the importance of including “a real-life scenario to the game due to the importance of being able to apply mathematical knowledge to the world”. Retrospectively, most students noticed that their designed game and task were not “suitable for introducing new mathematical concepts, however, it worked well as a consolidation activity” (Lorraine) or could be used as a formative assessment tool.
5.1.2. Content
Students attended to content-related aspects of the task such as general information about game rules and the mathematical content involved (e.g., mathematical concepts and/or procedures). As far as game rules are concerned, all students provided very detailed descriptions. In fact, based on our observations during the Fair, students were particularly careful in communicating rules and instructions to pupils as accurately as possible. Regina’s example, below, is typical and provides readers a brief, yet accurate description of the game:
Two groups of two work against each other in order to get the most questions correct. The questions come from each child throwing a ping-pong ball into a cup on the opposite side of the table. The pair work together to multiply the two numbers written on the disc within a time limit. Once the number has been used, a black card covers the cup so it can’t be used a second time. The children have two hint cards and an extra time card if they find questions challenging and require extra support. If the game results in a tie, there are real-life scenario questions to find a winner. Children have whiteboards, pens and counters which they can use to assist them when working out solutions.
Contrary to the detailed descriptions of the game rules by all students, very few of them explored the mathematical content involved or used mathematics-specific terminology to talk about their games. Nevertheless, those who did made attempts to bring in academic literature about the mathematical concepts that the task was based on. Sandra’s game, for instance, “Time Detectives” (
Figure 3), was based on time intervals. In her essay, Sandra discussed her game in relation to academic resources on the relevant concept:
Newell (2017) underlines the importance of activities that emphasise time intervals in teaching time. Using comparison and mental calculations are the most common methods of estimating intervals of time, therefore these were the methods applied in “Time Detectives” (Mooney et al. 2007). The children were provided with notebooks to note down any difficult calculations. As time is measured in non-metric units (Haylock 2006) it is an area of mathematics that requires adequate teaching time.
5.1.3. The Adaptive Potential of the Game & Improvements
All students noticed and commented on technical and/or pedagogical aspects of the task that could be improved. Technical improvements were the most common ones, and concerned issues such as the order of activities and the quality or design features of materials used. A typical comment is that of Justine, who wrote that “[m]aking the cards bigger and clearer would be first priority. For children with additional support needs, a clearer and more accessible concrete material would have made the game more approachable and user friendly”.
Some students made suggestions regarding changes that could improve the pedagogical and learning potential of the game. Even though these comments were less frequent than those regarding technical improvements, students who attended to those offered elaborate accounts. For example, Kyla commented on a potential improvement idea as she observed uneven participation in the game whilst using a collaborative learning approach:
If we used this game again, we would work more towards encouraging independence. Boaler (2006) gives several examples of how teachers “nurtured a feeling of responsibility… through the assessment system”, and I particularly like the “strategy of asking one member of a group to give an answer and an explanation, without help from his or her group-mates” to promote a sense of responsibility in students of their own and others’ learning.
A small number of students discussed how their game could be adapted for use with other mathematical concepts and/or procedures. Lisa was one example. Her game involved multiplication of integers. In her essay, she said “the game is easily adaptable to use numbers that suit all mathematical abilities and can be used across different mathematical concepts including addition, subtraction, division, fractions or decimals”.
5.2. Learning
In discussing issues related to pupils and how they interacted with the task or with their peers, students made a number of observations. The issues noticed correspond to different dimensions of learning: (a) the affective, (b) the cognitive, and (c) the social.
5.2.1. Affective Dimensions
One common topic explored across essays concerned pupils’ affective reactions, such as a (lack of) enjoyment and excitement, engagement, motivation, anxiety, and so on. Pupils’ excitement was widely discussed in most essays. This can be illustrated in Eliza’s quote: “Firstly, all children were excited and engaged because of the focus on active learning. Hopkins (2008) claims that children of all ages enjoy hands-on learning and learning becomes more valuable for children when they have opportunities to engage physically”.
Some students made task-specific observations, particularly related to the mathematical content. Kiara’s game, for example, involved measuring time with the use of an analogue clock:
Research has shown that several pupils have a fear of the clock; often struggling to focus on the questions, which negatively impacts upon their mathematical development (Faust et al., 1996). This was clear during the fair as pupils displayed signs of pressure.
The majority of students observed that pupils brought their own mathematics-related beliefs and attitudes to the Fair, such as Lorna, who commented on a child saying “I don’t like fractions”. Similarly, Evelyn wrote:
Some children vocalised concern in their abilities, expressing, “I’m bad at maths” or “I’m no good”. According to Grootenboer & Marshman (2016), a lack of confidence in maths can be detrimental to students and has a direct correlation with mathematical achievement, therefore, something must be done to increase the confidence of children within the game.
5.2.2. Cognitive Dimensions
Students noticed and discussed several issues related to the cognitive dimensions of learning. These include, inter alia, pupils’ cognitive development, preference towards specific representations, mathematical thinking (e.g., reasoning processes), mental engagement (e.g., paying attention), and the role of prior knowledge. Not knowing pupils prior to the Fair, most students focused on the variation in cognitive abilities among children. In her response, which was similar to others, Barbara said “[t]he children who participated in the fair had a wide range of abilities: some were capable with more challenging, second level maths whilst others seemed to be transitioning from first level into second”. For this reason, many students highlighted the importance of children’s prior knowledge in relation to their tasks. As Evelyn wrote:
During the game, I observed some students who were confident in explaining rules of patterns, however, for some pupils this only seemed to be the case when prior knowledge had been activated. When less confident learners were faced with a brand-new concept (for example, prime numbers) the conversations seemed to be ‘answer-getting’ rather than developing a deeper understanding.
Students described a range of strategies employed by different pupils to reach an answer. For example, Clara noticed that:
Some pupils would use their fingers connecting to concrete materials. Others could be seen breaking down the numbers to their tens and units; lastly, some would round up or down and then add or minus the remainders they used to complete the number to tens or up to the figure of the five times table.
5.2.3. Social Dimensions
Most games required pupils to work in pairs or small groups, either to solve something together or to compete against another team. As a result, in some essays, the ways that pupils collaborated and communicated with peers were explored. Specifically, students attended to pupil participation as a result of collaboration with peers, peer support in both cognitive and affective issues, the sharing of ideas, and communication. In this respect, some students agreed that “pupils working together showed greater confidence than the individuals who worked themselves” (Lena) and “performed better as they had extra support from their peers” (Nina). Others complemented that working in pairs or groups “promotes inclusive practice as all children will be able to participate” (Regina).
As far as affective issues of collaboration are concerned, Eliza wrote:
[T]he decision for children to work in pairs was successful because each pair had a shared outcome, which seemed less daunting than playing individually and it allowed competent and confident mathematicians to work collaboratively and explain their thinking with others (Stahl 1994, p. 4).
Rose, in turn, focused on cognitive aspects of collaboration, such as peer support in developing conceptual understanding of the mathematical content involved:
[W]orking in pairs allowed for discussion and for children to support each other. This is good because it is proposed that all learning occurs from social interactions with others where assistance is being provided. […] It also allows children to use language within the game, such as this decimal is bigger than that decimal. If this game was used in a classroom where you knew children’s abilities, this social support would be more effective as you could pair a ‘novice’ with an ‘expert’. This will scaffold the learner that is not as confident allowing both children to succeed in the task (Vygotsky, 1978).
Contrary to the students who discussed positive aspects of collaboration, some noticed that collaboration is not always effective, especially when issues of power dynamics are involved. For example, Kyla commented that “[a]s groups came up, often there was a student who was more confident in their mathematical ability, and they would take charge of the game” leaving little space to peers to express their views and contribute to teamwork.
Some of the students made observations which were concerned with pupil–pupil communication. As Ashley wrote in her essay, “I also felt that giving children time to investigate the clues and evidence together as a team helped build their communication skills with each other, share their thinking out loud and support one another’s learning”. Similarly, Charles commented on the composition of groups, arguing that there was better communication between children who came to the game already grouped with friends rather than individuals who had to form random groups:
When observing the learners throwing the ball or solving the equation it was noted that those who were in a pair with a friend performed better than those who weren’t. This observation agrees with Edward and Jones (2003), as the learners were able to communicate better and perform tactically if they were in a pair with their friend.
5.3. Teaching and Pedagogy
Another common theme across students’ essays regarded teaching and the teachers’ role, as well as general pedagogy. This operated in two ways, with students reflecting on (a) themselves as prospective teachers and (b) pedagogy in a broader sense. It should be noted, though, that most teaching-related references concerned the latter, as fewer references were explicitly directed to the students themselves.
5.3.1. The Self as a Mathematics Teacher
A small number of students reflected on their own beliefs and attitudes, knowledge, and teaching skills. For most, the Fair was an enjoyable event; “[C]reating the game and taking part in the maths fair was enlightening and enjoyable” (Sandra); “[T]he fair itself was something which I personally enjoyed” (Emily); “[it] provided me with inspiration from my peers for future maths lessons” (Julia). Others made more detailed comments on how this experience helped them develop their confidence as prospective teachers. In Karen’s words,
I believe the experience of the mathematics fair has allowed me to develop my knowledge and understanding of how pupils can interact with multiplication in an enjoyable and meaningful way, along with some of the challenges that can be faced.
Furthermore, the Fair provided opportunities for some students to reflect on and re-evaluate their own beliefs, knowledge, and practices. Ruth, for example, noticed that her questioning strategies and communication skills needed further development:
I felt I was not able to make best use of dialogic teaching and questioning during the activity due to my limited knowledge of teaching techniques. To resolve this, I would expand my readings more, and, by using different techniques in the activity, challenge my own beliefs about problem-solving and therefore effect the learning which takes place (Xenofontos et al. 2012).
5.3.2. General Pedagogy
Throughout the essays, students made links between their observations and general learning theories, topics, and concepts, such as collaborative learning, differentiation, assessment for learning, and so on. The quotes presented under this sub-theme may correspond to other themes as well, and could have been given multiple codes during the analysis process. Nevertheless, even though students may not have always written about teachers and/or teaching explicitly, we present this sub-theme here, as we believe that the underlying ideas of these quotes allude to general pedagogical theories and practices teachers employ in their professional lives. Below, we present some quotes that implicitly or explicitly refer to broader pedagogical ideas.
A number of students made observations related to play-based learning as an effective approach for raising pupils’ motivation in learning mathematics. Ashley, for example, wrote:
Pupils expressed how they found this method of learning a fun and interesting way to explore mathematical concepts, in comparison to alternative teaching strategies they have experienced. Listening to and interacting with the pupils has allowed me to see how using games can foster positive attitudes towards learning mathematics and has encouraged me to consider the implications in the classroom for my future pupils.
Collaborative learning, differentiation, and assessment strategies were other popular topics discussed in many essays. Particular references to differentiation were made by all students. Below is one such example by James:
The structure of our game, progressing in difficulty as the game went on was an excellent differentiation strategy. My partner and I were able to use observation and use formative assessment techniques to determine whether the two students playing the game would be capable of the later, more difficult rounds.
5.4. The Non-Formal Learning Environment
This final theme concerns the Fair itself and students’ remarks about the benefits and limitations of learning mathematics in a non-formal environment. Very few explicit references addressed this theme. According to Linda, the Fair was “a valuable learning experience that replicated scenarios that may occur in the classroom where intuition/flexibility need to come into play”. In a more critical spirit, Karen argued that the Fair provided her with opportunities “to reflect on mathematics outside the typical classroom environment”. She continued by writing that the setting of the Fair outside school made children less anxious and increased their enjoyment:
Some pupils expressed how they did not enjoy mathematics as a subject at school but enjoyed the afternoon of playing games at the fair as they were less nervous to take part in the learning. A study by Offenholley (2012) concurs that learning mathematics through games can decrease maths anxiety.
One of the students, Lorna, saw the non-formal character of the event as problematic. Having experienced some difficulties with the layout of the materials during the Fair, she commented that:
If this had been a normal lesson within a classroom environment it would have had much more of an impact on the children’s learning. Classroom layout is a key factor in education, and it not only affects children’s learning, but their behaviour too (Martin, 2006).
6. Discussion
The following section is organised in three sub-sections. In the first, we discuss how the Mathematics Fair as a non-formal learning environment provided opportunities for prospective teachers to notice several important aspects of the learning process. We move on by discussing key points from our findings, locating these in the wider noticing literature. In the final sub-section, we turn our attention to the implications of our work in mathematics teacher education and provide some ideas on how future research could move forward before reiterating the contribution and significance of this study.
6.1. Opportunities for Professional Noticing
As discussed earlier, the international mathematics education literature provides multiple examples of research programmes and activities aiming at developing pre- and in-service teachers’ professional noticing skills [
10,
18]. Nevertheless, all documented attempts are concerned with the formal classroom environment, either with participants analysing and reflecting on their own teaching [
17] or by observing others [
20]. The research reported here refers to a non-formal learning environment, a Mathematics Fair, designed to complement the formal system [
58]. Our intention is to unpack opportunities provided for prospective primary teachers to develop their noticing skills, within the mathematics classroom and beyond. This is important for the elevation of the quality of mathematics teaching through exploring different pedagogical strategies, collaborating with peers, and eventually improving the process of noticing in different contexts. We remind readers that this paper is based on a broad understanding of teachers’ professional noticing, in line with the work of van Es and Sherin [
7], who talk about identification, analyses, and response to important classroom situations or interactions. Informed by the work of Star and Strickland [
9], who argue that there is no standard answer to what one considers noteworthy and what one notices in an interaction/situation, we decided to broaden van Es’ and Sherin’s [
7] definition by referring to learning instead of classroom interactions/situations. Besides, in the work reported here, learning interactions/situations took place outside classrooms, but will ultimately foster pupils’ learning within the formal classroom settings.
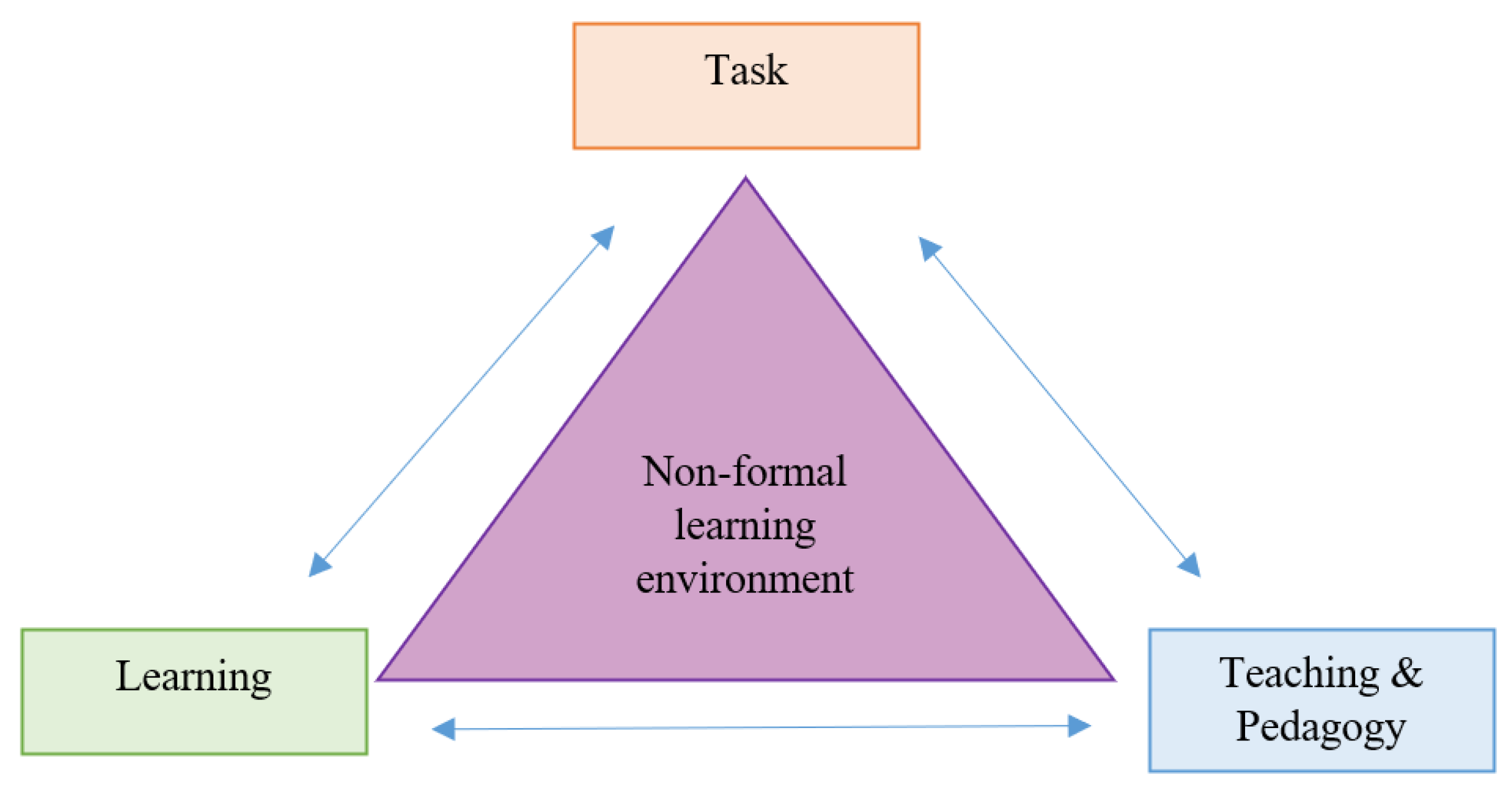
Our four identified themes, which correspond to what participants in this study considered noteworthy of reporting, may form a slightly adapted version of the well-known (in the educational research literature) pedagogical/didactic triangle (see
Figure 5). Even though we are aware that some colleagues consider this triangle to be narrow and problematic [
59], we believe that this schematic representation of our findings is quite accurate. We are aware there are no clear boundaries between the components of the triangle presented. For example, it is not always easy to talk about learning without referring to teaching as well, and vice versa [
60]. Similarly, drawing lines between task design, learning, teaching, and the non-formal learning environment is neither productive nor the purpose here. Yet, we consider these themes important in providing guidelines as to what one could potentially notice when mathematics-learning opportunities are taken outside classrooms, in non-formal settings.
Students in this study noticed important interactions/situations related to the task itself, pupils and learning, and teaching and pedagogy, as well as the particularities of non-formal learning environments. Even though not all themes were discussed by all students (certainly not to the same extent by everyone),
Figure 5 illustrates a mapping of the variation in different things noticed, in a phenomenographic manner [
54,
55,
56]. In this sense, we claim, the Mathematics Fair as a non-formal learning environment was successful in providing opportunities for students to notice similar issues as those reported in studies concerned with formal settings. Furthermore, it provided a platform for students to explore mathematics learning beyond formal education. As teacher educators, we are aware of many challenges which ourselves and colleagues around the world face concerning, inter alia, finding the balance between theory and practice in ITE programmes, developing effective partnerships with schools, and mentoring [
61]. Acknowledging the above, there are several reasons for which we consider the non-formal context of the Fair an important complementary activity in the development of prospective teachers’ noticing skills, especially when colleagues such as Sherin et al. [
48] call for more targeted attempts to promote noticing in-the-moment. Firstly, our students worked in pairs, switching roles between teacher-observers and researcher-observers. Secondly, within the duration of the event, they observed relatively large numbers of children working on the same activity, something that is not always possible in the context of the classroom. Thirdly, students received feedback on-the-spot from different people: each other, university tutors, teachers accompanying pupils, the mathematics/numeracy coordinators from RIC, and children. Formal classroom settings do not easily provide such opportunities. However, the particular nature of the organised event did not allow students to notice and report on issues such as classroom management, which we see in other published work [
9,
11]. It is, therefore, important for teacher educators to reflect on these themes and consider non-formal learning environments as spaces for professional noticing, as it has rarely been the focus of mathematics teacher education.
6.2. What Students Particularly Noticed
As already mentioned, the purpose of this paper is not to “quantify” what was noticed by students; instead, we aimed at mapping a range of events, features, dimensions, and opportunities for students to notice professionally. Nonetheless, it is worth mentioning that some aspects were, not least quantitatively, more extensively discussed in students’ essays than others.
Overall, we observe that students’ reflections and noticing had less mathematical focus compared to other things. This is in line with previous studies arguing that noticing skills are positively correlated to teaching experience. Specifically, prospective and novice teachers are less likely to notice issues related to mathematical content than teachers with more teaching experience [
12,
22,
25]. In our study, this can be seen in all four themes which were identified, highlighting the need for a more explicit focus on noticing mathematical content in initial teacher education. In regard to the task itself, all students made attempts to link their designed games and activities to curriculum documents and mathematics/numeracy benchmarks. However, this was rarely explored further. When students discussed the content of the task, the majority focused on general instructions and rules rather than the mathematical concepts and thinking involved. Although this may indicate that they had a clear picture of the design of the learner’s journey, there is still a lack of mathematical vocabulary and content knowledge referenced. From another perspective, it might be the particular design and content of the task itself that may limit the extent and type of noticing. As far as learning (our second theme) is concerned, more emphasis was placed on pupils’ affective and social reactions to the game than cognitive (i.e., mathematical thinking, pupils’ use of strategies, etc.). Those who noticed cognitive issues of learning mostly underlined the differences in individual pupils’ cognitive abilities, while few had an explicit mathematical focus. Weaknesses in noticing pupils’ mathematical thinking and strategies are likely to limit and compromise the quality of teachers’ responses [
8,
14,
21]. In discussing teaching-related topics, few students reflected on themselves as mathematics teachers, or their related beliefs and knowledge. All talked about issues of pedagogy, yet few touched mathematics-specific issues. The majority commented on general pedagogical issues such as differentiation, play-based learning, and assessment. Finally, the few students who made an explicit reference to the non-formal environment, made quite generic comments on how the setting allowed them or not to observe things related to mathematics learning. The fact that all students linked their task to the Scottish curriculum and associated their observations during the Fair with the general pedagogy literature may reflect general priorities of the undergraduate programme as a whole. Besides, before taking the mathematics methods module, all students had completed two semester-long modules on general pedagogy. On the one hand, it is encouraging to observe indications that students have developed transferable skills about professional vision and made links between knowledge across different undergraduate modules [
62]. On the other, as mathematics teacher educators, we believe it is important for initial teacher education programmes to provide several targeted opportunities for students to develop their mathematics-related noticing skills [
2,
4].
6.3. Implications for Teacher Education and Suggestions for Future Research
In closing, we would like to extrapolate several implications for mathematics teacher education by highlighting the structure of the programmes, and perspectives of teacher educators and students. Additionally, we offer suggestions on what future research could explore further. We end this paper by restating the significance and contribution of our research.
Firstly, we believe it is important for both initial and in-service teacher education programmes to address professional noticing more explicitly, along the lines of previous studies reporting successful attempts [
17,
20,
25,
27,
28]. Since there was much less emphasis on mathematical related insights in each theme, we suggest that particular focus be placed on mathematics-specific noticing, such as pupil thinking, teaching strategies, concepts, and processes involved in tasks. This would necessitate teacher-educators to be aware of their professional subject-specific knowledge, noticing, and professional judgements regarding the skills of students’ noticing. Previous research suggests that a lack of mathematical focus in regard to professional noticing by prospective and novice teachers is an issue. A greater communication regarding professional noticing between students and teacher educators may address this issue by offering different windows as to what one might notice. Hence, teacher educators should be equipped to design the learning environments and the subject content to support the professional noticing of students and in-service teachers. This research also suggests that the setting in which teaching is enacted may seize opportunities for students to enhance their noticing skills. As such, both initial and in-service teacher education programmes need to include elements of non-formal learning environments as complementary to formal settings [
58], in relation to the development of prospective teachers’ professional noticing skills. Within these settings, students would need to begin developing their professional self as teachers through, for example, constructing reflective portfolios and engaging in professional dialogues with peers and teacher-educators.
Secondly, we remind readers of the exploratory nature of this study. While students enrolled in the mathematics methods module had opportunities to analyse teaching videos, vignettes, transcribed dialogues, and pupils’ responses, their attention before, during, and after the Fair was not, at least explicitly, directed by tutors. Simply put, students had the freedom to observe and discuss any interaction/situation they considered noteworthy. In future work, we would like to use the themes which emerged as guidelines for students in order to provide more targeted support in terms of what they could notice. This support would include preliminary discussions about the framework, creating spaces for teachers and students to share what they notice during the fair and opportunities for sharing reflections with peers. In doing so, it should be clarified to students that these themes are not meant to be finite, and that, as professionals, they should have enough discretionary space to notice additional things that they consider important. This discussion could be enhanced by developing innovative work on noticing as a lens to develop noticing skills. We also underline the strong relationship between teacher-educators’ pedagogical views/positions and professional noticing with designing the teacher education programmes to navigate and reveal students’ noticing. Hence, we suggest that future research investigate this relationship in-depth to understand how to improve the professional noticing of students.
Thirdly, we focused on what students noticed. In future work, we, and others, could focus on how participants notice, and the extent to which their noticing is analytical, critical, and reflective. This would enable teacher education programmes to design their curricula according to a range of ways of noticing for more sophisticated reflections on teaching and learning. In addition, other data collection methods could be employed, such as individual and/or focus-group interviews before and after an event, to illuminate what and how students notice. These would also shed light on teacher-educators’ noticing skills and open up different arenas for noticing and/or offer different lenses to interpret the same events.
Finally, a core argument here is to suggest that students’ professional noticing also occurs in non-formal learning environments, which ultimately provides valuable insights into improving the formal learning of students through taking noticing forward, for example, to enhancing placement experience. Thus, we would like to encourage colleagues to carry out similar investigations in other non-formal learning environments, for example, visiting mathematics museums or outdoor learning activities.
To conclude, the contribution of our research is three-fold. First, we examined prospective teachers’ noticing outside of formal learning environments (i.e., a Mathematics Fair) to address a gap in the noticing literature, and offered methodological tools and a framework to explore noticing. This sheds light on our understanding of teacher noticing in non-formal learning environments and how this can be empirically studied. Second, our findings suggest that prospective teachers carry out noticing outside of formal learning environments and a Mathematics Fair, as a coursework in Initial Teacher Education, offers a good opportunity to enable this. Future research and Initial Teacher Education curricula can benefit from further exploring such opportunities to improve teacher learning. Third, our research provides some insights and evidence on how to document prospective teachers’ learning through the use of noticing as a conceptual lens. This is important for at least two reasons: reiterating the importance of noticing in teacher learning and maximizing alternative assessment opportunities to support prospective teachers.