1. Introduction
The need for ongoing professional support for teachers of mathematics using an instructional coaching model is an essential component of supporting and improving both teacher and student learning [
1]. Certain teacher certification characteristics such as holding a degree in the field one teaches, and certification status are strongly correlated to student achievement [
2]. Site-based mathematics coaches can support teachers’ ongoing reflection, collaboration and content knowledge to impact both teacher and student learning [
3,
4]. The role and implementation of a mathematics coach can take on many forms [
5] as this current study will also demonstrate. Generally, instructional coaches take a non-evaluative role in supporting teachers in increasing their capacity through reflection, dialogue, mentoring and modeling instruction [
6]. Three common models for coaching include cognitive coaching emphasizing one-on-one reflection with a teacher as they self-assess, content-focused coaching which focuses on content-specific knowledge and pedagogy, and instructional coaching utilizing a more holistic and collaborative approach to mutual improvement [
5]. Activities underlying the role of a typical instructional coach include, “creating intensive, job embedded learning opportunities for teachers through strategies such as offering ongoing workshops, leading professional learning communities, and working one-on-one with teachers to ‘coach’ their preparation for and execution of lessons [
7] (p. 440). The elementary mathematics specialist (EMS) role can include any of these types of coaching models as part of their responsibility to align their goals with the unique set of teacher needs and circumstances within an educational setting. For the purpose of this article, we use the term “instructional coach” or “instructional” or “teacher leader” to highlight the variety of roles the coach may adopt throughout their experience. Oftentimes, instructional coaches are considered to be formal positions while an “instructional leader” or “teacher leader” may be practically adopted as an informal leadership position or stance within the school while the teacher is still primarily teaching in the classroom. The participants in this project included all types of roles—both formal and informal instructional leaders or coaches. For this reason, these terms are used interchangeably throughout the article based on the context of the discussion. Similarly, the “coaching” or “leadership” roles may also encompass elements of all three coaching models, including content and cognitive coaching as described because of the common overlap that occurs [
5]. Previous researchers found that these positions are typically offered to teachers who excelled in the craft of teaching; however, they have not demonstrated their ability to effectively coach other teachers [
7]. Offering opportunities to engage in formal coaching programs to those interested in becoming mathematics specialists are needed to ensure proper training in this new set of skills and dispositions.
The lack of mathematics coaches in schools and insufficient programs to develop mathematics instructional coaches create barriers to building the skills and knowledge in both math content and pedagogy that teachers require for improving student achievement in mathematics [
1]. There are limited resources and certification programs to meet the needs of general instructional coaches [
1,
8]. Mathematics coaches require training in not only instructional leadership, but also in proficiency of high levels of mathematics, strong pedagogy, and curricular planning support for mathematics education [
9,
10]. The Center for Strengthening the Teaching Profession [
11] describes certain characteristics and conditions that must be present for teacher leaders to be effective. These include an overlap between the knowledge and skills, dispositions and roles and opportunities that teacher leaders must possess [
11]. This includes knowing how to collaborate with adult learners, understanding content and pedagogy and the ability to consider the system with which they are working. Dispositions that teacher leaders must possess include taking a stance of inquiry, practicing empathy, and taking a stance of curiosity when working with others. They need to be able to foster teacher engagement in effective dialogue, understand how adults learn effectively and facilitate opportunities to have conversations around their content [
11]. Developing characteristics of a successful mathematics teacher leader includes building a strong sense of self-efficacy though refining the knowledge, skills and dispositions needed for the role of supporting others. Part of this preparation also consists of a formal evaluation of the system-wide readiness to support emerging mathematical instructional coaches within existing school contexts. Preparation programs, whether formal or informal, ought to consider the context, including the opportunities and barriers that exist, to support teacher leaders as they grow in their craft through analyzing the readiness and/or environments within which they work [
11].
There is limited research on how to formally prepare elementary mathematics coaches that maximizes their ability to provide ongoing educator support [
10] through a combination of coursework and site-based internship or practical experiences. Understanding the features of an elementary mathematics specialist (EMS) preparation program that maximizes effectiveness for both the EMS and teachers they work with is crucial. This study focused on analyzing an effort that took the form of developing and implementing a newly established elementary mathematics specialist endorsement program in Washington State. The analysis of this current EMS program focused on three primary aspects of supporting an EMS candidate in their role as they emerge as an instructional leader. The first area was to analyze the level of specified content knowledge gained by the participants involved in the project. Instructional coaches adopt a variety of coaching methods [
5] so understanding the activities they engaged in as they were learning, but also as they delivered professional learning opportunities to others, were key components of this analysis. The second area of this examination was to better understand the types of professional learning opportunities the participants engaged in throughout the duration of the project that aligned with best practices for adult learning. Finally, the researchers were interested in better understanding the contextual, site-based opportunities and barriers that existed within each candidate’s context. These together impact the self-efficacy and growth of emerging mathematical instructional leaders and are important to further understand in order to inform program design in the future.
1.1. Social Cognitive Theory
Bandura [
12] noted the importance self-agency for success through the recognition of factors in influencing not only the individual’s experience, but also the environment around them through social cognitive theory. Bandura differentiated between three types of agency: direct personal agency, proxy agency and collective agency [
12]. Important to this conversation is the emphasis on the interdependence of individuals on one another and their environment through social interactions. Bandura [
13] explained the application of the social cognitive theory through reciprocal causation, emphasizing the interplay between the individual’s performance and the organizational characteristics that provide connected, yet unequal influence or outcomes on the system. The level of an individual’s self-efficacy also influences their ability to influence other individuals and create change within an organizational structure. Bandura [
14] noted that self-efficacy beliefs can be either self-aiding or self-hindering as realized through the attainment of goals. He emphasized that those possessing greater self-efficacy tend to persevere amid setbacks, inequities, and failures. This current study draws on Bandura’s social cognitive theory through analyzing the self-efficacy of teachers through their perseverance amid challenges, both environmental and personal. Especially relevant for this study is the notion that when failures or obstacles do arise, which they inevitably will, self-doubt tends to grow [
13]. Bandura argued that this self-doubt is natural. However, those with a greater sense of self-efficacy will recover faster, whereas others with more self-doubt and a lower sense of self-efficacy may lose faith in their capabilities.
In a more recent review of self-efficacy theory and associated research, Lippke [
15] reiterated that it is effective for predicting performance. This predictive theory was applied to the teaching profession by numerous researchers as recently noted by Morris, Usher and Chen [
16]. Some researchers noted that teacher self-efficacy is directly linked to student achievement portraying this construct as critical to effective teaching and learning [
17].
1.2. Andragogy
To support maximizing an individual’s ability to persevere for both the improvement of self and of the environment with which they work, it is important to connect social cognitive theory and self-efficacy to theory of how adults learn. Lindeman [
18] suggested that approaches to adult education will be through situations, not subjects. He posits that when students learn, they adapt to an established curriculum. When adult teachers learn, the curriculum is built around their needs as situated learning opportunities. Knowles [
19] reinforced Lindeman’s theory of adult learning with his concept of andragogy. He described andragogy where adults are self-directed learners who are interested in growing in their knowledge and are autonomous learners. He referred to it as “the art and science of helping adults learn” [
19] (p. 40). Adult learners require opportunities to direct their own learning, use life experiences that enhance their learning, and problem-centered situations where their learning is immediately applicable within their specific and ever-changing context [
20,
21,
22,
23]. This definition tends to characterize an idealistic or desirable personality of an adult. It does not necessarily account for the activities or supportive structures necessary to implement effective adult learning nor account for the context which may influence their self-efficacy. It is important to reiterate the interdependence of the individual, self-directed learner with the environmental and social influences that Bandura discussed to illustrate the challenge of designing educational opportunities for the adult learner. As Bandura [
24] wrote:
...schools in which the staff collectively judge themselves as powerless to get students to achieve academic success convey a group sense of academic futility that can pervade the entire life of the school. School staff members who collectively judge themselves capable of promoting academic success imbue their schools with a positive atmosphere for development.
(p. 141)
For learning systems, individuals can collectively influence and create the climate under which they work, thus creating not only a collective group efficacy, but also a norm for operating at the school level [
24]. In some situations, there are multiple learning systems that ought to be recognized as part of the wholistic story of adult learners that contribute to learning experiences. Morris et al. [
16] highlighted two modes of learning that are also applicable in this current context; the reinforcing model where there is more of a teacher-directed learning context where educators guide the learning objectives and adapting model of learning where the learner is encouraged to become adaptive in regard to their learning based on their context. This requires a level of reflective inquiry by the learner as facilitated by the educator. The authors [
16] make a case that knowledge is not secure and changes according to the contextual conditions. This suggests multiple implications for designing professional learning opportunities that promote learner reflection of how their educational environments may actually influence the ways in which they process new information. This current study seeks to analyze both the opportunities and barriers that are created within multiple professional learning environments that may impact the self-efficacy and growth of mathematics teachers and instructional leaders.
1.3. Ongoing Professional Learning Needs for Elementary School Mathematics Teachers
Tschannen-Moran and McMaster [
25] noted that one of the most important aspects of teacher self-efficacy is how it impacts the implementation of new teaching strategies based on professional development experiences. They found that “the most powerful professional development format included an authentic mastery experience embedded in the teacher’s regular teaching context” (p. 240). Their findings reiterated the need to align effective andragogical practices during the implementation of new learning, not simply the mastery of the learning itself, to increase teachers’ confidence and motivation to learn while receiving ongoing instructional coaching support. Elementary mathematics teachers, who typically also teach a myriad of other content areas, need support in learning deep levels of mathematics content aligned to their needs [
26,
27]. They also need to engage in active learning that includes opportunities for peer observation and collaboration, coherent with their needs and circumstances, and the learning must occur over a long period of time [
28,
29]. The results of a study by Caddle et al. [
30] indicated a need by mathematics teachers for their professional learning to be aligned with their specific needs, taking into consideration their experience, existing strengths and ways to improve. The authors suggest that while planning for professional learning support for mathematics teachers, there needs to be a consideration of their motivations and needs before creating a system of support. For example, some teachers may need specified math content knowledge while other teachers may need ongoing support for pedagogical instructional strategies. In order to provide specifically designed professional learning support for mathematics teachers that not only aligns with andragogical best practices for supporting adult learners, but includes specified knowledge of how to differentiate based on the needs of individuals, there is an urgency to ensure that mathematics instructional coaches are well equipped for handling this difficult task. Formal training for instructional coaches is critical to support systemic teacher improvement.
1.4. Preparing Mathematical Instructional Leaders
Fennell [
1] listed five main roles of a mathematics instructional leader as follows: mentoring/coaching, planning and providing professional development, assisting with curriculum and instruction, coordinating and monitoring interventions, and supporting professional learning communities (p. 10,11). Instructional leaders, or coaches, support teachers in improving their teaching practice through a variety of strategies. They co-teach, plan, and model lessons, facilitate opportunities for engaging in reflective dialogue, conduct peer observations, and generally promote shared practice amongst colleagues [
29,
31]. This “art and science of leading well” as described within the PRIME (Principles and Indicators for Mathematica Education Leaders) Leadership Framework [
32] more specifically described the stages from being aware of self to expanding that role to leading others through the development of their leadership skills. While the role of the teacher leader does vary across settings and context, most teacher leaders engage in a set of core activities [
32]. York-Barr and Duke [
33] asserted that many advantages of supporting the development of teacher leaders are for the benefits they obtain for themselves, in addition to the impact they make on other educators.
Given the vast continuum of roles and responsibilities of a math coach, a specific set of skills is needed to prepare mathematics coaches for supporting classroom teachers in effective mathematics instruction and improving student learning. A depth of mathematics content knowledge is critical for a successful coach and should not be assumed given many classroom teachers in elementary settings lack the confidence and skills to teach high level mathematics [
34]. Given this finding, intentional opportunities for increasing emerging math coaches’ content knowledge are critical. This is especially relevant, given that those who are being recruited for such positions primarily teach at the elementary level, where teachers have less confidence and experience in teaching high level mathematics. In addition, De Araujo et al. [
34], expand this list to include the need for mathematics coaches who possess high levels of pedagogical content knowledge and expertise in working with adult learners. Finally, they need to see themselves as mathematical leaders who can take on leadership roles within their respective schools and beyond that of their classroom. The PRIME Leadership Framework [
32], scaffolds this shift from “leadership of self” to “leadership of others” and finally “leadership in the extended community” (p. 6). Huggins, Lesseig, and Rhodes [
35] found that when early career teachers of mathematics were given intentional opportunities to reflect on their personal journey through these levels of leadership, they recognized this as an individual experience with their unique timetable for internalizing their leadership capabilities. Furthermore, McCauley et al. [
36], advocate for using a portfolio of leadership experiences in order to have opportunities for teachers seeking to grow in an instructional leadership role to recognize their progress. This portfolio would be organized based on the assumptions of andragogy as described by Knowles and predecessors [
19,
20,
36] in order for emerging instructional leaders to further develop their skills. This practice would provide a scaffold for becoming aware of not only one’s growth in leadership skills but also in allowing oneself to better understand the environment that also contributes to the progress towards increasing both self-efficacy as well as skills in instructional leadership.
1.5. System-Wide Readiness for Supporting Emerging Instructional Leaders
Often times the preparation of teacher leaders parallels that of general educator professional learning. Hopkins, Ozimek and Sweet [
37] noted a continuum of coaching development where coaches start out as intermediaries where they tend to share information and resources as requested by district leaders to leaders who create and facilitate connections and inquiry-based learning across grade levels and teams. As such, it is important to account for not only the readiness of emerging coaches, but also to consider the systems-wide readiness for supporting a coaching model. Swars et al. [
10], noted similar findings in their study of EMS candidates as they progressed through their preparation program that they began to look not only at improving their own teaching but advocating and supporting their colleagues as well. This in turn leads to the EMS program participants increasing in their own ability to become better mathematics teachers but also helps to support the greater initiatives of improving mathematics instruction.
There are many obstacles and constraints inherent to the preparation and implementation of teacher leaders within schools [
33]. Equipping instructional coaches, specifically as mathematics instructional leaders, is as varied as the needs are amongst those they serve. Hopkins et al. [
37] found that there were many variables that either interfered with or contributed to successful coaching implementation that were part of the greater system that school leaders ought to consider in order to create and sustain a successful coaching model [
37] that may contribute to both internal (self-efficacy) and external (support structures). Swars [
10] echoed this finding in that the teachers who participated in the EMS program found it difficult at times to implement new instructional strategies in their classrooms when students had previously been unfamiliar with these new methods, especially as teachers were still expected to adhere to strict pacing guidelines. Swars [
10] also found in their study of the implementation of an EMS program that time constraints and inconsistent administrative support were additional challenges. These challenges are also consistent with previous literature on supporting professional learning practices. The study by Swars [
10] is especially relevant to this current study that also sought to analyze both the growth in instructional leadership by individuals as well as the external factors that contributed to or diminished this growth.
In this current study, we specifically focus on analyzing the implementation of a pilot EMS preparation program in Washington State. While EMS preparation programs are growing, the preparation that program participants experience is vastly inconsistent [
10]. This current study builds on previous studies [
10,
29,
37,
38] who focused on ways to support professional learning to equip both elementary mathematics teachers as well as emerging elementary mathematics teacher leaders. The researchers wanted to better understand the ways in which the pilot EMS endorsement program was effective in preparing EMS candidates by improving their skills and dispositions as mathematics coaches as well as better understanding the challenges these candidates faced as they progressed through the program. We investigated the ways in which elementary mathematics teachers’ professional learning opportunities could be sustained through embedded elementary mathematics specialist instructional supports to impact teacher and student learning. There were two separate groups of teachers that the project wished to positively impact. Firstly, the teachers who enrolled in the formal elementary mathematics specialist endorsement pilot program—these teachers were identified as elementary mathematics specialist (EMS) candidates. The other group to be directly impacted by the pilot program was that of the teachers at each of the EMS candidates’ respective schools. These teachers were identified as core teachers; the core set of teachers who agreed to be participants for the EMS candidates professional learning “internship” activities. These core teachers were generally other grade level colleagues who were interested in participating in ongoing professional learning activities designed by the EMS candidate focused on furthering their mathematics instructional capacity. We recognized the need to analyze two separate contexts of learning communities as elements that impacted the learning and experiences of the EMS candidates. Though the EMS candidates shared a common environment with their identified set of core teachers because they worked in the same building and often experienced similar professional learning activities, the EMS candidates were also sharing a distinct learning setting alongside their EMS candidate peers throughout their program. It was also necessary to analyze these two settings for learning as both are distinct for EMS candidates and core teachers but at the same time part of a continuum of learning settings for the EMS candidates. As Bandura [
39] noted, those within a specific learning environment can influence learning, behavior and actions and it is critical to consider how contextual variables (i.e., people, structures, etc.) may impact the experiences of both sets of candidates distinctly. This included an analysis of both the EMS candidates themselves as well as a core group of teachers that the EMS candidates coached throughout the duration of their leadership internship experiences. Additionally, we sought to explore how teachers’ self-efficacy of their leadership potential changed over the course of the program. Finally, the researchers analyzed the growth of EMS candidate self-efficacy as they attempted to implement coaching practices within their individual school contexts.
1.6. Research Questions
The successes, lessons learned and next steps for implementing the program were addressed through the following research questions:
How are teachers’ knowledge and skills impacted by the program;
What professional behaviors and actions are supportive of teacher collaboration and student learning;
What structures and processes are needed to support the professional learning of teachers, thereby improving their levels of self-efficacy and the successful completion of the program.
3. Results
Research Question One: How did mathematical content knowledge change for each group of teachers impacted by the project based on the level of programmatic intervention?
Research question one sought to address how teachers’ knowledge and skills were impacted by the program; more specifically the level of intervention provided to each group. The EMS candidates participated in an intense course of study that included specific instructional opportunities to learn higher levels of math content knowledge. Core teachers were also given the opportunity to engage in professional learning around math instruction and pedagogy, but not necessarily to the degree of the EMS candidates in terms of focused professional learning on specific math content knowledge building. We were interested in understanding the degree to which the mathematics-based instruction impacted the level of math content knowledge for both groups distinctly, but also wanted to compare the groups to determine if there were differences in growth in math content knowledge over time. Math content knowledge was measured using the Diagnostic Teacher Assessments in Math and Science (DTAMS). The specific test from this series chosen for this study was the Middle Mathematics Teacher Assessment, developed by the University of Louisville’s Center for Research in Mathematics and Science Teacher Development. According to the developers, items captured both the teachers’ abilities to solve mathematics but also how to effectively teach the content and understand how students solve the problems. There are scales available for a variety of math topics. Based on mutual agreement between the project staff and EMS candidates, the Number Computation scale was used for this project since it represents common content necessary for all teachers of mathematics. This content test for teachers consisted of 33 items related to number computation. A pretest was administered in the fall of 2016 to EMS candidates (N = 11) and core teachers (N = 36). A posttest was administered in June 2017. Of the 11 EMS candidates that were present while taking the pretest, seven were able to take both the pre- and posttests.
The DTAMS was used to determine the level of specific mathematical content knowledge gained by both the EMS candidates and the core teachers. A mixed model analysis of variance (ANOVA) was used to explore the group differences between EMS and core teachers over the DTAMS number computation pretest and posttest. EMS candidate scores increased from a mean score of 25 to a mean score of 28.85. This is an increase in almost four points between the pre- and posttests. However, it was not statistically significant (F = 3.1, sig = 0.086). The small sample size of the EMS Teacher group may contribute to this finding. Core teachers also increased their scores from the pretest to the posttest, increasing from a mean of 18.44 to a mean of 23.52. This is a growth in about five points. However, this growth is not a statistically significant increase. There was, however, a statistically significant group difference between the EMS and core teachers with the EMS teachers showing higher mean scores on both the pre- and posttests.
Table 1 shows a comparison between the EMS and core teachers’ pre- and posttest DTAMS scores in number computation.
Research Question Two: What characteristics of effective professional learning were exhibited throughout the program for each group of teachers impacted?
Through the lens of social cognitive theory, it was important to recognize the ways in which the participants engaged in learning within their distinct environments. This included a need to analyze the various learning environments as well as those they collaborated with throughout the program. There were two separate sets of participants in this analysis. The EMS candidates had a distinct learning environment as they engaged in formal learning with their fellow EMS candidates throughout the duration of their formal coursework activities. They also had the separate learning environment of implementing their leadership internship at their respective school sites. This included a different set of individuals: their core teachers. Additionally, the core teachers also had a different learning experience as they were the ones receiving the professional learning by the EMS candidates as they implemented their internship experiences. This interaction brings with it a different experience for the core teachers, distinct from the EMS candidates themselves. Therefore, research question two sought to explore the characteristics of effective professional development that were exhibited throughout the program for both groups of teachers impacted by this project. The Characteristics of Teacher Professional Development (CTPD) Survey tool was used to gather data for this question. The CTPD Survey was given to both the EMS candidates and their core teachers during the summer of 2016 and again in spring of 2017 (see
Figure 1). The results showed an overall increase in the levels of effective professional development occurring over the year (see
Figure 1) and a statistically significant increase in two main areas: Active learning beyond the classroom and content (see
Table 2). Active learning beyond the classroom includes opportunities teachers have to engage in professional development outside of the context of their classroom and school. This would account for the courses in which the EMS candidates participated. Content refers to the focus on content-specific professional development activities; in this case, mathematics content. It should be noted that the degrees of freedom slightly vary across the six characteristics because some EMS candidates did not respond to all survey items.
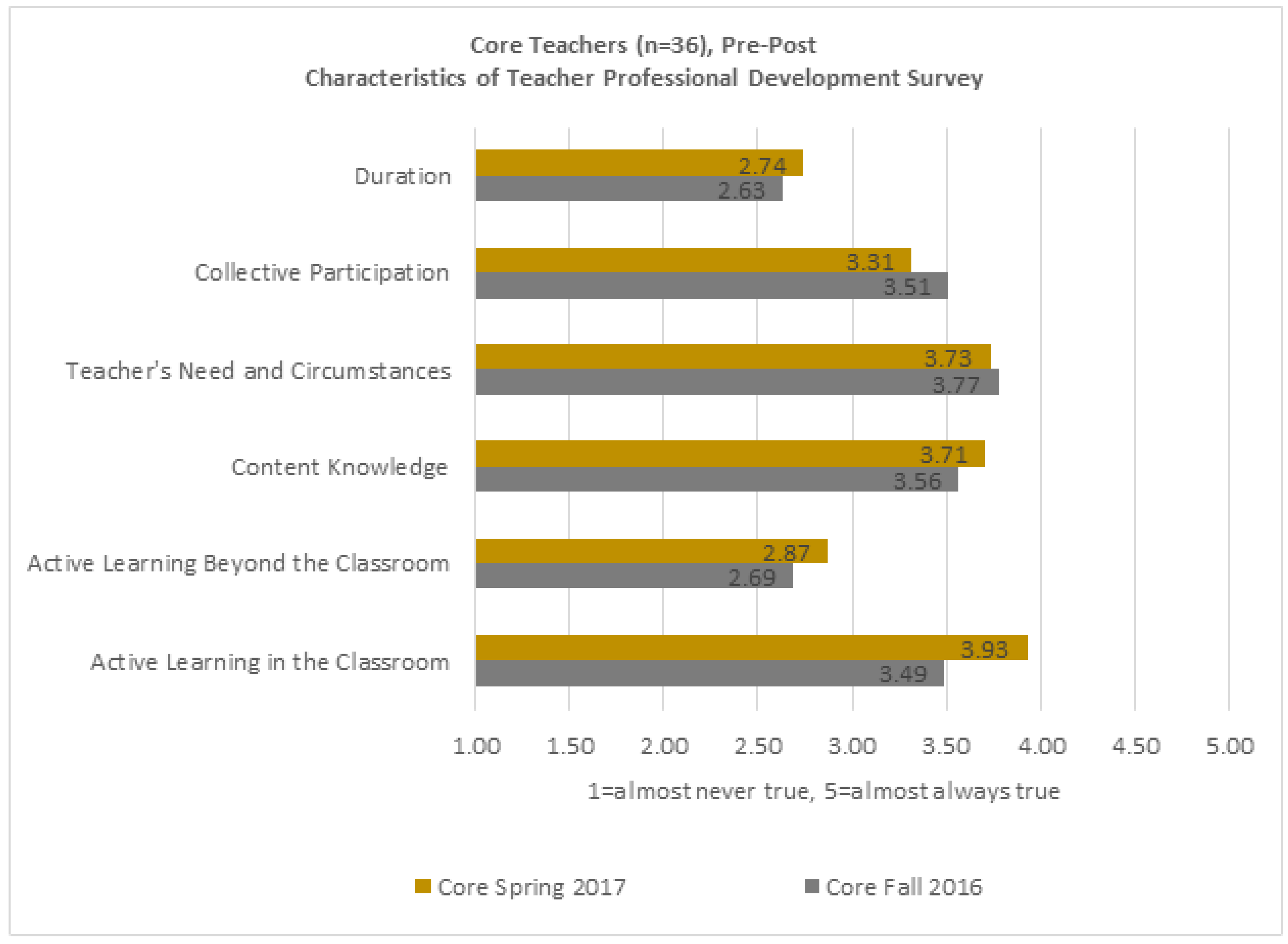
For core teachers, there were some slight areas of growth in practice of effective professional development activities while two areas dipped slightly (see
Figure 2). There was a statistically significant gain in the area of active learning in the classroom (see
Table 3). Active learning in the classroom relates to the frequency of professional learning opportunities that connect to immediate application within the context of the teachers’ classroom. This can take place in the form of professional learning communities, classroom observations, lesson planning and other activities that relate directly to job-embedded learning. Duration refers to the design of the professional learning as ongoing over a period of time rather than a single, finite, experience. Core teachers perceived an increase in these types of professional learning activities throughout the duration of the school year while the EMS candidates were completing their internship activities with them.
The researchers recognized that while the EMS candidates and core teachers often experienced similar professional learning activities as they collaborated at their common school sites, EMS candidates were also collaborating and learning in their own unique context amongst other EMS candidates throughout their program. It was important to consider these contexts through the lens of social cognitive theory to better understand whether these distinct contexts resulted in participants experiencing varied types of professional learning experiences. Therefore, the researchers were interested in comparing two groups, EMS candidates and core teachers, to determine whether the EMS candidates perceived experiencing different activities compared to the core teachers who were in the same schools with similar site-based professional development in order to determine whether there were differential programmatic features supportive of teacher collaboration.
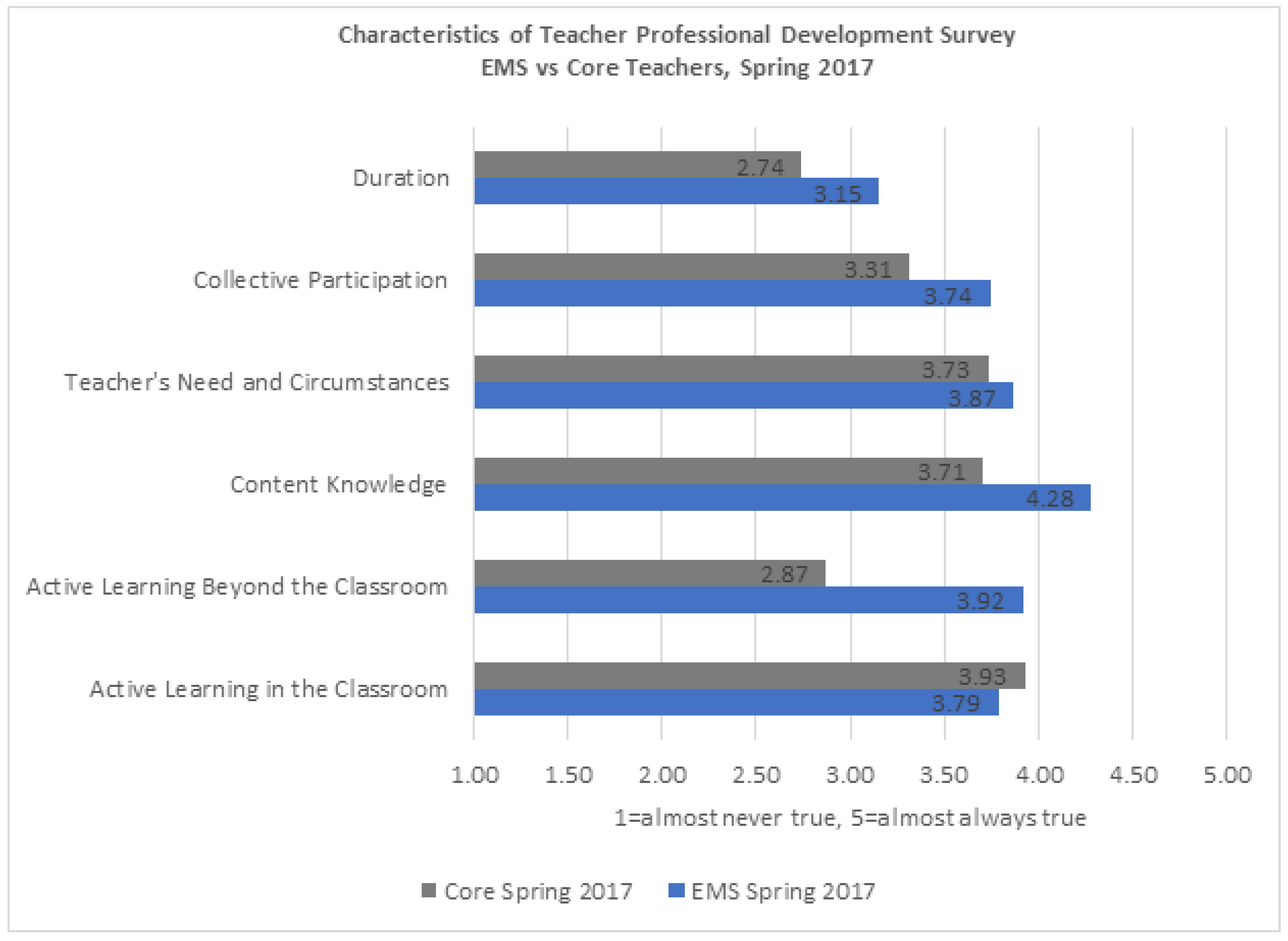
Figure 3 compares these two groups with two areas showing a statistically significant difference: active learning and math content knowledge (also see
Table 4). EMS candidates experienced significantly higher levels of professional learning activities focused on math content knowledge than their core teachers. EMS candidates also engaged in a higher frequency of professional learning activities that included such characteristics as external courses and workshops. Based on these results, EMS candidates experienced vastly different types of professional learning throughout their time in the EMS endorsement program compared to their fellow colleagues who, while they did experience ongoing, site-based professional learning, did not receive the same types of math content-focused professional learning.
Research Question Three: What opportunities and barriers existed within teachers’ educational contexts that contributed to teachers’ sense of self-efficacy and engagement in the EMS program activities?
The School Structure and Teacher Leadership Questionnaire [
46] was administered at the end of the project to EMS and core teachers to determine what types of supports (i.e., time, resources, collegial and administrator support) they had in order to be successful in improving mathematics instruction. Additionally, the researchers wanted to better understand the barriers that also prevented both EMS candidates and core teachers in maximizing this opportunity to grow as math teachers and leaders.
Drawing from end-of-program candidate self-assessment data and survey data using the School Structure and Teacher Leadership Questionnaire and EMS candidate reflections, [
46] several categories emerged using deductive coding due to the researchers’ prior knowledge of common themes related to professional learning readiness [
10,
33,
35,
49]. The pre-established themes set the parameters for coding the responses. These themes included a focus on growing in their self-efficacy and mindset pertaining to mathematics content and instruction. Understanding externally determined opportunities and barriers that also impacted the implementation of the professional learning plans were analyzed using two themes: time and administrator support, which are common themes within the existing set of literature on the variables needed to support ongoing professional growth.
3.1. Growth as a Mathematics Teacher
Comments from EMS candidates included, “This year I have learned the importance of anticipating what/how students will answer questions prior to having them do the work. This helps guide my instruction and better prepares me.” Another teacher noted, “Through the classwork and content I really learned a lot about the ‘new’ way to teach and learn math.”
Several other teachers also echoed their improvement in skills and knowledge around how to teach in alignment with the Standards for Mathematical Practice and being able to anticipate and interpret student learning data. One teacher reflected on her improvement in both areas when she wrote, “I feel like I have improved my ability to help other teachers implement new ideas about instruction. In addition to that, I have improved my own ability to teach mathematics to a depth I was previously unable to do.”
This qualitative feedback was triangulated with the results corresponding to research question one that sought to address the impact that this program had on an improvement in specific mathematical content knowledge. EMS candidates in fact did increase their math content knowledge significantly more than their core teacher counterparts.
3.2. Growth as a Mathematics Instructional Coach
As teachers transitioned to a role as a mathematics coach, there was also an increase in confidence and skills in how to facilitate and lead others. One EMS candidate stated, “I was extremely nervous prior to my practicum about how others would view my age and years of experience...I learned how to facilitate professional development opportunities that included asking questions to guide conversations instead of participating as a peer.” Another coach also wrote about their new ability to “facilitate adult discussions through a book study” and added, “I’d never done this before.” Professional learning had an impact on the greater system beyond the EMS candidates.
Responding to the questions on the School Structure and Teacher Leadership Questionnaire, one EMS candidate responded, “I have found that the teachers in the different grade bands are now collaborating to make the students ready for the upcoming years. It has also helped to make an organic flow for the students into upcoming grades.”
The commonly mentioned student impacts by the core teachers were the increased use of problem solving, increased student interaction and discourse, and an improvement in excitement and engagement amongst students. Several quotes from core teachers illustrate their sentiments regarding impact.
I have embraced math teaching now and my classroom is full of great math talks and learning.
I now look for different strategies to solve a problem. I have also learned that there may be more than one answer for a task or problem.
I am more excited and so are my students. They love being able to share their work and have multiple ways to come to an answer. My students talk about their mindset and encourage other.
The most stated impacts on the teachers themselves were the development of a growth mindset and increase in self-efficacy where they believe all students can learn mathematics, trying new strategies in the classroom, addressing student misconceptions, collaborating with other teachers, and the use of common core resources. Comments by Core teachers exemplify these impacts:
My participation in the project activities allowed me to have insightful discussions about the mathematics happening or not happening in my classroom.
I have changed the way that I view math and also my student answers;
By participating in this collaborative group, I have been able to work with my peers to look at how I can improve my teaching instruction and make math more collaborative.
There is a new enthusiasm for math throughout our building. Teachers are talking about math instruction with joy and asking each other questions.
3.3. Administrative Support and Involvement
Principal involvement was a critical element to the success of the EMS candidates. Over half of the candidates wrote that one of the challenges they needed to overcome was a lack of administrator support. This appeared to be very frustrating for candidates and caused a lack of opportunities to work authentically and consistently with colleagues.
Those candidates who perceived higher levels of support from their principals tended to complete the requirements of the endorsement more successfully. Even though most candidates expressed that one of the challenges was hindered by a lack of time to implement their action plans in their entirety, those who had administrator support were able to have more authentic leadership experiences. Furthermore, their attitudes regarding their experiences were generally more positive and proactive towards considering future opportunities for leadership. Comments from two core teachers reflect this sentiment:
“Administration has the power to either facilitate or impede the effectiveness of the EMS teachers.”
“Principal support is crucial. When you are trying to make changes in practice, having the support of the administration is definitely a crucial piece.”
3.4. Time
Another challenge included the lack of time available to meet with colleagues. One EMS candidate wrote, “[G]etting colleagues to participate and see the value in the PLC [professional learning community] opportunity was a challenge.” Another candidate reflected on the balance between her classroom teaching job and her new job as a mathematics instructional coach during her internship. “It has felt like I have two jobs. I poured all of my heart into meeting the needs of my building that I had very little left for my class.” Another candidate discussed the need to fit her mathematics coaching experiences into the predetermined professional development times. “We were granted time from our administrator for the book study, but one Wednesday a month didn’t allow for everything planned.” Interestingly, a candidate who had already taken a full-time position in her district as a mathematics instructional coach also echoed the need for more time, but also brought up the feelings of isolation she experienced. “I would like time to put into practice what I’ve learned… I don’t have time nor people to collaborate with.”
An external variable was the state requirement for candidates to pass the Middle Grades Mathematics Assessment (NES) to earn the endorsement. This test assesses upper-level high school mathematics skills. Passing this test was a barrier because many teachers simply lack the higher-level mathematics skills required. While the teachers were given a window of three months to study for and pass the test, only two teachers were successful after nine months and three passed after twelve months. They seemed to be overwhelmed and/or intimidated by the test. “I do not feel prepared to take or pass the test. Now that I have time, I will study, study, study.”
5. Conclusions
It is important to emphasize the importance of how the environment and other individuals influence the success of an individual as outlined in Bandura’s social cognitive theory [
12]. Bandura emphasized the interplay between self-agency as being one variable for success and other factors may also impact perceived success [
12]. The results of this study build upon this early work and work by other researchers that recognize external factors such as the school environment and leadership support which impact the experiences and perceived success of the EMS candidate.
Washington State’s EMS endorsement program requirements define expectations that candidates are not only proficient as elementary mathematics instructional coaches, but also demonstrate a competency of high-level mathematics content. This goal is in alignment with what previous research states about effective instructional coaches. Coaches need high levels of skill, content, and dispositions towards both knowing specified content knowledge as well as possessing effective instructional leadership skills [
51]. While there is much literature on the potential impact instructional coaches have on teaching and learning, there is insufficient evidence regarding the impact that an educator earning an elementary mathematics specialist endorsement has on both themselves as well as on the larger audience of teachers [
52]. The results of this study are important in that they reiterate the need for ongoing and supportive mentorship for emerging instructional coaches as also found in Myers et al. [
52]. The goal of an EMS endorsement program is to not only increase the skills and dispositions needed for being an effective EMS but also allow them to understand how their site-based environment may help or hinder their levels of success. This ongoing mentorship support has the potential to impact candidates’ levels self-efficacy as outlined by Bandura [
13] and aims to improve the capacity of all teachers at a location where there is an elementary mathematics coach for effective mathematics instruction. Promoting a rigorous EMS preparation program that reflects best practice for adult learning through supporting both the candidate in their endeavor as well as creating structures at the school site is essential.
It is important to recognize the interplay between the role of the EMS candidate as they fulfill the expectations of their endorsement and the variables within their school site that create opportunities or barriers to their success. Coaching candidates are also in need of opportunities for the ongoing reflection of their successes and barriers connecting their programmatic goals to their individual educational contexts in order to better understand how to maximize their internship experience. These successes are measured in many terms, which include reflecting on their self-efficacy as they view themselves as a continuum of an emerging instructional leader of one’s classroom to a leader of others [
32]. Success can be measured by examining increasing levels of skills, knowledge and disposition in mathematics and as an instructional coach [
20]. Success can also be measured by the impact coaches have on their colleagues’ levels of mathematics pedagogy and indirectly, student learning [
53].
While this represent one glimpse into a complex issue, the importance of effectively training mathematics instructional coaches to meet the needs of teachers and students is essential and pervasive across the United States. Ongoing improvements in program design, implementation and scaling up will continue to be important areas to study as more teachers look towards becoming instructional leaders in their schools. In this study, we found need to support teachers as they expand their role into instructional leadership positions within schools and districts [
54]. An additional facet of support for EMS programmatic improvements includes resources to equip school leaders to ensure they have the skills and capacity to support potential teacher leaders within their context by recognizing how the candidate has the potential to impact the school as a system of learners (both teachers and students) rather than solely considering the means to support the sole improvement of the individual EMS candidate [
29]. It is important to ensure they are entering their respective contexts with structures in place to promote a sustainable model for instructional leadership opportunities.