Understanding and Addressing the Deficiencies in UK Mathematics Education: Taking an International Perspective
Abstract
1. Introduction
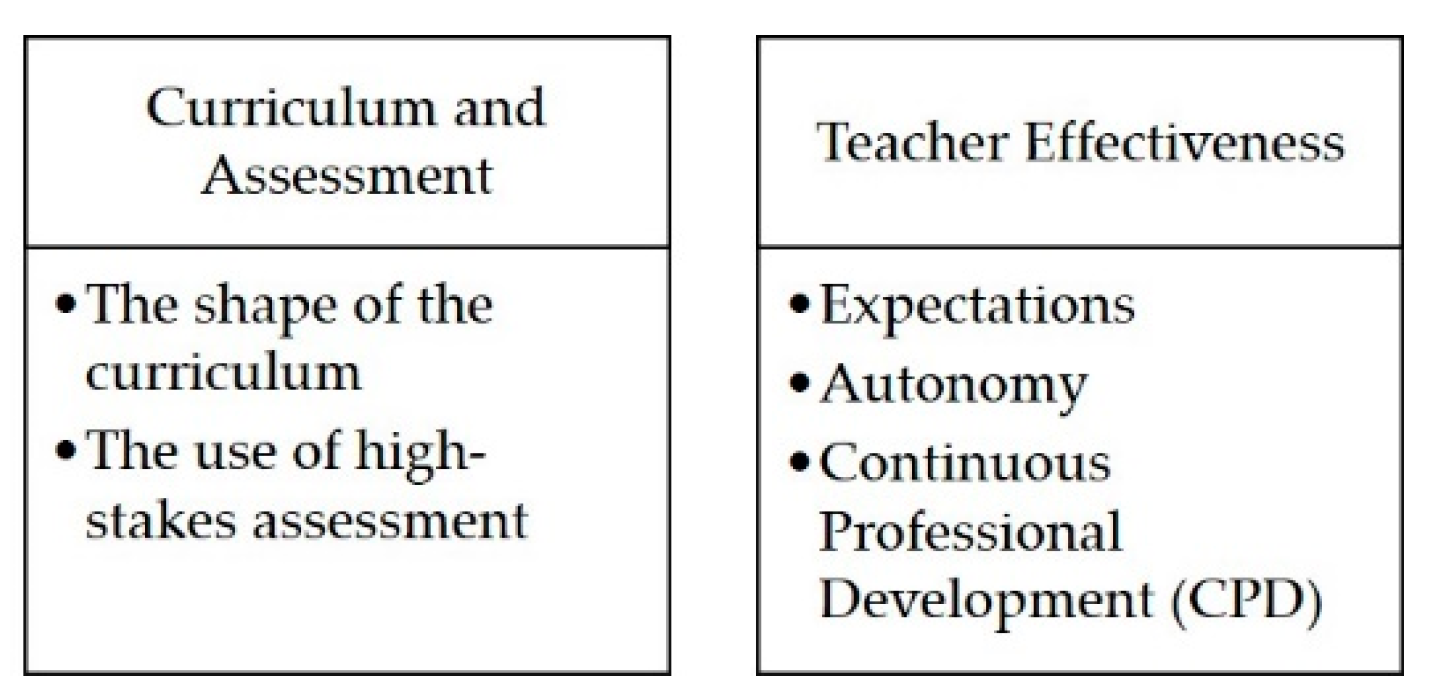
2. Curriculum and Assessment
2.1. Re-Shaping the Curriculum
2.2. Changing the Stakes of Assessments
3. Teacher Effectiveness
3.1. Teacher Expectations
3.2. Teacher Autonomy
3.3. Continuous Professional Development (CPD)
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Coughlan, S. Pisa Tests: UK Rises in International School Rankings. Available online: https://www.bbc.co.uk/news/education-50563833 (accessed on 4 January 2021).
- OECD. PISA 2018 Results What Students Know and Can Do; OECD: Paris, France, 2019; Volume 1. [Google Scholar]
- Sanz, M.T.; López-Iñesta, E.; Garcia-Costa, D.; Grimaldo, F. Measuring Arithmetic Word Problem Complexity through Reading Comprehension and Learning Analytics. Mathematics 2020, 8, 1556. [Google Scholar] [CrossRef]
- Ofsted. Mathematics: Made to Measure; Ofsted: London, UK, 2012.
- Gardiner, T. Background: Why focus on Key Stage 3? In Teaching Mathematics at Secondary Level; Gardiner, T., Ed.; Open Book Publishers: Cambridge, UK, 2014; pp. 5–8. [Google Scholar]
- Hodgen, J.; Pepper, D.; Sturman, L.; Ruddock, G. Is the UK an Outlier? An International Comparison of Upper Secondary Mathematics Education; Nuffield Foundation: London, UK, 2010. [Google Scholar]
- Jerrim, J. The 10 Key Findings from PISA 2015; FFT Education Datalab: London, UK, 2016. [Google Scholar]
- Oates, T. Could do better: Using international comparisons to refine the National Curriculum in England. Curric. J. 2011, 22, 121–150. [Google Scholar] [CrossRef]
- Marton, P.; Säljő, R. On qualitative differences in learning, I: Outcome and process. Br. J. Educ. Psychol. 1976, 46, 4–11. [Google Scholar] [CrossRef]
- DeLotell, P.J.; Millam, L.A.; Reinhardt, M.M. The use of deep learning strategies in online business courses to impact student retention. Am. J. Bus. Educ. 2010, 3, 49–56. [Google Scholar] [CrossRef]
- Moon, R.; Curtis, V.; Dupernex, S. How enterprise education can promote deep learning to improve student employability. Ind. High. Educ. 2013, 27, 433–448. [Google Scholar] [CrossRef]
- Shayer, M.; Ginsburg, D. Thirty years on–a large antieyrg, F effect/(II): 13fect 14fect/(II):e Piagetian tests of formal operations norms 1976stion/7. Br. J. Educ. Psychol. 2009, 79, 409–418. [Google Scholar] [CrossRef]
- Telegraph. UK children falling behind maths due to ‘superficial’ learning. Available online: https://www.telegraph.co.uk/news/uknews/12192892/UK-children-falling-behind-in-maths-due-to-superficial-learning.html (accessed on 4 January 2021).
- Silander, P. Digital Pedagogy; Center for Internet Excellence, University of Oulu: Oulu, Finland, 2015; pp. 9–26. [Google Scholar]
- Symeonidis, V.; Schwarz, J.F. Phenomenon-based teaching and learning through the pedagogical lenses of phenomenology: The recent curriculum reform in Finland. Forum Oświatowe 2016, 28, 31–47. [Google Scholar]
- Cogan, L.S.; Schmidt, W.H. Middle school math reform. Middle Matters 1999, 8, 2–3. [Google Scholar]
- Schmidt, W.H.; McKnight, C.C.; Houang, R.T.; Wang, H.; Wiley, D.E.; Cogan, L.S.; Wolfe, R.G. Why Schools Matter: A Cross-National Comparison of Curriculum and Learning. The Jossey-Bass Education Series; ERIC: London, UK, 2001.
- Greatbatch, D.; Tate, S. School Improvement Systems in High Performing Countries; Department for Education: London, UK, 2019.
- Jones, K.; Fujita, T. Interpretations of National Curricula: The case of geometry in textbooks from England and Japan. ZDM 2013, 45, 671–683. [Google Scholar] [CrossRef]
- Thomas, J. A Review of Research on Project-Based Learning; The Autodesk Foundation: San Rafael, CA, USA, 2000. [Google Scholar]
- Shepard, N. The Probe Method: A Problem-Based Learning Model’s Effect on Critical Thinking Skills of Fourth- and Fifth-Grade Social Studies Students; North Carolina State University: Raleigh, NC, USA; ProQuest Dissertations Publishing: Morrisville, NC, USA, 1998. [Google Scholar]
- Walker, A.; Leary, H. A problem based learning meta analysis: Differences across problem types, implementation types, disciplines, and assessment levels. Interdiscip. J. Probl. Based Learn. 2009, 3, 6. [Google Scholar] [CrossRef]
- Boaler, J. Experiencing School Mathematics Teaching: Teaching Styles, Sex and Setting; Open University Press: Buckingham, UK, 1997. [Google Scholar]
- Scott, D.M.; Smith, C.; Chu, M.-W.; Friesen, S. Examining the efficacy of inquiry-based approaches to education. Alta. J. Educ. Res. 2018, 64, 35–54. [Google Scholar]
- Adams, N.E. Bloom’s taxonomy of cognitive learning objectives. J. Med. Libr. Assoc. 2015, 103, 152. [Google Scholar] [CrossRef]
- Woodcock, N. State schools demand top GCSE grades to enter sixth form. Available online: https://www.thetimes.co.uk/article/state-schools-raise-the-bar-for-sixth-form-n0rrcj2sh# (accessed on 4 January 2021).
- UCAS. UCAS Undergraduate entry requirements. Available online: https://www.ucas.com/undergraduate/what-and-where-study/ucas-undergraduate-entry-requirements (accessed on 4 January 2021).
- Department for Education & Skills Funding Agency. Funding Guidance for Young People 2018 to 2019; Department for Education & Skills Funding Agency: London, UK, 2018.
- Curtis, P. Boys Overtake Girls in Maths GCSE as Coursework Dropped. Available online: https://www.theguardian.com/education/2009/aug/27/maths-gcse-coursework-dropped (accessed on 17 February 2021).
- Klenowski, V.; Wyatt-Smith, C. The impact of high stakes testing: The Australian story. Assess. Educ. 2012, 19, 65–79. [Google Scholar] [CrossRef]
- Wearmouth, J. Testing, assessment and literacy learning in schools: A view from England. Point and Counterpoint. Curric. Perspect. 2008, 28, 77–81. [Google Scholar]
- Harlen, W.; Deakin Crick, R. Testing and motivation for learning. Assess. Educ. 2003, 10, 169–207. [Google Scholar] [CrossRef]
- Wenglinsky, H. Using Technology Wisely: The Keys to Success in Schools; Teachers College Press: New York, NY, USA, 2005. [Google Scholar]
- Scot, T.; Heinecke, W.; Callahan, C.; Urquhart, J. “Yes… But…” The Unintended Effects of Accountability Policy on Technology Infusion and Innovation. In Proceedings of the Society for Information Technology & Teacher Education International Conference, Las Vegas, NV, USA, 3–7 March 2008; pp. 4313–4320. [Google Scholar]
- Singh, A.; Uijtdewilligen, L.; Twisk, J.W.; Van Mechelen, W.; Chinapaw, M.J. Physical activity and performance at school: A systematic review of the literature including a methodological quality assessment. Arch. Pediatrics Adolesc. Med. 2012, 166, 49–55. [Google Scholar] [CrossRef]
- Trudeau, F.; Shephard, R.J. Physical education, school physical activity, school sports and academic performance. Int. J. Behav. Nutr. Phys. Act. 2008, 5, 10. [Google Scholar] [CrossRef]
- Nelson, M.C.; Gordon-Larsen, P. Physical activity and sedentary behavior patterns are associated with selected adolescent health risk behaviors. Pediatrics 2006, 117, 1281–1290. [Google Scholar] [CrossRef]
- Amrein, A.L.; Berliner, D.C. The effects of high-stakes testing on student motivation and learning. Educ. Leadersh. 2003, 60, 32–38. [Google Scholar]
- Barksdale-Ladd, M.A.; Thomas, K.F. What’s at stake in high-stakes testing: Teachers and parents speak out. J. Teach. Educ. 2000, 51, 384–397. [Google Scholar] [CrossRef]
- Landry, D.E. Teachers’(K-5) Perceptions of Student Behaviors during Standardized Testing. Thesis, Oklahoma State University, Stillwater, OK, USA, 2005. [Google Scholar]
- Triplett, C.F.; Barksdale, M.A. Third through sixth graders’ perceptions of high-stakes testing. J. Lit. Res. 2005, 37, 237–260. [Google Scholar] [CrossRef]
- Buck, S.; Ritter, G.W.; Jensen, N.C.; Rose, C.P. Teachers say the most interesting things—An alternative view of testing. Phi Delta Kappan 2010, 91, 50–54. [Google Scholar] [CrossRef]
- Watson, C.E.; Johanson, M.; Loder, M.; Dankiw, J. Effects of high-stakes testing on third through fifth grade students: Student voices and concerns for educational leaders. J. Organ. Learn. Leadersh. 2014, 12, 1–11. [Google Scholar]
- Richardson, F.C.; Suinn, R.M. The mathematics anxiety rating scale: Psychometric data. J. Couns. Psychol. 1972, 19, 551. [Google Scholar] [CrossRef]
- Bellinger, D.B.; DeCaro, M.S.; Ralston, P.A. Mindfulness, anxiety, and high-stakes mathematics performance in the laboratory and classroom. Conscious. Cogn. 2015, 37, 123–132. [Google Scholar] [CrossRef] [PubMed]
- Carey, E.; Hill, F.; Devine, A.; Szücs, D. The chicken or the egg? The direction of the relationship between mathematics anxiety and mathematics performance. Front. Psychol. 2016, 6, 1987. [Google Scholar] [CrossRef]
- Ashcraft, M.H.; Moore, A.M. Mathematics anxiety and the affective drop in performance. J. Psychoeduc. Assess. 2009, 27, 197–205. [Google Scholar] [CrossRef]
- Else-Quest, N.M.; Hyde, J.S.; Linn, M.C. Cross-national patterns of gender differences in mathematics: A meta-analysis. Psychol. Bull. 2010, 136, 103. [Google Scholar] [CrossRef] [PubMed]
- Reimer, D.; Sortkear, B.; Oskarsson, M.; Nilsen, T.; Rasmusson, M.; Nissinen, K. Northern Lights on TIMSS and PISA 2018; Nordisk Ministerråd: Copenhagen, Denmark, 2018. [Google Scholar]
- Weinstein, L.; Laverghetta, A. College student stress and satisfaction with life. Coll. Stud. J. 2009, 43. [Google Scholar]
- Jerrim, J. Nine Key Findings from PISA 2018; FFT Education Datalab: London, UK, 2019. [Google Scholar]
- OECD. Country Note. Programme for International Student Assessment (PISA) Results from PISA 2018. Finland; OECD: Paris, France, 2019. [Google Scholar]
- OECD. Country Note. Programme for International Student Assessment (PISA) Results from PISA 2018. United Kingdom; OECD: Paris, France, 2019. [Google Scholar]
- Antaramian, S. The importance of very high life satisfaction for students’ academic success. Cogent Educ. 2017, 4, 1307622. [Google Scholar] [CrossRef]
- Berger, S.; Freund, A.M. Fear of failure, disorganization, and subjective well-being in the context of preparing for an exam. Swiss J. Psychol. 2012. [Google Scholar] [CrossRef]
- Buzinski, S.G.; Clark, J.; Cohen, M.; Buck, B.; Roberts, S.P. Insidious assumptions: How pluralistic ignorance of studying behavior relates to exam performance. Teach. Psychol. 2018, 45, 333–339. [Google Scholar] [CrossRef]
- Putwain, D.W. Assessment and examination stress in Key Stage 4. Br. Educ. Res. J. 2009, 35, 391–411. [Google Scholar] [CrossRef]
- Beilock, S.L. Math performance in stressful situations. Curr. Dir. Psychol. Sci. 2008, 17, 339–343. [Google Scholar] [CrossRef]
- Mathematics Education Innovation. Coursework in Mathematics. A Discussion Paper; 2006. Available online: https://mei.org.uk/files/pdf/CourseworkMEI.pdf (accessed on 4 January 2021).
- Helm, T. Coursework for GCSE Maths to be Dropped. Available online: https://www.telegraph.co.uk/news/uknews/1530008/Coursework-for-GCSE-maths-to-be-dropped.html (accessed on 16 March 2021).
- Elwood, J. Undermining gender stereotypes: Examination and coursework performance in the UK at 16. Assess. Educ. 1995, 2, 283–303. [Google Scholar] [CrossRef]
- Teodorczuk, A.; Fraser, J.; Rogers, G.D. Open book exams: A potential solution to the “full curriculum”? Med. Teach. 2018, 40, 529–530. [Google Scholar] [CrossRef] [PubMed]
- Gharib, A.; Phillips, W.; Mathew, N. Cheat Sheet or Open-Book? A Comparison of the Effects of Exam Types on Performance, Retention, and Anxiety. Online Submiss. 2012, 2, 469–478. [Google Scholar] [CrossRef]
- Block, R.M. A discussion of the effect of open-book and closed-book exams on student achievement in an introductory statistics course. Primus 2012, 22, 228–238. [Google Scholar] [CrossRef]
- Gharib, A.; Phillips, W. Test anxiety and performance on open book and cheat sheet exams in introductory psychology. IPEDR 2012, 53, 1–4. [Google Scholar]
- Brightwell, R.; Daniel, J.-H.; Stewart, A. Evaluation: Is an open book examination easier? Biosci. Educ. 2004, 3, 1–10. [Google Scholar] [CrossRef]
- Murphy, R.; Machin, S. Improving the Impact of Teachers on Pupil Achievement in the Uk-INTERIM Findings; Sutton Trust: London, UK, 2011. [Google Scholar]
- Dierking, R.C.; Fox, R.F. “Changing the way I teach” building teacher knowledge, confidence, and autonomy. J. Teach. Educ. 2013, 64, 129–144. [Google Scholar] [CrossRef]
- Rosenthal, R.; Jacobson, L. Pygmalion in the classroom. Urban Rev. 1968, 3, 16–20. [Google Scholar] [CrossRef]
- Friedrich, A.; Flunger, B.; Nagengast, B.; Jonkmann, K.; Trautwein, U. Pygmalion effects in the classroom: Teacher expectancy effects on students’ math achievement. Contemp. Educ. Psychol. 2015, 41, 1–12. [Google Scholar] [CrossRef]
- Rubie-Davies, C.M. Teacher expectations and student self-perceptions: Exploring relationships. Psychol. Sch. 2006, 43, 537–552. [Google Scholar] [CrossRef]
- Shapka, J.D.; Keating, D.P. Structure and Change in Self-Concept During Adolescence. Can. J. Behav. Sci. 2005, 37, 83. [Google Scholar] [CrossRef]
- Tiedemann, J. Parents’ gender stereotypes and teachers’ beliefs as predictors of children’s concept of their mathematical ability in elementary school. J. Educ. Psychol. 2000, 92, 144. [Google Scholar] [CrossRef]
- Szumski, G.; Karwowski, M. Exploring the Pygmalion effect: The role of teacher expectations, academic self-concept, and class context in students’ math achievement. Contemp. Educ. Psychol. 2019, 59, 101787. [Google Scholar] [CrossRef]
- Makarova, E.; Aeschlimann, B.; Herzog, W. The gender gap in STEM fields: The impact of the gender stereotype of math and science on secondary students’ career aspirations. Front. Educ. 2019, 10, 60. [Google Scholar] [CrossRef]
- Rattan, A.; Good, C.; Dweck, C.S. “It’s ok—Not everyone can be good at math”: Instructors with an entity theory comfort (and demotivate) students. J. Exp. Soc. Psychol. 2012, 48, 731–737. [Google Scholar] [CrossRef]
- Coe, R.; Aloisi, C.; Higgins, S.; Major, L.E. What Makes Great Teaching? Review of the Underpinning Research; The Sutton Trust: London, UK, 2014. [Google Scholar]
- Jerrim, J. England’s Schools Segregate by Ability More Than Almost Every Other Country in the World; FFT Education Datalab: London, UK, 2019. [Google Scholar]
- Wiliam, D.; Bartholomew, H. It’s not which school but which set you’re in that matters: The influence of ability grouping practices on student progress in mathematics. Br. Educ. Res. J. 2004, 30, 279–293. [Google Scholar] [CrossRef]
- Rubie-Davies, C.M.; Peterson, E.; Irving, E.; Widdowson, D.; Dixon, R. Expectations of achievement: Student teacher and parent perceptions. Res. Educ. 2010, 83, 36–53. [Google Scholar] [CrossRef]
- Deng, Z.; Gopinathan, S. PISA and high-performing education systems: Explaining Singapore’s education success. Comp. Educ. 2016, 52, 449–472. [Google Scholar] [CrossRef]
- Ker, H. The impacts of student-, teacher-and school-level factors on mathematics achievement: An exploratory comparative investigation of Singaporean students and the USA students. Educ. Psychol. 2016, 36, 254–276. [Google Scholar] [CrossRef]
- Salili, F. Learning and motivation: An Asian perspective. Psychol. Dev. Soc. 1996, 8, 55–81. [Google Scholar] [CrossRef]
- Crehan, L. Cleverlands: The Secrets behind the Success of the World’s Education Superpowers; Random House: London, UK, 2017. [Google Scholar]
- Parsons, S.; Hallam, S. The impact of streaming on attainment at age seven: Evidence from the Millennium Cohort Study. Oxf. Rev. Educ. 2014, 40, 567–589. [Google Scholar] [CrossRef]
- Francis, B.; Archer, L.; Hodgen, J.; Pepper, D.; Taylor, B.; Travers, M.-C. Exploring the relative lack of impact of research on ‘ability grouping’in England: A discourse analytic account. Camb. J. Educ. 2017, 47, 1–17. [Google Scholar] [CrossRef]
- Ruthven, K. Ability stereotyping in mathematics. Educ. Stud. Math. 1987, 18, 243–253. [Google Scholar] [CrossRef]
- Warwick, I. How Should Schools Respond to Ofsted’s Renewed Focus on G&T? Optimus Education: Oldbury, England, 2013. [Google Scholar]
- Kollmayer, M.; Schober, B.; Spiel, C. Gender stereotypes in education: Development, consequences, and interventions. Eur. J. Dev. Psychol. 2018, 15, 361–377. [Google Scholar] [CrossRef]
- López-Iñesta, E.; Botella, C.; Rueda, S.; Forte, A.; Marzal, P. Towards breaking the gender gap in Science, Technology, Engineering and Mathematics. IEEE Rev. Iberoam. Tecnol. Aprendiz. 2020, 15, 233–241. [Google Scholar]
- Hoyle, E.; John, P.D. Professional Knowledge and Professional Practice; Cassell: London, UK, 1995. [Google Scholar]
- Little, D. Learning as dialogue: The dependence of learner autonomy on teacher autonomy. System 1995, 23, 175–181. [Google Scholar] [CrossRef]
- Machin, S.; Vernoit, J. Changing School Autonomy: Academy Schools and Their Introduction to England’s Education; Centre for the Economics of Education, LSE: London, UK, 2011. [Google Scholar]
- Adams, G.; Povey, H. “Now There’s Everything to Stop You”: Teacher autonomy then and now. In Sociopolitical Dimensions of Mathematics Education; Springer: Berlin/Heidelberg, Germany, 2018; pp. 209–230. [Google Scholar]
- Hargreaves, A. Four ages of professionalism and professional learning. Teach. Teach. 2000, 6, 151–182. [Google Scholar] [CrossRef]
- MacBeath, J. Future of Teaching Profession; Education International Brussels: Brussels, Belgium, 2012. [Google Scholar]
- Price Waterhouse Cooper. Teacher Workload Study, Report of a Review Commissioned by the DfES; Price Waterhouse Cooper: London, UK, 2001. [Google Scholar]
- Sturman, L.; Lewis, K.; Morrison, J.; Scott, E.; Smith, P.; Styles, B.; Taggart, G.; Woodthorpe, A. General Teaching Council Survey of Teachers; National Foundation for Educational Research in England: London, UK, 2005. [Google Scholar]
- Department for Education. Factors Affecting Teacher Retention: Qualitative Investigation; Department for Education: London, UK, 2018.
- Foster, D. Teacher Recruitment and Retention in England; House of Commons Briefing Paper: London, UK, 2019. [Google Scholar]
- Pearson, L.C.; Moomaw, W. The relationship between teacher autonomy and stress, work satisfaction, empowerment, and professionalism. Educ. Res. Q. 2005, 29, 38–54. [Google Scholar]
- Rhodes, C.; Nevill, A.; Allan, J. Valuing and supporting teachers: A survey of teacher satisfaction, dissatisfaction, morale and retention in an English local education authority. Res. Educ. 2004, 71, 67–80. [Google Scholar] [CrossRef]
- Talbert, J.E.; McLaughlin, M.W. Teacher professionalism in local school contexts. Am. J. Educ. 1994, 102, 123–153. [Google Scholar] [CrossRef]
- Ingersoll, R.M. Teacher Professionalization and Teacher Commitment: A Multilevel Analysis. Statistical Analysis Report; US Department of Education, Office of Educational Research and Improvement: Washington, DC, USA, 1997. [Google Scholar]
- Santiago, P.; Levitas, A.; Radó, P.; Shewbridge, C. OECD Reviews of School Resources-Estonia; OECD: Paris, France, 2016. [Google Scholar]
- OECD. Education at a Glance 2008; OECD: Paris, France, 2008. [Google Scholar]
- OECD. PISA IN FOCUS. School Autonomy and Accountability: Are They Related to Student Performance? OECD: Paris, France, 2011. [Google Scholar]
- Butrymowicz, S. In Dutch Schools, More Time in School and More EDUCATOR control; The Hechinger Report: New York, NY, USA, 2015. [Google Scholar]
- Eyles, A.; Machin, S. The introduction of academy schools to England’s education. J. Eur. Econ. Assoc. 2019, 17, 1107–1146. [Google Scholar] [CrossRef]
- West, A.; Wolfe, D. Academies, autonomy, equality and democratic accountability: Reforming the fragmented publicly funded school system in England. Lond. Rev. Educ. 2019, 17, 70–86. [Google Scholar] [CrossRef]
- Cirin, J. Do Academies Make Use of Their Autonomy? Research Report; Department for Education: London, UK, 2014.
- Arbor. How Dixons Academies Trust Took Tips from Silicon Valley on Structuring Their MAT; Arbor Education: London, UK, 2018. [Google Scholar]
- Tickle, B.R.; Chang, M.; Kim, S. Administrative support and its mediating effect on US public school teachers. Teach. Teach. Educ. 2011, 27, 342–349. [Google Scholar] [CrossRef]
- Worth, J.; Van den Brande, J. Teacher Autonomy: How Does It Relate to Job Satisfaction and Retention? Natl. Found. Educ. Res. 2020. [Google Scholar]
- Cordingley, P.; Bell, M.; Isham, C.; Evans, D.; Firth, A. What do specialists do in CPD programmes for which there is evidence of positive outcomes for pupils and teachers. Res. Evid. Educ. Libr. 2007, 4, 1–24. [Google Scholar]
- Glover, D.; Miller, D.; Averis, D.; Door, V. The evolution of an effective pedagogy for teachers using the interactive whiteboard in mathematics and modern languages: An empirical analysis from the secondary sector. Learn. Media Technol. 2007, 32, 5–20. [Google Scholar] [CrossRef]
- Sellen, P. Teacher Workload and Development in England’s Secondary Schools: Insights from TALIS; EPI: Cobham, UK, 2016. [Google Scholar]
- Pedder, D.; Storey, A.; Opfer, V.D. Schools and Continuing Professional Development (CPD) in England-State of the Nation Research Project; Cambridge University/The Open University: Oxford, UK, 2008. [Google Scholar]
- Centre for the Use of Research and Evidence in Education (CUREE). Evaluation of CPD providers in England 2010–2011. Report for School Leaders; Training and Development Agency for Schools: Cumbria, England, 2011.
- Chew, L.C. Teaching training and Continuing Professional Development: The Singapore Model. In Proceedings of the Proceeding of International Conference on Teaching Training and Education, Surakarta, Indonesia, 23–26 November 2016; pp. 165–171. [Google Scholar]
- Sälzer, C.; Prenzel, M. Looking Back at Five Rounds of PISA: Impacts on Teaching and Learning in Germany. Sol. Polje 2014, 25, 53–72. [Google Scholar]
- Roback, P.; Chance, B.; Legler, J.; Moore, T. Applying Japanese lesson study principles to an upper-level undergraduate statistics course. J. Stat. Educ. 2006, 14. [Google Scholar] [CrossRef]
- Goulet, L.; Krentz, C.; Christiansen, H. Collaboration in education: The phenomenon and process of working together. Alta. J. Educ. Res. 2003, 49, 4. [Google Scholar]
- McArdle, K.; Coutts, N. Taking teachers’ continuous professional development (CPD) beyond reflection: Adding shared sense-making and collaborative engagement for professional renewal. Stud. Contin. Educ. 2010, 32, 201–215. [Google Scholar] [CrossRef]
- Imada, T. Cultural narratives of individualism and collectivism: A content analysis of textbook stories in the United States and Japan. J. Cross-Cult. Psychol. 2012, 43, 576–591. [Google Scholar] [CrossRef]
- Allen, R.; Benhenda, A.; Jerrim, J.; Sims, S. New evidence on teachers’ working hours in England. An empirical analysis of four datasets. Res. Pap. Educ. 2020, 35. [Google Scholar] [CrossRef]
- Clay, B.; Weston, D. No teacher thinks they have enough time for proper CPD. Here’s how schools can MAKE time. Times Education Supplement, 11 January 2018. [Google Scholar]
- Perrella, C.J. Exploring the Influence of an Early Talent Development Program on Teacher Perceptions of Giftedness in Culturally and Linguistically Diverse Students. Ph.D. Thesis, Northeastern University: Boston, MA, USA, 2017. [Google Scholar]
- Rubie-Davies, C.M.; Peterson, E.R.; Sibley, C.G.; Rosenthal, R. A teacher expectation intervention: Modelling the practices of high expectation teachers. Contemp. Educ. Psychol. 2015, 40, 72–85. [Google Scholar] [CrossRef]
- Weinstein, R.S.; Soule, C.R.; Collins, F.; Cone, J.; Mehlhorn, M.; Sintontacchi, K. Expectations and high school change: Teacher-researcher collaboration to prevent school failure. Am. J. Community Psychol. 1991, 19, 333–363. [Google Scholar]
- Britzman, D.P. Practice Makes Practice: A Critical Study of Learning to Teach; Suny Press: Albany, NY, USA, 2012. [Google Scholar]
- Hargreaves, A. Educational change takes ages: Life, career and generational factors in teachers’ emotional responses to educational change. Teach. Teach. Educ. 2005, 21, 967–983. [Google Scholar] [CrossRef]
- Orbell, S.; Verplanken, B. The automatic component of habit in health behavior: Habit as cue-contingent automaticity. Health Psychol. 2010, 29, 374. [Google Scholar] [CrossRef]
- Hsin, A.; Xie, Y. Explaining Asian Americans’ academic advantage over whites. Proc. Natl. Acad. Sci. 2014, 111, 8416–8421. [Google Scholar] [CrossRef] [PubMed]
- Heine, S.J.; Kitayama, S.; Lehman, D.R.; Takata, T.; Ide, E.; Leung, C.; Matsumoto, H. Divergent consequences of success and failure in japan and north america: An investigation of self-improving motivations and malleable selves. J. Personal. Soc. Psychol. 2001, 81, 599. [Google Scholar] [CrossRef]
- Ng, F.F.-Y.; Pomerantz, E.M.; Lam, S.-f. European American and Chinese parents’ responses to children’s success and failure: Implications for children’s responses. Dev. Psychol. 2007, 43, 1239. [Google Scholar] [CrossRef] [PubMed]
- Beaton, A.E.; Postlethwaite, T.N.; Ross, K.N.; Spearritt, D.; Wolf, R.M. The Benefits and Limitations of International Educational Achievement Studies. Trends in Education; ERIC: Wahsington, DC, USA, 1999.
- Wise, A. Behind Singapore’s PISA rankings success and why other countries may not want to join the race. The Conversation, 8 December 2016. [Google Scholar]
| Area | Recommendation |
|---|---|
| Curriculum |
|
| Assessment |
|
| Teacher expectations |
|
| Teacher autonomy |
|
| Continuous Professional development |
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skipp, C.S.; Dommett, E.J. Understanding and Addressing the Deficiencies in UK Mathematics Education: Taking an International Perspective. Educ. Sci. 2021, 11, 141. https://doi.org/10.3390/educsci11030141
Skipp CS, Dommett EJ. Understanding and Addressing the Deficiencies in UK Mathematics Education: Taking an International Perspective. Education Sciences. 2021; 11(3):141. https://doi.org/10.3390/educsci11030141
Chicago/Turabian StyleSkipp, Charlotte S., and Eleanor J. Dommett. 2021. "Understanding and Addressing the Deficiencies in UK Mathematics Education: Taking an International Perspective" Education Sciences 11, no. 3: 141. https://doi.org/10.3390/educsci11030141
APA StyleSkipp, C. S., & Dommett, E. J. (2021). Understanding and Addressing the Deficiencies in UK Mathematics Education: Taking an International Perspective. Education Sciences, 11(3), 141. https://doi.org/10.3390/educsci11030141







