Formative Potential of the Development and Assessment of an Educational Escape Room Designed to Integrate Music-Mathematical Knowledge

Abstract

In the particular case of Spain, student and teacher difficulties associated with the mathematical discipline have been evidenced in PISA and TEDS-M reports. As we consider that the teachers’ difficulties are connected to the students’ performance, we propose a multi-disciplinary approach to deliver specific didactic/mathematical knowledge to the trainee teachers. Such additional instruction shall be meaningfully connected to the real needs of the schools, so a service-learning approach is proposed here. In the present manuscript, the trainee teachers have co-designed educational escape rooms (in coordination with local schools) with the aim of mobilizing curricular knowledge. The goal of the educational escape rooms is to foster the mathematic-related competencies by establishing meaningful connections to other curricular disciplines (music-related knowledge, in the case of this study). This paper reports on the particular experience developed with a group of students (trainee teachers) while designing their educational escape rooms, focusing on the particular case of a specific student to evidence the formative potential of the procedure. The didactic suitability of the proposed escape room has been analyzed and professional development has also been discussed, showing the mobilization of relevant professional skills and fostering the related music and mathematical didactic competencies by shifting the teaching perspective from an algorithmic point of view to a more “reasoning and designing” strategy. This constitutes an evidence of the formative potential on the co-design of educational escape rooms, when designed in the frame of a service learning approach.

1. Introduction

A school’s curriculum may appear unrelated, fragmented or somewhat disjointed due to the lack of communication and connection among topics and subjects. This fragmentation often affects students’ performance inducing lack of interest and confusion, thus, perceiving some knowledge as useless and affecting the experience being delivered to them in school [1]. Indeed, some core curricular subjects seem to be clearly affected by these problems, particularly scientific and mathematical knowledge. For the particular case of Spain, schoolchildren show their worst results in scientific knowledge in PISA [2] tests (scoring below the OECD average). The PISA 2018 report indicates that such a result might be due to students’ lack of capacity to formulate, manage, and interpret mathematics in a variety of contexts. This bad performance might be related to the lack of connections of scientific/mathematical knowledge to other curricular topics, but might also be related to their teachers’ specific lack of knowledge. Indeed, for the sake of comparison, PISA statistic data can be compared to that of the TEDS-M report [3], thus, giving information on the teachers’ specific lack of mathematical knowledge. 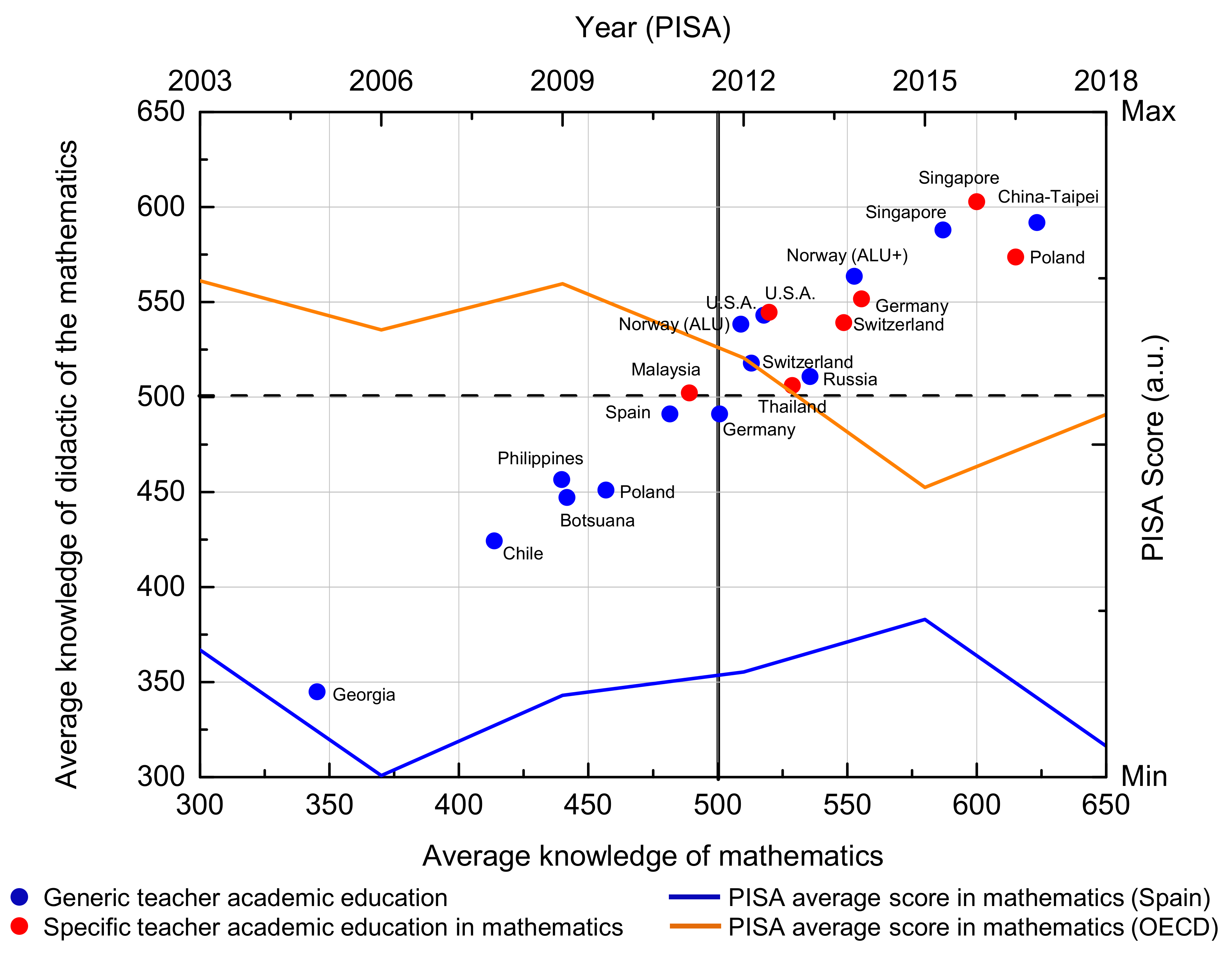In doing so, worrisome data regarding the mathematical and didactic knowledge of on-service teachers are revealed (see Figure 1). These results reveal the key importance of specific “mathematical training programs” for teachers’ education, with Spain teachers lightly below the mean score for both didactic and mathematic knowledge. In this regard, Figure 1 shows the average performance of 15-year-old students in mathematics (regardless of the school type and grade attended), evidencing a wide gap between the Spanish score (blue line) and the average OECD score (orange line). Figure 1 also shows the score provided by the TEDS-M report for the didactic-mathematical knowledge of on-service teachers, where Spanish teachers are also below the OECD average.

Attending to Figure 1 data, it is clear that countries with a specific teacher education in mathematics score higher that those with a generic teacher education. Furthermore, the poor performance of Spanish students could be related to the low didactic-mathematical knowledge of their own teachers.

Therefore, two main challenges should be attended: (i) To solve the “curricular isolation” of the mathematics discipline, promoting the ability to establish connections and (ii) designing a specific teacher academic education in mathematics as a way to improve didactic-mathematical knowledge.

This manuscript constitutes a research report, showing data corresponding to a “mentoring program” to deliver specific didactic-mathematic education to students (trainee teachers). We would like to face both challenges at once, creating a framework to treat the “isolation” and the low didactic knowledge in mathematics. To solve the perceived “curricular isolation” of the mathematics discipline, the use of curricular integration techniques can be an approach, which may help establish connections. In this regard, Anglin [4] insights that “integrating curriculum correctly requires more than combining two subjects, or turn teaching”. Therefore, in effective curriculum-integration models knowledge is meaningfully related, connecting in such a way that it becomes relevant to other areas of learning, as well as in real life.

In this contribution, the authors assume that a curricular integration approach may lead to a significant improvement in the students’ mathematical skills (including reasoning mathematically and using mathematical concepts, procedures, facts, and tools to describe, explain, and predict phenomena). It is also assumed that curricular integration may motivate students to perceive mathematical knowledge as useful. Finally, a schoolchild and future teachers should “enjoy while doing mathematics”, so a gamification approach is also considered. The main goals of this study can be summarized as:

• Explore the efficiency of a specific program designed to develop students’ mathematical competencies in the frame of an integrated curriculum, with the aim of:

  ◦

  Delivering specific didactic-mathematical knowledge in touch with on-service teachers and schools.

  ◦

  Designing, analyzing, and implementing problem-solving scenarios (educational escape rooms) as a way to mobilize professional didactic-mathematical skills.

• Manage students’ “math-phobia”: The trend of students and the schoolchild that fear the mathematical discipline. Math-phobia has to be treated since no knowledge can be built over a bad relation with the discipline. Thus, a gamification approach is used to boost students’ capacities to employ mathematical concepts in a variety of contexts. Curricular integration is used here as a tool to motivate students to develop didactic skills and mathematic knowledge taking the music discipline as a source.

To do so, the authors (researchers and teachers at the University) have created a mentoring program formalized as two academic year’s student/teacher cooperation. The goal of the mentoring program was to improve the didactic-mathematical knowledge of participant students (trainee teachers). This goal should be achieved in two stages (each one, corresponding to a different academic year). Both years would be dedicated to solve specific mathematical difficulties reported by on-service teachers in cooperating schools. Difficulties would be treated by designing gamified environments (educational escape rooms), specifically developed to mobilize mathematical competencies in a curricular integration approach. That is, students should design an educational escape room which shall mobilize curricular knowledge as a way to promote connections and relations among the different curricular subjects. In doing so, some research questions should be answered by the students: Can an educational escape room be used to work music and mathematical knowledge? How can music and mathematics didactic situations be analyzed?

The project started with a small group of five cooperating students, creating a team able to design, implement, evaluate, and re-design such educational escape rooms in close relation to cooperating primary education schools (CEIPs). This procedure allows students (future teachers) to enjoy a “specific mathematic education”, in close relation with their own interests, while providing valuable support to the CEIPs. Students should have accomplished the core mathematic education of the “Primary Education Degree” of the University career, so the 2-year cooperation was designed to go beyond the core instruction.

In this manuscript, we present one of the educational escape rooms designed by one of the five cooperating students, analyzing its didactic suitability, exploring the possibilities of curricular integration, and analyzing the professional development achieved by this specific student.

2. Background and Framework

As mentioned in the Introduction Section, this manuscript presents an educational escape room (EER) designed by students with the aim of mobilizing mathematic competencies, while emphasizing connections in a curricular integration approach. EER should be useful to treat specific mathematic difficulties reported by the on-service teachers. Therefore, as the aim of this procedure is the implantation and evaluation of the designed EER, students have been in touch with the cooperating schools (coordinating, scheduling, and programming the interventions). This section presents a brief discussion of the theoretical framework which inspired the core ideas of the study.

2.1. The Need for Curricular Integration

Criticism of a standards-based curriculum began when the National Council of Teachers of Mathematics (NCTM) [5] produced the Curriculum and Evaluation Standards for Schools in 1989 [6]. Since then, numerous evidences have been reported on the effects of changing from a traditional mathematics curriculum to an integrated mathematics curriculum on student mathematics learning [7,8]. In Europe, and as a consequence of the Bologna Process (a European process to adapt education to the new reality), an aptitude-based perspective has been used to inspire the new curricula [9,10]. In this context, adopting curricular integration approaches have been recommended in all educational stages.

Curricular integration is a way to promote interdisciplinary teaching, and can be defined as a method used to teach across curricular disciplines, with the aim of bringing together previously separated disciplines around common themes, issues or problems [11]. Literature [12] identifies seven common elements which are shared among different integrated curriculum approaches: (i) A combination of subjects, (ii) an emphasis on projects, (iii), the use of a wide variety of source material beyond textbooks, (iv) highlighting relationships among concepts, (v) thematic units, (vi) flexible schedules, and (vii) flexible student grouping. Curricular integration approaches have become more and more widespread as the emphasis of the learning process has emphasized on connections and skill development rather than on curricular disciplines [13].

One way curriculum developers have created a standards-based curriculum is by arranging consecutive integrated courses, which incorporate different content and process standards [14]. However, this can in fact lead to a disintegration of curriculum if great care is not taken to review and base learning on the previous year’s topics [15]. Since an integrated curriculum generally alternates between content strands, students can lose the understanding of mathematical systems [15], so a problem-based approach is required.

In the particular case of Spain, curricular integration approaches are being used to give an answer to students who ask “what is this knowledge useful for?”, since “meeting the reality is one of the aims of an educational system” [16]. In this regard, J. Torres [16] spotted that “some knowledge will only make sense when integrated with the living reality”.

In the present contribution, authors aim to educate students (future teachers) for an effective music-mathematical integration. In this regard, the proposal aims to encourage our students to allow children in primary and early childhood education to explore and play in both music and mathematics and to experience the synergy of exploring the two subjects as one. For future teachers to be confident in their ability to incorporate integrated approaches in the teaching of music and mathematics, teachers may need to re-conceptualize what it is that makes an activity “musical” and “mathematical”. This may require support from higher education tutors and teachers and is likely to take time to develop. However, experience to date indicates that, when experienced teachers and trainee teachers engage in appropriate activities for themselves, they quickly develop the confidence to explore the activities further and even go on to create activities of their own [17]. Finally, the proposed approach is supported by previous research [18], which reports that teachers became more comfortable at the global thought of integrating music and core academic objectives, with a slight increase in the confidence level in integrating music with reading, math, science or social studies objectives.

2.2. Co-Design of Didactic Situations

Some authors report that a real empowering in learning processes can be achieved by the educational co-design [19]. Participatory design (originally co-operative design, now often co-design) is an approach to design attempting to actively involve all the participants in the design process to help ensure that the result meets their needs and is usable. In the particular case of education, participatory design should allow students to investigate and develop their own learning processes via peer-to-peer discussions and teachers’ feedback [20]. In this regard, the co-design of didactic situations shall fit with the principles mentioned in literature [21,22], which can be summarized in:

• The activities should allow students to manipulate and control tools useful to fit the problem.
• The tasks should enable the skill to customize and explore the problem autonomously.
• The complete experience should provide opportunities to visualize the problem from a different role (as a reviewer, solver, etc.)

In the case of this manuscript, the co-design approach is used to fit creative tasks cooperatively developed by on-service school teachers, students, and the authors of this manuscript (researcher and teachers at the University). Participatory design processes should be based on a question to be solved, whose treatment could be supported and enhanced by the use of virtual learning networks [23]. With the aim of respecting such principles, the procedure employed in this research involved the creation of a small “designer team” (constituted of five students). To enhance the process, this “designer team” should be coordinated in the creation of problems, activities, tasks, tests, narrative, etc. to be taken into account when designing an EER. On-line and face-to-face meetings with the researchers in charge (authors of the manuscript) were scheduled, in order to provide feedback to the students. Moreover, virtual meetings with on-service teachers at the school were also scheduled to verify that the designed EERs were fitting with their needs, as well as to plan different implementations.

2.3. A Service-Learning Approach

In 1979, Robert Sigmon [24] defined service-learning as an experiential education approach that is premised on “reciprocal learning” suggesting that since learning flows from service activities, both those who provide the service and receive it “learn” from the experience. In Sigmon’s view, service-learning occurs only when both the providers and recipients of the service benefit from the activities. Since its original idea, service-learning has evolved to become a methodology, a teaching-learning tool (and even a pedagogy by itself) that combines the service to a community with the professional formation and the needed reflection, which enrich the learning experiences of students and teachers [25].

Nowadays, service-learning is considered an educational approach that combines learning objectives with community service in order to provide a pragmatic, progressive learning experience, while meeting societal needs. This methodology involves students in service projects to apply classroom learning for local agencies that exist to effect positive change in the community.

In this particular study, authors have assumed a service-learning approach to boost students’ learning experience, while meeting the school needs (specifically, schoolchildren’s mathematical difficulties). With this approach, researchers would like to simultaneously attend to the students and schoolchildren’s mathematical difficulties. This approach aims to contribute to solve the situation spotted in the Introduction (see Figure 1). In the presented experience, university students (primary education trainee teachers) have cooperated with several schools to design and implement educational escape rooms that fit the specific school needs.

2.4. Educational Escape Rooms as a Formative Tool

A conventional escape room consists of a live-action, team-based game where players are jailed in a room where they will have to solve puzzles in order to unravel a story and escape before the available time ends. Using mathematical puzzles (such as situations of calculus resolution, data acquisition, probability determination, etc.) the players get access to a combination of numbers that enables them to open mechanisms that grant access to other puzzles. The last enigma (or the combined result of some enigmas), grants the final code to escape the room. Finally, there is a “game master” supervising the escape room experience, who can eventually communicate with the players.

In this contribution, the authors’ starting hypothesis considers that an escape room-based activity might be a powerful educational resource to create learning opportunities for primary-school schoolchildren, but also to promote professional skills on trainee teachers by designing EERs. This approach is shared by other authors in literature [26]. Using an EER to tell a story, students are transformed into protagonists of an escapism tale and, to have success, they will have to mobilize curricular knowledge (conveniently fitted to the educational level of the students). In addition, this resource fosters collaboration, allowing the development of social skills (cooperation between players is essential to complete the adventure). Furthermore, the EER can be used to deliver an integrated experience, so that knowledge is not isolated but meaningfully connected to the different clues, tools, enigmas, scenery, and other elements of the ERR.

We have already demonstrated the potential of EERs to promote knowledge [27], by designing the experience of a problem-based game and emphasizing the equivalent game-problem [28,29]. In this regard, the literature reports that problem-based learning approaches may help mitigate the different mathematics performances evidenced in PISA reports [30]. Design criteria and guidelines were provided to students, but the proposal presented here could not be implemented (due to the COVID-19 pandemic). Therefore, the potential of the EER in terms of “useful teaching tool to be used in primary education” could not be presented in this manuscript. However, the students’ design of EERs will be evaluated in terms of professional development, analyzing the didactic suitability as well as the fit to the design criteria, needs of the school, and success as a curricular integration tool.

3. Methodology

In January 2017, the project started with the idea of co-designing gamified environments (educational escape rooms—EERs) so that students have a way to interact with on-service teachers, researchers (authors of the manuscript), and schoolchildren. The goal of the project was to promote didactic and mathematic knowledge in a meaningful way for both students and schoolchildren.

3.1. Design-Based Research and Didactic Engineering

Design-based research (DBR) is a family of methodological approaches for the study of learning in context [31]. It uses the design and systematic analysis of instructional strategies and tools, trying to ensure that instructional design and research are interdependent. In a first practical approach, DBR consists of orienting research to introduce innovations in education. One of the DBR main characteristics is the introduction of new elements that shall transform the situation [32]. DBR aims to provide answers to real problems (detected in the educational reality) taking scientific theories or theoretical models as a starting point which is available for solving such problems. To this aim, programs, didactic packages, tools, didactic strategies, etc. are designed, tested, and validated so, once improved, can be diffused to the school reality.

The design-based research process is often presented in two stages: (i) The research process until a new product is created and the successive improvements, and (ii) delivering knowledge so that new principles can contribute to the new design process. The product is not only composed of material tools (textbooks, video, computer apps or simulations, etc.) but also composed of processes and procedures (teaching methods, schoolchildren scheduling plans, didactic strategies, etc.).

On the other hand, “didactic engineering” (DE) was introduced in the French Didactic of Mathematics in the early 80s to describe a research approach in mathematics education comparable to an engineer’s work. Since its origin, didactic engineering was fundamentally connected to educational interventions (experiments) in classrooms, usually sequences of lessons. These experiences were guided by and tried to test some theoretical ideas. That is, DE is conceived as the design and evaluation of theoretically justified sequences of mathematical teaching, with the intention of triggering the emergence of some educational phenomena, and developing teaching resources scientifically tested. DE is based on the theory of didactical situations [31,32] and involves the experimentation (classroom teaching interventions) and validation via a priori and posteriori analysis. In this manuscript, a combination of DBR with DE (which have common terms, as stated in literature [33,34]) is used.

3.2. Participants and SAMPLING

By the year 2018, a group of five cooperating students voluntarily conform a mentored “designer team” (supervised by the authors of this manuscript). Such a team should act in coordination with different primary education schools (CEIPs) of the province. In the 2017/18 academic year, three different CEIPs were interested in the implementation of EERs. However, the demand highly increased in 2019 and the project was expanded to interact with conventional courses, so more students could cooperate on the initiative. This project is being developed at the University of Cadiz. Students belong to the “Primary education degree” and have a mean age of 21 years. Two lines are actually being developed:

• Design and implementation of EERs: This line is being developed by a group of five cooperating students in close relation with on-service teachers at schools. They have already finished their conventional curricular education in the university degree, so this project acts as a specific and additional didactic-mathematic formation (with a strong emphasis on establishing connections by curricular integration methodologies). This line is in the core of the present manuscript.
• Didactic analysis of EER experiences: This line uses the recorded data of the first line to share real didactic experiences with other trainee teachers (so more students could benefit). As EERs have been designed to mobilize mathematic skills and knowledge, the transcribed situations can be used to develop a variety of items of the conventional trainee teachers’ curricula. This line is out of the focus of the manuscript, but some results have already been published [17] and is briefly presented here to provide a full view of the picture.

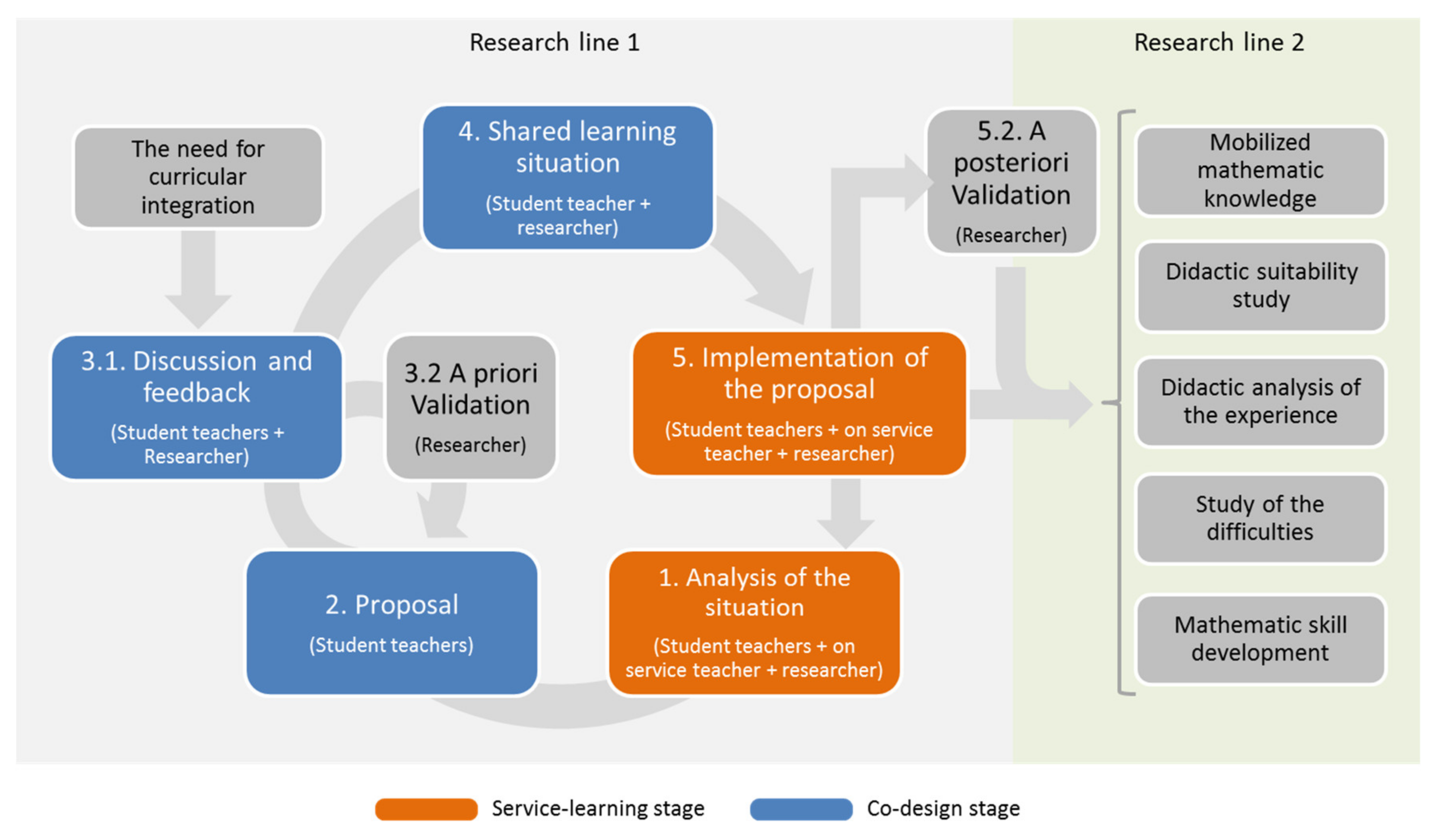
Figure 2 summarizes the procedure and methodologies used in line 1, emphasizing the use of the results provided by this line to ease real didactic situations that are used in conventional lectures with students. As presented in Figure 2, implementation of the designed EER occurs after a co-design phase, while service-learning stages are present at the beginning and the end of each cycle.

While the co-design of the EERs is carried out by a group of five cooperating students, the designed experiences are implemented in different schools of the province (to date, seven CEIPs have been cooperating with the project), so more than 200 schoolchildren have already participated in the project. The transcribed experiences are then used to carry the didactic analysis and to develop curricular elements/professional competencies of the students participating in line 2. Summarizing, to date:

• Line 1: Five cooperating students have been involved in designing, implementing, analyzing, and re-designing EERs (in touch with on-service teachers and local schools). The average age of these students was 23 years.
• Line 2: Results obtained in line 1 have been shared with other trainee teachers, showing the different didactic experiences in conventional lectures. Up to 142 students, with a mean age of 21 years, have participated in this line in the 2019–2020 and 2020–2021 academic years.
• As a consequence of the interaction with local schools, one meaningful byproduct of the project is that more than 200 schoolchildren have participated in EER experiences. The implemented EERs were designed and implemented in all primary education levels, so schoolchildren aged between 6 and 12 years have been participating in the different implementations.

The presented EER was co-designed by one of the five cooperating students, as a previous step of her final career work, let us label her as “cooperating student #4” (CS#4). She participated in designing EERs (as part of the first stage of the 2-year cooperation) prior to designing a whole EER by herself. The experience of this student takes the authors’ attention due to her initial bad emotional relation with the mathematics discipline, while exhibiting high performance in other areas. Knowing her math-phobia, this student requested to be incorporated in the group of cooperating students as a way to go further in her didactic-mathematical knowledge. Researchers seized the opportunity to connect her fears (the mathematics) with her passions (the music).

CS#4 started developing EER tasks as part of the “designer team”, following the conventional cycle proposed in Figure 2 for research line 1. She had the opportunity to implement a team-designed EER during the first year of cooperation (prior to the 2020 pandemic situation). CS#4 had completed her conventional didactic-mathematic formation available in the “primary education degree”, so she was familiar with the design criteria, [27] as well as the didactic situations theory [35]. Her goal was to establish connections among the mathematic and musical knowledge in the frame of an EER, so that the narrative and tasks contained concepts, procedures, strategies, and skills from both disciplines. This report focused on CS#4 achievements due to the limited extension of the manuscript. However, achievements of the complete “designer team” are also briefly presented and discussed.

3.3. Design Guidelines

Some educational escape rooms design guidelines are available in literature [36,37], lacking, in some cases, scientific references supporting such guidelines. The literature has plenty of “false” escape rooms [38,39]: Players are accompanied by the teacher or the escape room experience is reduced to an “opening a box” in a conventional lecture. Indeed, in such kind of approaches, players do not have to escape from any room. Educational escape rooms are yet in an emergent situation, so there is still some misinformation and confusion.

3.3.1. EER Design Criteria

The previously described situation sets the point to establish specific criteria for defining “what an educational escape room is”. In this regard, design criteria were established by the authors as presented in [27], so that students can apply such criteria when designing their proposals. Design criteria can be summarized as follows:

• Dynamism: Linked problems and enigmas should be designed to be solved in a brief time.
• Performance: The EER has to be fitted to the knowledge level of the student/players. Specific difficulties, detected during the conventional course, should be addressed during the game, creating a framework where peer-to-peer discussions help overcome such difficulties.
• Communication: Once the escape experience is finished, a final discussion is needed.
• Isolation: Players have to be isolated in a room, with an appropriate scenario recreating the narrative. Communication among players and the teacher is limited to a radio.
• Continuity: EER should be meaningfully connected to the concepts that are being worked on the conventional lectures. Moreover, scenery and storytelling might create an immersive experience [40] and be used to fit with an integrated curriculum approach.
• Curriculum: Enigmas and problems of an EER should mobilize the curricula (fitting with NTCM [41]) in the case of the mathematics curriculum.
• Assessment: Finally, as in any educational experience, an EER constitutes an activity where the development of certain competencies should be assessed.

Most of these criteria are coincident with traditional parameters used for designing and scheduling conventional educational situations [42].

3.3.2. EER Experience Analysis Model

As part of the formative process, students are committed to carrying a didactic analysis of the implemented experiences. Didactic analysis is a common term used in didactic of the mathematics’ research and includes a set of concepts and methods widely used by research groups, highlighting conceptual and procedural aspects [43]. In this project, a validated model created by Font [44] has been used. However, such a model was designed to perform the mathematic education practice analysis, while the experience proposed by the student aims to be curricularly integrated. This implies that Font’s model was to be “expanded” to cover the range of music-related practices. Such “expanded model” was co-designed by the student CS#4 in touch with the multi-disciplinary team of researchers in charge (authors of this manuscript). The resulting model is briefly presented as a result in the present contribution.

3.4. Evaluation: Tracking Students’ Learning Process

Evaluation is an essential part of every learning-teaching process. When considering how to evaluate students, one has to realize that different evaluation tools should provide different information [45]. Therefore, researchers designed a sequence of tasks, deliverables, and evaluation tools to assess students’ performance. For example, to track the students’ learning process, face-to-face and online meetings were scheduled. Furthermore, deliverables were required as part of the students’ practice interaction with schools:

• An on-line diary was to be delivered on-line and weekly reviewed by the researchers.
• Three to five practical interventions were to be designed, implemented, documented, and reported to the researchers in charge (this was an agreement with local schools).

In parallel, students were co-designing the EERs according to the documented schoolchildren’s difficulties. The design of the EER was tracked by meetings and interviews with the researcher, so that the creative process was not interrupted but boosted by new ideas. That is, the evaluation is conceived here as a way to support students in their creative look for didactic-mathematical knowledge [46]. The different evaluation tools, tasks, and learning goals are summarized in

Table 1. Deliverables and evaluation tools used in this research.

Task	Type	Educational Goal
On-line diary of the activity on the cooperating school	Diary deliverable, weekly review, and feedback	Identify, track, and discuss schoolchildren’s mathematical difficulties
Design, implement, and analyze 3–5 interventions	Flexible deliverable, on-line review	Identify, track, and discuss students’ own didactic difficulties
Report of the designer team	Monthly meeting, interview	Track the state of the co-designed EER
Questionnaire	Initial and final	Track students’ attitude through the formative process
Final degree thesis	Final deliverable, evaluated by a committee	Provide evidences of promotion in the didactic-mathematical knowledge

.

4. Results and Discussion

While the co-design of the EERs is carried out by a group of five cooperating students, the designed experiences are implemented in different schools of the province (additional information on the characteristics of the sample is provided in Section 3.2). The proposed experience [47] was co-designed to be implemented in a specific school with a medium-low social-cultural and economic level. All activities were designed to fit the sixth academic course of the Spanish Primary Education curricula, as well as to fit the psychological characteristics of students aged between 11–12 years. The whole escape room experience was designed to be autonomously accomplished in 45 min. Mathematical tasks of the presented experience were designed to connect spatial orientation, spatial quantification, maps’ interpretation, problem-solving skills, and mathematical reasoning. Mathematical tasks were designed to fully connect with music-related concepts such as active audition, timbral source recognition, and music style recognition. Finally, the proposal was designed to be solved by heterogeneous groups of 4–5 schoolchildren and to mobilize contents and skills from different academic fields: Mathematics (logic, arithmetic, geometry, and spatial orientation) and music (active listening, audio-visual timbre identification, and musical genres).

4.1. Result 1: Adapting the Original Didactic Analysis Model

As a service-learning approach, the “analysis of the situation” and difficulties reported by CEIPs set the starting point of the experience (see Figure 2). Since students have to reply to the CEIP-reported difficulties, the following research questions emerge: Can an educational escape room be used to work music and mathematic knowledge? How can music and mathematics didactic situations be analyzed? To provide the initial literature, students are initiated in Font’s model [44], applying such a model to analyze pure mathematic didactic situations. Once the students became familiar with the original model, they were invited to propose slight modifications to be introduced in the model (so that it covers a music-mathematical analysis). In this section, we present the adaptation of the original Font’s model co-designed by CS#4 and the authors.

4.1.1. Identification of Musical and Mathematical Practices

This level of analysis focuses on actions with different natures (discursive, operative, etc.) that schoolchild-players have to do in order to solve the situation-problem. As the problem in the EER belongs to different branches of knowledge, the analysis of the implemented experience should differentiate musical practices from mathematics. However, when involving students in situations of curricular integration problems, it may happen that the practices developed coincide in form, not in content.

4.1.2. Knowledge and Practice

In Font’s model, it is clear that students have to mobilize mathematical concepts and skills which enable a proper interpretation of the obtained results. Therefore, the language used as well as the procedures and arguments (as a fundamental part of the mathematic reasoning) have to be analyzed.

Taking the literature as a reference [48,49], music-related declarative and procedural knowledge (“knowing that” vs. “knowing how”) should be included in this level, due to its similarity with the original design of the model [50]. “Knowing music” involves both, the assimilation of contents (facts, propositions, theoretical systems, etc.) and the development of specific skills (such as audition, interpretation, and creation [48]). Musical declarative knowledge should be meaningfully connected to the proposed situation-problem. On the other hand, a proper analysis of the musical procedural knowledge should contemplate:

• Audition: In this stage, the focus of the analysis is the identification of sounds and recognizing its relation to the timbral source (depending on the musical style). The study of both dimensions is based on the theories and pedagogical principles presented in literature [51,52], which makes an emphasis on the soundscape and the acoustic ecology.
• Composition: In a music-mathematic environment, a situation-problem may require a compositional musical dimension, which should take into account the appropriate use of musical parameters in contrast to an intuitive performance of the compositional act [48].
• Interpretation: The solution of a problem-based situation may involve the interpretation of a musical piece or a melodic pattern on an instrument. In such a case, the technique used should be analyzed, taking into account the musical interpretation [48].

4.1.3. Interactions and Conflicts

The treatment of the interactions produced during the problem-solving process must be analyzed [44]. The different activities which compose the whole EER should motivate the communication among the participants. Such communication might involve different parameters, such as cognitive, epistemic, interactional, etc.

4.1.4. Norms

This level of analysis involves the creation of norms and generalities derived from the musical and mathematical practice.

4.2. Discussion 1: Towards a Curricular Integration Analysis Model

Based on the co-design of the “expanded didactic analysis model” and as a consequence of the multi-disciplinary research team co-authoring this manuscript, the need for a concretion of the indicators which are mobilized in a curricular-integration proposal arises. Taking the previous work of J. Torres as a reference [16], we define the following indicators, which might be checked in order to validate a curricular integration proposal:

• Establishing connections between disciplines: This item aims to assess the need for mobilizing curricular knowledge from different curricular disciplines (do the students have to mobilize multi-disciplinary knowledge?). Overcoming this item means that the problem is not being solved from a “split” perception of the knowledge, but invites the student to interconnect concepts from different curricular disciplines.
• Innovative teaching-learning experience: A meaningful experience is strongly related to the procedures and strategies involved during the problem-solving practice. In this regard, the experience should mean an attractive challenge, showing clear differences with traditional problems and pushing the student to investigate new strategies to solve the problem (does the problem involve mechanical or standardized strategies?).
• Motivation: The emotional dimension of problem-solving situations should not be neglected. Therefore, this item should be used to take into account the way in which “players” are living the experience. Emotions and attitudes have a meaningful impact on the consecution of curricular objectives, and have a strong influence on determining the success/failure ratio of a problem-solving situation (does the problem foster the implication, curiosity, and motivation of the student?).
• Critical thinking: An integrated problem-solving situation should be designed to stimulate reasoning and strategy development. Activities presenting a “single way” for reasoning should be avoided, so that students have to make questions, develop strategies, and provide answers in an autonomous way (does the problem provide multiple perspectives for its solution?).
• Team working: An integrated problem-based approach should prioritize the sharing of ideas. This should mean a coordination to reach a consensus answer to the problem, so that different points of view converge by promoting discussion and reflection (does the situation promote the sharing of ideas?).

The previously mentioned items might be useful to establish and design a model to study curricular integration approaches. These items emerge as a consequence of the adaptation of Font’s model [34] to fit with a curricular integration perspective. It can be concluded that the effort made by CS#4 has been fruitful not only from the formative point of view, but from the research output achieved. The similarity of the presented items with that of the original Font’s model is a consequence of the common roots of the music and mathematical knowledge [53].

4.3. Result 2: Extract of the Student’s Proposal

The complete and original proposal made by CS#4 is stored at RODIN [47], which is the institutional repository of Research and Learning Objects of our university. A translated, reduced version is available as supplementary material #1 for this manuscript. However, an extract of the proposal is presented here so a view of its formative potential (for both the student who was designing the proposal and the schoolchild playing the game) can be assessed.

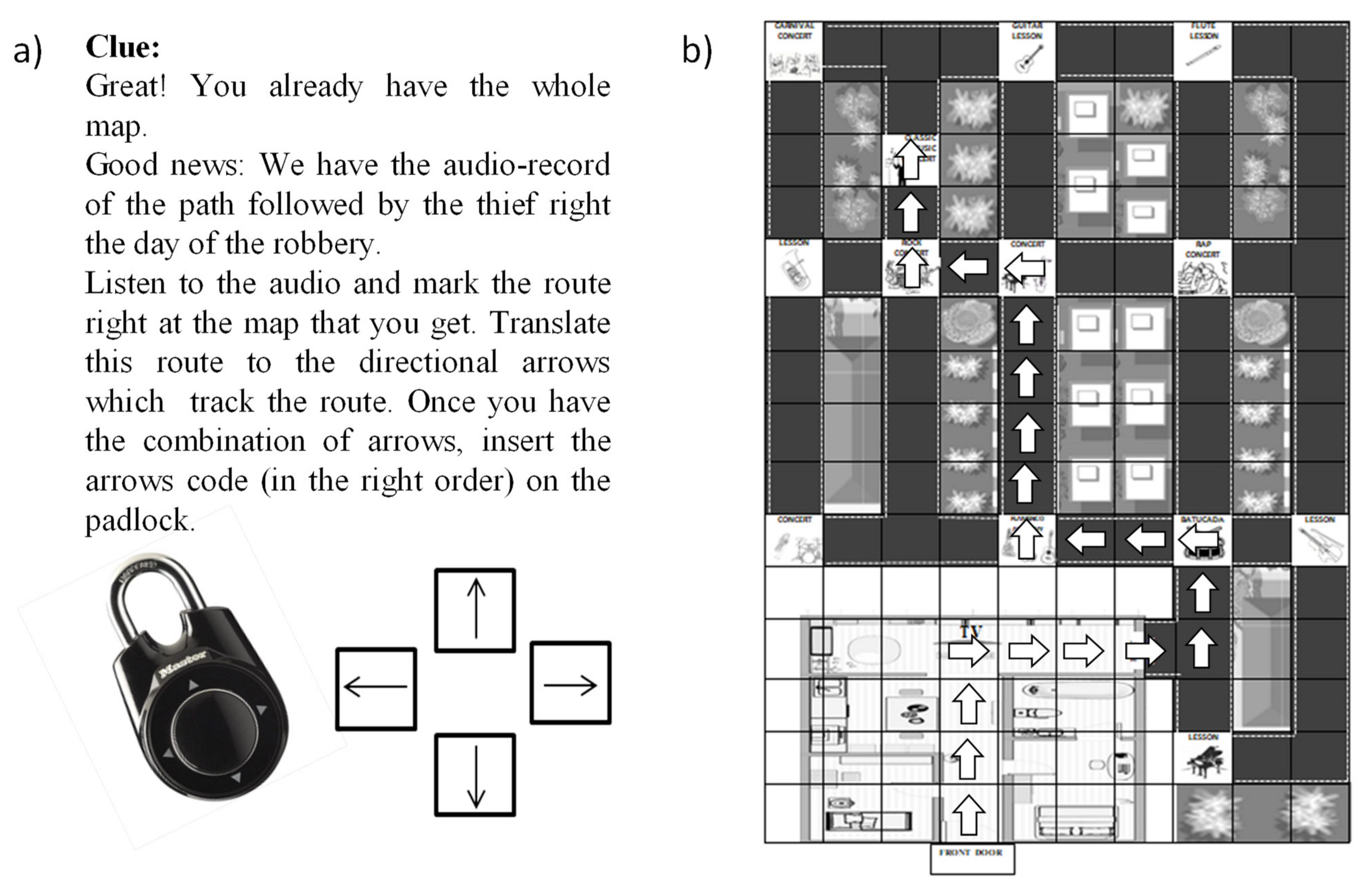
The original proposal is composed of three “missions” to be accomplished by the players during a 45 min EER experience. As the complete experience could not be reproduced here, a view of one of the activities is presented. In this activity, players can use an audio-recorded message to deduce the path followed by a thief. The corresponding audio track is available as supplementary material #2 for this manuscript. Using the audio, the schoolchild should track the thief’s path on a map (whose construction was the final activity of the previous mission). Once the path is drawn on the map, a combination of directions arises. Such a combination shall be coded in “arrows” and the code shall be introduced in a padlock to proceed to the next activity (see Figure 3).

4.4. Discussion 2: Didactic Suitability of the Proposal

In the particular case of an EER, the curricular content as well as the tools, guides, and supports have to fit with the specific characteristics of the course and school (in order to preserve the flow state). Furthermore, other key elements should be considered when analyzing the didactic suitability of a proposal. In this section, a didactic suitability analysis of the student’s proposal is carried out, according to literature [50].

4.4.1. Epistemic Suitability

Epistemic suitability aims to evaluate the implementation of institutional knowledge. From the point of view of the mathematic-related competencies, knowledge and mathematical procedures mobilized on the EER shall be considered “good mathematics” (which is useful in daily life). We consider that this item is fulfilled due to the agreement with the on-service teachers of the school. Indeed, the curricular topic (spatial-related knowledge and spatial orientation) was specifically chosen for its direct application. Concerning the music-related competencies, the knowledge and procedures mobilized in the EER refer to the active audition of sound fragments, as well as to the visual and timbral-auditory identification of different musical instruments. The latter means a concrete curricular application focused on the musical experience, an approach that should be meaningful for the students’ integral development.

4.4.2. Cognitive Suitability

The way in which the activities are distributed throughout the formative process is also an item to be considered on the assessment of the didactic suitability of a proposal. The designed proposal was developed in the frame of a conventional course and in agreement with the CEIP, so that the knowledge to be used in the room should be at a reasonable distance to what the students already knew. This is to ensure that cognitive conflicts, induced by cognitive limitations right in the moment of the experience, are overcome through experimentation and peer-to-peer discussion.

In the particular case of mathematic concepts mobilized in this proposal, the concepts are well fitting to those presented in literature [54], as part of the NTCM standards [41]. In the particular case in this proposal, the mathematic concepts can be listed as: Itinerary description and coding, itinerary building and interpretation, describing positions and displacements, representing positions and displacements in maps, etc. Musical concepts mobilized in this proposal fit well with the established standards, being interrelated with the mathematic concepts. Such interrelation is concreted in the active audition and the fragmented sound story which contributes to the identification of the itinerary. To build the corresponding itinerary, musical instrument timbral differentiation and different musical style fragments are correlated to the different locations and displacements annotated on the schematic map.

4.4.3. Media Suitability

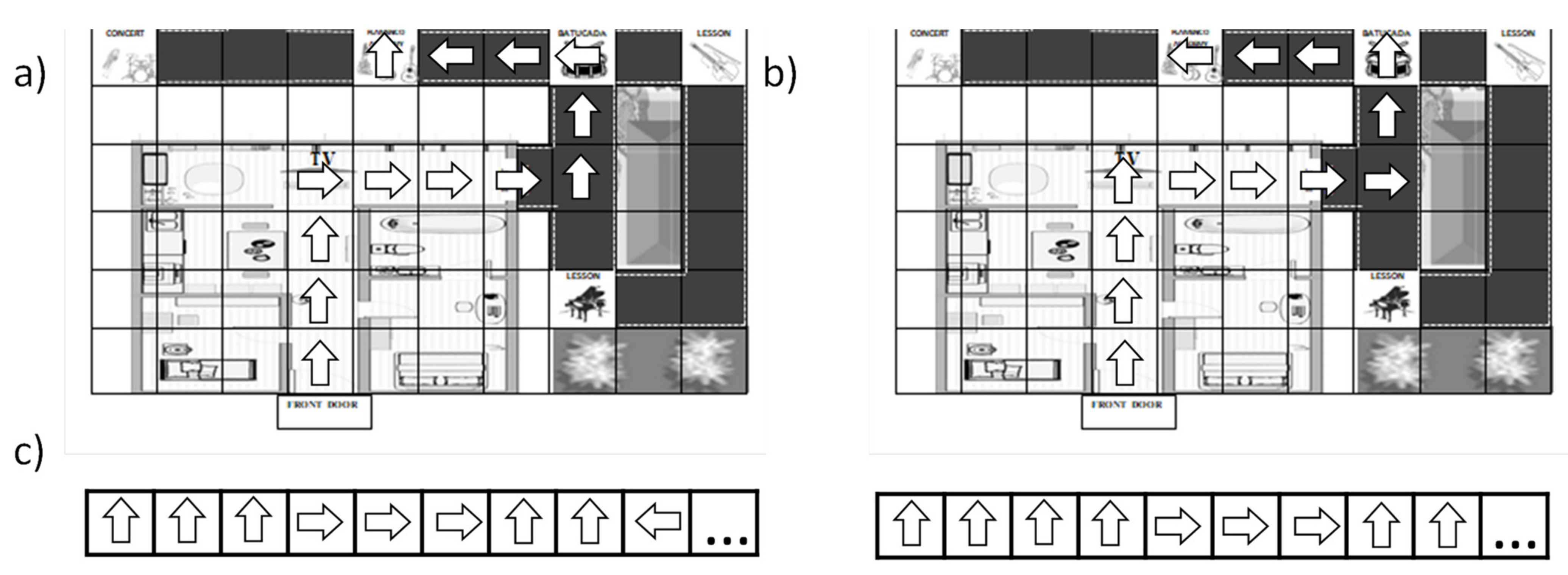
Here, the grade of adequacy of the materials and tools provided is discussed. In the proposed experience, the audio, speaker, paper, pencil, maps, padlock, radio communication, etc. are provided to the student-players. Such resources may help solve the problem by applying different strategies. Concerning the use of the tools, from a mathematic point of view, the provided resources ease the establishment of the code by providing a “squared pattern” on the map (see Figure 3b), which clarifies the possible paths, locations, and displacements. However, there are some aspects which may induce confusion. Particularly, the moment in which each “turn to the left/right” has to be made, may induce some confusions (see Figure 4). To solve this, a token/model of the thief could be provided, fixing its original position so that no mistakes on the final code are induced (note that both final codes are similar, differing on the starting position). Therefore, extrinsic difficulties could be presented on the experience, induced by the misinterpretation of the provided tools.

Concerning the musical resources used in the proposal, students would use a speaker to listen to the sound-story. Auditory and visual tools (which are the speaker and schematic maps) should provide enough support to solve the activity. The provided sound story can be reproduced on demand. Again, there is a complementary music-to-mathematics relation so that auditory and visual tools are meaningfully connected.

4.4.4. Interactional Suitability

Interactional suitability is the grade in which the activity allows identifying and solving semiotic conflicts by negotiating meanings. The presented proposal aims for peer-to- peer discussions since the experience is designed for five simultaneous players, which should negotiate mathematical terms such as “left”, “right”, “turn over”, “in front of” or “advance”. Relative positions and displacements must be coded in order to accomplish the activity, so the different perspectives of the map may induce discussions among players. This would require a negotiation about “which one is the right perspective” in order to reach a consensus on the code to be introduced on the padlock.

In the proposed EER, musical aspects are fully related and connected to the mathematical aspects. The EER requires the recognition of sound sequences in the sound story which determines the displacements in the schematic map in Figure 3 (the appropriate sequence of sounds-displacements will provide the code to the next activity of the EER). The potential interactional conflicts should be addressed by negotiation and discussion in a way that evidences auditory skills and the musical background of the students as a fundamental part of the activity, which are needed to accomplish the mission.

4.4.5. Emotional Suitability

The grade of motivation and interest of the students during the formative process should also be assessed. We consider that the proposed experience has an optimum degree of emotional suitability due to the originality of the proposal, the multi-disciplinary approach, and the game-based-learning perspective. However, as no implementation of the proposal was possible (due to the COVID-19 pandemic), this item could not be properly assessed. Even so, previous experiences designed and implemented by students in the frame of the mentoring program [27] provide enough evidence of meaningful emotional suitability of EERs.

4.4.6. Ecologic Suitability

Finally, the grade of fitting of the experience to the educational project of the school should also be considered. In this regard, we consider that ecologic suitability is quite appropriate since the topic, concepts, tools, and moment of implementation were negotiated with the on-service teacher due to the co-design approach.

4.5. Professional Development Analysis

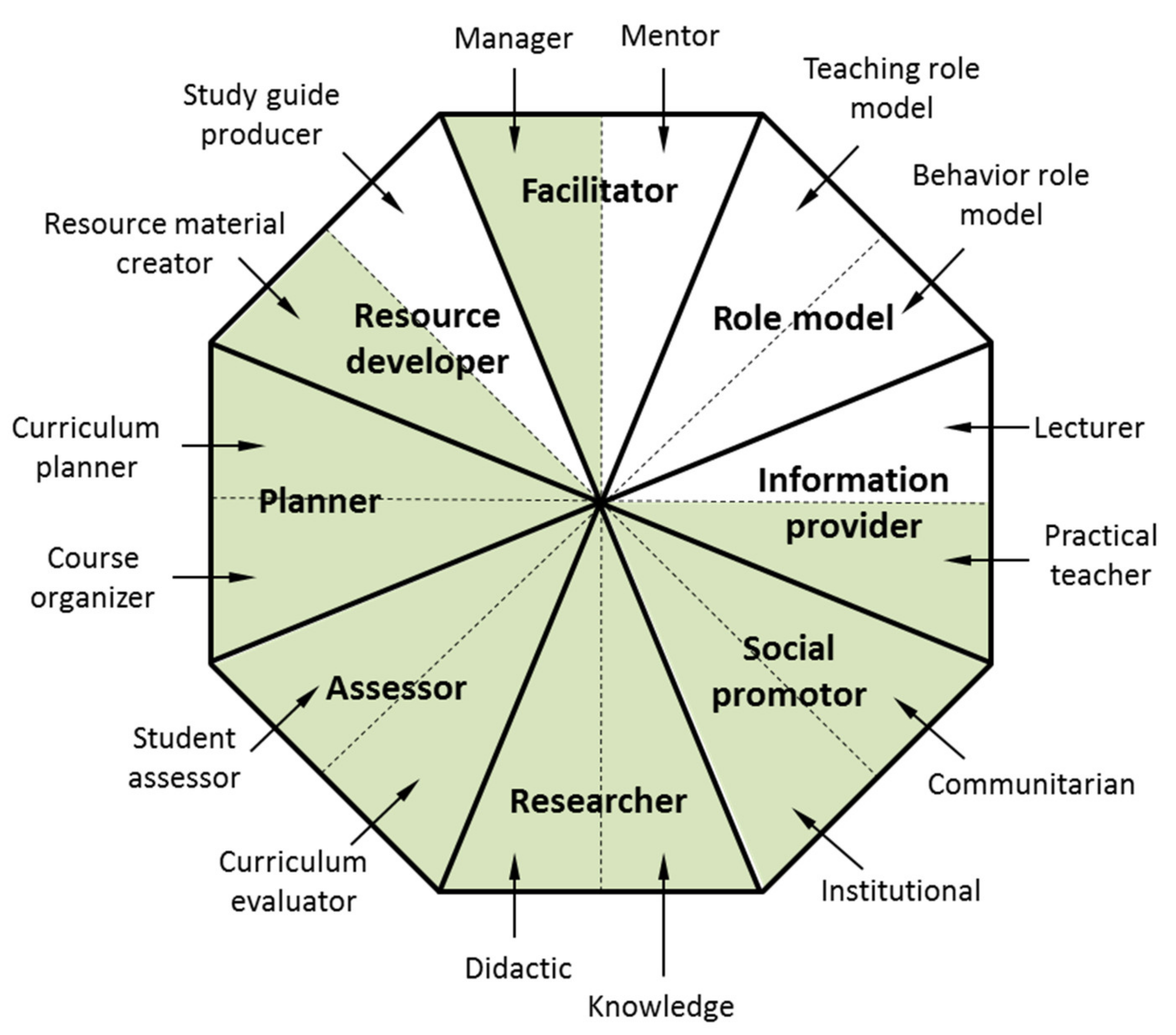
A brief analysis of the professional development reached by CS#4 during the experience is presented in this section. The “16 roles model” [55] (which is based on the discussion presented by Azcárate in literature [56]) is used here to perform the analysis. Of course, there are deeper and more complex models (such as MTSK model [57], for example). However, such models are approachless for those not specifically instructed on the model. The selected model was chosen for its simplicity, comprehensibility, and accessibility (even for non-specialized researchers), while being a validated model useful for the research in didactic of the mathematics. The selected model is schematically presented in Figure 5. According to the 16 role models, the presented experience fits with the 11 roles of the teacher, which means that the complete experience has mobilized several professional roles and skills:

• Developing an EER implies scheduling activities such as the solving time (“planner” role), as well as designing specific material (“resource developer” role).
• A proper design of the activities included in the EER should be accompanied by an analysis of the possible difficulties which may emerge during the experience (“practical teacher” role). Such activities should be designed to allow schoolchildren for an autonomous solution of the problem, displacing the “center of gravity” from the teacher to the student (“manager” role).
• A problem-based learning approach, which is in the base of serious game-based learning methodologies, involves a meaningful period of supervised self-formation, guided through the provided literature, seminars, and meetings. This stage requires months of formation on PBL-GBL methodologies (related to the “researcher” role). In this regard, the supplementary material including the corresponding research, carried out by the student, can be consulted in literature [47].
• Students are designing EERs in coordination with on-service teachers, as a result, the university and school worlds get approached. Familiars are updated about the content of the project (their child will be video-recorded, so an authorization is required), and are invited to follow the evolution of the project. As a result, the “social promotor” role is developed.
• Finally, students have to consider the curricula during the design of the EER. Once designed, the implementation of the EER is video-recorded and this resource is used to evaluate not only the schoolchild knowledge, but the EER performance itself (connecting with the “assessor” role).

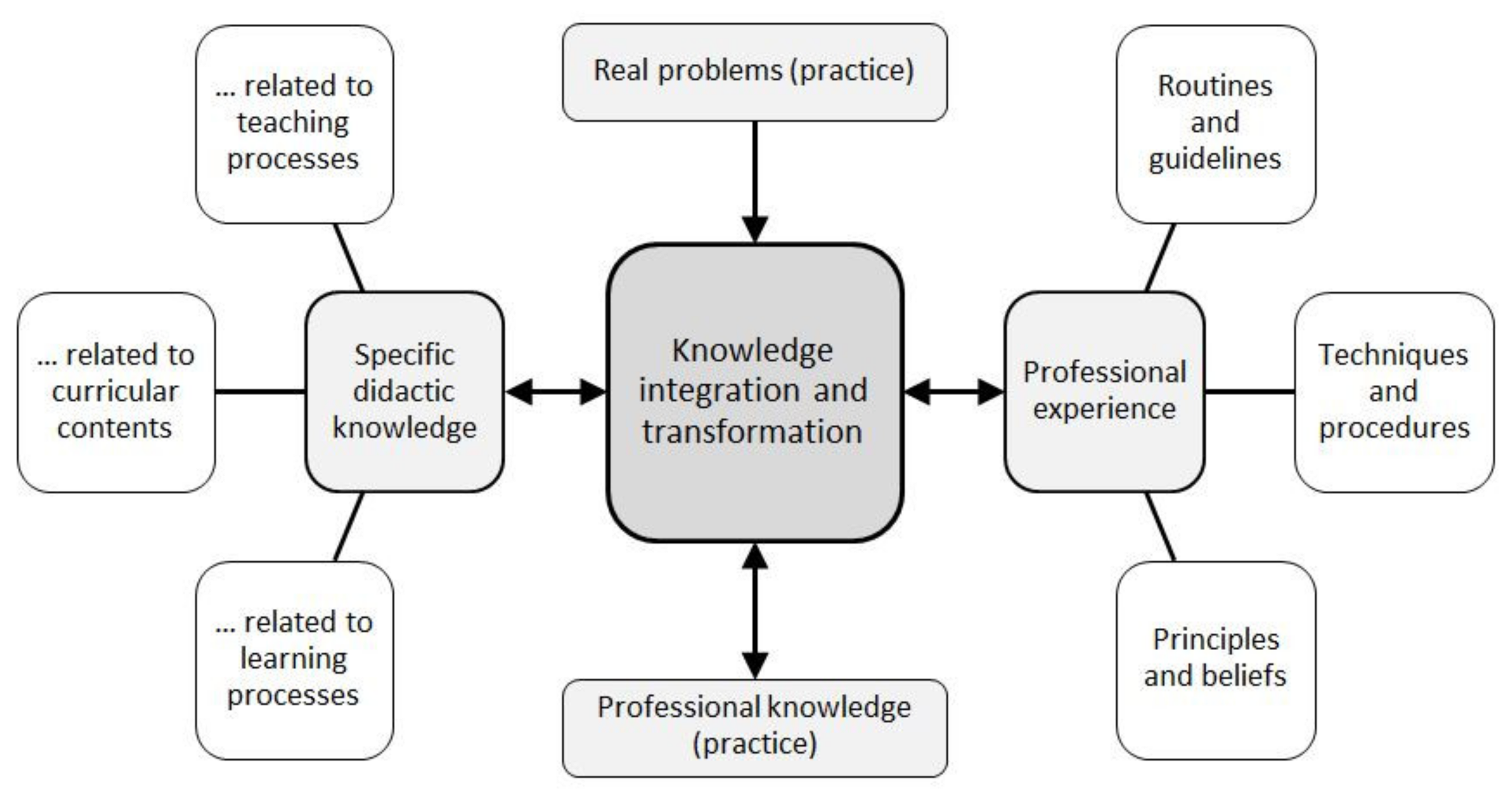
The previously described roles are strongly related with the development of professional competencies, which are developed by integrating and transforming the knowledge acquired during professional experiences, solving real problems, and mobilizing didactic-professional knowledge (according to literature [58], see schematic in Figure 6).

Students develop different professional competencies depending on the moment of the experience: (i) Professional competencies needed while implementing EERs:

• Meet and promote interaction processes, cooperation strategies, and team-working.
• Promote educational (to an active and democratic citizenship) and scientific values, fostering the democratic education of citizens and the practice of critical social thinking.
• To identify, report, and collaborate in the treatment of learning difficulties by identifying and planning the resolution of educational situations that affect students with different abilities and different learning rates.
• Evaluate the curriculum content and teaching resources and its influence on the promotion of basic skills in students.
• Communicative and interactional skills.

Additionally, (ii) professional competencies needed while developing EERs:

• Meet the curriculum.
• Understand the basic principles and fundamental laws of the experimental, social, and exact sciences.
• Develop and evaluate appropriate teaching resources able to promote the acquisition of basic skills in students.
• Problem-solving skills.
• Establishing connections among subjects and developing a problem-solving perspective strongly related to real problems.

4.6. CS#4 Achievements: A Love-Hate Tale

While we have presented several data concerning the whole students’ “designer team”, this manuscript focuses on the formative process of one of the students (CS#4) due to her initial “math-phobia”. To provide evidences of the evolution on the perceptions of CS#4,

Table 2. Extract of questionnaires provided to cooperating student #4 (CS#4) and a comparison of her responses with other students before and after the experience.

Question		Before					After
What do you understand by “knowing mathematics”?		Problem-solving skills					Reflection and justification based on mathematics arguments. Strategy building.
What is the importance of the emotional factors when teaching mathematics?		Determining the interest for the subject					Determining interest and attitude to explore mathematics
What is mathematic knowledge useful for?		Some aspects of the mathematics are useful (solving operations), while other are not useful in real life					Building critical and analytical thinking
Rate this questions (1–5)		Before					After
What is your relation to the mathematical discipline?		3	3	4	2	4	4	4	5	4	4
What is the importance of establishing connections to other subjects?		2	3	5	3	3	4	3	5	5	4
Do you feel well prepared to conduct mathematics lessons?		2	2	3	3	3	3	4	5	4	4
I have enough mathematical knowledge to teach in primary education schools		2	3	4	4	3	3	3	4	4	4
I have enough didactic knowledge to teach in primary education schools		3	3	4	3	4	4	4	5	4	4
Mathematics are only useful if applicable to real-life problems		4	3	5	4	5	4	5	5	5	5
The role of the teacher is a key factor that may determine the relation with the mathematics of my future students		5	5	5	5	4	5	5	5	5	5
Rate the importance of	Making operations	5	5	4	5	5	4	4	4	4	5
	Reasoning	2	3	4	3	3	4	4	5	5	4
	Developing strategies	2	2	3	3	3	3	4	5	5	4
	Tools provided	1	2	2	3	3	3	3	4	5	4
	Algorithms provided	5	4	5	5	4	4	3	3	3	3
	Discussions	1	2	2	3	1	3	3	4	5	4
Cooperating student		#1	#2	#3	#4	#5	#1	#2	#3	#4	#5

summarizes some answers to questionnaires. Such questionnaires were provided to CS#4 prior to the delivery of the core didactic of the mathematic subjects of the conventional curriculum and once the core subjects and additional “specific formation” was delivered. Meaningful changes in the perception of this student are evidenced. Particularly, her vision of the mathematic knowledge seems to have evolved from an algorithmic-centered perspective to a perspective where reasoning, strategy development, and hypothesis/discussion dynamics are much more relevant. Comparing the responses “before and after” the whole experience is delivered, we observe that:

• CS#4 relation with the mathematical discipline is meaningfully improved (her rating rises from 2 to 4).
• Her perceived importance of establishing connections to other curricular subjects and topics has been meaningfully increased (rating rises from 3 to 5).
• The student has gained self-confidence and she feels more comfortable about her didactic and mathematical knowledge when referring to teach in primary education schools. This is particularly important due to the motivations presented in the Introduction (see Figure 1).
• Her perception about the usefulness of the mathematical knowledge in real life situations, which was already high, has also been increased.
• The relative importance attributed to “making operations” decreased from 5 to 4. Therefore, she seems to have understood that “knowing mathematics” is much more than “making operations”.
• In connection to the previous point, her perception of the importance of “mathematically reasoning” and “developing strategies” rise from 3 to 5 in both items. This constitutes a major evidence of a meaningful change of her perception of the discipline.
• In addition, the importance attributed to the use of “algorithms provided” and “tools provided” are inverted: “Tools provided” items rise from 3 to 5, while “algorithms provided” items decrease from 5 to 3. This is also a meaningful change in her perception of the discipline, since the mathematical knowledge now seems to be a much more “applied” version than before.
• Finally, a dramatic increase in the role of peer-to-peer discussions is evidenced (the score rises from 2 to 5). This is probably due to her experience when implementing other EERs [27], where peer-to-peer discussions are evidenced to contribute to horizontal mathematization.

We can summarize that, while some insecurities still remain (concerning her perceived ability to conduct mathematical lessons), connections to other subjects and areas are more relevant for her, so that the experience seems to have fostered her capacity to “identify mathematical knowledge” in a wide variety of situations.

On the other hand, her perception about the applicability of mathematical knowledge has gained some relevance, making emphasis on connections among curricular areas and application of the knowledge in real-life scenarios.

4.7. Students’ Achievents: Educational Goals

The whole group of students was invited to develop their final degree thesis to complete the whole formative experience. This was a challenge for most of these students. Indeed, the participant students perceive the mentoring program as an opportunity to improve their mathematical skills, but most of them felt some anxiety with the idea of developing the final degree thesis focusing on the mathematical knowledge. The final degree thesis should consist of a 50–60-page document summarizing their experience, showing the theoretical background and evidencing a learning process. Furthermore, it should be defended on a committee and was mandatory to obtain the teacher’s degree. 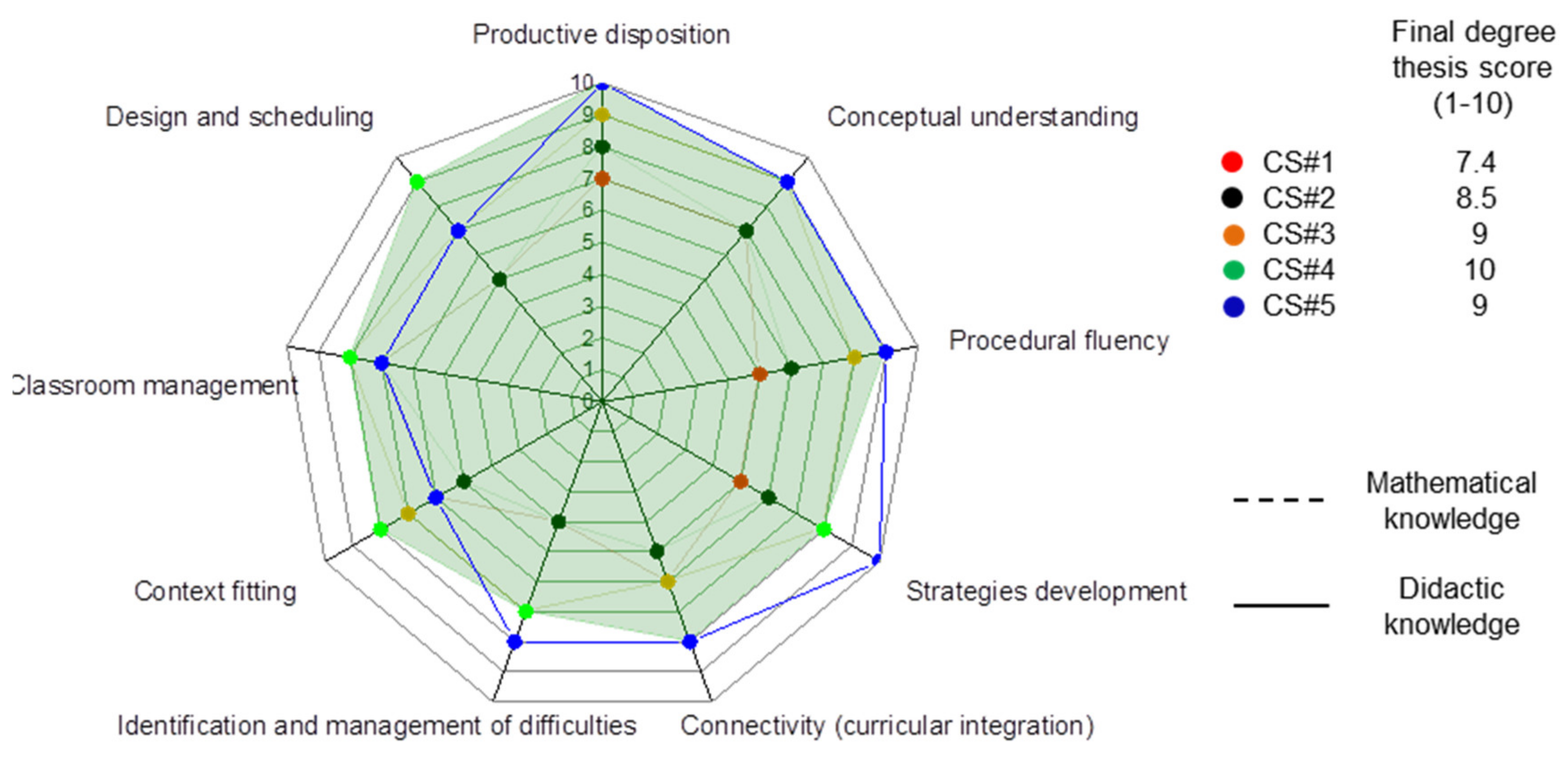Figure 7 shows a radar plot of the evaluation of professional skills corresponding to all the participant students. Professional didactic-mathematical knowledge was evaluated using the tools and tasks presented in Table 1. To the authors’ consideration, the final degree thesis committee reports are a key aspect fact to be considered for the evaluation of the performance of the whole experience, thus it is included in Figure 7.

Examining Figure 7, it can be observed that students succeed on all of the items related to mathematical knowledge. Concerning the didactic knowledge, some students still fail in identifying and managing the schoolchildren difficulties. While the size of the sample is too small to provide fully reliable conclusions, Table 2 and Figure 7 provide enough evidences of a positive evolution on both: Didactic and mathematical knowledge of participant students.

• Mathematical knowledge:

  ◦

  Conceptual understanding aims to check the global domain of the different mathematical concepts and its different interpretations. This is what is conventionally said to “know mathematics” in its most traditional way. Data presented in Figure 7 show that all students are presenting good/very good conceptual understanding.

  ◦

  Procedural fluency is related to the ability to efficiently use the mathematical concepts, regarding the precision and flexibility. Figure 7 shows meaningful differences among students, which can be explained by a different level of mathematical practice.

  ◦

  Strategies development is another item which shows meaningful differences among students. This item is related to the ability to identify a variety of perspectives to solve a problem, which should lead to the choice of an optimum and viable strategy. Most of the students still show a wide margin for improvement in this field.

• Didactic knowledge:

  ◦

  The ability to connect mathematical knowledge to real-life situations is taken into account in the “connectivity” item. This item is particularly important in a curricular integration approach. It can be observed that all the participant students’ score above 5/10, but some students still show limited ability to re-contextualize the mathematical knowledge.

  ◦

  The ability to identify and manage schoolchildren’s difficulties is closely related to students’ self-abilities to overcome their own difficulties. This may explain the obtained result, with two groups of students clearly differenced. While students 3–4-5 show a remarkable ability in this field, students 1–2 fail in identifying schoolchildren’s difficulties, which is coherent with the results obtained in the “mathematical knowledge” evaluation.

  ◦

  Context fitting and didactic transpositions are key professional skills. Teaching has to be adapted to the specific knowledge of the learner. Indeed, teachers should explore the previous ideas of the schoolchildren prior to the design of a lesson. In our experience, students’ ability to fit to the context could be considered as “good” for all participants.

  ◦

  Classroom management skill is the best scored skill in average. It is related to the ability to manage conflicts, structure schoolchildren, and coordinate the learning process in a learning-teaching experience.

  ◦

  Design and scheduling ability is related to the “context fitting ability”, since no good design can be performed without context. Scheduling a proper sequence of problems or ideas (even in a 45-min escape room) is a key aspect to be considered. Figure 7 evidences that, while all students score above 5/10, there is still some margin to improve.

• Finally, productive disposition is not an item directly associated to didactic or mathematical knowledge. However, it is a key feature in every aspect of life (indeed, a good attitude trends to influence a good problem solution). We can state that all participant students show an excellent productive disposition through the whole experience.

This result supports the usefulness of the mentoring program, evidencing that additional and specific didactic-mathematical education may help change the situation exposed in the Introduction (see Figure 1). Finally, authors would like to emphasize that the evolution of the five cooperating students was made by annotations, questionnaires, interviews, and deliverables: These items could not be attached to this manuscript (they are handwritten and/or presented in Spanish language). However, relevant evaluation notes are presented in Table 2 and Figure 7.

5. Conclusions

This manuscript presents and analyzes an extract of a proposal made by one student (a trainee teacher which was part of a five-member group). Such a proposal was designed in the frame of a mentoring program, whose aim was to explore the influence of a specific and additional formation on didactic and mathematical knowledge. Our approach was to “work mathematical concepts based on other curricular disciplines”, so that students could use their “favorite topics” to expand their didactic and mathematical knowledge.

As teachers and researchers, the authors’ aim was to establish a problem-based-learning approach by applying gamification strategies. Previous results [27] indicate that educational escape rooms can be used to foster cooperation, motivation, and exploration, thus becoming an optimum tool for working mathematic-related content. Therefore, students were invited to design (in cooperation with different schools) educational escape rooms, covering curricular aspects. A co-design strategy with a service-learning perspective allows fitting the escape room design to the real needs of the schoolchild, also stimulating the implication of the participant students in the process.

This study focuses on the formative potential of “co-designing educational escape rooms in a service-learning perspective”, evidencing the mobilization of professional skills and knowledge and showing a boost on the importance attributed to “reasoning”, “development strategies”, and other mathematic-related skills, which were previously perceived as secondary skills when considering the importance of “using algorithms”. Furthermore, the mentoring program has been proven as useful for developing students’ professional didactic-mathematical knowledge.

Analyzing our original objectives, we consider that: (i) The experience stimulates the capacity to use mathematic knowledge in non-conventional contexts, (ii) the student shows a positive evolution in their relation with the mathematic knowledge, and (iii) mathematical competencies have been meaningfully connected to other disciplines in the frame of an integrated curriculum approach. Therefore, we consider that educational escape rooms are suitable tools to build problem-based situations with an integral curriculum perspective. We also consider that co-designing educational escape rooms fosters the development of trainee teachers’ professional skills, mobilizing specific professional didactic-mathematical knowledge.

On the other hand, during the experience accumulated experience (considering the presented manuscript and previously published experiences [27]), we have detected three main obstacles to overcome in order to develop/apply EER. The first is to establish a clear narrative with a strong relation to the problems presented in the EER, so that all activities are narratively connected in a meaningful way. The second is to create connections among subjects, promoting an integrated view of the knowledge. In addition, the third is the design of real and meaningful problems which requires reasoning, experimentation, argumentation, and calculation, overcoming the pen-paper based activities.

During the experience, key didactic-mathematical professional skills were evaluated. In doing so, we have detected specific skills whose development requires special attention in future editions of the mentoring program. Thanks to this perspective, we have detected that the key competencies mobilized by the students during the development process were: (i) Meeting the curriculum, (ii) understanding the basic principles and fundamental laws of the experimental, social, and exact sciences, (iii) developing and evaluating appropriate teaching resources able to promote the acquisition of basic skills in students, (iv) developing problem-solving skills, and (v) establishing connections among subjects and developing a problem-solving perspective strongly related to real problems.

Finally, the 2020 pandemic scenario prevents us from implementing this specific experience. However, other EER experiences have been implemented in the frame of the mentoring program. As a result, we consider that the key competencies mobilized during the application of an EER experience are: (i) Meet and promote interaction processes, cooperation strategies, and team-working, (ii) promote educational and scientific values (for an active and democratic citizenship), fostering the democratic education of citizens and the practice of critical social thinking, (iii) identify, report, and collaborate in the treatment of learning difficulties by identifying and planning the resolution of educational situations that affect students with different abilities and different learning rates, (iv) evaluate the curriculum content and teaching resources and its influence in the promotion of basic skills in students, and (v) communicative and interactional skills.

Future editions of the mentoring program should emphasize on developing specific students’ skills. Particularly procedural fluency, strategies development, identification of difficulties, and problem design are skills to be specifically attended. We consider that designing and implementing educational, integrated, problem-based escape rooms constitutes an optimum procedure to expand students’ competencies, as well as to explore didactic/mathematic knowledge in a meaningful way. Furthermore, this procedure allows students to explore and grow over their own limitations, while providing a service to local schools.