Next Article in Journal
Quantitative Comparison between Traditional and Intensive Face-to-Face Education through an Organizational Model
Next Article in Special Issue
Cross-Cultural Comparisons of Home Numeracy and Literacy Environments: Canada, Mexico, and Chile
Previous Article in Journal
Remote Teaching in Professor Training: Three Latin American Experiences in Times of COVID-19 Pandemic
Previous Article in Special Issue
Facilitating Preschool Children’s Mathematics Development in China, Japan, and the United States: Is the Classroom Library Considered?
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Education Sciences
Volume 11
Issue 12
10.3390/educsci11120819
education-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Parental (STEM) Occupations, the Home Numeracy Environment, and Kindergarten Children’s Numerical Competencies

by
Anna Mues
*,
Efsun Birtwistle
,
Astrid Wirth
and
Frank Niklas
Department of Psychology, LMU Munich, D-80539 München, Germany
*
Author to whom correspondence should be addressed.
Educ. Sci. 2021, 11(12), 819; https://doi.org/10.3390/educsci11120819
Submission received: 20 October 2021 / Revised: 9 December 2021 / Accepted: 13 December 2021 / Published: 16 December 2021
(This article belongs to the Special Issue Mathematics Education: At Home and in the Classroom)
Browse Figures
Versions Notes

Abstract

:
Children’s early numerical competencies are of great importance for later academic achievement. Young children gain these competencies in the context of the home numeracy environment (HNE). Additionally, child characteristics and families’ socioeconomic status (SES) are associated with children’s competencies. In this study, we investigated parents’ occupations (i.e., STEM or non-STEM occupation) as a specific aspect of the SES to understand whether parental occupations are associated with children’s numerical competencies and whether such an association may depend on the HNE. We analysed data from a sample of N = 190 children (Mage = 63.58 months; SD = 4.41) at two measurement points. Correlational analyses and crossed-lagged models were conducted to predict children’s numerical competencies by a global measure of the HNE and parental STEM vs. non-STEM occupations. We found significant associations between parents’ learned and current occupations and the HNE. Further, significant associations between parents’ learned occupations and children’s numerical competencies were observed. However, parents’ current occupations were not significantly associated with children’s numerical competencies. Consequently, more specific facets of the SES instead of a global measure seem to be associated with children’s numerical competencies. A greater focus on specific differences between family characteristics and their potential impact on children’s HNE and the development of their numerical competencies seems expedient.

1. Introduction

1.1. Family’s Socioeconomic Status and Children’s Early Numerical Competencies

In the context of early child development, many studies consider the socioeconomic status (SES) of a family to be a key aspect [1]. Most of the research on SES-based disparities in children’s early academic skills and development focuses on literacy and language skills [2]. In comparison, numerical competencies, such as the comparison of numbers, the knowledge about counting principles and cardinality, and solving arithmetic problems, have not been the focus of many studies [1], despite being of great importance for later school achievement [3]. When children start school with lower numerical competencies, these school-readiness disparities often persist, which shows the fundamental role of early numerical competencies for children’s later advanced mathematical skills [4,5].
Several studies indicate that individual child characteristics and later school achievement are associated with families’ SES [1,6,7]. For instance, poverty and low parental education seem to be associated with children’s poor outcome scores, whereas parents with higher income and education often provide a higher-quality learning environments by having more conversations with their children, being more responsive, and providing more teaching experiences, all of which leads to better child performance [1,8,9].
Here, the SES can be conceptualized as a multidimensional construct that acts as an indicator of a family’s economic and social resources. SES is mostly measured with three objective parental factors: income, occupation, and education [10]. In addition, neighbourhood, social standing, and prestige are often considered as SES estimates as well [1,10].
Studies showed that differences in children’s early numeracy competencies depend partly on their SES background and that such differences are found even for very specific mathematical abilities, such as number sense or spatial skills [6,11]. Starkey, Klein, and Wakeley [12] reported significantly greater mathematical abilities in children from a middle-income family when compared to a lower-income family group in 10 out of 16 tasks assessing mathematical knowledge (e.g., ordering, comparing numbers, addition or subtraction). Jordan, Kaplan, Locuniak, and Ramineni [13] examined children’s basic number skills and mathematical achievement during kindergarten and first grade and showed that these seem to be associated with SES, with children from a higher income group achieving better outcomes than children from low-SES families.
Most studies consider a global SES construct in their analyses [1,14,15]. However, in their review, Elliott et al. [1] discussed specific aspects of SES, such as parental educational attainment, education, occupation, or income, as mediating factors for children’s numerical achievement and development. They pointed out that it would be useful to take a closer look at individual aspects of SES and not only to examine SES as a global construct to be able to establish more specific connections with child outcomes [1].

1.2. Parental Occupation and Other Aspects of Socioeconomic Status

In recent years, several studies focussed on the role that parents play in children’s development of numerical competencies [16,17,18]. Here, studies differ in their usage of various SES measures [10,19], and the most common aspects (i.e., parental occupation, education, and income) seem to be highly correlated [20,21].
Parental occupation and education seem to be important factors for students’ mathematical achievement [18,22,23]. For instance, Omolade, Kassim, and Modupe [23] showed that parental education was the best predictor of students’ achievement, followed by parental occupation and motivation.
Within data from the PISA study in 2012, the OECD established an association between parental occupations, students’ mathematical performance, and their learning [22]. Students whose parents had professional occupations outperformed students whose parents worked in elementary occupations in mathematics. Chi et al. [24] found similar results for students’ scientific competencies. Here, both mothers’ and fathers’ occupations were significantly linked to children’s scientific competencies. Differences between mothers’ and fathers’ socioeconomic characteristics and children’s mathematical outcomes or achievement have been considered in only a few studies so far [14,24,25,26,27].
The association between parental occupation and education and children’s mathematical achievement was also affirmed in longitudinal data. For instance, Shoraka et al. [18] used data from the Longitudinal Study of American Youth to examine the direct effect of parental education and occupation in STEM fields on students’ achievement gap in mathematics. As in the OECD report [22], students with at least one parent who was working in a professional occupation achieved higher mathematics scores compared to students whose parents were not working in professional occupations while controlling for students’ gender and parents’ education. Moreover, especially for parents working in STEM fields, a positive effect on students’ mathematical achievement was found.
Only a few studies addressed the differentiation of parental STEM vs. non-STEM occupations and the interrelation with children’s mathematical competencies [17,18,28]. In most cases, this relationship was examined with high-school students’ competencies and their career aspirations, rather than with early numeracy development [17]. Plasman et al. [17] provided a detailed overview that shows a positive effect of parents’ STEM occupations on students’ mathematical achievement.
Our study analyses the differences in parents’ learned and current STEM or non-STEM occupations. Parents’ learned occupations (German term: erlernter Beruf) are referred to as the professions that parents have learned and the skills that were gained in the course of training or studies. Parents’ current occupations refer to the professions that parents currently are working in, which they do not necessarily have to have learned. This distinction relies on previous reports that point out that, in Germany [29], in the year of 2005, 52% of the individuals working in the STEM field had actually been trained as STEM professionals, but 36% of the people working in STEM-related occupations were not specialised in STEM. Consequently, several people working in STEM professions have not learned STEM-related subjects or gained specific skills through training. These figures underline the need for a differentiation between the learned and current occupations of parents. It can be assumed that parents’ mathematical interactions with their children will vary depending on parents’ own experiences, attitudes, and beliefs [30]. As parents’ experiences are closely associated with both their occupational training and their current occupation, it is very likely that parents’ occupations will impact children’s numerical competencies through such mathematical interactions at home [1,17]. Consequently, parental occupation and the differentiation between learned and current occupation as specific aspects of the SES may be promising predictors of children’s early numeracy development.

1.3. Home Numeracy Environment

During early childhood, a child’s individual development is predicted by different aspects of their learning environment, such as kindergarten education [31], and the experiences that they make in the context of their family, which are summed up in the home learning environment [3,32]. According to Bronfenbrenner’s ecological theory [33], proximal aspects in children’s environment, such as direct parent–child interactions, are important for the development of children’s competencies. Similarly, Vygotski’s [34] idea of learning in social contexts highlights the importance of children’s experiences in their homes and of family characteristics, such as parental SES.
Experiences in the early years are not only important for the development of general knowledge, but also for developing domain-specific competencies [31]. In recent years, several studies [4,13,14,35,36] reported that children’s early numerical skills predict later mathematical skills [4,37]. Here, one of the predictors of early mathematical and numerical abilities is the home numeracy environment (HNE) [5,38]. The HNE can be defined as all of the aspects in the family that support children’s early mathematical learning, such as the frequency and quality of mathematical parent–child interactions, mathematical resources at home (e.g., books with numbers), and parental attitudes towards mathematics and teaching mathematics at home.
The HNE, especially in terms of mathematical activities and support at home, can be differentiated into formal and informal aspects. LeFevre et al. [39] described formal aspects as using number books and practicing number skills. These aspects are defined through active engagement of parents in numeracy with the goal of teaching their children about mathematics. On the other hand, informal aspects include the frequency of mathematical games and applications in everyday life that incidentally support children’s numeracy competencies [39]. For example, parents who play dice games with their children more frequently provide them with opportunities to learn numerical content, such as counting or adding, as well as number symbols and number words, in an environment that is fun and leads to greater motivation [40,41]. Both aspects of the HNE seem to support children’s mathematical competencies [1,39,42].
For German-speaking countries, only a few studies examined the construct of the learning environment at home and its impact on children’s domain-specific development [3,32,37,38,43]. Anders et al. [32] showed that mathematical competencies at age three are significantly predicted by the home literacy as well as the home numeracy environment. Further, Niklas and Schneider [37] found the HNE to be a reliable predictor of early initial mathematical abilities and children’s further development and competencies, even after controlling for several variables, such as SES, intelligence, and linguistic variables. These results are similar to those presented by LeFevre et al. [39], who also found significant correlations between the HNE and numerical competencies of children.
The HNE was investigated by several researchers as a predictor of numerical skills in its association with the SES [1,15]. Saxe et al. [44] were some of the first researchers to empirically investigate parents’ numerical practices in the context of varying SES. In their study, they found only minimal differences for the frequency of home learning activities that parents provided to their 2- and 4-year old children. However, higher levels of parental education were associated with greater engagement in more qualitative activities. Further, parents with a high SES reported including numerical activities in everyday life more often than other parents, albeit parents with a low SES engaged more often in formal schoolwork to improve mathematical skills directly [41].
In summary, evidence suggests that parental SES seems to be associated with parent–child interactions and, thus, the home learning environment and the HNE, which, in turn, are connected to children’s mathematical learning [1].

1.4. Early Development of Numerical Competencies in the Home

Different studies show that early numerical competencies, such as knowledge about numbers and quantities, are important predictors for later mathematical achievements [13,45]. Children who are better with counting, matching specific amounts of objects to numbers, or identifying more number symbols earlier than other children in their development [4] “also do better in mathematics later at school” [37] (p. 330).
Sarama and Clements [46] identified different important domains of numerical abilities. Here, numeracy skills can be described as a variety of number-based skills, including solving arithmetic problems, comparing numbers, and knowledge of counting principles and cardinality [4,35].
Despite children’s innate mathematical abilities [4], they develop and learn further mathematical competencies through interaction with their environment, and thus with people, objects, and events. Different opportunities (e.g., interacting, playing, discussing) can support their learning about numbers or may even engage them in advanced numerical thinking [38].
Various studies [39,47,48] examined children’s performance in relation to mathematical activities that they experience at home or to their parents’ characteristics. For instance, LeFevre and colleagues [39] analysed the associations between the frequency of mathematical parent–child activities, parental expectations and attitudes towards mathematics, and children’s early mathematical learning. Here, mathematical activities predicted children’s mathematical fluency significantly. Similarly, Kleemans et al. [47] showed that later mathematical achievement of children was associated with numeracy activities between parents and children. The more frequent such activities are, the better children’s early numeracy skills, such as mathematical knowledge and fluency, will be.
Therefore both parent–child activities, such as playing, reading, painting, or visiting a library, and the social characteristics of parents, such as the SES and, thus, their education, their income, and their occupation, have a great impact on the development of children’s early mathematical skills [39,49].

1.5. The Present Study

Although the impact of parents’ occupation on students’ mathematical and STEM achievements has been explored in several studies, most of these studies focused on late childhood and adolescents [16,22,24,27]. Assuming that parents act as socio-cultural agents and influence their children’s development, we expect that the expertise that arises from a scientifically based profession should have a specific impact on the development of the mathematical competences of young children.
Accordingly, we tested the following hypotheses:
(1)
We hypothesize that parents’ learned STEM vs. non-STEM occupations are associated with the HNE and with children’s numerical competencies. Here, the HNE acts as a mediator.
  • We hypothesize that parents’ learned STEM vs. non-STEM occupations are associated with the HNE.
  • We further expect an association between parents’ learned STEM vs. non-STEM occupations and children’s numerical competencies.
(2)
We further expect a similar interrelation between parents’ current STEM vs. non-STEM occupation, with the families’ HNE as a mediator, and children’s numerical competencies.
  • Here, we expect, similarly to H1a, an association between parents’ current STEM vs. non-STEM occupation and the HNE.
  • Additionally, we also hypothesize an association for parents’ current STEM vs. non-STEM occupation and children’s numerical competencies.
To our knowledge, this is the first study with young children that differentiates parental occupations into learned and current STEM vs. non-STEM occupations to test their associations with the HNE and child outcomes.

2. Materials and Methods

2.1. Sample and Procedure

We analysed data from two measurement points (t1 and t2) from the first cohort of the EU-funded, 5-year longitudinal study “Learning4Kids” conducted in Germany [50]. There was a period of five and a half months between the first and the second assessments. The sample comprised N = 190 children, including 98 girls and 92 boys, with an average age of M = 63.58 months at t1 (SD = 4.41). The assessments were carried out by trained psychologists, educators, and research assistants and included standardized mathematical tests to assess children’s numerical competencies. Further, parents were asked to fill out written surveys about the HNE, the family background, the children’s characteristics, their learned and current occupations. In total, 64.2% of the families spoke German as their main language, and the parental surveys were provided in several languages to the families who did not have German as their first language.
Before the beginning of the assessments, families were contacted and informal consent was obtained through kindergartens, public places, and a professional company for study recruitment. Afterwards, formal consent was obtained at the first family visit from the parents of children in the penultimate year of kindergarten. The child and parent assessments took place at families’ homes. Ethical approval for all research activities was acquired by the European Research Council Executive Agency, as well as the ethics committee of the Faculty of Psychology and Educational Sciences at LMU Munich.

2.2. Measures

2.2.1. Children’s Numerical Competencies

Children’s numerical competencies were assessed with different tests. Here, the “Mathematik- und Rechenkonzepte im Vorschulalter-Screening” (MARKO-S) [51] that included 21 items, an adapted version of the calculation subtest of the “Test mathematischer Basiskompetenzen im Kindergartenalter” [52] comprising addition and subtraction (R, eight items), and several subtests from the “Würzburger Vorschultest” [53] assessing number sequences forward (Zfv, eight items), number sequences backwards (Zfr, six items), number symbol knowledge (Zk, eight items), and knowledge of numerical representations (VuN, eight items) were used (Cronbach’s α between 0.70 and 0.87). The items of each subtest were summarized into one scale for each measurement point. Finally, children’s numerical competencies were measured with a latent variable for each measurement point (NumC t1 and NumC t2), including all numerical subtest scales.

2.2.2. Home Numeracy Environment

The global HNE was measured as a latent variable consisting of a combination of the formal and informal HNE. The formal HNE comprised five items and the informal comprised ten items (Cronbach’s α: 0.80 and 0.75).
Parents were asked about the formal and informal learning environments that they provided for their children. For example, this included questions about the engagement in everyday mathematical activities (e.g., “How often do you talk with your child about measurements (e.g., weight, temperature, or speed)?”) or teaching of mathematical concepts (e.g., “At home, I often explain to my child how to split apples for people or cakes in pieces”). This assessment was adapted from a survey used by Niklas et al. [54]. Parents rated the HNE items on a 5-point Likert scale (e.g., several times a week to never, or does not apply at all to does apply exactly). Values of 4 to 0 were assigned accordingly, with higher values indicating a higher-quality HNE, and the mean was used for the analyses.

2.2.3. Parental Occupations and Their Allocation to STEM

Further, parents were asked about their learned and current occupations with a survey. The answers were categorized into occupations involving a STEM background or non-STEM background based on the “Aggregatbestimmung MINT-Berufe” and “Aggregatbestimmung Ingenieurberufe”, which are based on the “Klassifikation der Berufe von 2010 (KldB)” of the Job Agency of Germany [55,56]. The coding was done independently by two coders. The intercoder reliability for the mothers’ learned occupation was Cohen’s K = 0.98, and for the current occupation, it was Cohen’s Κ = 0.89. The intercoder reliability for the fathers’ learned occupation was Cohen’s K = 0.96, and for the current occupation, it was Cohen’s Κ = 0.94. All discrepancies were discussed and solved in agreement. If one or two parents of the child had a STEM background, the occupational background was coded with 1 = STEM. In case neither the mother nor the father had a STEM background, this was coded as 0 = non-STEM. For our analyses, the current and the learned occupational backgrounds (STEM vs. non-STEM) were used, and there were almost no reported occupational changes in the current parental occupations between t1 and t2 (at least none that would have changed the STEM status). All families from whom information about at least one parental occupation was available were included in the analytic sample. Consequently, only participants for whom there was no information about the occupation for either the mother or the father were excluded.
All descriptive data and the sample sizes for all variables are shown in Table 1.

2.3. Analytical Approach

All analyses were conducted using SPSS 26 [57] and MPlus 8.6 [58]. Altogether, 9 cases out of the total number of child–parent dyads (N = 190) had to be excluded from analyses of the learned occupation and 26 cases had to be excluded from analyses of the current occupation. The main reasons for the exclusion were missing values of the occupational variables and a drop-out of two families at the second measurement point, as well as only partially completed parental surveys and missing test scores of a few children.
Considering the incomplete variables of children’s assessments, the percentage of missing values ranged between 0.5% (n = 1) and 1.6% (n = 3). For the items of the parental survey, the range of the missing values was between 0.5% (n = 1) and 4.2% (n = 8). There were more missing values for the occupational variables of mothers and fathers (from 8.9% (n = 17) for mothers’ and fathers’ learned occupations to 22.6% (n = 43) for mothers’ and 21.6% (n = 41) for fathers’ current occupations). The percentages of missing values for occupational background in a family were 4.7 % (n = 9) for the learned occupation and 13.7% (n = 26) for the current occupation.
To address the problem of missing values, maximum likelihood estimations with robust standard errors (MLR) were used for all models [59]. This led to a final sample of N = 181 for the analysis of the learned occupation and N = 164 for the analysis of the current occupation.
To test whether the drop-out was biased, independent t-tests were conducted for our study variables (HNE, NumC, SES, and migration background). We examined the differences between the excluded cases and all other cases of our dataset for the analyses of both the learned and current occupations.
The results showed that the excluded cases of the learned occupation dataset differed significantly in children’s numerical competencies at t1 (t (188) = 2.332, p = 0.021) and t2 (t (186) = 2.091, p = 0.038), the SES (t (185) = 5.550, p < 0.001), and the migration background (t (180,000) = −15.770, p < 0.001). Here, the children who were not included in the analyses showed lower numeracy abilities at t1 (M = 17.33, SD = 11.29) and t2 (M = 13.88, SD = 4.63), had a lower SES (M = −1.74, SD = 0.80), and were more likely to have a migration background. No significant differences were found for HNE.
For the current occupation, the excluded cases only differed significantly from the remainder of the sample concerning the SES (t (185) = 2.952, p = 0.004) and the migration background (t (32,362) = −2.643, p = 0.013). Consequently, the drop-out in our sample was biased and needs to be considered as a limitation of our study.
First, the measurement models will be described. In the next step, we analysed the correlations (Pearson’s r) between all study variables. Finally, crossed–lagged models were used with the final dataset and are described in detail below.

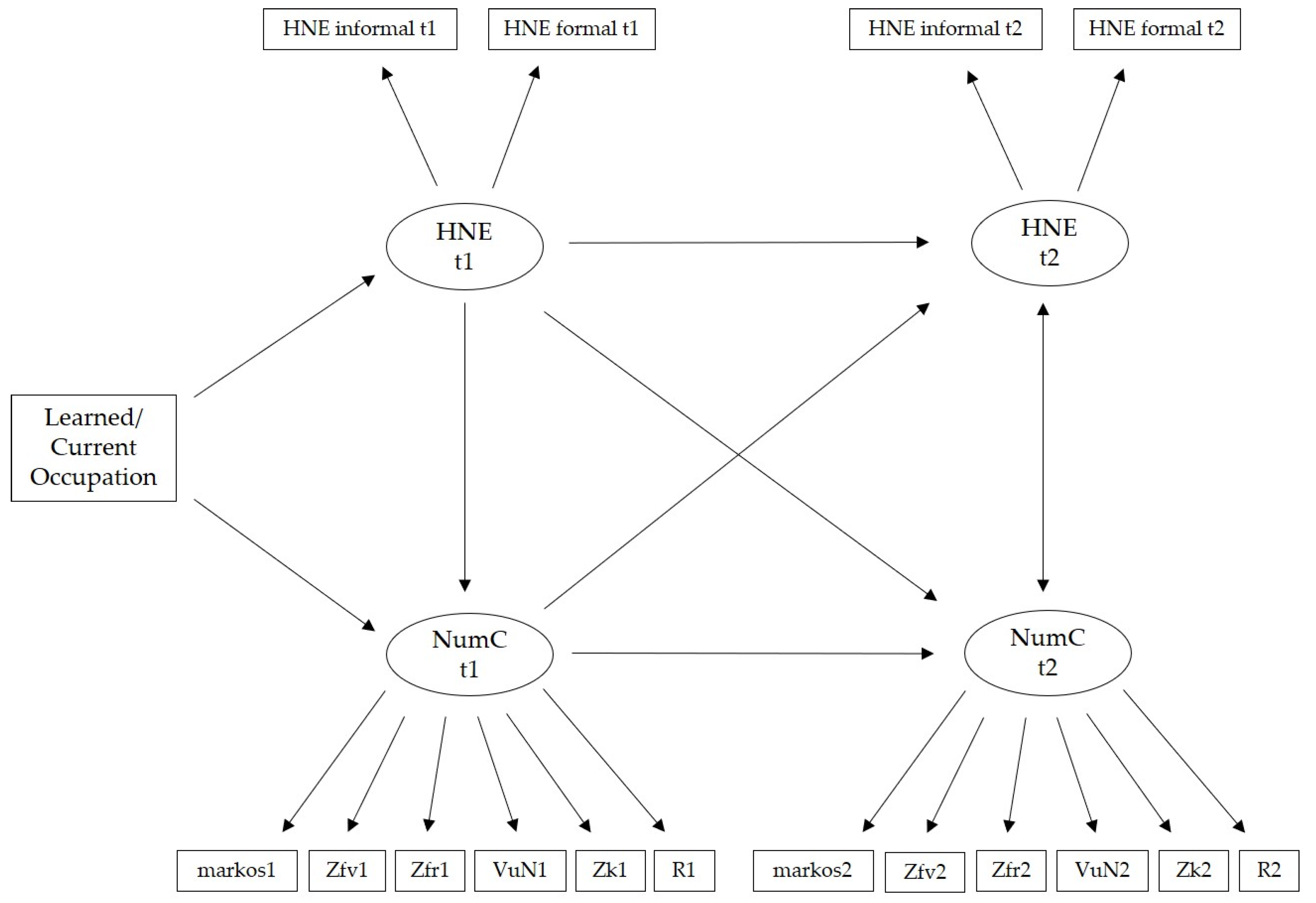
2.4. Measurement Model and Statistical Model Analysis

To test the relationships between the learned and current occupations, the HNE, and the numerical competencies of the children, we developed two different models (for learned and for current occupations). Here, learned and current occupations were introduced as manifest predictor variables, and the HNE was introduced as a latent variable comprising the formal and informal HNE. Similarly, the numerical competencies of the children (NumC) were assessed with the numerical tests and then combined in a latent variable.
Before testing the two final statistical models, we first assessed the fit of the measurement models for the four latent variables through confirmatory factor analysis (CFA). Second, we evaluated how well the statistical model fit the data [58]. To evaluate the fit of the measurement models and the statistical model, the Chi-square goodness-of-fit statistic and additional fit indices (the root mean square error of approximation (RMSEA), the comparative fit index (CFI), and the standardized root mean squared residuals (SRMR)) were used. The following values, which indicate good model fit between the hypothesized model and the observed data, were considered to assess the model fit: Chi square p ≥ 0.05, CFI ≥ 0.95, RMSEA ≤ 0.06, and SRMR ≤ 0.08 [60].
Modification indices were considered to improve the model fit; however, only modifications aligning with theory were applied. We added the highest modification indices one after another to the model to examine the changes in the fit values after each change. This process continued until a sufficient model fit was achieved [61]. All applied modifications are described in our section on the results.

3. Results

3.1. Measurement Models of Numerical Competence and the HNE

In the first step, the fit of the measurement models for numerical competence at t1 and t2 (NumC t1, NumC t2), including six variables each, and the HNE consisting of the formal and informal HNE, including five and ten items each, was evaluated using a CFA (see Table 2).
The latent variables of the children’s numerical competencies comprised the standardized numeracy tests of each measurement point. MPlus’ modification indices suggested to add a correlation for the tests calculation task with MARKO-S, and such a correlation was included in our model for t1 and t2, as both tests focussed on children’s calculation abilities.
The latent variables (see Figure 1) of the HNE were defined by the formal (five items) and informal HNE (ten items) of each measurement point. At both measurement points, MPlus’ modification indices recommended to correlate items two with three, five with six, five with seven, six with seven, eight with ten, and nine with ten for the informal HNE (for detailed information, see Appendix A). Given that we assessed various facets of the informal HNE, these correlations were appropriate and were included in our model. Overall, the measurement models for children’s numerical competencies and the formal and informal HNE showed a good model fit (see Table 2), with the exception of the informal HNE at t2, which showed slightly lower values. All models were included in the next step of the analysis.

3.2. Correlational Analyses

Table 3 provides an overview of the correlations between the latent variables of the HNE and mathematical competencies at t1 and t2, as well as the manifest variables of the learned and current occupations.
The cross-sectional correlational analyses showed a positive association between the HNE and children’s numerical competencies at both measurement points. A STEM-related parental occupation was significantly associated with the HNE that parents provide at home for their children. However, such an association was only found for the learned and current occupations at t1. Further, the learned occupation also correlated significantly with children’s numerical outcomes. Despite the small effect size of the correlations, no significant associations were found between the current parental occupation with or without a STEM background and children’s numerical competencies.

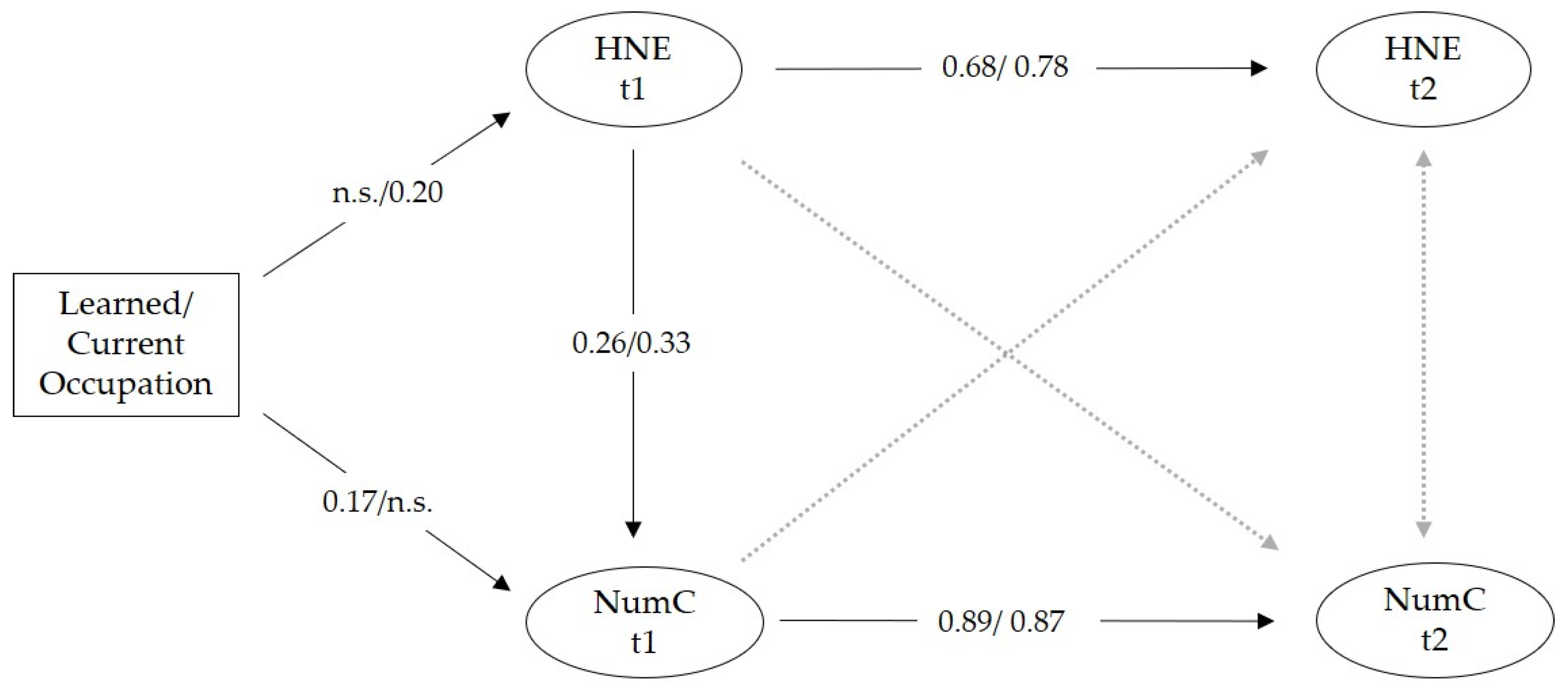
3.3. Statistical Models of Parental Occupation, HNE and Children’s Numerical Competencies

For our final statistical models, the direct paths from the first to the second measurement points of all latent variables were set as autoregressive paths. The paths from HNE t1 to NumC t2, NumC t1 to HNE t2, and NumC t1 to NumC t2, as well as for the relation between HNE t1 and NumC t1, were formed as regressions. Due to current research [42,62], we expected a direct cross-sectional association between the HNE and the numerical competencies of the children at the first measurement point. Table 4 shows the model fit for our two final models.
To address H1, we tested the association between the learned occupation (STEM vs. non-STEM background) of the parents with the HNE and NumC. In a second step, we tested the association for the current occupation (STEM vs. non-STEM background).
For our first hypothesis, the results from the crossed–lagged analysis (see Table 4) demonstrated that the data fit the model well. The learned occupation of the parents with a STEM background was significantly positively associated with the numerical competencies of the children at t1 (see Figure 2). To verify whether this association could also be found for the second assessment of children’s mathematical competencies, we conducted an exploratory mediation analysis, which showed a significant direct effect of 0.24 (p < 0.01) from learned STEM-related occupations of parents on t2 of children’s numeracy competencies. Within the mediation analysis, the model showed a significant specific indirect effect of 0.16 (p = 0.01) mediated by children’s numerical outcomes at t1 with an effect size of 0.19 (p = 0.01), as well as a significant total effect of 0.25 (p < 0.01). This indicates a relevant association between the learned occupation and children’s numerical development.
No significant association of learned occupation with the HNE was found. The autoregressive path of t1 onto t2 for the HNE was strong and significant (β = 0.68; p < 0.01), indicating that the HNE remained relatively stable across the two measurement points. The same was found for the stability of children’s numerical competencies (β = 0.89; p < 0.01). The expected direct path from HNE t1 to NumC t1 was also positive and significant (β= 0.26; p < 0.01). No other significant direct paths were found in our model. However, HNE t1 had an indirect effect on NumC t2 mediated by NumC t1 (β = 0.23; p < 0.001).
To address our second hypothesis, we conducted the same analysis again and used the current occupation of parents with a STEM background as a predictor variable. The results show (see Table 4) that our data fit the model well. The results of the standardized model show a significant association between the current occupation and the HNE at t1, but no significant association for the numerical competencies of the children at t1 (see Figure 2).
Other than that, this model resembles the first model. Again, the mathematical competencies at t2 were not directly predicted by the HNE at t1, but an indirect effect from HNE t1 on NumC t2 mediated by NumC t1 was found with 0.29 (p < 0.001).

4. Discussion

Early numeracy development and child and family characteristics that are associated with this development are intensively discussed in current research to understand how we can support children to improve their skills and abilities [62,63,64]. However, still, not much is known about the specific associations of parents’ learned and current STEM or non-STEM occupations with children’s numerical competencies and families’ HNE at an early age [17,18].
By means of a detailed analysis of STEM- and non-STEM-related occupations that parents learned and currently practice, we investigated the association of parents’ occupations with their children’s numeracy competencies and the HNE. Our results indicate that parents’ learned STEM occupations, but not their current occupations, are positively related to children’s numerical competencies. However, our findings did not support the hypothesis that parents’ learned occupation significantly predict the HNE. Instead, such an association was only found for their current occupations.

4.1. Direct Links between Parents’ STEM Occupations and Children’s Numerical Competencies

Consistently with the results from previous studies [17,18], children with at least one parent in a STEM-related occupation outperformed children with parents without a STEM-related occupation. However, unlike previous work [17,18], we differentiated between parents’ learned and current occupations. Our findings showed that only parents’ learned STEM occupations, but not their current STEM occupations, were associated with children’s numeracy competencies. In contrast to other studies, we examined these associations for preschool-aged children and not for high-school students or adolescents [17,18,23].
Unexpectedly, the link between parental occupation and children’s numerical competencies was found only for parents’ learned STEM occupation, but not for parents’ current STEM occupation. Here, different possible explanations can be put forward.
One can assume that parents who have studied an occupation in a STEM field already had a strong interest in this area before choosing their course of study or training [65]. Accordingly, they will show greater interest, as well as positive beliefs and attitudes, concerning STEM [66]. Such positive attitudes and beliefs may be related to children’s numerical competencies [67,68,69].
Further, it can be assumed that experiencing STEM education leads to certain skill sets (e.g., critical thinking, problem solving, active learning), which [70] may then be passed through by the parents to their children. These skills are also important skills for early STEM learning according to Steffensky [71]. Moreover, studies showed an interrelation between children’s mathematical and scientific competencies at an early age [4,27,44].
Further, we suppose that the education that parents went through shaped their skills, attitudes, motivation, and interests [72,73], which they are likely to pass on to their children. This may play a role in children’s numerical development and mathematical outcomes. Similarly, Sonnenschein et al. [74] pointed out that parents’ behaviours and practices, which reflect their cultural heritage, beliefs, and experiences, influence children’s development.
However, we could not find a link between parents’ current occupation and children’s numerical competencies. We assume that parents’ occupations that they currently perform can vary widely and are not necessarily related to their learned occupation. This means that a current STEM occupation does not equal a STEM education, or conversely, a STEM education does not equal a current occupation in that field [29]. For example, Cech and Blair-Loy [75] found that many parents left STEM occupations after the birth of their first child.
Consequently, it can be assumed that parental learned occupations (but not their current occupations) are connected to parents’ beliefs and attitudes and, in turn, are associated with parent–child interactions at home, which were not assessed within our HNE measurements. Here, clearly, more research is needed that focusses on the association of specific aspects of parental occupations, beliefs, and attitudes with specific aspects of the HNE [63].
Passing on good numerical and mathematical skills could also be influenced by parents’ genetics, as suggested by Puglisi et al. [76], who could not find a direct association of the informal home literacy environment with children’s literacy skills when parental skills were controlled for. Our findings may be interpreted as being in favour of the results of Puglisi et al. [72]. However, as pointed out above, a more differentiated look at parental factors, especially the influence of parents’ occupations, is needed.

4.2. Associations between Parents’ Characteristics and the Home Numeracy Environment

As expected, we found a significant association of parents’ occupations and families’ HNE, although this link was only affirmed for parents’ current occupation in our statistical models. We assume that parents’ current occupation is reflected in their everyday activities, which can be seen in the home numeracy environment that they provide for their children. Accordingly, it seems plausible to us that families in which at least one parent is currently working in a STEM field show a higher quality in their HNE, assuming that a current STEM background is related to more activity in and discussion of numerical and scientific topics in general [77].
Further, Zucker et al. [78] showed that parental involvement in helping children with science or math or doing more STEM-related activities was associated with parental values and self-efficacy. They also reported a direct association between mothers’ working in a STEM-related field and higher self-efficacy when engaging in informal STEM activities. Here, they suggested an indirect link between a maternal STEM career and parental involvement, mediated by a higher self-efficacy in encouraging children’s informal STEM learning.
These results underline our findings and raise the assumption that especially mothers who are currently working in a STEM profession are involved in particularly high-quality mathematical activities [78]. However, we can only speculate about this idea, as we have not investigated this association. It would be of great interest to check whether there is a difference in the quality of the HNE between mothers and fathers and the other factors (e.g., occupations) to which this may be related.
Unlike we expected, for parents’ learned occupation, we did not find a statistically significant link with the HNE. This could be related to the fact that the profession was learned further back in time and the questions about mathematical activities of the parents reflected more of their current activities and not those of the past. It can therefore be assumed that there is not such a strong link between the occupation learned in the past and the current interactions. Nevertheless, our cross-sectional correlations show a significant correlation between the learned occupation and the HNE at t1. This could indicate that learning a STEM profession also plays a (minor) role for later home numeracy activities.
In our sample, mostly fathers were educated and worked in STEM occupations [28,79,80,81]. However, about 80% of our parental surveys and, thus, the questions on the HNE were filled out by mothers. Consequently, it may be possible that the association between parental STEM occupation and the HNE would have been stronger if the individuals with STEM backgrounds would actually have answered our questions. This issue of potential differences in the answering patterns of fathers and mothers should be considered in the future, as only a few studies investigated such differences in socioeconomic characteristics, HNE, and interest, attitudes, and beliefs concerning science and mathematics [14,24,25,26,27,82].
Only a few studies investigated the link between different aspects of the SES and the HNE [e.g., 1,15,37]. Here, differences between high- and low-SES families concerning home math activities were found by DeFlorio and Beliakoff [15] and by Elliott and Bachman [1]. However, other studies did not find significant associations [e.g., 37], and most studies used the SES or aspects of it as control variables only. Our findings indicate that it is worthwhile to analyse specific facets of the SES in the context of the HNE and the development of children’s competencies during kindergarten.

4.3. The Role of the Home Numeracy Environment in Children’s Numerical Competencies

In addition to many different aspects that impact children’s numerical competencies and their development, such as parental factors, the SES, and child characteristics, such as intelligence, the HNE is an important predictor of children’s numerical competencies [42,62]. Our results replicated previous findings [39,42,47,77], with significant positive correlations and a direct link in our cross-sectional analyses of the families’ HNE and children’s numerical competencies. However, HNE t1 and NumC t2 were only indirectly correlated, with NumC t1 as a mediator, and no significant association was found for the correlation of HNE t2 and NumC t2 in our model. As our correlational analyses showed significant associations between all measures of HNE and NumC (see Table 3), we attribute the missing links of our HNE measures and NumC t2 in our model to the great stability of NumC across t1 and t2. Consequently, most of the variance of NumC t2 was explained by NumC t1. Previous studies also reported inconsistent findings for the association between the HNE and children’s numerical competencies. For instance, while some studies found positive associations [37,47], others found no such associations [15,67]. Clearly, more research on the HNE and its association with children’s early competencies is necessary, and studies should consider additional factors that might influence this association, such as parental beliefs, expectations, and cultural backgrounds [15,62].
Further, our CFA modelling indicates that the construct of the HNE has space for improvement. As also mentioned by Hornburg et al. [63], we recommend that the construct of the HNE needs to be used carefully and greater thought should be put into assessments and operationalisations. This could mean that it is not enough to capture caregiver-initiated activities, but also child-initiated ones or, additionally, aspects such as the family structure [63,82].

4.4. Limitations and Further Research

Some limitations need to be considered when interpreting our findings. First, our sample is not representative for the German population, and in addition, we could not use the whole sample of our study, leading to a reduced sample size for the final analysis. Consequently, the biased drop-out needs to be considered.
Second, we did not control for additional variables in our main analyses, such as a global SES measure, children’s intelligence, sex, age, or migration background [37], because we wanted to focus mainly on the associations of one specific aspect of the SES (STEM vs. non-STEM occupations) with the HNE and children’s mathematical outcomes. The inclusion of further control variables in exploratory analyses led to a very low model fit.
Although we used two measurement points in our study, it is necessary to exercise caution when interpreting the findings regarding causality. However, previous research based on longitudinal data also showed direct relations between the HNE and children’s mathematical abilities [42,47,83], and other studies with representative sample sizes undermined the assumption of a relation between STEM-related parental occupations and better mathematical competencies of children [17,18,22].
With additional methods of data collection, more detailed information about the associations between parents’ occupation, the HNE, and children’s mathematical abilities could have been examined. For instance, surveys on parental beliefs and attitudes, observational methods to directly capture the parent–child interactions, and interviews to obtain more qualitative data on parental occupations and the skills they learned would provide us with a greater insight [1,63].
Further research on differences in parents with STEM-related occupations regarding their educational qualification and highest degree and the associations of these differences with children’s mathematical competencies and development would be of great interest.
In order to find out more precisely why the learned STEM profession is a predictor for early numerical skills of the children, but not the current STEM profession of the parents, we also need further research. In particular, one should look at the potential link between parents’ occupations and children’s competencies in different fields and the potential influence of the content and skills gathered during their education as mediators for children’s early numerical competencies. Additionally, a greater sample size might show different results and would offer more opportunities for further statistical investigation, e.g., in which ways parents who learned STEM occupations, but do not currently work in a STEM-related field, may differ from parents with the same background and from parents who learned something else, but who are now working in STEM occupations.
In addition, looking at gender-related differences not only in the parents, but also between girls and boys, may provide a greater insight into mathematical learning and development and how mathematics are provided at home in different ways [28,84,85].
Altogether, it would be interesting to use the analysed and additional variables in a more comprehensive model and to examine them in a larger sample with a longitudinal design and more assessments.

5. Conclusions

Our findings indicate that parents’ learned occupations seem to play an important role in children’s early numerical development [17]. Further, the HNE was an important predictor for children’s early numerical competencies, which aligns with the results of prior studies [39,42,83]. Our study shows that concentrating on only SES as a global factor may not be sufficient to explain the development of children’s competencies [1]. This indicates that it is worthwhile to look at the construct of the SES in more detail and to differentiate between subcomponents. Consequently, depending on the research focus, future studies should consider which aspect (s) of the SES to assess. Despite our results, we still need more information about the specific associations and mechanisms that connect parental STEM vs. non-STEM occupation, the HNE, and children’s numerical outcomes. Here, research on parental beliefs and attitudes and on the clarification and specification of the HNE may be helpful [15,63,74] to provide policy and practise with more detailed information about how to best support children and their parents.

Author Contributions

Conceptualization: A.M. and F.N.; methodology: A.M.; formal analysis: A.M.; investigation: A.M., E.B., A.W. and F.N.; resources: F.N.; data curation: E.B.; writing—original draft preparation: A.M.; writing—review and editing: A.M., E.B., A.W. and F.N.; visualization: A.M.; supervision: F.N.; project administration: F.N.; funding acquisition: F.N. All authors have read and agreed to the published version of the manuscript.

Funding

This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant agreement No 801980). The design of the study, collection, analysis and interpretation of data and writing the manuscript were not influenced by the ERC.

Institutional Review Board Statement

The study was conducted according to the guidelines of the Declaration of Helsinki, and approved by the European Research Council Executive Agency as well as the ethics committee of the Faculty of Psychology and Educational Sciences at LMU Munich.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The raw data supporting the conclusions of this manuscript will be made available by the authors, without undue reservation, to any qualified researcher on reasonable request.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

Appendix A

Item description of the informal home numeracy environment.
ItemsItem Description
Item 1How often does your child count in everyday life (e.g., when setting the table with tableware or when counting down hours or days until a certain event)?
Item 2How often do you play counting games with your child (e.g., “Benjamin Blümchen: Lerne Zählen”, “Die Maus-Lern-Spiel-Sammlung”, “Kosmolino: 1,2,3…”)?
Item 3How often do you play arithmetic games with your child (e.g., “Ich lerne Rechnen”, “Zahlen und Rechnen”, “Zählen und Rechnen mit Ernie und Bert”, “1 + 2 = 3 Rechnen macht Spaß”)?
Item 4How often do you play dice games with your child (e.g., “Mensch ärgere Dich nicht”or “Tempo, kleine Schnecke”)?
Item 5How often do you involve your child in weighing and counting food and paying at the counter when you go shopping?
Item 6How often do you involve your child in counting, weighing, or measuring ingredients when cooking?
Item 7How often do you talk with your child about measurements (e.g., weight, temperature, or speed)?
Item 8In our family, we think that it is important to be able to calculate.
Item 9 My child shows interest in learning to calculate and to count and is looking forward to it.
Item 10Mathematics is important in our family.

References

  1. Elliott, L.; Bachman, H.J. SES disparities in early math abilities: The contributions of parents’ math cognitions, practices to support math, and math talk. Dev. Rev. 2018, 49, 1–15. [Google Scholar] [CrossRef]
  2. Rodriguez, E.T.; Tamis-LeMonda, C.S. Trajectories of the home learning environment across the first 5 years: Associations with children’s vocabulary and literacy skills at prekindergarten. Child Dev. 2011, 82, 1058–1075. [Google Scholar] [CrossRef]
  3. Niklas, F.; Schneider, W. Home learning environment and development of child competencies from kindergarten until the end of elementary school. Contemp. Educ. Psychol. 2017, 49, 263–274. [Google Scholar] [CrossRef]
  4. Krajewski, K.; Schneider, W. Early development of quantity to number-word linkage as a precursor of mathematical school achievement and mathematical difficulties: Findings from a four-year longitudinal study. Learn. Instr. 2009, 19, 513–526. [Google Scholar] [CrossRef]
  5. Duncan, G.J.; Dowsett, C.J.; Claessens, A.; Magnuson, K.; Huston, A.C.; Klebanov, P.; Pagani, L.S.; Feinstein, L.; Engel, M.; Brooks-Gunn, J.; et al. School readiness and later achievement. Dev. Psychol. 2007, 43, 1428–1446. [Google Scholar] [CrossRef] [Green Version]
  6. Bachman, H.J.; Votruba-Drzal, E.; El Nokali, N.E.; Castle Heatly, M. Opportunities for Learning Math in Elementary School. Am. Educ. Res. J. 2015, 52, 894–923. [Google Scholar] [CrossRef]
  7. Susperreguy, M.I.; Jiménez Lira, C.; Xu, C.; LeFevre, J.-A.; Blanco Vega, H.; Benavides Pando, E.V.; Ornelas Contreras, M. Home Learning Environments of Children in Mexico in Relation to Socioeconomic Status. Front. Psychol. 2021, 12, 626159. [Google Scholar] [CrossRef]
  8. Duncan, G.J.; Brooks-Gunn, J.; Klebanov, P.K. Economic Deprivation and Early Childhood Development. Child Dev. 1994, 65, 296. [Google Scholar] [CrossRef] [PubMed]
  9. Ho, E.S.C. Family influences on science learning among Hong Kong adolescents: What we learned from PISA. Int. J. Sci. Math. Educ. 2010, 8, 409–428. [Google Scholar] [CrossRef]
  10. Khundrakpam, B.; Choudhury, S.; Vainik, U.; Al-Sharif, N.; Bhutani, N.; Jeon, S.; Gold, I.; Evans, A. Distinct influence of parental occupation on cortical thickness and surface area in children and adolescents: Relation to self-esteem. Hum. Brain Mapp. 2020, 41, 5097–5113. [Google Scholar] [CrossRef]
  11. Reardon, S.F.; Portilla, X.A. Recent Trends in Income, Racial, and Ethnic School Readiness Gaps at Kindergarten Entry. AERA Open 2016, 2, 2332858416657343. [Google Scholar] [CrossRef] [Green Version]
  12. Starkey, P.; Klein, A.; Wakeley, A. Enhancing young children’s mathematical knowledge through a pre-kindergarten mathematics intervention. Early Child. Res. Q. 2004, 19, 99–120. [Google Scholar] [CrossRef]
  13. Jordan, N.C.; Kaplan, D.; Locuniak, M.N.; Ramineni, C. Predicting First-Grade Math Achievement from Developmental Number Sense Trajectories. Learn. Disabil. Res. Pract. 2007, 22, 36–46. [Google Scholar] [CrossRef] [Green Version]
  14. Dearing, E.; Casey, B.M.; Ganley, C.M.; Tillinger, M.; Laski, E.; Montecillo, C. Young girls’ arithmetic and spatial skills: The distal and proximal roles of family socioeconomics and home learning experiences. Early Child. Res. Q. 2012, 27, 458–470. [Google Scholar] [CrossRef]
  15. DeFlorio, L.; Beliakoff, A. Socioeconomic Status and Preschoolers’ Mathematical Knowledge: The Contribution of Home Activities and Parent Beliefs. Early Educ. Dev. 2015, 26, 319–341. [Google Scholar] [CrossRef]
  16. Giannelli, G.C.; Rapallini, C. Parental occupation and children’s school outcomes in math. Res. Econ. 2019, 73, 293–303. [Google Scholar] [CrossRef] [Green Version]
  17. Plasman, J.; Gottfried, M.; Williams, D.; Ippolito, M.; Owens, A. Parents’ Occupations and Students’ Success in STEM Fields: A Systematic Review and Narrative Synthesis. Adolesc. Res. Rev. 2021, 6, 33–44. [Google Scholar] [CrossRef]
  18. Shoraka, M.; Arnold, R.; Kim, E.S.; Salinitri, G.; Kromrey, J. Parental Characteristics and the Achievement Gap in Mathematics: Hierarchical Linear Modeling Analysis of Longitudinal Study of American Youth (LSAY). Alta. J. Educ. Res. 2015, 61, 280–293. [Google Scholar]
  19. White, K.R. The relation between socioeconomic status and academic achievement. Psychol. Bull. 1982, 91, 461–481. [Google Scholar] [CrossRef]
  20. Braveman, P.A.; Cubbin, C.; Egerter, S.; Chideya, S.; Marchi, K.S.; Metzler, M.; Posner, S. Socioeconomic status in health research: One size does not fit all. JAMA 2005, 294, 2879–2888. [Google Scholar] [CrossRef]
  21. Farah, M.J. The Neuroscience of Socioeconomic Status: Correlates, Causes, and Consequences. Neuron 2017, 96, 56–71. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  22. OECD. PISA in Focus; OECD: Paris, France, 2014. [Google Scholar]
  23. Omolade, A.; Kassim, A.; Modupe, S. Relative Effects of Parents’ Occupation, Qualification and Academic Motivation of Wards on Students’ Achievement in Senior Secondary School Mathematics in Ogun State. J. Educ. Pract. 2014, 5, 99–105. [Google Scholar]
  24. Chi, S.; Wang, Z.; Liu, X.; Zhu, L. Associations among attitudes, perceived difficulty of learning science, gender, parents’ occupation and students’ scientific competencies. Int. J. Sci. Educ. 2017, 39, 2171–2188. [Google Scholar] [CrossRef]
  25. Erola, J.; Jalonen, S.; Lehti, H. Parental education, class and income over early life course and children’s achievement. Res. Soc. Stratif. Mobil. 2016, 44, 33–43. [Google Scholar] [CrossRef] [Green Version]
  26. Lawson, K.M.; Crouter, A.C.; McHale, S.M. Links between Family Gender Socialization Experiences in Childhood and Gendered Occupational Attainment in Young Adulthood. J. Vocat. Behav. 2015, 90, 26–35. [Google Scholar] [CrossRef] [Green Version]
  27. Guo, J.; Marsh, H.W.; Parker, P.D.; Dicke, T.; van Zanden, B. Countries, parental occupation, and girls’ interest in science. Lancet 2019, 393, e6–e8. [Google Scholar] [CrossRef] [Green Version]
  28. Bowden, M.; Bartkowski, J.; Xu, X.; Lewis Jr., R. Parental Occupation and the Gender Math Gap: Examining the Social Reproduction of Academic Advantage among Elementary and Middle School Students. Soc. Sci. 2018, 7, 6. [Google Scholar] [CrossRef] [Green Version]
  29. Bott, P.; Helmrich, R.; Zika, G. MINT-Berufe—die Not ist nicht so groß wie oft behauptet! Analysen aus der ersten BIBB-IAB Qualifikations- und Berufsfeldprojektion. In Indikatoren und Benchmarks; Bundesinstitut für Berufsbildung: Bonn, Germany, 2010; pp. 40–44. [Google Scholar]
  30. Niklas, F.; Wirth, A.; Guffler, S.; Drescher, N.; Ehmig, S.C. The Home Literacy Environment as a Mediator between Parental Attitudes toward Shared Reading and Children’s Linguistic Competencies. Front. Psychol. 2020, 11, 1628. [Google Scholar] [CrossRef]
  31. Burghardt, L.; Linberg, A.; Lehrl, S.; Konrad-Ristau, K. The relevance of the early years home and institutional learning environments for early mathematical competencies. J. Educ. Res. Online 2020, 12, 103–125. [Google Scholar] [CrossRef]
  32. Anders, Y.; Rossbach, H.-G.; Weinert, S.; Ebert, S.; Kuger, S.; Lehrl, S.; von Maurice, J. Home and preschool learning environments and their relations to the development of early numeracy skills. Early Child. Res. Q. 2012, 27, 231–244. [Google Scholar] [CrossRef]
  33. Bronfenbrenner, U. The Ecology of Human Development: Experiments by Nature and Design; Harvard University Press: Cambridge, MA, USA; London, UK, 1979; ISBN 9780674224575. [Google Scholar]
  34. Vygotsky, L.S. Mind in Society: The Development of Higher Psychological Processes; Harvard University Press: Cambridge, MA, USA; London, UK, 1980; ISBN 9780674076686. [Google Scholar]
  35. Jordan, N.C.; Kaplan, D.; Nabors Oláh, L.; Locuniak, M.N. Number sense growth in kindergarten: A longitudinal investigation of children at risk for mathematics difficulties. Child Dev. 2006, 77, 153–175. [Google Scholar] [CrossRef]
  36. Passolunghi, M.C.; Vercelloni, B.; Schadee, H. The precursors of mathematics learning: Working memory, phonological ability and numerical competence. Cogn. Dev. 2007, 22, 165–184. [Google Scholar] [CrossRef]
  37. Niklas, F.; Schneider, W. Casting the die before the die is cast: The importance of the home numeracy environment for preschool children. Eur. J. Psychol. Educ. 2014, 29, 327–345. [Google Scholar] [CrossRef]
  38. Niklas, F.; Cohrssen, C.; Tayler, C. Improving Preschoolers’ Numerical Abilities by Enhancing the Home Numeracy Environment. Early Educ. Dev. 2016, 27, 372–383. [Google Scholar] [CrossRef]
  39. LeFevre, J.-A.; Skwarchuk, S.-L.; Smith-Chant, B.; Fast, L.; Kamawar, D.; Bisanz, J. Home Numeracy Experiences and Children´s Math performance in the Early School Years. Can. J. Behav. Sci. 2009, 41, 55–66. [Google Scholar] [CrossRef]
  40. Cohrssen, C.; Niklas, F. Using mathematics games in preschool settings to support the development of children’s numeracy skills. Int. J. Early Years Educ. 2019, 27, 322–339. [Google Scholar] [CrossRef]
  41. Gasteiger, H.; Moeller, K. Fostering early numerical competencies by playing conventional board games. J. Exp. Child Psychol. 2021, 204, 105060. [Google Scholar] [CrossRef] [PubMed]
  42. Skwarchuk, S.-L.; Sowinski, C.; LeFevre, J.-A. Formal and informal home learning activities in relation to children’s early numeracy and literacy skills: The development of a home numeracy model. J. Exp. Child Psychol. 2014, 121, 63–84. [Google Scholar] [CrossRef] [PubMed]
  43. Lehrl, S.; Ebert, S.; Blaurock, S.; Rossbach, H.-G.; Weinert, S. Long-term and domain-specific relations between the early years home learning environment and students’ academic outcomes in secondary school. Sch. Eff. Sch. Improv. 2020, 31, 102–124. [Google Scholar] [CrossRef]
  44. Saxe, G.B.; Guberman, S.R.; Gearhart, M.; Gelman, R.; Massey, C.M.; Rogoff, B. Social Processes in Early Number Development. Monogr. Soc. Res. Child Dev. 1987, 52, 2. [Google Scholar] [CrossRef]
  45. Krajewski, K. Vorschulische Mengenbewusstheit von Zahlen und ihre Bedeutung für die Früherkennung von Rechenschwäche. [Preschool awareness of quantities and numbers and their importance for the early detection of arithmetic weaknesses]. In Diagnostik von Mathematikleistungen; Hasselhorn, M., Marx, H., Schneider, W., Eds.; Hogrefe: Göttingen, Germany, 2005; pp. 49–70. ISBN 9783801718664. [Google Scholar]
  46. Sarama, J.; Clements, D.H. Early Childhood Mathematics Education Research: Learning Trajectories for Young Children; Routledge: New York, NY, USA, 2009; ISBN 9781135592509. [Google Scholar]
  47. Kleemans, T.; Peeters, M.; Segers, E.; Verhoeven, L. Child and home predictors of early numeracy skills in kindergarten. Early Child. Res. Q. 2012, 27, 471–477. [Google Scholar] [CrossRef]
  48. LeFevre, J.-A.; Polyzoi, E.; Skwarchuk, S.-L.; Fast, L.; Sowinski, C. Do home numeracy and literacy practices of Greek and Canadian parents predict the numeracy skills of kindergarten children? Int. J. Early Years Educ. 2010, 18, 55–70. [Google Scholar] [CrossRef]
  49. Melhuish, E.; Phan, M.; Sylva, K.; Sammons, P.; Siraj-Blatchford, I.; Taggart, B. Effects of the Home Learning Environment and Preschool Center Experience upon Literacy and Numeracy Development in Early Primary School. J. Soc. Issues 2008, 64, 95–114. [Google Scholar] [CrossRef]
  50. Niklas, F.; Annac, E.; Wirth, A. App-based learning for kindergarten children at home (Learning4Kids): Study protocol for cohort 1 and the kindergarten assessments. BMC Pediatr. 2020, 20, 554. [Google Scholar] [CrossRef] [PubMed]
  51. Ehlert, A.; Ricken, G.; Fritz, A. MARKO-Screening—Mathematik- und Rechenkonzepte im Vorschulalter—Screening [MARKO-Screening—Mathematics and Concepts of Calculation before School Entry]; Hogrefe: Göttingen, Germany, 2020. [Google Scholar]
  52. Krajewski, K. MBK 0. Test Mathematischer Basiskompetenzen im Kindergartenalter [MBK 0. Assessment of Basic Mathematical Competencies in Kindergarten Age], 1st ed.; Hogrefe: Göttingen, Germany, 2018. [Google Scholar]
  53. Endlich, D.; Berger, N.; Küspert, P.; Lenhard, W.; Marx, P.; Weber, J.; Schneider, W. WVT: Würzburger Vorschultest: Erfassung Schriftsprachlicher und Mathematischer (Vorläufer-) Fertigkeiten und Sprachlicher Kompetenzen im Letzten Kindergartenjahr [WVT: Würzburg Preschool Test: Assessment of Literacy and Mathematical (Precursor) Abilities and Linguistic Competencies in the Last Year of Kindergarten]; Hogrefe: Göttingen, Germany, 2017. [Google Scholar]
  54. Niklas, F.; Cohrssen, C.; Tayler, C. Parents supporting learning: A non-intensive intervention supporting literacy and numeracy in the home learning environment. Int. J. Early Years Educ. 2016, 24, 121–142. [Google Scholar] [CrossRef]
  55. Bundesagentur für Arbeit. Ingenieurberufe [Engineering Professions]. 2013. Available online: https://statistik.arbeitsagentur.de/DE/Statischer-Content/Grundlagen/Klassifikationen/Klassifikation-der-Berufe/KldB2010/Arbeitshilfen/Berufsaggregate/Generische-Publikationen/Steckbrief-Ingenieur.pdf?__blob=publicationFile&v=5 (accessed on 2 July 2021).
  56. Bundesagentur für Arbeit. MINT-Berufe [STEM-Occupations]. 2017. Available online: https://statistik.arbeitsagentur.de/DE/Statischer-Content/Grundlagen/Klassifikationen/Klassifikation-der-Berufe/KldB2010/Arbeitshilfen/Berufsaggregate/Generische-Publikationen/MINTBerufe.pdf?__blob=publicationFile&v=5 (accessed on 2 July 2021).
  57. IBM Corp. IBM SPSS Statistics for Windows; IBM Corp.: Armonk, NY, USA, 2019. [Google Scholar]
  58. Muthen, L.K.; Muthen, B.O. MPlus User’s Guide: Eighth Edition; Muthen, L.K., Muthen, B.O., Eds.; Los Angeles, CA, USA, 2017; Available online: https://www.scirp.org/(S(czeh2tfqyw2orz553k1w0r45))/reference/ReferencesPapers.aspx?ReferenceID=2123077 (accessed on 2 July 2021).
  59. Lai, K. Estimating Standardized SEM Parameters Given Nonnormal Data and Incorrect Model: Methods and Comparison. Struct. Equ. Modeling Multidiscip. J. 2018, 25, 600–620. [Google Scholar] [CrossRef]
  60. Hu, L.-T.; Bentler, P.M. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Struct. Equ. Modeling Multidiscip. J. 1999, 6, 1–55. [Google Scholar] [CrossRef]
  61. Schumacker, R.E.; Lomax, R.G. A Beginner’s Guide to Structural Equation Modeling, 3th ed.; Routledge: New York, NY, USA, 2010; ISBN 9781841698908. [Google Scholar]
  62. Susperreguy, M.I.; Douglas, H.; Xu, C.; Molina-Rojas, N.; LeFevre, J.-A. Expanding the Home Numeracy Model to Chilean children: Relations among parental expectations, attitudes, activities, and children’s mathematical outcomes. Early Child. Res. Q. 2020, 50, 16–28. [Google Scholar] [CrossRef]
  63. Hornburg, C.B.; Borriello, G.A.; Kung, M.; Lin, J.; Litkowski, E.; Cosso, J.; Ellis, A.; King, Y.A.; Zippert, E.; Cabrera, N.J.; et al. Next directions in measurement of the home mathematics environment: An international and interdisciplinary perspective. J. Numer. Cogn. 2021, 7, 195–220. [Google Scholar] [CrossRef]
  64. Del Río, M.F.; Strasser, K.; Cvencek, D.; Susperreguy, M.I.; Meltzoff, A.N. Chilean kindergarten children’s beliefs about mathematics: Family matters. Dev. Psychol. 2019, 55, 687–702. [Google Scholar] [CrossRef]
  65. Maple, S.A.; Stage, F.K. Influences on the Choice of Math/Science Major by Gender and Ethnicity. Am. Educ. Res. J. 1991, 28, 37–60. [Google Scholar] [CrossRef]
  66. Moore, R.; Burrus, J. Predicting STEM Major and Career Intentions With the Theory of Planned Behavior. Career Dev. Q. 2019, 67, 139–155. [Google Scholar] [CrossRef]
  67. Missall, K.; Hojnoski, R.L.; Caskie, G.I.L.; Repasky, P. Home Numeracy Environments of Preschoolers: Examining Relations among Mathematical Activities, Parent Mathematical Beliefs, and Early Mathematical Skills. Early Educ. Dev. 2015, 26, 356–376. [Google Scholar] [CrossRef]
  68. Tazouti, Y.; Malarde, A.; Michea, A. Parental beliefs concerning development and education, family educational practices and children’s intellectual and academic performances. Eur. J. Psychol. Educ. 2010, 25, 19–35. [Google Scholar] [CrossRef]
  69. Viljaranta, J.; Lazarides, R.; Aunola, K.; Räikkönen, E.; Nurmi, J.-E. The Different Role of Mothers’ and Fathers’ Beliefs in the Development of Adolescents’ Mathematics and Literacy Task Values. Int. J. Gend. Sci. Technol. 2015, 7, 297–317. [Google Scholar]
  70. Siekmann, G.; Korbel, P. Defining “STEM” Skills: Review and Synthesis of the Literature.- support document 1NCVER, Adelaide. 2016. Available online: http://www.ncvre.edu.au (accessed on 2 July 2021).
  71. Steffensky, M. Naturwissenschaftliche Bildung in Kindertageseinrichtungen. [STEM Education in Early Childhood Institutions]; WiFF Expertisen; Deutsches Jugendinstitut e.V.: München, Germany, 2017. [Google Scholar]
  72. Albarracín, D.; Wyer, R.S. The Cognitive Impact of Past Behavior: Influences on Beliefs, Attitudes, and Future Behavioral Decisions. J. Pers. Soc. Psychol. 2000, 79, 5–22. [Google Scholar] [CrossRef]
  73. Uğraş, M. The Effects of STEM Activities on STEM Attitudes, Scientific Creativity and Motivation Beliefs of the Students and Their Views on STEM Education. IOJES 2018, 10, 165–182. [Google Scholar] [CrossRef]
  74. Sonnenschein, S.; Galindo, C.; Metzger, S.R.; Thompson, J.A.; Huang, H.C.; Lewis, H. Parents’ Beliefs about Children’s Math Development and Children’s Participation in Math Activities. Child Dev. Res. 2012, 2012, 1–13. [Google Scholar] [CrossRef] [Green Version]
  75. Cech, E.A.; Blair-Loy, M. The changing career trajectories of new parents in STEM. Proc. Natl. Acad. Sci. USA 2019, 116, 4182–4187. [Google Scholar] [CrossRef] [Green Version]
  76. Puglisi, M.L.; Hulme, C.; Hamilton, L.G.; Snowling, M.J. The Home Literacy Environment Is a Correlate, but Perhaps Not a Cause, of Variations in Children’s Language and Literacy Development. Sci. Stud. Read. 2017, 21, 498–514. [Google Scholar] [CrossRef]
  77. Cheung, S.K.; Dulay, K.M.; McBride, C. Parents’ characteristics, the home environment, and children’s numeracy skills: How are they related in low- to middle-income families in the Philippines? J. Exp. Child Psychol. 2020, 192, 104780. [Google Scholar] [CrossRef]
  78. Zucker, T.A.; Montroy, J.; Master, A.; Assel, M.; McCallum, C.; Yeomans-Maldonado, G. Expectancy-value theory & preschool parental involvement in informal STEM learning. J. Appl. Dev. Psychol. 2021, 76, 101320. [Google Scholar] [CrossRef]
  79. Wang, M.-T.; Degol, J.L. Gender Gap in Science, Technology, Engineering, and Mathematics (STEM): Current Knowledge, Implications for Practice, Policy, and Future Directions. Educ. Psychol. Rev. 2017, 29, 119–140. [Google Scholar] [CrossRef]
  80. Anaya, L.; Stafford, F.; Zamarro, G. Gender gaps in math performance, perceived mathematical ability and college STEM education: The role of parental occupation. Educ. Econ. 2021, 6, 1–16. [Google Scholar] [CrossRef]
  81. Niepel, C.; Stadler, M.; Greiff, S. Seeing is believing: Gender diversity in STEM is related to mathematics self-concept. J. Educ. Psychol. 2019, 111, 1119–1130. [Google Scholar] [CrossRef]
  82. Del Río, M.F.; Susperreguy, M.I.; Strasser, K.; Salinas, V. Distinct Influences of Mothers and Fathers on Kindergartners’ Numeracy Performance: The Role of Math Anxiety, Home Numeracy Practices, and Numeracy Expectations. Early Educ. Dev. 2017, 28, 939–955. [Google Scholar] [CrossRef]
  83. Silinskas, G.; Di Lonardo, S.; Douglas, H.; Xu, C.; LeFevre, J.-A.; Garckija, R.; Gabrialaviciute, I.; Raiziene, S. Responsive home numeracy as children progress from kindergarten through Grade 1. Early Child. Res. Q. 2020, 53, 484–495. [Google Scholar] [CrossRef]
  84. Mejía-Rodríguez, A.M.; Luyten, H.; Meelissen, M.R.M. Gender Differences in Mathematics Self-concept across the World: An Exploration of Student and Parent Data of TIMSS 2015. Int. J. Sci. Math. Educ. 2021, 19, 1229–1250. [Google Scholar] [CrossRef]
  85. Niklas, F.; Schneider, W. Die Anfänge geschlechtsspezifischer Leistungsunterschiede in mathematischen und schriftsprachlichen Kompetenzen. [The beginning of gender-based performance differences in mathematics and linguistic competencies]. Z. Für Entwickl. Und Pädagogische Psychol. 2012, 44, 123–138. [Google Scholar] [CrossRef]
Education 11 00819 g001 550
Figure 1. Measurement model of the associations between the learned and the current occupations of the parents, the HNE, and the mathematical competencies of the children. Circles represent latent variables and rectangles represent measured variables.
Figure 1. Measurement model of the associations between the learned and the current occupations of the parents, the HNE, and the mathematical competencies of the children. Circles represent latent variables and rectangles represent measured variables.
Education 11 00819 g001
Education 11 00819 g002 550
Figure 2. Statistical models of the associations between the learned/current occupations of the parents, the HNE, and the mathematical competencies of the children. Note. Circles represent latent variables and rectangles represent measured variables. Lines indicate significant associations, and dotted lines indicate nonsignificant associations.
Figure 2. Statistical models of the associations between the learned/current occupations of the parents, the HNE, and the mathematical competencies of the children. Note. Circles represent latent variables and rectangles represent measured variables. Lines indicate significant associations, and dotted lines indicate nonsignificant associations.
Education 11 00819 g002
Table
Table 1. Descriptive statistics of the study variables (sample sizes, means, standard deviations, minima, and maxima).
Table 1. Descriptive statistics of the study variables (sample sizes, means, standard deviations, minima, and maxima).
VariablesNMSDMinMax
HNE_t11902.700.710.353.85
HNE_t21862.870.571.013.95
NumC_t119026.7012.500.0061.00
NumC_t218836.2012.809.0061.00
Learned Occupation1810.550.490.001.00
Current Occupation1640.440.490.001.00
Note: HNE = Home numeracy environment; NumC = Numerical competencies; Learned occupation (0 = non-STEM, 1 = STEM); Current occupation (0 = non-STEM, 1 = STEM).
Table
Table 2. Chi-square test (X2, df, p), confirmatory fit index (CFI), root mean square error of approximation (RMSEA), and standardized root mean square residual (SRMR) for the measurement models of children’s numerical competencies and HNE at t1 and t2.
Table 2. Chi-square test (X2, df, p), confirmatory fit index (CFI), root mean square error of approximation (RMSEA), and standardized root mean square residual (SRMR) for the measurement models of children’s numerical competencies and HNE at t1 and t2.
Χ2dfpCFIRMSEASRMR
Numerical Competence t13.93380.8610.000.01
Numerical Competence t210.57880.220.990.040.01
HNE formal t17.85350.160.980.050.03
HNE formal t27.08850.210.980.040.03
HNE informal t133.970290.240.990.030.04
HNE informal t263.196290.000.930.080.06
Note. The fit criteria for all measurement models and statistical models were Chi square p ≥ 0.05, CFI ≥ 0.95, RMSEA ≤ 0.06, and SRMR ≤ 0.08.
Table
Table 3. Cross-sectional correlational analyses for parents’ occupations, home numeracy environment, and children’s mathematical competencies.
Table 3. Cross-sectional correlational analyses for parents’ occupations, home numeracy environment, and children’s mathematical competencies.
23456
Learned Occupation0.508 **0.171 *0.1090.209 **0.255 *
Current Occupation (2)10.183 *0.1540.0950.152
HNE t1 (3) 10.866 **0.317 **0.278 **
HNE t2 (4) 10.333 **0.321 **
NumC t1 (5) 10.895 **
NumC t2 (6) 1
Note. Pearson’s correlation coefficients for manifest and latent variables. N = 160–190. * = p < 0.05, ** = p < 0.01, HNE = Home numeracy environment, NumC = Numerical competencies of the children.
Table
Table 4. Chi-square test (X2, df, p), confirmatory fit index (CFI), root mean square error of approximation (RMSEA), and standardized root mean square residual (SRMR) for the statistical models of the learned and current occupations.
Table 4. Chi-square test (X2, df, p), confirmatory fit index (CFI), root mean square error of approximation (RMSEA), and standardized root mean square residual (SRMR) for the statistical models of the learned and current occupations.
Χ2dfpCFIRMSEASRMR
Learned Occupation188.3101020.000.950.070.05
Current Occupation175.1261020.000.950.070.05
Note. The fit criteria for all measurement models and statistical models were Chi square p ≥ 0.05, CFI ≥ 0.95, RMSEA ≤ 0.06, and SRMR ≤ 0.08.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Mues, A.; Birtwistle, E.; Wirth, A.; Niklas, F. Parental (STEM) Occupations, the Home Numeracy Environment, and Kindergarten Children’s Numerical Competencies. Educ. Sci. 2021, 11, 819. https://doi.org/10.3390/educsci11120819

AMA Style

Mues A, Birtwistle E, Wirth A, Niklas F. Parental (STEM) Occupations, the Home Numeracy Environment, and Kindergarten Children’s Numerical Competencies. Education Sciences. 2021; 11(12):819. https://doi.org/10.3390/educsci11120819

Chicago/Turabian Style

Mues, Anna, Efsun Birtwistle, Astrid Wirth, and Frank Niklas. 2021. "Parental (STEM) Occupations, the Home Numeracy Environment, and Kindergarten Children’s Numerical Competencies" Education Sciences 11, no. 12: 819. https://doi.org/10.3390/educsci11120819

APA Style

Mues, A., Birtwistle, E., Wirth, A., & Niklas, F. (2021). Parental (STEM) Occupations, the Home Numeracy Environment, and Kindergarten Children’s Numerical Competencies. Education Sciences, 11(12), 819. https://doi.org/10.3390/educsci11120819

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop