1. Introduction
The constraints imposed by the COVID-19 pandemic in Portugal caused an exponential increase in the use of technology in teaching and learning processes, even among teachers who have always been reluctant [
1]. The importance of digital technologies in education systems is undeniable [
2], reinforced by the emergence of digital natives [
3] and the way they perceive it. It is important to discuss how technology can be used to benefit learning [
4]. Not only does it change the way of teaching but it also affects what can be taught, while providing opportunities for students to interact with mathematical ideas [
5] by allowing manipulation and visualisation of mathematical concepts [
4]. The role of the teacher in integrating technology is central and crucial. This requires teachers to possess a set of skills that allow them to choose, adapt, or create pedagogical resources suitable to the learning objectives [
6]. For the integration of technology in teaching processes to be properly achieved, it should stem from the context and serve the learning objectives [
7].
Appropriate integration of technology in mathematics education rests on three pillars: didactic design, teacher performance, and educational context [
8]. It is not enough for teachers to be competent in handling technological tools, they need to be able to mobilize specialized knowledge to create conditions that promote mathematical learning [
4]. It is therefore increasingly important to prepare future teachers to develop and articulate their pedagogical, technological, and content knowledge in practical and contextualized situations [
9], allowing them to develop skills necessary to create learning scenarios that promote an appropriate integration of technology [
10].
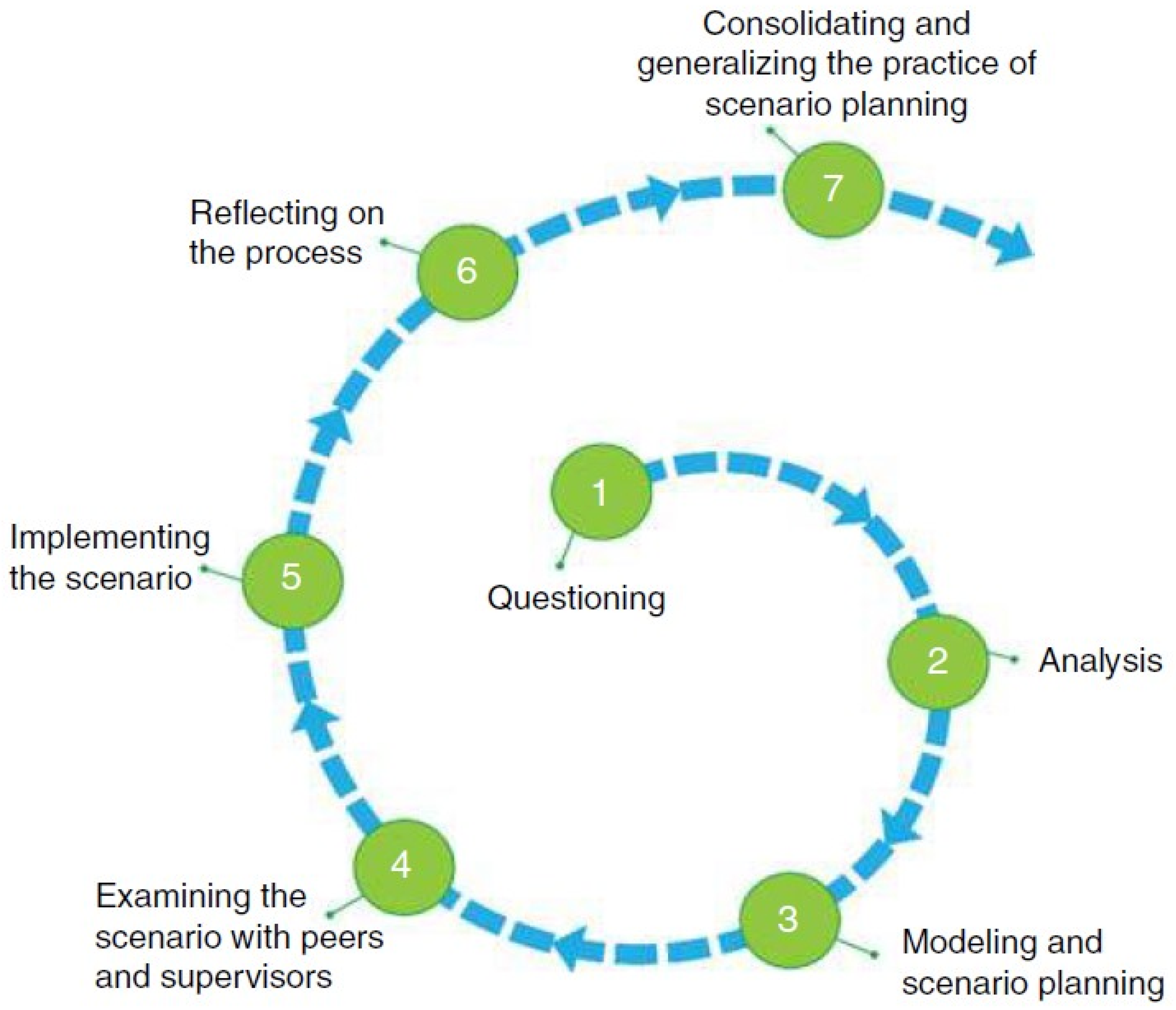
A learning scenario is a teaching and learning situation (fictional or anchored in reality) that describes the context in which learning occurs, based on its constituent elements: organizational design of the environment; roles and objectives of the actors; storyline, work strategy, performances, and proposals; and reflection and regulation [
11]. The design and implementation of learning scenarios have an intrinsic reflective nature, which promotes an understanding of the implications of the decisions made [
12]. This practice contributes to the professional development of pre-service teachers (PST), in a cycle of expansive learning [
10] (
Figure 1).
This article reports on the period of training of elementary school teachers—with a class of first-year elementary school students—during which difficulties in comprehending the meanings of subtraction by the students were identified. With the purpose of helping them to overcome the identified difficulties, the learning scenario presented in
Section 2.2. was designed and implemented. Appropriate solutions for the class context were sought in the literature, with particular attention to reading and writing skills, as well as to the group routines.
When preparing teaching sequences for subtraction, a learning trajectory and the students’ competencies necessary to understand and make use of the mathematical concepts involved should be taken into account [
13]. The positive contribution of word problems to learning subtraction [
14,
15] and of representations, including manipulatives, whether concrete or virtual, is also recognised [
16]. The use of computational tools to solve tasks should be done in such a way that teaching strategies promote comprehension of the mathematical concepts involved [
17].
A well-established tool in mathematics education, virtual manipulatives (VM) [
18], has evolved considerably in recent years [
18]. In this study, we adopted the definition proposed by Moyer-Packenham and Bolyard: “An interactive, technology-enabled visual representation of a dynamic mathematical object, including all of the programmable features that allow it to be manipulated, that presents opportunities for constructing mathematical knowledge” ([
18]). Its application in the classroom is no guarantee of learning. The teacher must be a mediator of mathematical meanings [
19], helping students to establish connections between the manipulation and mathematical concepts [
20].
The use of VM allows students to test and validate hypotheses on-screen without fear of negative feedback from peers or teachers; this experimentation can encourage students to establish connections between concepts and virtual representations [
21]. The teacher can take advantage of these features to help students overcome obstacles by using teacher scaffolding [
20]. VM allow visualisation and reduce abstraction, thus making mathematical concepts more understandable [
22,
23].
The selection of VM to be used should be careful and aligned with the learning objectives, according to their affordances and constraints, so that their integration into the teaching and learning processes may contribute to the comprehension of mathematical concepts [
24]. Shih [
25], in her case study, reports the positive contribution of VM to students’ ability to correct misconceptions related to subtraction.
The integration of computational tools in the classroom, using mathematical modelling (MM) as a learning environment, helps students to make multiple mathematical connections, fostering the development of mathematical comprehension [
26] and its concepts. Although different perspectives on MM exist, there is a consensus that it is a two-way translation process between the real world and mathematics [
27]. It is cognitively demanding since it operationalizes mathematical and non-mathematical skills and knowledge [
28]. When using MM as a learning environment, the teacher should seek a balance between minimal teacher guidance and maximal student independence [
29]. Supported by the diagnostic assessment of students’ mathematical knowledge, scaffolding strategies [
29] can be applied to help students make connections between mathematical and non-mathematical knowledge [
27]. In addition to representing the interaction between formal mathematics and reality, word problems are often the only means of providing students with opportunities to experience the basic principles of mathematisation and MM [
30]. By starting from real-world problems, MM as a learning environment is conducive to the construction of meaningful learning, promoting the active participation of students [
28].
The present study expands on previous work [
31,
32,
33,
34] dedicated to understanding how the integration of virtual manipulatives in classroom practices, using MM as a learning environment, generated positive impacts on students’ construction of mathematical knowledge. It was already established that the intervention contributed to improvements in participating students’ comprehension of the meanings of subtraction [
31].
Regarding integration of VM in classroom practices, there is already a body of studies about the teacher’s feedback that allow students to be able to use these tools and complete a task. However, the discussion is still in its early stages on how the teacher should support students to make mathematical connections between the manipulation and their interpretations of the representations [
35]. It is important to understand not only the characteristics of the teacher’s performance but also what influential relationships exist between the actions of the teacher and the students.
Thus, two research questions were established: (1) which characteristics of the learning scenario contributed to the students’ comprehension of the meanings of subtraction, and (2) what relationships exist between the constituent elements of the learning scenario? The search for answers to these research questions was based on the analysis of a mapping of constituent elements of the learning scenario and their relationships throughout the action units [
36]. Structural characteristics of the learning scenario were identified related to mathematical communication [
37]; collaborative learning [
38]; and self-regulation and co-regulation of learning [
39]. These identified characteristics are strongly aligned with how MM was integrated into the learning scenario, taking advantage of the affordances and constraints of the chosen VM.
3. Findings
The results are presented regarding the mapping of the constituent elements of the learning scenario along with its implementation. First, we present their relative frequency (
Section 3.1), then relationships are identified between the occurrences concerning their proximity (
Section 3.2) and co-occurrence (
Section 3.3).
3.1. Frequency of the Learning Scenario Elements
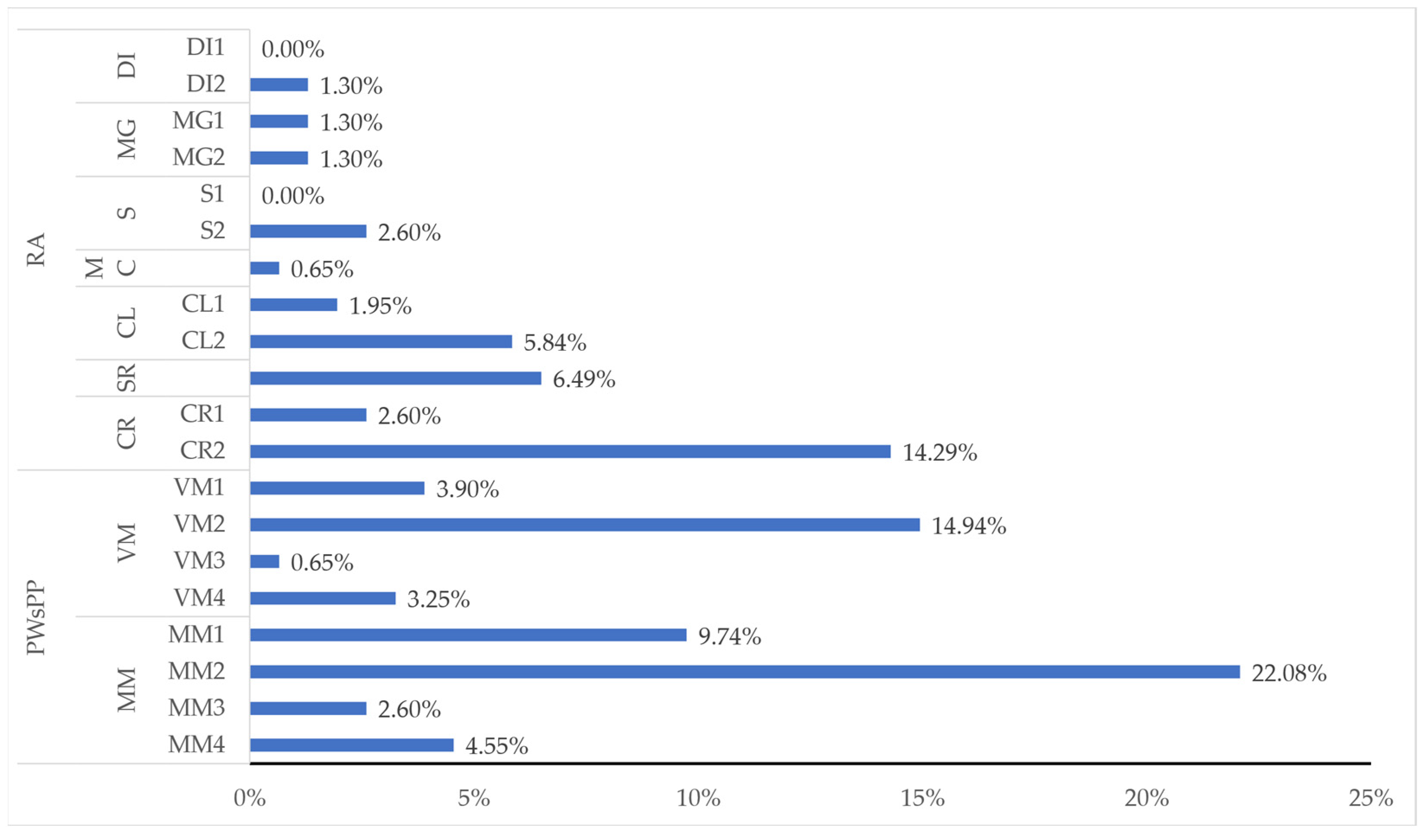
The frequency distribution of the learning scenario elements is summarised in the figure below (
Figure 2). The analysis of the collected data (
Table A1), according to the categories proposed in
Table 4, allowed the identification of the presence of all categories foreseen for the roles and actors (RA) dimension and most of the respective codes. No occurrence was identified of differentiated instruction concerning the teacher’s actions that encourage the student to assume an active role in the learning process (DI1) nor of planned scaffolding (S1). With regard to the dimension of plot, working strategies, performances, and proposals (PWsPP), the occurrence of all categories and codes was identified.
In the RA dimension, it was possible to observe a higher incidence of actions associated with the students’ expected role. This pattern is particularly visible in the students’ interactions related to collaborative learning (CL2), co-regulated learning (CR2), and self-regulated learning (SR). Regarding the PST role, it is noticeable that PST/student interaction frequency was significantly lower than the frequency of interactions between students.
Looking at the PWsPP dimension, within the VM category, the highest number of occurrences refers to VM allowing visualising mathematical concepts (VM2). Within the MM category, the results indicate a higher frequency of situations related to pair work (MM1 and MM2). The evidence of students’ mathematical communication (MM2) had the absolute highest value of all situations, considerably exceeding the number of situations mapped to interactions with VMs that allowed visualising mathematical concepts (VM2), whose frequency corresponded to the second-highest value. On the other hand, situations related to students being able to establish connections between mathematical concepts and reality (MM3) had the lowest frequency in the MM category.
3.2. Proximity between Elements of the Learning Scenario
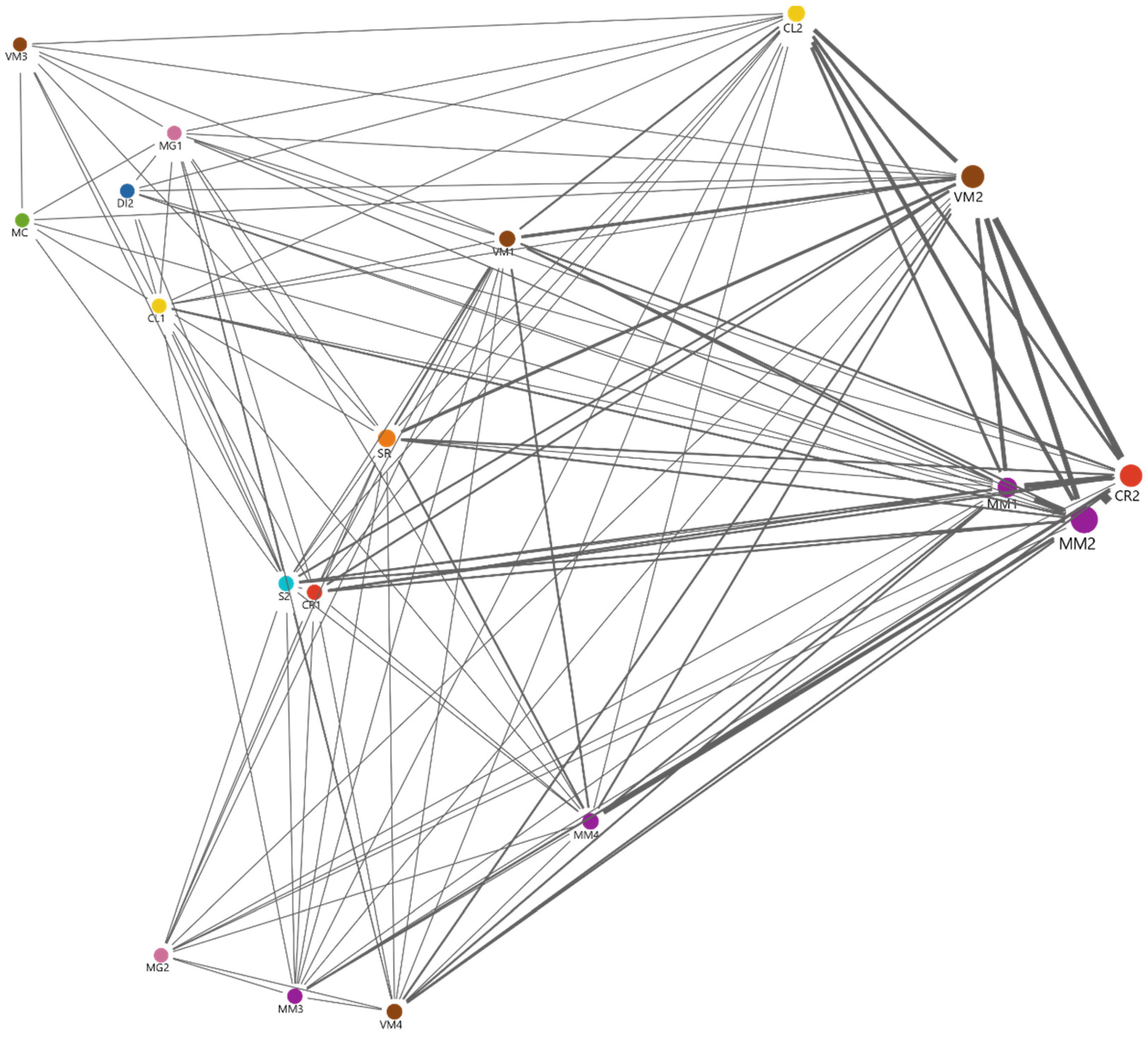
The proximity between elements of the learning scenario is represented in the graph below (
Figure 3), generated with the values presented in
Table A2, providing visual support for proximity relations found. The dimension of the nodes is directly proportional to the frequency of the codes found in the action units, whereas the thickness of the lines is representative of the number of relations between codes identified. From its interpretation, the most common patterns in the proximity relations between elements of the learning scenario stand out.
It is possible to identify a web of influences involving the codes MM1, MM2, MM4, CR2, VM2, and CL2. Consistent with the frequency mapping in the previous section, students’ mathematical communication (MM2), interactions between students that promote co-regulation of learning (CR2), and their interactions with VMs that allow visualising mathematical concepts (VM2) are a reiterated occurrence in the vicinity of most elements of the learning scenario.
It is considered relevant to point out the proximity relations of situations related to co-regulation of learning among students (CR2) and between teacher and students (CR1), spontaneous scaffolding (S2), and self-regulation of learning (SR). A relevant pattern is also identified in the proximity relations between students’ co-regulation of learning (CR2) and the virtual manipulatives category (VM1, VM2, VM3, and VM4).
3.3. Co-Occurrence of Elements of the Learning Scenario
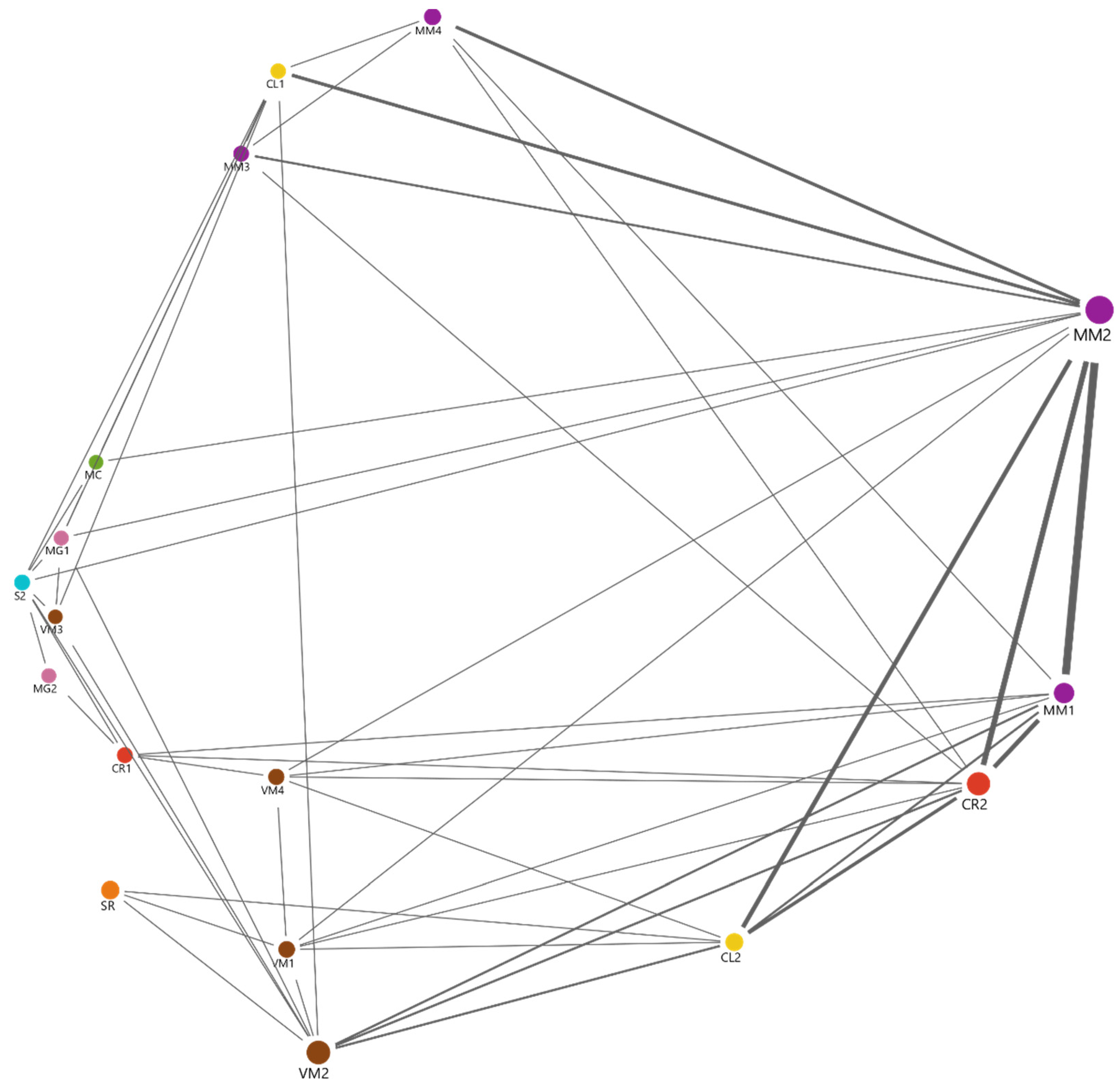
This section is dedicated to the presentation of results related to the co-occurrence of elements of the learning scenario, synthesized in the graph of the figure below (
Figure 4), generated with the values shown in
Table A3, providing visual support for the co-occurrences found. The dimensions of the nodes are directly proportional to the frequency of the codes found in the action units, whereas the thickness of the lines is representative of the number of relations between codes identified. The results of the co-occurrence of learning scenario elements reinforce the preponderance of mathematical communication among students (MM2).
It is possible to identify a pattern of simultaneous occurrences of the codes included in the mathematical modelling category (MM1, MM2, MM3, and MM4). A pattern of co-occurrence is also visible among situations involving mathematical communication (MM2), collaborative work (MM1), self-regulation of learning among students (CR2), and collaborative learning (CL2).
Mathematical communication (MM2) is also associated with situations in which students establish connections between mathematical concepts and knowledge and reality (MM3), solve a real problem through a mathematical description (MM4), and collaborative learning situations involving the PST and students (CL1). Although less frequent than the relations pointed out above, the co-occurrence of situations in which the manipulation of VMs allowed visualising mathematical concepts (VM2) with students’ collaborative work (MM1), their collaborative learning (CL2), and in which they co-regulate their learning (CR2) is also noteworthy.
4. Discussion
This study reports on a specific context. The PST skills are still at an early stage of development; the didactic sequence presented in this learning scenario was implemented only once; and the results refer to two pairs of students. Given these constraints, contributions are offered to discuss the structuring elements of the learning scenario that contributed to promoting students’ comprehension of the meanings of subtraction. Also discussed are the influential relationships existing between the roles intended for the PST and for the students in tasks that integrate VM, using MM as a learning environment. Mathematical communication, self-regulation, and co-regulation of learning and collaborative learning appear to be related to the integration of VM throughout the learning scenario. There is evidence to suggest that differentiated instruction, minimal guidance, and scaffolding may have contributed to students being able to establish mathematical connections between the manipulation and their interpretations of the representations offered by the VMs.
Answering the first research question (which characteristics of the learning scenario contributed to the students’ comprehension of the meanings of subtraction?), mathematical communication, collaborative learning, self-regulation, and co-regulation of learning are considered to be the characteristics of the learning scenario with the greatest influence on its structure.
By including MM and VM in the design of the learning scenario, we sought a minimalist intervention by the PST, creating conditions that would promote students’ autonomous work [
29], taking advantage of the affordances and constraints of VMs so that mathematical concepts would be correctly reinforced [
24,
47]. This design choice is validated by the results presented, where there is a higher frequency of elements of the learning scenario in the RA dimension related to the students’ role (CL2, CR2, and SR) as opposed to the idealised role for the teacher (DI, MG, S, CL1, and CR1).
The frequency of elements of the learning scenario included in the PWsPP dimension corroborates the importance of immediate feedback (VM1) from VMs, identified by Durmuş and Karakirik [
47], as well as allowing students to visualize mathematical concepts (VM2) [
22,
23] and pose and test hypotheses (VM4) [
20]. These results are considered to support the argument that the characteristics of the proposed learning scenario contributed to the promotion of student autonomy.
Mathematical communication is an integral part of collaborative word problem solving [
48], allowing students to express their mathematical reasoning in tasks that integrate CSCL [
37]. The frequencies of the MM1 and MM2 learning scenario elements are consistent with findings from Anderson-Pence and Moyer-Packenham’s [
49] study on the relevance of students’ collaborative work and mathematical communication in tasks that integrate VM. It is argued that these characteristics of the proposed learning scenario contributed to students being able to establish connections between mathematical concepts/knowledge and reality (MM3) and to solve real problems through a mathematical description (MM4).
To answer the second research question (what relationships exist between the constituent elements of the learning scenario?), the relationships identified between the occurrences of elements of the learning scenario regarding their proximity and co-occurrence are discussed.
From the analysis of the results, a close relationship emerged between the elements of the learning scenario MM1, MM2, MM4, CR2, VM2, and CL2. For a collaborative construction (MM1 and CL2) of a solution to a real problem (MM4) [
27] to take place, students must be able to express their reasoning and mathematical ideas (MM2) [
48]. The design of the learning scenario, in which the chosen VMs enable the visualisation of mathematical concepts (VM2), predicted that the idealised tasks, by integrating CSCL, would be conducive to the occurrence of CL2 and CR2 [
38]. Regulation of learning in collaborative learning situations is multifaceted, implying complex interactions between the various actors. For co-regulation of learning (CR1 and CR2) to occur, each of the actors needs to be able to regulate their motivations, behaviours, emotions, and cognitive processes (SR); these interactions include the decisions made by teachers (S2) [
39]. As such, the close relationships between the CR1, CR2, SR, and S2 codes are consistent with the literature.
A close relationship was also identified between students’ co-regulation of learning (CR2) and the elements of the learning scenario that constitute the VM category. By providing immediate feedback (VM1), allowing visualisation of mathematical concepts (VM2), and posing and testing mathematical hypotheses (VM4), they promote students’ autonomous work [
20]. These features of VMs also create opportunities for the teacher to help students establish mathematical connections (VM3) [
19], allowing students to develop comprehension of mathematical concepts [
26] conditions conducive to the occurrence of CR2.
As argued above, mathematical communication (MM2) is instrumental to the constituents of the learning scenario. As such, the co-occurrence of this element of the learning scenario with most of the others was expected—except for VM3, MG2, CR1, and SR—since the mathematical communication of the PST was not analysed. The co-occurrence of the learning scenario elements belonging to the MM category (MM1, MM2, MM3, and MM4) is consistent with the simplified modelling cycle presented by Ferri [
27]: (1) understanding the task, (2) searching mathematics, (3) using mathematics, and (4) explaining mathematics. Even though the data do not allow identifying patterns of sequences of the codes, it is argued that the co-occurrence of MM1 and MM2 is transversal to the four stages of the simplified modelling cycle; the co-occurrence of MM2/MM3, MM2/MM4, and of MM3/MM4 falls within that predicted for stages 3 and 4 of the simplified modelling cycle. In the specific case of the proposed learning scenario, the first three stages correspond to the resolution of the task and the fourth to its discussion.
The co-occurrence of the learning scenario elements MM2, MM1, CR2, and CL2 is supported by the literature. As pointed above, mathematical communication (MM2) is necessary for students to express their mathematical reasoning and ideas in CSCL [
37], contributing—in the specific circumstances of the proposed learning scenario—to the occurrence of CL2 and CR2 [
38].
Regarding the co-occurrence pattern MM2/MM3, MM2/MM4, and MM2/CL1, the first two have already been justified. Concerning the co-occurrence of MM2/CL1, the PST should be able to help students make connections between mathematical and non-mathematical concepts and find solutions to the problems posed (CL1) [
27,
29]. For this to happen, students must be able to express their mathematical reasoning and ideas (MM2) [
37,
48].
Finally, regarding the most significant pattern of co-occurrences concerning the category VM—VM2/MM1, VM2/CL2, and VM2/CR2—it is argued that by allowing visualising mathematical concepts, hence reducing abstraction, this feature of VMs facilitates the comprehension of the mathematical concepts involved [
22,
23], promoting the occurrences of CL2 and CR2 [
38], in the context established by the proposed learning scenario.
The results show that the elements of the learning scenario related to the PST actions present a low frequency. This is considered to be influenced by two factors: these relate to teaching competencies that require time and practice to develop [
50], and the context of the learning scenario refers to the systematization and remediation of learning.
5. Conclusions
This study identified the characteristics of the learning scenario with the greatest influence on its structure: mathematical communication, collaborative learning, self-regulation, and co-regulation of learning. The action planned for the PST, the conditions conducive to students’ autonomy, and the way technology was integrated into the design and implementation of the learning scenario contributed to the improvement of students’ comprehension of the meanings of subtraction.
The results presented suggest that differentiated instruction, minimal guidance, and scaffolding may be important for students to be able to make mathematical connections between the manipulation and their interpretations of the representations offered by VM. While these results may be conditioned by the PST developing skills, it is hoped that they can contribute to the discussion concerning how teachers should provide support to students in activities that integrate VM. Future work that includes multiple teachers and addresses multiple interventions may allow us to seek to understand whether the characteristics of the learning scenario identified represent statistically significant variables for student learning.
Considering the current prevalence of touchscreens in the daily lives of students at the first-year elementary school, it would be relevant to understand the potential of replacing computers with tablets in this proposed learning scenario, as well as adding an interactive whiteboard that students can use to support their arguments during task discussion.