Elementary Students’ Reasoning in Drawn Explanations Based on a Scientific Theory

Abstract

Constructing explanations of scientific phenomena is a high-leverage practice that promotes student understanding. In the context of this study, we acknowledge that children are used to receiving explanations from teachers. However, they are rarely encouraged to construct explanations about the causes and consequences of phenomena. We modified a strategy to elicit and analyze primary students’ reasoning based on scientific theory as a methodological advance in learning and cognition. The participants were fourth-graders of middle socioeconomic status in Chile’s geographical zone with high seismic risk. They drew explanations about the causes and consequences of earthquakes during a learning unit of eighteen hours oriented toward explanation-construction based on the Tectonic Plates Theory. A constant comparative method was applied to analyze drawings and characterize students’ reasoning used in pictorial representations, following the first coding step of the qualitative Grounded Theory approach. The results show the students expressed progressive levels of reasoning. However, several participants expressed explanations based on the phenomena causes even at an early stage of formal learning. More sophisticated reasoning regarding the scientific theory underpinning earthquakes was found at the end of the learning unit. We discuss approaching elementary students’ scientific reasoning in explanations based on theory, connected with context-based science education.

1. Introduction

Instructional practices that are central to learning are called high-leverage practices [1]. Constructing explanations based on evidence derived from inquiry processes [2] or underpinned by scientific theories or principles is relevant for mobilizing students’ understanding of natural phenomena in science classrooms [3].

Constructing better explanations continuously provides an organizational and educational framework for designing science teaching and learning experiences [4]. Elementary school students’ explanation construction has been researched primarily in developed countries, i.e., [5]. Nonetheless, in developing countries, this field of research is in its early years [6]. Moreover, most of the studies in elementary classrooms are based on students’ written explanations [6]. For instance, Forbes et al. [5] found that German classrooms supported students’ use of evidence to ground claims. At the same time, the teachers gave more robust opportunities to evaluate evidence-based explanations through comparison in the US. Hence, students learned to look for bias in their reasoning by analyzing other students’ explanations. In primary school, exploring and fostering students’ explanation construction at the same time is difficult because the students are at the entry points to learn the theories, concepts, or principles. They also start developing writing skills and knowing to use the diverse genres in science education [6]. Thus, misinterpreting students’ knowledge because of them having diminished writing skills is likely to happen.

Despite the different emphases of the international studies, there is agreement that explanation-construction is a challenging task for students and teachers which requires explicit support from linguistic and conceptual areas [6,7] or distributed scaffolding to help students gradually [8,9]. Linking phenomena with their underlying causes appears to be among students’ difficulties in constructing explanations. This process requires scaffolding and reframing the thinking mechanisms to include theories or concepts already existing in the individual’s system of theories [9,10,11,12]. Indeed, there is a need for research on evaluative approaches to scaffold students’ construction of scientific explanations [11].

Scientific explanations constitute a specialized genre of the discipline in the classroom, different from the report, arguments, or other text genres that children might be more familiar with [13,14]. Constructing explanations also involves the development of causal reasoning [15,16], disciplinary-specificities, i.e., [17], and the transformation of the individuals’ intuitive theories [18]. This transformation is influenced by formal knowledge [19], which usually occurs in a social dimension of learning in the classroom activity. Additionally, scientific reasoning skills and other cognitive, metacognitive and motivational—social—skills are related to one another [11,20]. Managing all these dimensions is relevant but also challenging for teachers and researchers when they identify the development of the explaining practice and engage primary students in making sense of phenomena [20,21,22,23,24].

The current study focuses on analyzing pictorial representations of a specific phenomenon, earthquakes, in elementary school students to understand better the process of eliciting their causal reasoning through drawn explanations during a learning sequence. The objective was to characterize students’ expressed reasoning through drawn explanations. Using drawings for this purpose advances an evaluative approach to younger learners’ thinking, who are just learning to write and talk in science. Additionally, analyzing drawings complements the classic methodological trends of verbal and written modes of making meaning. This knowledge is needed to analyze students’ reasoning in phenomena underlined by a scientific theory and identify alternative formats to benefit the growing number of students learning science through a foreign language or those with verbal/oral expression difficulties [24].

1.1. Explanation-Construction as a Meaning-Making Process

Creating or sharing meaning in science education involves multimodal languages, experiences, and interactions in the classroom [21]. The students’ construction of explanations as a source of expressing their ideas is crucial, as it provides a window to understanding and sensemaking [22]. A teaching approach responsive to meaning-making processes will anticipate students’ ideas about phenomena before instruction and then elicit and respond to these ideas during the lesson [23]. The materials and resources are other crucial elements for meaning-making processes [24].

From a sociocultural perspective, students’ explanation construction is a strategy for knowledge integration. It is an iterative and collaborative process in which they connect what is already known—by prior instruction or intuitive theories—with their experiences and conceptual elements to give scientific support for certain phenomena. From this perspective, the explanations constructed are learning artifacts rather than products or learning samples [25]. Explanations in the form of pictorial representations are considered in this study to be vehicles for thought, or reasoning artifacts [26] that trigger the creation of meaning [21] and, consequently, turn into steps in the development of precursor models. These are “cognitive schemata compatible with scientifically appropriate knowledge since they are constructed on the basis of certain elements pertinent to scientific models, which have a limited range of application, and which prepare children’s thinking for the construction of scientifically appropriate models” [27] (p. 2259).

In cognitive terms, explanation-construction requires a process of reasoning about phenomena [17] that is rarely easy to access as an external observer since it might require the recreation of the “image of the world” of the other, which contains not only concepts, but the images created through visual thinking [28]. Indeed, even when teachers know their students’ initial ideas, it is hard to build on those ideas while teaching to probe their students’ reasoning [29].

Even though interpreting and building new ideas based on students’ reasoning in the classroom is challenging for teachers, encouraging the students to construct explanations provides an optimal scenario to engage in understanding natural phenomena, such as those related to socio-scientific issues [30,31]. Moreover, these scenarios help them reconstruct their knowledge and reasoning about phenomena relevant to their lives [32,33]. The reasoning process elicited in the classroom is afforded by an interaction between two information processing systems: the individual’s intuitive and deliberative thinking [19]. Categories, as hypothetical entities in science education, fall under the umbrella term of “concept”. These entities are products of reasoning with theoretical inputs provided by formal education [34]. We understand explanations as a vehicle for triggering learning and expressing scientific reasoning that emerges when putting the ideas into a material form of communication (see the next section). Therefore, we interpret students’ drawings from the lenses of sociomateriality, both as processes that elicit reasoning and as outcomes of expressed scientific reasoning about a phenomenon that appears to be of high risk.

1.2. Explanations and Students’ Scientific Reasoning

Children at school learn about the underlying principles of phenomena and causal relationships, usually but not exclusively in science education. These learning processes are crucial to developing scientific thinking, which is applying the methods or principles of scientific inquiry to reasoning or problem-solving situations [35]. We understand scientific reasoning from a multiple component skills perspective [36], including hypothesizing, experimenting, and evaluating evidence (inferencing, evaluating data, and drawing valid conclusions) [37]. Generating valid conclusions in inquiry processes usually requires explanations. Explanations are particularly characteristic of everyday causal understanding appearing during early childhood [16].

This article studies a specific component, causal scientific reasoning expressed or demonstrated in children’s explanations [16] if we take them as a process of intentional knowledge-seeking [36]. Causal scientific reasoning emerges when they need to explain why a specific phenomenon occurs. Constructing explanations requires diverse causal connections [38], which means identifying particular circumstances that can trigger consequences to understand why observed changes or phenomena have a place under certain conditions. Explanations in science education involve scientific knowledge, and they can be based on theory, evidence, and mixed with daily life experiences. Children’s scientific reasoning reconciles different kinds of causal explanations about phenomena, such as scientific, natural, and supernatural [17].

Explanations in science education frequently involve abstract knowledge or concepts (i.e., explaining phenomena at an atomic or molecular level mediated by energy transfers). Into a framework for modeling competence, explanations in science classrooms trigger children’s abductive reasoning, which is the theory-based attempt of explaining a phenomenon by a cause [38]. Abduction means generating a cause as the best explanation for a phenomenon based on theoretical knowledge [39].

Considering scientific reasoning components, children’s use of information to make causal inferences is a complex cognitive task [35,40]. However, this does not imply that young learners cannot express causal reasoning about their natural environment [41]. Wang et al. [42] observed how children between 2 and 5 years old faced causal tasks related to the weight of objects and concluded that, even before primary school, children use causal reasoning in natural environments, although some age-dependent variations were found. Mayer and collaborators [20] measured four scientific reasoning dimensions in everyday situations, one of those was understanding theories. They worked with 155 fourth-grade students in a paper and pencil instrument test. The results showed that children developed their performance in the measured dimensions.

In terms of searching for explanations to make sense of a phenomenon, scientific reasoning is related to the construction of models. A model used for teaching and learning concepts serves as a medium for communication, describing, and explaining [39]. Perkins and Grotzer [40] proposed a selection of causal models based on the level of reasoning sophistication: (a) mechanism, where students can use their experience to make generalizations not always aligned with mechanistic reasoning, moving to more complex and accurate explanations; (b) interaction pattern, a dimension where students use different paths to connect causes and effects; (c) probability, referred to as what could happen; (d) agency, for example when students identify the presence of an agent involved in direct action. Within each of these dimensions, the authors note sublevels of complexity. Based on Perkins and Grotzer’s framework and other research studies of causal reasoning in science education, Moreira et al. [9] found that secondary students use complex causal reasonings to develop explanations in a specific chemistry topic. However, their results showed that using mechanistic reasoning does not always guarantee an alignment with scientific theory. Zangori et al. [31] built a rubric based on Perkins and Grotzer’s framework [40] and other studies related to reasoning about ecosystems to analyze the causal associations used by third-grade students when they learn about ecosystems. They found the students who had the opportunity to reason using models enhanced their causal reasoning, and intermediate steps towards the use of causal reasoning were identified.

1.3. Scaffolding Explanations in Science Learning

Other studies have developed instructional models or learning progressions to scaffold, assess, and analyze students’ explanations at the school level, e.g., [43,44]. These studies have common characteristics; they describe the explanation components and using evidence in their performances. McNeill et al. [43] constructed their instructional model considering Toulmin’s framework and standards for science education, describing three explanation components: claim, evidence, and reasoning in the following components:

Claim, an assertion or conclusion that answers the original question; evidence, scientific data that support the claim; the data need to be appropriate and sufficient to support the claim; and reasoning, a justification that links the claim and evidence and shows why the data count as evidence to support the claim by using the appropriate and sufficient scientific principles.

However, a few studies relate explanations and scientific reasoning in evaluative purposes, for instance, highlighting the reasoning expressed by students in their productions. A five-stage comprehensive learning progression of written scientific explanations for the school level was designed by Yao and Guo [44]. At the more basic stages, the students first relate, indirectly, facts and theory through models. When their scientific reasoning evolves, they progressively approach scientifically accepted models. The elements of reasoning appear as a simple causality, moving forward to more complex forms such as probabilistic or correlational reasoning to link the explanations logically [44].

The distinction between school explanations based on evidence versus those based on theory is an ongoing academic discussion. However, we know that the scaffolding process that children need to construct explanations based on their observations, inquiry processes, and evidence is different from the practical support for students to create explanations underpinned by theories, principles, or models that are more abstract entities [43,45]. Among the first group, the studies show that systematically helping students distinguish between the description of the facts, observations, and the emergence of an argument based on evidence is worthy of learning, e.g., [43]. The second group of students’ explanations—supported by theories—counts with empirical support of how the use of epistemic tools, such as the Premise–Reasoning–Outcome instructional strategy (P.R.O.) [45] facilitates not only writing of better explanations but enhancing students’ cognition and metacognition processes [46]. Thus, in the context of learning to explain phenomena based on theory, we found the research need of a domain-specific instrument to characterize students’ reasoning and apply it to explanations.

Previous studies of explanations as a product and process of learning have analyzed verbal or written answers separately, i.e., [9,47,48]. However, this type of analysis has insufficiently captured the complexity and advancement of children’s reasoning in learning new scientific concepts [47,49].

Consequently, we focus on generated pictorial representations in drawings, a complementary format vital for children’s expression and communication that has been less researched in this field [49]. In addition, Park et al. [50] argued that this type of representation contains implicit information that offers an opportunity to analyze students’ ideas and concepts. Indeed, analyzing non-linguistic forms of representation is a more inclusive method to approach students with difficulties with verbal/oral expression [24].

The focus of our work is highlighting and approaching children’s reasoning about natural phenomena underpinned by theory from a cognitive perspective. We centered the application of this purpose on student-generated drawings as an alternative form of constructing and communicating explanations to make sense of the causes of a natural phenomenon that might affect their lives, specifically earthquakes. We chose the earthquake phenomena because, in Chile, the country in which this study was conducted, earthquakes are a relatively frequent event that children are familiar with, as the country is in a seismic area. Thus, for the participants living in a geological fault zone, this phenomenon might be more quotidian/frequent or, at least not as unfamiliar as other natural phenomena. Nonetheless, the fourth grade is the first formal opportunity in which students start learning the underpinning theory of this phenomenon, known as Tectonic Plates Theory (henceforth, TPT). Moreover, the transmutation of the daily life self-explanations of phenomena towards scientific explanations based on theory begins at the stage this research took place.

Briefly explained, TPT states that layers and plates form the Earth’s internal structure in the static model. Plates move in different directions, giving place to continents as we currently know them. The inner movements of the plates occur mainly in three forms, convergent where plates move towards each other, divergent where plates move away from each other. Lastly, in transform movement, each plate moves sideways compared to the other. As a result of such movements, energy builds up, released through earthquakes, tsunamis, and related events. Therefore, TPT describes movements of plates, explaining the origin and mechanism of earthquakes [51].

We started from the assumption that supporting students in constructing explanations is a high-leverage practice in education [3], implying the development of reasoning processes and more authentic scientific practices in this study regarding TPT.

Our research question was: What characterizes students’ expressed reasoning in drawn explanations in the context of learning about earthquakes? The purpose of this article is to shed light on primary students’ scientific causal reasoning during a learning sequence at the school, in the context of current challenges in science, as well as to present a novel methodological coding rubric to approach this process. Science education needs to promote students’ thinking processes through authentic scientific practices, such as constructing explanations. Thus, this work will contribute to research on primary students’ causal reasoning and science education from a cognitive perspective.

2. Materials and Methods

The present study was exploratory with a descriptive and relational scope based on educational practices to inform educational processes. The data set was collected in Spanish and then translated into English by the article’s first author for dissemination purposes. The information from the participants was gathered during the science learning sequence about the “Internal Dynamics of the Earth” in 2019. Two stages during the learning sequence were crucial for collecting the data that compose this study, part of a larger project in science education research. These stages are denominated as stage one and stage two, henceforth S1 and S2. S1 represented when the learning unit was started by the teacher, and S2 when the unit finished. It is important to note that this study did not intend to estimate the effectiveness of the teaching unit or determine how the learning opportunities provided affected students’ scientific reasoning skills because the study design did not include an intervention or comparison groups to make those inferences.

Characterizing students’ drawings provides opportunities to analyze how instruction and the curriculum need to challenge students’ ideas. It is educationally relevant considering that students’ and scientific ideas coexist and interplay in their experience of making sense of the world [52]. The instruction helps with a reconstruction of these ideas in the sense of an explanatory coexistence [52].

The learning sequence in our study consisted of approximately 18 h of pedagogical work distributed throughout four weeks. The lessons comprised drawing activities, a group puzzle about Tectonic Plates and watching videos about the consequences of earthquakes, tsunami, and volcano eruptions. The teacher delivered some lectures about Earth Structure and Tectonic Plates’ interaction. The students completed learning workbooks about the more dangerous hazards in Chile and socialized a school security plan.

During the learning unit, the learning outcomes were formalized by constructing hand-drawn explanations about the phenomenon of earthquakes. However, the teacher also used other sources to facilitate learning advances regarding tsunamis and volcanic eruptions. The prompt for triggering student drawings used in this study was “Why does the ground move (in a seismic context)? Please draw your explanation in this blank sheet”. The instruments and steps of this study were approved by the Pontificia Universidad Católica de Chile’s Ethics Committee code number 180514006.

2.1. Participants and Paradigm

The participants were 22 fourth-grade students from families of middle socioeconomic status. The school was selected through purposive sampling and was in an area of Chile identified as being at risk for disaster if an earthquake occurs, near the San Ramon geological fault line in Santiago, the Chilean capital. The partnership with the teacher for the educational purposes of this research included the collaborative design of a learning sequence to help students reason about the causes and consequences of Earth phenomena and, therefore, to construct scientific explanations through drawings. This decision was founded on the participatory research paradigm [53], in which the communities of research are part of the analytic process and the decision-makers in the study.

Although the whole class that composed the group participated in the learning activities, only 22 of the students had parental authorization and their consent to use the drawings for research purposes. Moreover, one student did not attend school the day the teacher allocated time for drawing in S2, and he did not want to do it later. Thus, the final data set consisted of 22 illustrations in S1 and 21 in S2, and some results are presented as percentages.

2.2. Data Analysis and Processing

Our data processing was carried out in three different steps. First, we developed an instrument to categorize the scientific reasoning expressed through drawn explanations following the study by Park et al. [50] about pictorial representations. Then, we used the constructed instrument to analyze a group of students’ drawn explanations of earthquakes based on Tectonic Plates Theory (TPT). In the following paragraphs, we describe these two steps.

1. First, we developed an instrument to categorize the scientific reasoning expressed through drawn explanations following the study by Park et al. [50] about pictorial representations when qualitatively learning physics. Their work established three main levels for students’ expression: sensory that includes what students sense; unseen substance level, which provides for concrete substances that cannot be seen; and lastly, unseen non-substance that contains those representations about non-concrete and unseen aspects. This prior work was developed with talented students, representing a novel contribution to the field with a limited scope of applicability.

A panel of three experts, including teachers and cognitive psychologists, checked that this first version of the instrument was conceptually adequate, and the levels proposed would be observable in regular primary students learning samples.

2. To expand the applicability and address explanations of regular primary students, we developed a first pilot qualitative analysis of a set of learning samples composed of drawings using the constant comparative method as the primary coding process of Grounded Theory [54]. We created groups of similar drawings and contrasted their main features, discussing the expressed reasoning that could be identified. Then, we went through three flows of activity of the constant comparative method to adjust the instrument to the data: data reduction, data display, and conclusion verification. We also followed the indications by Tang et al. [55] for interpreting specific aspects of children’s drawing, such as types of lines for representing movement. Once we went through three rounds of discussion between the authors of this study, clarifications on the instrument were added. We modified the first version of the rubric by adapting the sensory level, the unseen substance level, and the unseen non-substance level of Park et al.’s framework [50], with specific emphasis on explanations of earthquakes based on TPT and an interpretation of the younger student’s context-related scientific reasoning.

3. We conducted a qualitative analysis of students’ explanations by three independent researchers—also authors of this article—all trained to code the drawings in a blind review process using the instrument developed in the previous steps. The final version of the rubric, which served as a coding framework, is presented in

Table 1. Coding rubric for primary students’ drawn explanations inspired by Park et al. [50].

	Level 0	Level 1	Level 2	Level 3
Description	It is not possible to interpret an explanation connected with the phenomenon from the pictorial representation.	The drawing represents elements within the child’s sensory plane, generally as effects of earthquakes, such as the ground’s surface movements or movement effects. The information in the representation was not enough to interpret an explanation beyond the child’s perceptible plane.	Some elements are beyond the immediate child’s sensory or perceptual plane. The drawings present changing aspects, for instance, beneath the ground or views from outside planet Earth. However, it is not evident that these changing entities are related to the interactive basis of TPT, such as movement, friction or a crash of plates, or the dynamics of the internal structure of the Earth.	The drawings include interacting elements that are outside or beyond the child’s sensory or perceptual plane (i.e., changing position or moving entities), expressed as a causal explanation of the earthquake, directly connected with TPT (i.e., movement, friction, or a crash between plates, or the dynamics of the internal structure of the Earth). Conceptual inaccuracies are expected even in this level of representation.
Details	Some students wrote “I don’t know”, drawing a non-related phenomenon from an external observer’s view, leaving the paper blank, or presenting incomprehensible elements.	These drawings frequently have a baseline to delimit the ground line (continuum, backstitch, oblique) or function as object support. Some graphics also wrote words related to “movement” or “seism”, etc., while others designed zigzags or wavy lines to represent the consequences of movement on the objects.	These drawings commonly represent a baseline to express a division between the elements perceived and the not perceived but conceptualized and represented as the possible causes of earthquakes. This conceptualization attempts to express a causal relationship between the consequences of the earthquake and its origin.	The drawings include the causes and consequences of the phenomenon, usually with arrows or labels indicating the name of the components (i.e., epicenter, interaction, etc.) or the direction of the movement. These drawings are precursor models used to express a causal relationship between the phenomena and the underpinning theory.
Reasoning (interpreted)	Students ‘ expressed reasoning is not possible to be interpreted from these types of drawings.	It is a sensory level of reasoning because the cognitive operation is based on entities or elements within the students’ perception of their senses.	The reasoning includes elements or processes beyond the sensory experience, attempting to express causality, nonetheless, not yet at a level that uses the parts of a theory to represent causal processes or ongoing mechanisms.	There is a qualitative leap of children’s reasoning towards thinking with non-visible theories or non-perceived elements to explain processes or ongoing mechanisms as the cause of phenomena, using theories, abstract concepts, or models. Thus, reasoning at this level is at a more sophisticated stage than in the previous levels.

. The coding process was performed by each researcher independently; a total of 30% of the students’ drawings were coded and compared among the three researchers in two rounds. The first round comprised 15% of the data, and the inter-rater reliability was 62%. After discussing the cross-cutting drawings, examples were selected to represent each level (see details in Section 3.3). The disagreements were discussed until a consensus was reached between the three researchers. The second round included a second set of drawings that comprised another 15% of the data set; the inter-coder agreement was 91%, which was considered a high measure of transparency for instrument implementation [56]. The remaining data were coded by one of the researchers considering the high level of prior agreement. The drawings were coded according to the three rows of the rubric. The first identified the main characteristics of the explanations represented in the students’ drawings, looking for causes or consequences of the characterized phenomena. The second one centered the attention on the specific elements or details found in the representations. The third one interpreted the type of reasoning the student expressed in each drawing.

3. Results

This section describes first the coding framework and the rubric developed to characterize the students’ expressed reasoning through drawn explanations. Secondly, we present the application results for fourth graders’ drawings based on the main elements that constituted the participants’ explanations based on theory. After this, we show the main trends of this group of participants’ reasoning levels coded at the beginning and the end of a learning unit in context-based science learning related to earthquakes to illustrate a practical application of this novel approach. These results are presented as an example of the possible analysis of drawn explanations using the developed instrument but do not limit the application to one phenomenon only. Finally, we illustrate the composition of each reasoning level with some drawing examples, highlighting their inferior and superior anchor to orient teachers and researchers on the transitions from one reasoning level to the next one in the case of TPT.

3.1. Instrument for Characterizing Scientific Reasoning in Drawings

The instrument developed in our study takes the form of a comprehensive rubric which works as a coding system to facilitate the assignment of levels, and the characterization of primary students’ expressed reasoning through drawn explanations. The rubric allows a description of both the characteristics of the domain-specific drawings and the reasoning level that might be externally interpreted.

Precisely, the rubric developed in this research (Table 1) consists of a three-level grid oriented to progressively identify levels of scientific reasoning in primary students, which are presented as columns. However, the first column represents a level 0 for drawings under the category of missing. As the instrument was applied to learning about earthquakes, its specification for Earth Science phenomena and TPT theory is included. We decided to base our work on distinguishing between perceptual planes expressed as input for interpreting reasoning and the connection between the explained phenomenon and its underpinning theory. This decision sought broader use of this approach to characterize early stages of students’ scientific learning based on theories for modeling and explaining phenomena. In the topic of this study application, this stage corresponds to the fourth grade.

Additionally, the instrument added a minimum level used to code the learning samples that could not be categorized or did not answer the cognitive demand of the task, which is quite frequent in young children or during initial learning processes. We expected that students’ drawn explanations move throughout the starting levels, from concrete or straightforward stages—based on their previous experiences, highlighting a sensorial focus—to more abstract ideas considering causal links, likewise expressing more complex reasoning. Furthermore, the rubric would make visible the sophistication of the students’ expressed reasoning and understanding of the underpinning theory. Thus, the levels proposed in our instrument could also be used as an emergent learning progression.

The three rows of the rubric present elements as follows.

• The first one describes the main characteristics of the explanations represented in the students’ drawings, emphasizing the differentiation between their expressed sensory plane and the connection with the theory.
• The second row presents the specific elements or details found in fourth-graders learning about a particular phenomenon, in this case, earthquakes, as an application of the first row to domain-specific learning samples.

The two first parts of the instruments may be adapted for working with other theories or phenomena.

3.

The third row describes the interpreted scientific reasoning in connection with the sensory planes, the causality, and the usage of theory as a more abstract step in the students’ cognitive processes when learning science. This part of the instrument is not associated with a singular theory; thus, it does not need adaptation to apply other topics.

The interpretation of reasoning is suitable to be used by educators or researchers in other learning topics or areas beyond Earth Science when students construct explanations based on scientific theories. It constitutes the first contribution of our work related to science learning research transcending the specific theory and expanding the cognitive process of causal reasoning rather than focusing on the learning accuracy of scientific concepts.

3.2. Trends in the Participants’ Reasoning Levels

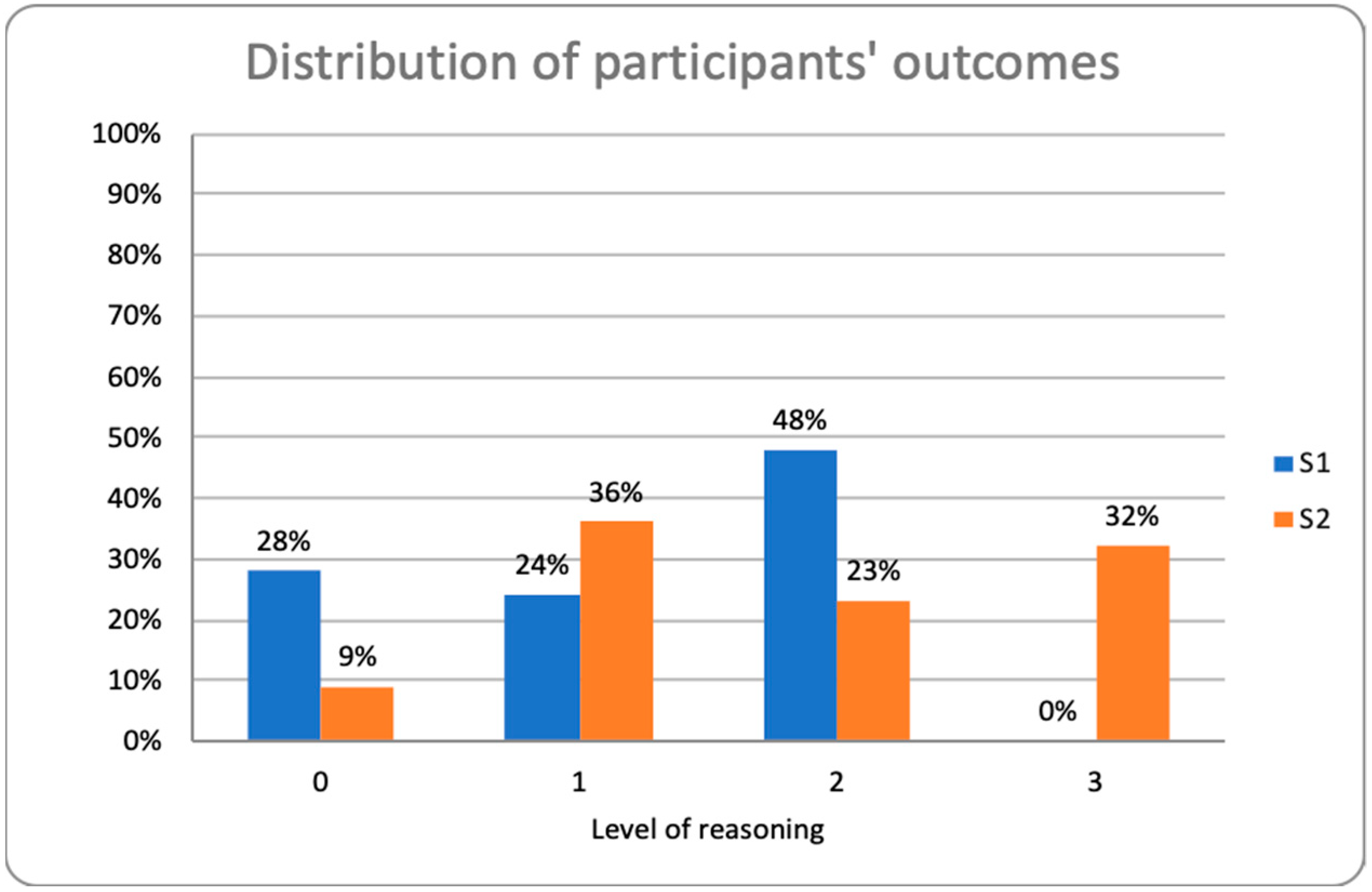
Considering the categorization results of the participants’ explanations using the instrument described earlier (Figure 1), we observe that in the early stage in the formal process of learning—called Stage 1—(S1) before the learning unit began at the school, 28% of the students’ explanations did not achieve the minimum level for categorization. Consequently, level 0 was assigned, as shown in Figure 1. In comparison, 24% of the drawings were categorized at level 1 for reasoning and 48% at level 2. This result means that most fourth-grade students could express reasoning about earthquakes with attempts to go beyond their immediate perception plane, representing elements that might constitute a causal explanation later, even with no formal instruction. However, none of the drawings reached level 3, causal reasoning based on aspects of TPT. Thus, we observed that some of them might have had an intermediate level of reasoning even with no formal instruction in this group of students. Nonetheless, establishing connections between the phenomenon and the theory in the form of a causal explanation in the drawings was difficult for the students.

In Stage 2—(S2), after the learning unit about the internal dynamics of the Earth was implemented, we saw a reduction in the percentage of drawings at level 0, with only 9% of the students’ samples categorized as such. There was a proportional increase in level 1 illustrations, with 36% classified as level 1 instead of the 24% obtained at S1. It is interesting to note that student representations categorized as level 2 decreased from 48% to 23% compared to S1; however, this fact is attributed to an increase in the drawings categorized in level 3, comprising 32% of the total. Thus, we conclude that, after participating in a formal learning process about earthquakes, it is likely that most of the participants in this group of students could express more sophisticated reasoning and a causal link in their drawn explanations. Nonetheless, 45% of children did not show cognitive operations with unobservable entities or logically connect the causes and consequences of earthquakes, even after the learning unit was finished.

3.3. Characterization and Examples of Reasoning Levels Interpreted from Drawings

This subsection presents descriptions, main features, and examples for each level identified, representing the finest-grain analysis of student drawings. It is worth remembering that, in the context of learning about Earth Sciences, the task demanded was “draw or represent here your explanation about Why does the ground moves?”

Level 0: It is impossible to interpret an explanation connected with the earthquake phenomenon from the pictorial representation. For instance, some students wrote “I don’t know”, drew a non-related phenomenon from an external observer’s view, left the paper blank, or presented elements that were incomprehensible for the researchers in the light of the question demanded by the task. Thus, we could not interpret the students’ expressed reasoning from these types of drawings. The authors of this work considered this level as missing data. This means that interpretable reasoning could not be obtained from an external viewer solely from drawings regarding the question given. However, other researchers might combine these types of illustrations with oral or written explanations; thus, the character of missing data would change. Some examples of pictorial representations categorized in this level in the current study are presented in Figure 2.

Level 1: The student drawing represents elements within their sensory plane, generally as effects or consequences of the earthquake phenomenon, recognizable as movements of the ground’s surface or results of the movement. The information derived from the representation was insufficient for the researchers to interpret an explanation beyond the child’s perceptible plane, for instance, based on non-visible entities. These drawings frequently have a baseline to delimit the ground line (in a continuum, backstitch, or oblique) or function as object support. Some graphics also wrote words related to “movement” or “seism”, etc., while others designed zigzag or wavy lines to represent the consequences of movement on the objects, as Figure 3 shows. Thus, we interpreted these drawings as a sensory level of reasoning because the cognitive operation is based on entities or elements within the students’ perception of their senses.

Level 2: Some representations or elements are beyond the students’ primary sensory or perceptual level. The drawings in this category (Figure 4, in which we have translated what the students wrote in their drawings) usually present changing elements, for instance, beneath the ground, or views from outside planet Earth, commonly represented by a baseline–ground line or object support–to express a division between the elements perceived by children and the elements not perceived but conceptualized and represented as the possible causes of earthquakes. In these types of drawings, we observed an attempt at expressing a causal relationship between the consequences of the earthquake (i.e., beyond the baseline) and their origin (i.e., beneath the baseline); however, it is not evident that these changing entities are related to the interactive basis of TPT, such as movement, friction or a crash of plates, or the dynamics of the internal structure of the Earth. Thus, we interpret a more complex level of reasoning than in level 1 because children are reasoning through elements or processes that are further from their immediate sensory experience and trying to express causal thinking, nonetheless not yet at a level that uses the parts of the theory to represent a causal process or ongoing mechanism.

Level 3: The representations in this level were more complex in comparison with level 2. The drawings include elements outside or beyond the children’s primary sensory or perceptual level. However, the difference with level 2 is that, in level 3, these components are interacting, changing position, or moving. These concepts are expressed as a causal explanation of the earthquake, directly connected with TPT, such as movement, friction or a crash between plates, or the Earth’s internal structure dynamics. We observed drawings that included the causes and consequences of the phenomenon, usually with arrows or labels indicating the name of the components (i.e., epicenter, interaction, etc., illustrated in Figure 5) or the direction of the movement. Thus, we interpret these drawings as precursor models used by the participants to express a causal relationship between the phenomena and the underpinning theory, which means a qualitative leap of children’s reasoning towards thinking with non-visible theories to explain processes or ongoing mechanisms. It is worth noting that we made no judgment of the conceptual accuracy presented through the representation.

Conceptual accuracy refers to the degree of content correctness in the scientific use of concepts, terms, or postulates in the drawing. Although in other works with secondary students’ explanation, a conceptual inaccuracy in the written explanation implies coding in level 0, e.g., [44], in this study, we consider that primary students can have inaccuracies expected because they had only started to learn about the content. Thus, we decided to give value even to explanations that were not totally precise but showed the advance in the reasoning process. For instance, in Figure 5, student’s drawing A represented the causes of earthquakes under the baseline, reasoning with abstract entities, represented a model of interaction, signaling a black point where the energy releases as “the epicenter.” Although the correct term should be “the hypocenter,” we made no judgment of the conceptual accuracy in the representation and consider it is an advance in the expressed reasoning regarding levels 1 or 2. Thus, we categorized it at level 3.

3.4. Boundaries for Interpreting “Qualitative Leaps” to a Superior Level

Our research found three qualitative leaps of expressed reasoning in students through drawn explanations, which help us interpret a hypothetical progression of reasoning. The first one (a) marks the level at which we can affirm interpretable reasoning about the phenomenon. The second one (b) refers to an advance from the upper anchor of level 1 to the inferior anchor of level 2. The third leap (c) occurs between the upper anchor of level 2 to the low anchor of level 3.

(a)

The entry point to the hypothetical progression of reasoning is the connection of the explanation with the phenomenon of interest. In this case, we observed the leap between level 0 and level 1 when the students represented the effects or consequences of earthquakes. In addition, they recognized that, in the context of learning about the internal dynamics of the Earth, the cognitive task that required drawing “why does the ground move?” involves a specific phenomenon—an earthquake. Level 1 is minor complex because the student only needs to identify a logical connection within the task’s context. For example, in Figure 2B, the planet Earth drawing was categorized at level 0, missing data. However, in Figure 3A, at the bottom anchor of level 1, we considered the black lines around the plants in the soil to represent movement, according to the categories by Tang et al. [55], which signal a consequence of the earthquake.

(b)

Comparing the upper anchor of level 1 to the inferior anchor of level 2, we can observe the qualitative leap that focuses beneath the ground level as a baseline. In Figure 3B, even though there is a line that might divide the perceptual plane from the non-perceptual plane, beneath this line, there are no recognizable elements. On the contrary, in Figure 4A, it is possible to observe the same ground line but with a representation of the Earth’s layers similar to the static model. Thus, we interpreted the increased complexity of the child’s recognition of possible causes of the phenomenon with an incipient link to the TPT.

(c)

Between the upper anchor of level 2 and the inferior anchor of level 3, we interpret a leap signaled by some representation elements connecting with the modeling process in science education, in the labeling of “Plates” in Figure 4B. However, no interaction between the components was expressed. The sophistication was demonstrated by the more explicit representation of the interaction between unobservable entities. Figure 5A,B represents cause, consequences, and activities between the components of TPT. They show reasoning with theory to explain a natural phenomenon.

4. Discussion

In this study, we sought to explore the characteristics of students’ expressed reasoning through drawn explanations in the context of learning about earthquakes at an early stage of formal instruction. We developed an instrument based on previous research to elicit and analyze fourth graders’ scientific reasoning based on theory through their drawn explanations. The analysis allowed the recognition of three levels of scientific reasoning, which were possible to characterize in the participants of this study. Consequently, our findings answer the question proposed: What characterizes students’ expressed reasoning in drawn explanations in the context of learning about earthquakes?

In summary, at level 0, topic-specific reasoning was not interpretable from the representational explanation. In contrast, at level 1, students’ reasoning was based mainly on the perceptible entities associated with the consequences of the phenomena. Drawings characterized as level 2 showed that children’s reasoning starts to connect some theory elements as a first attempt to explain the causes of a phenomenon. Despite this, levels 1 and 2 lack causal relations using the theory. Finally, in level 3, students could express their scientific reasoning about the phenomenon by linking elements of TPT to explain the causes and effects of a phenomenon as a precursor model, considered as cognitive schemata compatible with scientifically appropriate knowledge [27].

Moreover, our study found qualitative leaps between the children’s levels of expressed scientific reasoning focused on the connection with the phenomena under investigation, the emergence of the divisions of the perceptual and non-perceptual plane, and the presence of recognizable elements of the theory as part of the representation of the explanation. Some of the more advanced features expressed by the participants in our study presented similar characteristics to those of Perkins and Grotzer [40]. Specifically, we interpreted sophistication from static comprehension to an interactive activity between the non-observable or theoretical entities.

According to Yao and Guo [44], the students first relate indirectly to facts and theory through models before their scientific reasoning evolves, progressively approaching scientifically accepted models. Analyzing students’ drawings as an expression of their reasoning process gave us evidence for interpreting more sophisticated reasoning during the learning unit and students’ drawings as precursors of scientific models. This idea might be construed from a transformation of embedded intuitive theories through language [18] and deliberate thinking [19]. Moreover, our study expanded the literature to other forms of capturing advances of students’ reasoning through their creative activity of drawing explanations, which represents a complement to the current instruments to analyze students’ written explanations [31,43,44].

However, simultaneously analyzing and fostering students’ explanation construction based on theories, principles, or concepts is still a challenge at the early stages of formal learning [6]. Given this, we need to understand that students are still constructing the meaning of the scientific concepts involved when explaining. In primary education, they also develop essential skills such as explaining for scientific purposes or using models to explain the world. Thus, we emphasize the importance of supporting students to build these capacities and not underestimating their possible ability to express their scientific reasoning and knowledge through formats more familiar to them, such as drawings. Combining forms for approaching scientific reasoning and learning might mean a synergistic effort to scaffold the emergence and sophistication of reasoning, the conceptual understanding of children, and the development of essential skills. Our results resonate with prior research showing the need to combine diverse data sources to interpret children’s scientific learning [27].

Park et al. [50] discussed pictorial representation as a complementary format to explore students’ ideas. In this, they argued that drawings involve implicit information that is connected to other external representations. Indeed, the ways students express themselves about a concept or idea might be different when they do it verbally and pictorially, or exclusively verbally. We believe that for younger students, it is through drawings or representations that they are building scientific ideas and connecting them to other types of representations. We know that for students to construct scientific concepts, multimodal languages support processes related to sensemaking, scientific explanation construction, and scientific concept development [21]. It implies that employing exclusively visual or verbal representation during teaching might limit students’ learning process. Considering pictorial representations as part of multimodal language supports students in building concepts that are vehicles for expressing their reasoning. By having students use verbal communication only for concept construction, incorporating pictorial representations might result in more prosperous, more robust, and connected ideas for concepts construction, perhaps involving a re-conceptualization due to changing modalities. This is because constructing explanations seen from a sociocultural perspective is a knowledge integration learning artifact, in which the students connect what is already known with their experiences and conceptual elements to give scientific support for certain phenomena [25].

The instrument used to analyze scientific reasoning based on theory for primary students was demonstrated to be sensitive enough to detect the sophistication of these elements of reasoning during a learning unit of eighteen hours in the context of this study. Specifically, we observed an increase in level 1 and 3 categorized drawings between the learning sequence’s beginning—S1—and the end—S2 (Figure 1). Thus, we can conclude that, after participating in a formal instruction process, some participants in our study could express more sophisticated reasoning with a causal link in their drawn explanations. We agree that explaining phenomena provides an optimal scenario to connect students with socio-scientific issues [30,31], and our study adds that student drawings can be a source of expressed reasoning and, at the same time, a learning activity that activates and allows enacting or triggering of specific systems of reasoning.

Nonetheless, the instrument allowed the identification of a significant group of participants who did not show evidence of operating cognitively with unobservable entities to connect the causes and consequences of the phenomena under study. After the learning unit was finished, this gap was observed, with students immersed in a high-risk context, adding familiarity with the phenomenon. We recommend providing opportunities to learn to link phenomena and their causes in this and several other topics and conducting more research to determine the obstacles to student advancement in reasoning levels. Still, we observed instances of expressed reasoning regarding context-related situations before formal learning started at school. The entry point to the hypothetical reasoning progression was the connection of the explanation with the studied phenomenon. This finding coincides with studies that show the starting point for explanation-construction is the phenomenon [4], which helps to afford the need to generate explanations. By fourth grade, Chilean students have likely already had some daily life experiences with earthquakes and can nurture their reasoning process about the environment in which they live. Thus, the fact that our study considered the early stages of formal learning and identified what ideas the students had already formed in their representations for constructing explanations is valuable. Further research could illuminate the role of local context in early scientific reasoning levels, not only on how scientific reasoning about earthquakes develops throughout the school trajectory but also extending the use of such instruments to other subjects, areas, or demanding tasks.

This study has some limitations. First, using a strategy designed in a different context and language might cause cross-cultural issues. We adapted the frame suggested by Park et al. [50] according to the context of the study. Still, we also acknowledge the particularities of Chile as having a high risk of disaster (e.g., earthquakes). Thus, the learning approach to these phenomena may vary from those whose context does not include risk or whose geographical reality is very different. However, this point also represents a possible subject for future researchers to explore: the extent to which proximity to a phenomenon might imply a variation in the way students think about it.

Additionally, some elements of students’ drawn explanations went beyond the frames of our analysis, for instance perspectives from outside the planet that combined astronomical concepts. Although we treated those features as exceptions in our study, perhaps representing a limitation, we believe a second perspective on these types of data is crucial to challenge adults’ beliefs about the abstraction capacity of children and the way they visualize phenomena and their causes. Moreover, we recognize our study has a small sample size for going beyond descriptive analysis. Thus, we encourage further research to work with larger groups of students for complementary validation purposes.

Regarding the validation of the rubric, in this study, we went through a content validation through a panel of experts and a small pilot study before analyzing the data sets. Due to the small sample size and the study’s exploratory nature, we could not run factor analysis or more sophisticated processes, strengthening the significance and or generalizability of the results.

Nonetheless, we consider this study as a first approach interpreting primary students’ reasoning in phenomena explained by theory, with an educational significance in the field of science education. Other researchers might take the advances of our work and, for instance, compare pre–post drawings in specific groups of students, or use a repeated-measurements design focusing on learning the topic or conceptualization of the phenomena. Hence, we suggest future research gathering evidence of the leaps shown in our study but exploring them in the light of learning progressions of individual students. This exploration might complement the current results to emphasize the connections between understanding phenomena, theories, or concepts and learning, to establish learning trajectories in science education.

5. Conclusions

The current study allowed us to characterize students’ scientific reasoning through drawn explanations. We presented a helpful instrument to identify cognitive leaps between concrete expressed reasoning levels and more abstract ones, including causal links between phenomena and theory. It is a methodological innovation to approach young students’ learning and reasoning development from an interdisciplinary perspective that combines education and cognitive science. Our research explicitly links science learning and cognition by highlighting and approaching children’s reasoning about natural phenomena underpinned by theory. This development expands the current instruments available to notice the complexity of scientific reasoning of young children when they are at the first moments of learning models, theories, or abstract postulates that sustain the causes of phenomena. There is a methodological advance considering that most of the current instruments relate to explanations based on evidence in written formats.

In applying the developed rubric, we observed sophistication in students’ scientific reasoning when provided a formal learning opportunity, resulting in some students progressively connecting their ideas to a scientific theory. Our study allowed exploration of students’ progressive development of the causal reasoning required to construct explanations. Constructing explanations based on theory from primary school is a relevant teaching and learning practice to develop at an early stage of learning, considering that secondary and college students have limitations to using their scientific knowledge to establish causal links when they construct explanations. Furthermore, identifying scientific reasoning levels at the early stages of learning allows conceptualization of scientific reasoning as a trajectory. Thus, we can observe more precisely where students begin this form of complex knowledge and how it will eventually progress. By identifying and understanding this trajectory and the qualitative leaps, teachers, educators, and researchers can better scaffold the learning process and the development of context-related scientific reasoning, providing opportunities to support this development promptly. The detailed description of these findings helps researchers interested in this field adapt, reframe, and test in different ways the analysis we have done, allowing projection of transference of the interpreted reasoning of the rubric of this research to other topics. It would make the progressive approach to thinking in different disciplines visible and promote students’ reasoning in the school. This idea resonates with theoretical frameworks used for understanding of the construction of explanations as epistemic processes, which broadens the interest of this article to other areas beyond the content of the application in our study.

Teachers’ support of children’s reasoning in the classroom might take the form of distributed scaffolding. For instance, giving prompts with initial questions such as in the present study “why do you think this phenomenon happens”, and moving forward to students to revise and enrich their initial explanations during the learning of the content advance. The scaffolding seeks to transfer the responsibility gradually to the student, promoting autonomy. In primary education, where students are diverse in autonomy degrees, generating group discussions about explanations is an option, considering that science practices also imply peer-reviewing ideas and claims to compare and contrast to evaluate their scope and limitations. This strategy also connects with positioning science construction as a collective activity, introducing children to elements of Nature of Science. We strongly believe that classroom activities oriented to develop students’ reasoning processes should encourage students to express their ideas in diverse formats, such as the causes of phenomena. Then, linking those with the scientific support through concepts, theories, or postulates that are usually more abstract entities to reason. However, this approach needs teachers to consider that students’ common sense is part of their implicit theories that allow them to make sense of emergent phenomena, thus relevant for transformation and not represent merely knowledge to discard during science lessons. We know that teachers tend to suppress ideas that might look wrong as they are expressed in more traditional science classrooms. Still, we want to stress that responsive science teaching gives value to the students’ existing ways of thinking to construct new understanding, further develop their reasoning into a more scientific one, managing the supports strategically that students need promptly.

Furthermore, our work supports understanding primary students’ reasoning considering current educational challenges, affording students’ thinking processes through authentic practices, such as constructing explanations based on context-related phenomena. Moreover, we see the explanation-construction of relevant phenomena as a participatory action for responsible citizenship that can be implemented in primary education to promote high-leverage practices such as explaining and modeling, as was mentioned in our theoretical framework. Thus, we highlight that, even at the early stages of formal science learning, students can transform their ideas into expressions of context-related reasoning, for instance, through drawings that act as learning samples of explanations represented at the first stages of their models to explain natural phenomena. This fact emphasizes the importance of recognizing young children as active constructors of knowledge, showing that some can go beyond their immediate experience to logically link a phenomenon with its underpinning theory. Constructing explanations about world phenomena and expressing students’ reasoning in formats aligned with their action, drawing creative activity is a more abstract and complex process worthy of considering by researchers, educators, and teachers interested in the multidisciplinary innovations for understanding learning processes and outcomes.