Next Article in Journal
Learning to Teach: How a Simulated Learning Environment Can Connect Theory to Practice in General and Special Education Educator Preparation Programs
Previous Article in Journal
Using E-Learning to Deliver In-Service Teacher Training in the Vocational Education Sector: Perception and Acceptance in Poland, Italy and Germany
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Education Sciences
Volume 10
Issue 7
10.3390/educsci10070183
education-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Battle between the Correct and Mirror Writings of a Digit in Children’s Recognition Memory

by
Jean-Paul Fischer
1,* and
Christophe Luxembourger
2
1
Laboratory 2LPN, University Lorraine, 54021 Nancy, France
2
Department of Psychology, Laboratory 2LPN, University Lorraine, 54021 Nancy, France
*
Author to whom correspondence should be addressed.
Educ. Sci. 2020, 10(7), 183; https://doi.org/10.3390/educsci10070183
Submission received: 27 May 2020 / Revised: 8 July 2020 / Accepted: 14 July 2020 / Published: 17 July 2020
(This article belongs to the Section Early Childhood Education)
Browse Figures
Versions Notes

Abstract

:
Recent research into character reversals in writings produced by occidental children has shown that they mainly reverse the left-oriented digits (1, 2, 3, 7, and 9) and therefore appear to apply a right-orienting rule. But do they produce similar reversal errors when asked to recognize the digits? In an experiment, based on eye-tracking observations of 50 children (Mage = 5.4 years), children had to point towards a target digit in a 2 × 2 matrix also containing three distractor digits, one of which was the mirror-reversed writing of the correctly written target digit. This recognition task led to a true “battle” in children’s memory between the two writings of the target digit. This battle is shown in the graphical abstract that represents a heat map from a sub-sample of children (on the left side) and the fixation points map from an individual child (on the right side). Rather than following the predicted right-orienting rule, the children’s responses appeared to be biased towards digits in the right-hand column of the 2 × 2 matrices (when the reversed target digit was not in the same column as the correctly written target digit). As a whole, these findings support the hypotheses that many 4- to 6-year-old’s representations of the digit writings are unoriented in their memory and that these children may adopt different solutions to overcome this lack of orientation depending on whether they write or read.

Graphical Abstract

1. Introduction

Since the “discovery” of mirror writing by Buchwald in 1878 [1], the phenomenon of reversal of the characters (mainly letters, secondarily digits, for example ε instead of 3) by 3- to 7-year-old children has generated many theoretical accounts. We will distinguish two sorts of such accounts, depending on whether the theories seek the explanation of mirror reversal in the participants or in the composition of the characters.
Theories of the first sort attribute a differential role to the two cerebral hemispheres, which can support two different representations of a character. Orton’s account on dyslexia clearly pertains to this first sort [2]. These accounts do not clearly differentiate between the confusion of the characters in seeing them and their reversal in writing them. Orton’s theory was then mainly improved by Corballis and coworkers [3,4,5]. The double representation, one writing in each hemisphere, offers a simple explanation of confusion between a character and its mirror; that is, the use of the “wrong hemisphere” [6]. An original variant of this sort of theoretical account was suggested by Lachmann and coworkers [7,8,9]. These researchers see the confusion between a character and its mirror as a specific case of the holistic processing mode in younger children which will be replaced (suppressed) by an analytical one through experience (and automatization) in reading letters or digits. The differential mode of processing often attributed to the two hemispheres—the right hemisphere excels at holistic processing of information whereas the left excels at analytic [10]—and the typical perceptual and cognitive development going from the holistic toward the analytic mode [11] (but see also [12]), support this theory. Furthermore, the recent finding that adults who are the most sensitive to inversion of the words (rotation of 180° and right-to-left writing) are those who engage the right visual word form area the most [13], reinforces the possible role of the two cerebral hemispheres in the differential use of the two modes of processing. Importantly, this first sort of theoretical account leads to mainly attributing the problem of mirror reversal confusion to some persons or populations. For example, there is a considerable literature on the confusion between characters among children [14,15] or adults [16,17] who write with their left hand, and among learning-disabled children [14,18].
The second sort of theoretical account was initially developed through the analysis of the form of the characters [19,20,21,22]. Thus, these theories emphasize the characters rather than the persons. The authors of these theories have noted that many Latin letters have a roughly vertical stem with an appendage to the right (B, D, E, F, K, L, N, P, and R for the asymmetrical capital letters). This particularity of the letters makes them look toward the right; that is, in the direction of writing in our culture. Thus, when writing, one may be tempted to turn all capital letters, including J and Z, toward the right. However, this is not sufficient to explain confusion between a correctly written and a mirror written character and, furthermore, does not hold for the digits that, in majority, look toward the left (1, 2, 3, 7, and 9 for the asymmetrical digits). It was the process of mirror generalization in memory [3,23,24,25,26] that allowed us to complete the theory. Because this process results in an unoriented representation of the characters in memory, children who are asked to write a character on a sheet of paper should be in difficulty [27]. The empirical work by Fischer and coworkers [28] shows that a great number of these children adopt a simple, but reasonable, solution to overcome the difficulty. They merely orient the characters in the direction of writing [29,30]. Consequently, in writing, they reverse the left-oriented characters (J, Z, 1, 2, 3, 7, and 9). However, two interesting questions induced by this proposition remain unanswered.
First, because unoriented representations are also activated in reading or recognition tasks (see [28], Section 5.5), a “battle” should be observed when children must make a choice between correctly or mirror-written characters. Second, if such a battle occurs, do children apply the same solution; that is, to prefer the characters oriented in the direction of writing, whether correctly or mirror written? If not, how do they base their choice of the correct writing? The observation of the possible battle in recognition memory and these questions were the main aims of the present research.
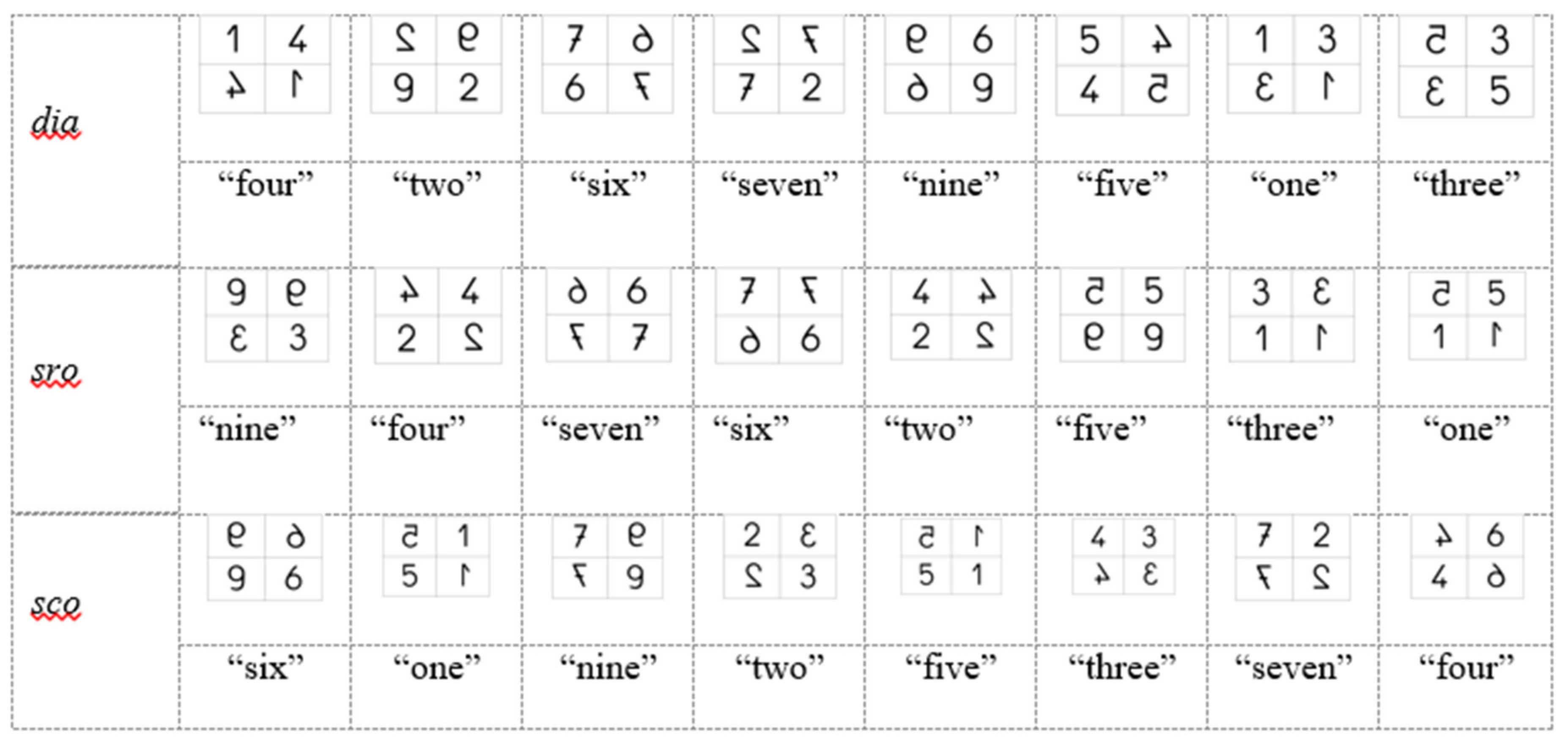
To achieve these aims, a very simple approach—asking the children to choose the correct writing when a target character is displayed beside its mirror image—was selected. If the representations of the characters are unoriented in recognition memory, the correct and mirror writings of a character will appear equally valid. This will result in considerable hesitation or even inability to correctly identify the correct writing. Presenting just these two writings simultaneously forces a child who has not overcome the problem of mirror generalization to choose between what he or she perceives as two valid writings. This problem does not disappear when the two writings are presented among other characters, but it may attenuate its apparent difficulty by enabling 4- to 5-year-old children to apply their knowledge of the characters’ shapes (without orientation) and thereby easily reject writings whose shapes are inappropriate. Consequently, we used this way of testing recognition memory. For practical reasons, most notably to facilitate the use of an eye-tracking system, we limited to four the number of writings simultaneously displayed in 2 × 2 matrices.
Another important methodological choice was the type of materials to use which, because we carried out the study in France, had to take into account the way children in France’s écoles maternelles are taught to write the characters. Écoles maternelles are divided into three “sections”: lower, middle, and upper. Children generally begin learning how to write in the middle section, starting with the uppercase letters and then the digits. They may be taught to write the lowercase letters when they are in the upper section, at which point teachers have to decide whether to teach printing or cursive writing. Most teachers prefer cursive writing. Consequently, uppercase letters and digits are the most appropriate material for systematic statistical studies of 4- to 5-year-old children’s knowledge of the characters. Eleven of the 26 uppercase letters are symmetrical about a vertical axis (i.e., a horizontal mirror reversal is indistinguishable from a correct writing). Of the 15 remaining asymmetrical uppercase letters, only two (J and Z) appear to be left-oriented, as reported by studies measuring adults’ ratings of the characters’ left or right orientations [31,32]. Conversely, most of the digits (1, 2, 3, 7, and 9) are reported as being left-oriented [32]. Thus, digits offer a greater possibility for observing reversal errors if these errors are induced by a character’s left orientation, as suggested for writing the characters [28].
Finally, in order to ascertain whether a battle between a correct and a reversed writing of a digit actually takes place, we used an eye-tracker. The eye-tracker allowed us to determine whether children who are trying to choose the correct writing of a target skip back and forth between the correct writing and the mirror target, and to compare the frequency of these skips of attention with other possible skips (e.g., between the correct and mirror writings of the distractor). As observed in writing, children seem to bootstrap the orientation of the digits. The active verb “bootstrap” means that they do this themselves, through improvised means, with a self-initiated process and with no apparent outside help [33]. Therefore, the use of an eye-tracker was not only original, but also very appropriate for observing the children’s choice of the digits’ orientation.
Because experiments on recognition of written digits in competition with their mirror writing are very scarce, a consequent pilot study was however desirable. A behavioral pilot study was possible as part of a more general test of an emergent numeracy project called LINUMEN (LIttératie et NUMératie Émergentes par le Numérique: see [34]). Hence, 169 children (Mage = 5.07 years; SD = 0.60; 75 girls) from 11 classes at three écoles maternelles participating in the project were recruited. They were successively presented with eight 2 × 2 matrices containing a correct writing of the target digit and three distractor writings, one of which was the mirror reversal of the target digit. Each matrix was devoted to one of the eight asymmetrical digits. For example, in the first matrix, the target 7 was located in the second column (i.e., right part of the matrix) and row (i.e., bottom part of the matrix) and its reversal Education 10 00183 i001 in the first column and row (i.e., diagonally opposite from target); the matrix was completed with the digit 3 (i.e., any other asymmetrical digit) and its reversal e. All the other seven matrices followed an analogous construction.
Two important conclusions could be drawn from this pilot study with respect to our initial purpose. First, it is unnecessary to observe a considerable number of children because the children’s choices concentrate on the target and its mirror. Indeed, an overwhelming majority of the children chose either the correct target (mean = 61.8%) or the mirror target (mean = 35.2%), with fewer than 5% of the children choosing one of the two distractors. Second, children’s choices were biased toward the right side of the matrix. We found a preference for responses in the right side column, with children choosing writings from the right side column in 60% of the trials and from the left side column in 40% of the trials. A paired participant’s t-test showed this difference to be highly significant, t(168) = 6.682, p < 0.001, η2 = 0.210. These findings fundamentally explain the rationale of our following experimental design.

2. Experiment

2.1. Material and Method

2.1.1. Participants

A sample of 50 children (28 girls, Mage = 5.38 years, SD = 0.52) from a single école maternelle was recruited (not a sub-sample of the children in the pilot study). The same experimenter tested all the children individually, during the second school term. At the beginning of the experiment, the children were given a pointer for pointing to the correct answer. Seven children spontaneously held this pointer in their left hand. All the children were instructed to use the same hand throughout the test. All administrative authorizations and ethical rules for experiments in schools were respected and we obtained informed written consent from the parents of the tested children.

2.1.2. Material

The stimuli were the three series of eight 2 × 2 matrices of digit writings shown in Figure 1. Each series included, in random order, all eight asymmetrical digits as targets, with a different target digit in each matrix. The positions of these targets were counterbalanced across each series so that four matrices in each series had correctly written targets in the top row, four matrices had correctly written targets in the bottom row, four matrices had correctly written targets in the left side column, and four matrices had correctly written targets in the right side column. The three series were created by placing the mirror targets either diagonally opposite (dia series), in the same row (sro series), or in the same column (sco series) as the correctly written target. Each matrix was completed by adding two versions (correct and reversed) of an asymmetrical digit as distractors. The distractors first were randomly chosen, with the important constraints that all 8 asymmetrical digits were assigned to each series and differed from the target digit of the concerned matrix, and then were added in such a way that four matrices in each series had correctly written distractors in the top row, four matrices had correctly written distractors in the bottom row, four matrices had correctly written distractors in the left side column, and four matrices had correctly written distractors in the right side column. The digits in the four cells of the 2 × 2 matrices were written using the ScriptEcole2 font (5 cm high on the screen).

2.1.3. Apparatus

We used a Tobii Pro Glasses 2 Eye Tracker to record eye movements during testing and a Tobii Pro Glasses Analyzer to analyze the data recorded [35]. Technical problems in tracking the eyes resulted in decentered fixation data for 12 participants. However, manual re-centering of these data enabled us to include all but a small percentage of trials (1.17%) in the eye-tracking analysis.
We defined the four rectangular cells in each 2 × 2 matrix as areas of interest (AOIs), although we excluded the small corner of each cell at the center of the matrix in order to avoid attributing a precise AOI to a gaze point near the center of the matrix. There was a bi-univocal correspondence between the four AOIs and the four writings of a digit (e.g., AOI#1 corresponds to a correct writing of a target digit). Successive fixations in the same AOI were counted as a single visit and the minimum duration of a fixation was 60 ms, which is the default value for the Tobii analyzer.

2.1.4. Procedure

The tests took place in a quiet room, near the children’s classroom but away from other children. Every participant was presented with the twenty-four 2 × 2 matrices. Each 2 × 2 matrix was displayed in the center of a computer screen, with a visual angle of approximately 21 × 16°, preceded by a fixation cross, the duration of which was decided by the experimenter. The children were given a 20-cm pointer, which they were told to use to point to the correct writing. This instruction was repeated many times (systematically at the beginning of the test). The matrix was displayed until the child had pointed to the chosen response. Transitions from one item to the next were controlled by the experimenter, who provided uniquely encouraging and positive feedback. The children were divided into two groups, one of which (n = 29) received the three series in the order dia, sro, sco. The series were reversed for the other group (n = 21). Because there were no significant differences in the number of correct choices between the two groups (p = 0.35), we collapsed the data across groups.

2.1.5. Hypotheses

Our experiment, and the relatively low number of participants more precisely, was based on the prediction (confirmed in the pilot study) that mirror writing of the target should be a very compelling distractor in the recognition task. We expected this distractor to be so compelling that we named it the “mirror target”, in order to distinguish it from the other two distractors in a 2 × 2 matrix.
Hypothesis 1—the battle hypothesis—claims that there is a true battle between the correct and mirror writings in children’s recognition memory. With our eye-tracking system, we were able to examine the stage preceding the choice of the children. With respect to this stage, the hypothesis predicts that children mainly hesitate between the two writings (correct or reversed) of the target digit when making their choice. The eye-tracking data allow us to verify if children will look at the two AOIs containing the correct and mirror targets more frequently and for longer times than they look at the AOIs containing the two distractors. The hypothesis may be investigated by systematically counting the saccades between two AOIs. If the hypothesis is correct, we should observe a substantially higher number of saccades between the AOIs containing the correct and mirror targets than between the other pairs of AOIs.
Hypothesis 2—the digit-orientation hypothesis—was based on an analogy with writing. When writing from memory, children who do not know the orientation of a character orient it in the direction of writing. Hence, we hypothesized that our participants, who live in a left-to-right writing culture, would apply the same implicit right-orienting rule when making forced choices in a character recognition task. Therefore, they should prefer the right-oriented characters. In the case of the digits, we expected them to choose the correct writings of 4, 5, and 6, but the incorrect writings of 1, 2, 3, 7, and 9; that is, Education 10 00183 i002 respectively. Note that the debatable right-oriented categorization of digit 4 was well argued in other studies [28,33].
Hypothesis 3—the right-side preference hypothesis—appears an alternative to Hypothesis 2 for explaining many erroneous mirror target choices. It claims the children’s preference for a choice located in the right column of the matrix when they hesitate between the two target writings. This preference was suggested by the pilot study but not properly demonstrated because the left or right target’s position was not perfectly counterbalanced across the study. Because our three series differed in the relative positions of the mirror target and the correct target, we could also explore a consequence of the right-side preference. When presented with the dia and sro series, children could differentiate the target digit writings on the basis of their position in the left-side or right-side column of the matrix, and choose the writing in the right-side column, whether correct or not. But this was not the case for the sco series, where the two writings of the target digit were in the same column. Therefore, we predicted that the left or right horizontal position of the target would have an effect on the children’s responses in the dia and sro series but not in the sco series.

2.2. Results

2.2.1. Behavioral Results

Minimum, first quartile, mean, median, third quartile, and maximum values (out of 24 choices per child) were 6, 12, 14.42, 13, 18, and 24, respectively, for correct target choices, and 0, 6, 9.20, 10, 12, and 18, respectively, for mirror target choices. Hence, the data were not subject to any floor or ceiling effects.
An overwhelming majority of the children chose either the correct target (mean = 60.1%) or the mirror target (mean = 38.3%), with less than 6% of the children (exactly 6% for the digit 9) choosing one of the two distractors (Table 1). In fact, in half of the matrices, none of the children chose the distractor.
As regards to Hypothesis 2, there was no significant difference between the left-oriented digits (1, 2, 3, 7, and 9) and the right-oriented digits (4, 5, and 6) in terms of the percentage of mirror target choices: 38.67% for left-oriented targets versus 37.78% for right-oriented targets, t(49) = 0.262, p = 0.79, η2 = 0.001. Therefore, Hypothesis 2 was not confirmed.
Somewhat logically, its alternative Hypothesis 3, that is, a choice based on the right-side position of the target writing rather than on the target digit’s orientation (Hypothesis 2), was clearly confirmed. The relative positions of the correct and mirror targets significantly influenced the children’s choices, F(2,98) = 13.46, p < 0.001, ηG2 = 0.125. As predicted, the number of right-side choices was significantly lower in the sco condition than in the other two conditions (Figure 2).
When the correct and mirror targets were in the same column, as in the sco condition, children could not differentiate these writings on the basis of their left/right position in the matrix. When the correct and mirror targets were in the same row, as in the sro condition, children could not differentiate these writings on the basis of their top/bottom position in the matrix. Consequently, in order to determine whether the children showed a preference for right-side column or top row choices we had to analyze the dia + sro and dia + sco conditions, respectively. Analyzing the dia + sro condition showed that children were much more likely to choose a response from the right-side column of the matrix (61.88% of choices) than from the left-side column, t(49) = 4.665, p < 0.001, η2 = 0.307. Similarly, in the dia + sco condition the children showed a preference for writings in the top row (55.13% of choices) over writings in the bottom row, t(49) = 2.236, p = 0.030, η2 = 0.093. It is important to add that the preference for writings in the right-side column of the matrix was marginally greater for the seven children who pointed to their choices with their left hand. In the dia + sro condition, 63.39% of these children’s choices were in the right-side column (versus 61.63% for children who pointed to their choices with their right hand).
Thus, as well as enabling us to enhance the confirmation of Hypothesis 3, including three conditions (dia, sro, and sco), the experiment allowed us to show what happens when the right-side decision-making rule does not apply (as in the sco condition). In such cases, the children’s responses were distributed equally between the left and right sides of the matrix, with some of the children appearing to replace the inoperative right-side rule with an upper-half rule.
Finally, in order to test for possible impacts of certain individual factors in the choice of mirror targets simultaneously with the role of orientation and digit position, we conducted a mixed-effects logistic regression using the glmer function of the lme4 package [37]. The binary dependent variable Y was 1 if the child chose the mirror target and 0 if not. The fixed effects were age (the only continuous variable, which was mean-centered), sex, pointing hand, digit orientation, and the digit’s horizontal and vertical positions. As regards the random effects, we only specified that we wanted the intercept to vary across participants. The full model yielded a significant fixed effect of the digit’s horizontal position, |z| = 5.167, p < 0.001. Sex also had a significant effect, |z| = 2.473, p = 0.013, reflecting the higher percentage of mirror target choices by boys versus girls (44.70% vs. 33.33%). Compared with a model with horizontal position as the only fixed factor, adding sex as a fixed factor improved the model significantly (χ2(1) = 6.05, p =.014) but ambiguously (the addition decreased the AIC criterion but increased the BIC criterion). No other effects were significant. In particular, the hand a child used to point to the answer had no significant effect.

2.2.2. Eye-Tracking Results

We first studied the influence of the type of writing—correct target, reversed target, correct distractor, reversed distractor—on the total number of visitations (TNV) and total duration of fixation (TDF). For comparison, we also studied the influence of the type of writing on the children’s point of first fixation.
Type of writing significantly but slightly influenced the children’s point of first fixation, F(3,147) = 6.76, p < 0.001, ηG2 = 0.121. The mean percentage of first fixations was significantly greater for the mirror target than it was for the correctly written target and the correctly written distractor (Figure 3a).
Type of writing significantly influenced the TNV, F(3,147) = 268.04, p < 0.001, ηG2 = 0.845. The percentages of the TNV accorded to each of the two target writings were comparable and each of these percentages was significantly higher than the percentages of the TNV accorded to each of the two distractor writings (Figure 3b).
Type of writing also significantly influenced the TDF, F(3,147) = 274.66, p < 0.001, ηG2 = 0.849. The percentages of the TDF accorded to each of the two target writings were comparable and these percentages were significantly higher than the percentages of the TDF accorded to each of the two distractor writings (Figure 3c).
Figure 3 also suggests that the children’s first fixations landed more randomly on one of the four AOIs or writings than their visitations or fixations. The latter appear to be concentrated on the AOIs containing the two writings of the target digit.
Regarding Hypothesis 1, that is, a genuine battle in children’s recognition memory between the two writings of the target digit, we compared the saccades between any one pair of AOIs by calculating the percentage of saccades a child allocated to each pair. We then calculated the mean percentage for the 50 participants (Figure 4). The percentage of saccades varied significantly and strongly across the six pairs of AOIs, F(5,245) = 257.62, p < 0.001, ηG2 = 0.840. Saccades between the correct target and the mirror target accounted for almost 50% of all saccades. This figure is substantially higher than the percentage of saccades for any other pair of writings.
The eye-tracking analyzer produced numerous illustrations of the intensity of the battle in the recognition memory between the two writings of the target digit. The left-part of Figure 5 shows the strength of the battle at a global level. To construct this image, all the fixation relative counts from the children were first added together; then, color values were added to all fixation points, with the warmest color representing the highest values. We see that the warmest colors are centered on the correct and mirror writings of the target digit 5. The right-part of Figure 5 shows the intensity of the battle between the target digit 6 and its mirror in the mind of a girl aged 5 years 9 months. Examination of the fixation points shows that the girl’s gaze skipped between the correct and mirror writings of ‘6’ six or seven times before she correctly selected 6.

3. Discussion

3.1. The “Battle” between Correct and Reversed Writings of Digits in Children’s Recognition Memory

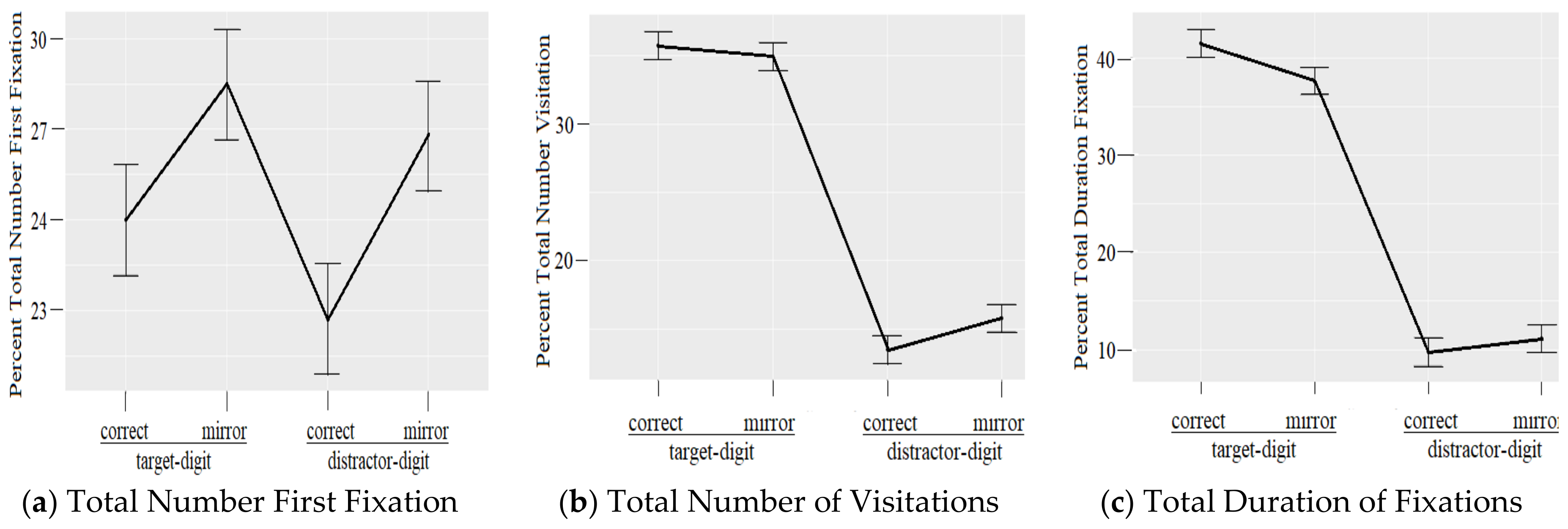
The behavioral results first showed that the children chose, as expected, the correct (60.1%) or mirror (38.3%) targets much more frequently than they chose the correct (0.8%) or mirror (0.8%) distractors. The eye-tracking data confirmed that the percentages of visitations and durations of fixations were higher (and approximately equal) for the AOIs containing the correct and mirror targets than they were for the AOIs containing the correct and mirror distractors.
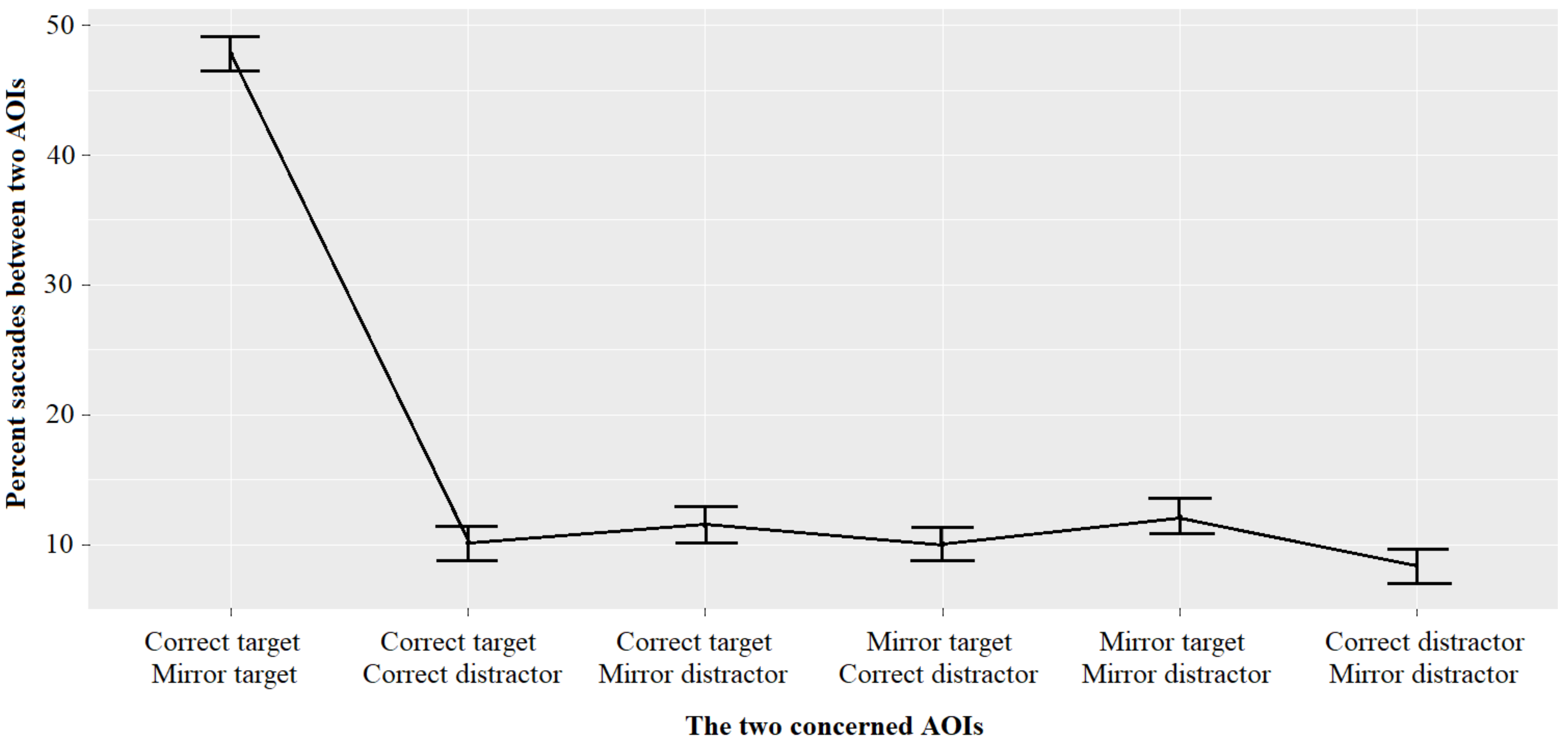
Eye movements showed a systematic relationship between the digit heard and where the eyes tended to go in the 2 × 2 matrix. After initially landing on one of the matrix’s four cells, the children’s gaze moved back and forth, mainly between the cells containing the correct and mirror targets. Despite the presence of the other two distractors, the children’s resulting choices were then essentially restricted to the two writings of the target digit.
Can these results not simply be explained by perceptual similarity? For example, 5 and its mirror are surely, additionally of their transformational relation, more similar to each other than 5 and 1 in terms of Gestalt (e.g., structure, complexity). However, 1 and its mirror also are more similar to each other than 1 and 5. Therefore, the perceptual similarity cannot explain why the children focused on 5 and its mirror, when 5 is the requested target, and on 1 and its mirror when 1 is the requested target. A simple physical similarity between a target and its mirror cannot account for the concentration on these two writings: children must use their memorized knowledge of the form of the requested digit. In fact, the similarity, or even the identity of a target digit and its mirror is a direct consequence of the unoriented representation.
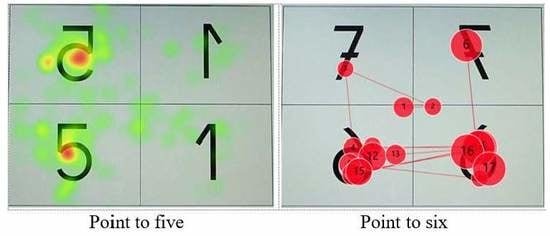
The distribution of choices concentrates on the writings of the target digits; the distractor digits (other than the reversed target digit) accounting for less than 1% of the children’s choices. Such a distribution could also occur if there was a binary division between two populations of children, with a majority population of children who know the correct writing and a minority population of children who have a mirror representation of the target. However, the predominance of saccades between the correct and mirror targets suggest that the true explanation for this distribution is a genuine battle in the children’s recognition memory between the two orientations of the target digit (Hypothesis 1). Spontaneous comments by some very few children provided incidental evidence corroborating the hesitation or embarrassment accompanying their choice between the two target writings. For example, when a 4-year, 10-month-old boy was shown the final matrix in the sco condition (see Figure 1) and instructed to point to “four”, he, somewhat vexedly, said: “They are all the same”. The systematic analysis of the saccades between the AOIs as the children made their choice clearly confirmed our battle hypothesis.
Many visual images provided by the eye-tracking system illustrate this battle between the two writings in the children’s recognition memory (see Figure 5). To our knowledge, this curious battle has never been demonstrated, despite the huge body of research conducted during the 142 years since Buchwald first introduced the notion of “mirror writing” [1].
The present results therefore support the theoretical account of character reversals in typical 4- to 6-year-old children, most notably the idea that representations of the digits in the memory of a great number of children are unoriented, at least at a certain stage of their development (see Introduction). They support both the theory as a whole and its individual components. Thus, both the neurological component—the process of mirror generalization—and the developmental component—which assumes that 4- to 6-year-old children know the shapes of the digits without orientation—are supported by our findings. The latter is specifically supported by the fact that our participants rarely confused the writings of the target digit with the writings of another digit and often confused the two writings of the target digit.

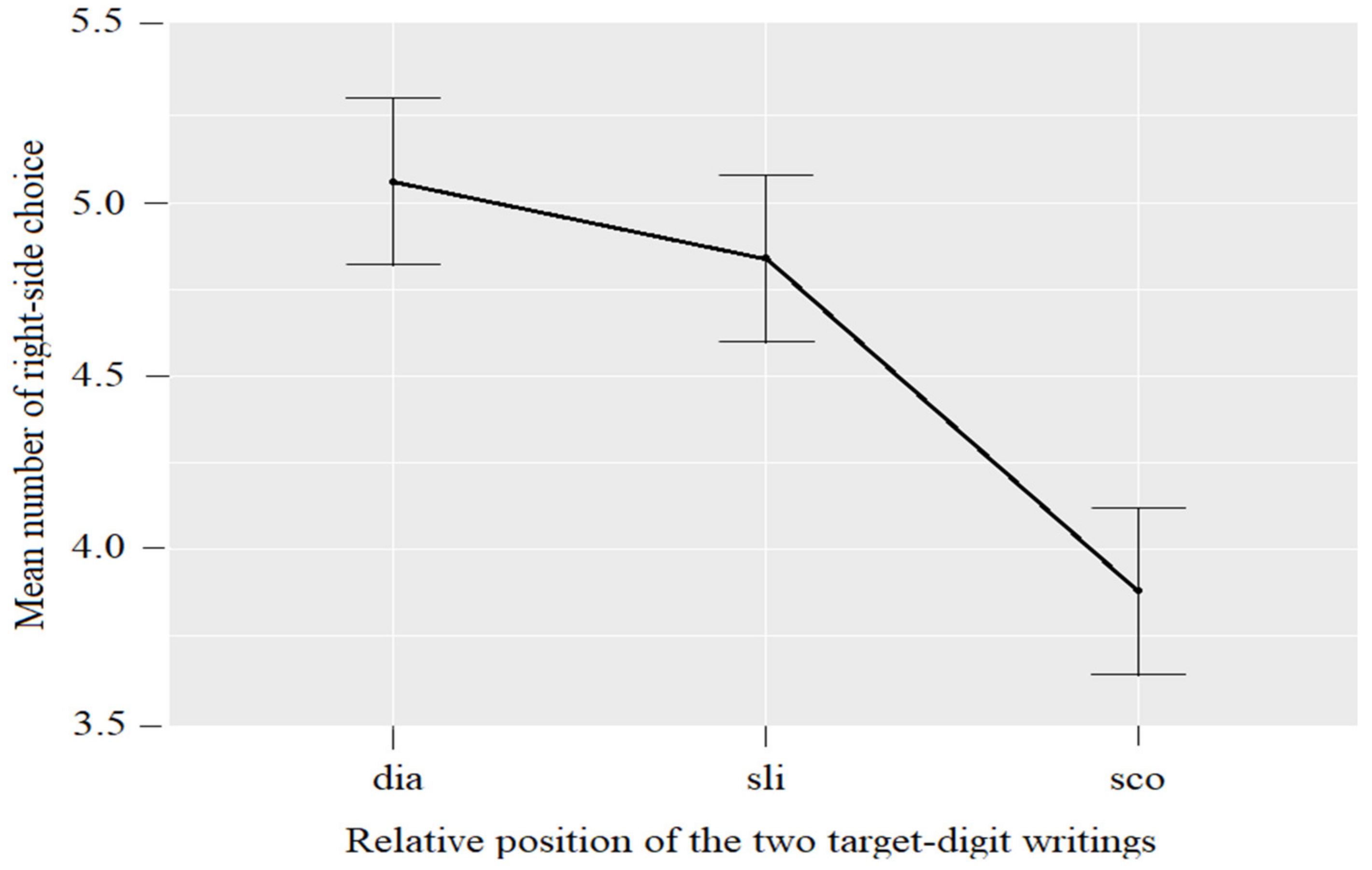
3.2. The Right Spatial Position Versus Digit’s Orientation Bias in the Children’s Recognition Response-Choices

The right spatial position bias was revealed incidentally in the pilot study and was confirmed by our present experience when the two writings of the target digit were not in the same column. Importantly, children who pointed with their left hand also showed the bias, making unlikely a simple biomechanical advantage toward the dominant-hand side of space. In addition, the three conditions included in this experiment allowed us to establish a consequence of the implicit right spatial position bias: when this choice is impossible, it may be replaced by another spatial bias, this time for the upper half of the matrix.
Mixed logistic regression modeling showed the right spatial position of the digits to be the main factor influencing choices of the mirror target. The influence of other individual factors was either insignificant, in the case of pointing hand and age (within the restricted age range of our participants), or ambiguous, in the case of gender. It also suggests that the left-right orientation of the digits, which appears to be a major explanation for their reversal in a left-right writing culture [28,29,30], plays only a minor role when children are prompted to choose between a digit and its mirror, differentiated by their left or right horizontal position. These results are in accord with the confirmation of our right-side response hypothesis (Hypothesis 3) at the expense of the digit orientation hypothesis (Hypothesis 2).
The right-side preference is consistent with the visual-spatial biases frequently reported in preschool children [38]. We suggest that it may be a direct result of the writing/reading direction in our culture, although a rightward directional bias was recently reported in art produced by cultures without a written language [39]. It was shown that writing/reading direction can affect many thoughts and actions [40], and an overall dominance of the left-to-right counting direction in 3- to 5-year-old children in a Western culture (Germany) was reported [41]. Moreover, this counting direction may be influenced by children observing the direction in which storybooks are read to them [42]. In addition, preliterate children may learn the direction of text when learning to write (notably their name) at école maternelle, in exercise books, and/or with their parents.
A right spatial bias in typical developing children was also attributed to a selective attention deficit [43]. For example, in a line bisection task, a rightward bias in attention diminishes the apparent leftward extent of the line and, thus, leads to a response at the right of the true half. This was effectively found in right-handed children (5-7 years) when they responded with the right hand [44]. Because the attentional system was clearly challenged in our experiments, the right-side choice could result from such attentional bias. Interestingly, Lange-Küttner suggests “that a right spatial bias lingers throughout the life-span and may reemerge” [43] (p. 844), particularly under performance pressure or, as was the case in our experiment, when a child hesitates and has no other means to choose the side of its response.
Can the Spatial-Numerical Association of Response Codes (SNARC) effect [45] contribute to explain this right-side preference? The SNARC effect was originally found in tasks in which magnitude (or parity, another numerical property) was assessed using a response-time measure. It describes the tendency for people presented with a mix of larger and smaller numbers to respond faster with the right hand for the larger numbers and to respond faster with the left hand for the smaller numbers (in a left-to-right reading culture). The tasks used in our experiments involved only the visual properties of the digits (not their magnitude), and we assessed just the accuracy (but not the speed) of digit recognition. However, the numerical line showing the order of the digits from 0 to 10 (and sometimes beyond) that is displayed in all classrooms, even in écoles maternelles, may act as a powerful source of magnitude information [46]. In addition, magnitude may be activated automatically, even in young children [47]. Given the generality of the SNARC effect, which has been extended to other tasks and stimuli (e.g., pitch: see [48]), and to preschoolers [47], a SNARC-like effect must be considered a possible explanation for our right-half preference finding. However, both in our pilot study and experiment (see Figure 1), half of the larger target digits (5, 6, 7, and 9) were displayed in the left-side column and the other half were displayed in the right-side column. This was also the case for the smaller digits (1, 2, 3, and 4). Now consider a theoretical child who hesitates between the two writings of the target digit and chooses responses in the right-side column for the larger digits and responses in the left-side column for the smaller digits. For the 24 matrices in Figure 1 this child would produce exactly the same number of right-side-column choices as left-side-column choices (12 of each). Therefore, the right-side preference revealed by our experiments is unlikely to be due to a SNARC-like effect.
Does other research confirm the right-side bias at the expense of choice based on a digit’s orientation in character recognition? To the best of our knowledge, there are only two studies to have examined in a single group of children the relation between left-right reversing when writing characters and falsely recognizing mirror reversed characters [49,50]. Both studies found the two phenomena to be similar. Because they also found the left-oriented characters—the letters j and z, and the digits 3, 7, and 9—to be more prone to reversal, they are at odds with the results of our experiment. Indeed, the reversed left-oriented digits were not chosen significantly more frequently than the reversed right-oriented digits, contrary to the prediction of Hypothesis 2. However, our experiment provides an explanation for this divergence in the form of a spatial position bias in the children’s recognition responses. This is a major, and perhaps sufficient explanation, for the divergence between these findings and our results. Neither the correct letter and word reading task used in the first study [49], nor the letter decision task used in the second [50] allowed a spatial choice.

3.3. Educational Implications

In reading normal arithmetic writings, a digit is rarely simultaneous seen with its left-right mirror reversed writing. An exception may come from the symmetrical (around a horizontal axis) digit 3 when children play—or see others play—with movable digits in cardboard, plastic, or wood. They can then simultaneously see two ‘3s′, one that appears the correctly written 3 and the other written ε, as shown in Figure 6a. This is the case in the Mathable game—a mathematical/numerical version of the better known Scrabble game of words. The problem of the veracity of a mirror written 3 is also exacerbated with a classical presentation of the Mathable board, as shown in Figure 6b. More generally, with the 52 classical playing cards, children can see simultaneously the two writings of the digit ‘3′, but not two left-right reversed writings for the other asymmetrical digits, because their two writings are obtained from each other through a 180° rotation (and not through a left-right symmetry). Drawing the attention of a child who is playing, or simply observing the game, to the two writings of 3 seems to be an elementary educational act. Nevertheless, when a child is at the stage of unoriented representation of digits, this act is fundamental. Of course, it will be accompanied by an emphasis on the validity of only one of the two writings, namely “3”, in our culture, especially at school.
However, in supporting the theory of an unoriented representation of the characters in memory, our results also concern writing of the digits. Moreover, it is highly probable that our demonstration extends to characters other than digits, notably lowercase letters. This extension, for example, accounts for the finding that 1st, 3rd, and 5th graders require more time to discriminate between two lowercase letters that are lateral mirror images of one another (e.g., b and d) than two lowercase letters that are not (e.g., f and t) [51]. It leads to emphasis on the confusion in reading between b and its mirror reversal d, because these are the most common letters that are reversed.
Parents are worried about this confusion as shown by their numerous thanks for tips and tricks helping their children correct b/d reversals, which one can find on the internet (e.g., multisensory activities, air writing, the “bed” visualization, …: see, for example, https://www.readandspell.com/b-and-d-letter-reversal). One wonders whether these tricks can be proved effective. According to Fischer and Tazouti, the effectiveness of many tools or techniques used by teachers for teaching writing of the digits are supported by their data [52]. However, there is less evidence for the effectiveness of these tricks. Therefore, it is worthwhile to note that a trick used by the French children for the writing of the uppercase letter N is so effective that N proved be the least reversed capital letter [28]. This trick is to notice that to trace the letter N one must “go up, go down, and finally go back up” while writing from left to right. This quasi-absence of reversals affecting the writing of the letter N is particularly impressive when one recalls Goodnow and Levine’s prediction that children might well “grow into reversals of the letter N as they acquire the rules of starting at the top-left, starting with a vertical stroke, and threading” [53] (p. 96).
Primary teachers should be informed that students have generally no difficulty in differentiating visually b and d, or p and q, but that all of them must initiate and consolidate their differentiation in memory and, most importantly, that some students struggle with this differentiation. This would allow teachers to take preventive actions (such as the above tricks) that would reduce the risk of embarrassment in these children and, ultimately, the resulting risk of loss of their self-esteem. Indeed, letter reversals are particularly noticeable errors and fear of making them may not only disrupt fluency in writing but also interfere with a child’s ability to express him or herself.

3.4. Limitations of the Study

Our study’s main limitation concerns the possibility of generalizing the results, most notably because each target digit did not appear equally frequently at each matrix position. We also have not taken into account factors such as visual similarity (e.g., 6–9, 7–1) and numerical magnitude (e.g., 6–7). However, the results of the pilot study (succinctly reported in the Introduction) argue against a significant biasing impact of these limitations. This is because we obtained similar results with different material in the pilot study than in the eye-tracking experiment. Nevertheless, while this study has investigated the impact of the digits’ orientation and of their place in the 2 × 2 matrix, further studies should control the possible influence of other factors that might affect the selection of the target item, such as visual similarity (6–9) or numerical magnitude (6–7).
In addition, our clear and significant results were all obtained with a recognition test involving a visual search in a 2 × 2 matrix in which the three distractors were a mirror writing of the target digit and two writings of another digit. Although we created three conditions and randomized (with some constraints) the positions of the distractors and the order in which we presented the matrices in our experiment, many other stimuli and procedures could have been used. Using an eye-tracking system does not preclude displaying two items [54], three items [55], or even five or more items. Thus, further studies are needed to ensure our findings concern recognition in general and are not specific to the format of our stimuli.
Another limitation arises from the eye-tracker system we used which, even with the latest version of the associated software [35], did not have the capabilities needed to examine the time course of the preferential viewing effect. Using a more sophisticated eye-tracking system would have enabled us to examine the children’s fixations at specific times, most notably the period immediately before they give their answers. This would allow a more detailed analysis of the response intention effect [56]; that is, the natural tendency to look at the writing that is about to be selected [55].

4. Conclusions

The 4- to 6-year-old participants in our experiment heard an auditory input corresponding to a target digit contained in one of the cells of a 2 × 2 matrix displayed in front of them. The other three cells contained distractors, one of which was a mirror-written version of the target digit.
The experiment provides evidence for a battle between correct and reversed writings which ensues when children are required to choose the correct writing in a display containing both correct and mirror writings of a digit. It is also, as far as we are aware, the first demonstration that the right-orienting rule explaining children’s character reversals in writing does not influence the visual recognition of these characters. More generally, the research supports the claim that a substantial number of 4- to 6-year-old children have unoriented representations of the writing of the digits in their memory.
When forced to choose between the correct and mirror writings of a digit, children’s choices are influenced by a right-side preference. However, if this right-side preference cannot come into play, as is the case when both writings are on the same side, children may resort to a vertical preference and choose the upper writing. This latter preference is less systematic. Importantly, these visual-spatial biases seem to minimize, or even exclude, choices based on whether the digit is left-oriented or right-oriented. When writing, Fischer and Luxembourger’s explanation of mirror reversals as arising from the left-orientation of the digits is very different [28].
Therefore the present findings challenge the accepted way of thinking that character reversal (digits and letters) by typical developing children is the same phenomenon in reading and writing. None of the numerous studies on reversal in reading [7,51,57,58,59,60,61,62,63,64] underlines such a difference between the two tasks, which are associated in teaching/learning and in the brain [65]. Nevertheless, a simple description of the behavior of children who have unoriented representations of digits can account for the difference between writing and reading: when writing, children make the digits face right and therefore reverse the left-oriented digits 1, 2, 3, 7, and 9; when choosing between a correct and a mirror writing in a recognition task, (if possible) they choose the writing on the right.

Author Contributions

Conceptualization, J.-P.F.; methodology, J.-P.F. and C.L.; software, C.L.; validation, J.-P.F. and C.L.; formal analysis, J.-P.F.; investigation, C.L.; resources, C.L.; writing—original draft preparation, J.-P.F. and C.L.; writing—review and editing, J.-P.F. and C.L.; visualization, J.-P.F and C.L. Both authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

We thank all the children who have taken part in the investigations. We are also grateful to the teachers and administrative officials who have facilitated their performing.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Buchwald, A. Spiegelschrift bei Hirnkranken [Mirror writing in patients with cerebral disease]. Berliner klinische Wochenschrift 1878, 5, 6–8. [Google Scholar]
  2. Orton, S.T. “Word-blindness” in school children. Arch. Neurol. Psychiatry 1925, 14, 581–615. [Google Scholar] [CrossRef]
  3. Corballis, M.C. The left-right problem in psychology. Can. Psychol. 1974, 15, 16–33. [Google Scholar] [CrossRef]
  4. Corballis, M.C.; Beale, I.L. The Psychology of Left and Right; Erlbaum: New York, NY, USA, 1976. [Google Scholar]
  5. Corballis, M.C. Mirror-image equivalence and interhemispheric mirror-image reversal. Front. Hum. Neurosci. 2018, 12, 140. [Google Scholar] [CrossRef] [PubMed]
  6. Mather, D.S. Does dyslexia develop from learning the alphabet in the wrong hemisphere? A cognitive neuroscience analysis. Brain Lang. 2001, 76, 282–316. [Google Scholar] [CrossRef]
  7. Lachmann, T.; Geyer, T. Letter reversals in dyslexia: Is the case really closed? A critical review and conclusions. Psychol. Beitr. 2003, 45 (Suppl. 1), 50–70. [Google Scholar]
  8. Lachmann, T.; Van Leeuwen, C. Differentiation of holistic processing in the time course of letter recognition. Acta Psychol. 2008, 129, 121–129. [Google Scholar] [CrossRef]
  9. Lachmann, T. Reading and dyslexia: The functional coordination framework. In Reading and Dyslexia: From Basic Functions to Higher Order cognition; Lachmann, T., Weis, T., Eds.; Springer: Cham, Switzerland; Birkhäuser: Cham, Switzerland, 2018; pp. 271–296. [Google Scholar] [CrossRef]
  10. Banich, M.T. Hemispheric specialization and cognition. In Encyclopedia of Neuroscience; Squire, L.R., Ed.; Elsevier: Amsterdam, The Netherlands, 2010; pp. 1081–1086. [Google Scholar] [CrossRef]
  11. Kemler, D.G. Holistic and analytic modes in perceptual and cognitive development. In Perception, Cognition, and Development: Interactional Analyses; Tighe, T.J., Shepp, B.E., Eds.; Erlbaum: Hillsdale, NJ, USA, 1983; pp. 77–102. [Google Scholar]
  12. Stiles, J.; Delis, D.C.; Tada, W.L. Global-local processing in preschool children. Child Dev. 1991, 62, 1258–1275. [Google Scholar] [CrossRef]
  13. Carlos, B.J.; Hirshorn, E.A.; Durisko, C.; Fiez, J.A.; Coutanche, M.N. Word inversion sensitivity as a marker of visual word form area lateralization: An application of a novel multivariate measure of laterality. NeuroImage. 2019, 191, 493–502. [Google Scholar] [CrossRef]
  14. Gordon, H. Left-handedness and mirror writing, especially among defective children. Brain 1921, 43, 313–368. [Google Scholar] [CrossRef]
  15. Lebrun, Y. Mirror-reading and mirror-writing in schoolchildren. ANAE 1990, 2, 177–182. [Google Scholar]
  16. Della Sala, S.; Cubelli, R. Directional apraxia: A unitary account of mirror writing following brain injury or as found in normal young children. J. Neuropsychol. 2007, 1, 3–26. [Google Scholar] [CrossRef]
  17. Kushnir, T.; Arzouan, Y.; Karni, A.; Manor, D. Brain activation associated with practiced left hand mirror writing. Brain Lang. 2013, 125, 38–46. [Google Scholar] [CrossRef]
  18. Mather, D.S. Ipsilateral printing in children’s mirror-writing: A cause of specific learning disabilities? Can. J. Exp. Psychol. 2012, 66, 172–180. [Google Scholar] [CrossRef]
  19. Kolers, P.A. Clues to a letter’s recognition: Implications for the design of characters. J. Typogr. Res. 1969, 3, 145–168. [Google Scholar]
  20. Simner, M.L. The grammar of action and reversal errors in children’s printing. Dev. Psychol. 1984, 20, 136–142. [Google Scholar] [CrossRef]
  21. Fischer, J.P. Vers une levée du mystère des écritures en miroir (des lettres majuscules) chez l’enfant: Une hypothèse nouvelle. Enfance 2010, 62, 371–386. [Google Scholar] [CrossRef]
  22. Treiman, R.; Kessler, B. Similarities among the shapes of writing and their effects on learning. Writ. Lang. Lit. 2011, 14, 39–57. [Google Scholar] [CrossRef] [PubMed]
  23. Dehaene, S. Reading in the Brain: The New Science of How We Read; Penguin Books: London, UK, 2010. [Google Scholar]
  24. Freiwald, W.A.; Tsao, D.Y. Functional compartmentalization and viewpoint generalization within the macaque face-processing system. Science 2010, 330, 845–851. [Google Scholar] [CrossRef] [Green Version]
  25. Kietzmann, T.C.; Swisher, J.D.; König, P.; Tong, F. Prevalence of selectivity for mirror-symmetric views of faces in the ventral and dorsal visual pathways. J. Neurosci. 2012, 32, 11763–11772. [Google Scholar] [CrossRef] [Green Version]
  26. Kietzmann, T.C.; Poltoratski, S.; König, P.; Blake, R.; Tong, F.; Ling, S. The occipital face area is causally involved in facial viewpoint perception. J. Neurosci. 2015, 35, 16398–16403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  27. McIntosh, R.D.; Anderson, E.L.; Henderson, R.M. Experimental confirmation of a character-facing bias in literacy development. J. Exp. Child Psychol. 2018, 170, 207–214. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  28. Fischer, J.P.; Luxembourger, C. A synoptic and theoretical account of character (digits and capital letters) reversal in writings by typically developing children. Educ. Sci. 2018, 8, 137. [Google Scholar] [CrossRef] [Green Version]
  29. Fischer, J.P. Character reversal in children: The prominent role of writing direction. Read. Writ. 2017, 30, 523–542. [Google Scholar] [CrossRef] [Green Version]
  30. Portex, M.; Hélin, C.; Ponce, C.; Foulin, J.N. Dynamics of mirror writing compared to conventional writing in typical preliterate children. Read. Writ. 2018, 31, 1435–1448. [Google Scholar] [CrossRef]
  31. Treiman, R.; Gordon, J.; Boada, R.; Peterson, R.L.; Pennington, B.F. Statistical learning, letter reversals, and reading. Sci. Stud. Read. 2014, 18, 383–394. [Google Scholar] [CrossRef] [PubMed]
  32. Fischer, J.P. Studies on the written characters orientation and its influence on digit reversal by children. Educ. Psychol.-UK 2018, 38, 556–571. [Google Scholar] [CrossRef] [Green Version]
  33. Fischer, J.P. Digit reversal in children’s writing: A simple theory and its empirical validation. J. Exp. Child Psychol. 2013, 115, 356–370. [Google Scholar] [CrossRef]
  34. Tazouti, Y.; Jarlegan, A. Les Apprentissages Premiers en école Maternelle à l’ère du Numérique: Contribution du Projet LINUMEN. The Conversation. Available online: https://theconversation.com/les-apprentissages-premiers-en-ecole-maternelle-a-lere-du-numerique-contribution-du-projet-linumen-94074 (accessed on 31 October 2018).
  35. Tobii, A.B. Tobii Pro Glasses Analyzer: User’s Manual (Version 1.41). Available online: https://bmslab.utwente.nl/wp-content/uploads/2018/03/Tobii-Pro-Glasses-2-Analyzer-manual.pdf (accessed on 31 October 2018).
  36. Lawrence, M.A. Easy Analysis and Visualization of Factorial Experiments (Package ‘ez’, Version 4.4-0). Available online: https://cran.r-project.org/web/packages/ez/ez.pdf (accessed on 22 September 2018).
  37. Bates, D.; Maechler, M.; Bolker, B.; Walker, S. Fitting linear mixed-effects models using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
  38. Patro, K.; Nuerk, H.C.; Brugger, P. Visuospatial biases in preschool children: Evidence from line bisection in three-dimensional space. J. Exp. Child Psychol. 2018, 173, 16–27. [Google Scholar] [CrossRef]
  39. Boiteau, T.W.; Smith, C.; Almor, A. Rightward directional bias in art produced by cultures without a written language. Laterality 2020, 25, 165–176. [Google Scholar] [CrossRef] [PubMed]
  40. Maass, A.; Suitner, C.; Deconchy, J.P. Living in an Asymmetrical World: How Writing Direction Affects Thought and Action; Psychology Press: London, UK, 2014. [Google Scholar]
  41. Patro, K.; Nuerk, H.C.; Cress, U. Does your body count? Embodied influences on the preferred counting direction of preschoolers. J. Cogn. Psychol. 2015, 27, 413–425. [Google Scholar] [CrossRef]
  42. Göbel, S.M.; McCrink, K.; Fischer, M.H.; Shaki, S. Observation of directional storybook reading influences young children’s counting direction. J. Exp. Child Psychol. 2018, 166, 49–66. [Google Scholar] [CrossRef] [PubMed]
  43. Lange-Küttner, C. Disappearance of biased visual attention in infants: Remediated tonic neck reflex or maturating visual asymmetry? Percept. Motor Skill. 2018, 125, 839–865. [Google Scholar] [CrossRef] [Green Version]
  44. Failla, C.V.; Sheppard, D.M.; Bradshaw, J.L. Age and responding-hand related changes in performance of neurologically normal subjects on the line-bisection and chimeric-faces tasks. Brain Cogn. 2003, 52, 353–363. [Google Scholar] [CrossRef]
  45. Dehaene, S.; Bossini, S.; Giraux, P. The mental representation of parity and number magnitude. J. Exp. Psychol. Gen. 1993, 122, 371–396. [Google Scholar] [CrossRef]
  46. Sella, F.; Lucangeli, D.; Zorzi, M. Spatial order relates to the exact numerical magnitude of digits in young children. J. Exp. Child Psychol. 2019, 178, 385–404. [Google Scholar] [CrossRef]
  47. Hoffmann, D.; Hornung, C.; Martin, R.; Schiltz, C. Developing number–space associations: SNARC effects using a color discrimination task in 5–year–olds. J. Exp. Child Psychol. 2013, 116, 775–791. [Google Scholar] [CrossRef] [Green Version]
  48. Weis, T.; Estner, B.; van Leeuwen, C.; Lachmann, T. SNARC (spatial–numerical association of response codes) meets SPARC (spatial–pitch association of response codes): Automaticity and interdependency in compatibility effects. Q. J. Exp. Psychol. 2016, 69, 1366–1383. [Google Scholar] [CrossRef]
  49. Richmond, J.; Taylor, M. Visual recognition difficulties: Identifying primary school students’ directional confusion in writing letters and numbers. S. Afr. J. Occup. Ther. 2014, 44, 2–6. [Google Scholar]
  50. McIntosh, R.D.; Hillary, K.; Brennan, A.; Lechowicz, M. Developmental mirror-writing is paralleled by orientation recognition errors. Laterality 2018, 23, 664–683. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  51. Ahr, E.; Houdé, O.; Borst, G. Inhibition of the mirror generalization process in reading in school-aged children. J. Exp. Child Psychol. 2016, 145, 157–165. [Google Scholar] [CrossRef] [PubMed]
  52. Fischer, J.P.; Tazouti, Y. Unraveling the mystery of mirror writing in typically developing children. J. Educ. Psychol. 2012, 104, 193–205. [Google Scholar] [CrossRef]
  53. Goodnow, J.J.; Levine, R.A. The grammar of action: Sequence and syntax in children’s copying. Cogn. Psychol. 1973, 4, 82–98. [Google Scholar] [CrossRef]
  54. Doi, H.; Shinohara, K. Attention allocation towards own face is pronounced during middle adolescence: An eye-tracking study. Dev. Sci. 2018, 21, e12490. [Google Scholar] [CrossRef]
  55. Urgolites, Z.J.; Smith, C.N.; Squire, L.R. Eye movements support the link between conscious memory and medial temporal lobe function. Proc. Natl. Acad. Sci. USA 2018, 115, 7599–7604. [Google Scholar] [CrossRef] [Green Version]
  56. Ryan, J.D.; Hannula, D.E.; Cohen, N.J. The obligatory effects of memory on eye movements. Memory 2007, 15, 508–525. [Google Scholar] [CrossRef]
  57. Brault-Foisy, L.M.; Ahr, E.; Masson, S.; Houdé, O.; Borst, G. Is inhibitory control involved in discriminating pseudowords that contain the reversible letters b and d? J. Exp. Child Psychol. 2017, 162, 259–267. [Google Scholar] [CrossRef]
  58. Davidson, H.P. A study of the confusing letters b, d, p, and q. Pedagog. Semin. J. Gen. 1935, 47, 458–468. [Google Scholar] [CrossRef]
  59. Fernandes, T.; Leite, I. Mirrors are hard to break: A critical review and behavioral evidence on mirror-image processing in developmental dyslexia. J. Exp. Child Psychol. 2017, 159, 66–82. [Google Scholar] [CrossRef]
  60. Fernandes, T.; Leite, I.; Kolinsky, R. Into the looking glass: Literacy acquisition and mirror invariance in preschool and first-grade children. Child Dev. 2016, 87, 2008–2025. [Google Scholar] [CrossRef] [PubMed]
  61. Liberman, I.Y.; Shankweiler, D.; Orlando, C.; Harris, K.S.; Berti, F.B. Letter confusions and reversals of sequence in the beginning reader: Implications for Orton’s theory of developmental dyslexia. Cortex 1971, 7, 127–142. [Google Scholar] [CrossRef]
  62. Orton, S.T. A physiological theory of reading disability and stuttering in children. N. Engl. J. Med. 1928, 199, 1046–1052. [Google Scholar] [CrossRef]
  63. Wechsler, D.; Pignatelli, M.L. Reversal errors in reading: Phenomena of axial rotation. J. Educ. Psychol. 1937, 28, 215–221. [Google Scholar] [CrossRef]
  64. Soares, A.P.; Lages, A.; Oliveira, H.; Hernández, J. The mirror reflects more for d than for b: Right asymmetry bias on the visual recognition of words containing reversal letters. J. Exp. Child Psychol. 2019, 182, 18–37. [Google Scholar] [CrossRef]
  65. Longcamp, M.; Anton, J.L.; Roth, M.; Velay, J.L. Visual presentation of single letters activates a premotor area involved in writing. NeuroImage 2003, 19, 1492–1500. [Google Scholar] [CrossRef]
Education 10 00183 g001 550
Figure 1. The three series of eight matrices used in the experiment. The two writings of the target digit were diagonally opposite each other (dia series), in the same row (sro series), or in the same column (sco series). The name of the target digit, shown in quotation marks below the matrix, was read aloud, not written.
Figure 1. The three series of eight matrices used in the experiment. The two writings of the target digit were diagonally opposite each other (dia series), in the same row (sro series), or in the same column (sco series). The name of the target digit, shown in quotation marks below the matrix, was read aloud, not written.
Education 10 00183 g001
Education 10 00183 g002 550
Figure 2. Mean number of right-side column responses (out of 8) as a function of the relative positions of the two target digit writings: diagonally opposite (dia), same row (sro), or same column (sco). The error bars show Fisher’s Least Significant Differences, which facilitate visual post-hoc multiple comparisons (see [36]).
Figure 2. Mean number of right-side column responses (out of 8) as a function of the relative positions of the two target digit writings: diagonally opposite (dia), same row (sro), or same column (sco). The error bars show Fisher’s Least Significant Differences, which facilitate visual post-hoc multiple comparisons (see [36]).
Education 10 00183 g002
Education 10 00183 g003 550
Figure 3. Mean percentages of (a) total number of first fixations, (b) total number of visitations, and (c) total duration of fixations for each type of writing. The error bars show Fisher’s Least Significant Differences [36].
Figure 3. Mean percentages of (a) total number of first fixations, (b) total number of visitations, and (c) total duration of fixations for each type of writing. The error bars show Fisher’s Least Significant Differences [36].
Education 10 00183 g003
Education 10 00183 g004 550
Figure 4. Mean percentages of the participants’ saccades between each of the six pairs of areas of interest (AOIs). The error bars show Fisher’s Least Significant Differences [36].
Figure 4. Mean percentages of the participants’ saccades between each of the six pairs of areas of interest (AOIs). The error bars show Fisher’s Least Significant Differences [36].
Education 10 00183 g004
Education 10 00183 g005 550
Figure 5. Fixation point plots showing the intensity of the battle between the correct and mirror writings of a target digit (5 in Figure 5a; 6 in Figure 5b) in children’s recognition memory. In Figure 5a, the colors red, yellow, and green show, respectively, the highest, intermediate, and lowest numbers of fixations. In Figure 5b, the size of the dots indicates the fixation duration, the numbers in the dots show the order of fixations, and the lines between the dots show the gaze trail from one fixation to another.
Figure 5. Fixation point plots showing the intensity of the battle between the correct and mirror writings of a target digit (5 in Figure 5a; 6 in Figure 5b) in children’s recognition memory. In Figure 5a, the colors red, yellow, and green show, respectively, the highest, intermediate, and lowest numbers of fixations. In Figure 5b, the size of the dots indicates the fixation duration, the numbers in the dots show the order of fixations, and the lines between the dots show the gaze trail from one fixation to another.
Education 10 00183 g005
Education 10 00183 g006 550
Figure 6. The problem of validity of a mirror written 3 is raised in the Mathable game, both by (a) the possibility of positioning the movable digits in any one orientation, and (b) the classical presentation of the board in which the symmetrically opposed 3s are in mirror one of the other.
Figure 6. The problem of validity of a mirror written 3 is raised in the Mathable game, both by (a) the possibility of positioning the movable digits in any one orientation, and (b) the classical presentation of the board in which the symmetrically opposed 3s are in mirror one of the other.
Education 10 00183 g006
Table
Table 1. Percentage of children who chose each response for each target digit.
Table 1. Percentage of children who chose each response for each target digit.
Choice12345679
Correct Target54.6768.6769.3360.0061.3360.0056.6750.00
Mirror Target45.3331.3330.6740.0037.3336.0042.0044.00
Correct Distractor0.000.000.000.000.000.670.675.33
Mirror Distractor0.000.000.000.001.333.330.670.67

Share and Cite

MDPI and ACS Style

Fischer, J.-P.; Luxembourger, C. The Battle between the Correct and Mirror Writings of a Digit in Children’s Recognition Memory. Educ. Sci. 2020, 10, 183. https://doi.org/10.3390/educsci10070183

AMA Style

Fischer J-P, Luxembourger C. The Battle between the Correct and Mirror Writings of a Digit in Children’s Recognition Memory. Education Sciences. 2020; 10(7):183. https://doi.org/10.3390/educsci10070183

Chicago/Turabian Style

Fischer, Jean-Paul, and Christophe Luxembourger. 2020. "The Battle between the Correct and Mirror Writings of a Digit in Children’s Recognition Memory" Education Sciences 10, no. 7: 183. https://doi.org/10.3390/educsci10070183

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop