Investigating Network Coherence to Assess Students’ Conceptual Understanding of Energy

Abstract

Conceptual knowledge is a crucial tool for students to understand scientific phenomena. Knowledge about the structure and function of mental concepts potentially helps science educators to foster the acquisition of this tool. Specifically, the coherence of students’ mental concepts is an intensely discussed issue within the related conceptual change discourse. While former discussions focused on the question of whether these conceptions are coherent or not, recent approaches describe them as dynamic systems behaving more or less coherently in different situations. In this contribution, we captured this dynamic behavior of individual concepts by means of network analysis. Transcribed video data of 16 pairs of students working on four subsequent experiments on energy were transformed into weighted networks, which in turn were characterized by standardized coherence parameters. These coherence parameters and more basic network parameters were correlated with students’ pre-post scores of a multiple-choice test on the energy concept. We found that the coherence parameter is significantly related to the students’ test scores. Even more intense relations are indicated if networks are calculated solely based on conceptual key terms. Implications as well as methodological constraints of this approach are discussed.

1. Introduction

Scientific concepts constitute powerful tools to make sense of the world, within the scientific community as well as in everyday life [1]. Accordingly, promoting conceptual understanding is a major aim of science education [2,3,4]. Also, research has put much effort on questions concerning the nature of individual concepts and their development, e.g., from naïve interpretations of the world to normatively accepted thinking tools [5]. In general, scientific concepts (like evolutionary theory, Newtonian laws, or energy) can be considered as relational categories that relate several variables to each other [6]. Acquiring a scientific concept requires the learner “to develop highly flexible relational knowledge representations to be able to successfully use these concepts,” in terms of classifying phenomena, problems, and situations “by their deep (common) relational structure and not (only) by superficial features” ([6], p. 733; cf. [7]).

During the last decades, different approaches to characterize the nature of individual conceptions as well as the process of concept development were discussed controversially. In a nutshell, some proponents argue that individual conceptions consist of several elements like presuppositions, beliefs, and mental models which coherently interact in a system and, thus, are best described as theory like themselves [8,9]. Others advocate for describing individual conceptions as more loosely connected clusters of intuitive fragments which are supposed to be of smaller grain size compared to theories [10,11,12]. Besides the fact that proponents of both views agree that individual conceptions might consists of smaller elements, they are still in opposition as they apply contrary notions of what Brown calls ‘regular things’ [13]. He argues that people are used to identifying (regular) static structures in their environment (e.g., rock, baseball, or chair), while having problems identifying emergent dynamic and relational structures (cf. [14]). Theory proponents might implicitly regard the structure of elements in a certain set of data as the regular thing while fragments supporters see the regularity in the pieces these structures are made of. Brown in turn argues that “the pieces in fragmented or elemental views interact dynamically to form emergent structures, which in some cases might be robust enough to be considered as coherent ideas across a particular domain” [13] (p. 1473). Thus, the central question of conceptual change research might not be whether individual conceptions are most accurately described as fragmented or coherent [15], but to which degree they appear to be more or less fragmented or coherent, respectively.

According to diSessa, the coherence question is “about the relational structure of the totality of domain-relevant knowledge” [16] (p. 39). He describes two ideas as being coherent “if one vaguely seems to imply the other, or even if they merely seem related in some unspecified sense” [16] (p. 39). While it is difficult to grasp ‘emergent’ structures in students’ conceptions directly, as these structures are dynamic [13] as well as contextually mutable [14], the connections and associations students are making between specific knowledge elements [17,18] and how they transition between conceptual and contextual features of a problem [19] or across problem settings [20] are more readily accessible. However, the question of accessibility has important implications concerning the assessment of students’ conceptual understanding, as it weakens the validity of singular snapshot analysis of students’ conceptions. In contrast, analyses covering a wider range of different contexts are needed to assess coherence as a relational measure of elements constituting a particular concept. For example, Wagner [21] or Kapon and diSessa [22] showed how knowledge fragments are applied differently in different contexts, leading to a more or less coherent picture of conceptual understanding (cf. [23]). However, as these studies focus on (possibly subjectively tinged) qualitative analysis of a few selected cases, comparisons on a larger scale or between different studies remain difficult. In this vein, network analysis approaches have recently gained prominence in science education research [24,25], as they allow a different perspective to students’ declarative knowledge that takes the interconnectedness and structure of the knowledge elements into account [26] and can be applied to larger samples.

In this study, we used network analysis to investigate how students apply and expand their conceptual knowledge as they work on a series of contextualized experiments related to the energy concept. Students’ verbal statements were transcribed and transformed into concept networks and corresponding network parameters like network coherence. Here, striving for coherence is assumed to be the driving force underlying learning processes and, thus, concept development in science [25,27]. To investigate this assumption, we statistically relate a measure of coherence to students’ pre-post scores of a written test addressing their conceptual understanding of energy. Comparing these findings to results based on more basic network and text parameters and further restricting the range of terms to establish students’ concept networks aims to provide insights to the question to which extent network-like structures provide means to capture students’ conceptual knowledge.

2. Literature Review

2.1. Network Analysis

If a given system is dynamic and sufficiently complex, understanding the properties and behavior of its constituents does not suffice to understand the behavior of the system as a whole. Therefore, approaches characterizing the dynamic interactions of the constituents on a larger scale are needed. Network analysis constitutes such an approach, successfully applied, for example, in neurology [28], biology [29], or the social sciences [30]. Networks depict systems of elements (e.g., brain cells, germs, persons) as nodes in a graph. The relations between these elements are characterized by edges. Basically, edges depict if two given nodes are connected with each other or not. Moreover, they can contain information on the intensity and direction of a given connection. Repeated interactions then result in higher edge weights. Accordingly, dynamics in the development of a system as well as in its activation can be captured to a certain extent by monitoring changes in edge weights over time.

Modeling a system as a network facilitates its characterization based on numeric parameters, in turn enabling comparisons of the system’s constituents (based on local parameters) as well as between different systems (based on global parameters). The total number of nodes and edges is the most basic global parameter. Furthermore, measures characterizing a system’s density, coherence, or diversity can be applied. On the local scale, degree centrality (number of edges connected to a given node), closeness centrality (reciprocal of the sum of the distance of a given node to all other nodes in a network), or betweenness centrality (characterizes how often a given node serves as a bridge within the shortest path between two other nodes) enable comparisons between the network constituents [31].

Besides such measures of graph theory that account for structural properties of a network, also content specific, semantic features such as the words used by learners are of interest. Text or word networks are considered to indicate the complex relations between a variety of conceptual terms which in turn are considered suitable to reveal the learners’ knowledge and even their problems of understanding [18]. In this analytical context, concepts are considered as single ideas that are represented by one or more words in a network (i.e., nodes). Edges between words indicate the semantic relationship between these words, in the perspective of the learner, and can differ in strength, directionality, and type. The entirety of all relations build the semantic network of the learner’s conceptual knowledge [18].

While concept maps (which are conceptually and structurally similar to text-based semantic networks [32,33,34]) are also used to trace students’ knowledge development, Jacobsen and Kapur [35] have suggested to conceive students’ knowledge as scale-free networks. This type of network is produced by two underlying mechanisms, namely growth (i.e., the addition of new nodes) and preferential attachment (i.e., new nodes are most frequently linked to those concepts that are already connected more densely than others [17]). Consequently, some nodes are more central than others and function as ‘bridge concepts’ that might link different contexts to which a particular concept is applied to [18,36].

2.2. Network Analyses of Conceptual Knowledge

Using conceptual knowledge productively implies to recognize a new problem or phenomenon as an instantiation of a particular concept. “This recognition process mainly requires learners to identify relational similarities, [but] sometimes superficial similarity concurs with relational similarity” [6]. When superficial features are not diagnostic for selecting the appropriate concept, learners might be misled and thus struggle in selecting an adequate procedure to solve a problem (cf. [37]). In consequence, students’ concepts project differently in different context as the activation of a particular concept depends on which knowledge elements are activated by the problem context. In turn, new knowledge elements must be integrated (or connected) with prior knowledge elements to be available for future problem solving [38]. Theoretically speaking, relating elements and variables to each other is foundational for scientific concepts and acquiring a highly interrelated set of concepts and principles is central in developing expertise [6].

In this context, Gupta, Hammer, and Reddish argue that “conceptual knowledge organization is likely to be network-like” [39] (p. 317). Accordingly, network-related approaches currently gain prominence in science education (research), as students’ written or spoken contributions concerning concept related tasks can be translated into networks, which in turn reflect their individual conceptions to a certain degree. For instance, Sherin [40] used spoken word transcripts to identify students’ concepts and the dynamics of their mental constructs (by means of automated analyses using vector space models and simple clustering methods). Koponen and Huttunen [25] or Koponen and Nousiainen [41] proposed possibilities to shed light on conceptual dynamics with the help of network- and graph-related analyses. Bodin [24] used network analyses to map students’ epistemic framing of computational physics or to characterize teachers’ and students’ simulation competence in physics. Koponen and Huttunen [25] explicitly address the coherence vs. fragmentation issue based on network parameters by modeling a concept’s coherence and utility in a given situation. Koponen and Nousiainen [41] furthermore suggest parameters to estimate the importance of single conceptual elements within a given network.

Koponen and Huttunen [25] give a definition to identify the coherence of a single node (as a local property, but taking the assembly of nodes into account) within a whole network, based on the weighted edges of other nodes connected to the node under investigation. Thereby, they regard some nodes as concepts on their own and other nodes as evidence explained by these concepts.

Rafols and Meyer [42] give a measure of coherence stemming from research on scientific knowledge integration. They use co-citations of authors “to measure the intensity of similarity relations within a bibliometric set […] which reveals the structural consistency (i.e., coherence) of the publications network” (p. 263). Among other things, they suggest indicating coherence as a function of the networks’ mean path length. Technically, network coherence (C_net) is equal to the reciprocal mean closeness centrality of all nodes in a network. Applied to the current aim of characterizing the coherence of a single concept, all nodes’ relative mean path lengths in a network consisting of conceptually relevant nodes describe its coherence. C_net applies for weighted networks; repeated connections of two given nodes increase the corresponding edge-weight and proportionally shorten the path length. While condensing the coherence of a learner’s conceptual knowledge to a single measure certainly leaves out potentially relevant aspects of coherence [26] or conceptual knowledge development [12], C_net captures the relational structure of elements constituting a concept and provides the possibility of gradual, intra-individual comparisons, also at a larger scale [42].

Generally, tools to analyze students’ individual conceptions as well as to compare them inter-individually by the means of network analysis are available. However, as network analysis remains a quite abstract and technical way to assess conceptual understanding, evidence for its meaning to actual students’ performance is needed [34]. Koponen and Huttunen [25] argue that striving for coherence can be considered as the driving force or mechanism underlying learning processes and, thus, concept development in science (cf. [27]). If this assumption holds, higher coherence of conceptual knowledge should also be reflected in higher performance in other measures of students’ conceptual understanding, e.g., success in problem-solving or written tests. Also, when growing expertise is indicated by acquiring an increasingly interrelated set of concepts and principles that is able to classify phenomena and problems “by their deep (common) relational structure and not (only) by superficial features” [6], then changes in coherence of the applied knowledge elements might reflect the dynamical process of knowledge integration [42]. This way, dynamics in concept application over the course of time could be analyzed to a certain extent.

Building upon this background, the current study attempts to statistically relate students’ test performance to their conceptual understanding captured during the learning process by means of network analysis. In particular, we relate a measure of coherence to students’ test scores and compare the results to more basic network and text-parameters.

2.3. Energy as a Concept

The scientific concept under investigation within this analysis is energy. It can be described as a law or fact relevant for all natural phenomena (cf. [43]). However, energy is not only a fundamental scientific concept; moreover, it constitutes a highly relevant issue in economy, politics, and philosophy. Accordingly, energy is awarded prominence in many science curricula worldwide [2,3,4]. Due to its multifaceted relevance and also its ambiguous scientific definition (cf. [44]), it is hard to sharply define what students should actually know about energy. For the sake of simplicity, we bypass the intense scientific and educational discourse on this issue (see [44,45] for an overview) and refer to some aspects of the energy concept persistently found in the science education discourse which is simultaneously relevant for this investigation.

Duit [46] distinguishes different key aspects of the energy concept: Forms, transport/transformation, degradation, and conservation. These key aspects are, albeit slightly different, constantly displayed in curricula and educational standards [3] as well as studies investigating students’ understanding of energy (e.g., [47,48,49,50]). The latter investigations indicate that some of the above aspects are easier to learn than others. For instance, Liu and McKeough [48] show that tasks on forms of energy are more likely to be solved by students than tasks on energy conservation (cf. [49,51]). In addition, there is evidence that students’ application of the energy concept depends on context [49]. The context dependent application of concepts in turn is a matter of conceptual coherence [16]. Thus, it might be insightful to apply a measure of coherence to characterize learning processes of students dealing with energy-related topics.

3. Research Objectives and Hypotheses

We aim to characterize verbal contributions students make while working on a series of experiments related to the energy concept by different network parameters. Based on students’ verbal contributions, we therefore analyzed which concept- and context-related terms students use and how they connect these terms to explain the phenomena addressed in the different experiments. These terms and their connections were then used to create word networks with different numbers of vertices and edges having different weights for each participant. With regard to the present study, a concept is represented by the whole network or at least by an assembly of nodes. Consequently, analytical approaches to capture coherence of whole networks or node clusters (as a more global property) are applied [42] to students’ word networks. These parameters are correlated with the students’ pre-post scores of a written test aiming at assessing students’ understanding of the energy concept. Besides coherence as elaborated above, more basic measures like the network size (number of nodes), or number of words stated by the participants are included in this analysis to check for the coherence measure’s added value. The explicit research questions are as follows:

• To what extent can network parameters deduced from spoken word transcripts explain students’ test scores after working on a series of energy-related experiments (taking into account students’ prior knowledge)?
• Do network parameters (i.e., coherence) and static parameters (i.e., number of nodes) differ in their predictive power regarding students’ test score?

4. Materials and Methods

4.1. Setting and Sample

The database of this investigation is a series of videotaped pairs of students working on four consecutive experiments related to the energy concept (for about two hours in total). The experiments were embedded in different contexts, all related to the common frame topic of sustainable use of energy. Within the contexts of wind turbines, photosynthesis, eco fuel, and power-to-gas technology, students conducted different experiments (one per context) that addressed different basic elements of the energy concept, e.g., energy forms, transformations, degradation, and conservation [52]. Thus, all contexts focused on the same core aspects of energy (cf. [52]), but differed with regard to situational (i.e., superficial [6]) features. To ensure comparability, scripts guiding students through the process of experimenting were provided. Within each context, the scripts included an introductory text (of equal length and complexity), a picture of the experimental set-up, a description of the experimental conduction, and five questions to guide the analysis [53]. Questions were structured in increasing order of complexity [54,55], ranging from naming relevant energy forms and describing energy transformations to calculating the experiments’ energy conversion efficiency and identifying possible spots of energy degradation. Participants’ verbal statements during working on the experiments and the corresponding questions were transcribed afterwards. All of the following steps were based on the students’ transcripts in German language. For the purpose of the present article, all relevant materials were translated to English.

Before and after the experiments, students’ knowledge was assessed with a test on the energy concept (N_items = 25; multiple choice and constructed response format; pre-test: Mean score 12.03 / 25 points (SD = 5.02), Cronbach’s α = 0.80, McDonald’s ω = 0.76; post-test: Mean score 15.84 / 25 points (SD = 4.27); Cronbach’s α = 0.77, McDonald’s ω = 0.78; identical tests were used pre and post; for details see [53]). Additional tests were issued to control for general intelligence [56], scientific self-concept, and interest [57].

Teachers in ten schools in the larger rural area of Kiel (Germany) were addressed to participate in this study. Four out of these ten schools officially replied, and students of these schools were invited to the laboratory (after providing parental consent). In total, 16 pairs of students (grades 9–11, aged 15–17 years) took part in this study (N_total = 32). The students represent a convenience sample of students that were willing to participate in this study. The intervention took place in a research laboratory at the university and was organized by the authors of this study. While the study took place in an out-of-school context, the content of the experiments was aligned to the schools’ curriculum [4].

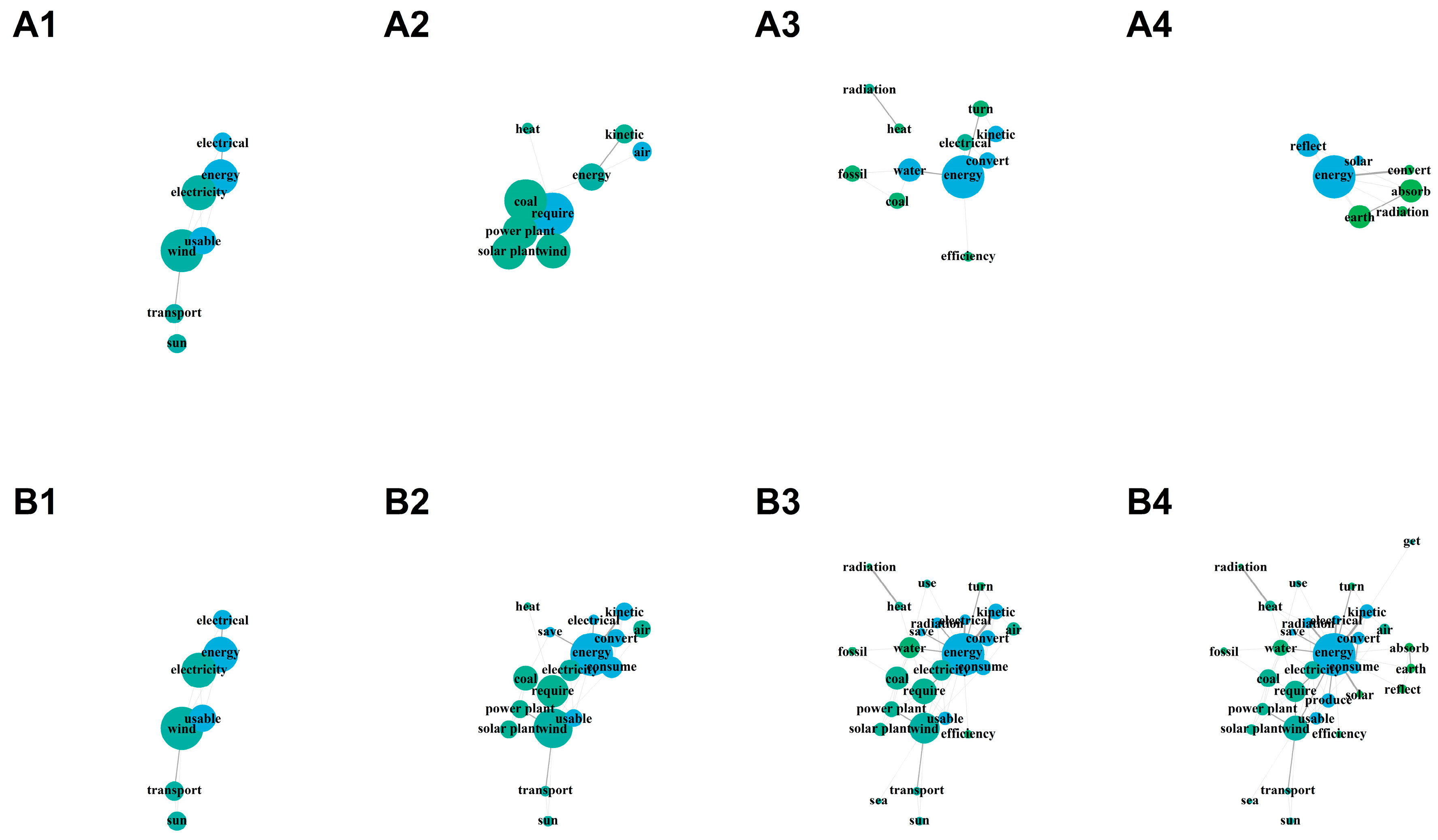
4.2. Methodology

To characterize the transcribed verbal contributions of the students while working on and talking about the experiments in terms of network parameters, the raw transcripts had to be cleaned in advance. We decided not to assign specific conceptual ideas to students’ statements and build the conceptual network based on such an assignment, but we chose single words as units of analysis. Simply stating a concept-related term of course does not necessarily reflect any understanding of this term. However, a recent study by Haug and Ødegaard [58], focusing on elementary students, suggests that the ability to apply and moreover combine concept-related terms in larger word networks indicates increased conceptual understanding. Thus, using concept-related terms for our analysis provides an efficient way to get access to students’ conceptual understanding.

In the first place, a list of all words used by the students was crafted. Afterwards, the authors went through this list focusing on words either relevant for the energy concept (e.g., kinetic energy, to transform) or for the contexts the experiments were embedded in (e.g., flashlight, fire, atom) to create positive-lists of words to be generally included in the network analysis (cf. Appendix A). The selected terms were generated individually by the authors, shared, and collaboratively revised until agreement was reached. While context terms are considered to reflect features of the different experimental settings, as they are partly provided in the text and scripts or can be derived from the experimental set-up, concept terms are considered to indicate the students’ recognition of the underlying conceptual structure in the different settings and, thus, their ability to see the deep structure below the superficial features of the contexts [6,23,37].

Additionally, a thesaurus script to standardize variations of the words included in the positive list was created (e.g., transforms, transforming, and transformed become ‘transform’). The following example is intended to clarify the process of transcript cleaning (all examples provided in this paper are translated from German to English by the authors).

Initial statement:

Yes, wait, well in the flashlight it is transformed from the chemical energy to electric energy.

Cleaned statement:

flashlight transform chemical energy electric energy

The cleaned transcripts then were split into segments, whereby every change in speaker indicates a new segment. Within these segments, every word constitutes a node and all nodes are connected with each other by edges of the weight 1, regardless of the total number of occurrences of a node in this segment. Self-connections of nodes (loops), like for the energy node in this example, are removed later. Afterwards, a word-word matrix for each segment can be created.

Table 1. Exemplary word-word matrix.

	Chemical	Electric	Energy	Flashlight	Transform
Chemical	0	1	1	1	1
Electric	-	0	1	1	1
Energy	-	-	0	1	1
Flashlight	-	-	-	0	1
Transform	-	-	-	-	0

illustrates the matrix for the example above.

A second segment of the transcript, stated later by the same student, is exemplified to show how matrixes add up over the course of the experiments (

Table 2. Exemplary word-word matrix after a segment is added.

	Chemical	Electric	Energy	Flashlight	Plug	Transform
Chemical	0	1	1	1	0	1
Electric	-	0	2	1	1	1
Energy	-	-	0	1	1	1
Flashlight	-	-	-	0	0	1
Plug	-	-	-	-	0	0
Transform	-	-	-	-	-	0

):

Initial statement:

Well it comes out of the plug as electric energy.

Cleaned statement:

plug electric energy

Notice that the verb ‘come’ for example is not included in the positive list, because we regarded this as being applied too generally, thus causing bias in the network. However, important conceptual connections might be missing due to such a decision.

The second matrix illustrates that repeated interactions of two nodes give higher weight to the edge connecting them (see electric and energy). Figure 1 depicts the transformation of this example network graphically.

Over time, increasingly complex networks with different numbers of vertices and edges having different weights are created for each participant. Technically, it is important to note that we treat the networks as undirected (every edge of node A to node B simultaneously constitutes an edge from node B to node A, whereby for later calculations, the corresponding edge weight is only incorporated once). Moreover, every connection is given a positive weight, regardless of the normative correctness of a certain statement. We decided for this approach of weighting the statements, as arguments on energy are generally hard to categorize as either clearly right or wrong as it heavily depends on context, the system under investigation, or agreed forms of language concerning the concept.

Networks can be described with a set of parameters. With reference to the conceptual change controversy between coherence and fragmentation views mentioned above, we apply a measurement of the total network coherence and compare its explanatory value concerning participants’ test performance to more basic parameters like network size (total number of nodes included in the positive list) and total number of all words mentioned by a student working on the experiments (which actually is no network parameter, but indicates the ‘volume’ of a students’ contribution).

As described above, the coherence indicator C_net is structurally suited to our data, as it applies for undirected, weighted, scale-free networks with only positively weighted edges. It is defined by Rafols and Meyer [42] as the reciprocal mean closeness centrality (cc) of a network of N nodes:

$${\mathrm{C}}_{net}=\frac{1}{\frac{{\displaystyle \sum }cc}{N}}$$

(1)

Closeness centrality, which is intended to characterize how closely the nodes in the network are generally connected, is in turn calculated based on the shortest paths by which all nodes in a network are connected. In this context, Opsahl, Agneessens, and Skvoretz [59] suggest a formula taking into consideration the sum of weights in a network that also emphasizes the number of nodes a shortest path is composed of. Calculations of closeness centrality based on [59] were performed on the basis of the closeness_w function from the tnet-package in R. We used closeness measures that are normalized by network size for further calculations. Brandes and Erlebach [31] found the C_net measure to be independent of network size on large scale, which is important to check for, since network parameters often increase proportional to a networks’ size. However, as the current sample is rather small scale, C_net will be checked for scale dependency again.

Statistics were done using R 3.6.2 (R Core Team, 2019) and several packages, notably tnet_3.0.14 [60], igraph_1.2.4.2 [61], matrixStats_0.55.0 [62], tm_0.7–7 [63], and tidyverse_1.3.0 [64].

5. Results

Before showing relations between the network parameters and students’ test data, some descriptive results are presented (cf.

Table 3. Sample statistics for test scores, number of words contributed as well as number of nodes and coherence of networks on the level of single transcripts (i.e., four per student, N = 28).

	mean	sd	median	min	max	Skew	kurtosis
Pre-test	0.45	0.17	0.42	0.20	0.92	0.52	−0.13
Post-test	0.61	0.16	0.64	0.28	0.92	−0.30	−0.53
N words	682.76	284.96	604.00	197	1456	0.66	−0.25
Vertices	12.31	5.70	10.50	5	29	0.90	−0.03
Cnet	316.66	355.84	159.43	7.32	1900.23	1.82	3.86

). Out of 32 participants, 28 networks were calculated (four participants did not contribute enough verbal statements on the topic to perform calculations). Therefore, the following analyses are limited to this sample of 28 students. The test scores follow a normal distribution, although the distribution of the pre-test scores is moderately skewed right. The number of words and vertices as well as the coherence measure C_net rather follow a Weibull distribution.

Students’ performance increased significantly from pre-test (M = 0.45) to post-test (M = 0.61; t = 6.21, df = 27, p < 0.001, d = 1.17; cf. Table 3). Based on a linear regression, there is a significant effect of students’ pre-test score on their post-test score (R² = 0.45, F(1, 26) = 21.47, p < 0.001, β = 0.62, 95% CI [0.38, 0.86], β = 0.67, p < 0.001).

To visualize its dimensions, a typical network (of a medium achieving student according to the pre-test score) is presented in Figure 2. Apparently, only a few terms from the positive list were used to establish the networks (on average of five to 29 terms per network; cf. Table 3 and Appendix B).

Although students worked in pairs during this study, small Pearson correlation coefficients for network coherence (r = −0.15, p = 0.45) and post-test scores (r = 0.17, p = 0.22) within dyads indicate very low level of interdependence between students [65]. Consequently, the nested data structure is not taken into account in the analysis, but results from students within dyads are treated as independent.

With regard to changes across the four contexts, no main effect of the order of the context was found (F(3, 81) = 0.59, p = 0.62). Consequently, the coherence of the single networks does not seem to change systematically across students over time, i.e., from working on the first to the fourth context. When considering the four consecutive contexts as separate instantiations of distinct problems (like items in a test), the internal consistency of the four networks (in terms of the average covariance between pairs of networks) across the four contexts is quite high (Cronbach’s α = 0.74; McDonald’s ω = 0.82). However, the effect of the mean coherence of the four context networks on students’ post-test score is not significant (F(2, 25) = 3.12, p = 0.10, R² = 0.12).

When taking in turn a more holistic perspective on students’ performance across the four contexts by considering students’ verbal contributions cumulatively across contexts, the coherence of the cumulative networks (cf. Figure 2, lower row, B1 to B4) increases significantly in the sequence of contexts with a large effect (F(3, 81) = 35.58, p < 0.001, η²_G = 0.31).

The following analyses will focus on the students’ final, cumulative network, i.e., covering their verbal contributions across the four contexts they worked on (cf.

Table 4. Sample statistics for the number of words contributed as well as number of nodes and coherence of networks on the level of students (i.e., cumulated across contexts).

	mean	sd	median	min	max	skew	kurtosis
N words	2468.37	958.72	2425.00	969.00	4518.00	0.44	−0.67
Vertices	35.33	16.48	35.00	6.00	65.00	0.01	−1.19
Cnet	3297.32	2671.19	2664.93	1.00	9114.42	0.61	−0.76

). Here, the mean number of total words per participant is 2468.37 (SD = 958.72). On average 35.33 (SD = 16.48) of the words included in the positive list were applied. However, only 10.60 words (SD = 2.02) were directly related to the concept and 35.73 words (SD = 15.34) to the contexts of the experiments. The mean network coherence is 3297.32 (SD = 2671.19). For the purpose of the following analyses, predictors in regression models are z-scaled.

The first research question addressed the explanatory value of the network parameters for students’ post-test score, taking pre-test scores into account. We calculated multiple regression analyses, successively incorporating network coherence, the number of network nodes, and the total number of words stated as independent variables to predict, under control of pre-test scores, students’ scores on the post-test. Independence of the parameters under investigation was checked. It turned out that all of the parameters under investigation are intensely correlated (cf.

Table 5. Correlation matrix.

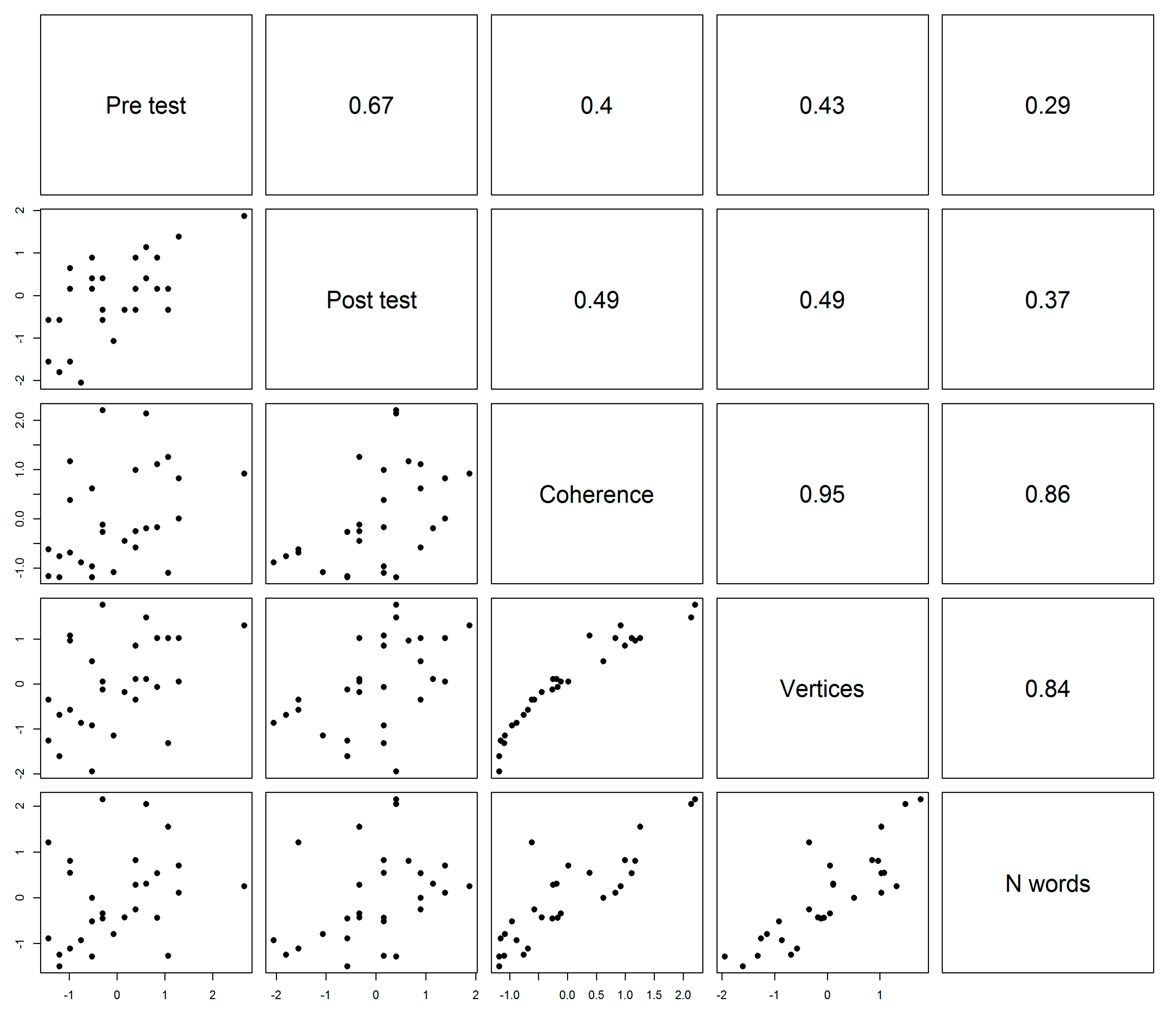
		Test Scores		Concept + Context terms			Concept Terms Only
		Pre-test	Post-test	Coherence	Vertices	Nwords	Coherence
	Post test	0.67 ***	-	-	-	-	-
Concept + context terms	Coherence	0.40 *	0.49 **	-	-	-	-
	Vertices	0.43 *	0.49 **	0.95 ***	-	-	-
	N words	0.29	0.37	0.86 ***	0.84 ***	-	-
Concept terms only	Coherence	0.34	0.49 **	0.99 ***	0.96 ***	0.84 ***	-
	Vertices	0.40 *	0.34	0.71 ***	0.85 ***	0.65 ***	0.73 ***

Note: * = p < 0.05; ** = p < 0.01; *** = p < 0.001.

and Appendix C).

The strong correlation between network coherence and number of vertices shows that, opposed to the results of Rafols and Park [42], the implemented measure of coherence is highly scale dependent at our scale of investigation. Therefore, we normalized the measure by the total number of nodes in a network for the following calculations. Nevertheless, the correlation between coherence and the number of nodes remains stable (r = 0.97, p < 0.001), raising issues of multicollinearity (cf. discussion).

In a multiple regression analysis, network coherence significantly predicts students’ post-test scores when taking pre-test scores into account (cf.

Table 6. Multiple regression of network coherence and pre-test score on post-test score (F(2, 25) = 14.79, p < 0.001, R² = 0.55).

	Estimate	Std. Error	β [95% CI]	p
(Intercept)	0.61	0.02		<0.001	***
Pre-Test Score	0.09	0.02	0.57 [0.28, 0.86]	<0.001	***
Network Coherence	0.05	0.02	0.31 [0.02, 0.60]	0.048	*

Note: * = p < 0.05; ** = p < 0.01; *** = p < 0.001.

). The effect size of network coherence is about half the size of the effect of the pre-test scores.

When changing the predictor to a more general parameter of students’ networks, the number of nodes also turns out to be a significant predictor of students’ post-test scores. The effect sizes and significance levels are nearly equivalent to the former calculation (cf.

Table 7. Multiple regression of the number of network nodes and pre-test score on post-test score (F(2, 25) = 15.47, p < 0.001, R² = 0.56).

	Estimate	Std. Error	β [95% CI]	p
(Intercept)	0.61	0.02		<0.001	***
Pre-Test Score	0.09	0.02	0.54 [0.25, 0.84]	0.001	**
Number of nodes	0.06	0.03	0.34 [0.04, 0.63]	0.034	*

Note: * = p < 0.05; ** = p < 0.01; *** = p < 0.001.

).

In contrast to network coherence and the total number of nodes in the network, the total number of words stated by a student does not predict their post-test score (cf.

Table 8. Multiple regression of total number of words and pre-test score on post-test score (F(2, 25) = 13.06, p < 0.001, R² = 0.52).

	Estimate	Std. Error	β [95% CI]	p
(Intercept)	0.61	0.02		<0.001	***
Pre-Test Score	0.10	0.02	0.62 [0.34, 0.91]	<0.001	***
Number of words	0.04	0.02	0.23 [−0.06, 0.52]	0.127

Note: * = p < 0.05; ** = p < 0.01; *** = p < 0.001.

).

Conceptual coherence relates to the stability of students’ conceptions from the perspective of a normative scientific concept. This means, how reliably students apply conceptually relevant terms and ideas. Thus, we additionally performed comparable calculations only incorporating the positive-list of concept related words into the network (e.g., kinetic energy, transform, etc., see Appendix A), i.e., excluding the context-related terms.

Using conceptual core terms for the network calculations produces results more clear-cut, associated with higher effect size (β_std. = 0.40) and a larger portion of total explained variance (R² = 0.61) compared to the former calculations incorporating the complete set of terms (cf.

Table 9. Multiple regression of network coherence and pre-test score on post-test score taking into consideration only directly concept related words (F(2, 22) = 19.05, p < 0.001, R² = 0.61).

	Estimate	Std. Error	β [95% CI]	p
(Intercept)	0.59	0.02		<0.001	***
Pre-Test Score	0.10	0.02	0.60 [0.33, 0.87]	<0.001	***
Network Coherence	0.08	0.03	0.40 [0.13, 0.67]	0.005	**

Note: * = p < 0.05; ** = p < 0.01; *** = p < 0.001.

). The number of nodes in turn is not significantly predictive and less explanatory compared to the coherence measure (β_std. = 0.20, R² = 0.50; cf.

Table 10. Multiple regression of the number of network nodes and pre-test score on post-test score taking into consideration only directly concept related words (F(2, 25) = 12.16, p < 0.001, R² = 0.50).

	Estimate	Std. Error	β [95% CI]	p
(Intercept)	0.61	0.02		<0.001	***
Pre-Test Score	0.10	0.03	0.61 [0.30, 0.92]	<0.001	***
Number of nodes	0.04	0.03	0.20 [−0.11, 0.50]	0.226

Note: * = p < 0.05; ** = p < 0.01; *** = p < 0.001.

).

Including both parameters in a combined regression model, which would be a better approach for direct comparison, results in insignificance of both predictors. This might be due to the small sample size in combination with the parameters’ high intercorrelation that make it hard to measure the marginal effects of these variables.

6. Discussion

The aim of the present study was to characterize the verbal contributions students make while working on a series of experiments related to the energy concept by means of different network parameters. These parameters were correlated with the students’ pre-post test results from a written test aiming at assessing students’ understanding of the energy concept. Results indicate that the calculated network parameters significantly relate to students’ performance in a quantitative test.

With regard to students’ test performance, the tight relation between students’ pre-test and their post-test scores seems plausible, especially since the intervention was quite short (about two hours). As students did not receive feedback on their pre-test answers and the tests were administered immediately before and after working on the four experiments, the large effect regarding the increase from pre- to post-test might be attributed to substantial learning gains, while re-test effects might play only a minor role. Consequently, we would argue that the participating students actually learned by working on the differently contextualized experiments and that the students’ final performance is a function of their prior knowledge and their learning in the course of participating in our study.

With regard to the coherence of students’ networks, which were based on students’ verbal contributions while working in the four contextualized experiments, network coherence turned out to be of predictive value for students’ post-test scores, beyond their pre-test scores. Taking into account that pre- and post-tests were identical, it may not be surprising that the predictive power of students’ pre-test scores is highest across all analyses. However, incorporating network coherence in the regression model proved to increase the amount of explained variance substantially. Simpler measures like the number of words a student contributes do not seem to fulfill this purpose, at least for the current set of data.

Restricting the creation of networks to a set of words that are conceptually or contextually relevant does seem to describe the learning process to a certain degree, as significant correlations of network coherence or the number of nodes to students’ post-test scores indicate. When analyzing students’ verbal contributions cumulatively, i.e., across the four experimental contexts, the development of students’ networks seems also to reflect the underlying mechanisms relevant for producing scale-free networks, i.e., growth and preferential attachment [17], resulting in increasingly coherent networks. However, when analyzing the four contexts separately, the derived network parameters (coherence, number of vertices) were rather constant. The structural similarity in the networks stemming from single contexts might reflect the circumstances that students were not prompted explicitly to make comparisons and connections across contexts and that students’ work on all four contexts was highly scripted.

With regard to the positive list of words deductively derived from students’ verbal contributions, there were a lot more context words than concept words included to establish the networks (cf. Appendix A). To our perception, the positive list reflects the features students are extracting from the problem situation or from their prior knowledge when working on the different experimental contexts and, thus, represents the knowledge elements activated by students during their problem solving [17,18]. When further restricting the analysis to only incorporate concept-related terms, the predictive power of the network coherence on students’ post-test scores increased. In addition, results suggest that network coherence is superior to more static parameters like the number of vertices, i.e., a measure that does not take the interconnectedness between terms into account.

Under this perspective, students’ individual networks within each of the four contexts do not seem to just ‘add up’ from context to context, but the cumulative analysis across contexts also takes into account changes in the interconnectedness of knowledge elements that are present across contexts, i.e., the deep structure of the concept. These conceptual knowledge elements on the one hand are connected to the respective context terms within each of the four contexts, but on the other hand, the repeated activation of these knowledge elements across contexts might additionally increase their interconnectedness. Working on a series of conceptually related problems might support students’ recognition of the underlying conceptual structure in the different settings [6,23,37], even when not explicitly prompted. This in turn might explain the high(er) predictive value of the network coherence when only taking the focused set of conceptually relevant terms into account for calculating the networks.

A major limitation of the present study is the small sample size. Despite significance of some relations, the obtained results have to be replicated in further studies on a larger scale. A larger sample would allow for testing differences in the predictive power of the distinct predictors that had to be incorporated in different analytical steps in the present study. Consequently, the present study rather represents an explorative account to illustrate how network analysis and network coherence might be used to analyze data from student interactions with learning materials as well as the relation of this measure with other variables. The following subsections seek to clarify implications of the presented findings.

6.1. Methodological Discussion

Although this study indicates a relation between network parameters and learning outcome (as measured by test scores), stability of such a result will have to be demonstrated in the future. Many choices had to be made in advance to the network calculations. For example, we pre-selected a fixed set of terms (based on all terms said by the participants) to include in the analysis, implying the dismissal of terms potentially relevant to the students’ conceptual understanding. Especially for the energy concept, which is characteristically influenced by everyday speech and vague expressions, students’ valuable intuitive ideas might be underrepresented by this approach due to a lack of ‘normative energy language.’ On the other hand, it can also be argued that confident use of scientific language can be regarded as a sign of expertise [66,67].

Unlike, for example, Koponen and Huttunen [25], we did not categorize relations between nodes as positively or negatively weighted, as students’ misinterpretations of the phenomena have not always been corrected. Even if a student is hinted to be in error, this does not necessarily result in a weakened conceptual connection on a cognitive level. Assigning always positive links can also differentiate between more or less appropriate relations, as the former are supposed to be used repeatedly and therefore have higher weights in the conceptual network relative to the latter.

Furthermore, relations between nodes are undirected in the networks here. This is due to the fact that the energy concept here is used as a tool to make sense of real-world processes [50], rather than a tool for causal explanations. Students mostly described the transformation processes occurring in the experiments using energy language [68] and did not give more detailed mechanistic explanations for these transformations. Thus, using network analysis to describe students’ conceptual application and refinement in the manner we did might be appropriate for the energy concept but not necessarily for other concepts that are more causally coined.

Additionally, it turned out that coherence as operationalized here remains dependent on the network size even after normalization. This undermines the measure’s validity as an indicator of mere strength of relations between elements, but the size dependency could alternatively also be regarded as an advantage when used as a measure of conceptual sophistication. Understanding a concept on the one hand means to deduce information reliably (coherence) out of a situation based on a set of rules, but on the other hand understanding means also to do so across a wide range of situations (or contexts; cf. [12]). Thus, the measure used here might capture the criterion of coherence simultaneously to the criterion of width of situations.

A specific limitation with regard to the network approach taken in this study is the high intercorrelations between the derived network parameters (cf. Table 5). This issue of multicollinearity creates difficulties when building regression models based on multiple network parameters to compare their marginal effects on the outcome variable, in this case students’ test scores [69]. Hence, comparisons among regression coefficients reported for different network parameters in this study need to be treated with caution. Further investigations are necessary to explore the individual contribution of these network parameters in explaining students’ test performance.

6.2. Theoretical Discussion

In theoretical regard, network analysis within the current study has been related to conceptual change research. In our view, it bears the potential to capture the very nature of concepts as dynamic emergent structures, selectively compiled on the spot as a function of individually available conceptual elements and contextual stimuli [12,13]. A fixed set of conceptually or contextually related words has been used as the set of elements to compile in a given situation. More detailed insights into the level of sophistication of an individual’s conception is then given over the course of several, authentic learning situations. However, the present study did not investigate conceptual change as a dynamic and temporal process. With regard to the analysis presented here, further studies might replicate the approach to investigate difference in network structures between students having particular (alternative or normatively accepted) conceptions [40]. In addition, longitudinal analyses of students’ verbal explanations might provide insights into structural changes in derived networks (or network parameters) that are indicative for conceptual change. This relates to diSessa’s claim of describing processes of conceptual change and conceptual application in process rather than as single snapshots of performance [11]. This study suggests that network analysis might be a means to do so.

If further investigations can confirm the relation of network parameters to students’ performance, network analysis of digitally written texts might help teachers to get a standardized way of comparing between students, but also an indicator of students’ longitudinal development [18]. Chiu and Linn [70] also characterize learning success based on students’ written responses in an online environment. Thereby, they assign students to a fixed level of knowledge integration [71] based on a standardized algorithm considering prior manually coded answers. The coherence measure proposed here in turn enables to capture a more gradual development, as it is not restricted by fixed levels. Moreover, the development of single connections of knowledge elements can be tracked. Teachers might get a quick glance of this development by comparing graphical networks of different stages in the learning process. However, further studies need to provide evidence for the validity of inference based on such network parameters.

Finally, this approach offers a possibility to take another perspective to the discussion of coherence as a crucial issue within the conceptual change debate. Sikorski and Hammer argue that “students’ ideas are not accurately described by coherent, qualitatively different levels” [72] (p. 1037), but also it is unlikely that they are completely loose without any regularity and coherence, as evidence for the stability of students’ alternative conceptions suggests [73]. Thus, coherence (or non-coherence) might be treated as a gradual indicator of conceptual sophistication rather than a binary term used to describe a concept’s very nature [13]. Network parameters could help to fill the scale between the binary poles. As they offer less space for interpretation after a certain set of network terms is agreed on, they are admittedly not objective, but at least standardized.